A full geometric and photometric calibration method for oblique-viewing endoscopes

Figures & data

Figure 1. Stryker 344-71 arthroscope Vista (70 degree, 4 mm). An oblique endoscope consists of a scope cylinder with a lens and point light sources at the tip (which is tilted at an angle from the scope cylinder axis), a camera head that captures video images, and a light source device that supports the illumination. The scope cylinder is connected to the camera head via a coupler. This connection is flexible to enable rotation of the scope cylinder and camera head separately or together.

Figure 2. The geometric model of an endoscope based on a tracking system. A new coupler (see Figure 1b) has been designed to enable mounting of an optical marker on the scope cylinder, ensuring that the transformation from the scope (marker) coordinates O₂ to the lens system (camera) coordinates O₃ is fixed. The optical tracker defines the world coordinates O₁. Two optical markers are attached to the coupler and camera head separately to compute the rotation θ between them.

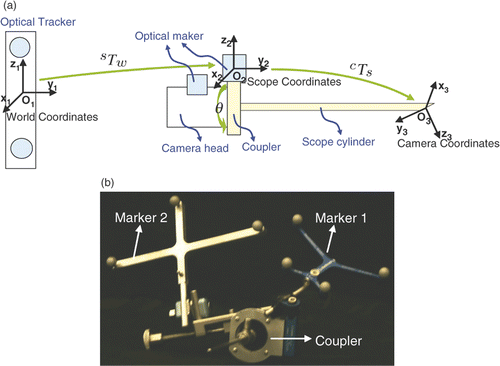
Figure 3. A comparison between the system of Yamaguchi et al. and our own system. In the former, the camera head is tracked such that the transformation from the marker to the lens system is not fixed but depends on the rotation angle θ. Using the marker coordinates as a reference, the lens system is rotated around the scope cylinder through θ, but the image plane (that is in the camera head) remains the same. Yamaguchi et al. use two additional transformations to describe the effect of rotation, so their model becomes complicated. Moreover, they must calibrate the axis of both the scope cylinder and the lens system by using another optical marker attached to the scope cylinder. Based on our observation, it is possible to simplify the model if we fix the transformation between the marker and the lens system. We designed a coupler that enables the optical marker to be mounted on the scope cylinder. We then set the marker coordinates as a reference; the lens system remains fixed. The rotation only affects the image plane since the camera head is rotated around the cylinder (reference), and the image plane only rotates around the principal point. Since the principal point is an intrinsic parameter, we need only estimate the rotation angle. As a result, we have a very simple model (see details in the text).

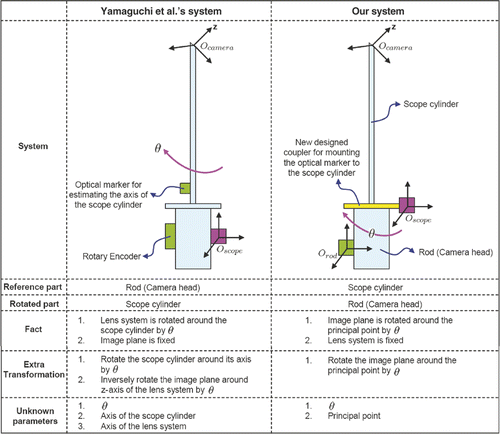
Figure 4. Relationship between the rotation angle θ and two marker coordinates. O₁ is attached to the scope cylinder and O₂ is attached to the camera head. A indicates the position of O₂ when θ = 0 and B indicates the position of O₂ given a rotation θ. Given any point P_r in O₂, its trace following the rotation of the camera head is a circle in Marker 1's coordinates O₁. It moves from position to in Marker 1's coordinates O₁. This circle is also on the plane perpendicular to the axis of the scope cylinder. O is the center of the circle.

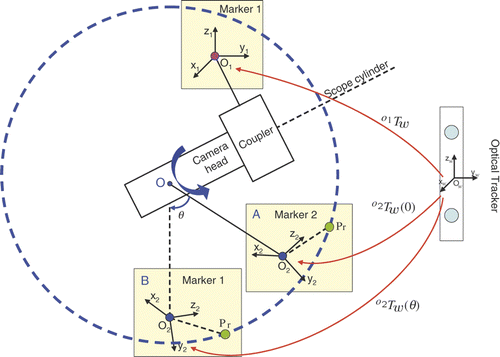
Figure 5. Estimated rotation angles for the two endoscopes. In each trial we rotated the camera head with respect to the scope cylinder and captured an image. We captured a few images for the initial position, then acquired two images for each rotation angle. The red curves are the estimated rotation angles from different RANSAC iterations; the black curve is the average rotation angle.

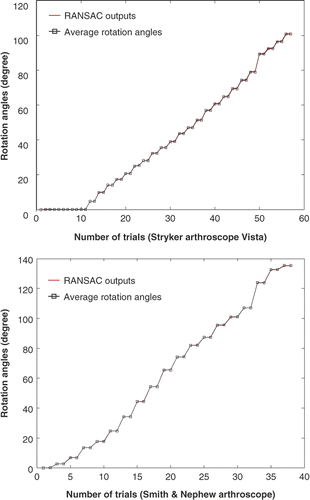
Table I.  Pseudo code of RANSAC for estimating the center of the circle

Loop k=1:K (K=2000)

Generate a random point Pr from 3D space

Generate random number x, y, z between [1, N]

Compute Px, Py, Pz using Eq. 4

Compute Ok using Eq. 6

Compute

Compute vk

Save Ok, vk

End loop

Return Oq, q = argkmin(vk)

Table II.  Pseudo code of RANSAC for estimating the rotation angle

Loop k=1:K (K=1000)

Generate a random point Pr from 3D space

Compute PA and PB using Eq. 4

Compute θk using Eq. 3

End loop

Return

Figure 6. The endoscopes used in the experiments. (a) Smith & Nephew video arthroscope–autoclavable SN-OH 272589 (30 degree, 4 mm). (b) Stryker 344-71 arthroscope Vista (70 degree, 4 mm).

Figure 7. (a) The back projection with and without rotation compensation. The green points are the ground truth–2D corner pixels on the image of the calibration pattern. The red points are the back projection of the 3D world positions of the corners using the first equation of Equation 2, which has no rotation compensation. The blue points are the back projection using both equations of Equation 2. Since the rotation is included in the camera model, the back-projected pixels are much closer to the ground truth than the red points. (b) An image used in the paper by Yamaguchi et al. [11], [12]. This image has higher resolution, better lighting and less distortion than our own.

Figure 8. Back-projection errors with respect to the rotation angles for the two systems. (a) Stryker 344-71 arthroscope Vista and Polaris optical tracker in our laboratory. (b) Smith & Nephew video arthroscope and OPTOTRAK optical tracker in the operating room. The three images above the graphs correspond to different rotation angles (specified above each image). The red curves represent the errors without rotation compensation; the blue curves are errors with rotation compensation.

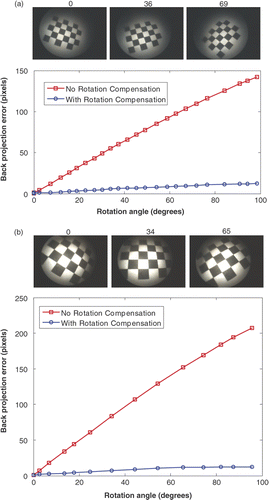
Figure 9. The perspective projection model for an endoscope imaging system with two near point light sources: O is the camera projection center; s₁ and s₂ indicate two light sources. We assume the plane consisting of O, s₁ and s₂ is parallel to the image plane. The coordinate system is centered at O and Z is parallel to the optical axis and pointing toward the image plane. X and Y are parallel to the image plane, F is the focal length, and a and b are two parameters related to the position of the light sources. Given a scene point P, the corresponding image pixel is p. Assuming a Lambertian surface, the surface illumination thus depends on the surface albedo, light source intensity and fall-off, and the angle between the normal and light rays.

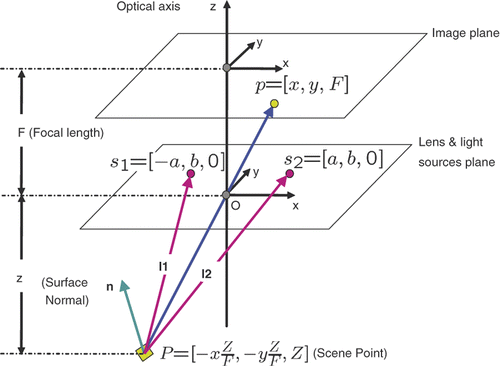
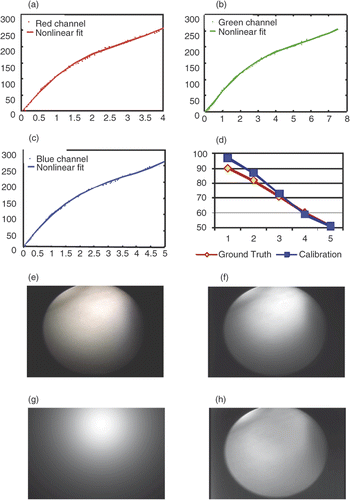
Figure 10. Results of photometric calibration. (a) Camera response function in the red channel. The red dots represent the data points and the magenta line represents the nonlinear fit. (b) Camera response function in the green channel. The green dots represent the data points and the magenta line represents the nonlinear fit. (c) Camera response function in the blue channel. The blue dots represent the data points and the magenta line represents the nonlinear fit. (d) Calibrated light intensity at different levels (blue) and the ground truth (green). We use level 6 as a reference and plot levels 1-5 with a small level corresponding to high light intensity. A bit variation in range for the high intensities may be caused by saturation. (e) Original image on color chart. (f) . (g) The cosine term . (h) The spatial distribution function m(x, y).

Yamaguchi T, Nakamoto M, Sato Y, Nakajima Y, Konish K, Hashizume M, Nishii T, Sugano N, Yoshikawa N, Yonenobu K, Tamura S, Camera model and calibration procedure for oblique-viewing endoscope. In: Ellis RE, Peters TM, editors. Proceedings of 6th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2003), Montreal, Canada, November 2003. Part II. Lecture Notes in Computer Science 2879. Berlin: Springer; 2003. pp. 373–381

 Google Scholar

Yamaguchi T, Nakamoto M, Sato Y, Konishi K, Hashizume M, Sugano N, Yoshikawa H, Tamura S. Development of a camera model and calibration procedure for oblique-viewing endoscopes. Comput Aided Surg 2004; 9(5)203–214

 PubMedGoogle Scholar