Development of a modified Cohen method of standard setting

Abstract

Background: A new ‘Cohen’ approach to standard setting was recently described where the pass mark is calculated as 60% of the score of the student at the 95th percentile, after correcting for guessing.

Aim: This article considers how two potential criticisms of the Cohen method can be addressed and proposes a modified version, with the assumptions tested using local data.

Methods: The modified version removes the correction for guessing and uses the score of the 90th, rather than the 95th percentile student as the reference point, based on the cumulative density functions for 32 modules from one medical school; and incorporates an indirect criterion-referenced passing standard by changing the 60% multiplier to the ratio of the cut score to the score of the student at the 90th percentile on exams that have been standard set using modified Angoff.

Results: The assumption that the performance of the 90th percentile student is consistent over time holds for multiple choice questions. Applying the modified Cohen method to the 32 modules generally reduced the variation in failure rate across modules, compared to a fixed pass mark of 50%.

Conclusion: The results suggest that the modified Cohen method holds much promise as an economical approach to standard setting.

Introduction

Standard setting is an essential part of an assessment strategy for medical education. The method of standard setting used should be fair, defensible, practical and transparent (Cusimano 1996; Norcini 2003; Cizek 2006) and the passing standard set should be valid (Cizek 2006), passing students who are truely competent and failing those who are incompetent. It is well known that there is no ‘gold standard’ approach to standard setting (Ben-David 2000; Norcini 2003; Downing et al. 2006) and that different methods of standard setting produce different results (Boursicot et al. 2006; George et al. 2006).

Cohen-Schotanus and van der Vleuten (2010) recently detailed a new method of standard setting in which the best performing students are used as the point of reference. Using this ‘Cohen’ method, the pass mark (PM) for an exam is calculated using the following equation (Cohen-Schotanus and van der Vleuten 2010):where C is the expected percentage score due to guessing and P the percentage score of the student at the 95th percentile. The results presented in Cohen-Schotanus and van der Vleuten's paper suggested that the Cohen method provides more stable pass rates when compared to both norm-referenced (mean minus one standard deviation) and fixed PM (of 60%) methods. Furthermore, the Cohen method is both practical and affordable, particularly when compared to exam-centred panel methods (Cohen-Schotanus and van der Vleuten 2010). The authors therefore advocate the use of the Cohen method for relatively low stakes tests where the cost of using exam-centred panel methods is prohibitive.

Two potential criticisms of the Cohen method are the fairness of the correction for guessing and the subjectivity of the ‘multiplier’ (0.6) used to calculate the PM. The Cohen method also relies on the assumptions that the score of the student at the 95th percentile is an accurate indicator of exam difficulty and is consistent over time (i.e. that successive cohorts of students are of similar ability). This article explores these criticisms and assumptions, which are tested using data from 16 first- and second-year modules each used in two student cohorts at one medical school. A modified version of the Cohen method is then proposed and used to explore the effect on the failure rate in the 32 modules when compared with a fixed 50% PM.

Criticisms and assumptions of the Cohen method

Correction for guessing

The benefits of correcting for guessing in terms of reliability may be outweighed by concerns regarding fairness, since answering strategies and risk-taking behaviour are being assessed as well as subject-specific knowledge (Betts et al. 2009). Since it has been noted that ‘correction for guessing formulas do not show significant benefits over conventional scoring’ (Chevalier 1998, p. 1) it may be more appropriate not to correct for guessing, but to maintain standards by increasing the multiplier.

Choice of the 0.6 multiplier

The 0.6 multiplier appears to have been chosen for the Cohen method as the previously used fixed PM was 60% (Cohen-Schotanus and van der Vleuten 2010), and hence could be accused of being subjective. As a result, the method is not criterion-referenced, as is desirable in medical education (Bandaranayake 2008). A potential solution is to use a criterion-referenced method of standard setting, such as Angoff (1971), to determine what the multiplier should be. After establishing the criterion-referenced PM and finding the score of the 95th percentile student on the exam, Equation (1) can be rearranged to find the value of the multiplier. This process would need to be repeated for other exams and the mean multiplier found, which can then be applied in the Cohen formula for subsequent exams.

The score of the 95th percentile student is an accurate indicator of exam difficulty

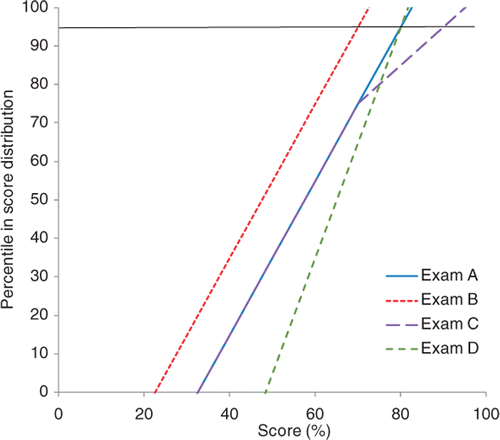
One approach to testing this assumption would be to use a criterion-referenced method of standard setting for a large number of exams and to assess the correlation between the PM established and the score of the 95th percentile student. A high positive correlation would provide evidence that this assumption is met, but would be time consuming to undertake. An alternative approach is to plot the cumulative density functions (CDFs) for the exams to be standard set using Cohen and evaluate if other students respond to test difficulty in the same way as the 95th percentile student, both within and across exams. Four example CDFs are shown in Figure 1 to illustrate this approach.

Figure 1. Example score CDFs.

Exam A is used as the baseline and with an expected score due to guessing (used in all four exams) of 20%, the PM is 56% and the failure rate 47%. A comparison of the CDFs for exam A and exam B suggests that exam B is significantly harder than exam A. The PM for exam B is 50% and the failure rate 55%. As both lines are straight and parallel, all students appear to respond in the same way to test difficulty within and between these two exams. The top performing students in exam C appear to do relatively better on the exam than other students (and the exam is more discriminating for these students), pushing the PM up to 62% and the failure rate to 59%. This means that the score of the 95th percentile student is not the most appropriate reference point. A more appropriate reference point would be where there is a distinct change in the gradient of the CDF; which can be determined by identifying the percentile where the second-order derivative is a local minimum (for exam C it is at the 75th percentile). The score of the 95th percentile student is the same for exams A and D, but the gradient of the CDF for exam D is much steeper than for exam A, indicating a difference in the way students below the 95th percentile respond to the difficulty of these two exams (exam D is less discriminating). The PM for exam D is 56%, but the failure rate is 23%.The Cohen method may therefore result in spurious failure rates if exams are not (approximately) equally discriminating between good and poor students, when considering discrimination both within and between exams.

The score of the 95th percentile student is consistent over time

To test this assumption, it is necessary to analyse data on student performance in exams which include questions that have been repeated for two or more cohorts. Where a number of questions have been used for more than two cohorts, a simple comparison of performance on these questions can be undertaken. An alternative approach, again providing there is some linkage between exams used in different cohorts, is to use Item Response Theory to establish and compare student ‘ability’ estimates across cohorts (de Ayala 2009).

Testing the assumptions and modifying the Cohen method

The components of the Cohen method that should be considered prior to local implementation are whether to use the correction for guessing, what the percentile reference point should be and what the multiplier should be. Due to concerns over the fairness of the correction for guessing identified above, this component has been removed. This simplifies the formula for finding the PM to:where K is the multiplier and P_x the score of the student at the xth percentile.

To determine the value of x to be used and to assess whether the exams were similarly discriminatory, the CDF for each of the 32 modules was compared to the combined CDF of the three exams that would be used to find the multiplier (see below). For 22 (69%) of modules, and for the combined multiplier CDF, the second-order derivative was at a local minimum between the 90th and 95th percentiles. The local minimum was between the 80th and 90th percentiles for two modules (6%), and between the 95th and 100th percentiles for 8 (25%) modules (Appendix). These results suggest that the 90th percentile is a more appropriate reference point than the 95th percentile, since students in the top 10% of the cohort respond differently to exam difficulty than other students.

The multiplier to be used was found by considering three fourth and fifth year exams that have been standard set using the Angoff (1971) method incorporating group discussion of questions with significant inter-judge disagreement. The PM, after scaling using the Angoff PM, was 50% for each exam and the scaled score of the 90th percentile student was 76%, 76% and 78% for the three exams. Rearranging Equation (2) and solving for K for the mean score of the 90th percentile student over the three exams (76.7%) gives K = 0.65. The modified Cohen formula to be used to determine the PM for this medical school is therefore:

The gradient of the CDF between the Cohen PM (as calculated using Equation (3)) and the 90th percentile student was calculated for the combined multiplier and each of the 32 modules. The Cohen PM was used as the starting point, since some of the module CDFs have a distinct ‘tail’ of poorly performing students. The combined multiplier gradient was 3.37 and the module gradients ranged from 2.67 to 3.76 (Appendix). A potential threshold range for the module gradients can be identified by keeping the score of the student at the 90th percentile and the failure rate constant, but adding and subtracting one standard error of measurement (3% for each of the multiplier exams used) from the PM and recalculating the gradient of the CDF. This gives a threshold range of 3.03–3.80: six modules (19%) are outside of this range, all with lower gradients (meaning these exams are more discriminating and will have a slightly higher PM and failure rate).

Finally, to test the assumption that the score of the 90th percentile student is consistent over time, the scores of students on 59 multiple choice questions (MCQs) that have been reused in six second-year module exams in 2007/2008, 2008/2009 and 2009/2010 have been disaggregated from individual module scores and analysed together. These 59 MCQs represent 42% of the MCQs for these modules. The score of the 90th percentile student for these MCQs was 86% in 2007/2008 and 2008/2009 and 88% in 2009/2010, suggesting that the performance of the 90th percentile student is consistent over time.

Applying the modified Cohen method to historical data

To illustrate the effect of the modified Cohen method (Equation (3)), it has been applied to the first- and second-year module results for the 2008/2009 and 2009/2010 cohorts. Figure 2 shows, for each year and cohort, the failure rate for each of the eight modules using a fixed PM of 50% and the modified Cohen PM, with modules sorted by the failure rate with the fixed PM. If modified Cohen is applied, the failure rate falls in 27 out of the 32 modules (84%), as the modified Cohen PM is less than 50%. Applying the modified Cohen method reduces the variation in failure rates compared to a fixed PM of 50% for three out of the four year/cohort combinations, as shown in Table 1.

Figure 2. Effect of applying modified Cohen on failure rates, Years 1 and 2, 2008/2009 and 2009/2010. PM, pass mark.

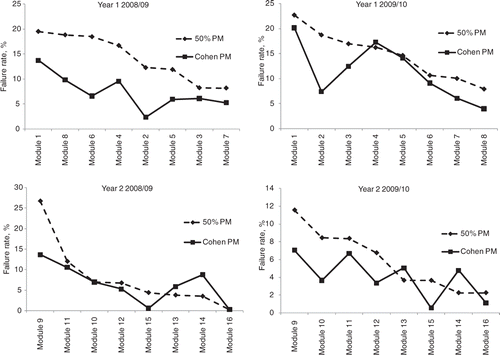
Table 1.  Variation in failure rates across modules

	Standard deviation of failure rate
Year of course and cohort	Fixed 50% PM	Modified Cohen PM
Year 1 2009/2010	4.95	5.66
Year 1 2008/2009	4.71	3.48
Year 2 2009/2010	3.42	2.35
Year 2 2008/2009	8.28	4.61
Combined	6.63	4.81

Discussion

This article had outlined two potential criticisms of the Cohen method of standard setting and proposed solutions for these. First, the correction for guessing can be removed, since this correction means that students’ marks are partly determined by their attitude to risk (Betts et al. 2009). Second, the subjectivity of the 0.6 multiplier was addressed using data from exams that have been standard set using a criterion-referenced method to find a ‘local’ multiplier. In addition, this article has identified the two key assumptions of the Cohen method and shown how these can be tested using local data. Such tests show that the score of the student at the 95th percentile may not be the most appropriate reference point, depending on the shape of the CDF of students’ scores. Furthermore, the gradient of six module CDFs was below the minimum of the proposed ‘threshold’. This will inflate the risk of a false negative error (failing a student who should have passed), although such errors are often seen as less consequential than false positives (Cusimano 1996). Nevertheless, it would be useful to run a criterion-referenced method of standard setting, such as Angoff, alongside modified Cohen, in order to assess whether the two methods give similar results, particularly for these six modules. The other key assumption, is that the performance of the 90th percentile student is consistent over time, was met for the MCQ part of the exams, but ideally should also tested for the short answer questions (this was not possible with the exams used for this article, since none of the short answer questions were repeated). As one potential explanation for this consistency is the large size of the cohort (approximately 370 students), this assumption would need to be checked before the Cohen method is used with smaller cohorts.

Applying the modified Cohen formula was successful in reducing the variation in failure rates across modules. Testing the assumptions of the Cohen method and identifying a ‘local’ Cohen formula, with or without correcting for guessing, a local multiplier and the most appropriate reference point is important for ensuring the fairness and credibility of the method. While this is a little time consuming at the outset, the modified Cohen method retains the advantages of the standard Cohen method, since it is still easy to understand and practical to use (Cohen-Schotanus and van der Vleuten 2010).

Assessing the validity of the PM established from any method of standard setting is difficult for four reasons. First, an evaluation of this kind is necessarily retrospective, since information on later performance is required before undertaking the analysis. Second, such analysis assumes that criterion pass/fail decisions are accurate and that the initial examination is predictive of performance on the criterion (Kane 2001). This latter assumption may not hold if different skills are being assessed (e.g. in the transition from pre-clinical to clinical studies at medical school). Third, criterion data are missing for those students who are deemed to have failed the initial examination, making it almost impossible to answer the question ‘is the PM too high?’ Finally, a trade-off between false positive and false negative error rates must be made and this requires subjective weights to be put on each type of classification error. Notwithstanding these difficulties, research to evaluate the effect of using different PMs/different methods of setting PMs on subsequent false positives and false negatives is required. This study needs to be a long-term effort, to ensure that PMs for all examinations are being set appropriately, such that students who are deemed ‘just competent’ are in fact safe doctors when then begin their postgraduate training.

Practice points

• The Cohen method of standard setting has been proposed as both practical and affordable for low stakes exams.

• The method can be modified to suit individual medical school policies on correcting for guessing, relating the standard to existing criterion-referenced methods and choosing an appropriate reference point based on existing score cumulative density functions.

• The assumptions of the Cohen method generally hold good when assessed using data from one medical school.

• Applying the Cohen method reduces the variation in failure rate across modules when compared to using a fixed PM of 50%.

• Assessing the validity of any PM or method of standard setting is difficult, but data should be collected to attempt such work.

Acknowledgements

I thank Charlotte Price, Prem Kumar and Beverley Merricks for their comments on the work reported in this article and on initial drafts of the paper.

Declaration of interest: The author declares that she has no conflict of interest.

Appendix

Table A1.  Percentiles between which the second-order gradient is a local minimum and the gradient of the CDF between the Cohen PM and the 90th percentile, by module and year

	Module 1	Module 2	Module 3	Module 4	Module 5	Module 6	Module 7	Module 8
Year 1 2008/2009
Percentiles between which second-order derivative of CDF is a local minimum	90–95	90–95	90–95	90–95	90–95	80–90	90–95	80–90
CDF gradient	3.11	3.65	3.24	3.19	3.38	3.45	3.32	3.27
Year 1 2009/2010
Percentiles between which second-order derivative of CDF is a local minimum	90–95	90–95	90–95	95–100	90–95	90–95	95–100	90–95
CDF gradient	2.70	3.42	3.08	2.70	2.93	3.12	3.33	3.46
	Module 9	Module 10	Module 11	Module 12	Module 13	Module 14	Module 15	Module 16
Year 2 2008/2009
Percentiles between which second-order derivative of CDF is a local minimum	90–95	95–100	90–95	90–95	95–100	95–100	95–100	90–100
CDF gradient	3.16	3.14	3.03	3.23	2.97	2.67	3.76	3.37
Year 2 2009/2010
Percentiles between which second order derivative of CDF is a local minimum	90–95	90–95	90–95	90–95	90–95	90–95	95–100	90–95
CDF gradient	3.29	3.51	3.22	3.38	3.15	2.90	3.70	3.53

Note: CDF gradients outside the local ‘threshold’ range are shown in bold.