Psychometric evaluation of a knowledge based examination using Rasch analysis: An illustrative guide: AMEE Guide No. 72

Abstract

Classical Test Theory has traditionally been used to carry out post-examination analysis of objective test data. It uses descriptive methods and aggregated data to help identify sources of measurement error and unreliability in a test, in order to minimise them. Item Response Theory (IRT), and in particular Rasch analysis, uses more complex methods to produce outputs that not only identify sources of measurement error and unreliability, but also identify the way item difficulty interacts with student ability. In this Guide, a knowledge-based test is analysed by the Rasch method to demonstrate the variety of useful outputs that can be provided. IRT provides a much deeper analysis giving a range of information on the behaviour of individual test items and individual students as well as the underlying constructs being examined. Graphical displays can be used to evaluate the ease or difficulty of items across the student ability range as well as providing a visual method for judging how well the difficulty of items on a test match student ability. By displaying data in this way, problem test items are more easily identified and modified allowing medical educators to iteratively move towards the ‘perfect’ test in which the distribution of item difficulty is mirrored by the distribution of student ability.

Introduction

The quality of assessment methods and processes is as important as the quality of the teaching and learning process in any form of educational activity. Undergraduate and postgraduate medical examination data needs to be evaluated using psychometric methods in order to understand, monitor, control and improve the quality of assessments. Medical educators and standard setters need to provide a stable and predictable measure of student performance over time to minimise sources of variation in examination data. The post-examination analysis of objective test data can provide the diagnostic feedback to not only improve the validity and reliability of assessments, but also improve curricula and teaching strategies (Tavakol & Dennick 2011b, 2012a, 2012b).

These analyses also allow for the identification of aberrant questions or individual skills assessment items (OSCE), which are outside of defined control limits and consequently could reduce the quality of the assessment questions (Wright & Stone 1979).

The importance of such analyses and their interpretations for improving student assessment are displayed in Table 1.

Table 1.  Ways in which psychometric methods can improve medical education assessments

1. Modifying and improving individual questions and individual stations continuously: aberrant questions and stations can be detected and then restructured or discarded.  2. Improving examination blueprinting by deciding on the number of stations, cases, standardised patients (SPs) and detecting sources of measurement error in cases/SPs; psychometric methods, such as the many-facets Rasch model, enables us to consider student ability, item difficulty, the difficulty of the rating categories and the severity of examiners and their interactions simultaneously.  3. Improving the practical organisation of examination (e.g. sites, SPs, examiners, marking procedures); do SPs represent patients in a standardized and consistent way? and are all sites fair for all students?  4. Improving and developing new approaches for analysing and interpreting exam data; using IRT faculty are able to obtain further information about the item difficulty and the student ability.  5. Improving the credibility of the competence-based pass mark; using cluster analysis and Rasch analysis.  6. Optimising duration of OSCE stations; if many students fail a given station, this could be due to the fact that they did not have enough time to demonstrate their performance.  7. Improving the validity and reliability of checklists, rating and global rating scales; the construct validity and the check-lists that are interpreted by examiners can be examined by the Rasch model.  8. Improving the reliability of total OSCE scores and knowledge-based tests; improving item discrimination indices, stations and questions or increasing the number of question and stations can increase reliability.  9. Improving inter-station reliability (the global rating scale versus checklists); using Cronbach's coefficient alpha faculty can estimate the reliability of the checklist score. In addition, it is possible to compare independent alpha coefficients of global rating scales and checklists using the Hakstian-Whalen test. 10. Evaluating and improving the internal structure of multiple choice questions and OSCE stations. (This helps to identify the domains that are being measured which are important in test score interpretation.) 11. Recognising, isolating and estimating measurement errors associated with students’ scores to gain a clearer picture for estimating the true score (e.g. the effect of examination sites on students’ scores); the use of Generalisabilty (G) theory and the Rasch Model. 12. Generalisability (G) theory; monitoring and improving the quality of an OSCE through aggregate analytical methods (i.e. G studies). 13. Providing useful information about inconsistent ratings; if a category in a checklist has not been used by examiners, this category can be combined with other categories. 14. Improving cases/SPs by detecting whether they are easy or difficult. 15. Mapping item difficulty to student ability using the Rasch model. This helps faculty to compare the range of student ability and item difficulty. 16. Improving the construct validity of a test by the Rasch model; PCAR will provide diagnostic information about the construct validity of the test. 17. Identifying guessing strategies using the IRT models. 18. Investigating the variability of students’ scores on different knowledge cases or stations. 19. Improving inter-rater reliability, particularly using Rasch Modelling 21. Using the Rasch model to reveal abnormal scoring patterns and to see whether the category responses employed in OSCE rating scales are being interpreted correctly. 22. Developing item banks which can be used in national assessment databases and for CAT.

The purpose of this Guide is to generally explore in some detail the way that assessment scores can be affected by various influences and specifically how the use of Rasch analysis can aid in detecting these influences, in order that minimalisation will improve quality.

Table

Practice points

Rasch analysis is a particular method used in IRT. IRT supersedes CTT, in that it takes into consideration the interaction between student ability and item difficulty. The characteristics of a test that fits the Rasch model can be identified, so that test developers can iteratively move towards the ‘perfect’ test. The ‘perfect’ test is one on which the distribution of student ability is perfectly mirrored by the distribution of item difficulty.

Comparing Classical Test Theory with Item Response Theory

This section of the Guide describes and compares the concepts and methods that underpin Classical Test Theory (CTT), which is the more traditional approach to psychometric analysis, and Item Response Theory (IRT), which is a more developed and contemporary approach.

CTT is relatively easy to understand and has some useful techniques and outputs; by contrast IRT is conceptually more complex but produces a much more comprehensive analysis of an assessment, which takes into account both student and exam item behaviour. As this Guide attempts to explain, the practical user of IRT methods does not have to deal with its complex mathematical constructs. By using the examples in the text of this Guide, we hope the reader can concentrate more on interpreting the post analytical outputs.

Traditionally the post examination results that are relayed back to faculty are often based on CTT models, such as descriptive reports of means, standard deviations, skewness measures, box plots, item difficulty, item discrimination, Cronbach and Kuder-Richardson reliability calculations, point-biserial correlation coefficients, standard error of measurement and Generalisability (G) studies. CTT concentrates purely on the items in the assessment and attempts to identify sources of measurement error and unreliability in the aggregate scores. With CTT, student ability is based on the number of questions that he or she answered correctly and the ability of a group of students is reported in terms of aggregate statistics. The analysis and interpretations of objective tests using these CTT techniques has been outlined elsewhere (Tavakol &Dennick 2011a). Sometime the association between aggregate student marks on variables, such as OSCE sites, cases or examiners, are identified using statistical procedures (e.g. chi-square and t-tests). As the CTT model focuses on the test and its errors, it provides little insight into how individual students interact with the test and its questions or how questions interact with individual students. Furthermore, as CTT statistics are all based on the aggregate, their values are sample size dependent. This means that the correlation of individual questions with the total score will be higher or lower purely on the basis of sample size, independently of the quality of the question. Because of this sample size effect, CTT may not always provide a greater understanding of the quality of questions being tested compared to IRT. Using the CTT model, investigators relate test scores to true scores by understanding the nature of errors and factors influencing the reliability of the test. In addition, if different students have the same mark on the test it is difficult to assess their ability, in terms of item difficulty, if they have different response patterns to the test questions. Just because students have the same mark does not mean they have answered the same questions correctly. Using the CTT model, it is not possible to calculate how individual students behave with particular questions (Hambleton & Jones 1993).

Although the results of CTT provide a preliminary and exploratory analysis of exam data, medical educators need to further investigate the relationship between the ability of students (independent of item sample size) and the ease or difficulty of questions (independent of student sample size). In order to look at this relationship, faculty need to use IRT which overcomes the limitations of the CTT model and provides a global picture of the distribution of student marks in relation to the range of difficulty of the questions. An assumption of IRT is that the probability of a student answering an item correctly is a function of the item difficulty (B) and the student ability (D). However, despite the theoretical advantages of the IRT measurement model compared with the CTT model in the medical education literature, it has received little attention, despite the fact that medical educators have acknowledged its existence (Downing 2003; de Champlain 2010).

One of the main models of IRT is known as the ‘Rasch’ model; however this too has received little attention in test item analysis. Using the search terms: ‘Rasch’, ‘Rasch analysis’ and ‘the multi-faceted Rasch model’, in searching all medical education journal articles published between 1990 and January 2012 revealed only a few articles reporting on the application of the Rasch measurement model for analysing individual questions and individual OSCE stations (de Champlain et al. 2003; Bhakta et al. 2005; McManus et al. 2006; Iramaneerat et al. 2008; Houston 2009; Chang et al. 2010; Yang et al. 2011).

Two parameter IRT (2PL) or three parameter IRT (3PL) models are also available where item discrimination, item difficulty, gender, student guessing behaviour or year of study can be included in the analysis.

Given the limitations of the CTT model previously described, the purpose of this Guide is to explain how the Rasch model can be used for analysing and constructing tests for assessing the knowledge and practical skills of medical students. In this Guide, we will demonstrate that Rasch analysis is a more sophisticated tool for the psychometric evaluation of assessments providing a detailed and forensic analysis of exam data that can be practically used to improve test quality.

Methods

The Rasch model

Despite the complexity of the statistical and measurement methods, used by the Rasch model, the results can answer some simple questions given below.

• How well does a student answer a question if we know the student's ability and the item's difficulty?

• What is the probability of a student answering an item correctly given a measure of item difficulty?

• If student ability equals item difficulty, what is the probability of answering the item correctly?

• What is the probability of a less or more able student answering an easy or difficult item?

The Rasch model identifies, isolates and estimates student and item measures to provide these probabilities.

In Rasch analysis, student ability and item difficulty need to be measured in the same units, namely ‘logits’. Student ability is the natural logarithm of the ratio of the probability of success divided by the probability of failure, ln(p/1-p). Higher logits (positive values) imply greater levels of ability. Lower logits (negative values) imply lower levels of ability. For example, if a student answers 60% of a test's questions correctly, the odds ratio for the whole test is  = +0.4 logit, which is the student's ability. The logit for item difficulty is calculated by reversing the numerator and denominator in the above formula. For example, if an item is answered correctly 80% of the time, its difficulty is  = −1.38 logit. Student ability and item ability can therefore be displayed on the same scale of logits. Zero on the scale represents the centre of the ability range and the centre of the difficulty range. A student with an ability of 0 logits has an average ability concerning the knowledge being tested. Under the Rasch model, the difference between student ability and item difficulty predicts the likelihood of a correct answer. For example, if student ability equals item difficulty, the difference is zero and hence the probability of a student answering a question is 50%. If student ability is greater than an item's difficulty this predicts the probability of a correct answer. If a student has an ability of +3 logits and an item has a difficulty of +1 logits then the probability of answering the question is 0.88. A key advantage of the Rasch model is that item difficulty and student ability are measured independently from each other (Andrich 2004), i.e. the distribution of items on the test cannot influence the student ability estimates and the distribution of students cannot influence the item difficulty estimates.

With Rasch analysis the relationship between student ability and item difficulty is displayed in an Item Characteristic Curve (ICC) as shown much later in Figure 4. The ICC provides informative data about each item and the probability of answering a question correctly given the student ability. The ICC also shows how an item contributes to the underlying construct of interest which either can be the relevant cognitive or psychomotor domain being assessed. The ICC displays those items that do not contribute to the underlying construct of interest as outliers on the scale. Investigating these items and removing them from the test can improve the construct validity of the test. For example, in a test we would not expect to see low performing students having a high probability of answering a given item correctly. We have explained how to draw an ICC using student ability and item ability elsewhere (Tavakol & Dennick 2012a, 2012b). To draw an ICC, readers should calculate the item difficulty of a question and then calculate the ability of all students. The ICC can then be drawn using Excel™. In order to use Rasch analysis to evaluate an assessment and to make valid predictions, the data should fit the Rasch model as closely as possible. Within Rasch analysis, there are a number of statistical processes used which can provide evidence as to how well the observed data fits the model. Lack of fit does not invalidate the model, on the contrary, it identifies test factors and items which should be examined further and which, if appropriately modified, will improve the validity of the test. It is a goal of Rasch analysis to produce a test that fits the Rasch model as closely as possible. These concepts and processes are discussed in more detail below.

Unidimensionality

One of the assumptions of Rasch modelling is that a test optimally measures a single underlying construct; this is termed unidimensionality. For example this underlying single construct can be identified with cognitive ability in a knowledge-based test or practical performance in an OSCE. Unidimensionalty implies that all items in a test or all OSCE stations assess a single construct or dimension. Therefore, we need to ensure that the dimensionality assumption of a test is not violated by some aberrant items. Simply speaking, if a question or item cannot contribute to the underlying construct of a test it should be excluded from the test. Removal of such items or questions will also increase the construct validity of the test. One aspect of Rasch modelling therefore is the identification of the dimensionality of the test. In this Guide, principal-component analysis of residuals (PCAR) is used to examine the unidimensionality of the test. The first or major factor identified is commonly termed the Rasch Factor or primary factor. If the data contributing to this factor are removed analysis of the residual data may reveal further factors termed for example the 1st, 2nd or 3rd ‘contrast’. However, if the first ‘contrast’ identified has an eigenvalue (a statistical measure of the number of questions making up a construct) of less than two this means that the data contributing towards this factor do not support an additional underlying construct and the uni-dimensionality of the test is supported (Linacre 2011). However, if an eigenvalue of 3.6 is found in the first contrast this indicates that approximately four items are measuring an alternative construct, by rounding up to the nearest whole number. In order to make a decision about this, we need to examine these items to see if they are related to different content as this is a sign of the multidimensionality of the test. However, if there is no meaningful difference in the item content, this may not support the multidimensionality of a test and the difference has occurred by chance.

Response dependency

Another assumption of Rasch analysis is local independency of items. This means that the probability of answering one item correctly should be independent of the answer to other items. When the value of an item is predicted by the value of another item, the assumption of independency is violated. In the context of the Rasch model, items with a high positive correlation indicate that one of the two questions is redundant for the test. Correlations greater than 0.50 between items are considered an indication of response dependency and items should be investigated. For example if item 1 has a correlation coefficient of 70% with item 2 this indicates a local item dependency between item 1 and item 2, suggesting both item 1 and item 2 are required for the test.

Reliability and separation estimates

In CTT, the reliability of a test is reported via the Kuder-Richardson or Cronbach reliability coefficient, with a single value ranging from 0 to 1, indicating the average inter-item correlation among the question responses. In Rasch analysis reliability is associated with the range of item difficulty as well as student ability. As reliability measures are a function of the interactions between students and items, multiple reliability values can be reported. In the case of student ability reliability is presented as ‘person separation reliability’ (PSR), which tells us whether the test discriminates or spreads out a cohort of students into groups according to their abilities on the test (Wright & Masters 1982). In addition, the value of the PSR indicates the reliability of the location of students among the items measuring the same construct (Bond & Fox 2007). A satisfactory value of PSR is similar to the value of Kuder-Richardson or Cronbach's alpha co-efficient, ranging from 0.70 to 0. 95 (Tavakol & Dennick 2011a). However, a useful reformulation of the PSR as the ‘person separation index’ (PSI) provides further information about the reliability of a test. It is equal to . The higher the value (>2) of the PSI the more student groups can be differentiated (Bond & Fox 2007). For example, if a Cronbach's alpha of 0.63 is reported the PSI is or 1.64. This suggests that the test was not sensitive enough to discriminate high and low ability students as the value is less than 2.

Rasch item fit

‘Rasch item fit’ statistics show how well or accurately data in the test fit the Rasch measurement model, i.e. how well item difficulty or student ability contributes to the underlying construct of the test (Linacre 2002). This can be used to identify ‘mis-fitting’ items and to measure the ‘dimensionality’ of the test. The Rasch process calculates an expected score from each observed score using a chi-squared technique or t-test for each item. Large deviations between observed scores and expected scores can give a distorted picture of the test although data which fits the Rasch model should show smaller deviations. There are two types of items in terms of Rasch fitness that can be identified by means of infit and outfit statistics. Infit statistics are expressed as ‘infit Mean Square’ (infit MNSQ) or ‘infit t’ (infit ZSTD). Outfit statistics are reported as ‘outfit MNSQ’ or ‘outfit t’ (outfit ZSTD). MNSQ values can be used to judge the compatibility of the observed data with the Rasch model, values between 0.70 and 1.30 indicating a good fit. A value of 1 indicates there is a perfect fit but values less than 0.70 and greater than 1.30 are termed misfitting and over fitting, respectively, and should lead to an analysis of the items (Bond & Fox 2007). ‘Infit t’ values also show the degree to which a question fits the Rasch model. Observed data follow the Rasch model if the results of infit t are non-significant (t between +2 and −2). Outfit and infit statistics also indicate the degree to which a student fits the Rasch model.

Although acceptable values of outfit statistics are similar to infit statistics, it should be noted that infit statistics provide more useful information about the relationship between the ability of the students and the difficulty of items as they are more sensitive to unexpected responses to items close to the student's ability level. Outfit statistics are more sensitive to unusual observed data where students find questions very easy or very hard or responses to items are far from the student ability (Linacre 2011). For example, since less able students struggle to answer difficult questions correctly if they do answer some difficult questions the outfit statistic will reflect it by creating a ZSDT value outside the acceptable limit. In addition, if an item was very easy, say a logit of −3.0, we would expect a large value for the outfit statistic suggesting the item should be examined or removed from the test.

Test information function

Another useful feature of Rasch modelling is the ‘item information function’ which is calculated by mathematically combining information from student ability (D) and item difficulty (B). The sum over all items gives the ‘test information function’ (TIF). Under the Rasch model, the TIF provides useful knowledge about the reliability of the test at different levels of student ability. Calculating a single value for the reliability (e.g. Kuder-Richardson reliability or Cronbach alpha, as in CTT) does not take into consideration that reliability is actually influenced by student ability and item difficulty. Therefore, if a test has a high reliability coefficient, one can ask for which group of students is it reliable (low, moderate or high ability students?).The Rasch method provides a test information curve, where the sum of all item information is plotted against student ability, which enables us to estimate reliability at different levels of student ability, with higher information indicating more reliability. A test containing highly discriminating items will have a tall narrow curve. Less discriminating items provide less information but over a wider range. That is the test has poor reliability and should be investigated and improved using psychometric methods.

Item difficulty invariance

Another feature is ‘item difficulty invariance’ which provides valuable information about the invariance or stability properties of item values within a test. Invariance in this context means that the properties of an item are not influenced by the ability of the students answering the item. A scatter plot of item difficulty values from high- and low-ability students can display a correlation that reveals the extent to which item difficulties vary between the two groups. By inserting 95% confidence interval control limits onto such plots items that are not invariant or unstable with respect to ability can be easily identified. Item difficulty invariance also allows us to identify items that are useful across the ability range in order to calibrate questions for item banks. This means that assessors will have convenient access to a large number of tested questions which are classified according to student ability and item difficulty. Such questions can also be used for computer adaptive testing (CAT) where the questions administrated to students can be modified according to their performance on the previous questions.

Item Characteristic curve

As previously mentioned, an important feature of the Rasch model is that the probability of a student answering an item correctly in a test is a function of the student's ability (B) and the item difficulty (D). This function is depicted graphically in an ICC. We have already shown how to draw the ICC elsewhere (Tavakol & Dennick 2012a, 2012b). We indicated that if the student ability is equal to the item difficulty (B-D = 0), the probability that the student will answer the question correctly is 50% which can be seen in the ICC. By knowing the student ability–item difficulty values for each student we can draw, in Excel, the ICC to display the response probability for any student attempting to answer any particular item. (In fact, using ICCs it is possible to estimate a student's ‘true’ score on a test). To simplify, if a test has two questions, a student might receive a mark of 0, 1 or 2. If the student has an ability of 0 logits they could have a probability of 0.23 of answering question 1 correctly and a 0.56 probability of answering question 2 correctly. Therefore, their calculated ‘true’ score is 0.79/2. However, their ‘actual’ score can be different.

Participants

The examination data used in this Guide was processed from results obtained from 355 medical students in their final clinical knowledge-based exam. We used Winsteps® software (Linacre 2011), to produce simulated modifications of the data to create examples for the purposes of this Guide. We did not require approval from our research ethics committee as this study was carried out using data acquired from normal exams within the curriculum with the goal of monitoring the quality of individual questions in order to improve student assessment.

Data collection

Knowledge-based test

The simulated knowledge-based questions were used to assess cognitive performance of students in this study. The test consisted of 43 questions to assess two clinical cases. Case 1 consisted of 24 questions on Clinical Laboratory Sciences and Case 2 consisted of 19 questions on chronic illness in General Practice. Each question was marked dichotomously, i.e. students received 1 mark if they answered the question correctly and 0 if they answered incorrectly. The potential score for Case 1 and Case 2 was 24 and 19, respectively. There was no negative marking for incorrect answers. Students responded to the questions through an online assessment system (Rogo, University of Nottingham) during a normal summative examination.

Psychometric software

The Rasch measurement model (Rasch 1980) was used to analyse the different response patterns obtained using Winsteps® software.

Results

In this section, we will demonstrate the results of the Rasch analysis of our simulated exam data under the headings previously discussed. For each section, we will discuss the following.

Unidimensionality

PCAR was performed to investigate the unidimensionality for the combined cases and for each case. The eigenvalue for both cases was 2 indicating that the test measured a single underlying construct. For the 1st contrast both cases had an eigenvalue of less than 2 indicating they also measured a single underlying construct. Therefore the unidimensionality for each case is supported and both cases are potentially measuring the same underlying construct (Table 2).

Table 2.  Rasch factor analysis of the whole test, cases 1 and 2

Test	No. of questions	Rasch factor (eigenvalues)	Factor 1 (1st contrast) (eigenvalues)
The whole test	43	19.4	2.0
Case 1	24	13.3	1.5
Case 2	19	9.7	1.7

Table 3.  Item difficulty, standard error and infit and outfit statistics in case 1

			Infit		Outfit
Question	Item difficulty logits^a	SE^b	MNSQ	ZSTD	MNSQ	ZSTD
Q1	1.86	0.12	1.00	0.10	0.97	−0.40
Q2	0.71	0.13	0.96	−0.87	0.91	−1.02
Q3	0.71	0.13	1.00	0.09	0.96	−0.48
Q4	−1.52	0.23	0.97	−0.12	0.76	−0.75
Q5	2.85	0.14	1.04	0.60	1.01	0.15
Q6	−0.48	0.16	1.02	0.25	1.02	0.16
Q7	1.56	0.12	1.03	0.60	1.05	0.75
Q8	2.01	0.12	1.02	0.49	1.05	0.68
Q9	−0.28	0.15	0.98	−0.19	0.87	−0.80
Q10	0.38	0.13	1.00	0.04	0.95	−0.48
Q11	−0.78	0.17	1.04	0.38	1.63	2.59
Q12	−0.97	0.19	1.03	0.25	0.96	−0.09
Q13	−1.28	0.21	0.97	−0.14	1.00	0.08
Q14	−2.1	0.29	1.01	0.11	0.87	−0.21
Q15	−3.1	0.45	1.00	0.14	0.82	−0.15
Q16	3.09	0.15	1.01	0.10	1.03	0.30
Q17	−0.15	0.15	1.04	0.57	1.20	1.34
Q18	−0.28	0.15	1.01	0.15	1.12	0.80
Q19	−1.08	0.19	1.01	0.15	1.46	1.71
Q20	−0.63	0.17	0.99	−0.03	0.93	−0.33
Q21	−0.13	0.15	0.99	−0.14	0.98	−0.06
Q22	−1.68	0.24	0.99	0.03	0.85	−0.35
Q23	−0.28	0.15	0.96	−0.49	0.82	−1.17
Q24	1.59	0.12	0.92	−1.85	0.90	−1.60
Mean	0.00	0.17	1.00	0.00	1.00	0.00
SD	1.52	0.07	0.03	0.50	0.19	0.90

Notes: ^aItem difficulty measured in logits (negative values indicate easier questions).

^bStandard error.

MNSQ: mean square (values between 0.70 and 1.30 are within acceptable limits for the Rasch model).

ZSTD: value of t-test (values between −2 and +2 are within acceptable limits for the Rasch model).

Figures in bold indicate questions outside Rasch model (Q11 and Q19).

Table 4.  Item difficulty, standard error and infit and outfit statistics in case 2

			Infit		Outfit
Question	Measure logits^a	SE^b	MNSQ	ZSTD	MNSQ	ZSDT
Q1	1.81	0.12	1.05	1.12	1.07	1.20
Q2	2.57	0.13	1.04	0.62	1.10	1.06
Q3	1.46	0.12	0.99	−0.32	0.98	−0.27
Q4	0.21	0.13	0.93	−1.13	0.91	−0.89
Q5	−4.05	0.71	0.99	0.21	0.36	−0.99
Q6	−0.06	0.14	1.05	0.63	1.19	1.56
Q7	0.80	0.12	0.96	−1.01	0.91	−1.42
Q8	−0.47	0.16	1.04	0.42	0.94	−0.31
Q9	2.23	0.13	1.01	0.13	1.06	0.76
Q10	0.94	0.12	1.02	0.43	1.06	0.97
Q11	−0.42	0.15	0.93	−0.73	0.87	−0.85
Q12	−2.63	0.36	0.98	0.06	0.54	−1.04
Q13	−1.83	0.25	0.95	−0.16	0.78	−0.60
Q14	−2.51	0.34	0.95	−0.07	0.56	−1.06
Q15	1.06	0.12	0.98	−0.51	0.96	−0.65
Q16	0.97	0.12	1.03	0.78	1.03	0.55
Q17	−1.11	0.19	0.98	−0.08	0.82	−0.77
Q18	−0.91	0.18	1.02	0.23	1.02	0.14
Q19	1.93	0.12	1.06	1.23	1.11	1.79
Mean	0.00	0.20	1.00	0.10	0.91	0.00
SD	1.77	0.14	0.04	0.6	0.21	1.00

Notes: ^aItem difficulty measured in logits (negative values indicate easier questions).

^bStandard error.

MNSQ: mean square (values between 0.70 and 1.30 are within acceptable limits for the Rasch model).

ZSTD: value of t-test (values between −2 and +2 are within acceptable limits for the Rasch model).

Figures in bold indicate questions outside Rasch model (Q5, Q12 and Q14).

In the whole test, the Rasch factor explained 19.4 items (eigenvalues) of the variance. In Case 1, the Rasch factor explained 13.3 items (eigenvalues) of the variance. In Case 2, the Rasch factor explained 9.7 units of the variance. Factor loadings in the whole test indicated that only one question (Q28) had a factor loading greater than 40. Based upon these values, it is unlikely that the item residuals (data left after data supporting the first factor have been removed) identify a further factor and therefore a unidimensionality model of the whole test is supported. Following the removal of question 28 from the whole test, there was little effect on the value of factor 1 (eigenvalue = 1.9) and therefore, we kept it in for the next analysis.

Response dependency

The local independence assumption is not violated if the order of the questions in an examination does not affect their difficulty. Test Response dependency was assessed for the complete test and for each case. Inter-correlations between item standardised residuals for the whole test were less than 0.50, ranging from −0.18 to 0.29. Similar results were also found for both cases 1 and 2, ranging from −0.13 to −0.18 for case 1 and −0.17 to 0.37 for case 2. These results suggest that items were locally independent and the local independence assumption is not violated. The order of the questions therefore does not appear to affect item difficulty.

Reliability and separation estimates

The PSR for the whole test was 0.65 with a PSI of 1.37. A PSI value less than 2 indicates that the spread or separation of students on the construct being measured was not satisfactory, suggesting that the questions had low discrimination. Similar findings were also found in Case1 (PSR = 0.60; PSI = 1.21) and Case2 (PSR = 0.44; PSI = 0.88).

Rasch item fit

Table 3 shows item difficulty, standard error and item fit in each case. The outfit statistics show that Q11 and 16 are not within the acceptable range (both for MNSQ and ZSTD) implying they needed to be investigated as they did not contribute towards the underlying test construct. This could also show that item difficulty does not map to student ability. The infit mean square statistic shows that all questions are within the acceptable range with a mean of 1.0. As we can see from Table 4, the outfit MNSQ has a mean less than 1.00 and Q5, 12 and 14 are outside the acceptable range of the outfit MNSQ, indicating questions outside the 0.7–1.3 range. For example, these items are too easy for all students and do not fit the Rasch model and can hence distort the single underlying construct of the test. In addition the ability of the students goes beyond the ability of these items. These questions therefore should be investigated.

Test information function

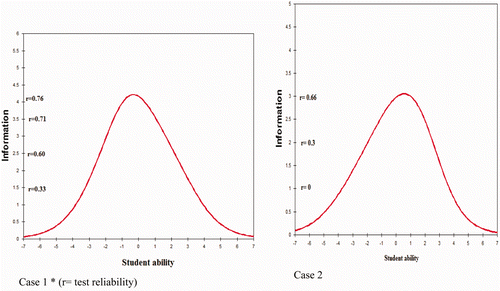
Figure 1 displays test information values for questions in cases 1 and 2, respectively. The TIF shows the reliability of the test at different levels of student ability. The highest reliability values are 0.76 and 0.66 in cases 1 and 2, where the ability of the student is equal to 0. These curves indicate that both cases are less reliable for low- and high-level students.

Figure 1. Test information function. Note: r = test reliability.

The graphs in Figure 1 illustrate the relationship between student ability (measured in logits) and the sum of the item information measures for the whole test. Reliability values are calculated from the graphs. For example, in case 1 the reliability value for individuals with ability 0 logits is calculated as 0.76, whereas for students with ability −3.5 the reliability estimate is 0.33.

Comparing students and questions

In case 1, students had a mean ability of 1.52 logits with a standard deviation of 1.01, while in case 2, they had a mean ability of 1.42 logits with a standard deviation of 0.89. This indicates that case 1 was slightly easier than case 2. The mean of item difficulty is 0 logits, by definition, since the mean value is where 50% of items are answered correctly, (ln(50/50) = 0). But, case 1 had a standard deviation of 1.52, whereas case 2 had a standard deviation of 1.77. We can confirm that the vast majority of questions are located between −1.52 and +1.52 in case 1 and between −1.77 and +1.77 in case 2. Standard deviations (and spread) of item difficulty are greater than standard deviations (and spread) of student ability. The item–student map clearly shows the relationship between student ability and item difficulty of both cases (Figure 2).

Figure 2. Item–student maps Each # represents four students and each ‘.’ represents one to four students. The values on the left of each scale are logits. T = 2 standard deviations from the mean, S = 1 standard deviation from the man, M = mean.

Figure 2 displays the difficulty hierarchy of questions as answered by the students for both cases. It can be seen that student ability is greater than item difficulty for both cases and hence, overall, students are more likely to answer questions correctly. There are some questions with difficulty measures below the least able student and few questions with difficulty beyond the most able one. In case 1, student measures range from approximately −1.0 logits to +5.0 logits and the item difficulties range from −3.5 to +3.5 logits. This means that the range of item difficulty is not as good as it could be as most items are located on the ‘easy’ side. Similarly, such findings can be calculated for case 2. It should be noted that a difficult test has negative mean student ability and therefore, we would expect to see the majority of questions at the top right side of the map and students at the bottom left-hand side of the map.

In order to demonstrate an ideal situation we have created some simulated data as depicted in Figure 2 (simulation 3). It can be seen there is a range of item difficulties which match the ability of students. It is worth noting that if the students’ mean ability in the test approaches 0, the ability of the students will map directly to the difficulty of the items. This is the aim of ‘best test design’, to match student ability to item difficulty.

Item difficulty invariance

Item difficulty values are divided into group of students (high and low performance on exam data) in both cases. (Figure 3)

Figure 3. Item difficulty invariance in cases 1 and 2, respectively.

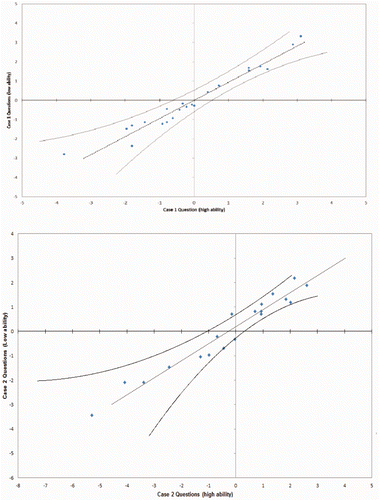
The graphs in Figure 3 show scatter plots of item difficulty from high versus low ability student groups. 95% confidence limits indicate the boundaries of questions that are within invariance limits.

As can be seen in Figure 3, all the plotted questions (highlighted in blue) for 24 questions lie along the diagonal line. This is not a regression line, but the Rasch-modelled relationship required for invariance. The values of item difficulty are located inside the control limits (95% confidence interval around the diagonal line), indicating that the item difficulty values are invariant. In case 2, one of the questions (Q4) lies outside the control limits indicating that this item should be investigated in order to improve the psychometric properties of the test among different groups with low and high levels of student performance.

Item Characteristic curve

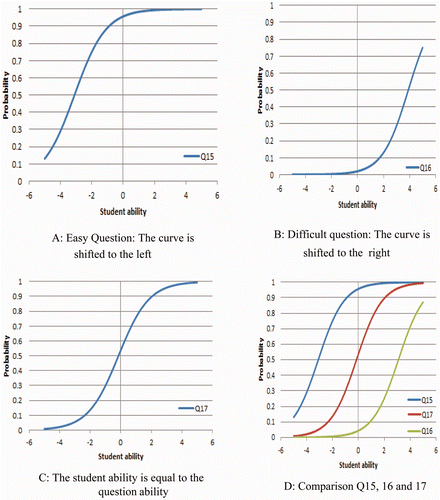
From Table 3, the ICC can be drawn for items in both cases and two or more ICCs can be drawn together (Figure 4) for comparison. For the purposes of this Guide, we have selected three item difficulty values to display their ICC differences. In Figure 4, Case 1, Q15 and 16 are easy and hard, respectively and Q17 is close to 0 logits. As we can see from Figure 4, there is a 95% probability that students with an ability of 0 logits will answer question 15 correctly, whereas the probability of answering question Q16 is very low. Q17 is a good question as there is a 50% probability that students with an ability of 0 logits will answer this question correctly. Comparison of these curves provides a better picture of the location of students and questions. In general, if a question shifts the curve to the left along the student ability axis, it will be an easy question and a harder question will shift the curve to right. The ICCs show examples of easy, intermediate and difficult questions.

Figure 4. ICC for questions 15, 16, 17 from Table 3.

Discussion

The purpose of this Guide is to demonstrate how to use the Rasch model as an alternative to CTT, to obtain diagnostic information about objective tests in order to monitor and improve the quality of assessments in medical education.

Developing valid and reliable tests of student performance is necessary to improve assessment quality and to ensure that curricula standards of fairness and objectivity are maintained.

In Rasch analysis, a sequence of steps must be taken in order to analyse the exam data. The first step is to assess the dimensionality of the test using the PCA of residuals (Linacre 1998). This analysis will reveal whether or not the test is unidimensional and is based on one underlying cognitive construct or practical performance. Before running the PCAR, however, an investigation of point–biserial correlation using the CTT approach is recommended to investigate problem questions. For example, if negative or low values are observed this may be either an indication of data entry errors, items are that are too easy or too difficult or easy items that have not been answered correctly by students of high ability.

The second step in Rasch analysis is to look for the eigenvalues of the unexplained variance remaining after the Rasch factor has been removed. These left over items constitute the ‘contrasts’, PCA of which demonstrates whether there may further underlying constructs or dimensions. Along with the assumption of unidimensionality, standardised residual correlations between questions are inspected to detect local independence. Locally, independent questions have low inter-item correlations, indicating that differences in responses to items are reflective of difference in the underlying trait or ability being measured (Cohen & Sweedlik 2010).

Thirdly, we need to investigate miss-fit of items in the test. Items that do not fit the Rasch model imply a lack of unidimensionality and should be investigated. Lack of fit may indicate either a misunderstanding of the item or that it is measuring some other construct.

Fourthly, we need to make sure an item provides useful information about the construct being measured by the test. The item that all students answer either correctly or incorrectly does not provide useful information about the test. The item information curve can illustrate how an item discriminates between students at different ability levels and the sum of item information measures does this for the test as whole. The item information curve also shows that different reliabilities are measurable for the test according to different student abilities. (Nunnally & Bernstein 1994; Cohen & Sweedlik 2010).

Fifthly, the item–student map provides a quantitative and visual display of the interaction between student ability and item difficulty. On this diagram, one can see the whole distribution of student abilities and the whole distribution of item difficulty on the same logit scale. This enables a comparison of the two ‘abilities’ and displays whether the items are easier or harder than the abilities of the students. It can be seen from this that a good test would have the student ability and item difficulty distribution mirroring each other as shown in Figure 2(c). A ‘perfect’ test that completely fitted the Rasch model would have both mirrored distributions around a mean of 0 logits.

Sixthly, item difficulty invariance needs to be measured to ensure that item difficulty is constant across the student ability range.

Finally, the ICCs need to be examined to compare and identify easy and difficult items. Probabilities associated with each item can be used in future standard setting procedures to improve the accuracy and credibility of the pass mark.

Summary

1. Rasch analysis is a method of post-examination analysis that goes beyond CTT to investigate the relationship between item difficulty and student ability. As such, it deals with how students interact with an exam and how exam items interact with students of different ability.

2. Rasch analysis provides diagnostic and quality feedback about test items and student ability to help medical educators improve the exam cycle.

3. The Rasch model provides useful information about the intrinsic quality of test items which is independent of student ability.

4. Rasch analysis provides useful graphical displays that enable test constructors to evaluate the effectiveness of their assessments.

5. ICCs can be used to compare and identify easy and difficult items.

6. A good test that fits the Rasch model should have the following characteristics.

   1. It should be unidimensional i.e. it should be aimed at a single underlying construct, either cognitively or practically.

   2. When analysed for dimensionality by PCAR, all items in a perfect test should load into the Rasch Factor. (In practice this is unlikely due to natural randomness in the data set).

   3. All items should display local independence and should not be correlated with a sub-set of other items.

   4. Item difficulty should be independent of student ability as measured by item difficulty invariance.

   5. Items should ‘fit’ the Rasch model using ‘infit’ and ‘outfit’ statistics.

   6. The TIF should have high values across the majority of the student ability range leading to high reliability and better differentiation.

   7. The item map should display item difficulty and student ability mirroring each other about a mean of 0 logits.

Although we have used a knowledge-based test as an example in this guide, the methods described here can equally be applied to the data obtained from individual OSCE stations.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of this article.