Level-spanning proof-production strategies to enhance students’ understanding of the proof structure in school mathematics

Abstract

This study focused on improving students’ learning mathematical of proofs and proving by using combinations of proof strategies that span different levels of understanding of proof structure; we refer to these as ‘level-spanning proof-production strategies’. We analysed the level-specific proof-production strategies evident in the lessons and class tests of two Grade 8 classes (students aged 13–14). Our analysis revealed the level-spanning proof-production strategies by students and teachers that emerged during lessons to enhance the students’ understanding of the proof structure. The idea of combining strategies at different levels is not found in previous studies and can be applied outside of proof studies, provided that the students’ levels are well developed. It can be expected that the conscious use of these strategies by teachers in their proof teaching will enhance students’ ability to produce proofs according to their understanding of proof structures.

Keywords:

• Proof-production strategies
• proof structure
• levels of understanding
• mathematics education

1. Introduction

The teaching and learning of proof is internationally recognised as a key component of mathematics education (Hanna & de Villiers, 2008, 2012). Yet, students in secondary education (and beyond) struggle to understand proof in mathematics, in general, and geometry, in particular. For example, research suggests that when learning proofs, students tend to rely too much on empirical data or concrete examples (e.g. Harel & Sowder, 2007; Küchemann & Hoyles, 2006; Martinez & Pedemonte, 2014), do not know where to start (e.g. Hoyles & Healy, 2007), or do not use existing knowledge (e.g. Weber, 2001). Moreover, students at school and even at the undergraduate level demonstrate difficulties when trying to read proofs presented to them (e.g. Inglis & Alcock, 2012; Lin & Yang, 2007), when asked to judge the adequacy of a proof (e.g. Hoyles & Healy, 2007), when asked to write a proof (e.g. McCrone & Martin, 2004; Senk, 1989), and when constructing an empirical numerical proof (Stylianou et al., 2015).

Within such extensive evidence of students’ difficulties in understanding proof and proving in mathematics education, there are three aspects of proof and proving that complement each other in the course of teaching proof: proving as an intellectual activity (e.g. Balacheff, 1987); the functions and meaning of proof (e.g. de Villiers, 1990); and understanding the structure of the proof (e.g. Miyazaki, Fujita, and Jones, 2017).

An essential core task of proof teaching is to enable students to view proofs as structural objects (Miyazaki, Fujita, & Jones, 2017). This is because such an understanding provides the foundation for students to engage in the intellectual activity of proving and to understand the roles, functions, and meanings of proof and proving. Accordingly, our focus is on the teaching process that enables students to see proofs as structural objects. We see such teaching as the key to eliminating or reducing the challenges of teaching proofs.

As structural objects, proofs consist of logical networks of singular propositions (of the form A is B) and universal propositions (of the form all As are B). As explained later (in the section ‘Three levels of understanding the structure of proofs’), there are different levels at which students understand this structure. Therefore, an important task for teachers is to use effective strategies to improve their students’ understanding in order to overcome the difficulties in learning proof.

Thus, the central research question that this research addresses is as follows: In proof classes, what students’ and teachers’ proof-production strategies emerge during lessons from the viewpoints of levels of understanding about proof structure?

To answer this question, we first contextualise the strategies for producing proofs that correspond to each level of understanding of the evidential structure. We call these level-specific strategies. We then use analytical coding to analyse two grade 8 junior high school proof lessons for Japanese students aged 13–14, and the results of a test that the students took after the lesson sequence. We identify level-spanning proof-production strategies as those strategies encompassing different levels of understanding about the proof structure. Finally, we argue that level-spanning proof-production strategies are based on the idea of combining strategies for different levels of understanding, which has not been considered in previous studies, and that these strategies are effective in improving students’ levels of understanding in proof teaching.

2. Theoretical framework

The main ideas for our theoretical framework are the understanding of the structure of deductive proofs and the level-specific proof-production strategies. The former has been previously introduced, and its use is illustrated in a series of papers, including Miyazaki et al. (2015), Miyazaki, Fujita, and Jones (2017), Miyazaki, Fujita, Jones, and Iwanaga (2017), and Fujita et al. (2018). The latter has developed a teaching tool to support strategies for constructing/reconstructing proofs (Miyazaki et al., 2019). In this paper, we extend this framework to characterise proof-production strategies that enhance students’ understanding of the proof structure.

2.1. Three levels of understanding of the structure of proofs

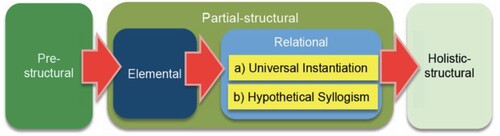
A deductive proof has a logical network of singular and universal propositions between premises and conclusions, connected with universal instantiation (which derives a singular proposition from a universal proposition) and hypothetical syllogism (which logically connects singular propositions to bridge the premises, intermediate propositions, and conclusion); we call this the structure of proof. Among many other factors that complicate the understanding of proofs (e.g. Moore, 1994), we focus on the logical relations within proofs (e.g. Duval, 2002). The following three levels of understanding have been proposed and reviewed for the structure of deductive proofs (Miyazaki, Fujita, & Jones, 2017), as shown in Figure 1:

• Pre-structural: The basic status in relation to an understanding of proof structure, where learners view proofs as a kind of ‘cluster’ of possibly symbolic objects.

• Partial-structural: Once learners have begun to pay attention to the individual elements, they are at the partial-structural elementary sub-level. To reach the next sub-level, learners need to recognise some relationships between these elements (e.g. universal instances and syllogism). Suppose learners have started paying attention to each relationship. In that case, we consider them to be at the partial-structural relational sub-level, with this sub-level being further divided into (a) universal instantiation and (b) syllogism (see Figure 1).

• Holistic-structural: At this level, learners understand the relationships between singular and universal propositions and can see a proof as a ‘whole’ in which premises and conclusions are logically connected by universal instantiation and hypothetical syllogism.

Figure 1. Framework of understanding of the structure of deductive proofs (source: Miyazaki, Fujita, & Jones, 2017)

Previous research used this framework to illustrate why some students accept proofs with logical circular reasoning (Miyazaki, Fujita, & Jones, 2017), how teachers support student learning (Miyazaki et al., 2015), and the design of a web-based learning platform to support students’ understanding of proofs (Miyazaki, Fujita, Jones, & Iwanaga, 2017).

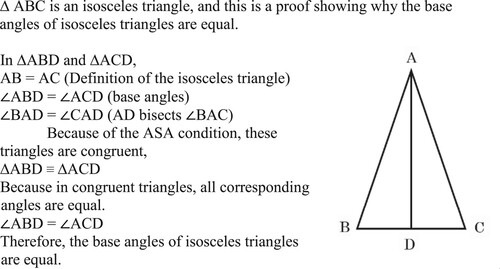
To illustrate the framework for understanding the structure of deductive proofs, consider that students can accept the proof shown in Figure 2.

Figure 2. Proof with a logical circularity

The proof shown in Figure 2 contains logical circularity because the conclusion ∠ ABD = ∠ ACD is used as an assumption. That some students may accept this as a correct proof can be explained by the fact that students’ understanding is at the partial-structural relational sublevel (as shown in Figure 1) because their understanding of the hypothetical syllogism is insufficient; that is, they do not understand how propositions can be logically bridged by the hypothetical syllogism (Miyazaki, Fujita, & Jones, 2017; see also Heinze et al., 2008).

2.2. Level-specific proof-production strategies

While students need an understanding of the structure of proofs when constructing and reconstructing them, they also need domain-specific knowledge (Chinnappan et al., 2012; Fujita et al., 2020) such as statements about triangles, congruence, parallel lines, and so on. Moreover, they need to be able to plan proofs carefully (e.g. Polya, 1945), monitor and control their thinking (e.g. Schoenfeld, 1985), use different mathematical representations (e.g. Weber & Alcock, 2009), etc. Among these factors for successfully constructing (and reconstructing) proofs, strategic knowledge plays an important role for students to ‘recall actions that are likely to be useful or to choose which action to apply among several alternatives’ (Weber, 2001, p. 111).

We focus on students’ construction and reconstruction of proofs in the context of geometry (especially congruent triangles), one of the topics frequently found in the school mathematics curriculum. When constructing proofs, students use a given condition to derive a conclusion: for example, when they want to prove that the opposite sides of a parallelogram are equal. Reconstructing proofs entails proving activities in which students create new proofs based on already completed proofs (such proofs may be incorrect ones), such as replacing one of the assumptions or using different theorems. Both constructing and reconstructing proofs are valuable because these activities make proofs more exploratory (Miyazaki et al., 2015) as students establish propositions, produce proofs (planning and constructing), and look back (examining, improving, and developing).

Previous work (Miyazaki et al., 2019; see also studies such as Anderson et al., 1995; Heinze et al., 2008; Schoenfeld, 1985; Zazkis et al., 2015) has shown that the following types of strategic knowledge are particularly relevant when working on deductive proofs:

• Strategic knowledge for constructing proofs (SKC): distinguishing between conclusions and assumptions, deciding on a method of proof, either by thinking backwards from a conclusion to an assumption, or by thinking forwards in the opposite direction.

• Strategic knowledge for the reconstruction of proofs (SKRc): checking the assumptions (definitions, axioms, etc.) and validity of the theorems used in the reconstruction of proofs and organising the elements of proofs to overcome any errors.

Both SKC and SKRc are based on Zazkis et al.’s (2015) ‘directed strategy’ of ‘understanding the task well, using that understanding to see why the result is true, and then formalising that understanding’ (p. 24). SKC is required to construct a proof from a problem, while SKRc is required to construct an alternative proof from the original proof. This latter process of deriving an alternative proof from the original proof corresponds to the ‘strategic use of examples’ (Zaslavsky, 2019, p. 269), as it involves the notion of multiple proofs that can be constructed from the original proof.

SKC and SKRc are notable for being generic instead of appertaining to certain problem-specific properties. These forms of knowledge can be used by students to produce proofs and by teachers to model/demonstrate proofs at any of the three levels of understanding of proof structures shown in Figure 1.

Once at the elemental sub-level (within the partial-structural level), students can grasp singular propositions as elemental aspects of proofs. Thus, at this level, one useful strategy for constructing proofs would be to find or modify the problem-specific properties (e.g. AB = AC in the proof in Figure 2). Further, students at this level may make successive connections between the problem-specific properties without reference to a universal proposition (such as a theorem). Thus, another strategy for constructing proofs would be to find or change the sequence of the problem’s properties (e.g. ΔABD ≡ ΔACD, then ∠ABD = ∠ACD in the proof in Figure 2).

At the relational sub-level (also within the partial-structural level), students grasp universal instantiation and hypothetical syllogisms as relational aspects of proofs. Thus, at this level, one useful strategy for constructing proofs is to find or modify a universal proposition (such as a theorem); another is to find or change the sequence for applying the universal proposition (if the universal proposition is the Side-Angle-Side Theorem: SAS → The two triangles are congruent). In the case of reconstruction proofs, changing the selected universal proposition to the more appropriate one and changing the sequence is useful.

Once the holistic level has been reached, students can grasp the logical network of singular and universal propositions. Thus, at this level, a useful strategy for constructing proofs is to clarify or review/change the premise(s) and conclusion of the proof to avoid circular logic. In the case of reconstruction proofs, reconsidering or modifying them is useful. Another strategy is to formulate or reorder the direction of the construction of the whole proof, from the conclusion to the premise(s) or from the premise(s) to the conclusion after deciding the premise(s) and the conclusion(s).

The strategies presented so far are organised as codes in Table 1 shown in Methodology to analyse the data from the lessons and tests. As far as the pre-structural level is concerned, we are concentrating here on the elementary sub-level (within the partial-structural level) and beyond it.

Table 1. Coding for proof-production strategies

Level of understanding		SKC	SKRc
Holistic-structural		C1: Find the premise and conclusion	Rc1: Review/modify the premise and conclusion
		C2: Formulate the proof (conclusion to premise/premise to conclusion)	Rc2: Reorder the proof (conclusion to premise/premise to conclusion)
Partial-structural	Relational	C3: Find the sequence for applying the theorem (e.g. congruence condition → property of congruent shape)	Rc3: Change the sequence for applying the theorem (e.g. congruence condition → property of congruent shape)
		C4: Identify the potentially applicable theorem (e.g. congruence condition)	Rc4: Modify the potentially applicable theorem (e.g. congruence condition)
	Elemental	C5: Find the sequence of the problem’s properties	Rc5: Change the sequence of the problem’s properties
		C6: Identify the problem-specific properties (e.g. AB = AC)	Rc6: Modify the problem’s properties (e.g. AB = AC)
Pre-structural		None	None

2.3. Teachers’ scaffolding for students’ use of strategies

Schoenfeld (1985) argued that simply describing the strategies themselves does not give students enough information; one must also show students how to use them. That is, it is necessary to create prescriptive and descriptive versions of the strategies. Prescriptive versions are particularly important in non-routine problem solving. Teachers’ scaffolding is likely to make students’ proof-production strategies more prescriptive.

Students acquire a variety of strategies for proof production in their daily lessons. Some of these are prescriptive of students’ learning situations, while others are not. In addition, as students make progress in their studies, they need to acquire more sophisticated strategies. Therefore, teachers’ coaching and articulation or students’ reflections are necessary to enable students to acquire and use appropriate proof-production strategies according to their learning situation (Brown et al., 1989; Nunokawa, 2005), and teachers incorporate them in their lessons intentionally or unintentionally.

Teachers’ coaching and articulation or students’ reflections in the classroom are a result of the teachers’ eagerness and desire to support the students’ production of proofs. In particular, the proof-production strategies that students can use vary depending on their level of understanding of the proof structure, as mentioned earlier. Thus, it is essential that teachers support students cognitively, technically, and affectively to enable them to use higher-level strategies in the classroom (Sharma & Hannafin, 2007; Yelland & Masters, 2007). In providing such support, it is assumed that teachers may demonstrate proof-production strategies, encourage students to use such strategies, and repeat, reflect, strengthen, and amplify them, depending on the students’ understanding of proof structure. Eventually, teachers should also assume that such scaffolding will no longer be needed (Rittle-Johnson & Koedinger, 2005, p. 342).

Elia et al. (2009) distinguished between flexibility and adaptivity as follows: ‘The term “flexibility” is primarily used to refer to using multiple strategies and switching between them, while the term “adaptivity” emphasises the ability to consciously or unconsciously select and use the most appropriate approach for solving a certain mathematical item or problem, by a particular person, in a given socio-cultural context (p. 606). It is expected that the teachers’ scaffolding will improve the flexibility and adaptability of students’ proof-production strategies. Thus, this study focuses on the use of proof-production strategies by teachers, in addition to students, in the classroom. In particular, this study will code the proof-production strategies of teachers and students that appear during the process of understanding the problem, sharing the prospect of a solution, and discussing individual problem-solving, as the teachers’ scaffolding.

3. Methodology

3.1. Classes and tests

In Japan, deductive proof is explicitly taught in geometry in Grade 8 (students aged 13–14) in junior high schools. Several studies have described current approaches to geometry teaching (Miyakawa, 2017; Miyazaki, Fujita, Jones, & Iwanaga, 2017; Shinno et al., 2018). Described below are the content and time allocated to geometry teaching for Grade 8 (34 lessons on the topic ‘geometry’). The course generally runs from mid-October to mid-January.

The contents include:

• How to investigate geometric shapes: parallelism and congruence (10), meaning and method of proof (4), summary (2)

• Properties of geometric shapes and learning to prove: properties of triangles (7), properties of squares (9), summary (2)

For our study we examined two data sets. The first data set consists of observational data from two Grade 8 classes (each with 40 students) at a junior high school affiliated to a national university. The classes ran from 21 to 26 November 2017. The results of the periodic tests indicated that both classes had similar mathematical attainments. No attainment differences were observed in terms of proof construction between the classes prior to the topic of geometry.

One class was taught by a teacher with 20 years of experience in teaching mathematics (Teacher A), while the other class was taught by a teacher with less than 2 years of experience (Teacher B). They shared the same lesson plan, but it is expected that there will be commonalities and differences in how the two teachers deliver their lessons (Webel & DeLeeuw, 2016). The aim is to identify them in strategies emerged in the classroom that have a certain impact on students’ understanding of the proof structure, irrespective of teachers’ competence and experience. The commonalities will increase the generality of the strategies, and the differences will have effective usage of the strategies to improve students’ understanding of proof structure. Based on this analysis we recommend that the strategies identified in the conclusion of this study be actively used by teachers in the long-term teaching of proofs as students’ levels of understanding increase. This is both a confirmation of the conclusions and a further development of the study.

We focused on the first two hours of four hours of course content on the properties of geometric shapes and how to prove them. The learning goals of each hour-long lesson were as follows:

• First lesson: construction of several ‘flowchart’ proofs using a triangle congruence condition and summary of ‘mathematical thinking’ (called ‘tips’ by the teacher) for constructing the proofs. During the lesson, ‘pen-ended problems’ were used, which ‘allow learners to construct multiple solutions by making the necessary assumptions and intermediate propositions to derive a particular conclusion’ (Miyazaki et al., 2015, p. 1216) as these support students’ construction and reconstruction of proofs.

• Second lesson: constructing a flowchart proof using a triangle congruence condition and the properties of geometrically congruent figures, constructing an alternative proof based on the original proof, and summarising the mathematical thinking (as tips) for constructing the alternative proof.

• Third and fourth hours: producing a ‘paragraph’ proof based on the flowchart proof.

Our reason for focusing on the first two hours of the course was Japan’s approach to proof teaching. Before Grade 8, students are gradually introduced to deductive proof in a non-geometric context. In the first two of the four lessons of geometry in Grade 8, students begin to apply their knowledge in a geometric context, so that by the end of Grade 9 they have begun to deductively investigate the properties of geometric shapes. In this gradual progression, the first two lessons of the four-hour content are a critical point, as the actions the teacher uses during this proof teaching play an important role and significantly influence future teaching and learning.

The second data set is from the test (shown in Appendix A), which was completed by the students in each class after the total 34 proof lessons (on 25 January 2018 for one class and 26 January 2018 for the other class). The strategies seen in the classroom observation data are mainly those expressed by teachers, while the strategies seen in the test data are those expressed by students. These two datasets are necessary to grasp the strategies of the teachers and those of the students and the relationship between the two. The test was administered to 39 students in teacher A’s class and 30 students in teacher B’s class. In the test, students were tested on the material they had learnt in the two lessons by constructing a flowchart proof in an open problem situation, reconstructing it by changing theorems and/or geometric properties, and repeating this reconstruction two more times, ending up with a total of four different proofs. Between the constructions of each flowchart proof were boxes on the test paper where students were asked to write down their ‘tips’ for how they transformed one proof into another.

All students were able to construct the four proofs correctly. This may seem obvious, since the students had been working for a long time on a series of proofs teaching until just before the test. However, the boxes for describing how to convert one proof into another were left blank by a number of students in Teacher B’s class. The recorded student tips are examined as data in the Results section below.

3.2. Data coding

As explained above, strategic knowledge for (re)constructing proofs (SKC and SKRc) can be specific to a particular level of understanding of the proof structure (Figure 1). On this basis, the codes shown in Table 1 were configured to analyse both data sets, from the lessons and the tests.

The analysis of the classes was carried out in several steps. After establishing the protocol for filming the two-hour lesson, three researchers from the field of mathematics education, working separately, coded the proof-production strategies that appeared in the lesson protocols. Direct teacher instructions and teacher–student interactions were counted as SKC/SKRc made explicit by teachers during the lessons. Strategies voiced by individual students were not counted as these strategies were not intended to be demonstrated by teacher A/B and learned by students in the classroom. The procedure for analysing the test response took only the codes of strategic knowledge for reconstructing proofs (SKRc), because the tips that the students wrote when reconstructing the proof were analysed in the test.

In the cases where the coding of the lessons differed, the researchers looked at the video footage and decided together on the appropriate code. We assigned a single code for the cases where a single strategy was used to (re)construct a proof. Multiple codes (e.g. C4 and C6) were assigned when more than one strategy was mentioned for the same objects (universal or singular propositions) of the proof in one statement separated by a protocol. When counting the number of strategies, two or more codes assigned to multi-strategies were counted as one strategy.

The procedure for analysing the test results followed similar steps. The three researchers coded the answers students gave in the three sections of the test sheet to describe how they rearranged one proof into another. The coding method was the same as for the analysis of the lesson content. Particular attention was paid to ensuring consistency between the class coding and test coding; all data were reviewed and checked for congruence multiple times, with codes being modified as necessary to achieve consensus.

4. Results

In reporting the findings, we use the codes for the proof-production strategies, C1-6 and Rc1-6, as laid out in Table 1. To address our research question, we exemplify, as noted in our methodology, the ways in which differences in the strategies that emerged in the two classrooms affected the students’ level of understanding (in the class and in their test results).

4.1. Strategies that emerged in lessons

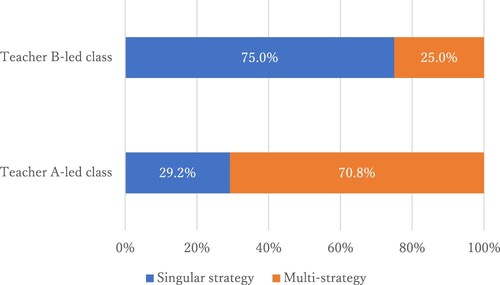
The proof-production strategies in each class, summarised in Table 2 and Figure 3, showed two differences when the lessons led by teacher A were compared with those led by teacher B:

• Teacher A-led lessons featured three times as many strategies as Teacher B-led lessons.

• In Teacher B-led lessons, singular strategies were deployed in 75% (6/8) of cases. By contrast, in Teacher A-led class, multiple strategies (multi-strategies) were deployed in 70.8% (17/24) of cases.

Figure 3. Percentage of proof-production strategies featuring in each class

Table 2. Proof-production strategies featuring in each class

Class	Teacher A-led class	Teacher B-led class
Number of strategies	24	8
Singular strategy	7	6
Multi-strategy	17	2

Thus, multi-strategy was more prevalent in the lessons led by Teacher A than in those led by Teacher B.

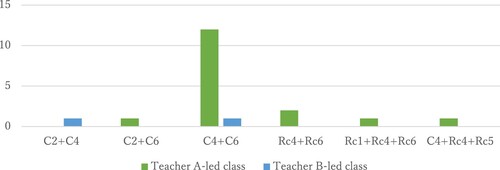
In terms of the numbers of proof-production strategies that featured in each class, shown in Table 3 and Figure 4, the following inter-class differences were found regarding the multi- strategies:

• All observed multi-strategies belonged to proof-production strategies.

• The Teacher A-led class featured 8.5 times as many multi-strategies as the Teacher B-led class.

• Of the multi-strategies featuring in the Teacher A-led class, 70.6% (12/17) combined C4 (identify potentially applicable theorem) and C6 (identify the problem-specific properties [e.g. AB = AC]).

• Of the multi-strategies featured in the Teacher A-led class, 82.4% (14/17) combined either:

  1. C4 (identify potentially applicable theorem) and C6 (identify the problem-specific properties [e.g. AB = AC]), or

  2. Rc4 (modify potentially applicable theorem) and Rc6 (modify the problem’s properties).

Figure 4. Number of multi-strategies featuring in each class

Table 3. Multi-strategies featuring in each class

	C2 + C4	C2 + C6	C4 + C6	Rc4+Rc6	Rc1 + Rc4+Rc6	C4 + Rc4+Rc5
Teacher A-led class	0	1	12	2	1	1
Teacher B-led class	1	0	1	0	0	0

These are interesting findings in light of the level of understanding (about proof structure) embodied by the multi-strategies. Given that C2 and R1 exemplify the holistic-structural level, C4 and Rc4 exemplify the relational sub-level, and C6, Rc5, and Rc6 exemplify the elementary sub-level, it was much more likely that the multi-strategies used in the class led by Teacher A spanned different levels of understanding in the class than the class led by Teacher B. The strategies used in the class led by Teacher B were not the same. Many of the strategies spanned the relational and elementary sub-levels in particular.

4.2. Strategies that emerged in tests

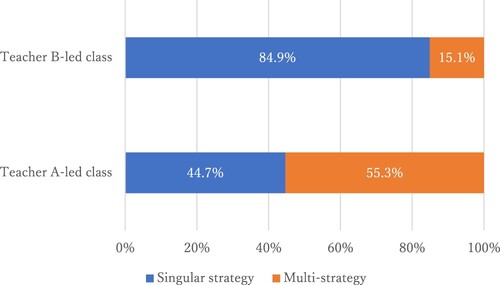
When analysing the two test series (for the pupils in the class led by teacher B and teacher A, respectively), the following differences were found (see Table 4 and Figure 5):

• Test responses featuring a singular strategy were almost three times more prevalent among the Teacher B-led class students than among those taught by Teacher A.

• Conversely, answers containing a multi-strategy were almost three times more frequent in the test answers of students taught by teacher A than in the test answers of students taught by Teacher B.

Figure 5. Percentage of proof-production strategies featuring in the test responses

Table 4. Proof-production strategies featuring in the test responses

Class	Teacher A-led	Teacher B-led
Respondents	30	39
Number of strategies	103	106
Singular	46	90
Multi	57	16

Thus, multi-strategy was more prevalent in the test responses of students taught by Teacher A compared with the test responses of students taught by Teacher B.

With regard to the students’ strategy combinations, which are summarised in Table 5 and Figure 6, the following differences were found between the classes:

• All identified multi-strategies belonged to proof-production strategies.

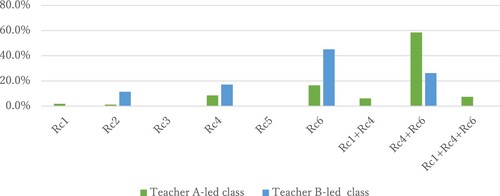
• The combination Rc4 + Rc6 featured more than twice as much in the test responses of students taught by Teacher A compared with those of students taught by Teacher B.

• The combinations Rc1 + Rc4 and Rc1 + Rc4 + Rc6 featured in some of the test responses of students taught by Teacher A (6.1% and 7.4%, respectively) but not in any of the test responses of students taught by Teacher B.

• Rc4 featured around twice as much in the test responses of students taught by Teacher B compared with those of students taught by Teacher A.

• Rc6 featured around three times as much in the test responses of students taught by Teacher B compared with those of students taught by Teacher A.

• No test responses of students taught by Teacher B showed the use of Rc1 as a part of a multi-strategy.

• No student of either class used Rc3 or Rc5 as a part of a multi-strategy.

Figure 6. Percentage of proof-production strategies observed in the test responses

Table 5. Proof-production strategies observed in test responses

	Rc1	Rc2	Rc3	Rc4	Rc5	Rc6	Rc1+Rc4	Rc4+Rc6	Rc1+Rc4+Rc6
Teacher A-led class	3	2	0	14	0	27	5	48	4
Teacher B-led class	0	14	0	21	0	55	0	16	0

As an example of a student’s response coded to ‘Rc1 + Rc4 + Rc6’, student (‘KO’) gave the following response concerning how they constructed Proof 2 from Proof 1 (see Figure 7): ‘Insofar as the proof cites BD, it cannot cite ∠ABD; therefore, the congruence condition must be SAS, with BD as one of the pairs of sides of equal length’. KO argued that using the premise BD = DB (the premise that the overlapping pair of sides are equal in length) would preclude the use of the premise ∠ABD, as that would assume the conclusion. Accordingly, KO identified the only possible congruence condition as Side-Angle-Side (two pairs of sides of the two triangles are equal in length, and the included angles are equal in measurement). KO misunderstood the conclusion as ‘∠ABD = ∠CBD’ (judging from the equiangular symbols they drew on the figure). For this reason, KO avoided citing ∠ABD, believing that this would beg the question. Then, marking a change from the previous proof, KO invoked SAS because this congruence condition works with the premise BD = DB. In turn, KO replaced the proposition AB = CB with ∠ABD = ∠CBD. Thus, in their response, KO used a multi-strategy combining Rc1 (review/modify the premise and conclusion), Rc4 (modify the potentially applicable theorem), and Rc6 (modify the problem’s properties).

Figure 7. Student KO’s test response

4.3. Emergence of combinations of proof-production strategies in lessons

To illustrate how the combinations of proof-production strategies emerged, we show a scene from a lesson by Teacher A.

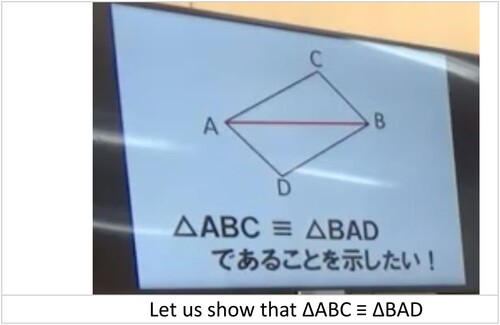
The lesson was the first of the four hours on the ‘meaning and method of proof’. The goal for the first lesson was as follows: ‘In the spaces provided, construct multiple flowchart proofs using triangle-congruence conditions, and summarise the mathematical idea (tips) for constructing the proofs’. During the lesson, Teacher A presented the problem on the blackboard (see Figure 8): ‘Which pairs of sides/angles should we cite to prove ΔABC ≡ ΔBAD?’ The teacher then discussed the prospects for resolving the problem, eventually sharing the idea of invoking a triangle-congruence condition. Then, Teacher A presented the next challenge: ‘Prove ΔABC ≡ ΔBAD by referring to the appropriate pairs of sides/angles and then relating them to the condition of congruent triangles’. The students then used the worksheet’s five spaces for flowchart proofs (see Appendix A) to state the pairs of sides/angles forming the premises, the relevant condition of congruence, and properties of the triangles. All students managed to construct at least four kinds of proofs.

Figure 8. Scene from the first hour of the unit

After a tour of the classroom to observe the students’ progress, Teacher A selected five students to present their answers in turn. The answers of the first four students to the congruence conditions were as follows (see Figure 9).

1. ‘Three pairs of sides are equal in length’ (Side-Side-Side).

2. ‘Two pairs of sides of the two triangles are equal in length, and the included angles are equal in measurement’ (Side-Angle-Side).

3. ‘Two pairs of angles of the two triangles are equal in measurement, and the included sides are equal in length’ (Angle-Side-Angle)

4. ‘Two pairs of sides of the two triangles are equal in length, and the included angles are equal in measurement’ (Side-Angle-Side).

Figure 9. Students’ work presented on the blackboard during the first-hour lesson (Teacher A-led class)

While Students 2 and 4 both used Side-Angle-Side as the congruence-condition, their answers differed in respect to the other pair of sides and the included angle. Nevertheless, both cited using AB = BA as one of the two pairs of sides. Indeed, in completing their proofs, all four students postulated that AB = BA (a proposition that was self-evident at the figure) as a tentative condition of congruency. It was evident that the structure of the proofs constructed by these four students was expected by Teacher A.

Then came the turn of Student 5 to present (line 95). As the student read out the answer, Teacher A transcribed the answer into a space on the flowchart proof attached to the blackboard, at which point the other students gasped in surprise. Teacher A, likewise, did not hide his surprise at the student’s answer (lines 96, 97).

―――

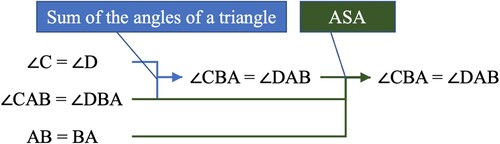
95 S If angles CAB and DBA are equal, sides AB and BA are equal, and angles C and D are equal, then, given that the sum of a triangle’s interior angles is always 180, angles CBA and DAB must be equal too. Thus, one pair of sides, and the two pairs of angles that form them, must be equal.

96 S (Gasp of surprise)

97 T What do you mean? What do you mean?

―――

Teacher A then remarked that the student’s answer seemed to miss the Angle-Side-Angle condition (lines 98–100). The student replied by arguing that ∠C = ∠D must entail ∠CBA = ∠DAB, given that the sum of a triangle’s internal angles is 180° (line 101). Teacher A then sanctioned the student’s idea (lines 102–103, 105–106) and checked whether the class understood the three pairs of items that should be cited when invoking the condition (line 107).

―――

98 T But it looks like these conditions don’t match the congruence condition (ASA).

99 T They don’t correspond to the condition of congruence.

100 T You’re saying that it implies congruence nonetheless?

101 S The interior angles of a triangle add up to 180°. On this basis, we can say that if angles C and D are equal, angles CAB and DBA must be equal too. So, if these two pairs of angles are equal, one pair of sides (the pair of sides formed by the two pairs of angles) must be equal too.

102 T Did everyone see what he was thinking?103 T The sum of the angles of a triangle is 180°. So, using this proposition, which pairs of things can we conclude are equal?104 S We can conclude that angles CBA and DAB are equal.

105 T Right, so you ultimately concluded that these here are equal.

106 T OK, did everyone get that?

107 T Now then, if we use this congruence condition, what three pairs of items should we cite?

108 T Which pair of sides?

109 (Students en masse) AB equals BA.

110 T That’s right. (Draws a circle around AB = BA on the blackboard to indicate that it is correct)

111 T Now, find one of the pairs of angles.

112 (Students en masse) Angles CAB and DBA.

113 T Angles CAB and DBA, right. What is the third pair?

114 (Students en masse) Angles CBA and DAB.

115 T That’s right. So [Student 5] didn’t write down all three of them here, but they are all present by implication.

―――

In the above exchange, Student 5 postulated that ∠C = ∠D implies ∠CBA = ∠DAB, citing the universal proposition that the sum of the angles of a triangle is always 180° (line 101). Teacher A then checked what the student had derived from the universal proposition (line 103), and the student answered that it was the equality of angles CBA and DAB (line 104). Teacher A then asked the whole class to find the pair of sides and the two pairs of angles that should be cited when using the universal proposition Angle-Side-Angle (line 107). The students gave the answers (AB = BA, ∠CBA = ∠DAB, ∠CAB = ∠DBA), and the teacher wrote the answers on the blackboard (lines 109–115). (See Figure 10)

In the above scene, the two universal propositions (the sum of the angles of a triangle = 180° and angle-side-angle) were not simply quoted, but instantiated. To facilitate this universal instantiation, Teacher A repeatedly checked whether the student had understood the equivalences (singular propositions) that were to be quoted in the problem in question and what further equivalence (singular proposition) they entailed. In this way, Teacher A treated the two universal propositions as logical connectives to be applied to the singular propositions of the problem in question. Indeed, Teacher A used combinations of proof-production strategies consisting of the relational sub-strategy ‘Identify the potentially applicable proposition’ and the elementary sub-strategy ‘Identify the problem-specific properties’.

Figure 10. Student 5’s idea emerged in the interaction with the teacher

5 Discussion

In our findings, we have illustrated how the combinations of proof-production strategies emerged during the lessons and show that the combinations of proof-production strategies were more prevalent in the lessons led by Teacher A than in the lessons led by Teacher B. Moreover, the combinations used by students led by teacher A were much more likely to be used than those used by students led by teacher B. We now discuss the characteristics of the combinations of proof strategies and their effectiveness for teaching proofs.

5.1. Level-spanning proof-production strategies

Through classroom observation and test analysis, proof-production strategies were identified that combined proof strategies at different levels of understanding. We call these strategies ‘Level-spanning proof-production strategies’. The fact that the level-spanning proof production strategies were identified in both Teacher A's and Teacher B's classes suggests that this strategy is a common one in proof classes.

Regarding proof-production strategies, a number of previous studies already have identified different strategies (Miyazaki et al., 2019; see also studies such as Anderson et al., 1995; Schoenfeld, 1985; Weber, 2001; and Zazkis et al., 2015). They include a strategy that starts from the premise to the conclusion, or from the conclusion to the premise (Heinze et al., 2008). There are also strategies that are closely related to the knowledge of geometry, such as one that alternates among the three congruence conditions for triangles (Chinnappan et al., 2012). In contrast, this study organises strategies based on students’ level of understanding. By analysing the class lessons, the study points out that the teachers combine the strategies that students can actually use with strategies that require a higher level of understanding of proof structure. Such a combination of strategies based on the level of understanding of proof structure has not been addressed in previous studies.

Strategic knowledge for constructing proofs (SKC) and Strategic knowledge for reconstructing proofs (SKRc) are essential for making the learning of proofs exploratory (Miyazaki et al., 2015). In particular, SKRc is used to produce alternative proofs using the ORIGINAL proofs as examples (Zaslavsky, 2019, p. 269). Activities to construct proofs as well as updating and remaking proofs are needed in various situations, and the possibilities and accuracy of these activities strongly depend on the students’ understanding of the proof structure. Level-spanning proof-production strategies comprise identifying SKCs and SKRc in accordance with the level of understanding of the proof structure (Miyazaki, Fujita, & Jones, 2017) and combining them across multiple levels (e.g. elementary/relational sub-level). Therefore, when using level-spanning proof-production strategies, students are able to grasp the structure of the original proofs in accordance with their level of understanding, and on the basis of this structure, they can also see what is needed to move to a higher level of understanding. In this way, it is strongly expected that making use of level-spanning proof-production strategies in proof lessons explicit will ensure that students’ understanding of the structure of proofs will be further enhanced.

Moreover, the idea of level-spanning strategies is not limited to the teaching of proofs but may potentially exist in a wide range of effective teaching. Perhaps level-spanning strategies are gradually developed as the lesson progresses, involving higher-level strategies, and teachers may have tacit knowledge of them. If this is the case, the identification of level-spanning strategies in different types of teaching, and their long-term development, would be of significant academic value.

5.2. The effectiveness of level-spanning proof-production strategies for teaching proofs

There is abundant literature on the strategies needed to produce proofs. Previous studies have also identified some effective strategies in proof constructions (e.g. Weber & Alcock, 2009; Zazkis et al., 2015). However, a problem with existing literature is that the levels of understanding required for the strategies are not specified. This means that even if a strategy is described by the teacher, the students will struggle to use the strategy if they lack the requisite level of proof-structure understanding; likewise, a teacher would struggle to teach the strategy to the students in such a case.

Regarding the use of the level-spanning proof-production strategies, it is necessary to integrate the higher-level strategy appropriately with the lower-level one. The individual, level-specific proof-production strategies (as described in the section ‘Level-specific proof-production strategies’) required ‘adaptability’ in that students had to choose strategies that were compatible with their level of understanding. Alternately, level-spanning proof-production strategies involved ‘flexibility’ (Elia et al., 2009) insofar as the students combined higher-level strategies on the basis of lower-level strategies that they could understand to enhance their level of understanding about proofs.

In order to allow the flexibility of level-spanning proof-production strategies to work, we can recommend an approach for teachers to use proof-production strategies in their proof classes: teachers can encourage their students to use proof-production strategies that consist of a strategy that is immediately above the student’s current level of understanding and a strategy that the student has already mastered. For example, for students who are currently at the elementary sub-level, the teacher can encourage the use of proof-production strategies that include the relational and elementary sub-levels. For students currently at the relational sub-level, the teacher can encourage using proof-production strategies encompassing holistic- and partial-structural levels (the relational and elemental sub-levels). This approach can result in a steadily increasing learning progression over time, where students can move up the levels of understanding of the proof structure.

Comparing Teacher A’s and Teacher B’s classes, it appears that the more level-spanning proof-production strategies emerged in the class, the more students expressed these strategies in their tips on the test. This suggests that level-spanning proof-production strategies can improve students’ understanding of proof structure. Moreover, using a universal proposition in this way leads to an understanding of universal instantiation and the hypothetical syllogism, both of which belong to the relational sub-level of understanding proof structure.

On this basis, we suggest that the use of level-spanning proof production in the classroom enhances students’ understanding of the structure of proof. To give an example, proof-production strategies that span the holistic and partial levels of structure enable students to move from the partial to the holistic level of structure. In particular, such proof-production strategies require students to use universal propositions while distinguishing the premise from the conclusion and (re)formulating the proof from the conclusion to the premise(s) or from the premise(s) to the conclusion; it is actions like these that enable students to see proofs as structural objects. Indeed, the results of this study show that if the trend shown in the above persists over time, it is reasonable to expect that the Teacher A-led class would increasingly feature proof-production strategies exemplifying the holistic- and partial-structural levels and that the Teacher B-led class would increasingly feature singular strategies exemplifying the holistic-structural level.

Thus, it may be effective for teachers to provide scaffolding by demonstrating level-spanning strategies and encouraging students to use them so that the students will be able to use proof-production strategies that require a higher level of understanding by teachers’ coaching and articulation or students’ reflections (Brown et al., 1989; Nunokawa, 2005). This scaffolding makes level-spanning proof-production strategies more prescriptive for students and makes them more aware of their use (Schoenfeld, 1985). However, teachers cannot provide hands-on assistance forever since the ultimate goal is for students to be able to use the proof-production strategies on their own. For this reason, teachers need a long-term teaching design to transform the scaffolding in stages. The teachers need to gradually weaken the scaffolding and eventually remove it so that students will be able to use higher-level strategies by themselves (Rittle-Johnson & Koedinger, 2005, p. 342).

6. Conclusions

From the evidence we provide in this paper and the answer to our research question, we can conclude that in proof classes, level-spanning proof-production strategies emerge through teacher–student interactions, from the point of view of levels of understanding of the proof structure. These level-spanning proof-production strategies emerged in the classrooms taught by Teacher A and Teacher B.

The above discussions and conclusions are based on data from the two observed classes and students’ tests and cannot be over-generalised. In particular, the test was carried out two months after the two lessons that were the subject of the lesson observations, but immediately after the end of 34 consecutive lessons. Therefore, further tests are needed to determine, in the long term, whether the students are able to express level-spanning proof-constructing strategies.

We have argued that level-spanning proof-production strategies are key to improving students’ understanding of proof structures. In the section titled ‘Level-spanning proof-production strategies’, we proposed the approach of combining higher- and lower-level strategies depending on the complexity of the proof structure. This approach has not been consciously implemented in the usual proof teaching, and we believe it is an effective method for teaching proof structure. We have also found that this approach is tacitly used by teachers (and perhaps tacitly imitated by their students). This approach, then, cannot be replicated by some teachers simply by having them observe lessons in which level-spanning proof-production strategies emerge. Further, we suspect that a teacher who has a greater knowledge of ‘situations for proving’ (Stylianides & Ball, 2008, p. 311) might tacitly understand when to mobilise opportunities for level-spanning proof-production strategies to achieve a steadily increasing progression of learning over long-term proof teaching. If so, the implication of our study is that the following two approaches are central to mathematics teacher education: the introduction of proof-structure-spanning proof-production strategies and their use to achieve a steadily increasing learning progression throughout the process of teaching proof.

A number of questions still remains unanswered. First, it is still not clear that the use of level-spanning proof-production strategies encompassing the relational- and elemental-structural levels enable a wider range of students to understand proof structure at the relational-structural level in proof classes. We also do not have a clear answer for a question how the use of level-spanning proof-production strategies encompassing the holistic- and partial-structural levels enable a wider range of students to understand proof structure at the holistic-structural level. Finally, studying how teachers progressively escalate the sophistication of the level-spanning proof-production strategies over the long course of proof teaching to enhance students’ levels of understanding about proof structure is also something we would like to undertake in our future research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by Grant-in-Aid for Scientific Research, Ministry of Education, Culture, Sports, Science, and Technology, Japan: [Grant Number No. 16H03057, 20H00098, 20H01675, 20H00092].