Effective hamiltonian of crystal field method for periodic systems containing transition metals

Abstract

Effective Hamiltonian of Crystal Field (EHCF) is a hybrid quantum chemical method originally developed for an accurate treatment of highly correlated d-shells in molecular complexes of transition metals. In the present work, we generalise the EHCF method to periodic systems containing transition metal atoms with isolated d-shells, either as a part of their crystal structure or as point defects. A general solution is achieved by expressing the effective resonance interactions of an isolated d-shell with the band structure of the crystal in terms of the Green's functions represented in the basis of local atomic orbitals. Such representation can be obtained for perfect crystals and for periodic systems containing atomic scale defects. Our test results for transition metal oxides (MnO, FeO, CoO, and NiO) and MgO periodic solid containing transition metal impurities demonstrate the ability of the EHCF method to accurately reproduce the spin multiplicity and spatial symmetry of the ground state. For the studied materials, these results are in a good agreement with experimentally observed d-d transitions in optical spectra. The proposed method is discussed in the context of modern solid state quantum chemistry and physics.

GRAPHICAL ABSTRACT

Keywords:

• Transition metals
• strongly correlated systems
• optical spectra
• quantum embedding methods
• point defects in solids

1. Introduction

Ever since the early 19th century, transition metals (TM) complexes have been a major focus of research, from theoretical and experimental standpoint, leading to major developments in molecular orbital, crystal field, and ligand field theories. Molecular TM compounds have been successfully used as photocatalysts [1], as an appropriate choice of ligand coordination environment can support the desired reactivity and balance the catalytic properties with robustness and durability. Some basic issues confounding the use of molecular TM photocatalysts reappear in solid state systems, including possible rapid deactivation of excited states and sensitivity of materials to degradation. In heterogeneous catalysis, additional uncertainties arise regarding the chemical nature of the active photocatalytic intermediates at the interface. When photocatalysis occurs, it is often unclear which electronic states are involved. The active species may have different density of states, populate with charge carriers at different rates, and may also interact with one another. The complex relationship between electronic and physical structure in both molecular and solid state systems containing transition metals can be effectively probed by optical absorption and photoelectron spectroscopy techniques [2,3].

According to Zaanen et al., [3] TM compounds can be classified by the relative energies of the following charge fluctuations: in Mott-Hubbard insulators, $d_i^n{d}_j^n\to d_i^{n+1}{d}_j^{n-1}$ excitations involving the d-d Coulomb and exchange (U) interactions (i, j are TM sites); and in charge-transfer insulators, $d_i^n\to L^{\pm }{d}^{n\pm 1}$ excitations (L is a hole in the valence band of an anion). In TM oxides, the energies involved in these excitations are typically high: 7–10 eV for Mott-Hubbard insulators [3] and above 5 eV for charge-transfer compounds [3].

Electronic excitations localised inside the d-shell, known as crystal field (CF) excitations, are of the order of 1–4 eV, and these excitations define the optical properties (colour which fascinates first-year chemistry students) and chemical properties (catalysis which fascinates all chemists) of TM solid compounds [4,5]. This applies not only to well-studied TM oxides but to a wide range of materials from metal-organic frameworks [6] to single-atom catalysts deposited on substrates such as ionic oxides, halogenides and amorphous carbon [7,8]. The properties of TM compounds in the energy range of 1–4 eV correspond to the electronic states of partially filled isolated d-shells [9].

Over the years, various pseudopotential and linear augmented-plane-wave methods within density functional theory (DFT) have been used to study the electronic structure of solids containing TMs (see, for example, [10–15] and references therein) claiming good computational efficiency. Although DFT methods typically provide reliable estimations of the geometry and ground state energy, it is difficult to capture finer details of the correlated electronic structure using standard DFT approaches. A correct description of the ground state d-shell multiplicity and its d-d excitation spectra are known to be a considerable challenge for DFT, which is a direct consequence of the incomplete description of important electronic correlations therein. A relevant representation of the underlying electronic structure is that of the band states of an (ionic) insulator supplied with the local multiplets of d-electrons. This prompts the development of quantum chemical methods that can achieve an accurate description of the d-shell embedded into a solid phase/matrix.

This is a challenging theoretical problem which remains open despite many established and more recent significant advances in the field, and where the celebrated models of quantum chemistry, such as molecular orbital (MO) or valence bond (VB) theory, do not provide a description of the required quantitative accuracy [16]. Main difficulties in providing a quantitatively accurate description of the d-shell weakly coupled to a solid state matrix are due to the highly correlated nature of the problem. The emphasis is to be placed on a correct account of electronic correlations in the d-shell, which inevitably becomes a substantial issue once models of a realistic size are considered.

A detailed description of electronic correlations can be, in principle, provided by configuration interaction (CI) method, which, for most chemical problems, can hardly be used in its original formulation due to extremely high computational costs. Therefore, less expensive and approximate methods are favoured such as hybrid approaches where electronic sub-systems are considered at different levels of theory. For example, strongly correlated d-shell can be described using the fully correlated CI approximation, whilst the rest of the system, where correlations are weaker, can be treated with more approximate and less expensive methods. In such hybrid approach, the required approximations can be derived systematically [17]. A specific realisation of this idea has led to the development of the effective Hamiltonian of crystal field (EHCF) method, dating back to 1991, which was originally developed and successfully applied to TM molecular complexes [18–22], including spin-crossover compounds of iron (II) [23,24]. Previously, EHCF has been applied to predict the ground state and optical spectra of insulating TM containing solids in the cluster approximation [25–27]. Although, the results were quite successful, the inherent limitations of a cluster model in predicting properties of ionic bulk crystals remain. This long standing problem requires significant efforts in accurate description of the boundary or in studying the convergence to bulk properties of clusters of increasing size [28–30].

In this work, we generalise the EHCF method to study the electronic structure and optical spectra of periodic systems containing transition metals, we test the developed theoretical framework on well known examples of TM oxides such as MnO, FeO, CoO, NiO, and we study TM impurities in the MgO matrix. In the proposed approach, EHCF procedure is combined with the Green's function (GF) formalism [31,32] suitable for describing local perturbations in periodic solids, such as atomic scale defects. In the combined approach, the band structure of a perfect crystal is first calculated and then transformed to GFs of the crystal in the basis of local atomic orbitals. Either perfect crystal (if the TM ions occupy the periodic lattice of solid phase) or defect crystal (if the TMs are impurities or point defects randomly embedded in the periodic matrix) are produced, whilst d-shell(s) are excluded at this stage. The influence of d-shell(s) on s- and p-electrons is taken into account following the methodology described below, which was adopted from Ref. [17]. The EHCF method, in turn, is also modified so that the defined Green's functions serve as EHCF input.

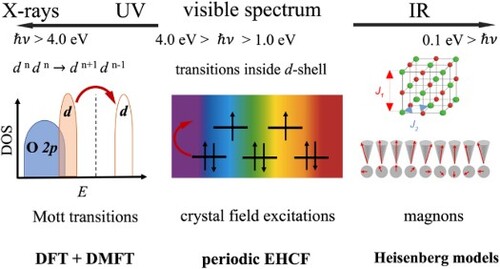
A brief classification of the experimentally observed transitions in TM oxides is summarised in Figure 1, together with the main computational methods used for their interpretation. Typical Mott insulators cannot be adequately described by conventional band theory of solids due to the shortcomings in a correct treatment of the electron correlation and in description of the localised d-states in the vicinity of the Fermi level. The band gap in a Mott insulator is between bands of like character, such as d electron bands, whereas the band gap in charge-transfer insulators exists between anion and cation states, such as between O 2p and Ni 3d bands in NiO [33]. Recent improvements of conventional DFT offer more accurate methods to describe the band gap and electronic structure of highly correlated materials. Some examples include single-determinant methods such as self-interaction correction [34], or using hybrid DFT functionals [35], adding explicitly the onsite Coulomb interaction through various implementations of DFT + U [36–38], or accounting for the electron correlation through random phase approximation [39].

Figure 1. Classification of the experimentally observed low-lying transitions in TM oxides.

The periodic EHCF method, suitable for description of crystal-field transitions inside an individual d-shell, shares several common ideas with the dynamical mean field theory (DMFT) [40–45] as well as with less expensive DMET [46] and RISB [47] methods which can be combined with DMFT into a unified framework [48]. These methods are related to embedding of strongly correlated atom(s) into a weakly correlated bath (for a recent review on embedding methods, see e.g. Ref. [49]).

In this manuscript, we compare and contrast the basic features of both approaches, however, we do not discuss the delocalised magnetic excitations – magnons – which are characteristic of transition metal compounds on the energy scale of several hundredths of electron-volts. These are described by Heisenberg and anisotropic exchange interactions models developed for magnetic materials with correlated electronic structure and significant spin-orbit coupling and lay beyond the scope of this paper.

2. EHCF theory for periodic systems

Derivation of the EHCF theory for periodic systems follows the same general steps as those for the method developed for molecules and finite clusters and described previously in Refs. [17–20]. In the framework of EHCF, the space of one-electron states, spanned by local atomic orbitals, is divided into two sub-spaces: (i) l-space spanned by s- and p-orbitals of TM atoms and all orbitals of other (light) elements; (ii) d-space spanned by d-orbitals of TMs. This division exploits the fact that s- and p-orbitals experience significant hybridisation and subsequent delocalisation to such degree that the atomic (many-electron) states completely lose their identity. The d-shells, however, are less affected by hybridisation so that electrons in d-orbitals retain atomic-like character, and these are only split by the (effective) crystal field. This argument conforms with the model ideas [9] on the electronic structure of TM oxides, assumed to be formed by sp-valence bands of an insulator (similar, for example, to MgO for TM oxides in the rock-salt structure) augmented with the local multiplets of d-electrons.

When multiple TM atoms are present in a periodic solid, such as TM oxides, the d-space cannot be simply divided into separate d-shells unless the resonance interactions between them are neglected. To overcome this, we recollect the two-step procedure, proposed by Anderson [50,51], for estimating the magnetic interaction of local momenta residing in different d-shells. The Anderson's recipe [50,51] prescribes that the states of an individual d-shell of a magnetic ion embedded into insulating diamagnetic medium (l-space) are obtained using kind of ligand field theory. At this stage, the exchange interactions between TM ions are neglected, and the entire d-system is divided into separate d-shells. After an adequate description of individual d-shells is obtained, an estimation of the interactions between electrons residing in the defined magnetic orbitals is constructed. Here, when describing periodic solids with multiple TM atoms, we perform the first stage of Anderson's procedure and postpone the account of the exchange interactions to a later stage [21,52].

Once the division of one-electron states into correlated and uncorrelated subsets is performed, the total wave function of the system, Ψ, is presented in a form prescribed by the group function approximation [53] with a fixed number of electrons in each subset: (1) $\Psi ={\Psi }_d\left(n_d\right)\wedge {\Psi }_l(N-n_d),$(1) where ${\Psi }_l$ and ${\Psi }_d$ are the many-electron wave functions built in the l- and d-subspaces, respectively ($n_d$ is number of d-electrons in the d-space, and N is the total number of electrons; $\wedge$ stands for the anti-symmetric product of the wave functions). Since d-shells are the most correlated part of the chemical system, the wave function ${\Psi }_d$ is treated using the configuration interaction (CI) method [53], whilst the many-electron states built in the l-subspace can be considered within a one-electron approximation.

Representation (1(1) $\Psi ={\Psi }_d\left(n_d\right)\wedge {\Psi }_l(N-n_d),$(1) ) of the electronic structure of a solid containing a TM ion is, of course, approximate. The exact wave function contains additional terms describing various distributions of electrons between the d- and l-(sub)space. These additional terms are taken into account by the Löwdin partition technique [54], which projects the exact wave function with multiple distributions of electrons between subspaces on the subspace spanned by the functions with a fixed number of electrons (1(1) $\Psi ={\Psi }_d\left(n_d\right)\wedge {\Psi }_l(N-n_d),$(1) ). The exact Hamiltonian of the system is then replaced by the effective Hamiltonian of the form: (2) $H^{eff}=P{H}_{0}P+H_{RR},$(2) where (3) $H_0=H_d+H_l+H_c,$(3) and (4) $H_{RR}=P{H}_{r}Q{(EQ-Q{H}_{0}Q)}^{-1}Q{H}_{r}P.$(4) In Equations (2(2) $H^{eff}=P{H}_{0}P+H_{RR},$(2) )–(4(4) $H_{RR}=P{H}_{r}Q{(EQ-Q{H}_{0}Q)}^{-1}Q{H}_{r}P.$(4) ), P is a projector to the subspace of the many-electron functions in the form (1(1) $\Psi ={\Psi }_d\left(n_d\right)\wedge {\Psi }_l(N-n_d),$(1) ), Q = 1−P, $H_d$ and $H_l$ are bare Hamiltonians for the d- and l-(sub)systems excluding all mutual interactions, $H_c$ describes Coulomb interactions between sub-systems without changing the number of electrons, and $H_r$ describes resonance interactions between sub-systems. Operator $H_{RR}$ is the key element as it renormalises the bare Hamiltonian on the account of coupling between the model many-electron states (1(1) $\Psi ={\Psi }_d\left(n_d\right)\wedge {\Psi }_l(N-n_d),$(1) ) and charge-transfer states which present in the theory only implicitly. This assumption is only acceptable when, within each d-shell, charge transfer states are significantly higher in energy than the d-d excited states, which is, ultimately, the boundary condition for the applicability of the present approach [19].

Averaging the effective Hamiltonian (2(2) $H^{eff}=P{H}_{0}P+H_{RR},$(2) ), obtained by the Löwdin partition, over the multiplier functions ${\Psi }_d$ and ${\Psi }_l$ yields two separate Hamiltonians for the d- and l-(sub)systems: (5) $\begin{array}{rl}& H_d^{eff}=H_d+{⟨⟨H_c⟩⟩}_l+{⟨⟨H_{RR}⟩⟩}_l,\end{array}$(5) (6) $\begin{array}{rl}& H_l^{eff}=H_l+{⟨⟨H_c⟩⟩}_d.\end{array}$(6) In expressions (5(5) $\begin{array}{rl}& H_d^{eff}=H_d+{⟨⟨H_c⟩⟩}_l+{⟨⟨H_{RR}⟩⟩}_l,\end{array}$(5) ) and (6(6) $\begin{array}{rl}& H_l^{eff}=H_l+{⟨⟨H_c⟩⟩}_d.\end{array}$(6) ), $⟨⟨⟩{⟩}_{d,l}$ stands for averaging over the ground state of the d- (or l-) system. The effective Hamiltonian (6(6) $\begin{array}{rl}& H_l^{eff}=H_l+{⟨⟨H_c⟩⟩}_d.\end{array}$(6) ) for the l-system requires an estimate of $⟨⟨H_c⟩{⟩}_d$ for which a density matrix ρ of the d-shell (system) is required. Due to the above mentioned atomic-like character of the TM d-shell in a crystal environment, the following simple approximation can be employed [19]: (7) ${\rho }_{\mu \nu }={\delta }_{\mu \nu }\frac{n_d}{5},$(7) where μ and ν numerate d-orbitals. Then $⟨⟨H_c⟩{⟩}_d$ can be split into (8) $\begin{array}{rl}{H}_c^{intra}& =\sum _{i,j\in TM}\sum _{\sigma }\frac{n_d}{5}\\ & \times \left[\sum _{\mu }\{(\mu \mu |ij)-\frac{1}{2}(\mu i|\mu j)\}\right]l_{i\sigma }^{+}{l}_{j\sigma }+h.c.\end{array}$(8) and (9) $H_c^{inter}=\sum _{i\notin TM}\sum _{\sigma }\frac{n_d}{5}\sum _{\mu }(\mu \mu |ii)l_{i\sigma }^{+}{l}_{i\sigma },$(9) where i, j runs over the atomic orbitals of the l-space, μ runs over d-orbitals, σ stands for the spin projection, $l_{i\sigma }^{+}$ ($l_{i\sigma }$) are the operators creating (annihilating) an electron in the ith AO of the l-space, $(\mu \mu |ij)$ are Coulomb two-electron integrals, $h.c.$ stands for the Hermitian conjugate. The term $H_c^{intra}$ describes repulsion of electrons residing on s-, p-orbitals of the TM atom from d-electrons of the same atom, while $H_c^{inter}$ corresponds to the two-centre two-electron repulsion of electrons of the l-space from d-electrons.

Having defined the effective Hamiltonian, the wave function of the l-system can be obtained using one-electron (Hartree-Fock) approximation and then used to calculate the averages $⟨⟨H_c⟩{⟩}_l$ and $⟨⟨H_{RR}⟩{⟩}_l$ entering the effective Hamiltonian of the d-system, which yields (10) $\begin{array}{rl}{H}_d^{eff}& =H_d+\sum _{\mu ,\nu }\sum _{\sigma }(H_{\mu \nu }^{intra}+H_{\mu \nu }^{cf}+H_{\mu \nu }^{res})\\ & \times d_{\mu \sigma }^{+}{d}_{\nu \sigma }+h.c.,\end{array}$(10) where $d_{\mu \sigma }^{+}$ ($d_{\mu \sigma }$) are the electron creation (annihilation) operators for the μth d-orbital. Effective terms in $H_d^{eff}$ involve the following contributions: (i) $H_{\mu \nu }^{intra}$ describes interactions of d-electrons with the electronic density located on the s-, p-orbitals of the same TM atom; (ii) $H_{\mu \nu }^{cf}$ describes interactions of d-electrons with the electron density located on other atoms/nuclei; it has the form of classical (Coulomb) ionic crystal field matrix elements [55]; (iii) $H_{\mu \nu }^{res}$ represents resonance (covalent, charge transfer) interactions between d- and l-systems, coming from the Löwdin partition procedure (perturbation theory) – the terms specific to the EHCF approach.

The above description can be applied to any chemical system containing a transition metal atom. Specific to periodic systems is the form of the solution for the electronic problem of the l-system. In a crystal, it is given as an assembly of the Bloch states $|n\mathbf{k}⟩$ (n is the band number) expressed as linear combinations of the Bloch sums (11) $|a\mathbf{k}⟩=\frac{1}{\sqrt{\mathrm{K}}}\sum _{\mathbf{r}}{e}^{i\mathbf{k}\mathbf{r}}|a\mathbf{r}⟩,$(11) where $|a\mathbf{r}⟩$ are atomic (spin-)orbitals of the l-space located in the $\mathbf{r}$th unit cell of the crystal, $\mathbf{k}$ is a vector in the 1st Brillouin zone, $\mathrm{K}$ is a number of unit cells in the crystal model with periodic boundary conditions. For the periodic l-system, the resonance contribution to the effective Hamiltonian of d-shell is given by Tokmachev and Tchougréeff [4] (12) $H_{\mu \nu }^{res}=\sum _n\sum _{\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}(\mathrm{\Re }{G}_{n\mathbf{k}}^{+}(-I_d)+\mathrm{\Re }{G}_{n\mathbf{k}}^{-}(-A_d)),$(12) where the first term in the brackets takes into account the effect of the charge transfer states with an electron transferred from the d- to the l-system, the second term – from the l-system to the d-shell, upon the effective potential felt by the electrons in the d-shell; β denotes the resonance (hopping) integrals between the l-Bloch states and the d-orbitals, $I_d$ and $A_d$ are ionisation potential and electron affinity of the d-shell. Since the electron transfer to (from) the l-bands happens only for unoccupied (occupied) orbitals, the Green's functions $G_{n\mathbf{k}}^{\pm }$ entering the last equation are (13) $\begin{array}{rl}& G_{n\mathbf{k}}^{+}\left(\epsilon \right)=\underset{\delta \to 0^{+}}{lim}(1-f_{n\mathbf{k}})\frac{|n\mathbf{k}⟩⟨n\mathbf{k}|}{\epsilon -{\epsilon }_{n\mathbf{k}}+i\delta },\end{array}$(13) (14) $\begin{array}{rl}& G_{n\mathbf{k}}^{-}\left(\epsilon \right)=\underset{\delta \to 0^{+}}{lim}{f}_{n\mathbf{k}}\frac{|n\mathbf{k}⟩⟨n\mathbf{k}|}{\epsilon -{\epsilon }_{n\mathbf{k}}+i\delta },\end{array}$(14) where $f_{n\mathbf{k}}$ is the occupation number of the given l-Bloch state, which can only have two possible values: 0 for the vacant states and 1 for the occupied states. Due to the Kramers-Kronig relations, the real part of these GFs is the negative Hilbert transform of the imaginary part. Note that both functions are defined as the analytic continuation from the lower complex half-plane to the real axis. These functions are evaluated from the GF of the l-system which is as usually defined as (15) $\mathbf{G}\left(\epsilon \right)=\underset{\delta \to 0^{+}}{lim}\sum _{n\mathbf{k}}\sum _{\sigma }\frac{|n\mathbf{k}⟩⟨n\mathbf{k}|}{\epsilon -{\epsilon }_{n\mathbf{k}}+i\delta }.$(15) When addressing $H_{\mu \nu }^{cf}$ in (10(10) $\begin{array}{rl}{H}_d^{eff}& =H_d+\sum _{\mu ,\nu }\sum _{\sigma }(H_{\mu \nu }^{intra}+H_{\mu \nu }^{cf}+H_{\mu \nu }^{res})\\ & \times d_{\mu \sigma }^{+}{d}_{\nu \sigma }+h.c.,\end{array}$(10) ), we note that these interactions of d-electrons with the electron density on other atoms include the long-range Coulomb part ($\sim 1/R$). In ionic lattices, these long-range contributions are described using the Ewald summation [56]. This gives a correct energy shift of d-orbitals in the crystal field of ionic solid, which indirectly affects the splitting by changing the energies of electron transfer between d- and l-systems (see below). At the same time, the Coulomb splitting induced by the ions of the crystal itself is not affected by this as more than 99% of its value comes from the interactions with the 1st and 2nd neighbours of a TM atom (dipole and quadrupole terms are proportional to $1/R^3\mathrm{and}1/R^5,$ respectively).

Another important difference to the molecular case comes from the fact that the transfer of electrons takes place within the d-shell, and not between molecular orbitals and vacuum. To account for this, one has to shift the poles of the $G_{n\mathbf{k}}^{\pm }$ by the interaction $g_{dn\mathbf{k}}=-(dd|n\mathbf{k},n\mathbf{k})$ of the electron (hole) placed to the l-Bloch state (d-shell) with the hole (electron) located in the d-shell (l-Bloch state). This shift, however, becomes negligible in the periodic solid since each individual l-Bloch state is delocalised over a large (asymptotically infinite) number of atomic orbitals, and the electron-hole interactions over atomic orbitals decay as $\sim 1/R$ with the distance from a TM atom. These intercations are represented by two-centre Coulomb integrals; other interactions decay even faster. The value of $g_{dn\mathbf{k}}$ is, therefore, inversely proportional to the number of unit cells in a periodic model (see Appendix 1). Following the main assumption of the EHCF method, denominators $(-I_d-{\epsilon }_{n\mathbf{k},\sigma })$ and $(-A_d-{\epsilon }_{n\mathbf{k},\sigma })$ entering GFs in Equation (12(12) $H_{\mu \nu }^{res}=\sum _n\sum _{\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}(\mathrm{\Re }{G}_{n\mathbf{k}}^{+}(-I_d)+\mathrm{\Re }{G}_{n\mathbf{k}}^{-}(-A_d)),$(12) ) must be larger than the energies of the d-d excitations, so that the integrals $g_{n\mathbf{k}d}$ are negligible in comparison.

To evaluate the resonance integrals ${\beta }_{\mu n\mathbf{k}}$ over the d-orbitals localised on the TM atom, it is convenient to expand l-Bloch states over local atomic orbitals, which gives (16) ${\beta }_{\mu n\mathbf{k}}=\sum _i⟨n\mathbf{k}|i⟩{\beta }_{\mu i}.$(16) Resonance integrals ${\beta }_{\mu i}$ decay exponentially with the distance from the TM atom, therefore, the summation is reduced to a small number of l-AOs. Inserting (16(16) ${\beta }_{\mu n\mathbf{k}}=\sum _i⟨n\mathbf{k}|i⟩{\beta }_{\mu i}.$(16) ) into Equation (12(12) $H_{\mu \nu }^{res}=\sum _n\sum _{\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}(\mathrm{\Re }{G}_{n\mathbf{k}}^{+}(-I_d)+\mathrm{\Re }{G}_{n\mathbf{k}}^{-}(-A_d)),$(12) ) and rearranging the terms leads to the following expression for $H_{\mu \nu }^{res}$: (17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) where the GFs $G_{ij}^{\pm }$ are now represented in the local atomic basis. These can be calculated from the retarded GF of the l-subspace in the same basis, obtained for an ideal periodic l-system or for a defected system if a TM atom/ion represents a point defect.

3. Implementation

The general methodology described in Section 2 can, in principle, have various implementations depending on the chosen method of calculating the required matrix elements. One may recollect ab initio methods [57] where the integrals are calculated exactly (and the number is substantial due to the presence of two-electron integrals), projector augmented wave PAW-DFT [58] where the required matrix elements are derived through various localisation/projection procedures, as implemented e.g. in lobster [59–61] or wannier90 [62] packages, or semi-empirical methods [63,64] where some parameters are extracted from experimental data and additional assumptions are made to express the matrix elements.

As proof-of-concept implementation, we find a semi-empirical setup to provide a reasonable compromise between an agreement with experimental optical lines and computational efficiency. The main features of our parameterisation scheme are:

• one-centre core attraction integrals and Slater – Condon parameters are extracted from the experimental atomic data as described in Ref. [19];

• the number of multi-centre two-electron integrals is reduced by either zero differential overlap (ZDO) or neglect of diatomic differential overlap (NDDO) approximations, the central and most successful semi-empirical methods of quantum chemistry;

• the resonance integrals are calculated using the following approximate expression involving the overlap integral, $S_{\mu \nu }$: ${\beta }_{\mu \nu }=1/2({\beta }_{\mu }^0+{\beta }_{\nu }^0)S_{\mu \nu },$where the resonance parameters ${\beta }_{\mu }^0$ and ${\beta }_{\nu }^0$ are fitted to experimental spectral data;

• the remaining integrals are evaluated analytically over STO-based atomic orbitals expressed as a linear combination of Slater-type primitives.

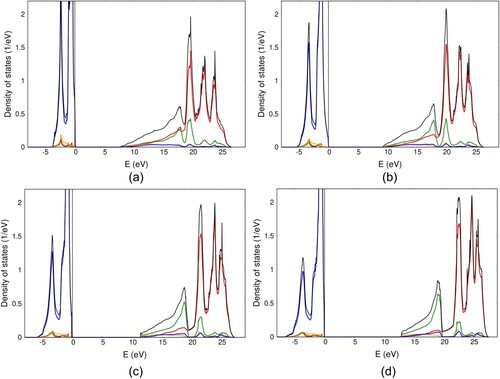
The GoGreenGo software [31], developed previously for modelling local perturbations in periodic systems due to chemisorption or point defects, provides the necessary information on the l-system (geometry, density matrix, the GF matrix) which is used as an input for the EHCF program. For the case of TM impurities, GoGreenGo calculates the density and GF matrices, perturbed due to the presence of a defect, from the band structure of an ideal, defect-free solid by solving the Dyson equation. Popov et al. [31] The band structure of a perfect crystal can also be pre-calculated using any available software of choice, including most commonly used VASP [58], ABINIT [65] or $\mathit{\Theta }\mathit{\Phi }$ (ThetaPhi) [66–68]. More details on GoGreenGo software can be found in Refs. [31,32].

The combined approach, proposed here, allows to use GoGreenGo together with the EHCF method for description of TM point defects in solids starting from the band structure of an ideal solid. Visual representation of the data exchange between GoGreenGo and ECHF is given in Figure 2. Additional input information includes the type of parameterisation and basis. The EHCF program currently supports several semi-empirical parameterisations: complete neglect of differential overlap (CNDO), one of the first semi-empirical methods of ZDO-type; modified neglect of diatomic overlap (MNDO), AM1, and PM3, all based on the NDDO integral approximation. Several basis sets of STO type are available such as single STOs, MAP [69], Bunge [70], and Koga [71]; these choices can be readily extended upon demand, and an option of using arbitrary atomic parameters defined by the user is currently under development.

Figure 2. Schematic representations of the proposed methodology and data exchange between EHCF and GoGreenGo modules.

All calculations performed in this work use parameterisation reported in Ref. [19] for both d- and l-systems, where one-centre parameters were derived from the spectral data available for neutral atoms and doubly charged ions of the first-row TMs. The resonance parameters were fitted to the optical spectra of [M(H₂O)₆]²⁺ – molecular aqua-complexes [72]. For all oxides, the band structures of the l-systems were calculated using the semi-empirical Hartree-Fock method in the basis of local atomic orbitals. Long-range parts of two-centre integrals entering matrix elements of the Fockian were summed over the lattice by the Ewald summation. The 1st Brillouin zone spans ($11\times 11\times 11$) Monkhorst-Pack k-grid [73]. Green's functions were calculated using GoGreenGo software on an energy grid with a step of 0.01 eV.

4. Results and discussion

4.1. Transition metal oxides

In this section, we test EHCF approach against periodic metal oxides of the first row transition metals (MnO, FeO, CoO and NiO) with rock-salt structure. We compare our numerical results with available experimental data on optical spectra and previous EHCF calculations performed within the finite cluster approach [25] keeping the same set of parameters. For NiO crystal with the rock-salt structure, band structure calculations of the l-system consisting of s-, and p-orbitals, performed with the effective Hamiltonian $H_l^{eff}$, yield the density of states presented in Figure 3. The low-lying wide 2s band located in the energy interval between – 38 eV and – 17 eV is not shown in the figure, which focuses on the vicinity of the Fermi level. 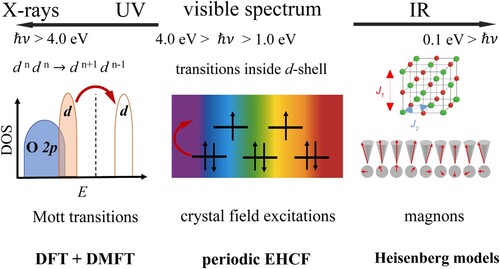The position of the d-multiplets is set to $-\frac{1}{2}(I_d+A_d)$, which, however, does not reflect the whole complexity of the electronic structure. Density of states of the l-system has the shape typical for insulators with the rock-salt structure, and it is similar for all studied oxides. NiO is a typical example, and fairly similar graphs of the density of states for the l-systems of the remaining oxides can be found in Appendix 2.

Figure 3. Periodic EHCF calculations of (a) total (black) and orbital projected density of states for NiO: orange – O 2s, blue – O 2p, green – Ni 4s and red – Ni 4p; (b) resonance term $V_{\mu \mu }^{res}(\epsilon )$ defined in Equation (18(18) $V_{\mu \nu }^{res}\left(\epsilon \right)=\sum _{n,\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}\delta (\epsilon -{\epsilon }_{n\mathbf{k}}),$(18) ) for both $t_{2g}$ (blue) and $e_g$ (red) d-orbitals.

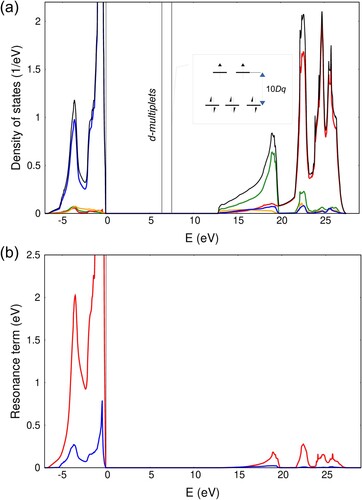
Figure 3 shows orbital projected density of states. The highest occupied band, has a shape of two narrow, high peaks, consisting mainly of oxygen 2p-orbitals with some fraction of 2s-orbitals, while the wide low-lying band corresponds to 2s orbitals. Transition metal 4s- and 4p- orbitals, on the other hand, provide major contribution to the conduction band: the first peak has a distinct 4s-character while the others have 4p-character. These features become particularly important in the discussion of the resonance contributions to the effective Hamiltonian Equation (17(17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) ) for the d-shell.

Atomic charges (Q) and the values of the energy gap between valence and conduction s,p-bands ($E_{gap}^{sp}$) are presented in Table 1. The quantity $E_{gap}^{sp}$ should not be confused with the experimentally observed band gap, which is evaluated by taking into account partially filled d-multiplets lying between the s,p-valence and similar conduction bands. The predicted charges on the metal and oxygen are significantly lower than the formal charges of $\pm 2$ due to delocalisation of the electron density over the bands of the crystal. The charges obtained for periodic solids are noticeably greater than those obtained in the cluster approximation. This can be explained by the Madelung electrostatic field, which cannot be fully captured in the cluster approach. The values of charges tend to increase with the cluster size [25], so that somewhat higher values in periodic calculations are anticipated. Another noticeable difference between these two approaches is that the effective atomic charges in the periodic model vary only insignificantly for different TM oxides.

Table 1. Periodic EHCF parameters of the electronic band structure of l-system: $E_{gap}^{sp}$ is the energy gap between valence and conduction s,p-bands, and $Q(M),Q(O)$ are effective atomic charges on metal and oxygen.

	$E_{gap}^{sp}$, eV		$Q(M)=-Q(O)$
	periodic model	cluster model	periodic model	cluster model
	this work	[25]	this work	[25]
MnO	7.72	9.71	1.21	1.03
FeO	9.30	10.61	1.25	0.96
CoO	11.53	11.25	1.24	0.89
NiO	12.74	11.82	1.23	0.85

Effective Hamiltonian $H_d^{eff}$, calculated with the density matrix and Green's functions obtained from the band structure of the l-system, gives the position and splitting of d-orbitals into triply ($t_{2g}$) and doubly ($e_g$) degenerate levels as must be expected for the octahedral point symmetry of the TM environment. The splitting can be characterised by a single spectroscopic parameter $10Dq$, which is usually known experimentally from the data on low-lying transitions observed in optical absorption spectra. Calculated values of $10Dq$ in comparison with experimental data and previous cluster model results can be found in Table 2. For all oxides, our results obtained in the periodic solid approach reproduce experimental values for the splitting with a fairly good accuracy; the relative errors are $<1\mathrm{\%}$ for NiO, c.a. 10% for MnO and CoO, and 15% for FeO. Periodic EHCF yields better quantitative agreement with experiment than the cluster approximation, which tends to underestimate the splitting. This can be explained by higher charges and higher population of oxygen orbitals in the periodic model and by an improved representation of the electronic structure of the l-system and the covalent terms in the effective Hamiltonian $H_d^{eff}$.

Table 2. Periodic EHCF splitting parameter of d-orbitals compared to the experimental data and cluster model calculations [25]; MAE and MPAE for optical spectra lines are calculated based on Tables 3–6.

	$10Dq$, eV
	periodic model	cluster model	experiment	MAE, eV	MPAE, %
	this work	[25]
MnO	1.35	0.84	1.21 [74], 1.25 [75]	0.08	3.67
FeO	1.38	1.04	1.20 [76,77]	0.16	8.17
CoO	1.27	0.90	1.17 [74]	0.15	7.22
NiO	1.13	0.87	1.13 [2]	0.09	3.47

Table 3. Periodic EHCF d-d transitions in MnO compared to the experimental data [74] and cluster model calculations [25].

Term	periodic model	cluster model	experiment
	this work	[25]	[74]
${}^6{A}_{1g}$	0.00	0.00	0.00
${}^4{T}_{1g}$	1.90	2.92	2.03
${}^4{T}_{2g}$	2.47	3.30	2.58
${}^4{A}_{1g}$	2.96	3.45	2.95
${}^4{E}_g$	2.96	3.45	–

Table 4. Periodic EHCF d-d transitions in FeO compared to the experimental data [76,77] and cluster model calculations [25].

Term	periodic model	cluster model	experiment
	this work	[25]	[76,77]
${}^5{T}_{2g}$	0.00	0.00	0.00
${}^5{E}_g$	1.38	1.05	1.20
${}^3{T}_{1g}$	1.42	1.72	–
${}^1{A}_{1g}$	1.40	2.02	–
${}^3{T}_{2g}$	1.92	2.14	–
${}^3{T}_{1g}$	2.58	2.58	2.64
${}^3{T}_{2g}$	2.78	2.79	–
${}^3{E}_g$	2.98	2.94	–
${}^3{T}_{1g}$	3.04	3.00	3.28

Table 5. Periodic EHCF d-d transitions in CoO compared to the experimental data [74] and cluster model calculations [25].

	periodic model	cluster model	experiment
Term	this work	[25]	[74]
${}^4{T}_{1g}$	0.00	0.00	0.00
${}^4{T}_{2g}$	1.13	0.77	0.90−1.03
${}^2{E}_g$	0.84	1.64	1.61
${}^2{T}_{1g}$	1.88	2.32	2.03
${}^2{T}_{2g}$	1.95	2.35	2.05
${}^4{A}_{2g}$	2.38	1.67	2.14
${}^4{T}_{1g}$	2.39	2.45	2.26−2.33
${}^2{T}_{1g}$	2.41	2.91	2.49−2.56
${}^2{A}_{1g}$	2.90	2.93	2.60

Table 6. Periodic EHCF d-d transitions in NiO compared to the experimental data [2], cluster model calculations [25], and recent DMFT calculations of the triplet-triplet transitions [78].

Term	periodic model	cluster model	DFT + DMFT	experiment
	this work	[25]	[78]	[2]
${}^3{A}_{2g}$	0.00	0.00	0.00	0.00
${}^3{T}_{2g}$	1.13	0.87	0.93	1.13
${}^3{T}_{1g}$	1.86	1.48	1.55	1.75
${}^1{E}_g$	1.94	2.12	–	1.95
${}^1{T}_{2g}$	3.02	2.92	–	2.75
${}^1{A}_{1g}$	3.11	3.04	–	2.95
${}^3{T}_{1g}$	3.25	3.28	2.91	3.25
${}^1{T}_{1g}$	3.60	–	–	3.52

Comparing ionic and covalent contributions to $10Dq$ we notice that the electrostatic crystal field interactions cause only ca. 10% of the total splitting, while the major fraction of it comes from the resonance interactions (17(17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) ). The resonance interactions (17(17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) ) contain a few different terms, and their influence on the splitting needs to be analysed further. It is obvious that the orbitals centred at the oxygen atoms nearest to the d-shell of TM play a central role as the overlap (and resonance integrals) with the d-orbitals is higher, at least by an order of magnitude, than for any other atomic orbital in the system. The contribution of the Bloch states $|n\mathbf{k}⟩$ to the resonance matrix element $H_{\mu \nu }^{res}$ at the energy ε can be characterised by the quantity (18) $V_{\mu \nu }^{res}\left(\epsilon \right)=\sum _{n,\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}\delta (\epsilon -{\epsilon }_{n\mathbf{k}}),$(18) which reflects the strength of the resonance between d-orbitals and the Bloch states, taking into account their density on the energy scale ($\delta (\epsilon )$ is the Dirac delta-function). The resonance matrix elements, $H_{\mu \nu }^{res}$, in (17(17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) ) are the Hilbert transforms of the functions $V_{\mu \nu }^{res}(\epsilon )$ taken at the particular points $-A_d$ and $-I_d$. Note that Equation (18(18) $V_{\mu \nu }^{res}\left(\epsilon \right)=\sum _{n,\mathbf{k}}{\beta }_{\mu n\mathbf{k}}{\beta }_{\nu n\mathbf{k}}\delta (\epsilon -{\epsilon }_{n\mathbf{k}}),$(18) ) resembles the imaginary part of the hybridisation operator characteristic to the DMFT theory (for the discussion see Section 4.3).

Due to the high-symmetry of TM ions in the studied oxides, both $H_{\mu \nu }^{res}$ and $V_{\mu \nu }^{res}(\epsilon )$ are diagonal with two eigenvalues: one triply degenerate corresponding to $\mu =\nu =t_{2g}$ and another doubly degenerate for $\mu =\nu =e_g$. The resonance term $V_{\mu \mu }^{res}(\epsilon )$ in Figure 3b shows that the occupied states have much stronger (by order of magnitude) effect on the d-shell. This indicates the importance of the states corresponding to an electron transferred from the valence bands to the d-shell. The valence band mostly consists of 2s and 2p orbitals of oxygen atoms (Figure 3(a)). Therefore, major contributions to the total splitting are due to $2p_{\sigma }\to e_g$ and $2s\to e_g$ charge transfer, in the descending order. The $2p_{\pi }\to t_{2g}$ charge transfer provides a small contribution to the splitting (compared to the interactions with $e_g$ orbitals) by slightly shifting $t_{2g}$ states upwards on the energy scale.

We are reminded that the EHCF method represents the electronic structure of TM oxides as a band structure of the l-system augmented with local d-multiplets treated with quantitatively accurate CI method. This makes EHCF methodology conceptually different from a variety of solid-state methods widely used to calculate electronic band structure. The differences manifest themselves in the most apparent way when we attempt to compare density of states. Although interpretation of density of states produced by the EHCF method for the l-system is straightforward, introducing d-multiplets is not trivial due to an ill-defined character of the conventional concepts within the approximation of electronic structure underlying ECHF. Due to the local nature of d-multiplets, a concept of d-band does not naturally appear in EHCF, and the d-orbital projected density of states can only be represented as a set of two discrete peaks (δ-functions) corresponding to $t_{2g}$ and $e_g$ orbitals. In addition, there exists an uncertainty in the position of these peaks on the energy scale, because ionisation potential and electron affinity of d-states are not equal. It means that different positions of d-multiplets are set depending on the process of interest: if an electron is removed from the d-shell, the position of d-multiplets is set at $-I_d$, and if an electron is added, the position corresponds to the value of $-A_d$. To avoid this problem, one can use the value of $-\frac{1}{2}(I_d+A_d)$ as a conventional position of d-multiplets, as it is done in Figure 3, although it is obvious that such representation does not reflect the whole complexity of the electronic structure. Finally, we note that due to the above mentioned factors the concept of the Fermi level also becomes ill-defined.

The CI calculations of the d-shell with effective Hamiltonian $H_d^{eff}$ produce spin and symmetry of the ground state along with the energy of excited states corresponding to the observable d-d transitions in optical spectra. These results are compared to experimental lines in Tables 3–6, whilst the mean average and mean percentage average errors (MAE and MPAE) between the calculated and experimental spectral lines are given in Table 2. In general, the proposed methodology gives the correct spin multiplicity and spatial symmetry of the ground state in all cases, and it allows to predict the energy of the low-lying excited states in a very good agreement with experimental observations (MAE does not exceed 0.16 eV, MPAE – 9%). As in the case of $10Dq$ parameter, the periodic version of EHCF method shows an improvement over the cluster EHCF calculations in terms of numerical accuracy. Note that in the case of CoO, we obtain a different order of the excited ${}^4{T}_{2g}$ and ${}^2{E}_g$ terms as compared to Ref. [74]. In all other cases, the calculated order of excited states and their multiplicity agree with the cited experimental data.

4.2. Transition metal impurities in magnesium oxide

Another experimentally well-studied case is provided by substitutional impurities in MgO where a small fraction of Mg ions is replaced by doubly charged transition metal ions. In this Section, we consider the electronic structure and optical properties of Co:MgO and Ni:MgO solids using the developed periodic EHCF approach. TM impurity, which forms a point defect in periodic solid, is treated differently to TM in pure oxides, namely the parameters describing 4sp-orbitals of the TM impurity are different to those of the 3sp-orbitals of Mg. Starting from the ideal MgO band structure, we evaluate the effect of a local defect on the l-system by applying perturbation theory as implemented in GoGreenGo. The perturbed Green's function of the modified l-system is then used to construct effective Hamiltonian for the d-shell of TM impurity and calculate its spectrum.

The periodic EHCF density of states for pure MgO is shown in Figure 4(a). The calculated charge of the ions is $\pm 0.958$. GoGreenGo calculations of Co:MgO and Ni:MgO show that in both cases perturbations of the orbital-projected GFs and density matrix elements decay very fast with the distance from the impurity site, as anticipated for a 3D insulator. For instance, the atomic charges (and diagonal density matrix elements) demonstrate no significant changes starting from the 3rd neighbours. Changes in the atomic charges for the impurity site and its 1st and 2nd neighbours are collected in Table 7. The perturbed site-projected density of states for these sites are shown in Figures 4(b,c) in comparison to the ideal MgO crystal. From these data we conclude that impurities have a rather small yet noticeable effect on the electronic structure, which is localised in the vicinity of the impurity site. The calculated splitting parameters $10Dq$ for the d-shell of the TM impurity and the energy of optical transitions are collected in Tables 8–10 where they are compared to experimental data. As one can see, the predicted theoretical values of $10Dq$ are overestimated for both Co:MgO and Ni:MgO. A significant discrepancy of 0.47 eV is observed for Co, whereas for Ni the deviation is much smaller and lies within an acceptable accuracy of 0.14–0.20 eV.

Figure 4. Periodic EHCF calculations of (a) total (black) and orbital projected density of states for MgO: orange – O 2s, blue – O 2p, green – Mg 3s and red – Mg 3p; (b) perturbed (red) and unperturbed (blue) density of states on the impurity site in Ni:MgO; (c) same as (b) but for the oxygen sites surrounding the TM point defect.

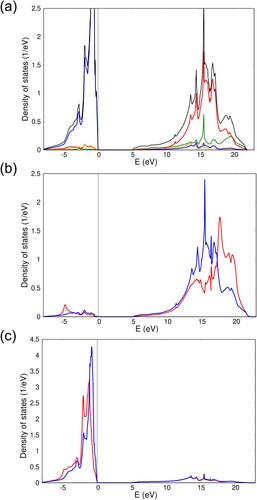
Table 7. Periodic EHCF atomic charges induced by the point defect in Co:MgO and Ni:MgO compared to the corresponding values in the ideal MgO crystal.

	impurity site	1${}^{\mathrm{st}}$ neighbours	2${}^{\mathrm{nd}}$ neighbours
MgO	0.958	$-0.958$	0.958
Co:MgO	1.083	$-0.983$	0.954
Ni:MgO	1.043	$-0.978$	0.953

Table 8. Splitting parameter of d-orbitals for Co:MgO and Ni:MgO compared to the experimental data.

		$10Dq$ (eV)
	periodic EHCF	corrected value	experiment
Co:MgO	1.67	1.49	1.20 [80]
Ni:MgO	1.21	1.07	1.07 [81]; 1.00 [82]

Note: Corrected values correspond to the shifted 2p O band as discussed in the text.

Table 9. Periodic EHCF d-d transitions in Co:MgO compared to the experimental data [80].

Term	periodic EHCF	corrected value	experiment [80]
${}^4{T}_{1g}$	0.00	0.00	0.00
${}^4{T}_{2g}$	1.50	1.34	1.05
${}^2{E}_g$	0.46	0.63	1.13
${}^2{T}_{1g}$	1.86	1.87	2.13
${}^2{T}_{2g}$	1.95	1.95	2.13
${}^4{A}_{2g}$	2.43	2.42	2.32
${}^4{T}_{1g}$	2.75	2.58	2.43
${}^2{T}_{1g}$	3.18	2.83	2.54
${}^2{A}_{1g}$	3.28	3.11	3.05

Table 10. Periodic EHCF d-d transitions in Ni:MgO compared to experimental data [81].

Term	periodic EHCF	corrected value	experiment [81]
${}^3{A}_{2g}$	0.00	0.00	0.00
${}^3{T}_{2g}$	1.20	1.07	1.07
${}^1{E}_g$	1.95	1.78	1.68
${}^3{T}_{1g}$	1.97	1.94	1.83
${}^1{T}_{2g}$	3.10	2.96	2.69
${}^1{A}_{1g}$	3.13	3.08	3.04
${}^3{T}_{1g}$	3.36	3.16	3.21
${}^1{T}_{1g}$	3.67	3.54	3.50

Our analysis indicates that the errors in the splitting parameters originate from a poor quality of the ideal MgO band structure used as a starting point in our calculations. The most significant contribution to $10Dq$ comes from the resonance interaction with the 2p O band located just below the Fermi level. Consequently, its position on the energy scale, relative to d-orbitals, is an important factor affecting the splitting. The position of the 2p O band in MgO is located higher than that of NiO by 2.88 eV; at the same time, the experimental NIST X-ray photoelectron spectroscopy results [79] indicate that the difference between the Auger parameters 1s – KL${}_{2,3}$L${}_{2,3}$ for MgO and NiO is 1.1 eV. If the 2p O band of MgO is shifted down by 1.78 eV to make its position to agree with the experimental data, then the calculated values of $10Dq$ and optical transitions demonstrate a much better agreement with experiment. These results are shown in the third column in Tables 8–10.

4.3. Conclusive remarks

In this work, we propose a quantum chemical method for computing the electronic structure and optical spectra of periodic solids containing transition metals with open d-shells. It combines the EHCF approach, previously used for finite clusters, with GoGreenGo software designed to model electronic structure of materials in the periodic boundary conditions. The developed computational framework has been used to reproduce optical spectra of the well-studied materials such as transition metal oxides with the rock-salt structure and transition metal impurities in the MgO matrix. This combined approach can be readily employed in more extensive studies on ideal and defected periodic structures containing transition metals.

The EHCF method has apparent similarities with the dynamical mean field theory (DMFT), widely used in condensed matter physics, in particular, in the DFT + DMFT implementation. In DMFT, the problem of a strongly correlated orbital or atom(s) is mapped onto another problem known as the Anderson impurity problem (AIP). This simplifies its solution as, in principle, AIP can be solved exactly, e.g. using quantum Monte Carlo, Lanczos diagonalisation, or with various approximations. However, the mapping comes at a cost of neglecting the spatial correlations by focussing on the exact temporal correlations instead. Within DMFT, information about the connection of a correlated atom (or subsystem, in general) to the bath is contained in the quantity called 'hybridisation', which is a finite temperature Green's function encapsulating the finite temperature dynamics of electrons hopping between the correlated atom and the bath. In DFT + DMFT approach, one has to distinguish between the Kohn-Sham, or lattice space, and the correlated, or local sub-space. A connection between these two unequal spaces is accomplished by downfolding – for going from the lattice to the correlated space and upfolding – for going from the correlated to lattice space. The full lattice Green's function (in the lattice space), if downfolded and averaged over the Brillouin zone, gives rise to the local Green's function in the correlated sub-space. An analogous operation of integration over the frequencies, up to a constant coefficient, produces the occupation matrix of the corresponding Green's function states, either lattice or correlated.

The output of the AIP solver is another Green's function named the impurity Green's function. The DMFT solution proceeds self-consistently, i.e. when the Green's functions of the impurity converge. Upon the convergence of DMFT procedure, the electronic density is updated according to the occupancies of the Kohn-Sham levels determined from the lattice Green's function, and Kohn-Sham Hamiltonian is re-derived with the updated density giving rise to the new lattice Green's function. This outer self-consistency loop proceeds until the electronic density is converged.

In the EHCF method, the effective Hamiltonians, $H_d^{eff}$ and $H_l^{eff}$, play a role analogous to the impurity and bath Hamiltonians of DMFT, whereas the CI solution to the effective Hamiltonian, $H_d^{eff}$, in EHCF corresponds to the AIP solution within DFT + DMFT. The Löwdin partition acts as the downfolding within DFT + DMFT, however, there doesn't appear to be an upfolding counterpart. This restricts the applicability of the EHCF method to the systems where the density reconstruction in the correlated sub-system is relatively weak, such as in the case of d-shells in TM impurity or, equivalently, where the electronic structure of the l-system/bath is not affected.

Furthermore, within EHCF, calculations are performed at the CI level of theory thus implying $T=0K$, whilst DFT + DMFT calculations are usually done at finite temperature. In addition, the EHCF hybridisation is only taken into account in the static limit at two frequency points, $I_d$ and $A_d$, as evidenced by Equation (17(17) $H_{\mu \nu }^{res}=\sum _{i,j}{\beta }_{\mu i}{\beta }_{\nu j}(\mathrm{\Re }{G}_{ij}^{+}(-I_d)+\mathrm{\Re }{G}_{ij}^{-}(-A_d)),$(17) ). This corresponds to the previously mentioned requirement of a significant energy separation between the d-shells excited states and the states of the electrons transferred between d-shell and the band l-states. Finally, it is worth noticing that the d−d optical transitions in NiO and MnF${}_2$ have recently been reproduced within DFT + DMFT [78].

The periodic extension of the Effective Hamiltonian of Crystal Field (EHCF) method presented here is tested on exemplary transition metal oxides (MnO, FeO, CoO, and NiO) with rock salt structure and MgO with transition metal impurities. The tests demonstrate the ability of the EHCF method to accurately reproduce the spin multiplicity and spatial symmetry of the otherwise problematic highly correlated ground states of the studied materials. The obtained results are in a good agreement with experimentally observed d-d transitions in optical spectra.

Acknowledgments

With this contribution, we mark the 60th Birthday of Professor Peter Gill and celebrate 20 years of friendship.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

EB acknowledges the awards of a Royal Society Wolfson Fellowship and a Royal Society Leverhulme Trust Senior Research Fellowship for financial support. This work was also supported by the Engineering and Physical Sciences Research Council (EPSRC) Programme Grant ‘Metal Atoms on Surfaces and Interfaces (MASI) for Sustainable Future’ (EP/V000055/1) and by the grant number 122011300053-8 of the Russian Federation, ‘Surface phenomena in dispersed and colloidal systems; physico-chemical mechanics, adsorption and chromatographic processes’.

Appendices

Appendix 1.

Electron-hole interactions in the electron transfer energies

Integral $g_{dn\mathbf{k}}$ describing electron-hole interactions has the following form (A1) $g_{dn\mathbf{k}}=-(dd|n\mathbf{k},n\mathbf{k}),$(A1) where d and $n\mathbf{k}$ refer to atomic d-orbitals and Bloch-states of the l-system respectively. As it is written in the main text, the latter is expressed as a linear combination of the Bloch-sums Equation (11(11) $|a\mathbf{k}⟩=\frac{1}{\sqrt{\mathrm{K}}}\sum _{\mathbf{r}}{e}^{i\mathbf{k}\mathbf{r}}|a\mathbf{r}⟩,$(11) ): (A2) $|n\mathbf{k}⟩=\sum _a|a\mathbf{k}⟩⟨a\mathbf{k}\mid n\mathbf{k}⟩.$(A2) Inserting this into Equation (A1(A1) $g_{dn\mathbf{k}}=-(dd|n\mathbf{k},n\mathbf{k}),$(A1) ) and employing the ZDO approximation for two-centre Coulomb integrals we get: (A3) $g_{dn\mathbf{k}}=-\frac{1}{K}\sum _{a,\mathbf{r}}{|⟨n\mathbf{k}|a\mathbf{k}⟩|}^2(dd|a\mathbf{r},a\mathbf{r}).$(A3) Inter-atomic Coulomb integrals entering the last equation decay as $1/R$ with the distance from the atom where the atomic orbital d is located. Therefore, the sum in the equation converges to a finite number describing Madelung field acting on electron (hole) in the d-shell. It means that $g_{dn\mathbf{k}}\sim 1/K$, where theoretically $K\to \mathrm{\infty }$ and in practical calculations K is equal to ${10}^3-{10}^4$.

Appendix 2.

Densities of states for all studied oxides

Total and orbital projected densities of states for MnO, FeO, CoO and NiO are depicted on Figure A1.

Figure A1. Total and orbital projected densities of states for MnO (a), FeO (b), CoO (c) and NiO (d). Low lying wide 2s bands located in the interval from are not shown for clarity. Color code is the same as in Figure 3(a).