A contribution to the amaranthine quarrel between true and average electrical mobility in the free molecular regime

ABSTRACT

Landau and Lipschitz's approach—termed here H&B due to the use of Happel and Brenner's slow rotation approximation—for calculating the average electrical mobility over all orientations of an ion in the free molecular regime is shown in this manuscript to be an invalid assumption for non-globular ions when a fixed electrical field is present. The reason behind the invalidity seems to be the confusion between average “settling” velocity (the calculation intended by H&B) and the average mobility (drag) in the direction of the field. When a missing orientation is taken into account by rotating the drag tensor, the average mobility obtained through Landau's approach coincides with well-known orientationally averaged Kinetic Theory Methods such as those of Mason and McDaniel (M&M). H&B's averaging approach, however, can be related to the true mobility displacement of the ion or, in other words, the displacement occurring in the direction of the velocity. This true mobility displacement only agrees with the average mobility displacement if ion velocity and electrical field have always the same direction, which only happens under special cases. Analytical and numerical calculations of collision cross-sections of linear and planar structures using a momentum transfer kinetic theory approach are chosen here as a means to prove that a single rotation of the drag tensor is sufficient to show agreement between both methods. A projected area approach is also used to prove the inadequacy of the H&B method.

© 2017 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction

From a semi-classical point of view, it is becoming more self-evident that there is a need to understand the microscopical behavior of systems in order to correctly define transport and thermofluid properties. It is far more evident that as science and technology progresses, the need to accurately define these properties could signify the difference between correct and incorrect modeling. In the free molecular regime, most transport properties are defined using a “directional” cross-section defined by the interaction of the species of interest with the surrounding medium. The ensemble average of all possible orientations, speeds, and fundamental force interactions define the collision integral or the collision cross-section (CCS), which can then be used to define the mobility diameter. Among many of such CCS-defined transport properties, electrical mobility is extensively used in the physical characterization of ions, clusters, and nanometer-sized aerosol particles (de la Mora et al. 1998; Bohrer et al. 2008). Under standard temperatures and pressures, Knudsen numbers of nanometer-scale particles that move at slow velocities fall within the momentum transfer free molecular regime, in which ion mobility, i.e., the average drift velocity acquired per unit electrical field experimented by a charged ion, can be expressed using the Mason–Schamp equation (Mason and McDaniel 1988):[1] where m_red is the reduced mass, k is Boltzmann's constant, T is the temperature, z is the net number of integer (positive or negative) charges on the particle, e is the unit charge, ρ_gas is the density, and Ω is the particle's averaged collision cross-section. The collision cross-section Ω is a gas momentum-transfer-based collision integral that is orientationally averaged, i.e., calculates all gas molecule impingements onto an ion that is randomly oriented. Equation (1[1] ) is the basics of gas dynamics and has been extensively used analytically and numerically to infer collision cross-sections and mobilities (Shvartsburg and Jarrold 1996; Ruotolo et al. 2008; Pease et al. 2009; Tsai et al. 2009; Hogan and de la Mora 2011; Jiang et al. 2011; Larriba et al. 2011; Larriba and de la Mora 2012; Larriba et al. 2014).

Arguably, the most accepted simplifications for acquiring an average Ω for an ion or aerosol nanoparticle are (1[1] ) the consideration that all directions are equally probable and (2[2] ) that non-inertial effects can be ignored. The first of such simplifications has had the most controversy in the last few years due to the application of two different approaches. The first approach follows the work of Mason and McDaniel (M&M; Li and Wang 2003a,b) based on Chapman-Enskog's theory, which defines an orientationally averaged collision integral and agrees with Equation (1[1] ). The second approach, which we will refer to as the Happel and Brenner method (H&B; Epstein 1924; Happel and Brenner 1981; Landau and Lifshitz 1987), is a momentum transfer approach that calculates a drag tensor for the particle of interest. This drag tensor is positive definite, when dynamic effects of rotation are neglected, and therefore can be diagonalized and, if inverted, an average value of the mobility, and thus of the collision cross-section, is said to be found by averaging the sum of the trace of the inverse tensor (see Landau and Lifschitz, equation 59-6[6a] ). The controversy relies in the fact that these two methods (M&M and H&B) do not yield the same results even though both methods have been amply supported (Dahneke 1973a,b; Chan and Dahneke 1981; Landau and Lifshitz 1987; Garciaybarra and Rosner 1989; Bird 1994; Mackowski 1994, 2006; Tammet 1995; Mesleh et al. 1997; Shvartsburg et al. 1997; de la Mora 2002; Garcia-Ybarra et al. 2006; Larriba and Hogan 2013a,b; Li et al. 2014a,b).

In this work, it is shown that the drag tensor calculated in H&B, when used to calculate the average mobility in the direction of the field, does not consider all possible orientations of the ion (H&B section 5–2.12) and that a small geometrical consideration leads to both approaches being equivalent. Averaging the inverted tensor using the H&B approach (H&B section 5–8) does however have a physical meaning that is equivalent to calculating the average settling velocity—probably the one intended by H&B and perhaps later misinterpreted. The total displacement in the direction of the velocity is termed here true displacement and its value differs from the average mobility displacement in the direction of the field. Theory is corroborated first analytically using a cylinder/disk and later on through numerical calculations using IMoS (Zhang et al. 2012; Ouyang et al. 2013; Larriba-Andaluz and Hogan 2013, 2014; Larriba-Andaluz et al. 2015; Oberreit et al. 2015), an all-atom momentum transfer model that can mimic both approaches, H&B and M&M (see the online supplementary information [SI] for results in calculations). Although not pursued in this work, special attention should be taken when using the mean diffusivity (Basser et al. 1994; Alexander et al. 2007; Basser and Pierpaoli 2011), which can lead to averaging errors for planar and linear ions due to the similarities between diffusion and electrical mobility (Einstein's relation). Given that the charged particles studied herein this manuscript are large polyatomic entities (up to 5000 atoms), we will refer to them as ions, particles, or nanoparticles indistinctively with the only precaution that these ions must fall within the free molecular regime.

2. Theory

2.1. Average non-dynamic mobility of charged polyatomic nanoparticles when all orientations are equally probable

Let a random amorphous polyatomic charged structure with mass m and charge q be pulled by a constant electric field E in a gas medium. The resulting equation of motion (for slow velocities) is given by[2] where the translational inertia of the ion is given by the balance of the electrical force, , and the collision-induced drag force, . One can argue that the equilibration between the forces will happen fast enough that the LHS will almost immediately become negligible under small changes in velocity. In order for such equilibration to happen, one can also hypothesize that the speed of rotation of the nanoparticle must not significantly affect singular collisions between gas molecule and ion. In order to simplify the picture, let us assume the following hypotheses:

1. The particle reaches terminal velocity instantly. This terminal velocity and its direction are determined by the equilibrium of forces in Equation (2[2] ). After terminal velocity is reached, any inertial acceleration, rotational or translational, is assumed to be negligible.

2. All orientations of the ion are equally probable.

3. For (ii) to be true, the nanoparticle is continuously reorienting itself after a random number of gas collisions as it drifts through space. This reorientation happens enough to allow pure statistical randomness.

4. The nanoparticle speed of rotation can have any value as long as it is slow enough that the angular velocity of the nanoparticle contributes negligibly to the momentum transfer upon collision of a gas molecule with the ion. If the ion speed of rotation is high, individual collisions with gas molecules would be affected by the speed of rotation and the analysis assumed herein would need to be modified.

5. The averaged drift velocity (<v_i>) under assumptions (i) through (iv) must be in the direction of the electrical field (E_i).

Under these hypotheses, both forces, electrical and drag must be equal in direction and magnitude at all times during the flight (in Einstein's notation):[3a]

Given that, when neglecting angular velocity (hypothesis iv), the drag tensor K_ij is symmetric, the tensor can be diagonalized and an average value calculated by assuming all orientations are equally probable. Since the tensor can be diagonalized, the average value is the sum of the trace divided by three.

Averaging leads to two options:[4a] [5a]

The first possibility is to average the tensor K_ij directly by “assuming” that it is independent of the velocity and then inverting it. The second approach is to first invert the tensor and then take the average of the inverted tensor K_ij⁻¹. The two results, which differ for any non-spherical ion, are given by[4b] [5b] where K_ii are the principal directions of the tensor.

The purpose of this work is to understand the qualitative difference between both calculated mobilities Z₁ and Z₂. While a derivation will not be shown here, the calculation of the mobility using an orientationally averaged calculation, e.g., first collision integral, such as that of Mason and McDaniel, M&M, using Equation (1[1] ) agrees with averaging K_ij first (Equation (4a[4a] )) and then inverting it (see analytical example). The average mobility using Equation (5a[5a] ) on the other hand agrees with the work of Landau and Lifschitz and that of Happel and Brenner, H&B. There has to be an underlying reason or a misconception to why these two ways of averaging lead to different mobility results.

Given that Equation (3a[3c] ) is correct under given assumptions, how is it possible that averaging the tensor does not provide a mathematically correct description regardless of whether the regular or inverse tensors are used? The answer, as will be shown, is that not all orientations are considered in Equation (3a[3c] ) and therefore averaging Equation (3a[3c] ) is not necessarily “equivalent to the assumption that all orientations are equally probable” and hypothesis (ii) will not be satisfied.

To mathematically calculate the drag tensor for a polyatomic ion with a fixed orientation, a possible option is to use three perpendicular directions to calculate the corresponding drag tensor K_ij (see analytical example of disk/cylinder). The electric field can be defined in Equation (3a[3c] ) as a function of two Euler angles () as , so that for a fixed (with principal directions :[3b] where . The velocity satisfying Equation (3b[4b] ) iswhere the values can be termed orientation weights. This process only uses two of the three Euler angles for a fixed tensor , which is key to the argument developed here. If one were to integrate Equation (3b[3c] ) over the third angle, an angle of revolution along the axis (termed ), the equation would be invariant to the integration:[3c]

Except for particular cases, this cannot be the correct equation to average assuming all orientations are equally probable as it is invariant under the integration of one of the angles. Imagine, for example, a simple finite rotation of the ion along the axis. Physically, a new drift velocity is produced, v_j2, for the same E_i, which is not satisfied by Equation (3a[3c] ). Figure 1 provides detailed insight of the missing rotation for an L-shaped ion (used here to easily represent the rotation). Initially, Figure 1a shows an ion drag tensor that can be produced by randomly selecting three perpendicular directions of E_i. A new orientation that was not accounted for in Equation (3a[3c] ) is now provided in Figure 1b.

Figure 1. (a) Given a molecular structure with a fixed orientation, one can infer the tensor K_ij from three perpendicular directions (Ex, Ey, Ez). Black arrows correspond to the direction of the field, light gray (red) arrows correspond to the drag force response, and dark gray (blue) arrows correspond to the drift velocity resulting from the equilibrium. Only one drift velocity v_j can be produced from each drag-Field pair for a given K_ij, i.e., . (b) A rotation of the ion around E_x should still produce the same reaction F_x but a different drift velocity v_j2. The tensor K_ij does not contain this orientation of the ion so that will not produce F_xi. Instead a rotation of the tensor must also be made to produce this new orientation .

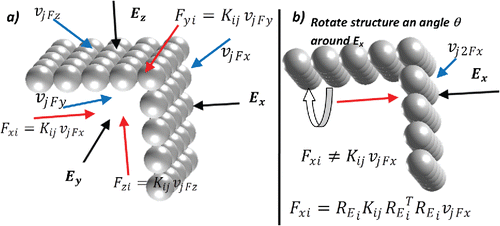
Therefore, to account for all possible orientations, one must include a rotation of the ion along the E_i axis. In such a case, Equation (3a[3c] ) can be rewritten as

[6a] where R_Ei is the rotation matrix of an angle θ along a unit vector û = (a, b, c) = in the direction of E_i (or v_i):[7]

The first term in brackets in the right-hand side of Equation (6a[6a] ) represents the rotation of the tensor K_ij while the second term in brackets represents the rotation of the velocity vector v_j. Equation (6[6a] a) remains valid and equivalent to Equation (3a[3c] ) regardless of how much the ion is rotated along the E_i axis. Only one position of this particular θ-rotation would be taken into account when only the tensor K_ij in Equation (3a[3c] ) is averaged. Since every θ-rotation is independent of each other, Equation (6a[6a] ) and not (3a[3c] ) should be employed and the resulting tensor, not K_ij, should be used when averaging.

To average such tensor, one can make use of Equation (6a[6a] ) to get the average θ-rotated tensor for a fixed E_i:[8]

Equation (8[8] ) needs further explanation to prove that the product of the averages is indeed the average of the products. The result can be proven by brute force. However, since the product of the averages, D_ijv_i, yields qE_i, as shown at the end of the derivation, the covariance must indeed be zero.

At a first glance, it is particularly interesting to note that the average of R_Eiv_j is in this case always in the direction of the field (v_i) regardless of the value of v_j (average rotation along the E_i direction). The average value D_ij for that particular position of E_i (assuming K_ij is given as a diagonal matrix with three principal axes) is given by the following matrix:

where

Since the tensor is symmetric and the product of D_ijv_i must still be in the direction of v_i, diagonalizing the above matrix gives:[9a]

with[9b]

Finally, averaging over all positions of vector û:[10] gives[11]

Note that u is described as expected by only two angles (χ,φ) of the total three needed to describe the orientation of an object. It is true that in the derivation of H&B, a third Euler angle, with the same orientation as θ, is used to average the settling velocity. However, as shown in Equation (3c[3c] ), Equation (3[3c] a) is invariant under such rotation making the average of the angle meaningless. The average value of D_ij″ is[12] which coincides with in Equation (4[4a] a). The most significant property of is that the average of its inverse is . It is therefore indifferent whether Equation (6a[6a] ) or[6b] is used. For a fixed field and when all orientations are taken into account, the Mobility is given by tensor M_ij (to differentiate from Z) as[13]

A general conclusion is therefore that when all orientations are considered and when the rotations that produce such orientations do not affect the gas molecule collisions, there is one and only one solution to calculating the average value of the mobility in the direction of the field and that is the one given by Equation (13[6b] ). This result also agrees with that of M&M.

2.2. True vs. average mobility

So far, we have seen that the average mobility should be obtained by averaging the tensor D_ij and not the tensor K_ij (despite the coincidence). This average mobility is what is calculated in an ion mobility spectrometer (IMS). What remains to do now is to understand the reasoning behind why Equation (4a[4a] ) yields the same value as Equation (13[6b] ) despite its averaging being in principle mathematically incorrect while Equation (5a[5a] ) yields a different value. To do so, let us first imagine an ion that travels a given distance with a fixed orientation. After such distance is covered, it instantly rotates and travels a new distance in a new fixed orientation. This is repeated until all orientations of the ion are covered. See Figure 2 for a sketch of the process.

Figure 2. Shows the comparison between true and average displacements for two equivalent structures rotating fast (dotted line) and slow (dashed line). True mobility displacement is not in the direction of the Field but, when all directions are equally probable, the average displacement in the direction of the Field is given by <x_i>. On the other hand, true displacement x_j occurs in the direction of the velocity and is given by the true mobility Z₂. It must always be true that <x_j> ≥<x_i>. Δt is the time taken for a single rotation while τ is the total time to cover a given distance.

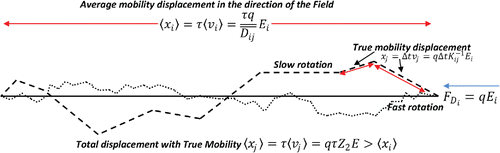
Since Equation (6a[6a] ) must remain valid, then the true drift velocity of a particle along a path before rotating will be given by v_j and therefore its mobility must be given by qK_ij⁻¹. Generally, under a fixed orientation, the drift velocity will not be in the direction of the field. Overall, however, if all directions are equally probable, the distance traveled in the direction of the field would be given by the projection of v_j on the direction of Ei (average drift <v_i>) times the total displacement in time. This is shown in Figure 2 for two particles that are rotating at different speeds. As long as hypothesis (iv) is in effect, the average displacement regardless of the speed of rotation is taken from averaging Equation (6a[6a] ) as[14] where τ is the total drift time.

Before describing the physical meaning of Equation (5a[5a] ), let us first interpret why Equation (4a[4a] ) and Equation (12[11] ) coincide. When Equation (6a[6a] ) is used, the right-hand side always yields the drag force (F_D = K_ijv_j = D_ijv_i) regardless of the value assigned to the angle θ. Every θ-rotation gives exactly the same information so the average of D_ij or K_ij must be equal even though K_ij is missing one orientation. This is similar to projecting v_j in the E_i direction.

However, when K_ij is inverted using Equation (3[3c] ):[15] rotating K_ij⁻¹ an angle θ using E_i as the axis will yield different values of v_j given by R_Eiv_j (v_j ≠ R_Eiv_j). In such case, so that Equation (5a[5a] ) wrongly describes the average value of mobility in the direction of the field and should not be used.

An interpretation can nonetheless be extracted from Equation (5a[5a] ) by trying to calculate the displacement in the direction of the velocity. In such a case, the third orientation angle can be thought of a rotation using the velocity as an axis (instead of using as in Equation (6[6a] a)):[16] where R_vj is the rotation of the ion an angle θ using the velocity v_j as an axis. Note that Equation (16[15] ) and Equation (6b[6a] ) have very different meanings and yield different results when averaged. Averaging or will yield in this case the same result and which coincides with Equation (5a[5a] ). Indeed, this is equivalent to H&B's approach that ultimately calculates the average “settling velocity” and should not be mistaken with calculating the average mobility in the direction of the field. Given that the ion's true displacement is in the direction of the velocity, one can define a true mobility displacement, x_j, different from the average displacement in the direction of the field given by[17]

Since any angle θ used to rotate E_i is valid in Equation (16[15] ), we can choose the angle that makes E_i be a vector fixed in the horizontal direction as is shown in Figure 2. Averaging over the rest of possible orientations yields[18] where the <x_j> is now termed true mobility displacement. <x_j> is always larger or equal to <x_i> and represents how much distance the ion has traveled regardless of direction vs. the average mobility displacement <x_i>, which represents the distance covered in the direction of the field. Perhaps, the intention of H&B was to define this true drift velocity (displacement), which they refer to as “settling velocity” and it was misinterpreted later to be the averaged displacement in the direction of the field. It is quite clear however that Z₂ cannot be used to calculate the electrical mobility of the particle given by a regular IMS instrument as regular instruments cannot interpret how far the ion deviates from the straight path given by a constant electric field. Not even in such cases where an ion does not rotate at all during flight since the average displacement in the direction of the field would still be given by Equation (14[13] ).

3. Results and discussion

In order to understand the error associated with using Z₂ instead of using the corrected average Mobility , an analytical as well as a numerical method is employed. The analytical method calculates the true as well as the average mobility for a disk/cylinder and compares both. The numerical method IMoS has been used to demonstrate the validity of the theory for any structure (not only a disk/cylinder) using all atom models (see the SI). In particular, linear structures up to 1000 atoms and planar structures were studied up to 5000 atoms were computed using the Projected Area and Exact Hard Sphere Methods (EHSS). For the EHSS method, three different models of orientation for the ion are used to obtain independent values and , which are then compared using Figure S1 and Table SI.

3.1. True vs. average electrical mobility of a disk/cylinder

The net drag force on an element of area dA with an outward normal is given by (de la Mora 2002):[19]

Here N is number concentration, T is the temperature, k is the Boltzmann's constant, m_g is the mass of the gas (much smaller than the mass of the ion), is the normal diadic, is the unit diadic, and a is the accommodation coefficient.

For elastic and specular collisions (a = 0), the drag force can be written as[20] where the friction tensor is given by[21] and where dA is integrated over the complete surface of the ion.

In the case of a cylinder or a disk, with each of the bases having a surface and side surface , the friction tensor is given by[22]

The average mobility depending on whether we use the average of the tensor or its inverse yields:[23] [24]

We wish to compare the average of the friction tensor and/or its inverse with the well-known Mason–Schamp equation (repeated from Equation (1[1] )):[25]

Here, , is the first collision integral, which, when specular and elastic collisions are considered and the body is convex (such as in the case of a cylinder or a disk), coincides with the average projected area of the ion. For a disk/cylinder, Cauchy's theorem states that[26]

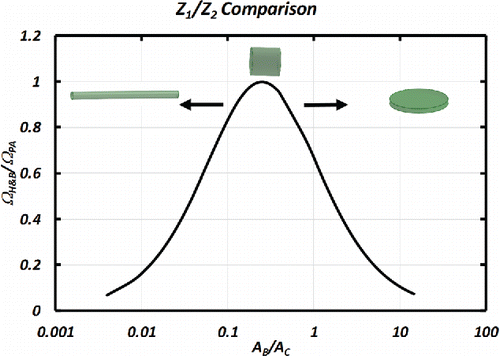
Using the above expression in the Mason–Schamp equation, one arrives at[27] which is exactly equivalent to . However, when is compared to , we arrive at the following equality:[28] which has a solution (or the diameter is equal to the length of the cylinder/disk). By analogy, one can term the collision cross-section from as . Figure 3 shows the ratio ( as a function of the ratio of /. As can be observed, is always equal or smaller than and they are only equal at the particular value specified. Moreover, the bigger the difference between and , the smaller the ratio becomes. A rotation of the tensor in Equation (22[21] ) using Equations (6)–(13) would lead to the tensor and to the agreement of both mobilities in Equations (23[22] ) and (24[23] ).

Figure 3. Ratio of as a function of the ratio of for a disk/cylinder molecule. Note that at , has its maximum value of 1.

4. Conclusions

In this manuscript, it is shown that previous approaches to calculate average collision cross-sections agree when the same considerations are applied. The previously used H&B approach using the inversion of the drag tensor assuming all directions are equally probable is shown to be invalid due to the omission of one of the angles of rotation of the ion in Equation (3[3c] ). A small geometrical consideration to rotate the tensor in the axial direction of the electric force is sufficient to demonstrate that same identical results can be obtained through the tensor or the inverse. We show however that the H&B method gives instead a total displacement of the ion in the direction of the velocity, which we have termed the true mobility displacement to differentiate it from the average mobility displacement.

Analytical calculations of a disk/cylinder molecule show that the ratio between true and average mobility can be quite large. Indeed, there is only one value where the true mobility is equal to the average mobility of the ion. In all other cases, the mobility inferred using H&B, can be several times smaller than that inferred from using the average projected area.

Numerical calculations of the collision cross-section of linear and planar structures using four different approaches has been pursued using IMoS, a momentum transfer kinetic theory approach using all atom models. By calculating both H&B and M&M approaches and comparing them to the regular projected area approximations the inadequacy of the H&B method to predict average mobility values is confirmed.

Acknowledgments

Carlos Larriba-Andaluz would like to acknowledge Juan Fernandez de la Mora for the fruitful discussions that have helped put together this manuscript.