Developing classroom formative assessment in dutch primary mathematics education

Abstract

In the last two decades Dutch primary school students scored below expectation in international mathematics tests. An explanation for this may be that teachers fail to adequately assess their students’ understanding of learning goals and provide timely feedback. To improve the teachers’ formative assessment practice, researchers, curriculum experts and teachers worked together to develop a model for classroom formative assessment (CFA). In three pilot studies, six teachers from three different schools implemented the CFA-model and evaluated its feasibility together with the researchers by means of checklists. The CFA-model was primarily changed with regard to the assessment techniques. Teachers indicated that classroom management and preparation time were preconditions for an optimal implementation. Analysis of covariance was used to explore students’ learning outcomes. The results showed that a correct implementation of the CFA-model might result in the enhancement of students’ mathematical performance. The implications of the three pilots for the implementation of the CFA-model on a larger scale are discussed.

Key words:

• Educational design
• classroom formative assessment
• formative assessment
• mathematics
• primary education

Introduction

In the last two decades, Dutch primary school students scored below expectation on different mathematics tests (Janssen et al. 1999; Van Weerden, Hemker, and Mulder 2014). In fact, it was reported that 10–18% of all Dutch primary school students was underachieving (Mulder, Roeleveld, and Vierke 2007). This was most likely caused by the fact that teachers hardly assessed their students’ progress systematically by means of standards-based tests in order to provide feedback to adhere to their students’ needs (Dutch Inspectorate of Education 2008). In other words, teachers did not use formative assessment adequately in their teaching. Formative assessment refers to the process of gathering and analysing information about the students’ understanding of a learning goal to provide instructional feedback that helps the students forward (Black and Wiliam 2009; Callingham 2008; Shepard 2008).

As in other western countries (Mandinach 2012), the first initiative in the Netherlands to improve the teachers’ formative assessment practice was the introduction of a type of formative assessment called Data-Driven Decision Making (DDDM). In the Netherlands, DDDM entailed that the teacher would analyse student data gathered from half-yearly standardised mathematics tests in order to set goals for subgroups within the class (e.g. low-achieving, average and high-achieving students) and to develop different instruction plans for these groups (Dutch Inspectorate of Education 2010). In contrast to the expectations, several studies in the Netherlands and other western countries showed that DDDM hardly enhanced student performance (Carlson, Borman, and Robinson 2011; Quint, Sepanik, and Smith 2008; Van Weerden, Hemker, and Mulder 2014). An explanation for the lack of improvement might be that teachers find it difficult to analyse student data and to use this information to provide timely and appropriate feedback to students who need it (Mandinach 2012; Shaw and Wayman 2012; Wayman, Stringfield, and Yakimowski 2004).

A different type of formative assessment, called Classroom Formative Assessment (CFA), might be more effective in enhancing student performance. Within CFA the teacher assesses the students’ understanding during lessons and provides immediate instructional feedback, such as small group instruction or individual help. Especially for conceptual and procedural skills, which are often practiced in mathematics education, immediate instructional feedback is effective in enhancing student proficiency (Shute 2008). Often, CFA is used to steer the teacher’s instruction. CFA-techniques, such as questioning, classroom discussions or games, allow the teacher to get a global overview of the class’s understanding of the learning goal and make instructional decisions, such as slowing down or speeding up the instruction or instructing in a different manner (Leahy et al. 2005; Shepard 2000; Veldhuis et al. 2013). Although the use of such CFA-techniques will ensure that the teacher provides an instruction that fits the majority of students in the class, it is questionable whether the techniques will help the teacher to gain insight into the students’ individual needs and provide feedback accordingly. For instance, if a teacher starts a classroom discussion to assess the students’ understanding of a particular mathematical problem, he or she will not know which specific student is experiencing difficulties with the task at hand and what these difficulties entail. As a consequence, the teacher cannot provide feedback that will help individual students forward. Therefore, we focused on CFA for the purpose of differentiation after the instruction. This means that the teacher should use an assessment after the instruction to determine each individual student’s understanding of the learning goal and to provide immediate instructional feedback to those students who need it.

Although CFA and differentiation have been linked to each other in the past, often only suggestions for CFA for differentiation purposes are provided (e.g. Falkoner Hall 1992; Moon 2005). To our knowledge, a model for CFA in order to differentiate after the instruction has not been developed. Therefore, in this study, researchers, curriculum experts and teachers worked together to develop such a model. The model should improve teachers’ formative assessment practice and ultimately enhance students’ mathematics performance.

Theoretical background

Classroom formative assessment

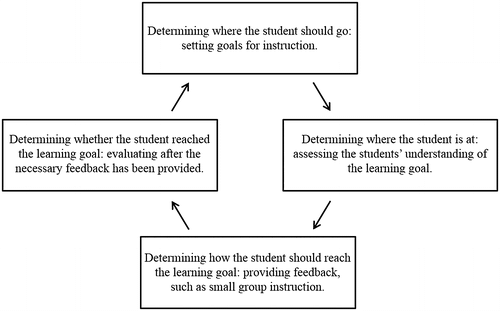
Formative assessment is considered to consist of four elements that are depicted in Figure 1 (Sadler 1998; Wiliam and Thompson 2008).

Figure 1. Four elements of formative assessment.

It is possible to distinguish types of formative assessment when looking at the place, timing and purpose of the four elements. In CFA all elements are incorporated in the lessons to move the student forward as quickly as possible. As was mentioned in the introduction, in this study, we focused on CFA for the purpose of differentiation after the instruction. By planning the assessment after the instruction, the teacher has enough time to determine whether each student understands the learning goal and which difficulties he or she is encountering. This information allows the teacher to give specific instructional feedback that focuses on the individual student’s problems.

The elements in Figure 1 imply that there is a certain degree of coherence between them: one step seems to lead to the other. However, it appears that teachers do not use CFA in a coherent way (Wylie and Lyon 2015). For instance, teachers tend to assess their students’ understanding without setting clear goals and criteria for success (Antoniou and James 2013) or do not provide adequate feedback based on the information gathered during the assessment (Furtak et al. 2008; Wylie and Lyon 2015). Therefore, in this study, we tried to develop a model in which a teacher uses all four elements coherently during mathematics lessons.

Educational design: a collaboration

In order to ensure that CFA is feasible in practice, it is necessary for researchers, curriculum experts and teachers to work together to design a CFA-model. Such a collaboration gives the researchers, curriculum experts and teachers the opportunity to share knowledge and develop new knowledge through interaction (Brandon et al. 2008). A collaboration acknowledges the fact that teachers often are too busy and ill trained to design and develop a CFA-model based on scientific literature. Similarly, most researchers do not have knowledge of the complexities of teaching practice to create a feasible model (Anderson and Shattuck 2012).

The feasibility of a CFA-model might be enhanced by embedding it in the curriculum. The curriculum materials provide information about lesson plans, learning goals and suggestions for instruction (Nicol and Crespo 2006). Often, both the teacher and the researcher lack an in-depth knowledge of the curriculum materials to fully understand its limitations and, more importantly, its opportunities. Therefore, the knowledge of a curriculum expert is of substantial value.

In this study, the development of a CFA-model consisted of four phases (Richey, Klein, and Nelson 2003; Van Den Akker 2010):

•	Phase 1 (researchers and curriculum experts): Definition of the research problem and reviewing related literature in order to create a concept of the model;
•	Phase 2 (researchers and teachers): Developing the concept in close collaboration and interaction with a small group of teachers including systematic documentation and analysis of the intervention by means of observations, evaluations and tests;
•	Phase 3 (researchers and teachers): Refining the model continually based on the observations, tests and feedback of teachers.
•	Phase 4 (researchers and teachers): Implementing the prototype for the model a second and third time to further develop the model by means of observations, evaluations and tests.

Research questions

In this article, we report on a study in which two researchers, two curriculum experts and six teachers from three different schools shared theoretical and practical insights in order to develop a curriculum-embedded model for CFA. The aim of the study was to develop a fully operational CFA-model based on theoretical considerations about effective CFA that should improve teachers’ formative assessment practice and consequently enhance students’ mathematics performance. The questions we seek to answer in this article are:

(1)	Out of which elements should a model for CFA in Dutch primary mathematics education consist of?
(2)	Which amendments should be made to the CFA-model for it to be feasible in practice?
(3)	Do students of a teacher who uses the CFA-model during mathematics education perform better on a mathematical test than students of a teacher who does not use the CFA-model during mathematics education?

Study design

Participants

Six female teachers participated in three pilot studies. Each pilot was held at a different school in order to evaluate whether the developed model would be feasible for teachers with different amounts of teaching experience and within a variety of teaching environments (e.g. high, average and low SES-students). During the first pilot two second-grade teachers implemented a concept CFA-model. Teacher A had one year of teaching experience; teacher B had approximately 15 years of teaching experience. During the second pilot, one second-grade teacher and one third-grade teacher implemented the CFA-model. Teacher C had approximately seven years of teaching experience, teacher D had approximately 20 years of teaching experience. Another second-grade and third-grade teacher participated in the third pilot. The second-grade teacher (teacher E) had approximately 40 years of teaching experience, whilst the third-grade teacher (teacher F) had approximately seven years of teaching experience. These six teachers seem to reflect the Dutch population of teachers with regard to teaching experience and gender adequately (Dutch Ministry of Education, Culture and Science 2014).

During the first pilot, 28 students (boys: 50%) in a class where the teacher used the concept CFA-model took three different mathematics tests: one pre-test and two post-tests. The students’ performance was compared to the performance on these tests of 29 students (boys: 59%) in a parallel class within the same school. The classes did not differ significantly to each other with regard to gender (χ² = .43, df = 1, p = .51). The pre-test scores of the students were used in the analyses to correct for possible differences in performance between the two classes prior to the intervention.

Procedure

Phase 1: reviewing literature in order to design a concept CFA-model

Based on a review of literature about effective CFA, the researchers designed a concept for a CFA-model in collaboration with curriculum experts. The researchers and curriculum experts analysed two curricula that were predominantly used in Dutch mathematics education. The analysis of the curriculum materials was focused on the four elements of CFA (see Figure 1):

•	Setting goals for instruction: The number of learning goals that were covered per lesson, the description of these learning goals and the extent to which the curriculum materials provided the teacher guidance (e.g. examples of mathematical representations or procedures) for instruction.
•	Assessing the students’ understanding of the learning goal: The assignments and activities present in the curriculum materials that could be used to assess the students’ understanding.
•	Providing feedback: The description of small group instruction to enhance the students’ understanding of the learning goal (e.g. description of previous knowledge or suggestions for instructional materials); The assignments and activities present in the curriculum materials to facilitate small group instruction.
•	Evaluating after the necessary feedback has been provided: Suggestions and materials for the evaluation of students’ understanding.

Phase 2 and 3: developing the concept model in collaboration with teachers

In the first pilot, a school team that was interested in improving their teaching practice, received information about the rationale of CFA and the concept CFA-model that was developed so far. During this first meeting in week 1 the school team had the opportunity to suggest amendments to the model. After the meeting two teachers were willing to further discuss and then implement the concept CFA-model in their mathematics lessons in order to help develop the model. The second meeting with the two teachers in week 2 was used to explain the concept CFA-model in more detail, which allowed the teachers to provide in-depth feedback about its feasibility. The researchers also demonstrated how they envisioned the use of a classroom response system to assess the students’ understanding of the covered learning goals at the end of a week. The teachers were asked to suggest amendments to the entire CFA-model to make it more feasible to use in daily practice.

Subsequently, the teachers implemented the CFA-model in their mathematics lessons. From week 3 until week 5, the researchers visited the teachers six times. At the end of every visit, the researcher and teachers discussed about a particular topic concerning (a key element of) the CFA-model in order to make amendments to the model. After this first part of the pilot, the researchers returned to the classroom for two more visits: once in week 7 and once in week 10. This second part of the pilot was used to let the teachers experience the use of the CFA-model on their own and suggest further amendments.

In order to get an indication of the CFA-model’s efficacy, the students in the participating teachers’ class (experimental group) and a parallel class in the same school (control group) took a mathematics pre-test during the second week of the pilot. During the fifth and tenth week the two classes took two different post-tests. Table 1 shows the entire procedure for the first pilot.

Table 1. Procedure of the first pilot.

Week	Participants	Activity	Topics for discussion
	Researchers and curriculum experts	Meeting	Literature study; analysis of curriculum materials; development concept CFA-model
1	Researchers and teachers	Introduction and discussion	Rationale of CFA; first amendments
2	Idem	Mathematics test for students
		Meeting with teachers	The CFA-model in more detail; set-up quiz
3	Idem	Classroom visit (lesson) and discussion	Goal setting for instruction; selecting assignments and activities for assessment
		Classroom visit (quiz) and discussion	Duration of quiz; technical issues
4	Idem	Classroom visit (lesson) and discussion	Duration assessment; small group instruction
		Classroom visit (quiz) and discussion	Duration of quiz; technical issues; analysis results
5	Idem	Classroom visit (lesson) and discussion	Content of assessment; content small group instruction
		Classroom visit (quiz) and discussion	Technical issues; providing feedback
		Mathematics test for students
7	Idem	Classroom visit (lesson) and discussion	Experiences teachers
10	Idem	Classroom visit (lesson) and discussion	Experiences teachers
		Mathematics test for students

Phase 4: implementing the concept model a second and third time

Four more teachers implemented the CFA-model during a second and a third pilot. The procedure for these pilots was the same as the procedure of the first pilot with the exception of the mathematics tests for the students and the extra visits in the seventh and tenth week. Once again, during a first meeting the school team received information about the rationale of CFA and the amended concept CFA-model. During this first meeting both school teams had the opportunity to suggest amendments to the model based on their own experience as teachers. The second meeting was used to discuss the concept CFA-model in more detail with two teachers from a second-grade and a third-grade class in both schools. The researcher demonstrated how the use of the classroom response system to assess the students’ understanding of the covered learning goals at the end of the week was developed so far. The teachers were asked to suggest amendments to the entire CFA-model.

Hereafter, the teachers implemented the CFA-model in their mathematics lessons. The researchers visited the teachers six times over the course of three weeks. At the end of every visit the researchers and teachers discussed about the CFA-model in order to make amendments to the model. During these visits, the same topics were discussed as the topics in the first pilot.

As neither school had parallel classes, the students’ performance in the CFA-classes could not be compared to other classes in the school.

Instruments

Checklists for visits

During the pilots, the researchers visited the teachers six times: three times for a lesson and three times for a quiz (weekly assessment). The researchers used a checklist to make notes about the lesson or quiz. This checklist was also used to guide the discussion with the teachers afterwards. The discussion consisted of three parts:

(1)	Preparation of the lesson/quiz: Question example: To what extent were you able to identify the learning goal for this lesson?
(2)	The lesson/quiz with specific topics for discussion: Question example: To what extent were you able to assess the individual students’ understanding within a short amount of time?
(3)	Input from the teachers: Question example: What kind of teacher knowledge or skills are preconditions for implementing the CFA-model?

Mathematics tests in the first pilot

During the first pilot, the students in the experimental group (CFA-class) and the control group took one pre-test and two post-tests. We screened the psychometric qualities of these tests by calculating p-values, corrected item-total test score correlations and Cronbach’s alpha values. We deleted items with item-total test score correlations lower than .10 from any of these tests as such items discriminate poorly (cf. Nunnally and Bernstein 1994).

The pre-test consisted of 24 items about adding and subtracting up to 20. The students had 10 s to answer each item. The internal consistency of the pre-test was good with Cronbach’s α = .88. The mean difficulty of the items was .67 (SD = .21) and the corrected item-total correlations ranged from .23 to .50. These results indicate that although the test may have been somewhat difficult, it discriminated well between students with high and low mathematics ability.

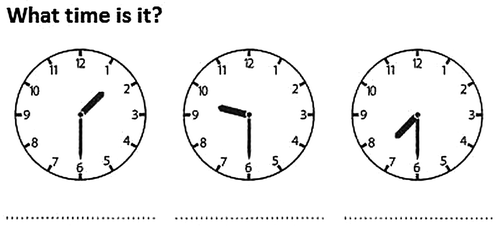
The first post-test was a curriculum-embedded test that consisted of 60 items. These items were about the learning goals that were covered during one chapter (approximately a month), such as adding and subtracting up to 20, jumping on a number line or telling time. Figure 2 depicts three items from the pre-test about telling time. The internal consistency of the first post-test was high with Cronbach’s α = .95. However, the corrected item-total correlation of one item was very low, indicating that it did not discriminate between students. Therefore, we removed this item from the test, resulting in 59 items with a mean difficulty of .82 (SD = .10) and corrected item-total correlations ranging from .14 to .71.

Figure 2. Three items from the first post-test.

Approximately a month after the first post-test the students took a second post-test. The second post-test was a curriculum-embedded test covering a different chapter and different learning goals, for example jumping on a number line, multiplications and reading a calendar. An example of an item in the second post-test is provided in Figure 3. The test initially consisted of 55 items. As six items had negative corrected item-total correlations, we removed these items from the test. The second post-test therefore consisted of 49 items with a mean difficulty of .85 (SD = .10) and r² ranged from .14 to .50. Its internal consistency was high with Cronbach’s α = .90.

Figure 3. Item from the second post-test.

By means of an independent samples t-test, we tested whether the students in the two classes differed significantly from each other with regard to their mathematics performance prior to the intervention. We used an analysis of covariance to test whether the students in the experimental group outperformed their peers in the control group in the post-tests. The analysis of covariance allowed us to test the efficacy of the teachers’ use of CFA whilst controlling for the students’ pre-test scores.

Results

Phase 1: reviewing literature in order to design a concept CFA-model

The researchers and curriculum experts determined how CFA could best be embedded in two widely used mathematics curriculum materials in Dutch primary education. Our analyses showed that the curriculum materials provided daily lesson plans with one main goal per lesson, suggestions for instruction (including examples of mathematical representations and procedures) assignments for students and achievement tests at the end of each chapter. Both curriculum materials contained several “assessment feedback loops”:

•

A short-term assessment feedback loop: Sometimes suggestions for the assessment of the class’s understanding of the learning goal during the instruction were provided, such as assessment games. Furthermore, the teacher was advised to check the work of the students after each lesson. There were few suggestions for instructional feedback after these assessments.

•

Two long-term assessment feedback loops: The curriculum material provided suggestions for small group instruction during the lesson to the low-achieving students. It was implicitly stated that these students would be identified by means of an analysis of the standards-based test (half-yearly). The curriculum materials also provided some instructions on how to provide the students who failed the curriculum-embedded test, instructional feedback a final time.

The analysis of the curriculum materials and the literature led us to believe that the main focus of the curriculum materials lay on the two long-term assessment feedback loops. These assessment feedback loops allow for a rather large time span between the assessment and the instructional feedback. As a consequence, students can practice with faulty mathematical knowledge and procedures that may turn out to be difficult to correct later on. Therefore, the researchers and curriculum experts decided that a CFA-model should, in addition to the two long-term assessment feedback loops, consist of a short-term assessment feedback loop and an intermediate assessment feedback loop.

Applied to a weekly lesson schedule, the concept model required that for each lesson the teacher decided upon a basic learning goal for the entire class and gave an instruction accordingly. By setting a goal for instruction the teacher determines which knowledge and skills need to be taught and assessed. Goal setting makes it possible to assess the students’ understanding, give appropriate feedback and subsequently improve proficiency (Ashford and De Stobbeleir 2013; Locke and Latham 2006; Marzano 2006). This first “step” of the concept model should be easy to implement, since most of the required information was already present in the curriculum materials.

Hereafter, the teacher should assess each individual student’s understanding of the learning goal. In a class with an average of 25 students, the most efficient way of collecting evidence about the students’ understanding is to give them specific tasks and subsequently assess their mathematical proficiency (Ginsburg 2009). In our concept model, such an assessment could be done by (1) asking questions that the students answered by holding up cards, (2) an assessment round during which the teacher would check the students’ individual, or (3) standing up/sitting down games (“When you think the correct answer is A, please stand up”). All three techniques would provide the teachers information about the individual students’ understanding of the learning goal. In addition, the teacher would ask the students to use a mathematical representation when making their assignments or answering questions. By doing so, the teacher gains more in-depth insight into the student’s understanding of the learning goal and should be better able to accommodate the feedback to the student’s needs (Heritage and Niemi 2006).

Subsequently, the teacher was expected to use the information gathered during the assessment to provide immediate instructional feedback in the form of small group instruction to those students who did not show a sufficient understanding of the learning goal. In this way, the time span between the assessment and the feedback would be kept to a minimum. At the end of the day the teacher would check the work of the students to assess once more whether all students understood the learning goal. This sequence of lesson episodes constituted the short-term assessment feedback loop.

Whether the short-term assessment feedback loop would suffice in identifying and correcting all students’ misconceptions was uncertain. Therefore, it seemed reasonable to assess the students’ understanding of the learning goal by using longer assessment feedback loops. Moreover, assessment and instructional feedback that is spaced over a longer period of time is beneficial for the memorisation of (mathematical) facts (Butler, Karpicke, and Roediger 2007). In order to give teachers the opportunity to assess and provide feedback a second and third time, our concept model consisted of two more assessment feedback loops: an intermediate and a long-term assessment feedback loop.

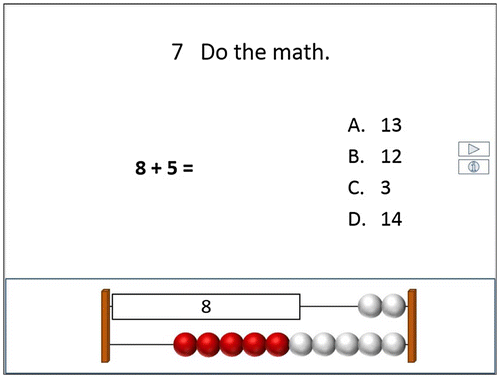
The intermediate assessment feedback loop referred to weekly assessments. In our concept model, the progress of the students would be evaluated every week by means of a digital quiz on the digital whiteboard consisting of eight multiple choice questions based on the four learning goals that were covered during the weekly programme. Figure 4 depicts an example of a multiple-choice question in the quiz.

Figure 4. Example of a multiple-choice question in the quiz.

The multiple-choice questions help to detect well-known misconceptions (Ginsburg 2009). The students could answer these questions by means of a clicker (voting device). This approach was chosen to enhance the participation of the students (Lantz 2010). During the quiz, the strategy of peer instruction would be used (Mazur 1997). This strategy entailed that the students had the opportunity to answer the question one time, get a hint (e.g. the abacus in Figure 4), discuss with a peer and finally answer a second time. Afterwards, the teachers discussed with the students how the question should be solved. At the end of the quiz the teacher was expected to analyse the individual scores of the students to determine which students still needed instructional feedback about one of the learning goals that was covered during the lessons. During the last lesson of the week the teacher would give small group instruction to students who did not perform satisfactorily on some of the learning goals assessed by the quiz. The teacher would give the other students who performed satisfactorily more challenging tasks.

Finally, the teachers would use the long-term assessment feedback loop that was described in the curriculum materials. This loop refers to the provision of remedial feedback when students fail on the curriculum-embedded test. The information that the teacher gathered from this test would be used to give instructional feedback, in the form of small group instruction, to those students who failed a particular learning goal and to give more challenging tasks to those students who mastered the learning goals. The information was not used to form fixed level groups within the class. Table 2 shows this concept model in a condensed form.

Table 2. Concept CFA-model: bold parts are the adjustments the teachers should make in their teaching.

	Short-term assessment feedback loop	Intermediate assessment feedback loop	Long-term assessment feedback loop
Goal-setting and instruction	• One learning goal for the entire class • Short instruction entire class • Use of mathematical representations	• Goals that were covered during the week	• Goals that were covered during a chapter of the curriculum
Assessment	• Holding up cards, assessment round or sitting/standing-game • Assessment of students’ use of mathematical representations or procedures • Selecting students for immediate instructional feedback	• Digital quiz • Peer instruction • Immediate feedback • Analysis of individual quiz results and selecting students for instructional feedback or more challenging assignments the next day	• Curriculum-embedded test • Analysis of tests based on tutorial curriculum materials • Selecting students for instructional feedback or more challenging assignments
Instructional feedback	• Immediately after the assessment to the students that were selected based on the assessment	• Goal-directed instructional feedback with use of a mathematical representation to the students that were selected based on the assessment	• Goal-directed instructional feedback with use of a mathematical representation to the students that were selected based on the assessment
Evaluation	Checking students’ work	Checking students’ work	Checking students’ work

Phase 2 and 3: developing the concept model in collaboration with teachers

During the first meeting the researchers and teachers discussed what needed to be amended within the model before it could be put into practice. The concept CFA-model was changed with respect to the short-term assessment feedback loop and the intermediate assessment feedback loop. The teachers remarked that they preferred to walk around the classroom and observe the students’ mathematical procedures instead of playing assessment games during the instruction. The teachers expected that an assessment round would take less time and demand less classroom management. Furthermore, the teachers predicted that the discussion between students and answering the question a second time during the quiz would lead to turmoil in the classroom. The researchers and teachers decided to let the students answer a first time, show the hint after answering and let the students answer a second time.

After the first meeting the two second-grade teachers put the concept CFA-model into practice. The researchers visited the teachers during the lessons and quizzes and discussed with the teachers which other changes had to be made to the CFA-model. Practical issues such as registration of the students who needed small group instruction were discussed as well as theoretical issues such as the necessity of repeating the assessment feedback loop during small group instruction (i.e. How does one assess the students’ understanding of the learning goal during small group instruction and how (many times) does one provide instructional feedback?). The teachers stated that choosing the right mathematical representation for (small group) instruction was difficult. Sometimes, the curriculum materials would suggest more than one mathematical representation or suggest one that was not in accordance with their own knowledge about mathematical representations. The researchers decided to provide the teachers with mathematical representations and strategies in line with the learning trajectory. These issues were taken up in the CFA-model. Based on the teachers’ experiences with the quizzes and the analyses of the quiz results it appeared that the opportunity to answer the same question twice confused the students. Some students answered the question correctly the first time, but thought they should better change their answer the second time. This complicated the interpretation of the quiz results: Should the teacher base the selection of students for small group instruction on the first answer or the second answer or a combination of both? The most practical solution was that the teacher would show the hint during the question – when it took students long to answer the question or when the teacher knew that the question was difficult – and let the students answer just once.

At the end of the first four weeks the teachers expressed that they enjoyed working with the CFA-model. Teacher A indicated that she had noticed that different students than the low-achieving students from the fixed level groups, needed small group instruction based on her assessment. She also stated:

I expected I had to change my lessons drastically, but that was not the case at all.

Teacher B found it difficult to refrain herself from helping students who were experiencing difficulties, during the assessment round. However, at the end of the four weeks she commented that the CFA-model gave structure to her lessons and saved her and her students time. At the end of the week, all students were able to finish their tasks, whereas before this was not the case.

Despite the optimistic nature of these statements, the visits in the seventh and tenth week of the pilot showed, that the teachers did not teach according to the concept CFA-model anymore. Both teachers stated that for a period of time extracurricular activities prevented them from optimally planning their lessons, fully executing the lessons according to the CFA-model and administering the digital quiz. The teachers indicated that after three weeks of implementing the CFA-model they were not comfortable enough with it. Another issue was the fact that the teachers did not always exactly know how to give and organise small group instruction after their assessments, seeing that the group composition – and with it the students precognition – could differ per lesson. It was easier to teach the lesson as described in the curriculum materials: giving small group instruction to the fixed level groups and responding to questions of individual students at their workplace. This required the teachers less preparation time before the lesson and less flexibility during the lesson. These statements might mean that teachers need coaching on the job for more than three weeks.

As was mentioned in the procedure section, the students of the experimental group and the students of the control group were tested three times. Due to illness, one student in the experimental and one student in the control group were unable to take the first post-test. For the same reason, two students in the control group were not able to take the second post-test.

The students showed no significant differences on the pre-test with t(53) = 1.29 and p = .20. The results of an analysis of covariance showed that the students in the experimental group scored somewhat higher on the first post-test than the students in the control group after correcting for the pre-test scores with a partial η² of .03, which is considered to be a small to medium effect (Cohen 1988). However, this difference failed to reach significance with F(1,52)= 1.66 and p = .10 (one-sided). The difference between the students’ performance on the second post-test was comparable to the difference on the pre-test. After correcting for the pre-test scores this difference was not significant with F(1,52) = .68 and p = .22 (one-sided). Table 3 provides an overview of the student performance on all mathematics tests.

Table 3. Student performance on the pre-test, post-test 1 and post-test 2 during the first pilot.

Condition	Pre-test (0–24)			Post-test 1 (0–59)			Post-test 2 (0–49)
	N	M	SD	N	M	SD	N	M	SD
Experimental group	28	17.14	4.68	27	50.04	7.78	28	42.68	6.98
Control group	29	15.07	5.65	28	44.96	13.57	27	40.11	8.55

Phase 4: implementing the concept model a second and third time

In the second pilot, the teachers used the same curriculum materials as the teachers in the first pilot. During the first two meetings the teachers did not suggest any amendments to the latest version of the CFA-model. However, once the teachers implemented the model, they encountered some unforeseen difficulties. The teachers indicated that they found it difficult to determine what to do if their assessment indicated that every student understood the learning goal or – the other way around – hardly any student understood the learning goal. These findings led to further changes in the CFA-model with more suggestions for the follow-up upon the assessment. The assessment should not necessarily lead to immediate instructional feedback to a small group, but could also consist of immediate instructional feedback to the entire class or instruction about more challenging tasks if all the students understood the learning goal. The teachers indicated that the weekly assessments by means of the quizzes went well. However, there was one issue that needed to be discussed, seeing that teacher C stated:

One student out of my class needed to get small group instruction based on the quiz results. But it turned out she already understood everything, which made her insecure about herself.

Teacher D indicated that she also noticed that some students did not perform as expected on the quiz. When the teachers were asked to elaborate upon their observations, they added that some students showed anxiety during the quiz. The researchers and teachers discussed what to do when such students would perform below expectation on the quiz due to – personal – circumstances. As a result, the CFA-model was adjusted by incorporating the teacher’s daily assessments in the analysis of the quiz results. The teachers would use both their daily assessments and the weekly quiz results to determine whether a student needed small group instruction.

The teachers in the third pilot were also introduced to the rationale of CFA and the concept CFA-model as was developed so far. During the first two meetings the teachers indicated that they wanted to use the CFA-model the way it was described. However, both teachers did have some remarks after implementing the CFA-model in their teaching. Teacher E noticed that she had the tendency to help the students during the assessment round, which resulted in a prolonged assessment round. This teacher also indicated that the model made sense to her, but it also entailed that a teacher should flexibly use the curriculum materials and have a clear understanding of the mathematical learning trajectories. Teacher F had more difficulties in implementing the CFA-model. She remarked that sometimes her class was too unsettled for her to implement the CFA-model as intended. Despite the fact that both teachers each had issues in implementing the model, these issues did not lead to substantial changes to the CFA-model. Table 4 shows the final CFA-model after the three pilots. All of the changes to the concept CFA-model are underlined.

Table 4. Final CFA-model: bold parts are the adjustments the teachers should make in their teaching; Underlined parts are the amendments the teachers made to the concept CFA-model.

	Short-term assessment feedback loop	Intermediate assessment feedback loop	Long-term assessment feedback loop
Goal-setting and instruction	• One learning goal for the entire class • Short (max. 15 min) instruction entire class • Use of mathematical representations	• Goals that were covered during the week	• Goals that were covered during a chapter of the curriculum
Assessment	• Assessment round • Assessment of students’ use of mathematical representations or procedures • Selecting students for immediate instructional feedback and registration of these students	• Digital quiz • Hint during answering the question • One chance to answer • Immediate feedback • Analysis of individual quiz results and selecting students for instructional feedback or more challenging assignments the next day	• Curriculum-embedded test • Analysis of tests based on tutorial curriculum materials • Selecting students for instructional feedback or more challenging assignments
Instructional feedback	• Immediately after the assessment in a small group, for the entire class or instruction about more challenging tasks (depending on the results of the assessment) • Including assessment	• Goal-directed instructional feedback with use of a mathematical representation to the students that were selected based on the daily assessments and the weekly quiz results • Including assessment	• Goal-directed instructional feedback with use of a mathematical representation to the students that were selected based on the assessment • Including assessment
Evaluation	• Checking students’ work	• Checking students’ work	• Checking students’ work

Conclusion

The aim of this study was to design a coherent, curriculum-embedded CFA-model for primary mathematics education in order to improve teachers’ formative assessment practice and consequently enhance students’ mathematical performance. Researchers, curriculum experts and teachers worked together and shared theoretical and practical insights in three pilot studies to develop a CFA-model that would consist of coherent elements and be easy to implement.

Based on a thorough review of scientific literature, the researchers and curriculum experts designed a concept CFA-model consisting of a short-term assessment feedback loop, an intermediate assessment feedback loop and a long-term assessment feedback loop. Each assessment feedback loop contained the four elements of effective CFA: goal setting for instruction, assessment, instructional feedback and evaluation (Ashford and De Stobbeleir 2013; Butler, Karpicke, and Roediger 2007; Ginsburg 2009; Heritage and Niemi 2006; Lantz 2010; Locke and Latham 2006; Marzano 2006; Mazur 1997; Shute 2008; Wiliam and Thompson 2008).

Although the curriculum experts mainly took part in this first phase of the development of the CFA-model, their input was indispensable, as the researchers were sometimes unaware of all the available materials in the curriculum. Some issues that the researchers addressed could be easily solved with the available materials in the curriculum. The curriculum experts’ input thus helped to keep the concept CFA-model as straightforward as possible. On the downside, it sometimes seemed that the curriculum experts were hesitant to admit a shortcoming in the curriculum materials that they developed, which strained the development process of the CFA-model somewhat. In future research, it might be advisable to involve curriculum experts that did not create the curriculum materials themselves, in the development of an educational innovation to ensure a more objective point of view.

The teachers in the three pilots indicated that the concept CFA-model should be changed on several points for it to be feasible in practice. The main changes concerned the use of an assessment round during the lesson, including an assessment during small group instruction and limiting the duration of the quiz by letting the students only answer a question once. After these amendments, the teachers indicated that the CFA-model could be implemented in their mathematics teaching rather easily. Though, for the implementation of the CFA-model on a larger scale, the teachers did indicate that many teachers will probably have difficulties with the classroom management skills needed for the CFA-model to be used appropriately and the time that is required for the quiz.

The issues that the teachers touched upon show the necessity of a collaboration between researchers and teachers to develop a CFA-model or any other educational innovation. It seemed that the concept CFA-model as developed by the researchers and curriculum experts was oversimplified. This is not uncommon, since most researchers are not fully aware of the complexities of teaching (Anderson and Shattuck 2012). The researchers and curriculum experts clearly underestimated the preconditions – with regard to the lesson preparation time and skills in classroom management – for implementing the concept CFA-model in practice. The preconditions might be of value once the final CFA-model will be implemented on a larger scale.

To get a glimpse of the CFA-model’s efficacy, the students in the first pilot made three mathematics tests: one pre-test and two post-tests. The difference between the students in the CFA-class and the students in the parallel class increased in favour of the CFA-class when the teachers used the CFA-model and decreased once the teachers stopped using the model. Although the sample of students was too small to draw any definite conclusions about the efficacy of the model and the difference on the first post-test failed to reach significance, these results might indicate that the CFA-model can be effective if it is implemented over a longer period of time.

The visits in the first pilot during the seventh and tenth week indicated that there might be some issues concerning the sustainability of the model. The teachers reported that they were not comfortable enough with the model after just three weeks of implementation. Stress coming from extracurricular activities made them relapse into old routines. It is not uncommon that teachers find it difficult to change their teaching routines. Usually, it takes teachers a vast amount of time and effort to make an educational innovation their own (Guskey 2002). For this reason, it is often recommended that teachers are coached on the job intensively to ensure the implementation of an educational innovation, such as the CFA-model (Guskey and Yoon 2009; Kretlow and Bartholomew 2010).

Overall, the final CFA-model is not as easy to implement as we had hoped it would be. All the small details that a teacher needs to change in his/her lesson taken together seem to end up in a rather invasive change in teaching routines. Although the teachers of the pilots were capable of implementing the CFA-model for a short period of time and were optimistic about the feasibility of the final CFA-model, it is unclear whether other teachers with other backgrounds will be able to implement the model. It is also uncertain whether this larger number of teachers can implement the CFA-model for a longer period of time, seeing that our study only dealt with six teachers that implemented the CFA-model for no longer than two months. Thus, it is advisable to follow this study up with an implementation study, in which the CFA-model is implemented by more teachers at different schools and for a longer period of time. Such a study should shed light on the feasibility of the CFA-model as well as the sustainability of the model.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

The study was supported by a grant from the Netherlands Organisation for Scientific Research (NWO-PROO), The Hague

Notes on contributors

Marian van den Berg is a PhD candidate at the Groningen Institute for Educational Research (GION education/research) of the University of Groningen. Her main research project focuses on the use of classroom formative assessment by teachers in primary mathematics education. The project consists of studies regarding the development, implementation and effectiveness of a classroom formative assessment model.

Egbert G. Harskamp is a Professor Emeritus at the Groningen Institute for Educational Research (GION education/research) of the University of Groningen. His research has concentrated on effective digital learning environments and the implementation of mathematics education curricula in primary and secondary education.

Cor J. M. Suhre is a senior researcher in the teacher education department of the University of Groningen. His research interests include the assessment of computational thinking in secondary education, the contribution of computer-assisted instruction to improve problem solving in physics and mathematics and the professional development of teachers. Currently, he is involved in instrument development research aimed at the assessment of critical and creative thinking skills in university degree programmes.