The Madden-Julian Oscillation

ABSTRACT

There are rich variabilities in the global atmosphere and climate system on the intraseasonal time scale. This review article focuses on the Madden-Julian Oscillation (MJO), which is the dominant mode of tropical intraseasonal variability. The MJO has a tremendous global impact and represents a major source of skill for subseasonal to seasonal predictions. Our knowledge on the MJO has been advanced in recent decades, but challenges remain in understanding, simulating and predicting the MJO and its global influence. Here we review the basic observed features of the MJO, possible mechanisms, the related teleconnections and tropical-extratropical interactions, its interannual variation, and its simulation and predictions.

RÉSUMÉ

[Traduit par la rédaction] L’atmosphère mondiale et le système climatique présentent de riches variabilités à l’échelle intrasaisonnière. Le présent article porte sur l’oscillation de Madden-Julian (OMJ), qui est le mode dominant de la variabilité tropicale intrasaisonnière. L’OMJ a une incidence mondiale considérable et constitue une source majeure de compétences pour les prévisions sous-saisonnières et saisonnières. Nos connaissances liées à l’OMJ ont progressé au cours des dernières décennies, mais il reste des défis à relever pour comprendre, simuler et prévoir l’OMJ et son influence globale. Nous examinons ici les caractéristiques fondamentales observées de l’OMJ, les mécanismes possibles, les téléconnexions connexes et les interactions tropicales-extratropicales, sa variation interannuelle, ainsi que sa simulation et ses prévisions.

Keywords:

• Madden-Julian Oscillation
• tropical waves
• teleconnection
• intraseasonal variability
• subseasonal prediction

1 Introduction

The intraseasonal or subseasonal time scale falls in the range from two weeks to a season, i.e. 14–90 days. It lies across the boundary between weather and climate. In the field of climate, the intraseasonal variability is the fastest time scale, but with respect to weather, it is slow and often called the low-frequency variability.

There are rich variabilities in the global atmosphere and climate system on the intraseasonal time scale. For example, in the Northern Hemisphere middle latitudes, synoptic-scale cyclones and anticyclones travel eastward along the tropospheric westerly jet stream, which have the maximum strength near the east coasts of East Asia and North America. When these weather systems move from the land to the ocean, they slow down and amplify over the warm water, contributing to the strong intraseasonal variance in geopotential height and sea level pressure over the central North Pacific and central North Atlantic (e.g., Blackmon, 1976; Blackmon et al., 1984; Dole & Gordon, 1983; N.-C. Lau, 1988).

The focus of this paper is not on the intraseasonal variability in the extratropics. Instead, we discuss primarily on that in the tropics. The tropical intraseasonal variability plays a special role in climate variability and subseasonal predictions. It should be stressed, however, that the tropical and extratropical intraseasonal variabilities are closely connected to each other. They interact with each other through teleconnections, so that the tropical intraseasonal variability can influence extratropical weather and its predictions and the extratropical variability impacts on the tropics as well.

There are varieties of tropical variabilities on intraseasonal time scales. For example, in boreal summer intraseasonal disturbances in the South and East Asian region tend to propagate northeastward that influence monsoon rainfall (e.g., Murakami et al., 1984; Yasunari, 1979). Our discussion here will in particular be around the Madden-Julian Oscillation (MJO) that is the dominant mode of intraseasonal variability in the tropics, with a planetary scale and propagating eastward. The MJO was discovered by Roland Madden and Paul Julian in early 1970s (Madden & Julian, 1971). Through spectrum analysis of 10-year radiosonde observations obtained at Kanton Island, which is located in the central Pacific near the equator, they found a remarkable oscillation in sea level pressure and zonal winds with a period of 40–50 days. With observational data from 20 tropical stations in a follow-up study, this signal was found to be part of a slowly eastward moving (∼5 m s⁻¹) planetary scale disturbance associated with convection and vertically overturning circulation anomalies (Madden & Julian, 1972).

In the past five decades since its discovery, numerous studies have been carried out to document and to understand the MJO, and substantial progress has been made, as summarized in several review articles (e.g., Madden & Julian, 1994; C. Zhang, 2005; Jiang et al., 2020; K.-M. Lau & Waliser, 2012). Prediction skill of the MJO using dynamical models has also been improved significantly in the past 20 years (e.g., H.-M. Kim et al., 2014; Vitart, 2017). However, the mechanism of the MJO is not fully understood. The current general circulation models still have poor representation of the MJO (e.g., Ahn et al., 2020; Jiang et al., 2015), and there is a considerable gap between actual MJO prediction skill and its potential predictability (e.g., Neena et al., 2014).

There has been increasing interest and enthusiasm in the research and development of operational subseasonal predictions (e.g., NAS, 2016). The subseasonal forecasting has been identified as a critical research issue by both weather and climate communities. It bridges the gap between numerical weather and short-term climate predictions and thus helps building a “seamless” weather-climate prediction system (e.g., Brunet et al., 2010; Hoskins, 2013; Shapiro et al., 2010). Several internationally coordinated activities have been developed to improve forecast skill and understanding on the subseasonal to seasonal timescale, including the World Climate Research Programme (WCRP) / World Weather Research Programme (WWRP) Subseasonal-to-Seasonal (S2S) prediction project (Vitart & Robertson, 2018) and the North American subseasonal experiment (SubX; Pegion et al., 2019). It has been well recognized that the MJO has a tremendous impact on weather and climate not only in the tropics but also in the middle and high latitudes, and it provides an important source of predictability on subseasonal time scales (e.g., NAS, 2016; Waliser, 2012). Therefore, improving the understanding and prediction of the MJO is crucial for subseasonal predictions.

This paper is organized as follows. Section 2 describes the basic observed features of the MJO. In Section 3, several current theories for the MJO are summarized. The global impact of the MJO and the related tropical-extratropical interactions are described in Section 4. In Section 5, the interannual variability of the MJO and its link to several other slow modes of variability are discussed. Section 6 reviews MJO modelling and predictions. Some final remarks are given in Section 7.

2 Basic observational features

The main observational features of the MJO have been extensively documented in the literature (e.g., Hendon & Salby, 1994; Madden & Julian, 1972, 1994; C. Zhang, 2005). The MJO is the dominant mode of variability in the tropics on the intraseasonal time scale. It represents large-scale zonal overturning circulations that extend throughout the entire depth of the troposphere that propagates eastward along the equator. It is coupled with deep convection and largely resides in the tropical warm pool region from the Indian Ocean to the central Pacific.

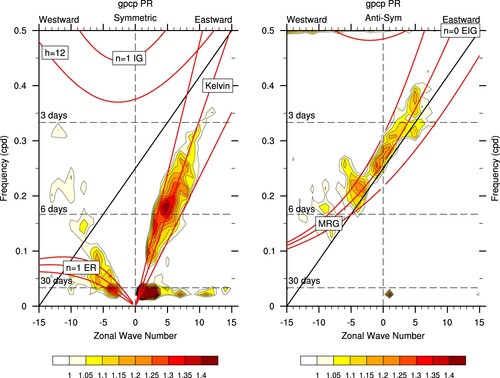
The large-scale and low-frequency features of the MJO can be clearly seen from a wavenumber-frequency power spectrum analysis of zonal winds at 200 hPa or 850 hPa in the tropics that displays spectral peaks at 30–60 days dominated by eastward propagating wavenumbers 1 (Fig. 1). Figure 2 illustrates the wavenumber-frequency spectrum of the 15°S–15°N equatorially symmetric and anti-symmetric components of OLR divided by the background spectrum using the Wheeler-Kiladis method (Wheeler & Kiladis, 1999). The MJO corresponds to the strong spectral density at 30–60 days of eastward propagating wavenumbers 1–3, which is not associated with any theoretical tropical waves derived from the shallow water equations (e.g., Matsuno, 1966).

Fig. 1 Wavenumber-frequency spectra of (a) 200 hPa and (b) 850 hPa zonal wind anomalies averaged over 10°S-10°N based on ERA-interim reanalysis (Dee et al., 2011) for the winter half year (November-April) from 1980–2018. Frequency values 0.02 and 0.05 correspond to periods of 50 and 20 days, respectively. Positive (negative) frequencies are for eastward (westward) propagating waves.

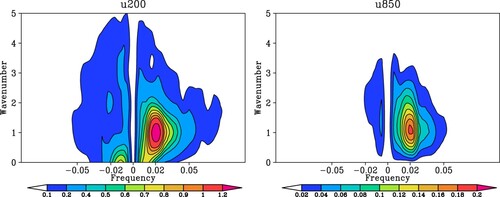
Fig. 2 Wavenumber-frequency spectra of 15°S–15°N symmetric (left) and antisymmetric (right) components of precipitation rate divided by the background spectrum based on the Global Precipitation Climatology Project one-degree daily data (GPCP 1DD V1.2; Huffman et al., 2001) for the period of 1997–2013, following the approach of Wheeler and Kiladis (1999). Superimposed are the dispersion curves of equatorial waves for the equivalent depths of 12, 25 and 50 m.

The circulation anomaly of the MJO is closely linked or coupled with the convection. The association of circulation anomaly and the MJO convection resembles atmospheric response to imposed tropical heating as described in Gill (1980) with a baroclinic vertical structure. To the east of the MJO convection are upper-level westerly and lower-level easterly anomalies similar to a Kelvin wave structure. To the west, a pair of anticyclonic (cyclonic) gyres of circulation straddling the equator with easterly (westerly) wind anomalies near the equator in the upper (lower) troposphere, resembling the equatorial Rossby wave (e.g., B. Wang & Rui, 1990). Such a coupled pattern propagates eastward along the equator at an average speed of 5 m s⁻¹ (e.g., Hendon & Salby, 1994; Knutson et al., 1986). The convective anomaly is largely confined to the eastern Hemisphere, while the circulation anomaly continues to propagate in the western hemisphere as dry Kelvin waves at a speed of 30–35 m s⁻¹ (e.g., Matthews, 2000; Milliff & Madden, 1996).

The large-scale vertical structure of the MJO shows a marked zonal asymmetry in thermodynamic and dynamic fields. To the east, there are boundary layer convergence (e.g., Hendon & Salby, 1994; Sperber, 2003), increased moisture in the lower troposphere (e.g., Johnson & Ciesielski, 2013; Kemball-Cook & Weare, 2001; Kiladis et al., 2005), and warm SST anomalies (e.g., Woolnough et al., 2000). Shallow cumulus clouds dominate and the maximum diabatic heating is concentrated in the lower troposphere (Jiang et al., 2011; J.-L. Lin et al., 2004). Horizontal advection of column-integrated moist static energy (MSE) leads to a positive tendency of MSE favouring the development of MJO convection (e.g., Adames & Wallace, 2015; Arnold et al., 2015). To the west of the MJO convection are low-level divergence, descending motions and negative anomalies in humidity. Enhanced low-level westerlies result in increased surface fluxes and negative SST anomalies (e.g., Hendon & Glick, 1997). Upper tropospheric stratiform clouds prevail (e.g., Kiladis et al., 2009) where the diabatic heating is large, while diabatic cooling occurs in the lower levels due to evaporation when precipitation from these high clouds falls through a relatively dry environment (e.g., Benedict & Randall, 2007). The contribution of horizontal advection of MSE on the west side of the MJO convection is opposite as to the east, suppressing the MJO development. The zonal asymmetry is an important feature of the MJO convection, which favours the development and eastward propagation of the MJO.

The eastward propagating large-scale MJO convection represents an envelope consisting of multiscale higher-frequency, smaller-scale convection systems that travel both eastward and westward (e.g., Hendon & Liebmann, 1994; Kiladis et al., 2009; Nakazawa, 1988). These smaller-scale systems include the disturbances associated with eastward moving coupled Kelvin waves (e.g., Nakazawa, 1988; K.-M. Lau et al., 1989), and westward travelling equatorial Rossby and mixed Rossby-gravity waves (e.g., Wheeler & Kiladis, 1999). High frequency variability of convection and clouds can also be associated with diurnal cycle of deep convections (e.g., S. Chen & Houze, 1997) and inertia-gravity waves (e.g., Haertel & Kiladis, 2004; Takayabu, 1994). These small-scale systems are organized within the MJO envelope by the large-scale circulation and can feedback to influence the MJO through upscale momentum transport (e.g., Houze et al., 2000; Majda & Biello, 2004; Miyakawa et al., 2014; Moncrieff, 1992).

The MJO activity is observed to have an apparent seasonal dependence, with the strongest MJO in boreal winter and spring (e.g., Salby & Hendon, 1994). During this time of the year, warm SST is along the equator and has maximum longitudinal extent in the eastern hemisphere (e.g., Shea et al., 1992), and the convergence of moisture in the equatorial boundary layer is strong (e.g., Hendon & Salby, 1994). The latitudinal location of the MJO undergoes a north–south shift, with strong signals slightly south of the equator in boreal winter and north of the equator in summer (e.g., C. Zhang & Dong, 2004).

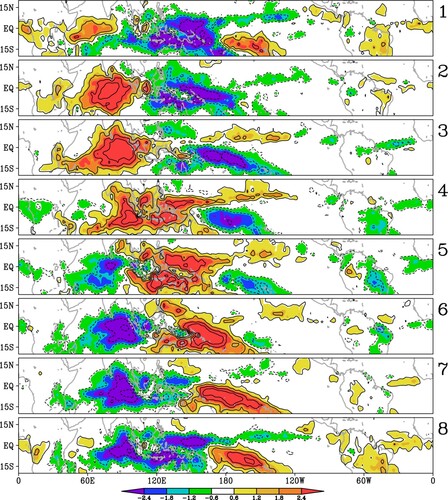
The MJO has long been identified through the use of empirical orthogonal function analysis (EOF) on a bandpass-filtered variable such as outgoing longwave radiation (OLR) and 200-hPa velocity potential (e.g., Ferranti et al., 1990; Knutson & Weickmann, 1987; K.-M. Lau & Chan, 1985; Matthews, 2000; Slingo et al., 1996). The Real-time Multivariate MJO index (RMM) introduced by Wheeler and Hendon (2004) is obtained as a pair of principal components (PCs) of the two leading EOFs of combined fields of 200-hPa and 850-hPa zonal winds and OLR, each averaged over the latitudes of 15°S–15°N. Because the RMM index captures the baroclinic convectively coupled circulation structure of the MJO without the need of time filtering, it has been widely used for MJO monitoring and prediction applications, as well as impact studies. Shown in Fig. 3 are composites of tropical precipitation rate anomalies for eight MJO phases as defined by the RMM index of Wheeler and Hendon (2004). It is clearly seen that the MJO convection starts in the western Indian Ocean in phase 1, propagates eastward to the central Pacific and dissipates in the eastern Pacific. MJO phases 2–3 and phases 6–7 correspond to a zonal dipole structure of tropical convection, which has strong global impact, as will be discussed in section 4.

Fig. 3 Composites of the precipitation rate anomaly in the tropics for eight phases of the MJO, during extended boreal winter based on the pentad data of the Climate Prediction Center (CPC) Merged Analysis of Precipitation (CMAP) (Xie & Arkin, 1997). The phase numbers are marked on the right of each panel. The calculation procedure is the same as for Fig. 3 of Lin et al. (2009), except that an updated CMAP data version (v1708) with the period of 1979–2017 is used here.

It has been acknowledged in several studies that the RMM index is dominated by zonal winds and perhaps does not represent very well the convection component of the MJO (e.g., Straub, 2013; Ventrice et al., 2013). Several MJO indices based only on OLR have been developed in recent years. For example, Kikuchi et al. (2012) developed two separate OLR extended EOFs for boreal summer and winter. An all-season OLR-based MJO index (OMI) was constructed using an EOF analysis of spatially gridded OLR in Kiladis et al. (2014). The gross features of the circulation and OLR of the MJO associated with these different indices are in general similar.

It should be noted that the MJO, with its dominant period in a range of about 30–60 days, is not a regular oscillation. Instead, it is highly episodic and discrete (e.g., Salby & Hendon, 1994). Although on average the MJO propagates in the Indian Ocean and western Pacific sector at about 5 m s⁻¹, individual MJO events have different propagating speeds. There are diversities in the MJO structure and in the equatorial wave activity imbedded in the MJO envelope (e.g., Dias et al., 2013; Kikuchi et al., 2018). B. Wang et al. (2019) identified four groups of MJO events, i.e. slow eastward propagating, fast eastward propagating, standing and jumping, which have different Kelvin wave response properties.

3 Mechanisms

The MJO is a phenomenon involving moist processes and coupling between circulation and convection, which cannot be explained by the tropical wave theory with dry shallow-water equations on a β-plane (e.g., Matsuno, 1966). The MJO shares some similarities with the equatorial convection-coupled Kelvin wave, e.g., they both propagate eastward, but the Kelvin wave propagates much faster than the MJO. Chang (1977) showed that the speed of the Kelvin wave can be reduced by the damping effect of convection, but it is still too fast comparing to the observed MJO. In early studies, the convective instability of the second kind (CISK; Charney & Eliassen, 1964) and wave-CISK (Lindzen, 1974) were used to understand the MJO (Chang & Lim, 1988; K.-M. Lau & Peng, 1987). However, the maximum growth rate for the unstable wave-CISK Kelvin modes occurs at smallest scales, and the waves propagate at speeds faster than the MJO. With the inclusion of the frictional effect on moisture convergence in the atmospheric boundary layer (BL), the small-scale wave-CISK modes are damped, resulting in planetary-scale, slowly eastward propagating coupled Rossby-Kelvin waves (B. Wang, 1988; B. Wang & Rui, 1990; B. Wang & Li, 1994). Another early MJO theory is based on the wind-evaporation feedback (Neelin et al., 1987), or wind-induced surface heat exchange (WISHE; Emanuel, 1987; Yano & Emanuel, 1991), which provides an instability for the MJO. A detail review of the early MJO theories can be found in B. Wang (2005) and C. Zhang (2005).

There are several MJO theories that have been developed in recent years. They focus on different processes, but most of them emphasize the interaction between convection and moisture. Strong precipitation over the tropical oceanic region associated with deep convection occurs mostly in moist environments (e.g., Bretherton et al., 2004; Peters & Neelin, 2006; Thayer-Calder & Randall, 2009; Y.-H. Kuo et al., 2019). The variability of MJO precipitation is closely related to the sensitivity of convection to atmospheric moisture (e.g., Adames, 2017; Jiang et al., 2016). To the east of the MJO convection centre, boundary layer convergence of moisture and detrainment and rain evaporation of shallow cumulus clouds gradually moisten the atmosphere (e.g., Johnson et al., 1999; Slingo et al., 2003), which sets a stage for the development of deep convection and eastward propagation of the MJO.

Comprehensive reviews and detailed discussions of most of the current MJO theories have been provided in C. Zhang et al. (2020), D. Yang et al. (2020), and Jiang et al. (2020). Here a brief summary is given, focusing on the most fundamental features of the MJO, i.e. its planetary spatial scale, intraseasonal temporal scale, and slow eastward propagation.

a Trio-Interaction theory

The “trio-interaction” theory of the MJO emphasizes the interaction between convection, circulation and moisture (B. Wang et al., 2016; B. Wang & Chen, 2017; F. Liu & Wang, 2017; G. Chen & Wang, 2018a). It is an extension of the original frictionally coupled Rossby-Kelvin wave theory (B. Wang, 1988; B. Wang & Rui, 1990), with an additional prognostic moisture variable. Based on the equatorial wave dynamics of the Matsuno-Gill model (Gill, 1980; Matsuno, 1966), interactive diabatic heating, BL convergence and moisture are considered essential for the MJO.

In the trio-interaction theory, the BL convergence plays a key role in producing planetary-scale, eastward propagation and the coupled Rossby-Kelvin wave structure of the MJO. BL low pressure and frictional convergence occur to the east of the MJO convection, consistent with the observations (e.g., Hendon & Salby, 1994; Sperber, 2003). This leads to upward motion, shallow and congestus clouds, moistening of the atmosphere and generation of eddy available potential energy, thus favours the eastward propagation of the coupled waves. The generation of wave energy by the BL convergence for longer wavelengths is more efficient than for shorter ones, so the unstable waves have preferred planetary scales (G. Chen & Wang, 2018a).

It is found from the trio-interaction theory that the MJO eastward propagation speed is closely associated with a westerly intensity index, which is the ratio of the maximum Rossby wave westerly and Kelvin wave easterly winds in the lower troposphere. When the westerly intensity index increases, i.e. Rossby wave component increases or Kelvin wave component is reduced, the eastward propagation of the MJO slows down (B. Wang & Lee, 2017; B. Wang et al., 2018). The propagation speed depends on convection parameterization scheme and SST. The Betts-Miller parameterization scheme (Betts & Miller, 1986) produces a slower eastward propagation for the coupled Rossby-Kelvin wave than the Kuo scheme (H. Kuo, 1974), and the eastward propagation speed decreases with the increase of SST (B. Wang & Chen, 2017).

There is some disagreement in the literature on role of BL friction for the MJO (e.g., D. Kim et al., 2011; Shi et al., 2018). In addition, the value of BL damping coefficient remains uncertain. Further studies are needed to test if the results can be reproduced in different models.

b Moisture mode theories

The “moisture mode” concept of the MJO stems from the close connection between moisture variation and convection (Raymond, 2001; Sobel et al., 2001). There are three theories that are related to “moisture mode”, which have different mechanisms for planetary scale instability and eastward propagation.

In the moisture mode theory under weak temperature gradient (WTG) approximation (Adames & Kim, 2016; Sobel & Maloney, 2012, 2013), it is assumed that the vertical motion is in balance with the diabatic heating, and anomalous wind field is in a steady balance with the diabatic heating as in the Matsuno-Gill model (Gill, 1980; Matsuno, 1966). Moisture tendency is the only prognostic equation. In this theory, the eastward propagation of the MJO is largely caused by large-scale horizontal advection of moisture, which moistens (dries) the free troposphere to the east (west) of the MJO convection. The propagation speed is determined by the magnitude of moisture advection, dry static stability and the convective moisture adjustment timescale. The planetary scale selection of the MJO is accomplished through the interactions between convection and longwave radiation. In the upper troposphere, clouds spread out far away from the precipitation region, which reduces the outgoing longwave radiation and warms the troposphere. This leads to anomalous upward motion with upward moisture advection, moistening the troposphere, which favours large-scale convection development. This theory predicts that the MJO has a westward group velocity, which is yet to be confirmed by the observations (e.g., G. Chen & Wang, 2018b).

In the WISHE moisture mode theory (Fuchs & Raymond, 2005, 2017; Raymond & Fuchs, 2009), the tendency in the momentum and thermodynamic equations is included. WTG is not strictly required. The meridional wind component is not considered (v = 0), so the horizontal structure of the moisture mode does not include the Rossby wave component. In this theory, the eastward propagation of the MJO is due to the moistening process of WISHE, assuming that the mean state zonal winds are easterlies. WISHE is also responsible for the planetary scale selection.

Another theory related to the WISHE-moisture mode is the boundary layer quasi-equilibrium proposed by Khairoutdinov and Emanuel (2018). It assumes that the increase of MSE in the BL is balanced by the import of free troposphere air with low MSE resulting from convective downdrafts (Emanuel, 1995; Raymond, 1995). Similar to the WISHE moisture theory discussed above, the eastward propagation of the MJO is due to WISHE. For the planetary scale instability, the longwave radiative heating is the dominant factor (Emanuel, 2019; Khairoutdinov & Emanuel, 2018).

One limitation for the WISHE based theories is that they require the mean state to be easterly for the induced waves to propagate eastward. In reality, the MJO convection is strongest in the tropical Indian Ocean where the mean state lower troposphere is westerly (e.g., B. Wang, 1988).

c Skeleton theory

The skeleton theory aims to explain the fundamental features of the MJO with a minimum number of processes and equations (Majda & Stechmann, 2009). It emphasizes the multiscale interactions of the MJO. In this theory, the MJO is described as a neutrally stable planetary-scale envelope of synoptic-scale and mesoscale systems. A wave activity is introduced to represent the average effect of synoptic-scale and mesoscale convective energy, which is expressed by a parameterization scheme. The wave activity and lower-tropospheric moisture are in quadrature, resulting in propagation of the convection anomalies. An eastward propagating planetary-scale solution is obtained with moistening to the east of the convection, which has a structure consistent with the observed Kelvin and Rossby waves. The propagation speed is controlled by the background moisture gradient, wave activity parameter and gravity-wave speed.

By including nonlinearity and stochastic noise, this theory can simulate reasonably well several aspects of the observed MJO including its structure, amplitude and the irregularity (Stachnik et al., 2015; Stechmann & Majda, 2015; Thual et al., 2014; Thual & Majda, 2015). Stochastic processes help to dissipate small-scale waves, leading to scale selection for the MJO development.

The skeleton theory depends on the unique treatment of wave activity of small-scale activities, which may be its main limitation. In addition, it applies the observed MJO structure instead of a scale selection mechanism. Further analysis and validation of the wave activity parameterization would be helpful.

d Gravity wave theory

The gravity wave theory of the MJO was developed by D. Yang and Ingersoll (2013, 2014). The high-frequency equatorial westward and eastward inertia-gravity waves are considered essential to the MJO. The eastward inertia-gravity waves propagate slightly faster than the westward inertia-gravity waves due to the beta effect, leading to the eastward propagation of the MJO. The planetary scale of the MJO is determined by the average distance for the inertia-gravity waves to propagate without intercepting a convective storm. In this theory, there is no explicit representation of moisture. It applies a cumulus parameterization with the convective available potential energy (CAPE) as its closure, thus treats convection as a triggered process.

Based on a 2-dimensional shallow-water model, the MJO is simulated reasonably well (D. Yang & Ingersoll, 2013). The MJO is seen as a planetary-scale envelope propagating eastward at around 3 m s⁻¹.

In the gravity wave theory, the convective parameterization has a threshold behaviour, making it difficult to obtain linear analytical solutions. Further investigation to test convection triggering and scaling parameters would be helpful.

e Vortex dynamics

There are another two MJO theories that have been proposed recently. They suggest that the dominant mechanism for the MJO to propagate slowly eastward is related to the dynamics of an equatorial vortex pair to the west of the MJO. Under the framework of solitary wave (Rostami & Zeitlin, 2019; Yano & Tribbia, 2017), the vortex pair propagate slowly eastward due to nonlinear potential vorticity advection. On the other hand, in Hayashi and Itoh (2017), the pair of cyclonic Rossby gyres move eastward because of strong vortex stretching in the lower troposphere through the coupling with deep convection.

The above-discussed MJO theories emphasize different dynamical processes. They also differ in approximations and parameterizations. Further studies are required to identify what processes are the most important for the MJO, and what parameter ranges are required for a realistic MJO.

4 Global impacts and tropical-extratropical interactions

a Observed MJO influences

The MJO has tremendous impacts on the global weather and climate system. In the tropical region, it has a direct influence by organizing convection and precipitation. The onset and variation of global monsoons are closely associated with the MJO (e.g., Hendon & Liebmann, 1990; K.-M. Lau & Chan, 1986; Lorenz & Hartmann, 2006; Sultan et al., 2003; Webster et al., 1998; Mo et al., 2012; B. Wang, 2006). The genesis and tracks of tropical cyclones are modulated by the MJO activity (e.g., Liebmann et al., 1994; Maloney & Hartmann, 2000; Nakazawa, 1988; C.-Y. Lee et al., 2018).

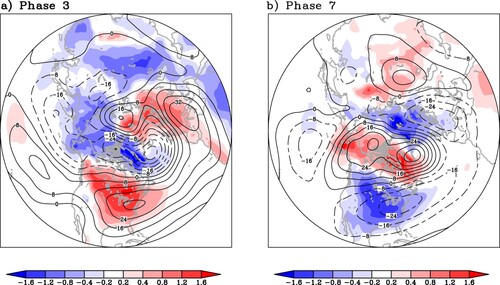
Although the MJO is a tropical phenomenon, it influences substantially on a wide range of extratropical weather and climate activities, including persistent and extreme weather events. Variabilities of surface air temperature over many extratropical regions are connected with the MJO. For example, Jeong et al. (2005) showed that the spatial pattern and magnitude of wintertime surface air temperature anomalies over East Asia vary significantly with respect to MJO phases, and the MJO induced circulation anomaly may reinforce cold surges. The MJO influences on the middle latitude region of East Asia was found to be related to a local Hadley-cell overturning and Rossby wave response (e.g., He et al., 2011). Over North America, subseasonal variability of wintertime surface air temperature is closely associated with the MJO phase (e.g., Baxter et al., 2014; H. Lin & Brunet, 2009; Zheng et al., 2018; Zhou et al., 2012). Warm anomalies tend to occur about two weeks after MJO phases 2–3, while about two weeks following MJO phases 6–7 there is increased probability of colder than normal temperature in Canada and the eastern United States (e.g., H. Lin & Brunet, 2009; NAS, 2016). The MJO was also found to correlate with wintertime temperature anomalies in the Arctic region (e.g., Vecchi & Bond, 2004; Yoo et al., 2012; H. Lin, 2020). Shown in Fig. 4 (in colour) are lagged composites of 2-meter air temperature (T2m) anomaly over the Northern Hemisphere in winter 11–15 days after the occurrence of MJO phases 3 and 7. As is seen from Fig. 4(a), following MJO phase 3, T2m tends to be warmer in North America and colder in central Eurasia than normal. In the high latitudes, cold anomalies are observed north of the Bering Strait and North America, while warm anomalies are seen north of Western Europe. A general opposite situation is evident after the occurrence of MJO phase 7 (Fig. 4(b)).

Fig. 4 Lagged composites of T2 m (in colour) and Z500 (in contour) anomalies 11–15 days after (a) MJO phase 3, and (b) MJO phase 7, during extended boreal winter season from November to March, based on the ERA-interim reanalysis over the 1981–2013 period. The contour interval is 8 m. Contours with negative values are dashed.

Variability of precipitation in extratropical regions has been found to be associated with the MJO as well. Precipitation anomalies in the North American west coast are correlated with the tropical convection activity associated with the MJO (e.g., Becker et al., 2011; Bond & Vecchi, 2003; Higgins et al., 2000; Mo & Higgins, 1998; H. Lin, Brunet, & Mo, 2010). Extreme rainfall over the contiguous United States was observed to be more frequent when the MJO convection centre is over the Indian Ocean (e.g., Barrett & Gensini, 2013; Jones & Carvalho, 2012). The MJO was found to modulate atmospheric river (AR) activity that is associated with heavy precipitation near the North American west coast (Baggett et al., 2017; Guan et al., 2012; Mundhenk et al., 2018). Jeong et al. (2008) found that the MJO modulates the distribution of precipitation over East Asia. A near-global impact of the MJO on precipitation was reported in Donald et al. (2006).

In the Southern Hemisphere, temperature and precipitation anomalies in many places were also observed to have a coherent variation with the MJO phase (e.g., Barrett et al., 2012; Marshall et al., 2014; Naumann & Vargas, 2010; Wheeler et al., 2009).

Not only does the MJO influence temperature and precipitation in many places, its impact is felt in many aspects of the global earth system. For example, the MJO is observed to also influence the frequency of extreme weather events (e.g., C. Zhu et al., 2003; T.-W. Park et al., 2010; H. Lin et al., 2019), polar sea ice variability (e.g., H.-J. Lee & Seo, 2019), and chemical and biological components in the atmosphere and ocean (e.g., Li et al., 2010; Tian et al., 2007). The MJO influence extends to sudden stratospheric warming events through upward wave propagation, and changes in polar vortex (e.g., Garfinkel et al., 2014; Garfinkel & Schwartz, 2017).

b Extratropical teleconnection of the MJO

The MJO influence on the extratropics is associated with atmospheric response to tropical diabatic heating and its interaction with extratropical variabilities. The extratropical climate variability is usually characterized by recurring patterns known as modes of variability (e.g., Wallace & Gutzler, 1981; Barnston & Livezey, 1987). Among them are the North Pacific – North American pattern (PNA) and the North Atlantic Oscillation (NAO) in the Northern Hemisphere, and the Pacific – South American (PSA; e.g., Mo & White, 1985) in the Southern Hemisphere. They have substantial impact on regional and global weather and climate, especially on persistent and extreme weather events.

The basic understanding of the dynamical processes for the extratropical intraseasonal variability was established as early as in 1980s through a large amount of observational, modelling and theoretical studies (e.g., Hoskins & Pearce, 1983). A large part of these variabilities are generated through atmospheric internal dynamics within the extratropical region and develop by extracting kinetic energy from both the time mean flow and high-frequency synoptic-scale transients (e.g., Simmons et al., 1983; N.-C. Lau, 1988; Sheng & Derome, 1991). Extratropical intraseasonal variability can also be excited by tropical thermal forcing and can be explained by Rossby wave propagation (e.g., Hoskins & Karoly, 1981). The MJO convection represents large-scale variability of diabatic heating, which provides an important tropical forcing to the global circulation.

It may be helpful to compare the MJO teleconnection with that of the El Niño – Southern Oscillation (ENSO). It is well known that on the interannual time scale ENSO is the dominant mode of tropical variability, which has a global impact and represents the most important source of predictability in seasonal predictions (e.g., Shukla et al., 2000). The diabatic heating anomalies of ENSO in the equatorial central Pacific can excite extratropical Rossby waves in boreal winter with typical extratropical atmospheric patterns similar to the PNA (e.g., Wallace & Guztler, 1981), and the Tropical – Northern Hemisphere (TNH) pattern (e.g., Mo & Livezey, 1986). Similarly, the MJO with its variability of tropical convection and diabatic heating in the tropical Indian Ocean and western Pacific represents a fluctuation in tropical forcing, which can induce extratropical Rossby waves and lead to variability of extratropical circulation on the intraseasonal time scale. Therefore, the MJO provides an important of source of predictability for the global atmosphere on the subseasonal time scale (e.g., Waliser, 2012; NAS, 2016).

The MJO convection can induce a wave train across the North Pacific and North America, with a pattern similar to the PNA (e.g., Ferranti et al., 1990; K.-M. Lau & Phillips, 1986; Mori & Watanabe, 2008). The analysis of Riddle et al. (2013) suggests that the MJO may not excite a pure PNA pattern, but rather a PNA-like response with its own unique signature. The eastward propagation of the MJO convection activity is associated with a shift in the tendency and sign of the Arctic Oscillation (AO) index (L'Heureux & Higgins, 2008). Flatau and Kim (2013) showed that on the subseasonal time scale enhanced MJO convection in the Indian Ocean leads to changes in the Antarctic Oscillation (AAO). The Southern Hemisphere PSA pattern has also been found to be modulated by the MJO phases (e.g., Mo & Higgins, 1998).

The NAO, which has its action centres in the North Atlantic, was observed to have a robust lagged connection with the MJO (Cassou, 2008; H. Lin et al., 2009). A significant increase in the probability of a positive (negative) NAO happens about 10–15 days after the occurrence of MJO phases 2–3 (6–7). This lagged MJO-NAO connection can be explained by extratropical Rossby wave propagation (e.g., Cassou, 2008; H. Lin, Brunet, & Mo, 2010) and can be simulated in dynamical models (e.g., Straus et al., 2015; H. Lin & Brunet, 2018; Shao et al., 2019; Yadav et al., 2019). Most S2S models can reproduce the MJO-NAO lagged connection, although the amplitude is weaker than in the observations (e.g., Vitart, 2017; Vitart & Molteni, 2010). Subseasonal prediction of the NAO has been found to benefit from the MJO influence (e.g., H. Lin, Brunet, G., & Fontecilla, 2010; Tseng et al., 2018; P.-N. Feng et al., 2021). The NAO substantially influences weather and climate in a large area in Europe and North America (e.g., Hurrell et al., 2003). Shown in Fig. 4 (in contour) are lagged composites of 500-hPa geopotential height (Z500) anomaly over the Northern Hemisphere in winter 11–15 days after the occurrence of MJO phases 3 and 7.

The tropical thermal forcing patterns with a west–east dipole structure in the Indian Ocean and western Pacific corresponding to MJO phases 2–3 and 6–7 are found to be the most effective in exciting extratropical Rossby waves and teleconnections. Through a series of numerical experiments with tropical heating at different longitudes, H. Lin, Brunet, and Mo (2010) demonstrated that the amplitude of the extratropical response is dependent on the longitudinal location of the equatorial forcing relative to the East Asian subtropical jet. The response is weak when the thermal forcing is near the Maritime continent longitudes. A heating in the Indian Ocean and that in the western Pacific excites a similar PNA-like teleconnection pattern but with opposite signs. Therefore, a dipole tropical thermal forcing with heating in the equatorial Indian Ocean and cooling in the western Pacific (MJO phases 2–3) or vice versa (MJO phases 6–7) produces considerably strong extratropical circulation anomalies. Early studies have shown that barotropic instability of zonally varying mean flow in the middle latitudes results in growth of low-frequency disturbances in preferred locations, e.g., the eastern North Pacific and North Atlantic (e.g., Branstator, 1985; Simmons et al., 1983). The tropical forcing that is optimal to excite the North Pacific response changes sign from the west Pacific to the Indian Ocean (e.g., Ferranti et al., 1990; Simmons et al., 1983). In a recent study, Tseng et al. (2018) confirmed that the MJO phases 2–3 and 6–7, which have dipole heating over the tropical Indian Ocean and western Pacific, are effective in exciting the PNA-like response. These authors showed that such a tropical forcing leads to a dipole pattern of Rossby wave source on each side of the subtropical jet that can increase the pattern consistency of teleconnections due to the constructive interference of similar teleconnection signals.

The MJO teleconnection can in broad terms be simulated by numerical models (e.g., Matthews et al., 2004; H. Lin, Brunet, & Mo, 2010; Vitart & Molteni, 2010; K.-H. Seo & Son, 2012; H. Lin & Brunet, 2018). In the North Pacific sector, there is good agreement among various studies that the MJO thermal forcing can excite a cyclonic or anticyclonic anomaly near 45°N, 180°, which forms the North Pacific centre of the PNA-like pattern. However, many models produce a too strong North Pacific response centre comparing to the observation (e.g., Vitart, 2017), which is likely related to errors of MJO propagation in the models. On the other hand, in the North Atlantic sector, most models can produce a positive NAO following MJO phases 2–3 and a negative NAO following MJO phases 6–7, but the signal is usually weak and less consistent (e.g., Vitart, 2017; Vitart & Molteni, 2010). Numerical experiments with linear models can well reproduce the North Pacific response to the MJO forcing, but only a weak signal in the North Atlantic (e.g., H. Lin, Brunet, & Mo, 2010; H. Lin & Brunet, 2018). This indicates that atmospheric nonlinear processes are likely more important for the response to tropical forcing in the North Atlantic than in the North Pacific, consistent with previous studies (e.g., H. Lin, Derome, & Brunet, 2007). Using the Community Earth System model, Straus et al. (2015) showed that the positive NAO 15–25 days after the MJO phase 3 is supported by synoptic vorticity flux convergence and Rossby wave source.

The MJO was found to influence the stratospheric sudden warming and polar vortex (e.g., Garfinkel et al., 2012, 2014; Kang & Tziperman, 2018; C. Liu et al., 2014). This leads to changes in the Arctic Oscillation (AO) or the Northern annular mode (NAM; e.g., Thompson & Wallace, 1998) and the signal can propagate downward to affect the troposphere and surface condition (e.g., Baldwin & Dunkerton, 2001). The stratospheric polar vortex may condition the background flow for the MJO induced tropospheric Rossby waves to propagate into the stratosphere, which provides a stratospheric pathway for the MJO to influence the NAO (e.g., Barnes et al., 2019).

c Tropical-extratropical interactions

There is considerable influence from the extratropics on the tropics as well. Extratropical waves can propagate into the tropics to influence tropical convection activity on a wide range of timescales (e.g., Liebmann & Hartmann, 1984; Matthews & Kiladis, 1999; Webster & Holton, 1982). Tropical waves can be forced by extratropical disturbances (e.g., Hoskins & Yang, 2000; C. Zhang & Webster, 1992). Some MJO events are found to be induced by Northern Hemisphere middle latitude atmospheric variabilities (e.g., Hall et al., 2017; H. Lin, Brunet, & Derome, 2007; Ray & Zhang, 2010; Vitart & Jung, 2010).

Tropical-extratropical interactions are an important aspect for the MJO and its global teleconnections (e.g., Frederiksen & Lin, 2013; H. Lin et al., 2019; Stan et al., 2017). In H. Lin et al. (2009), it was found that the NAO activity could modulate the MJO. About 20 days following a positive and negative NAO, the MJO tends to occur in phase 7 and 3, respectively. H. Lin and Brunet (2011) analysed the influence of the NAO amplitude on the MJO prediction skill, and found that the MJO prediction skill is higher when initialized with a strong NAO than a weak NAO. However, the understanding for the dynamical mechanism on how the extratropical NAO influences the tropical MJO is limited.

5 Interannual variations

In addition to the seasonal variation as discussed in section 2, the MJO activity changes from year to year. The MJO can be modulated by slow processes in the climate system. One of such processes on the interannual time scale is ENSO. During El Niño, the Pacific trade winds relax and the warm pool in the tropical western Pacific spreads eastward (e.g., McPhaden et al., 2006a). The MJO activity tends to extend eastward along with the edge of warm pool during the development of El Niño (e.g., Bergman et al., 2001; Fink & Speth, 1997; Hendon et al., 1999; Woolnough et al., 2000). In the Pacific, the MJO appears more active prior to the peak phase of an El Niño than before the extreme of La Niña (C. Zhang & Gottschalck, 2002). The MJO in the Pacific and ENSO SST indices are correlated (Kessler, 2001). J. Feng et al. (2015) showed that during various stages of eastern Pacific and central Pacific El Niño, the MJO activities are different. The observed relationship between ENSO and the MJO indicates that ENSO may modulate the MJO activity regionally in the tropical western Pacific, and/or the MJO activity may contribute to the development of ENSO through westerly wind burst and ocean Kelvin waves (e.g., K.-M. Lau & Chan, 1988; K.-M. Lau et al., 1989; Hendon et al., 2007; McPhaden et al., 2006b; Tang & Yu, 2008; C. Zhang & Gottschalck, 2002). However, the simultaneous correlation between the overall level of seasonal mean MJO activity and ENSO during boreal winter appears weak (e.g., Hendon et al., 1999; Jones & Carvalho, 2006; Slingo et al., 1999), implying that much of the interannual variability of the MJO is likely independent of the boundary ENSO related SST forcing and may result from atmospheric internal dynamics.

The extratropical atmospheric response to ENSO leads to changes in the seasonal mean state, through which the MJO induced Rossby wave propagates. Therefore, the MJO teleconnection can be modulated by ENSO. For example, Roundy et al. (2010) observed that the MJO teleconnection is stronger during the La Niña winters than during El Niño winters. R. Lee et al. (2019) reported that the MJO to positive NAO regime tropospheric teleconnection is enhanced during El Niño years and suppressed during La Niña, whereas the MJO to negative NAO regime stratospheric teleconnection is enhanced during La Niña years and suppressed during El Niño. Henderson and Maloney (2018) found that the ENSO phase-dependent teleconnection patterns influence the Pacific and Atlantic high-latitude blocking activity. The MJO teleconnection and impacts in the Pacific-North America region are found to be amplified by anthropogenic warming (e.g., W. Zhou et al., 2020).

Recent studies revealed that the interannual variability of the MJO is modulated by the stratospheric quasi-biennial oscillation (QBO), which is a prominent oscillation of tropical stratospheric zonal winds between easterlies and westerlies with a period around 28 months (e.g., Baldwin et al., 2001). During winters when the lower stratosphere is in an easterly phase of the QBO, the MJO tends to be stronger and more active than during a westerly phase of the QBO (e.g., Son et al., 2017; Yoo & Son, 2016). It is found that about 40–50% of interannual variance of the boreal winter MJO activity can be attributed to the QBO. During easterly QBO phase, the MJO propagates more slowly eastward and farther into the western Pacific than in boreal winters of westerly QBO (e.g., Nishimoto & Yoden, 2017; S. Wang et al., 2019; C. Zhang & Zhang, 2018). Several possible mechanisms have been proposed to explain the QBO-MJO connection. One of them is the QBO temperature stratification effect that changes the upper tropospheric static stability and the vertical zonal wind shear (e.g., Hendon & Abhik, 2018; Nishimoto & Yoden, 2017; Son et al., 2017). Cloud-radiation feedbacks may also contribute to the QBO-MJO connection (e.g., Son et al., 2017; Sun et al., 2019), as cold temperature during easterly QBO is likely accompanied by high-altitude cirrus clouds which in turn may influence the lower stratosphere temperature (e.g., Hartmann et al., 2001; Q. Yang et al., 2010).

The different behaviours of the MJO during easterly and westerly phases of the QBO lead to changes in extratropical teleconnection patterns. During easterly QBO winters, the PNA-like Rossby wave teleconnection pattern in the North Pacific is more pronounced than in westerly QBO winters (e.g., Son et al., 2017; Toms et al., 2020; J. Wang et al., 2018). The QBO is also found to modulate the MJO teleconnection in the North Atlantic indirectly through its influence on the seasonal mean westerly flow (P.-N. Feng & Lin, 2019). The MJO-related precipitation in East Asia is observed to be modulated by the QBO (H. Kim et al., 2020).

Our understanding of the connection between the MJO and the QBO is limited. There has not been a conclusive dynamical explanation for the QBO-MJO connection. Current global climate models cannot simulate the observed correlation between the MJO activity and the QBO (e.g., H.-M. Kim et al., 2020b; Lim & Son, 2020). H.-M. Kim et al. (2020a) showed that the relationship between the MJO prediction skill and the QBO is not statistically significant in the state-of-the-art S2S models. All these indicate that some key processes connecting the stratosphere and the tropical MJO are missing or not well represented in the modern GCMs, and further observational, modelling and theoretical studies are needed.

The interannual variability of the MJO activity has an important implication and impact on the global climate system. H. Lin et al. (2015) investigated the interannual variability of the MJO and its impact of the NAO in boreal winter. They found that the preferred location of the MJO activity shifts between the Indian Ocean and the western Pacific from one year to another, which is reflected by the year-to-year variation in the occurrence frequency of individual MJO phases. This interannual shift of the MJO location is not correlated with the ENSO and the QBO. During winters when the MJO convection occurs more frequently in the Indian Ocean (western Pacific), a positive (negative) seasonal mean NAO tends to occur (H. Lin et al., 2015). Similar shift of MJO activity between the Indian Ocean and western Pacific was observed in Bellenger and Duvel (2012).

6 Modelling and predictions

a Modelling the MJO

It has been a challenging job for GCMs to simulate the MJO. In an early study with the first Atmospheric Model Intercomparison Project (AMIP I) models, Slingo et al. (1996) found that all of the models failed to capture the pronounced spectral peak in the upper winds associated with the observed MJO. Tropical variability in many models was too fast and too weak. J.-L. Lin et al. (2006) assessed the fidelity of MJO simulation in 14 coupled GCMs participating in the third Coupled Model Intercomparison Project (CMIP3), and reported that only one model was able to simulate a realistic spectral peak in equatorial precipitation similar to the MJO. Some improvement in the performance of the CMIP5 models was shown in Hung et al. (2013) and Ahn et al. (2017). With the more recent CMIP6 models, Ahn et al. (2020) demonstrated that in general the ability of representing the MJO is improved, especially for the eastward propagation across the Maritime continent. Many models were able to simulate the eastward propagation of the MJO in the zonal wind, but the signal in precipitation was too weak and several other important features of the MJO were not captured (e.g., C. Zhang et al., 2006; D. Kim et al., 2009). Jiang et al. (2015) analysed the MJO simulation in 27 models in a GCM inter-comparison for MJO project, and found that the eastward propagation feature of the observed MJO was captured by about 25% of the participating models.

Many studies have demonstrated that the simulated MJO is highly sensitive to the configuration of convection parameterization scheme of the model (e.g., C.-K. Park et al., 1990; Slingo et al., 1994; Wang & Schlesinger, 1999), which can be expected as the tropical convection process is crucial for the MJO. Convection processes are on the sub-grid scale and cannot be resolved in current conventional weather and climate models, therefore their representation has to depend on parameterization. In a standard parameterization scheme, the amplitude of convection is determined by the large-scale state, a procedure referred to as closure. A closure condition is usually derived as a vertically-integrated physical quantity. Two common choices are moisture (e.g., H. Kuo, 1974) and the convective parcel buoyancy (e.g., Arakawa & Schubert, 1974). The latter is often associated with a form of convective available potential energy (CAPE). Models with convection schemes that depends on moisture convergence are found to perform poorly in simulating tropical intraseasonal variability. For example, Slingo et al. (1996) showed that models using convection schemes closed on buoyancy simulated better intraseasonal variability than those depending on moisture supply. Wheeler (2003) found that switching the closure of the convection scheme from moisture convergence to CAPE leads to increased power spectrum in the eastward-propagating MJO frequencies.

In addition to closure, entrainment-detrainment is another important factor in a convection parameterization scheme (e.g., Yano et al., 2012). Increasing the fractional entrainment in the deep convection scheme was found to have a positive impact on the MJO simulation (e.g., Maloney & Hartmann, 2001; D. Kim et al., 2012). To capture the preconditioning and moistening of the lower troposphere to the east of the MJO deep convection, a proper representation of shallow convections in a GCM is also important (e.g., G. Zhang & Song, 2009). Bechtold et al. (2008) found that when the entrainment rate of the cumulus scheme was formulated to vary vertically and depend on the environmental humidity, model representation of tropical waves including the MJO was improved. Further analysis on the impact of this method on the MJO was given in Hirons et al. (2013a, 2013b). Several other studies also emphasized the impact of environmental moisture on convection parametrized in the GCM (e.g., Chikira & Sugiyama, 2010; D. Kim et al., 2012).

On the other hand, modification to the convection scheme that improves the MJO representation often results in degradation of the simulated mean climate (e.g., D. Kim et al., 2011). However, several recent modelling studies demonstrated that it is possible to improve the MJO simulation without negatively affecting the mean climate (e.g., Ahn et al., 2019; B. Chen & Mapes, 2018). Ahn et al. (2019) showed that an important factor to have a skilful simulation of both the mean state and the MJO is to have the entrainment rate situation adaptive, i.e. a higher entrainment rate for suppressed than active MJO convection.

Models that do not depend on convection parameterization have been developed recently in several research groups and were used in MJO simulation (e.g., Miura et al., 2007; Nasuno et al., 2009; P. Liu et al., 2009). For example, with the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) cloud resolving global ocean-atmospheric coupled model, Sasaki et al. (2016) demonstrated that an MJO event was realistically simulated. The high-resolution simulation makes it possible to conduct detailed analysis to provide insight for the MJO dynamics especially that related to multiscale interactions. However, simulations using these cloud resolving GCMs often have a short duration with a small number of MJO cases which is limited by computing resources. It is usually difficult to produce a statistically robust conclusion from such simulations.

Another approach to represent clouds and convections in a GCM is to replace the convection parameterization by embedding a 2-D could-resolving model (CRM) at each grid column (e.g., Grabowski, 2001; Khairoutdinov & Randall, 2003). Such a “super-parameterization” approach was found to produce a better performance of MJO simulation than its parent model using a conventional cumulus parameterization scheme (e.g., Khairoutdinov et al., 2005; Benedict & Randall, 2009; H. Zhu et al., 2009). However, the success of the super-parameterized models in simulating the MJO is model dependent. Some models with embedded CRM still have strong biases in model climate (e.g., D. Kim et al., 2011; Jiang et al., 2015).

It has been recognized that the air–sea interaction is an important aspect of the MJO. There is a coherent relationship between the MJO convection, surface fluxes and sea surface temperature (SST) (e.g., DeMott et al., 2015; Woolnough et al., 2000). Processes involved in this interaction include changes in solar radiation, surface evaporation, winds and vertical mixing. Therefore, a proper representation of the air–sea coupling may be required for a realistic simulation of the MJO. This includes a proper representation of the diurnal cycle of the SST and thus a fine vertical resolution near the surface of the ocean is needed (e.g., Woolnough et al., 2007; H. Seo et al., 2014). Some previous studies found that the time scale and intensity of intraseasonal variability, and phase speed are more realistic when a coupled GCM is used (e.g., Flatau et al., 1997; Kemball-Cook et al., 2002; Sperber et al., 2005; Waliser et al., 1999). In contrast, several previous studies showed that the air–sea coupling either has a small impact or degrades the MJO simulation (e.g., Gualdi et al., 1999; Hendon, 2000; Pegion & Kirtman, 2008). Factors affecting the MJO simulation when coupled with the ocean include increased biases in the model mean climate and deficiencies in representing surface flux anomalies, as discussed in Gualdi et al. (1999) and Hendon (2000).

b Predicting the MJO

Given the important role of the MJO in subseasonal to seasonal predictions, it is crucial to produce skilful MJO predictions. The performance of numerical models in predicting the MJO has been considerably improved in the past 20 years. The main factors contributing to this MJO prediction skill improvement are improved model representation of clouds and convection (e.g., Bechtold et al., 2008; Hirons et al., 2013a), better initial conditions and advanced ensemble techniques (e.g., Neena et al., 2014; Vitart, 2017).

An estimation of potential predictability of the MJO is useful which provides an intrinsic limit for MJO predictions. The potential predictability can be estimated from an ensemble forecast using the “perfect model” approach, where one member of the ensemble is taken as the “truth” and compared with forecasts of other members (e.g., Pegion & Kirtman, 2008; Waliser et al., 2003). By analysing the ensemble hindcasts of eight coupled models participating in the Intraseasonal Variability Hindcast Experiment (ISVHE), Neena et al. (2014) estimated the potential predictability of the MJO in boreal winter, defined as the lead time at which the mean-square error becomes as large as the model MJO standard deviation. They found that the potential predictability of the MJO could reach up to 50 days. Such an estimation of potential predictability is highly model dependent. However, the actual prediction skill of the MJO verified against the observation is significantly lower than the potential predictability for a given model, implying that there is room for improvement.

Most studies on MJO predictions use the RMM indices of Wheeler and Hendon (2004) as a measure for the MJO. The evaluation is often performed on the forecast against the observed MJO indices using the bivariate correlation coefficient for each lead-time (e.g., Gottschalck et al., 2010; H. Lin et al., 2008). The lead time in days when the correlation drops to 0.5 is usually defined as MJO prediction skill, as used in many previous studies (e.g., Lim et al., 2018; Murphy & Epstein, 1989). Most current dynamical models are able to produce skilful MJO predictions with a lead time longer than 20 days, with the best models up to around 30 days (e.g., Rashid et al., 2010; H.-M. Kim et al., 2014; Lim et al., 2018; Pegion et al., 2019; Vitart, 2017). Vitart (2017) evaluated the MJO prediction skill in the operational models participating in the S2S project, and found that the skill scores vary widely among the models, with the ECMWF model standing out with the best MJO prediction skill of 34 days.

The RMM index consists of three components, U200 and U850 for circulation and OLR for convection. When the forecast skill of these three components of RMM is evaluated separately, the circulation component of the MJO in general has a better prediction skill than the convection component (e.g., H.-M. Kim et al., 2014; H. Lin et al., 2008).

In addition to model and initial condition quality, several factors are found to influence the MJO prediction skill. Forecasts initialized with a strong MJO in general have a higher MJO prediction skill than those starting from a weak MJO (e.g., H.-M. Kim et al., 2014; Lim et al., 2018; Rashid et al., 2010). This implies that a strong MJO tends to have a more coherent large-scale structure, and is more predictable than a weak MJO. The dependence of MJO prediction skill on the initial MJO phase has also been investigated, but the result is inconsistent among models (e.g., Lim et al., 2018; H. Lin et al., 2008). Most models produce a higher MJO prediction skill in winter than in summer, which is likely related to the fact that the MJO is stronger in boreal winter than in summer. However, it is interesting to see that the ECMWF model, which has the highest MJO prediction skill among the operational S2S models, is an exception that a higher MJO forecast skill occurs in boreal summer than winter (Vitart, 2017).

As discussed in section 5, the stratospheric quasi-biennial oscillation (QBO) has considerable influence on the MJO (e.g., Son et al., 2017). Predictions performed during boreal winters when the QBO is in its easterly phase in the lower stratosphere in general have a better MJO prediction skill than when the QBO is in its westerly phase (e.g., Lim et al., 2019; Marshall et al., 2017; S. Wang et al., 2019). However, it remains inconclusive whether the QBO-dependent MJO prediction skill change is statistically significant (e.g., H.-M. Kim et al., 2019).

There is evidence that atmospheric variability in the middle latitudes can influence the MJO prediction skill. For example, Vitart and Jung (2010) showed that improved MJO prediction skill is achieved when the extratropical atmosphere is realistically represented through a set of relaxation hindcast experiments. H. Lin and Brunet (2011) demonstrated that MJO prediction skill is higher when initialized with a strong NAO compared to a weak NAO, which is associated with the lagged NAO-MJO connection as discussed in H. Lin et al. (2009). Further studies are necessary to clarify the mechanism for the influence on the MJO from middle latitude processes and the degree of impact on the MJO prediction skill.

Dynamical models tend to have difficulty simulating the propagation of the MJO across the Maritime Continent from the Indian Ocean to the western Pacific (from phase 2/3 to phase 6/7), leading to a predictability barrier for the MJO (e.g., H.-M. Kim et al., 2016). This problem may result from model bias in the diurnal variability over the complex terrain of the Maritime Continent, longwave feedback and deep convection parameterization (e.g., H.-M. Kim et al., 2019; Lim et al., 2018; Ling et al., 2019). Vitart (2017) showed that all the S2S models have difficulties propagating the MJO across the Maritime Continent, with a higher percentage of MJO events not reaching the western Pacific. Capturing the realistic propagation feature of the MJO from the Indian Ocean to the western Pacific in dynamical models is thus crucial to improve the MJO prediction. It has been identified in several studies that the horizontal moisture advection over the Indian Ocean is one of the key processes for the eastward propagation of the MJO across the Maritime Continent that influences the MJO prediction skill (e.g., H.-M. Kim et al., 2014, 2019; Lim et al., 2018). Model biases in mean moisture lead to errors in moisture advection and are found to be partly responsible for the degradation in MJO propagation and forecast skill. Other processes including air–sea coupling, cloud-radiation feedbacks are likely also important. Improved understanding of processes for model errors is beneficial for MJO predictions.

A common issue for ensemble prediction systems in MJO prediction is that the ensemble spread is too small, i.e. under-dispersive (e.g., H.-M. Kim et al., 2014; Vitart, 2017). In an ideal ensemble system, the spread should provide an estimate for the forecast uncertainty and be related to skill of the system. The underdispersion of MJO forecast implies that the S2S models do not produce well calibrated ensemble MJO forecasts. To improve the spread-error relationship and MJO prediction skill, improved ensemble generation with better representation of uncertainties in model physics and initial condition are required.

7 Final remarks

The intraseasonal time scale resides between weather and climate. As the dominant mode of intraseasonal variability in the tropics, the MJO has substantial global impacts and represents a major source of predictability on the subseasonal time scale (e.g., NAS, 2016). Over the past few decades since its discovery, a great number of studies have been conducted and significant progress has been made in understanding, modelling and predicting the MJO. The MJO dynamics involves complex feedbacks among processes including circulation, convection, moisture, clouds and radiation. Multiple theories for the mechanism of the MJO have been proposed, indicating that a clear picture of the MJO dynamics is yet to come. Further observational, theoretical and numerical modelling studies and internationally coordinated efforts are warranted to advance the MJO science and to improve the subseasonal and seasonal predictions.

Disclosure statement

No potential conflict of interest was reported by the author(s).