How Children Individualize Numerical Routines: Elements of a Discursive Theory in Making

Abstract

Conceptualizing numbers as discursive constructs generated in, and for the sake of, communication, we investigated the development of the numerical discourse of Milo, a boy who was 2 years and 8 months old when we first met him and whom we then followed for 18 months. Our analyses of the child’s evolving responses to the question “Where is there more X?” (WiTM) corroborated the basic theoretical tenet, according to which numerical thinking begins in our culture with the independent appearance of (1) the quantitative–non-numerical discourse and (2) numerical–non-quantitative discourse. In Milo’s case, these two discourses, although constantly evolving, remained separate for months. A number of clearly distinguishable developments preceded the eventual consolidation of the independent numerical and quantitative “rituals” the child performed in response to WiTM-question into one compound routine of quantitative–numerical comparison. It is at this point that the numerical and quantitative ways of thinking began coalescing into a single discourse and the initial binary relation of order gave rise to the unary relation of cardinality. All this is summarized in a three-stage model of the development of numerical discourse. Three additional case studies that corroborated this model are reported briefly.

How do children become able to deal with the abstract object called number? This question has been guiding our research for the last 15 years. It was not for the paucity of studies on children and numbers that we have been engaging in this sustained effort. Indeed, numerical thinking has been attracting researchers’ attention at least since Piaget’s seminal publications on the subject (Piaget, 1965). Yet, the burgeoning field has also been fraught with controversies. Research has been producing fractioned accounts, infested by lacunas which we could not help noticing while trying to make sense of some previously unreported phenomena (Sfard & Lavie, 2005).

Convinced that the key to the problem may be the way researches have been thinking about numbers and learning, we began creating a conceptualization that we called “commognitive” (Sfard, 2008). This combination of communication and cognition is an epitome of our foundational tenet, according to which thinking is a form of communication. We have been refining the commognitive framework time and again in our consecutive studies (Sfard, 2008, 2015). This paper is yet another interim report from this longitudinal project. After an attempt to synthesize what is known so far about the origins and early development of numerical thinking, we offer a brief introduction to the commognitive discourse. We continue with a detailed presentation of our most recent study: the investigation of the evolving numerical thinking of a boy whom we followed for 18 months since he was 2-year 8-month old.

RESEARCH ON ORIGINS AND DEVELOPMENT OF NUMERICAL THINKING

The question of origins and development of numerical thinking has always been drawing attention of psychologists (e.g. Piaget, 1965), educational researchers (e.g. Fuson, 1988), linguists and biologists (Hauser, Chomsky, & Fitch, 2002), mathematicians and historians of mathematics (Seidenberg, 1962) and philosophers, beginning with Plato. More recently, it was taken up also by neuroscientists (Nieder & Dehaene, 2009). Because the resulting accounts are coming from diverse research discourses, it is not easy to combine them into a single coherent story. The task is additionally hindered by the fact that even relatively homogeneous niches are often hosting several diverging takes on seemingly the same phenomena. We shall now try to adumbrate this heterogenic field, grouping the different accounts according to their onto-epistemological foundations.

All the existing approaches can be roughly divided into two categories, differing in their vision of the nature and origins of numerical thinking. The larger and arguably better established of these strands may be called acquisitionist, because it treats numerical thinking as the activity of manipulating mental entities and describes its development as the process of “acquiring” these intangible objects. This shared conviction notwithstanding, the acquisitionists are divided over the question of the nature and mechanism of the acquisition. The different positions run from Piagetian constructivist stance (Piaget, 1965; 2001/2014) to full-blown nativism, championed, among others, by Chomsky (1980). According to the constructivist vision, further developed by neo-Piagetians (e.g. Case, 1992; Ferrari & Vuletic, 2010), the child constructs her “mental scheme” of number herself, by drawing on her experiences in the world. On the nativist pole, numerical thinking becomes a genetically determined human trait.

Today, most studies on the earliest forms of numerical thinking, and mainly those led by researchers trained as psychologists or neuroscientists, fall close to this latter extreme. Here, numerical thinking is considered to be genetically determined, with social interaction regarded as potentially helpful but not indispensable for this thinking to emerge (Carey, 2001; Condry & Spelke, 2008; Dehaene, 1997; Feigenson, Carey, & Spelke, 2002; Gallistel & Gelman, 1990; Geary, 2017; Holloway & Ansari, 2015; Sarnecka, Goldman, & Slusser, 2015; Siegler & Lortie-Forgues, 2014; Wynn, 1992). In that research, participants are usually faced with tasks considered by the researcher as testing one’s inborn “sense” of cardinality. The latter idea comes together with the claim about “inner representations” of numbers, which are believed to exist in children already at the pre-verbal, or pre-symbolic, stage. Findings from studies conducted among babies as young as two months of age (Wynn, 1992) have been interpreted as showing that even newborns may have expectations with regard to how cardinality of small sets should change when an item is added or removed.

Within the acquisitionist research, the focus on the property of cardinality (as opposed, for instance, to that of order) continues beyond the pre-verbal stage and is characteristic also of studies on toddlers who begin communicating in language. More generally, researchers have been testing preschool children’s ability to count, to name the cardinality of a given set (Gelman & Gallistel, 1978), to construct a set with a named number of elements (e.g. “Give me five blocks”; Mix, 1999), to tell the cardinality of a set constructed by matching its elements to those of a set whose cardinality has already been established (Frydman & Bryant, 1988), and similar. Relatively small portion of acquisitionist research deals with comparisons (e.g., “Which doll has more cookies?”; Fuson, 1988; Piaget, 1965) and thus not much attention is given to the relation of order.

Acquisitionist researchers may differ in their description of the range of abilities (or “acuities”) the child typically displays upon her birth versus those that she will develop only latter (Condry & Spelke, 2008; Starkey, 1992), but they have a widely shared opinion on what children can or cannot do with numbers while at the verge of the verbal stage, just after being introduced to the numerical vocabulary. According to this common vision, children’s representations of numbers can be split into two categories (or “systems”; Condry & Spelke, 2008; Sarnecka et al., 2015), one of which consists of cardinalities 1, 2, 3, and sometimes also 4, and the other of which contains all the larger ones (Condry & Spelke, 2008; Dehaene, 1997; Geary, 2017; Siegler & Lortie-Forgues, 2014). For simplicity, the word ad, the common suffix of dyad, triad and quadrad, will be used in this paper for the elements of the former category, whereas the name crowd will be given to the latter. Ads and crowds differ in the degree of precision with which the pre-symbolic child identifies different cardinalities: while being able to name the ads accurately, the young child tends to refer to crowds indiscriminately either with terms such as a lot or many or with any number word from four up (Condry & Spelke, 2008; Mix, 2009). With time, there will be an increase in the child’s ability to differentiate crowds at a glance, without counting (the fraction 11:10 has been found to be the lower bound of the ratio between distinguishable cardinalities; Halberda & Feigenson, 2008). When it comes to the binary relation of order, young children may be expected to respond correctly when a pair with at least one ad is involved but will often fail if presented with two crowds (Condry & Spelke, 2008). Whether considered as present at birth or as emerging sometime later, the abilities to execute these tasks are seen by the acquisitionists as determined by the human genetic makeup.

This vision has been countered by a newer, admittedly less numerous but steadily growing group of developmentalists and learning scientists who, following Vygotsky, reserve the term “numerical thinking” for an activity that is unique to humans and has its origins at the social rather than individual “plane” (Vygotsky, 1987, p. 11). These thinkers claim that mathematics, like any other “higher cognitive function”, can be “defined as a cultural practice” and that “to learn mathematics is to become socialized into the ways of knowing used in the community of mathematicians and mathematics teachers” (Nunes, 1999, p. 33). This strand can be called participationist, because it follows children’s increasingly competent participation in the historically established activities with numbers. While claiming the utmost importance of the cultural shaping, participationists do not deny the role of genetic factors. Unlike the nativists, however, they see genes as enablers of this thinking, and not as its independent generators. Without the cultural input, the uniquely human potential for activities known as numerical would have been unlikely to materialize.

If so, children can begin engaging in numerical thinking only when they are already capable of deliberately coordinating their actions with those of other people. Accordingly, Nunes and Bryant, the leading representatives of the latter strand, declare that they have little interest in “research that is presented as evidence of infants’ numerical abilities” and they justify this omission by saying that their own approach is “radically different from that adopted by researchers who argue that infants know the number of objects in small sets and can compute addition and subtraction on numerical representations.” (Nunes & Bryant, 2015, p. 725). This “radical difference” is not just a matter of diverging epistemologies, but also of ontological disagreements. In spite of their common terminology, the two schools seem to hold incommensurable visions of their focal entities, such as “numbers” or “conception of number”. The acquisitionist-nativist account rests on the tenet of ontological dualism, according to which numerical thinking involves manipulation of representations of numbers, either “inner” (Geary, 2017; Siegler & Lortie-Forgues, 2014), or in the form of numerical symbols. The participationist school, on the other hand, avoids the talk about inner representations, thereby eliminating inner/outer, or mental/physical (mind/body) dichotomies.

Renouncing the dualist ontology, however, requires an even more thorough revision of language. For instance, many of the participation-minded researchers retain the term representation. Although now referring only to tangible numerical symbols, icons and manipulatives, this notion tacitly pushes them back into the trap of the ideal/material dichotomy: the talk on representations implies that words and symbols are but avatars of the “real things”, of numbers “as such”. According to this Platonic assumption, the child may experience numbers prior to getting acquainted with their properties, just as she experiences moon before realizing its place in the universe as an astronomic body that orbits the Earth. This view of things may be the main reason for the phenomenon about which we complained from the outset: for the fact that researchers often tend to talk about what children do not yet “know about numbers” rather than attending carefully to what they say and do when invited to participate in numerical discourse (Sfard, 2015). Those researchers who succumb to this tendency remain oblivious to the possibility that the child’s response to the adult’s “numerical task” may be about something else than numbers. Clearly, awareness of this possibility is crucial in teaching.

The approach to be introduced in the next section is the product of our attempt to avoid looking at children’s activities through the prism of our own “grownup” mathematical discourse. A change in our language was indispensable if we were to free ourselves from the implicit assumption, according to which the young learner deals with the same mathematical objects as educated grownups, except that she may have wrong ideas about the nature of these objects. To eliminate “the dominant ‘deficit’ view in which learners have robust scientific [or mathematical] misconceptions that must be confronted and replaced” (Luce, Tanner, Goldman, & Conlin, 2018, p. 1192), we had to clean our research discourse from the last vestiges of dualist ontology.

COMMOGNITIVE APPROACH TO THE STUDY OF NUMERICAL THINKING

According to commognitive conceptualization, numerical thinking is a discursive activity evolving around number words. Thus, within the commognitive vision, baby’s spontaneous reactions to a certain type of change in cardinality, although relevant to her latter ability to think about numbers, is not, in itself, an act of numerical thinking any more than is one’s spontaneous reaction to a falling glass of water the activity of thinking about forces and energy.

Numerical Thinking as a Discourse

In the spirit of participationism, the focus of our research is on those forms of numerical activities that are unique to humans. Collectively shaped over numerous generations, these activities now enter the child’s repertoire through individualizing, the process in which one gradually becomes capable of agentive participation. Activities known as numerical, which aim at producing statements on particular properties of objects, constitute a subset of activities of communicating. When individualized, they become a form of child’s thinking.

In the light of this, to say that a child is engaged in numerical thinking is to claim that she is participating in a special kind of communication – in a discourse known as numerical or as discourse about numbers. Four features set numerical discourse apart from any other. First, it is characterized by its keywords, such as number names, terms related to quantities (big, bigger, more, etc.) and words signifying numerical operations. Second, it is recognizable by its special visual mediators, which may come in the form of either concrete counters or numerical symbols (digits and numerals). Third, an important part of numerical discourse are endorsed narratives on numbers, that is, statements such as “seven is more than five” (symbolically, “7 > 5”) or “three plus four is seven” (“3 + 4 = 7”), which mathematicians consider as useful and describe as true.

Finally, this discourse, as any other, has its own characteristic ways of doing things, that is, its own routines. In informal terms, numerical routines are patterns of action that appear when people participate in numerical discourse. Numerical routines are performed when, for instance, one counts, creates narratives on number, substantiates those narratives, writes a formal proof of a claim about numbers, etc. In other words, numerical routines are generally accepted, repetitive forms of actions one undertakes to produce narratives about numbers and to make sure they would be endorsed by the community of the discourse. Another way to describe a routine is to say that it is as a task–procedure pair, where the task indicates what needs to be achieved by executing the routine (for instance, one has to produce an endorsable narrative about the sum of a given pair of integers) and the procedure is a prescription for how it could be done (in this example, the long algorithm for addition, for example; see also Lavie, Steiner, & Sfard, 2019).

Within commognitive approach, to study development of numerical thinking means to follow successive transformations in the four characteristics of numerical discourse. This is what needs to be done whether historical or ontogenetic changes in numerical discourse are considered. In the spirit of Vygotsky’s remarks “on the importance of ‘genetic’ analysis” and in concert with his insistence on “seeking the origins of current phenomena by studying their history” (Cole & Packer, 2016), we will now take a glance at the development of numerical discourse over centuries before turning to its individualization by the child.

Historical Development of Numerical Thinking: Co-constitution of Numerical Discourse and the Activity of Choosing

As discursive constructs, numbers have a social rather than “natural” history. They originated in interactions between people, not in nature. Our first job, therefore, is to identify those human needs that were likely to give rise to numerical communication. We will then have to answer the question of why and how this communication subsequently evolved until it reached its present form. The empirical basis for reconstructing past forms of numerical discourse or for figuring out the circumstances that led to their emergence is, of necessity, shaky and insufficient, and is particularly problematic when the object of study is a discourse. A proper analysis of historical changes in numerical discourse would require extensive samples of everyday numerical talk, as practiced by past generations. Since such data are mostly unavailable, we have to make do with the speculative nature of historical investigations.

To be sure, historians of mathematics have much to say about the emergence of numbers. The existing visions of the origins of numbers can be divided into two types. According to the mainstream accounts, the emergence of counting was spurred by its prospective applications (see e.g. Ifrah, 1998). Being supposed to satisfy some universal human needs and desires, counting was bound to appear, sooner or later, practically in every culture. The other school, represented by Seidenberg (1962), among others, professes the view that numbers came into being in the ancient Greek rite, known as ritual of creation. Here, the routine of counting expressed itself in reciting a constant sequence of labels that dictated the order in which the rite participants appear on a stage. If this version is adopted, all the numerical systems in the world must be seen as a product of the diffusion and transformation of this one-time invention.

Our commognitive version, while different from both these theories, adopts an element of each. On the one hand, we opt for the more widely held hypothesis on the invention of numbers as stimulated by a prospective use. On the other hand, while unconvinced by Seidenberg’s thesis on the role of rites in the creation of number talk, we do share his belief that it was the binary relation of order (more precisely, of quantitative order) that gave rise to the unary relation of cardinality. This, of course, counters the acquisitionist assumptions on the developmental primacy of cardinality. Our argument for this vision begins with two tenets on development of discourses. First, new discourses originate in discrete routines, usually involving some new words. Second, such “germinal” discursive routines are byproducts of human efforts to improve or extend certain practical activities, that is, activities that aim at a change or reorganization of objects. In recent years, these assumptions were reinforced by findings of cross-cultural studies (Morris, 2014; Saxe, 2012).

In the case of numerical discourse, the obvious candidate for the germinal routine is the routine of counting. Historical deliberations, therefore, must include the quest after a practical activity likely to be the one that has triggered the invention of counting. Such activity must have a restricted initial version implementable with the help of a number-free procedure, and it must be undoable in its extended form as long as counting is unavailable. These two conditions are neatly fulfilled by the elementary practical activity of choosing the more numerous of two sets. Usually, the routine of choosing begins in the act of comparing the sets quantitatively. Such comparing leads to a statement, either explicit or just hinted at, of the form “Set X has more elements” and ends with opting for X as the set of choice. For small sets, this routine does not require numbers: it can be performed simply by mapping one set into the other in the 1-to-1 manner. This, however, is not possible if the two sets are very large or are distant in space or time. In these latter cases, numbers become indispensable. Our first claim about the emergence of number talk, therefore, is that it had to do with the desire to extend and refine the practical routine of choosing by quantitative comparisons.

Figure 1 outlines the possible historical developments of this routine together with its “numerical” extension. The model originates in the conjecture that humans have been occasionally engaging in the activity of choosing almost from the beginning of history. Initially, the choosing could express itself in a direct action of selecting one set without considering any other (see A in Figure 1). Later, the choices could be based on comparisons stemming from considerations other than quantity (B). The earliest quantitative choices (C) did not have to be numerical. The term” quantitative” signals that the comparison requires deciding whether one of the compared items constitutes (is isomorphic to) a part of the other. Such decisions can often be made on the basis of visual assessments. In the case of small sets, one can map one of the sets 1-to-1 into the other. As described in the previous paragraph, the wish to extend this latter routine to sets that could not be physically aligned with each other gave rise to choosing by numerical comparison (D).

Figure 1 Historical origins of numerical discourse.

Two basic assumption underly the above historical model:

• Quantitative discourse, made distinct by its use of words of comparison such as more/less and words for sizes, such as large/larger/largest or small/smaller/smallest, began emerging within the context of the practical activity of choosing. Initially, it was restricted to the discourse of quantitative order, that is, one in which it was possible to say that object or set S “is larger” or “has more” than object or set T whenever T appeared isomorphic to a proper part of S. This discourse did not yet support the unary relation of cardinality and did not contain words for describing stand-alone quantities, such as large, small, and was also free from number words¹.

• Numerical discourse developed from this initial talk of quantitative order when the routine of counting was introduced as a means for comparing sets too large or too distant in space or time to allow for a direct mapping of one into the other. This new discourse made it possible to talk about unary relation of cardinality, that is, to make statements about numerosity as a property of a set (“The set S is large” or “S has five elements”).

We will now argue for the relevance of these two claims also for the ontogenesis of numbers.

Ontogenesis of Numerical Thinking: Individualization of the Historically Established Numerical Discourse

The fact that in our globalized world the numerical discourse is already around when the child is born implies some obvious differences between the historical and ontogenetic developments. Indeed, the learners individualize the historical product rather constructing an all new discourse on their own. The process starts with the child’s exposure to other people’s numerical exchanges, proceeds with her “scaffolded” participation in such interactions and reaches completion when the learner is able to participate in an independent, agentive way. In constructing a hypothetical model of this development, we built on two tenets about the individualization of number talk in the modern societies.

• Today, two discourses, the quantitative non-numerical (Q-nN) and the numerical non-quantitative (N-nQ), are usually introduced to children in parallel; they then remain separate for months, if not for years.

• Gradually, these two discourses begin to coalesce until they turn into a single quantitative numerical (QN) discourse.

Much evidence for the first of these claims can be found in research done, or just inspired, by Piaget (1965, 2001/2014). The existence of numerical non-quantitative discourse finds its confirmation in observations according to which “children who know how to count may not be counting to compare sets with respect to number” (Nunes & Bryant, 1996, p. 35; see also Fuson, 1988; Hannula & Lehtinen, 2001; Sfard & Lavie, 2005). Other studies seem to corroborate the claim about the lingering presence of quantitative non-numerical discourse when they show that children are capable of quantitative comparisons long before they are ready to implement the task with the help of numerical discourse (Starkey & Cooper, 1980; Strauss & Curtis, 1981; Wynn, 1992). In tune with all these claims is the suggestion that quantitative non-numerical thinking should be fostered prior to, and as a foundation for learning about numbers (Davydov, 1982; Nunes & Bryant, 2009). In the light of all this, also the second tenet, the one about the eventual coalescence of Q-nN and N-nQ discourses, seems valid. After all, most individuals in our society do become, sooner or later, competent users of numbers as measures of quantity.

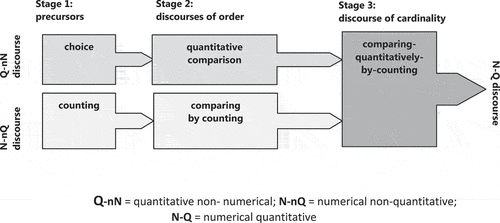
Based on the above two premises and on the previous observations occasioned by our historical deliberations, we can now propose a rough model of three initial stages in the individualization of numerical discourses (Figure 2).

Figure 2 Ontogenetic origins of numerical discourse.

Stage 1, which is called here the stage of precursors – of the initial non-quantitative and non-numerical routines, begins when the child is first exposed to the two routines, the routine of choosing and that of counting, that will latter give rise, respectively, to the discourse of quantities and to that of numbers. At Stage 2, two independent discourses of order are likely to develop: the discourse of quantitative order (cf. element C in Figure 1) and the discourse of comparing-by-counting. The claim about the independence of these two routines is grounded in our former research (Sfard & Lavie, 2005), which has shown that in the process of development of numerical discourse, there is a period during which the child can order sets according to the results of counting, but she does not see this order as equivalent to the quantitative order, reflective of the relation of inclusion. It will be by realizing this equivalence that, at Stage 3, the two discourses, Q-nN and N-nQ will eventually consolidate into one, giving rise to the unary relation of cardinality. We take this tripartite model as the point of departure for our research, which may now be described as aiming at a further corroboration of this model and at its refinement.

METHOD

The case study to be reported in this paper is a part of the ongoing research project, whose overall aim is to map the process of individualizing numerical discourse from its earliest stages until the moment the child goes to school. 16 preschool children, all of them native Hebrew speakers from a small middle-class community in the north of Israel, have been participating in the study. Our data consist of video recordings and transcripts of the first author’s interviews with the children. In one-on-one conversations, taking place every 4 to 5 months in the presence of a parent, the children are presented with task-situations likely to evoke quantitative, possibly numerical, discourse. Some of the tasks involve sets of concrete objects, such as blocks or small bite-size snacks; other ones are to be implemented with the help of a specially designed tablet app. With the parental approval, each child participates in the study for a period of one to two years.

Considering our intention to investigate processes of individualization, the interviewer acts as both researcher and teacher. Thus, the study belongs to the tradition of teaching experiments (Stefee, Thompson, & von Glasersfeld, 2000)². The teaching episodes take place whenever a new type of task-situation is introduced. The procedure consists of three steps. Once a task is presented, the children are given an opportunity to respond in their own way. In the second phase, the interviewer performs the standard routine, which the children are supposed to individualize. While acting as a leader, she encourages the young learners to execute for her any part of the procedure – counting, for instance – they may be already able to perform. The third step is to invite the children to try to deal with the same or similar situation again, this time on their own, but with interviewer’s scaffolding, as necessary. This 3-step cycle is repeated according to needs.

The story of our first interviewee, Milo, and his grappling with the routine of numerical comparison has been chosen for presentation in this article because this was the case study we completed ahead of all the others. Below is its more detailed description.

Participants

Interviews with Milo began when he was 2(8) (2 years and 8 months old) and lasted until he was 4(2). During all these 18 months, Milo attended a nursery school. His mother was present during all the interviews, albeit mostly as a passive observer. The two authors performed preliminary analyses of the data “on the go”, so as to use the insights thus gained to refine further data-collecting. Three other case studies have been completed before submitting this article, and we complement this report by comparing their findings briefly to those reported below in detail.

Data and the Collection Procedure

Our developmental models, whether historical or ontogenetic, feature the routine of comparing as the primary generator of numerical discourse. Because of this, it is the routine of comparison rather than that of counting that is in the focus of our research. To follow Milo’s progress toward the standard comparison routine, we had to expose the child to situations, in which the question “Where is there more X?” (WiTM-question) is asked in the presence of two sets of Xs. We call such situation WiTM-situation rather than “the situation of comparison”, because we are aware that the task the child may see himself performing in response may not be the task of comparison.

To explain this last claim and to prepare grounds for our future analyses, let us add a few words about how routines emerge and how they are recruited when necessary. Routines – patterns of action describable as task-procedure pairs – result from our tendency to react to task-situations – those situation in which one feels obliged to act – by trying to recapitulate what was done in similar situations in the past. Thus, the first step in dealing with any task-situation is to identify a precedent - a previous task-situation that seems to us similar enough to the present one to justify repeating what was done then. Subsequently, we replicate those elements of the precedent events that we consider as relevant to the present task-situation. The task we perform in result is thus a product of our personal interpretation of this situation. The same can be said about procedures we choose to accomplish the task: different people may draw their procedures from different precedents or may try to replicate different elements of what was done in the past event. In sum, a given task-situation may lead different people to different routines, deviating in both their tasks and procedures.

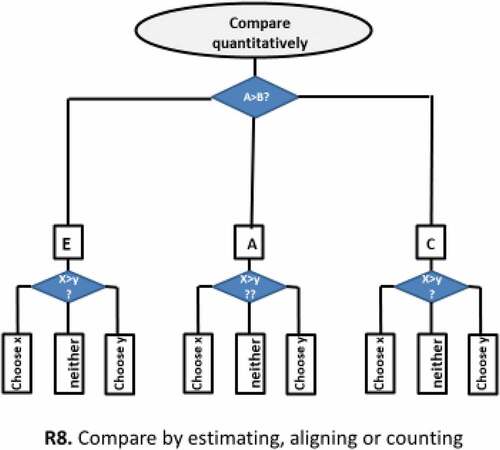
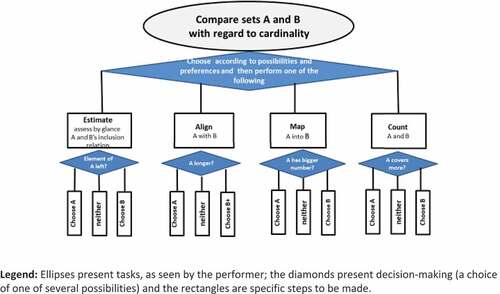
Of course, experienced numerical thinkers do opt for quantitative comparison while asked a WiTM-question. The comparison can be performed in several ways. Four options appear in the summarizing Figure 3 as different branches of the procedure (as sub-procedures). The task is marked here with the large ellipse on the top, whereas the beginning of the procedure, the act of deciding which of the four possible trajectories to follow, is marked below the ellipse by the diamond-shaped element. Each subsequent alternative is a sub-procedure consisting of two steps, with the output of the first one to be used as the input for the second – for the act of choosing (thus marked with diamond-shaped elements) of the set to be pointed to in response to WiTM question. The initial steps of the four sub-procedures can be described as follows:

• estimate (E): at a glance which of the sets is (isomorphic to) a subset of the other;

• align (A): order each set into a row and align the rows;

• map (M): construct an injection (1–1 mapping) of one of the sets into the other; and

• count (C): count the elements of the two sets.

Figure 3 The standard routine for comparing sets A and B with regard to cardinality, to be individualized by the participants of the study.

The subroutine of estimate & choose is grounded in one’s perceptual assessment of the binary relation of set inclusion, that is, in an attempt to decide which of the given sets constitutes a sub-set of the other one or is isomorphic to such sub-set. This inclusion may be called discrete, because it depends on the sets’ topologies rather than on their specific contents. The closer the ratio of the set cardinalities to 1, the more difficult it is to assess the relation of discrete inclusion at a glance. When the two sets are of similar density, we may also draw on the kind of inclusion that can be called continuous, because it is similar to the one we employ while comparing continuous objects: by assessing the areas or volumes occupied by the two sets. And vice versa: when the shapes and dimensions are the same, the assessment of discrete relation of inclusion can be based on the visual assessment of densities. Overall, the visual estimate & choose procedure is not always possible, and when it is applied, it is imprecise, that is, may lead different assessors to different results.

Visual estimation routine is challenging for teachers, if only because of the fact that its deciding step cannot be explicitly demonstrated or explained to very young learners. This problem is gradually alleviated in three other routines. These other routines are also more precise, that is, improve chances of agreement between performers. Yet, align & choose, which involves assessing the relation of continuous inclusion between two similarly arranged, aligned sets cannot be properly performed unless all the elements of both sets are identical in their shapes and sizes. The map & choose procedure, in which the answer to WiTM-question is given by assessing the relation of discrete inclusion scores high on precision, but its applicability is limited to pairs of relatively small, concurrently appearing sets. The count procedure overcomes all the limitations of the other procedures by extending the number-mediated assessment of discrete inclusion to sets of any cardinality.

These four subroutines do not exhaust all the options a competent person may consider, but this version clearly suffices as the foundation for the discourse of quantitative comparison. This is why it was chosen as the one to which participants of our study would be exposed. The teaching sessions, as all our meetings with Milo, were held in the university lab. The meetings have been video- and audio-recorded, with one camera directed exclusively on the child and positioned in such a way as to show his whole body and all the relevant elements of the setting. In the teaching episodes, we exposed Milo to expert performances of the routine from Figure 3. This was done in a gradual manner, with the different sub-procedures introduced sometimes separately and sometimes in combination. We helped ourselves with a battery of task-situations, each of which involved WiTM-question asked with reference to two small sets of identical objects. We varied the formulation of WiTM-question, so as to make children aware of the equivalence of the different forms. Two types of objects were used: those we termed desirable, because the children were likely to crave them (e.g. their favorite bite-size snacks, such as small pretzels or Bamba, the Israeli children’s favorite) and those we regarded as neutral, such as crayons or colorful plastic blocks. Desirable mediators were used to reduce the dependence of the child’s interpretations of the task-situation on his linguistic skills and to make it more likely that he sees it as requiring quantitative choice.

When deciding about the sizes of sets to be presented to children along with WiTM-question we were guided by what is known from previous research on children’s ability to distinguish between cardinalities. Since the same collection of tasks-situations was to be repeated with only minor modifications in all the rounds of interviewing, the battery included possibilities which were deemed in advance as being beyond the discerning capabilities of the youngest participants.

The data considered in this paper consist of video recordings and transcripts of all the WiTM-events. The transcripts have been segmented into episodes, each of which begins with the act of constructing a task-situation by the interviewer and ends when the activity generated by this task-situation is completed. In this report, only activities with concrete objects are considered. The full list of these episodes can be found in Appendix 1 (see Supplementary Materials—online only).

Data Analysis

Two questions have guided our data analyses:

Q1: In interactions with experienced participants, how did the child individualize comparison routine presented in Figure 3?

Q2: In this process, how did his use of quantitative and numerical keywords gradually evolve, especially with regard to coalescence of the quantitative and numerical discourses?

In our report, we will also remark on Milo’s routine of counting. Along the way, we will raise conjectures about how the boy used the interviewer’s actions as precedents.

To answer Q1 we had to derive Milo’s routines from his performances, which we did in a number of steps. Given a performance, we began with the question of whether Milo gave a standard response. If he did, we considered in addition his performances in several other comparable task-situations, so as to eliminate the possibility of an accidental success. In the case of a non-standard answer, we had to decide between two possibilities: either Milo’s task was as intended, but his procedure (or just its implementation) was incorrect; or Milo performed, possibly correctly, an entirely different task. Deciding between alternative interpretations required constant comparisons between the episode under scrutiny and the child’s other performances.

The most demanding analytic assignment was to figure out Milo’s non-standard interpretations of WiTM-situations. Theoretically, this required identifying all those features that were common to the current performance and to those past performances that the child was likely to consider as precedents. In practice, however, searching among all comparable past situations was unnecessary. From research on situatedness of learning (Brown, Collins, & Duguid, 1989), we knew that while faced with a certain task-situation in a given social, institutional or discursive setting, people are inclined to look for precedents only among those past events that took place in the same contexts. It was thus reasonable to assume that the most significant source of Milo’s precedents where to be found among the events that took place during our meetings (this is also why we believed that we would be able to tell a reliable story of Milo’s learning in spite of the fact that these were the only events to which we had a direct access).

The first few rounds of analyses were performed by the two authors independently, with each of them discussing her initial insights with her students. The two sets of results were then compared, argued for and successively adjusted until an agreed version was reached. Additional minor revisions of the analyses were made following reviews of the first report on this study, published in Hebrew (Lavie & Sfard, 2016). They were subsequently tested and found robust in eight workshops, conducted during the meetings of the authors’ research group (15 attendants, in average), at educational conferences, and during the second author’s visits to universities in other countries.

FINDINGS

We begin the report with a review of Milo’s performances prior to our intervention. We follow with detailed descriptions of the series of developments that took place during our subsequent meetings with him and led from the earliest precursors to fully-fledged comparison routine. While presenting our findings, we exemplify the analyses with the help of selected episodes. The sample set instantiates all routines observed in the study (no cherry-picking here!). These and additional representative episodes mentioned in the text can be found at the web (see the Appendix 2 in Supplementary Materials).

Milo’s Performances Prior to Instruction

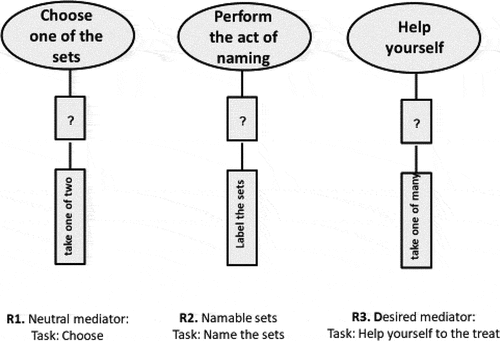
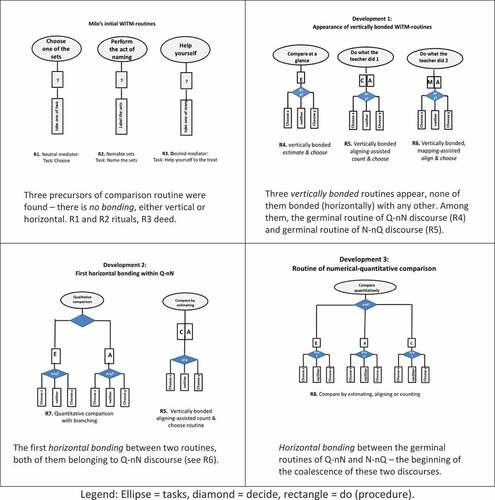
Our analyses of Milo’s earliest performances are based on the data collected in the first two rounds of interviews, when Milo's age was, respectively, 2(8) and 3(1). The analyses have shown that in this initial stage, Milo’s choice of procedures was highly sensitive to the type of mediator (natural vs. desirable) and to the question of whether the child could name the set with a number word. We identified three different routines Milo performed in response to WiTM question, none of them quantitative. We called these ways of acting routines, because each of them appeared a number of times. Together, they exhausted all Milo’s repetitive performances.

Routine R1: Choosing (as-if) for Oneself

This was the routine that we observed already in Milo’s first performances. It is exemplified in Episode I.

Episode I ³ Blocks <4,3 > ⁴ [round 1, Age 2(8)]

speaker	said	done	miscellaneous
1. Interv:	Tell me, in which bowl are there more blocks?		The bowls contain 4 and 3 blosks.
2. Milo:		Points to the bowl with 4 blocks
3. Interv:	Here? Or there?
4. Milo:	Here.	Points to the bowl with 4 blocks.

On the face of it, Milo did what he was expected to do: he evaluated the two sets visually and chose the more numerous one. Yet, the next few episodes with different pairs of cardinalities (see e.g., Episodes II, III in Appendix 2—online only) have shown that his choices did not depend on the relation between numbers. For instance, in the case of the pairs <4,5> and <1,5> the child answered WiTM-question by choosing the smaller set (which he did either by lifting it or by pointing to it). In the longer run, we did not manage to identify any common principle behind those choices. Although in some cases Milo’s “failures” could appear as related to the insufficient difference between the two collections, the more pronounced gaps did not make him more successful.

Given this, it is reasonable to conjecture that these task-situations reminded the boy of past events in which a choice had to be made from among a number of sets. In our society, even very young children are already familiar with this kind of situations. We thus concluded that the task Milo was trying to accomplish was simply to choose one of the sets, and to do it in whatever way he wished. This simple WiTM-routine, schematically presented as R1 in Figure 4, is probably the earliest precursor of the routine of comparison.

Figure 4 Milo’s initial WiTM-routine.

Routine R2: Naming the Sets

This routine, presented in Figure 4 as well, could be seen during our first meeting with Millo in Episode V.

Episode V Bamba <5,2> [round 1, Age 2(8)]

	speaker	said	done
76.	Mother:	Where is there more [pieces of] Bamba?	Milo holds two bowls, one with 5 pieces of Bamba, his favorite snack, and the other with 2 pieces.
77.	Milo:	Here there is a lot	Puts down the bowl with the larger amount
78.	Milo:	and here there are two	Puts down the bowl with 2 pieces of Bamba

On the face of it, the child did choose the larger set. Yet, although he correctly named the contents of one bowl as “two” and of the other one as “a lot”, we did not really see him choosing any of the two sets. Of course, we may assume that the ingredient of choice had been there implicitly, in the move of lifting the larger set first (see turn 77), or in the very act of uttering the term “a lot”. Yet, it is also reasonable to assume that Milo was simply trying to do what he probably saw done by people around him in WiTM-task-situations, except that he did not replicate all the elements that a competent performer considers as necessary. In his recall of the precedent events, he missed, this time, the fact that the act of labelling was followed by yet another one. The reason for this omission may be that in this present case he was able to name the sets. Since in the precedent events his ability to do so was probably rewarded by adults with expressions of pleasant surprise and with praise, once the names were stated the child was likely to consider his mission as complete. This way of acting repeated itself a number of times, and not only in the case of the tasty bites, but also in events with neutral mediators (see for instance Episode III in the Appendix 2). In short, when naming was possible, Milo tended to see it as his task to perform the labelling rather than to end up opting for a single label.⁵

Routine R3: Helping Oneself to a Treat

The last type of routine presented in Figure 4 was observed in many task-situations involving as-yet unnamable desirable mediators (see, for instance, Episode VII in the Appendix 2, where the two bowls contained pretzels.) In this kind of situation, Milo often tried to take hold of the bowls, evidently in an attempt, sometimes successful, to eat a piece or two. Given this procedure, the boy’s task was to help himself to the snacks. It was thus a special case of the routine of choosing, one that involved picking up individual pieces rather than the whole set. Because of the fact that, in general, Milo’s behaviors with desirable mediators caused much distraction, we decided to limit ourselves in the rest of this paper to tasks with neutral mediators (blocks).

Vocabulary

In Round 1 Milo responded to WiTM-questions mainly with gestures. The only exceptions were his uses of the words one in Episode III (25) and two and a lot in Episode V (in Hebrew, there is no lexical distinction between large amounts of discrete and continuous quantities, captured in the English words many and much; this is why we translated the Hebrew harbe – הרבה – into the neutral a lot). Beyond two, all sets were crowds (a lot). He used the words one, two and a lot as stand-alone labels, usually not accompanied by other words. Other number words, up to six, appeared in counting sequence evoked by the question “How many blocks are here?”. On this occasion, Milo responded by uttering the words “one, two, three, four, five, six” without really looking at the blocks and without any apparent reason for arriving at the word six (there were 5 blocks in the pile). There was also no active use of words of comparison.

Implications: What Needs to Change in Milo’s Discourse

The above outline of Milo’s initial reactions to WiTM-situation gave us preliminary ideas about the kind of transformations we should expect to happen in his routines and vocabulary on his way towards the standard routine of numerical comparison. Our subsequent teaching and analyzes were to be geared toward these changes.

Two differences strike the eye when one compares the two sets of routines presented in Figures 3 and 4. First, whereas Figure 3 presents a single routine that branches into a number of subroutines, Figure 4 features three separate single-branch routines. In the former case, the four subroutines (branches) are unified by a common task (see the ellipse in the top). Such uniting element is missing in the latter case one: Milo interpreted task-situations that gave rise to performances of R1, R2, and R3 as defining different tasks. Drawing on a metaphor taken from chemistry, we will say that in contrast to the four subroutines in Figure 3, the three routines in Figure 4 were horizontally (inter-procedurally) unbonded.

Another notable difference between Figures 3 and 4 can be found in the inner structure of the procedures. In each subroutine in Figure 3, the two vertical rectangles representing required actions are connected by a diamond shape, signaling that the second action – the action of choosing one of the two sets – will depend on the result of the first one – counting, aligning, mapping or estimating. In R1, R2, and R3 in Figure 4, there is no such connection. Here, the action marked by the lower rectangle is not related in any systematic way to the one marked by the upper rectangle. Indeed, even when Milo successfully named the contents of the sets, his subsequent choice did not necessarily match the naming. For instance, in one case (Episode III in Appendix 2—online only), after being presented with bowls of 1 and 5 blocks and naming the first one correctly, he chose the bowl with the single blocks as the one that “had more”. Here, we shall say that contrary to the routine in Figure 3, those in Figure 4 were vertically (intra-procedurally) unbonded.

It is not difficult to understand why bondedness was missing in all Milo’s routines. Lack of bonding, whether vertical or horizontal, signals that the performer does not ascribe any significance to the products of his actions. Instead, his attention is fully given to the actions themselves. Yet, these are the products of processes that bond different procedures: the criterion for horizontal bonding is that the procedures—say that of visual estimation and that of numerical comparison—produce the same outcome. In the case of vertical bonding, one needs to use the outcome of the first part of the procedure as an input to the second. All these products, often only tacitly present in expert performances of routines, are likely to remain invisible to the uninitiated observer, and so is their role in tying the different actions together.

Thus, whereas routines intended by the interviewer were product-oriented – their tasks was to produce a narrative of the form “There is more X in bowl Y”, Milo’s routines were process-oriented: in the eyes of the child, it was the performance of the procedure as such that constituted the task. The name exploration fits the first type of routine (it’s the defining feature of exploration that it produces a new endorsed narrative), whereas the term ritual fits the latter, standalone process-oriented routine, one that does not feed into any other. Milo’s initial routines R1 and R2 were clearly rituals. Routine R3 was an exception, in that its outcome – a few tasty bites the child could enjoy – were of significance. Since this product came in the form of tangible objects, this routine can be seen as practical (as opposed to routines such as quantitative comparison, which are discursive). We will call it deed. More generally, deeds are practical product-oriented routines, whose products express themselves in changes in objects or in arrangements of objects. Quite unlike rituals, both deeds and explorations tend to constitute elements of tightly interconnected nets, in which outputs of one routine may be used as inputs for some others. They can be combined with one another, thereby giving rise to ever more complex routines.

The absence of bonding, either horizontal or vertical, is the most obvious manifestations of ritualization, but there are other signs as well. Thus, when there is no interest in the product of performances, only social reasons, such as expectations of rewards or a fear of punishment, can motivate the implementation of ritualized routine. Also, since the performance is judged exclusively by its fidelity to the procedure, the performance is rigid, and there is not much space for the performer’s independent decisions.

The fact that Milo’s initial discursive routines, R1and R2, were rituals is in tune with the basic commognitive tenet, according to which, in the process of individualization, ritual is inevitably the initial form of germinal discursive routines (Sfard & Lavie, 2005). Under proper conditions, the rituals will morph into explorations. In our study, we expected that this process of de-ritualization—of shifting the attention from processes to products⁶ —would happen gradually, as the amount of intra- and inter-procedural bonds grows.

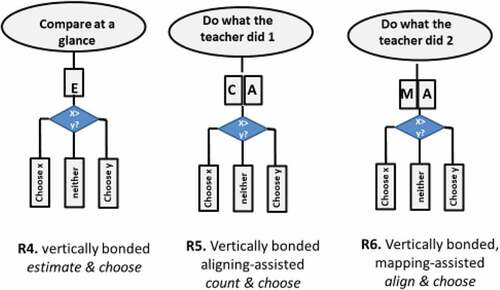
First Development: Appearance of Vertically Bonded WiTM-routines

In Round 2, which took place 5 months after the initial series of meetings, when Milo was 3(1), neither the first teaching event (Episode VI in Appendix 2—online only), nor the teaching that took place in the course of Round 2 seemed to have much impact. Also, not much improvement was noted in Milo’s procedure of counting, repeated numerous times in Rounds 1 and 2 as a part of WiTM-tasks execution. The first significant development was identified in Round 3, when Milo was 3(6). It expressed itself in the appearance of three vertically bonded routines that replaced the precursors R1 and R2.

Routine R4: Vertically Bonded Estimate & Choose

The first performances of this routine were observed in Episode IX.

Episode IX Blocks <5,3> [round 3, Age 3(6)]

	speaker	said	done
1.	Interv:	There are two piles of blocks here. Which pile do you choose?	Puts her hands over one pile of blocks, then over the other
2.	Milo:		Looks at the piles. Points at the one of five.

In this episode, as well as in some later ones (e.g. Episodes XII and XIII in Appendix 2—online only) Milo produced canonic answers. Later, in the case of equality, <5,5>, he answered by putting his hands over both piles and saying, “In both”.⁷ All this, as well as the fact that his responses were often preceded by a prolonged visual scanning of the two piles (see 1, 2 in Episode IX) support the conclusion that in all these cases, Milo’s choices, rather than being a matter of lucky guesses, resulted from visual quantitative estimation.

We concluded that Milo performed the vertically bonded estimate & choose procedure (R4 in Figure 5). This routine was more product-oriented than its precursors R1 and R2 from rounds 1 and 2, and thus not a pure ritual any longer. Its appearance constituted the first significant step towards Milo’s participation in the discourse on quantities.

Figure 5 Development 1: appearance of three vertically bonded routines.

Routine R5: Vertically Bonded Count & Choose Accompanied by Aligning

Two other unprecedented ways of acting appeared in Routine 3 immediately after the new teaching event (Episode XII, Appendix 2—online only). In this event, the interviewer led the performance, in which counting, aligning, and mapping were implemented one alongside the other. The performance involved counting the blocks in the piles, while also arranging them in adjacent rows. Moreover, after the blocks in one pile have been counted and arranged in a row, the blocks from the other pile, while counted, were being put one after another next to subsequent blocks in the first pile. It was now easy to see which of the two resulting well-aligned rows was isomorphic to a proper part of the other. The demonstration had an immediate impact on Milo’s performances, but because the task of emulating all three procedures at once might have been too demanding, Milo repeated just two of them at a time. Here, we report on his combination of count and align procedures, and in the next section, his performance of aligning-through-mapping will be described. In both cases, we illustrate our claims with the initial performance of the new routine. From what happened later in our study we do know that these were the beginnings of patterns of action that were to recur and develop in the future.

Although the routine of counting accompanied by arranging the counted piles into aligned rows was taught as early as the end of Round 1 (Episode VI, Appendix 2—online only), it was not until the similar teaching event in Round 3 (Episode XI, Appendix 2—online only) that Milo’s first attempt to perform this routine was observed⁸:

Episode XII Blocks <4,5> [round 3, Age 3(6)]

	speaker	said	done	misc
51.	Interv:	No, wait, no, no, the piles are separate. Which pile do you choose?	Separates the piles
52.	Milo:	one, two, three, four .four	While saying “four”, he lines them up; he smiles, rests his head on his hand and looks at the interviewer
53.	Interv:	Great
54.	Milo:	Four
55.	Interv:	There is four here	points at the pile of 4 blocks
56.	Milo:	one, two. Thrrrree, fooour, five	Pulls the second pile towards himself and starts arranging it in a line while counting
57.	Interv:	Good. So what does it mean?
58.	Milo:	This is more and this is less
59.	Interv:	Which is more and which is less? Show me.	Plays with the pile with 4 blocks
60a.	Milo:	This is a little and this is a lot	Points respectively to the pile with 4 blocks and then to the pile with 5 blocks
60b.	Interv:	Great! How did you know? Because … ?
61.	Milo:	Because you told me	Smiles at the interviewer
62.	Interv:	Because I told you what?
63.	Milo:	That we count

The first thing to note here is the impressive improvement in Milo’s counting skills. His count & choose procedure also seemed vertically bonded. We did consider an alternative possibility, according to which the correct answer to WiTM-question was the result of the accompanying performance of align & choose routine. This interpretation, however, was deemed less convincing. Indeed, Milo began to perform the aligning of the first pile only after its elements had already been counted and later, he did not carefully align the two rows. In counting the second pile, aligning seemed more like an auxiliary action, meant to make sure that the counting is performed correctly. It is also possible that aligning was implement for no other reason than the child’s wish to replicate what was done just a moment ago in the teaching episode. Our final evidence for the irrelevance of the aligning was Milo’s own stress on counting and on the fact that he claimed he counted because of the interviewer’s request (see 61–63 in Episode XII). To summarize, we interpreted what we saw here as a performance of the vertically bonded procedure, the first step of which included counting combined with aligning, and the later choice was made according to the order of the final numerical labels.

Since this procedure was very much like the one just demonstrated by the interviewer in the preceding teaching event and was also quite different from Milo’s performances prior to that event, it seems justified to say that the boy saw it as his task to replicate the teacher’s performance. This also means that the count & choose, while vertically bonded, was not yet bonded with any other routine. True, there was a connection between counting and aligning, but this connection was not one of horizontal bonding between two independent routines. Rather, combining counting and aligning constituted the first step of one procedure, and there was no awareness of the fact that each one of them, if used separately as the first step, would have led to the same outcome. As such, R5, in spite of its vertical bondedness, was still closer to ritual than to exploration.

R6: Vertically Bonded Align & Choose Routine Accompanied by Mapping

In the subsequent episode, after several attempts to just count blocks in the piles of 7 and 8 (which he executed successfully, but eventually abandoned), Milo turned to aligning accompanied by mapping.

Episode XIII Blocks <8,7> [round 3, Age 3(6)]

	speaker	said	done	misc
119.	Milo:	Look	Interrupts the interviewer	The piles of 7 and 8 are arranged in non-parallel rows.
120a.	Milo:		Takes blocks from the row of 7 and puts them one-by-one next to the blocks in the row of 8.
120b.	Milo:	And this … And this goes to that one And this goes to that one And this goes to that one And this goes to that one	Puts the fourth block. While matching, he skips one block. Ends up with two rows, one next to the other, that appear to be of equal lengths.
121.	Interv:	So, what do you say? Where is there more and where is there …
122.	Milo:	All of them have more

In the previous episode, aligning was deemed as but an auxiliary action, supposed to help in the proper performance of the deciding first step (counting). In the present case, it seems to have overtaken the leading role, with the accompanying mapping used only to make sure that the aligning is performed correctly. Indeed, the correct answer to WiTM-question, admittedly based on incorrectly implemented aligning, was clearly given on the basis of the result of this aligning. The mapping-assisted align & choose procedure was thus vertically bonded.

To sum up, all three routines observed in Round 3, R4, R5, and R6, can be described as ritualized, although to a lesser degree than Milo’s earlier routines. For one thing, all three were vertically (internally) bonded. Still, there was no sign for the horizontal bonding between any two of them. The present estimate & choose routine can be seen as the beginning of quantitative discourse of order and the aligning-assisted count & choose routine as an initiation of the numerical discourse of order.

Vocabulary

Just like his routines, Milo’s use of words indicated that he had already begun participating in both Q-nN and N-nQ. Number words appeared in his talk in counting, thus as labels. For the first time, Milo used such words also in a sentence: “There is four here” (55 in Episode XII). It is significant that the four was not yet followed by the phrase “of X”, thus was not yet used as an adjective but rather as a label for the set. Quantitative predicates, such as more or less (58 in Episode XII) were applied the way a lot and a little were used before and were unconnected to numbers. There was a new quantitative label, the same, which Milo used idiosyncratically.

Second Development: Appearance of a Horizontal Bonding Between WiTM- Routines

In Round 4, which began 4 months later, when Milo was already 3(9), the aligning-assisted count & choose routine, R5, has been implemented several times, with a growing proficiency. At the same time, the first horizontal bonding appeared, leading to the branching of quantitative comparison.

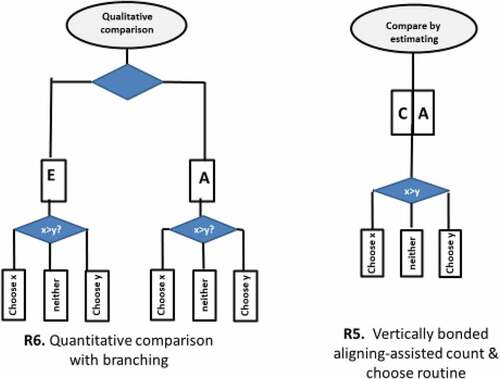
Routine R7: Branched Quantitative Comparison, Composed of Bonding of Count & Choose and Align & Choose

The branching of Milo’s routine of quantitative comparison (see R7 in Figure 6) was first observed in Episode XIV.

Episode XIV Blocks <5,3> [round 4, Age 3(9)]

	Speaker	said	done
69.	Interv:	And how do you know that in the purple pile there are more blocks?	Milo had just pointed at the pile of 5 purple blocks; the other pile contains 3 brown blocks
70.	Milo:	Because I put it for myself	Playing with the larger pile
71.	Interv:	Because you put it for yourself?
72.	Milo:	Yes
73.	Interv:	What did you put?
74.	Milo:	If we build this, we will see that it is not tall	Puts the brown blocks one on top of another and builds a tower.
75.	Milo:	And if we build this, we will see that it is tall.	Puts the purple blocks one on top of another and builds a tower.

Figure 6 Appearance of the first horizontal bonding between WiTM-routines.

Here, Milo justified his former answer by proposing that the procedure align & choose would have led to the same outcome as the procedure estimate & choose he implemented a moment earlier (see 74, 75: “If we build this, we will see that it is not tall; and if we build this, we will see that it is tall”). This imagined equivalence is striking and constitutes a strong evidence that the two routines were now bonded by the common task, that of quantitative comparison (ordering) – and were significantly de-ritualized.

Vocabulary

In this round, Milo’s discourse was still free from utterances combining number words with quantitative predicates. The only novel phenomenon was the appearance of expressions such as “It is [not] tall” (74 and 75 in Episode XIV) or “There are a few blocks here and a lot here”, in which the effect of comparison was attained by attaching opposite quantitative labels a few and a lot to the compared sets. Although Milo labeled objects with these kinds of words already during our first meetings, their use in as-if comparative sentences was a novelty. The appearance of these kinds of utterances, together with the significant development in the quantitative comparison routine, signaled a considerable rapprochement between Milo’s quantitative and numerical talk.

Third Development: Coalescence of Quantitative and Numerical Discourses

It was in Round 5, when Milo was 4(2), that his numerical and quantitative discourses began to coalesce.

Routine R8: Quantitative–Numerical Comparison

Episode XVI was the first event that made us aware of the fact that counting was becoming quantitative.

Episode XVI Blocks <4,6> [round 5, Age 4 (1)]

	speaker	said	done	misc
32.	Interv:	And this is a few, okay. Uuh, can you tell me which in which pile … there is a larger number of blocks?	The episode begins after Milo has already announced at a glance that the pile of 4 red blocks has “a few” (ktzat) and the one of 6 green blocks has “a lot” (harbeh).
33.	Milo:	In … one, two, three, four	Counts the 4 red blocks
34.	Interv:	Mmm …
35.	Milo:	One	Begins counting the green blocks-from the leftmost block
36.	Milo:	No, one, two, three, four, five	Milo changes his mind and starts to count again from the green block that is closest to him. Counts the fourth block twice, then stops.
37.	Milo:	one, two, three, four, five, six	Begins counting again. Counts from the closest block to the farthest one.
38.	Milo:	Here there is a few, and here there is a lot	“A few” refers to the pile of red blocks (4) and “a lot” refers to that of green blocks (6)
39.	Interv:	O.K
40.	Milo:	six, six	Points to the pile of 6 green blocks and then turns to the pile of red blocks and starts counting
41.	Milo:	one, two, three, four.	Counts the red blocks
42.	Interv:	And where are there less blocks?
43.	Milo:	In four	Selects the pile of 4 red blocks
44.	Interv:	In four? And where are there more blocks?
45.	Milo:	In fiv … in six

Let us first note that whatever the arrangement of the blocks, Milo’s counting was now performed according to rules, and the boy was capable of retracing and correcting the procedure whenever necessary (see 36), whereas his use of the last number words as labels for the sets (see 40, 43, 45) indicated his awareness of the principle of cardinality.

We now wish to claim that in this episode, procedure count & choose revealed itself as horizontally bonded with estimate & choose. The conjecture that this might be the case arose after Milo performed a (correct) visual estimation (in turn 31, not shown here, one pile was said to have “a few” and the other “a lot”) and began to count (33) in response to the repeated WiTM-question (32). If we still hesitated, it was because the counting might also be due to the presence of the word number in the second formulation of the WiTM-question. Our doubt was then dispelled by Milo’s utterances 33, 37 and 38, which testified to his being aware of the correspondence between the orders of visually estimated magnitudes and of the corresponding number words.

Because align & choose was already bonded with estimate & choose and closely associated with count & choose, we concluded that at this point, all three of them combined into a single, vertically and horizontally bonded routine of quantitative comparison (see Figure 7). This meant a decisive step in the process of de-ritualization. As long, however, as count & choose was not evoked by the child spontaneously, to provide input to another one (e.g. to the deed of choosing a pile for himself), we cannot claim that a fully satisfactory de-ritualization has been achieved.

Figure 7 Third development: the bonding of count & choose routine and quantitative comparison routines (coalescence of quantitative and numerical discourses).

Vocabulary

The analysis of Milo’s use of quantitative and numerical keywords provided additional evidence for the incipient consolidation of the corresponding discourses. It was signaled by the appearance of such cross-discursive expressions as “this is four and this is a few” (108, not shown in Appendix 2), where a few was used as a substitute for three. Number words began also functioning as adjectives in expressions such as “five blocks”.

Among other relevant novelties let us mention Milo’s use of the word yoter (more)⁹ , which has not appeared in his talk in the previous rounds and was now applied in non-standard expressions such as “yoter harbe” (verbally, “more many”; saying yoter should have sufficed). In addition, for the first time Milo was now describing sets that looked as equinumerous with the term the same. The word was used standalone as a descriptor of two equal towers, not yet numbers. In the context of numbers, this kind of talk was evidently still beyond his reach. When in a certain episode the counting of each of the two sets ended with the word five, he declared “two fives!” (67) and in a similar situation sometime later he described the result as “they are both five” (142). As argued in Sfard and Lavie (2005), the same cannot become a fully-fledged part of a numerical discourse until this discourse is sufficiently objectified, that is, until one talks about numbers as if they were self-sufficient objects, existing “in the world” independently of sets and humans who count them.

Summary of Milo’s Case and Comparison With Three Other Cases

Summary of all the above findings is presented below in the form of responses to questions Q1 and Q2. The answer to question Q1, regarding the evolution of Milo’s WiTM-routines over the five rounds of interviews, is offered in Figure 8. The response to Q2 about the evolution of Milo’s use of keywords of quantitative and numerical discourses and the coalescence of these discourses is presented in Table 1.

Table 1 Development of Milo’s Use of Numerical and Quantitative Vocabulary

Step	Use of keywords
	In the quantitative discourse	In the numerical discourse
Beginning (Rounds 1,2)	q1. Sporadic uses of quantitative predicates, such as a lot.	n1. One and two are the only number words in Milo’s talk
Development 1 (Round 3)	q2. Appearance of some comparative expressions, but never together with number words. q3. Equality is recognized, but not described with the expression the same.	n2. Number words are used as labels for sets
Development 2 (Round 4)	q4. Appearance of the first idiosyncratic comparative expressions, such as more a lot and more few; q5. the expression the same is used with regard to continuous quantities, but not to numbers
Development 3 (Round 5)	qn1. First appearances of cross-discursive sentences such as “This is four and this is a few”. Quantitative and numerical discourses begin coalescing. qn2. Number words are used to describe sets of concrete objects.

Figure 8 Development of Milo’s WiTM-routine.

While writing this paper, we were able to complete three other case-studies. The details on the participants’ ages in the different rounds of interviewing are presented in Table 2. Table 3 summarizes the development of children’s routines (the responses to Q1 in all the cases) and Table 4 presents their word use (responses to Q2). In constructing Table 3, we considered the child’s performance as signaling a given routine, say R7 (see its definition in Figure 5), if (a) it involved the same subroutines – in this example, estimate & choose and align & choose; and (b) it displayed the same bonding structure – in this case, both sub-procedures were vertically bonded and were horizontally bonded with one another.

Table 2 Children’s Age in Different Rounds in Years(months)

Child	Round 1	Round 2	Round 3	Round 4	Round 5
Milo	2(8)	3(1)	3(5)	3(9)	4(2)
Tal	2(1)	2(9)	3(2)	3(7)	4(1)
Yoni^i	2(10)	3(1)	3(7)	4(2)	4(6)^ii
Hala	2(6)	2(11)	3(5)	4	4(4)

ⁱ Yoni’s Round 3 took place twice (22.10.16; 24.10.16).

ⁱⁱ For several reasons, this round included only activities with tablet, thus its results are not included here.

Table 3 Development of WiTM-routines in the Four Cases (R1, R2, etc. Defined in Figure 5)

Child	Round 1	Round 2		Round 3	Round 4	Round 5
Milo	R1, R2, R3	R1, R2, R3		R4, R5	R5, R6	R8
Tal	R3, R4^a	R3, R4^a		R4, R5	R5, R6, R7	R8
Yoni	R3, R4^b	R3^c, R4, R6		R4, R5, R6^d	R5, R7
Hala	R3	R2, R3, R4^e		R4, R6	R5	R8

^a For <2, 2>, he chose both piles.

^b Observed for <1, 5 >.

^c Apparently, he estimated the areas occupied by the sets.

^d Round 3 was not completed the first time; it was repeated after two days. R7 was seen on the second day.

^e Observed for <1, 5 >.

Table 4 Development of Quantitative and Numerical Vocabulary in the Four Cases (Q1, Q2, etc. Defined in Table 2)

Child	Round 1	Round 2	Round 3	Round 4	Round 5
Milo	q1 n1	q1 n1	q2, q3 n2	q4, q5	qn1, qn2
Tal	q1, q3^a	n2	q1 n1, n2	q2, q4 n1, n2	qn1, qn2
Yoni	-	q1 n2	q1 n2^b	q4, q5^c n?^d
Hala	q1 n1, n2	q1, q2 n2	qn1^e, q3 n2	q3, qn2	qn1, qn2

^a Observed for <2, 2 >.

^b Performs “count all.”

^c Says “it’s the same.”

^d Counts each set separately.

^e Observed for <2, 2 >.

As can be seen from Tables 3 and 4, the findings from the additional three cases strongly corroborate what was found in that of Milo’s. More specifically, the mechanisms of change, as well as the resulting intermediary forms of in WiTM-routines and of keywords use observed in Milo’s case were found also in all other ones. Moreover, in spite of marginal idiosyncrasies of individual performances (see the notes in Tables 3 and 4), and despite the fact that the cases diverged slightly in the pace of the developments, no forms or mechanisms were noted in this additional corpus that would not be already observed in Milo’s case. Notably, the order of development of both WiTM-routines and word use was quite similar in all the four cases.

DISCUSSION

This study corroborated our initial tri-stage model of numerical development (Figure 2) and gave rise to its refinement. It also led us to some suggestions for teaching.

Corroboration of the Model of Individualization of Numerical Discourse

Findings from the initial two rounds of our conversations with Milo fit the description of the first stage in our model – the stage of precursors, where the discourse used by the learner in WiTM task-situations is supposed to be neither quantitative nor numerical. Indeed, at that time, the child’s responses to WiTM-question were not grounded in a systematic ordering of sets, and thus his use of the word more – which at this point appeared to be only passive – could not yet count as quantitative. The discourse was not numerical either, because number words were used only in purely ritualized counting or for labeling ads on the basis of their topologies and with no attention to their counting order.

The following two developments in Milo’s discourse, observed in Rounds 3 and 4, fit our characterization of the second developmental stage, that of discourses of order. At this stage, quantitative and numerical discourses, Q-nN and N-nQ, came into being, each one with its own relation of order. These two forms of talk remained separate throughout their continuous evolvement. The vertical bonding of the estimate & choose routine (R4) and its subsequent horizontal bonding with align & choose routine (R7) marked the emergence of quantitative-non-numerical discourse. The appearance of the numerical-non-quantitative discourse expressed itself in Milo’s growing proficiency in counting and in the vertical bonding of his count & choose procedure (R5).

The third development, observed 18 months after our first meeting with Milo (Round 5), brought the change expected at the third stage of the discourse development: the beginning of the coalescence of quantitative and numerical discourses, and thus the emergence of the discourse of cardinality. This was achieved through the horizontal bonding of estimate & choose and count & choose routines (R8).

REFINEMENT OF THE MODEL OF THE DEVELOPMENT OF NUMERICAL DISCOURSE

We now wish to argue that the results of the study go beyond mere corroborations of our initial developmental model from Figure 2. For this, we need to justify the claim that some of our findings may be generalized in spite of the limited size of our “sample”.

Of course, in studies such as ours, there may be considerable variations between cases or even within a single one. What the learner is doing constitutes a product of individualization and is thus function of what this learner has been exposed to. There is also no guarantee that in the out-of-lab situation the child would recruit any of the routines learned in the lab. Yet, all these are differences in routines, whereas our attempt at generalizing does not regard the routines as such but rather the mechanisms of the process of their individualization. It is here that we expect to find features that can reasonably be considered as more or less universal. We believe that just as watching the construction of a single house would be sufficient to realize that the roof can be added only when all the floors have already been erected, so may a single, closely observed case of individualization be sufficient to detect those features of the process that are a function of the properties of numerical discourse – of its structure and inner workings – rather than of the particular way of teaching or of the unique skills of the learner. In both cases, the universality of those changes may also be defended with analytical argument.

In the present context, it is reasonable to claim that the initial ritualization of the learner’s routines and then their gradual deritualization in the processes of vertical and horizontal bonding constitute basic mechanisms, thus relative invariants, of the process of individualizing of numerical discourse. Teaching may affect the pace of these transformations, can make slight shifts in their order, and may even introduce more intermediary forms than observed in our study; nevertheless, we claim that these transitions constitute the necessary “skeleton”, a set of features that stay more or less the same whatever the student’s individual skills and the kind of instruction to which she is exposed. Our developmental model may now be elaborated by incorporating these and related insights from our study. The refined version presented below is supported also by our own past findings and by those reported by other researchers.

Stage 1: Discourses of Quantitative and Qualitative Precursors

The pre-quantitative discourse appears when the child begins engaging in diverse choices in response to words of comparison, such as more. In this initial stage, however, this use is not yet grounded in genuine quantitative comparisons (cf. Sfard & Lavie, 2005; Walkerdine, 1988). At a more or less the same time, the emergence of pre-numerical discourses is triggered by the child’s exposure to the routine of counting. The learner begins using number words, but their counting order is irrelevant and does not impact the child’s responses to WiTM-question – there is no vertical bonding in her routine. The words one, two, and three are learned more or less the way one learns to name such properties as color or shape. This learning is grounded in the child’s ability to identify ads by their distinct topologies, without counting (this ability is known as one of “subitizing”; e.g. Mix, 2009).

Stage 2: Discourses of Order

At this stage, the quantitative non-numerical discourse emerges as a result of the child’s exposure to the activity of set comparisons. Numerical non-quantitative discourse evolves as well, with the child becoming increasingly proficient in the routine of counting (Gelman & Gallistel, 1978). She also starts responding to WiTM question with a number of vertically bonded routines. One of them is the routine grounded in the evaluation of the order of number words with which the sets are labeled in result of counting, which at this stage is a pure ritual. The other involves a visual estimation of the quantitative order of the sets, which is done in different ways, depending on the kind of sets that are being compared: two ads, two crowds or one ad and one crowd (see also Condry & Spelke, 2008; Sfard & Lavie, 2005). While vertically bonded, the routines of numerical ordering and of quantitative ordering are not yet bonded to one another (horizontally): at this stage, the child does not expect that she would get the same result whether ordering by counting or by inclusion.

Stage 3. Discourse of Cardinality

When these latter routines are eventually bonded together, Q-nN and N-nQ discourses coalesce, creating a single NQ discourse. The awareness of the connection is likely to arrive first for ads, where the fact that ordering by numbers (1,2, and 3) and ordering by inclusion must produce the same response imposes itself naturally after a certain amount of trials. From here, the bonding will extend to the crowds, probably quite rapidly. When this happens, ads and crowds collapse into a single category of sets. On this occasion, the binary relation of quantitative order gives rise to the property (unary relation) of cardinality. Since this scenario of coalescence of Q-nN and N-nQ discourses brings to mind the movement of a zipper consolidating hitherto separate sheets of cloth, we will refer to the refined three-stage developmental scheme as zip model.

It must be stressed that this model is offered here as not much more than a reasonable hypothesis in the need of further testing and refinement. Having completed our analyses we concluded at hindsight that our assortment of tasks-situations, as wide and diverse as it was, did not suffice for testing all the constituent claims. Thus, for instance, the two-ad pairs included in our battery were not sufficiently numerous and diverse to verify the claim that ads are the context within which the child first realizes the connection between the orders of counting and of inclusion. At the time we prepared the interview questions, the model was simply not yet fully developed and we were not yet aware of the kind of evidence that would be needed for its corroboration.

Some Implications for Teaching

At least three non-trivial lessons can be learned from this research by those who wish to usher young children into the world of quantities and numbers. First, considering the separate emergence of quantitative and numerical discourses, it may be advisable to foster quantitative, non-yet-numerical discourse from early on. Second, teachers need to keep in mind that the child’s unexpected (or “unsatisfactory” or “not yet correct”) performance may signal her idiosyncratic interpretation of task-situations rather than a mere failure to choose a proper procedure or to implement correctly the proper one. Remaining alert to this possibility may be the key to the teacher’s ability to support the learners in their attempts to individualize standard numerical routines.

Finally, our research highlights the role of rituals in learning and, in particular, may help the teacher in recognizing their inevitability in the initial stages of the process. On the basis of our theoretical assumptions and empirical findings it is also possible to formulate some suggestions about how to induce and support the process of de-ritualization. Thus, for instance, it seems advisable to renounce the standard practice of initiating the child to numerical discourse via the stand-alone, decontextualized activity of counting. This induction may be more effective if carried out within the context of the deed of choosing. Applied in our study, this instructional move might have been the one that accelerated Milo’s progress toward de-ritualization of counting: at the age of 4(2) he was already doing what in previous research was repeatedly found to be absent in most cases of 5-, or even 6-year-old children: spontaneously turning to counting in response to WiTM-question (Nunes & Bryant, 1996). Another suggestion is to try to spur de-ritualization by supporting the child in the task of horizontal bonding. For this, the learner must be made aware of the existence, and equivalence, of multiple correct responses to the same task-situation. Particularly effective may be relating the end products of those procedures that she now performs ritually to the results of those that she already practices as explorations or deeds. All these, however, are only initial, tentative proposals. This study leaves us acutely aware of the need for a systematic research, in which different conjectures with regard to possible ways of encouraging de-ritualization would be raised and thoroughly tested.

Concluding Meta-Remark: On Benefits of the Discursive Approach to Numbers

We conclude with a comment on what is new in our vision of child’s numerical development and, in particular, on how this vision differs from the predominant ones, with their roots in Piagetian and neo-Piagetian theories. We wish to claim that the major differences between them result from their ontological disparity—from the fact that what in the Piagetian, and more generally acquisitionist, vision of learning has been conceptualized as the development of mental schemes, for us has been a matter of changes in discourses.

Space limitation does not allow for counting all the other differences entailed by this one, so let us just mention two most basic ones. First, within the discursive approach to numerical thinking, development stops being a series of more or less universal changes in the child. Instead, it is understood as a chain of complexity-building transformations in the discourse. This time, the different developmental stages have little to do with genetics and follow no definitive timeline. It is now clear that the actual course of developmental events depends mainly on the child’s exposure to the discourse he or she is supposed to individualize and on the support he or she gets from other participants.

Second, putting communication at the heart of our approach to numerical thinking helped in overcoming the common tendency to present processes of learning in terms of deficit, of those things that children do not yet do. The discursive slant led to the realization that in the processes of learning, constant changes occur not only in the learners’ procedures – in the way they do things – but also in their interpretations of task-situations. So far, the study of this latter type of change has not been a regular part of research on the development of children’s mathematical thinking. The acquisitionist language bears the main responsibility for this relative negligence. For instance, consider the classical formulation of the “cardinality principle” in counting: the child is claimed to have a command of this principle if “[she knows that] the last word uttered in a (correct, rule-governed) count expresses the number of items in the whole set” (Sarnecka & Wright, 2013, p. 2). This statement implies that the young child is typically aware of the property called “number of items” even before she knows that it is identifiable by counting. With the developmental primacy of number (thus cardinality) engraved in the language and thus taken for granted, researchers remain oblivious to the possibility that the property of “having a given number of elements” emerges from the activity of counting rather than being inherent to sets and just detected by counting.

It is thus the acquisitionist language that leads the researcher to an impoverished, “deficit” image of learning processes. Aware of this, we have been reforming our research discourse all along the way. On this occasion, we learned that a small change in words we say can make a big difference in the world we see. We concluded that the considerable effort required to transform, and then practice, our way of talking was not too high a price to pay for what we got in return: the richer and more helpful vision of children and numbers.

Supplementary material

Supplemental data for this article can be accessed on the publisher’s website at https://doi.org/10.1080/10508406.2019.1646650.

Notes

¹ This is in line with the position of Nunes and Bryant (2015) who criticize acquisitionist researchers for “attribut[ing] numerical and computational ability to infants [without distinguishing] between quantities, relations, and number.” (p. 725).

² The method of teaching experiment grew from the acquisitionist tradition, but it shares with participationism the assumption that uniquely human learning occurs in interaction with other humans and must thus be always considered together with teaching, the other side of the same process. As such, this method is appropriate for participationist research as well.

³ The episodes have been recorded and analyzed in Hebrew, and then translated to English for the sake of this paper. They have been labeled chronologically with Roman numerals, but in this report they do not necessarily appear in the same order.

⁴ The phrase “<4, 3> Blocks” is short-hand for “4 blocks in the bowl the child sees on the left side and 3 blocks in the one he sees to the right”.

⁵ In most task-situations, more than one of the three routines described in this section could be chosen, and we did not see much regularity in the boy’s decisions about which one to use.

⁶ The notion of de-ritualization may be seen as the commognitive operationalization of expressions such as “coming to understand” or “moving form procedural to conceptual understanding” (see Lavie, Steiner, & Sfard, 2019).

⁷ In our previous studies, 4-year-old children’s answer to WiTM-question regarding equal sets was “In none” (Authors, 2005). Milo’s current response may count as equivalent, because it also says that there is no preference for any of the piles. In the past, we ascribed this response to the fact that the child’s quantitative discourse is not yet objectified  (numbers are not yet thought about as self-sustained objects) and thus there are no mathematical objects that could be claimed to be “the same” or “equal”.

⁸ On one previous occasion in Round 3 (Episode X, Appendix 2—online only) we witnessed a pretended counting that followed a response given by estimation.

⁹ In Hebrew, yoter is used also to create the comparative form of adjectives or adverbs; for instance, larger translates into the Hebrew is gadol yoter, the verbatim English equivalent of which is “more large.”