Markov Processes: Exploring the Use of Dynamic Visualizations to Enhance Student Understanding

ABSTRACT

Finding ways to enhance introductory students' understanding of probability ideas and theory is a goal of many first-year probability courses. In this article, we explore the potential of a prototype tool for Markov processes using dynamic visualizations to develop in students a deeper understanding of the equilibrium and hitting times distributions. From the literature and interviews with practitioners, we identified core probability concepts, problematic areas, and possible solutions from which we developed design principles for the tool and accompanying tasks. The tool and tasks were piloted on six introductory probability students using a two-person protocol. The main findings highlight that our tool and tasks seemed to assist students to engage with probability ideas, to develop some intuition for Markov processes, to enhance their distributional ideas, to work between representations, and to see structure within the mathematics representations. The implications for teaching and learning are discussed.

KEYWORDS:

• Animations
• Equilibrium distribution
• Hitting times distribution
• Introductory probability students
• Statistics education

1. Introduction

Probability for the last 30 years has provided a fertile ground for documenting seemingly intractable misconceptions prevalent in people's reasoning processes (e.g., Kahneman 2011). Many attempts have been made to ameliorate people's misconceptions (e.g., conditional probability; Gigerenzer 2014) but some misconceptions have proved difficult (e.g., p-value; Falk and Greenbaum 1995). Within probability education research, however, there is now a call to reform the approach to teaching probability from a traditional mathematical base to include more emphasis on modeling using technology and an investigative approach to probability (e.g., Pratt 2011). Within this spirit of reform, we undertook an exploratory study to build a tool to enhance students' probabilistic reasoning of Markov processes (Grimmett and Welsh 2014).

Similar to other introductory probability courses our students are given an introduction to Markov processes. The students experience a theoretical mathematical approach using transition diagrams and matrices and an algebraic approach to calculate the equilibrium distribution and the expected mean for the number of hitting times. They do not see visual representations of the equilibrium distribution or the distribution of hitting times. The problems the students encounter are mostly context-free or are set in coin and dice-type contexts. Therefore, our study sought to explore alternative ways to better develop their understanding of Markov processes. Furthermore, a literature search on Markov processes resulted in articles on teaching ideas (e.g., Rotondi 2010; Wilson et al. 2011) but no research was able to be sourced that sought to understand students' reasoning as they engaged with Markov concepts. This suggests that this study could make a useful contribution to the research knowledge base.

The purpose of this study is two-fold. The first purpose of the study was to develop an interactive visualization prototype tool for Markov processes based on the premise that visualizations might enhance students' conceptual understanding and assist students' ability to construe and construct more robust conceptualizations. The second purpose was to trial the prototype tool and accompanying tasks, which we designed, on some students to learn how the tool together with the tasks might enhance their learning. Therefore, in this article the research question is: Given that the introductory probability students in this study have learned about Markov processes from a mathematical perspective, what new understandings seem to emerge when they are exposed to a different learning environment which includes the use of dynamic visualization simulations?

2. Related Research

As part of a larger project, within which this study is situated, we interviewed seven practitioners whose professional lives are centered on probability modeling. The practitioners were involved in a diverse range of fields (e.g., ecology, queueing and networks, hydroelectricity, operations management, agriculture, commerce, and development of probability theory). One component of the interviews was to gauge the practitioners' perspectives on probability modeling and on ways of thinking probabilistically. To them, seeing structure and applying structure were two key elements for probabilistic thinking, which were built on, in their opinion, the core concepts of: randomness, distribution, conditioning, and mathematics (see Pfannkuch et al. in press). They believed students needed to develop a sense of intuition when encountering situations, which would assist them in seeing the underlying structure. Since most of these practitioners were also teachers, we asked them about problem areas for their students when learning probability and about possible strategies to mitigate these problems. Using a thematic analysis method, we identified the following main perceived problem areas for their students: disposition or the willingness to engage, persevere, and understand probability; the idea of distribution; ability to move between and within representations including the representation of the problem in words; mathematics; and randomness and decisions. Not surprisingly there seemed to be a strong connection between the core concepts and these problem areas because the practitioners would be concerned about and focused on helping students to understand what they considered were essential probability ideas. When they were asked about possible strategies to enhance student understanding of probability some of the main themes that emerged were to

1. incentivize students to engage in understanding the ideas;

2. use visual imagery;

3. allow students to play around with chance-generating mechanisms;

4. develop strategies to enable students to link across representations including extracting information from word problems;

5. use contexts that students can relate to.

Taking each of the five proposed strategies, we will discuss them in terms of the literature and how they could inform the design of the tool and tasks for this study.

One method for providing students with incentives or motivating them to engage with probabilistic ideas is through allowing students to make conjectures about features of the simulated or actual data before they start a problem and to use technological tools to test their conjectures (Cobb and McClain 2004; Konold and Kazak 2008; Garfield, delMas, and Zieffler 2012). Garfield et al. (2012) used the making and testing of conjectures as a principle for designing activities for statistical modeling and thinking which was based on Cobb and McClain's (2004) research on how students learn and develop statistical reasoning. Cobb and McClain discussed the importance of cultivating students' interest in an investigative spirit and of allowing students to “have multiple opportunities to test and revise their ideas” (p. 393). Konold and Kazak (2008) agreed that making conjectures can motivate student interest but also took a cognitive dissonance perspective and believed making conjectures leads to students confronting their misconceptions when they test their conjectures. This is particularly important in probability where intuitions can lead one's thinking astray and result in impoverished probabilistic reasoning (Kahneman 2011).

Technological tools have the capacity to support and enhance students' probabilistic reasoning. The tools not only offer the ability for students to test their conjectures but also offer dynamic visual representations that can make concepts that were previously inaccessible in mathematical symbolic representations accessible and visible (e.g., Konold and Kazak 2008; Arnold et al. 2011; Garfield et al. 2012; Pfannkuch, Budgett, and Arnold 2015). Hence, visual imagery is gaining increasing visibility and credence in statistics education. Statistical concepts, ideas, and phenomena reside in an abstract unseen perceptually nonexistent world that cognitive technologies can help students transcend through visual tangible means (Arcavi 2003). The purpose of visualization tools is to invoke the development of and thinking about new ideas and to advance understanding. Arcavi (2003, p. 220) also claimed “visualization can accompany symbolic development” since a visual image can reveal properties of a concrete nature that algebraic expressions cannot. Visualization is gradually being recognized as a major and integral part of reasoning and doing statistics, which can facilitate a deep level of engagement with concepts (see Presmeg 2006). Visualizations, however, are not a panacea to solve problematic probability areas but rather another avenue to enable students to grasp and make sense of how to reason probabilistically (see Budgett et al. 2013).

Linked to dynamic visualizations is the ability to play around with, experience, and feel the nature of chance-generating mechanisms using technological tools. Similarly hands-on activities can allow students to physically experience the nature of chance and randomness. Drawing on developmental psychology research Martignon and Krauss (2009) stated that learning by playing is essential for the development of probabilistic thinking. Although their research was focused on young students we believe, as well as the practitioners we interviewed, that older students could benefit from interacting with chance-generating mechanisms in order to foster and stimulate intuitions and knowledge of randomness, variation, and distribution. Pratt (2005) described his research where he enriched young students' views of randomness through facilitating them to play around with fair and biased spinners and observe the results and fix biased gadgets to make them fair. Technology was a crucial element in fostering these students' understanding of probability. Hence, educators such as Pratt (2005) believe that technology can play a significant role in developing probabilistic reasoning.

Technology also allows students to link representations. For example, in the case of Markov processes, the state diagram, transition matrix and equilibrium distribution, or hitting times distribution could be linked. Thomas (2008) asserted that using and thinking with representations plays an essential role in the development of mathematical thinking, which would equally apply to probabilistic thinking. He also stated that the flexible use of representations assists students to develop rich schema and conceptual understanding in mathematics. His versatile thinking framework (Thomas 2008, p. 10) refers to three elements, which we relate to Markov processes:

• process/object versatility—the ability to switch at will in any given representational system between a perception of a mathematical entity as a process or an object (e.g., the limiting distribution can be viewed as an object or a long-run process that stabilizes to a distribution);

• visuo/analytic versatility—the ability to exploit the power of visual schemas by linking them to relevant logico/analytic schemas (e.g., linking the visual representation of the equilibrium distribution to an algebraic analysis);

• representational versatility—the ability to work seamlessly within and between representations (e.g., transition diagrams and matrices) and to engage in procedural and conceptual interactions with representations (e.g., calculating the equilibrium distribution and conceiving it as a conceptual entity with its own properties).

Furthermore, Graham, Pfannkuch, and Thomas (2009) demonstrated how the development of concepts in statistics could arise using technology-linked representations while Pfannkuch, Budgett, and Thomas (2014) provided indirect evidence that technology designed for learning inferential concepts through linking representations seemed to promote concept formation. Representations can also be expressed in words and therefore changing a word representation into a state diagram is also an example of linking representations. The translation of a word problem into a Markov or other probability model can be difficult for students as the context can hinder them unless it is very similar to other problems they have experienced.

Despite the practitioners being aware that students seemed to have difficulties with extracting information from problem scenarios, they nevertheless believed that contexts that students could relate to were important for engaging them in probabilistic reasoning and in appreciating how probability is used in actual practice. Probability modeling often starts with a contextual situation problem and the resultant models are tested against the real-world situation as to whether they make sense. This integration of statistical and contextual knowledge is fundamental to statistical and probabilistic thinking (Cobb and Moore 1997; Wild and Pfannkuch 1999). Furthermore, according to proponents of the Realistic Mathematics Education teaching theory (de Lange 1987; van den Heuvel-Panhuizen and Drijvers 2014), mathematical concepts are formed through initially involving students in problem situations that are meaningful to them or able to be realized. Through mathematizing, which is an activity that involves organizing and structuring, students can start to identify the specific mathematics in the context, formulate, and visualize the problem in different ways and discover relationships. Hence, relatable contexts can help drive students' engagement and conceptual understanding.

Based on the practitioners' suggestions for improving students' probabilistic reasoning and the literature, we developed a six-principle framework to guide the designing of the tool and tasks. The principles were to encourage students to (1) make conjectures, (2) test their conjectures against simulated data, (3) link representations, (4) perceive dynamic visual imagery, (5) relate to contexts, and (6) interact with chance-generating mechanisms. We also used this framework to analyze the data.

3. Methodology

The aim of this research study was to explore the potential of a dynamic visualization tool and its accompanying tasks to enhance introductory probability students' understanding of Markov processes. As an exploratory study, it is equivalent to a pre-clinical trial where one investigates, experiments, and modifies the tool and tasks based on student responses during and after the trial (Schoenfeld 2007). To encourage students to think out loud while doing the tasks, we used a two-person protocol whereby students could discuss with one another proposed actions and what they were thinking. Occasionally the two authors would intervene to clarify what the two students were thinking or to move them forward if time became an issue as we could only allow 2 hr for the tasks.

3.1. Participants, Data Collection, and Analysis

The participants in this study were six first-year students (ages 18 and 19) who had completed an introductory probability course. The course covers basic probability set theory, random variables, discrete probability distributions, joint and conditional distributions, covariance and conditional expectations, and an introduction to Markov chains. Because of our university's ethical requirements, whereby it was determined that students participating in our study could be perceived as having a potential grade advantage over other students, we could not recruit them before or during the course. Hence, the student participants in our study could be presumed to already have acquired a working knowledge of Markov processes from a mathematical perspective. They were volunteers, who responded to an email sent to 50 randomly selected students from a cohort of 200. All volunteers were used in the wider study and they were compensated for their time. The names (pseudonyms) of the pairs of students who worked on the Markov tasks were: Mike and Lisa, Mark and Cameron, and Simone and Harvey. Apart from Simone, all were articulate and able to explain how they were thinking and reasoning. Simone appeared to have the characteristics of a rote learner who memorized procedures. She also seemed to have difficulty in interpreting problems in an unfamiliar context and explaining her reasoning.

The students worked for at least 2 hr on the tasks during which time they were video- and audio-taped including the use of Camtasia to capture a record of what was on the computer screen. Camtasia is software that simultaneously records the students' faces, their voices, and images of the tool as students interact with it on the computer. After the tasks, the students were given an opportunity to reflect on their learning and to give suggestions for improving the tool and tasks in a half-hour interview, which was also taped. Transcriptions of their interactions were qualitatively analyzed against the six-principle framework to identify critical features of the students' understanding that seem to emerge within the new learning environment.

3.2. Tool and Tasks

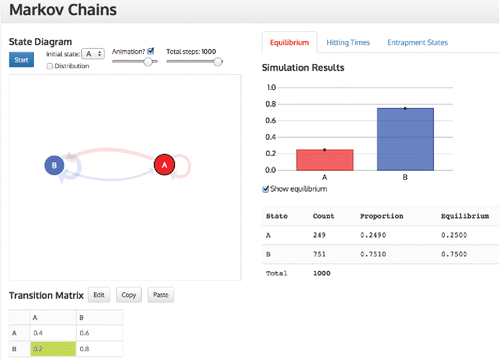
The Markov chains tool (see: https://www.stat.auckland.ac.nz/∼wild/MarkovChains/) was based on a dynamic visualization developed by Victor Powell on the Setosa blog (see: http://setosa.io/blog/2014/07/26/markov-chains/). Our prototype tool was developed in conjunction with the wider project team. The tool has three screens but for this study we only used the screens for equilibrium (Figure 1) and hitting times (Figure 2). Data are entered in the transition matrix and then a state diagram with arrows in proportion to their probabilities appears, which can be repositioned in its designated space. The simulation can start in any state and, in the case of determining the hitting times, can end in any state. As the simulation progresses, the three representations (state diagram, transition matrix, and distribution) are active and linked while the distribution gradually builds up. For example, in Figure 1 the transition from D to B is simultaneously highlighted in the matrix and state diagram. The animation can be sped up or turned off and up to 1000 simulations can be conducted. For the hitting times distribution, a sound feature was added to denote a hit on the end state, which simultaneously visually enlarges. Current and previous hitting times are also recorded (see Figure 2).

Figure 1. Screenshot of equilibrium distribution screen for Markov chains task two for four rental car offices at different locations.

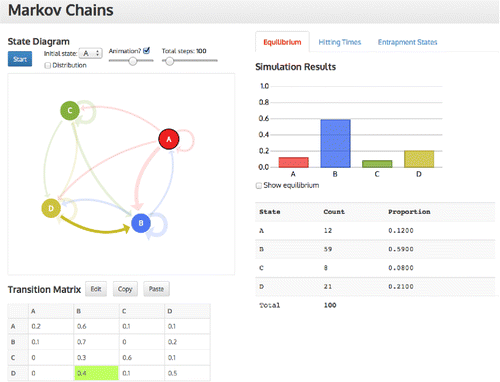
Figure 2. Screenshot of hitting times distribution screen for Markov chains task two for four rental car offices at different locations.

The three tasks used in the study are given in Appendix 1 (the Appendices are available in the online supplementary files). The first two tasks are in the context of a car rental agency, while the third task is a cut-down version of a Snakes and Ladders game. The tasks build on students' prior knowledge and then extend them to make conjectures about the equilibrium and hitting times distributions before they interact with the tool to test their conjectures. As this was an exploratory study, the tool and tasks were modified during the three interviews. After the first interview a “Show equilibrium” check box was added as we realized the automatic showing of the theoretical distribution focused the students on that rather than watching the distribution stabilize. Also, we added in new ways of conjecturing possibilities as the interviews progressed, which are italicized in the tasks to show these modifications. In Appendix 2, we show our analysis of how each part of the tasks operationalizes the six-guiding principles we used to design them.

4. Results

Using their prior knowledge, all the students were able to draw the transition state diagram and put it into matrix format for the scenarios given. Apart from Simone, the students were able to explain how the dynamic representations of the transition matrix and state diagram in the tool related to the context of the problems and how the Snakes and Ladder game, which they physically played with a board and die, was related to the matrix. That is, five out of the six students seemed to be able to interpret and understand the information the visual imagery was depicting and communicating.

We will now examine in more detail the results of the students' interactions with the other parts of the tasks and the consequent emergent understandings that arose. The first part of the results covers their reasoning about the equilibrium distribution; the second part their reasoning about the hitting times distribution. To obtain a sense of the students' reasoning, we begin by following one pair of students, Mark and Cameron, as they engaged with the tasks. References to the reasoning of the other two pairs are also included.

4.1. The Equilibrium Distribution

For Task One the students were asked to calculate the equilibrium distribution using their prior knowledge (see Appendix 1). After some time one of students in the pair remembered the formula. Therefore, they were interested in whether their calculation was correct when they were directed to use the tool. When Mark and Cameron were asked what they expected to happen as they watched the equilibrium distribution being constructed (Figure 3) the following conversation ensued. (Note, in this research we only considered Markov chains where the equilibrium and limiting distributions were the same.)

Figure 3. Screenshot for Markov chains task one for two rental car offices at different locations.

Table

Mark:	Would it oscillate around them (theoretical values) or would it get closer and closer to them? No, it would get closer and closer, yeah?
Cameron:	Yeah, I think it would get closer.
Mark:	Cause remember how the theory states that it is the limiting distribution, so in an infinite amount of time.
Author:	So are you saying it would not oscillate around those values?
Mark:	Would it ever go above it or would it always stay below? Would it approach from the bottom or the top or is it both? Yeah I'm interested actually now. [Watches the simulation at a slow speed.] Oh yeah it's going to oscillate at any individual time but in the long run it is going to approach and stay and become it (theoretical value) and in an infinite amount of time it will actually be it. [Reflecting on what he saw.] Saying that the equilibrium distribution is defined as such (limiting) is not helpful.

In this exchange, we noted that the students' conjecture about how the equilibrium distribution would build up was based on a possible misinterpretation of the term limit, as they seemed to visualize a process converging to a limit rather than a process that oscillated in the short run before stabilizing in the long run to the equilibrium distribution. Harvey was also amazed at the amount of variation before stabilization occurred, particularly for the second task: “Oh wow. Oh gosh. That was amazing, that was a big blip … [further on in the simulation] Oh so they're getting pretty close now.” Hence the simulation seemed to provide these students with a new awareness about long-run processes, variation and distribution stabilization.

For Task Two with four rental car offices, (Auckland central city (A), Auckland airport (B), Christchurch (C), and Wellington (D)), Cameron and Mark, using a modification of the original task, were asked to rank intuitively the probabilities for the equilibrium distribution from highest to lowest (see Appendix 1). Mark suggested B would have the highest probability because it is the “one with the biggest probability coming in.” They looked at the matrix (see Figure 1) and came up with the idea of summing the probabilities in the column to rank the equilibrium distribution probabilities.

Table

Cameron:

I think it is the sum. Cause for this like [refers to Column B, see Figure 1] you add like, even if you do the equilibrium you add them up [we believe he is referring to how the equilibrium distribution is calculated], right you add them up

Using this conjecture they ranked the probabilities as B > D > C > A. They then watched the simulation to test their conjecture (see Figure 1):

Table

Mark:	Oh no!
Cameron:	A is actually bigger than C. [They realize it is a simulation and check the theoretical values.] Yeah, B is the highest, D is next which is right, C is …
Mark:	So you were right. So you can just sum down it (the columns) effectively.
Cameron:	It may not be that accurate but it should be around (that) …
Mark:	Don't know if it (the conjecture) is true. Might be. …And the reason I say that it is (true), because these are the probabilities coming in (to each state) and the probabilities coming in should be directly related to the equilibrium distribution, if there is one.

They were really pleased with themselves that they had discovered this relationship and specifically mentioned this insight in their post-interview. Harvey also discovered this relationship by thinking about the probabilities going into each state: “Auckland airport looks like its going to be the highest … cause it's got cars most likely to go to it.”

The interaction of Mark and Cameron with this task is an illustration of how all the students operated throughout all the tasks: make a conjecture, do the simulation, test the conjecture against the simulation, analyze why conjecture is correct or incorrect. The first three actions were inherent in the setup of the task. The action, analyze why, was a surprise in that the students went to great lengths at times to try and understand and to reason how the simulated answer could be made sense of from the information they were given. From these students' interactions with the equilibrium distribution, we note they were engaged, and reasoning at quite a deep level from the numerical matrix representation to conjecture how it could be linked to the distribution representation. The context seemed to help them to reason with the probabilities as they could think in terms of the number of cars going to and within an office.

When Mark and Cameron were asked to interpret the equilibrium distribution (see Figure 3) in terms of the rental agency with two offices (Task One) Cameron said the following.

Table

Cameron:

In the long run like that much cars will be in the city [points to 0.25] and that much cars will be at the airport [points to 0.75].

Harvey and Simone struggled for a while to interpret the distribution in context but finally Simone responded by referring to her calculations.

Table

Simone:	If we just keep running this car, this transition diagram, the probability that the car goes to the city should be two over eight and the probability that the car goes to the airport is six over eight.
Harvey:	Yeah or I guess another way of saying it is if you had like 100 cars in total at the start you would end up with like 25 at the city and 75 at the airport, yeah.

All the students seemed to appreciate the context-based scenarios and mentioned in their post-interviews the lack of context in their probability course with Mark stating that he had never realized rental cars could be modeled by Markov chains.

4.2. The Hitting Times Distribution

In the probability course completed by the students they had calculated expected hitting times but had not seen or considered the distribution of hitting times. Initially Mark and Cameron were baffled about how to conjecture the expected number of times a car would be hired out or sketch the distribution for the first task on the two-office car rental agency based on their transition diagram and matrix (see Figure 4). They asked if they could skip this part of the task. On being asked to just give an intuitive guess they came up with the idea that the hitting times may be related to the geometric distribution “yeah it is like the geometric because you just keep going until you go to the airport” (Cameron) and in contrast to the equilibrium distribution they intuited that they needed to look at the probabilities going out from each state. Knowing that the mean for the geometric distribution was 1/p they decided the expected time (number of steps) for a car going from the central city to the airport would be 1/0.6 = 1.67 while from the central city to the central city would be 1/0.4 = 2.5. Before and after this decision, however, they spent a lot of time debating and wondering how to combine multiple geometric distributions, and thinking about how many ways a car could move. Even though their discussion got very involved and detailed they were obviously enjoying thinking about this problem because as Mark said, “I'm having fun” and “the fact that it had never been stated to me before is interesting in itself.”

Figure 4. Student transition diagram and matrix for Markov chains task one for two rental car offices at different locations. (A is Auckland airport, C is Auckland central city–shown as B and A, respectively, in Figure 3.)

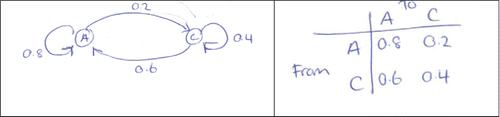
Lisa and Mike, using similar reasoning, gave the same answers for the expected times except they did not explicitly mention the geometric distribution. Hence, each of these students sketched right-skewed distributions; the exception being one fairly symmetrical distribution, which Cameron drew for a car picked up and returned to the central city. Harvey, on the other hand, intuitively guessed 1–4 and 1–2 for the expected times and sketched right skewed distributions saying “I would guess it would be asymptotic” while Simone estimated 16 and 6 for the respective situations and produced sketches of an increasing step function up to her expected means. Harvey did not give a reason for a lower estimate for the second situation, only that he thought it was, while Simone did explain her rationale: “because the probability of the car return back to the central city in total is actually lower than it will go to the airport so that's why I think it should be lower.” Simone focused on the 0.4 probability of returning back to the city and because this probability was lower than the 0.6 to the airport then she reasoned that the mean would be lower. Even though we thought she understood the problem based on the questions she asked when clarifying the problem, her sketches and reasoning suggested that she did not.

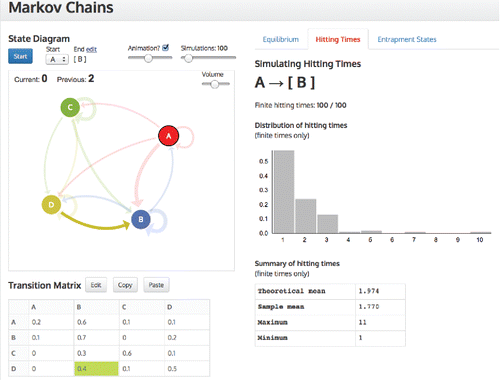
Returning to the tool, the students performed the simulations for Task One. Mark, Cameron, Lisa, and Mike were very happy that their first conjecture for the expected hitting time was correct and that their sketches for the distributional shape were roughly right. All the students, including Harvey and Simone, were very surprised at the range or variation in the hitting times. When Mike and Lisa were asked for the reason why the maximum for the second situation was larger than the first one (see Figure 5) they said:

Figure 5. Screenshot of hitting times distribution for Markov chains task one for two rental car offices at different locations.

Table

Lisa:	Because the probability is closer to 0.5, it's less close to one.
Mike:	It looped around here seven times before it went to there, what 12 times, 11 times before it got back to there? Yeah its looping around here lots before its coming back …
Lisa:	You're going to get something that's going in to itself more if the probability is higher.

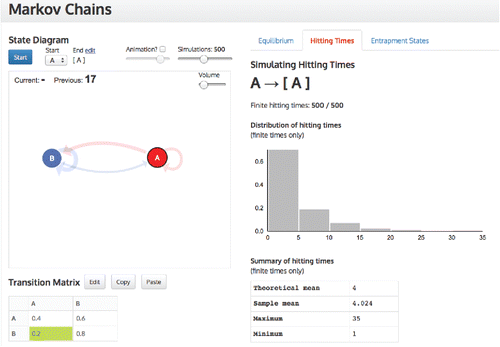
Their surprise at how many times a car could loop around in one state was shared by the other students. However, these students' second conjecture for the expected time was incorrect. Mark and Cameron tried to analyze why the mean was four and went into a deep discussion with written mathematical expressions and arguments until they felt they could see why it might be 4. On the other hand, Mike gave an intuitive argument about why the mean might be 4.

Table

Mike:

You've got 0.6×1 + so to get to four you've got to be going there once which is one, round there a few times then back which is one so it makes sense in my head but I'm not sure how to work it, write it down. So to go round here once, that's going to give you all the ones and that happened 0.4 but then it means the rest of the time you're going over here, looping round here and coming back and I can't remember how you get to number four but it makes sense in my head.

We conjecture that these students were gaining an awareness and appreciation of distribution and of variation through not only seeing the creation of the distribution but also seeing the process in action and the effect of probabilities on the process. Moreover, the task stimulated some of these students to think of some theoretical mathematical arguments to explain the mean hitting times. The linking of representations and the context also seemed to play a role in developing new ideas and visual imagery for students to think about.

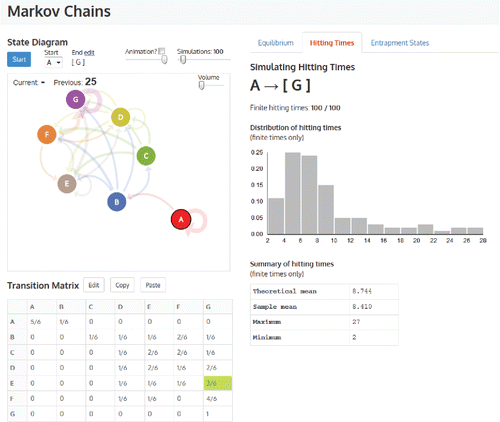
By the second task, all the students were producing skewed distributions for the hitting times. In order to ascertain a possible rank order for the expected times for a car picked up in Auckland central city (A) and arriving at Auckland airport (B), Christchurch (C), Wellington (D) or Auckland central city (A), they either looked at the rows of the matrix to determine the probabilities going out or looked at the transition diagram and thought about or traced possible routes where cars could be going (see Figure 2). Basically, as Harvey said, they used “the most probability going from each state.” They all conjectured that A to B would have the lowest mean and A to C the highest mean. Where there was disagreement was the order of the middle two; A to A and A to D. Harvey's intuitions for the actual means ranged from 1.2 to about 6, which seemed to be a typical expectation as the students were very surprised by the actual means (1.97 for A to B (see Figure 2), 6.087 for A to D, 13.789 for A to A, and 25.455 for A to C). They were also amazed at the variation and range of the distributions. The following excerpt shows Mike's interaction with the tool, which was typical of the students who articulated what they saw. In the excerpt, there is evidence of engagement when he tests his conjectures, awareness of variation within and between the distributions, an intuitive analysis of the Markov process to explain the variation and connecting the probabilities to the process.

Table

Mike:

This is an exciting thing to watch … 1.97 to get to the airport (B). Oh, because you are going directly there and then you are going the whole route as well. Then A to A, theoretical mean 13, oh, there's all the other self loops with quite high probabilities so it's spending heaps of time looping round everywhere else … [then realizing initial thinking was way off in terms of mean expected and the range]… I'm scared to see what the theoretical mean for this one is (A to C), 25. Yeah it is just doing lots and lots of self loops before it gets anywhere else … it took 61 (steps) … [later on] we got 114 (steps) … I'm surprised we haven't got a single one (step) yet. Oh there we are, we just got one (step) … Christchurch is C. I said it was going to take longer because you have to go, if we got to B it would take longer because you have to go via D before you get to C rather than you going from A because B doesn't go to C so I said it would take longer … [later on]… yeah nothing hardly goes into A … I thought the self loop would have done a little bit more than that but it's the idea of 0.2.

Through conjecturing the mean times and the distributional shapes the students were thinking and reasoning about the Markov processes, relating the numerical probabilities to possible expected times, and to how the process actually operated. Through the tool allowing them to visualize the process and to see the effect of differing probabilities, they realized they did not anticipate how long the process would stay in a state. Mark and Cameron also related the numerical probabilities to geometric distribution properties. As Lisa said “It's really cool because it makes you think a lot more about what you are actually doing, well if you are calculating or whatever, rather than just doing it because you know the formula.”

For Task Three the students played the Snakes and Ladders game (see Appendix 1) physically with a board and die so they now had a more intuitive idea of the expected time. Mike and Lisa theorized that since they had to get a six to start the game, the average number of rolls would be six to get started, and therefore the mean hitting time would be more than six. Mike said: “To me it would feel like there could be more … it would be a little bit more than six” to which Lisa replied “eight or nine or something” and Mike agreed. They then sketched a right-skewed distribution with a minimum of two, on the basis that one could toss a six then a four and would be able to finish the game. Mike: “So you'd start very low, one in 36 chance of getting two, then so like nine or 10 would be your best. And then it would just sort of tail out.” They decided on a maximum of ∞, as Lisa explained, “you theoretically could … it's unlikely, well it's impossible, kind of.” When they used the tool (see Figure 6) they were pleased with their conjectures with Lisa exclaiming: “That's (the mean) between eight and nine … look at that distribution. Perfect.” Harvey and Simone drew a right-skewed distribution with a mean between 12 and 15 and with a minimum of 2 based on the game. Similarly, Cameron guessed a mean of around nine while Mark inexplicably guessed between 6 and 41 and although both were not surprised at the distributional shape they were surprised at the maximum number of steps (144) that occurred in their simulation.

Figure 6. Screenshot of hitting times distribution for Markov chains task three for cut-down version of the board game Snakes and Ladders.

Playing the game of Snakes and Ladders and their prior experience with the other tasks seemed to assist students in getting a feel for the hitting times distribution. When they viewed the equilibrium distribution for the game they were not surprised to see it go into an absorbing state as the game finished when the player reached the ninth square. They were engaged in the game and could relate the game to the visual representations afforded by the tool. The hands-on experience seemed to be a useful adjunct to the visual experiences.

4.3. Post-Task Reflections

In their post-task reflections on their interactions with the dynamic visual imagery of the tool the students were very positive, comparing it to their mathematical course experience.

Table

Cameron:

It makes it a lot easier to understand because you just think about writing those probabilities down like you get confused with all the notations and stuff like all the letters and everything else but with that graph it is really clear.

Harvey even suggested teaching should start with students' intuitions then move to simulations before introducing the mathematics.

Table

Harvey:

like go through a process of using your own intuition… like in class you are given this formula which makes no sense to you …but in those questions how it said like: What would be your prediction? I kind of think that's a really good way of introducing the idea.

Mark and Cameron also liked the idea of conjecturing and testing out their conjectures to see if they had intuitively got the answer right as they thought this type of reasoning was important to see if an answer was sensible and reasonable.

Table

Mark:

It is just not us, other people I talk to, the hitting times, people wouldn't know whether their answer was even reasonable. When I ask about hitting times they are like I don't know.

The students also appreciated being able to visually see the equilibrium and hitting times distributions, something that had not occurred to them as possible. To Lisa the visual imagery made a “lot of things clearer now than they were before” while Mike rejoined with: “visuals just help you understand more what it's doing.” They also liked following the process and seeing the self-looping or as Lisa said, “how random it can be.” Simone was able to articulate that the tool and tasks gave her “a quite flexible way to think about it [and] I do not know how to describe it just like what I think before when I think about that question and now shh shh shh…” which we understood to mean that she now had a dynamic image of Markov processes.

5. Discussion

Since our study was exploratory our research question was interested in finding any new understandings that might emerge in some students' thinking about Markov processes as they interacted with the dynamic visualization tool. To guide the discussion, we draw on the components of our six-principle framework and their potential influence in stimulating students' thinking.

A major aspect that emerged from this study was student engagement. Through making conjectures, doing the simulations, testing their conjectures against the simulated data, and then analyzing why their conjectures were roughly correct or incorrect, the students not only engaged with probabilistic ideas and reasoning but also persevered in trying to grasp how the Markov process worked. Incentivizing students to engage in understanding probability ideas was a concern of the practitioners and therefore it seems that research and teaching which seeks students' conjectures before tackling a task (e.g., Garfield et al. 2012) is a promising avenue. Moreover, giving reasons for the conjecture and then analyzing the consequent result seemed to stimulate in students a search for the underlying structure inherent in the Markov process. Hence, they seemed to be developing some intuition for seeing structure in the scenarios and for determining the reasonableness of results, some core elements for thinking probabilistically (Pfannkuch et al. in press).

The tasks and tool, including the use of a context that the students could relate to, seemed to facilitate students' awareness of random behavior or how probabilities operated in a Markov process through being able to see the dynamic images of the Markov process and the formation of the distributions. Having an image of the equilibrium distribution also seemed to give students a better appreciation of long-run stabilization while the image of the hitting times distribution seemed to give students a better appreciation of the expected times and the extent of the variation. Our findings for these students seem to suggest that dynamic visual imagery and experiencing chance-generating mechanisms, as other researchers have indicated (e.g., Konold and Kazak 2008; Martignon and Krauss 2009; Arnold et al. 2011), may assist in the development of probabilistic reasoning.

The tasks and tool also seemed to facilitate students to seamlessly switch between representations, an indication according to Thomas (2008), that they were being assisted to develop richer schema and conceptual understanding. Starting with a context in the spirit of Realistic Mathematics Education teaching theory (van den Heuvel-Panhuizen and Drijvers 2014), the students changed the representation to a state diagram and then to a transition matrix. When viewing the tool, which dynamically linked three representations simultaneously (state diagram, matrix, and distribution), the students could visually see the connections. This linking of the representations seemed to be developing in students a probability sense similar to what people term a number or measurement sense. However, the power of the linking was realized when the students made conjectures from either the state diagram or transition matrix to predict properties of the distributions. Mark and Cameron, and implicitly Mike and Lisa, went beyond the representations given to consider the geometric distribution and its properties. Furthermore, their conjectures gleaned information from the numerical probabilities and mathematical structuring. For example, by honing in on the structural properties within the mathematized matrix they added the probabilities in the columns to determine the relative probabilities of the equilibrium distribution outcomes. Although summing the columns of the matrix will not, in general, give the relative probabilities for the equilibrium distribution, it may sometimes be approximately correct, suggesting that it may be a useful first step for students. Therefore, our findings seem to indicate that the tool and tasks were assisting these students to develop versatile thinking (Thomas 2008) and consequently probabilistic thinking.

Our research question was interested in any new understandings that might emerge when students were exposed to a different learning environment from that previously experienced. We conjecture that for Markov processes these students seem to have a new awareness and appreciation of: distribution, variation, randomness, and the underlying structure within the mathematized representations. Considering that Pfannkuch et al. (in press) proposed that the core concepts for probabilistic thinking were: randomness, distribution, conditioning, and mathematics, we believe that our tasks and tool were contributing towards enriching these students' conceptual repertoire.

The implications for using these tasks and tool in teaching and learning are not simple. As the students in this study said, if they were given the tasks and tool to explore on their own they would simply work out how to use the tool and then get the answers. Asking students to spend time on making conjectures, and rationalizing those conjectures before using the tool was a necessary precursor for stimulating the desired thinking. For teaching purposes the cycle of conjecture, do, test and analyze, would need very careful consideration around the pedagogy about how to scaffold the students' thinking and how to draw their attention to salient features of the Markov process. If the tool and tasks were used to introduce students to Markov processes, further activities would need to be developed to induct students into considering how to mathematize or represent a Markov process and further questions would be necessary to prompt thinking about equilibrium and hitting times distributions. Research is therefore needed on the effectiveness of such a learning approach before introducing students to the theoretical mathematical approach.

As an exploratory study, where the students have already learnt about Markov processes mathematically, the findings are tentative and limited. However, we believe there is merit in considering how dynamic visualizations and tasks, which engage students in making and testing conjectures, could enhance the development of students' probabilistic reasoning. Our findings suggest the tool and tasks have the potential to deepen and enhance students' understanding of Markov processes. Further research in other settings is recommended.

Supplementary Materials

Appendices referred to in this article can be accessed on the publisher's website.

Acknowledgments

This work is supported by a grant from the Teaching and Learning Research Initiative (http://www.tlri.org.nz/). The authors thank David Banks, the software developer, and Ilze Ziedins for her helpful comments on this article.