Methodological Aspects of Determining Apple Mechanical Properties During Impact

Abstract

The influence of cylindrical sizes of samples and velocity of impact on its course and strength parameters for the “Braeburn” variety apples was studied. Three sample lengths of 17, 19, and 21 mm, three diameters of 10, 15, and 20 mm and four impact velocities of 0.25, 0.5, 0.75, and 1 ms^–1 were applied. Failure stress and strain, impact energy, absorbed energy as well as tissue stiffness and toughness were determined as dependent variables. The influence of the sample diameter on maximum force response, impact energy, absorbed energy, and tissue stiffness was studied. The other independent variables: Sample length and impact velocity did not show significant influence on the strength parameters of the apple tissue. The shock wave speed in the apple tissue was independent of both sample sizes and impact velocity. Its mean value amounted to 292 ms^–1. Under the experimental conditions the mean value of the absorbed energy contribution to the impact energy amounted to 9.9%. The experiment confirmed importance of a critical stress criterion as regards cylindrical samples of apples under impact conditions.

Keywords:

• Impact
• Apple
• Cylindrical sample
• Mechanical strength
• Mechanical properties

Introduction

In Poland the average annual apple production under favorable weather conditions amounts from 2.5 to 2.9 million tons. The bruise is the main cause of apple quality deterioration amounting even up to 50% as far as grade reduction in some varieties is concerned^[1,2] though the average level of losses is in the range 10–25%.^[3] Based on the 12-year New York fruit market research Knee and Miller^[4] showed that 6% of the apples were bruised. In 2000 and 2001 it was found in Belgium that as a result of selection 15 and 8% of the apples were bruised, respectively.^[5] Bartram et al.^[6] found out a similar amount of losses studying apple bruising of the “Golden Delicious” variety on the packing lines. They showed that 14% of the apples were bruised as a result of packing operations.

The costs resulting from bruises in fruits and vegetables are enormous. According to Brook^[7] reduction in number of impact causing potato tuber damage by 1% in the United States would give 7.5 million dollars savings. Comparing the prices of high- and low-quality apples, Van Zeebroeck et al.^[5] estimated that the decrease in the low-quality apples amount by 10% could lead to the increase of Belgian fruit growers income by 892,000 euros in 2000 and 595,000 euros in 2001. In Poland there are not accurate data concerning this problem. However, in the United States it is estimated that annual losses caused by bruising amount to 300 million dollars for potatoes, 1.2 billion dollars for apples, and 280 million dollars for pears.^[8] It is found out that up to 20% of potato producers income depends on damages due to impacts.^[9,10] These losses in the form of physical changes occur during harvest, transport, and handling, which results in decay or deterioration of external appearance at a later time.

Therefore, the knowledge of the basics concerning the mechanisms of bruising allows improving production output and cost reduction. This must be preceded by research of fruit mechanical properties which are related to the parameters describing impact effects. ^[11–16] There is a large number of papers presenting the impact research carried out on the cylindrical samples of fruits and vegetables.^[17–21] The question arises whether the tests performed on the samples of different sizes and at various impact velocities can be compared.

The aim of the research was determining the influence of sample diameter, sample length, and impact velocity on the quantities regarding impact course and strength properties of fruit samples under impact loading conditions. As a result from the experiments, it was possible to compare failure stress values for the cylindrical samples and the whole fruits in the impact process.

Material and Method

Measuring Device

The device for cylindrical samples impact measuring consists of a pendulum with a rigid arm ended with a cylindrical hammer, in which a piezoelectric force sensor is placed. The pendulum arm length was 940 mm, and the hammer displacement during a contact with a sample did not exceed 6 mm, hence you can assume that the sample deformation proceeded along a straight line. The anvil in the form of a cylinder was attached to a vertical concrete wall. The piezoelectric force sensor was mounted to the anvil. The cylindrical sample was fixed to the vertical plate screwed in the sensor with the use of technical vaseline. To the pendulum axis there was mounted the WMU45SK angle sensor which allowed measurement of pendulum angular displacement perpendicularly and as a result, determination of drop height and impact velocity. The hammer mass was adjusted so as kinetic energy was much bigger than that of sample deformation. The hammer velocity difference at the beginning and at the end of the sample crushing amounted to 0.01 ms^–1 including the increase of hammer energy at the end of the test and sample resistance. Thus it can be assumed that the sample was deformed at constant velocity. The force measurement during the impact was performed by means of the piezoelectric force sensors, ENDEVCO 2311-100 with the sensitivity 22.5 mV/N and the measurement range ± 220 N. The microprocessor recorder, which next transmitted the data to a computer, cooperated with the force sensors. The sample frequency of the microprocessor recorder was 153.6 kHz.

Experimental Material

The object of the research were cylindrical samples of the “Braeburn” variety apples of three diameters of 10, 15, and 20 mm. The samples were cut out by means of a manual punching die in the perpendicular direction to the longest apple diameter. The right sample length was obtained by cutting them out in the sleeve of a specific diameter and height. The distance between the surface of the plate screwed in the sensor and the resistance surface of anvil amounted to 15 mm. The sample lengths were 17, 19, 21 mm, which corresponded to the three levels of samples strain 12%, 21% and 29%. The samples were impacted with the velocities 0.25, 0.5, 0.75 and 1 ms⁻¹, which for the pendulum arm length amounted to 940 mm corresponding to the angular displacement of a pendulum by 4.7, 9.4, 14.2, and 18.9. For each length and diameter of a sample as well as impact velocity, 10 repetitions were made. As the research was carried out on three sample lengths and three sample diameters as well as four impact velocities, totally 360 impact tests were made.

Measurement Method

The research consisted in impacting the sample with a hammer and the simultaneous recording of the force response in time on both ends of the sample (Fig. 1). To determine the shock wave propagation speed in the sample, the time Δt between the beginning of the force response increase in the sensors installed in the hammer and anvil was measured. Knowing the sample length l, the shock wave propagation speed v_w was calculated from the formula:

(1) $v_w=\frac{l}{\mathrm{\Delta }\mathrm{t}}$(1)

FIGURE 1 A: A typical course of the sample force response recorded in the sensors installed in the hammer and anvil during the impact; B: The way of determining time between the beginning of the force response increase in the sensors installed in the hammer and anvil.

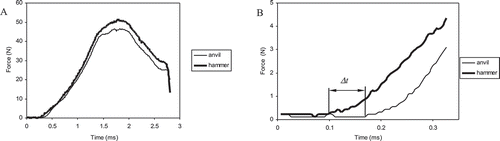
where l is the sample length (m); Δt is the time between the beginning of the force response increase as shown by the sensors installed in the hammer and anvil(s). The impact energy required for the sample damage was also calculated. On account of the large hammer mass (3.4 kg) and the moment of inertia around the pendulum rotation axis (3.7 kgm²) in comparison with the sample mass, it can be assumed that the hammer kinetic energy is much bigger than the sample deformation energy, as previously mentioned. As a result, the constant value of the hammer displacement velocity during the impact was assumed. Hence, the impact energy e_i required for the sample damage can be expressed by the formula:

(2) $e_i=v\cdot \underset{0}{\overset{t_c}{\int }}{F}_h\left(t\right)\cdot dt$(2)

v is the impact velocity (ms⁻¹), F_h(t) is the force response course on the hammer during the impact (N), t_c is the time counted from the impact beginning to obtaining the maximum force response on the hammer(s). The absorbed energy e_ab developed as a result of the shock wave propagation through the sample was determined from the formula:

(3) $e_{ab}=v\cdot \underset{0}{\overset{t_c}{\int }}\left[F_h\left(t\right)-F_a\left(t\right)\right]\cdot dt$(3)

F_a(t) is the force response course recorded by the sensor placed on the anvil (N). The values of secant modulus E and the tissue stiffness k were determined from the formulas:

(4) $E=\frac{F_{hmax}\cdot \mathrm{\Delta }l}{A\cdot l}$(4)

(5) $k=\frac{F_{hmax}}{\mathrm{\Delta }\mathrm{l}}$(5)

F_hmax is the maximum force response value in the sensor installed in the hammer during the impact (N), Δl is the displacement corresponding to the maximum force response in the sensor installed in the hammer (mm), A is the sample cross section area (mm²), l is the sample length (mm)

(6) $A=\frac{\pi \cdot d^2}{4}$(6)

(7) $\mathrm{\Delta }l=v\cdot t_c$(7)

d is the sample diameter (mm). Mohsenin^[22] defined the concept of apple tissue toughness as the work required to cause the damage for the unit of volume of the tested material. This quantity can be approximately determined as the surface area below the stress-strain curve. Hence, the tissue toughness T is calculated from the formula:

(8) $T=\frac{v\cdot \underset{0}{\overset{t_c}{\int }}{F}_h\left(t\right)\cdot dt}{A\cdot l}$(8)

The failure stress σ_f and the failure strain ε_f were determined from the formulas:

(9) ${\sigma }_f=\frac{F_{hmax}}{A}$(9)

(10) ${\epsilon }_f=\frac{\mathrm{\Delta }l}{l}$(10)

Statistics

Statistical analyses of the obtained results were performed with Statistica 5.5 software. There were studied the relationships between 10 dependent variables and three factors. The results of the analyses were: variability ranges of all parameters, correlation coefficients for all pairs of dependent and independent variables, and models of multiple linear regression to estimate the effect of the factors on dependent variables. For each factor, 10 repetitions were made. The total number of data used in the regression was 360.

Results

Table 1 shows the value ranges of the quantities obtained as a result of direct measurements and calculations for the samples of the “Braeburn” variety apple flesh. However, Table 2 is the correlation matrix, which presents the coefficient values of the correlation between the independent and dependent data vectors.

TABLE 1 The value ranges obtained experimentally

Variable	Mean	Minimum	Maximum
Fhmax (maximum force response on the hammer, N)	75.9	18	168
σf (failure stress, MPa)	0.4	0.196	0.612
εf (failure strain, –)	0.049	0.033	0.07
Δl (displacement corresponding to Fhmax, mm)	0.927	0.622	1.367
vw (shock wave speed, ms^–1)	292	163	486
ei (impact energy, J)	0.032	0.0057	0.092
eab (absorbed energy, J)	0.0032	0.0004	0.008
E (secant modulus, MPa)	8.45	3.5	13.6
k (stiffness, Nmm^–1)	83.9	16.7	203.2
T (tissue toughness, MPa)	0.0085	0.0035	0.0142

TABLE 2 The correlation coefficients for all independent and dependent variable pairs

Variable		v	l	d	Fhmax	σf	εf	Δl	vw	ei	eab	E	k	T
v	1		0	0	–0.04	–0.06	0.57*	0.51*	–0.28*	0.05	0.07	–0.35*	–0.14*	0.14*
l			1	0	0.06	0.21*	–0.08	0.46*	–0.15*	0.21*	0.20*	0.13*	–0.10	0.16*
d				1	0.95*	0.26*	0.32*	0.31*	0.05	0.90*	0.90*	–0.04	0.91*	0.51*
Fhmax					1	0.50*	0.29*	0.31*	0.05	0.95*	0.94*	0.12	0.94*	0.63*
σf						1	0.06	0.15*	–0.07*	0.48*	0.46*	0.56*	0.40*	0.73*
εf							1	0.85*	–0.24*	0.45*	0.42*	0.46*	0.13*	0.51*
Δl								1	–0.27*	0.53*	0.50*	–0.32*	0.07	0.54*
vw									1	–0.11	–0.06	0.10	0.13*	–0.16*
ei										1	0.98*	0.05	0.82*	0.75*
eab											1	0.05	0.81*	0.71*
E												1	0.28*	0.20*
k													1	0.49*
T														1

*denotes statistical significance on the level 0.05.

The multiple regression analysis was made in order to determine the influence of the three selected independent variables: the impact velocity v, the sample length l, and the sample diameter d on such dependent variables as: the maximum force response on the hammer F_hmax, the failure stress σ_f, the failure strain ε_f, the displacement Δl, the shock wave speed v_w, the impact energy e_i, the absorbed energy e_ab, the secant modulus E, the tissue stiffnes k, and the tissue toughness T.

The analysis showed that the sample diameter was the parameter correlated with the maximum force response on the hammer F_hmax, the impact energy e_i, the absorbed energy e_ab, as well as the tissue stiffness k. The other parameters such as sample length and impact velocity are not advisable for predicting the dependent variables, which is proved by the small values of multiple determination coefficient R² (Table 3).

TABLE 3 The multiple regression models

General form of the model: dependent variable = A0 + A1v + A2l + A3d
Dependent variable	A0	A1	A2	A3	R^2
Fhmax	–106	–0.04	0.067	0.952	0.91
σf	0.183	–0.06	0.215	0.262	0.11
εf	0.038	0.58	–0.09	0.327	0.44
Δl	–0.221	0.507	0.451	0.315	0.56
vw	415	–0.28	0.08	–0.09	0.09
ei	–0.089	0.042	0.205	0.898	0.85
eab	–0.009	0.076	0.212	0.908	0.86
E	7.44	–0.35	0.133	–0.04	0.143
k	–2.92	–0.14	–0.1	0.913	0.86
T	0.0005	0.15	0.165	0.51	0.3

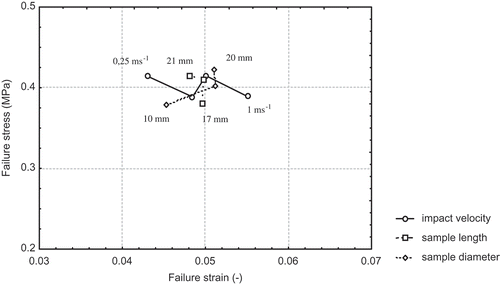
Figure 2 shows the influence of the impact velocity, sample length, and diameter on the location of the failure point determined by the failure stress and strain. The increase of the impact velocity caused the shift of the failure point in the direction of larger strain values. However, the failure stress remained on the same level. The secant modulus and tissue stiffness of apple flesh decreased with the increasing impact velocity. The sample length did not affect the failure strain whose value was close to 0.05, but resulted in the failure stress increase. The sample diameter rise shifted the failure point in the direction of both larger stresses and strains.

FIGURE 2 The influence of the impact velocity, the sample length and diameter on the failure stress and strain for the “Braeburn” variety apple flesh.

The shock wave speed v_w was determined from Formula 1. As follows from the calculations, the mean values of the shock wave speed were not statistically significantly dependent on the values of the impact velocity as well as the sample length and diameter. The further analysis showed that the mean values of the shock wave speed for the three independent variables had very similar values. This confirms the fact that the shock wave speed is the constant quantity characteristic of the tested material. The mean value of the shock wave speed for the “Braeburn” apple flesh amounted to 292 ms^–1.

The percentage contribution of the absorbed energy, e_ab, developed as a result of the stress wave propagation through the sample to the impact energy, e_i, damaging the sample was also determined. The data analysis showed that this contribution was constant for the tested values of the impact velocity, sample length, and diameter. The mean value of the percentage contribution of the absorbed energy to the impact energy amounted to 9.9% (Fig. 3).

FIGURE 3 A: The mean values of the shock wave speed for different impact velocities, sample lengths and diameters; B: The percentage contribution changes of the absorbed energy e_ab to the impact energy e_i depending on the impact velocity and the sample length and diameter.

Discussion

Bajema et al.^[23] stated that the shock wave speed in the “Red Delicious” variety apple flesh amounted to 48 ms^–1 and in the potatoes this value varied from 150 to 200 ms^–1. In another publication of Bajema et al.^[24] for the same apple variety and the same sample sizes, the obtained shock wave speed values were about 160 ms^–1. Baritelle et al.^[17] studied the influence of tissue hydration on the damage impact properties and bruise threshold. They determined the shock wave speed for four varieties and obtained: for “Golden Delicious”—144 ms^–1, for “Red Delicious”—174 ms^–1, for “Fuji”—162 ms^–1, and for “Rome”—196 ms^–1. The results given above refer to fresh apples.

These large variances in the values of the shock wave speed can result from different hydration levels of apple tissue. Baritelle and Hyde^[25] reported the research results, in which the shock wave speed suddenly decreased together with the mass loss due to low dehydration. The “Braeburn” variety apples tested in this article were fresh fruits just after the harvest. The impact tests of the cylindrical samples of “Braeburn” variety apple flesh showed that the tissue failure point corresponded to the stress of about 0.4 MPa and the strain of about 5%, which was confirmed in another research. Bajema et al.^[24] determined the failure point for the “Red Delicious” variety apples with the similar stress level, but for the higher strain values about 8%.

The apple tissue toughness was determined from Formula 8. The value changes of the sample length and the impact velocity did not affect the tissue toughness. The only factor which influenced the tissue toughness was the sample diameter. The mean values of the tissue toughness of the “Braeburn” variety apples were in the 0.008–0.009 MPa range. The tissue toughness of the “Red Delicious” variety apple was determined by Bajema et al.^[24] from 0.016 to 0.017 MPa. Bajema et al.^[24] as well as Baritelle and Hyde^[26] determined the tissue toughness from the simplified formula being the product of 0.5·σ_f ·ε_f. The data analysis showed that the above formula always gave higher values than Formula 8. The tissue toughness of four apple varieties was also determined by Baritelle et al.^[17] who obtained the values for fresh fruits: “Golden Delicious”—0.022 MPa, “Red Delicious”—0.018 MPa, “Fuji”—0.019 MPa, and “Rome”—0.020 MPa, respectively.

The secant modulus was calculated from Formula 4. In the tested range of the independent variables, the changes of the sample length and diameter as well as the impact velocity did not have the influence on the secant modulus values. The mean value of the secant modulus for the “Braeburn” variety apple flesh was in the 8–9 MPa range. Determined from Formulas 2 and 3, the values of the impact energy causing tissue damage and those of the absorbed energy, which developed as a result of stress wave propagation, allowed to calculate the contribution of the absorbed energy to the impact energy. It turned out that the mean values of the contribution of the absorbed energy to the impact energy were constant and amounted to 9.9% for all three independent parameters: sample length, sample diameter and impact velocity.

Though the e_ab quantity was called the absorbed energy as a result of the stress wave propagation, the authors realize dissipation of energy could occur due to other processes, which can be found in other articles. Bajema and Hyde^[27] applied the constant height multiple impact (CHMI) method for determination of the impact energy including: the elastic energy, the plastic deformation energy and the viscous deformation energy. They assumed that the viscous deformation energy is constant at each impact and contains the vibration energy. Dintwa et al.^[28] found that the kinetic energy is transformed into three forms. The first is the potential energy connected with the material strength. The second is the vibration energy connected with the stress waves propagation in bodies during the impact. The third is the dissipated energy connected with the inelastic deformation resulting from plastoelastic, viscoelstic, or visco-elastic-plastic character of the material and the fracture in the material structure.

As we can see various researchers use different ways of interpretation of the energy division during the impact. As a result, the quantity estimation of the energy dissipation during the impact can be made only in a general way. The research results allow to confirm that exceeding a particular value of stress causes damage of apple tissues under dynamic load conditions. In Fig. 2 it is shown that along with the increase of the impact velocity, the failure strain increased and the failure stress remained on a similar level and equalled around 0.4 MPa. Therefore, the experiment confirms the importance of the critical stress criterion as regards the cylindrical samples of apples under the impact loading conditions. The obtained mean value of the failure stress can be also interpreted as the maximum stress which apple tissue can bear under impact conditions.

There is an interesting question how this value determined for the cylindrical samples of apples is similar to the same parameter defined for the whole fruit. In the article,^[29] the authors studied strength parameters under impact conditions of whole fruits for the “Freedom,” “Rubin,” and “Rajka” apple varieties. Another way of presentation of the obtained results in that article showed the linear relationship between the maximum force response and the bruise surface area of whole fruits in the 0.125–1.66 ms^–1 range of the impact velocity. The linear relationship means the constant value of the failure stress for the impact velocities. The mean value of the failure stress 0.47 MPa for the whole fruits was a bit higher than the mean value determined for the cylindrical samples which results from testing the samples without skin which is the fruit strengthening element. The difference can also result from various apple hydration levels, which was not the research object in both experiments. Taking into consideration that the “Braeburn” apples firmness^[30] is in the range of variability of the “Rubin,” “Rajka,” and “Freedom” apples firmness, it can be found that both experiments show quality and quantity compliance as regards the obtained values of the failure stress.

Conclusions

The shock wave speed is the quantity independent of the sample sizes (length and diameter) as well as the impact velocity. It was 292 ms^–1 for the “Braeburn” variety apple flesh. In the tested range of the sample length and diameter as well as the impact velocity they did not have any influence on the percentage contribution of the absorbed energy to the impact energy, which was 9.9%. The analysis of the linear multiple regression showed that the values of the maximum force response F_hmax in the sensor installed in the hammer, the impact energy e_i, the absorbed energy e_ab and the tissue stiffness k were influenced by the sample diameter. The experiment conditions determined by the sample length and diameter as well as the impact velocity had a small effect on the values of basic strength parameters such as ε_f, σ_f and T. The highest value of correlation coefficient 0.57 was found for the relationship between the failure strain ε_f and the impact velocity. However, it seems that to compare apples strength parameter values, sample sizes should be standardized. The experiment confirmed the importance of the critical stress criterion for the impact of samples. The mean values of the failure stress obtained for the samples and whole fruits under the impact loading conditions were similar. Therefore it seems feasible to replace complicated measurements of the whole fruits strength properties with cylindrical samples measurements.