A numerical study of the sensitivity of ethanol flux to the existence of co-factors in the Central metabolism of a yeast cell using multi-substrate enzymes kinetic modelling

Abstract

Metabolic engineering of a yeast fermentation process with an intention of increasing ethanol production is a challenging engineering task since the fermentation system involves multi-enzymes and multi-substrates systems. When a certain reaction is disturbed, the other reactions are also influenced since it is a connecting system coupled with co-enzymes/co-factors which also controls the metabolic process. In this study we numerically investigate the complex system by formulating a multi-enzymes and a multi-substrate kinetic model as a tool to study system regulatory opportunities. Based on the sensitivity analysis for the maximal reaction changes, the glucose transpose is predicted to yield the largest improvement in ethanol productivity while the reaction catalysed by acetaldehyde dehydrogenase is with the highest negative effect in reducing the amount of ethanol. The existence of NAD⁺ and NADH affect the performance of ethanol production that shows ups and downs behaviour when the maximal activity of some enzymes is disturbed. This is due to the inverse role of NADH and NAD⁺ in the certain reactions whether NAD⁺/NADH acts as a substrate or as a product.

Keywords:

• Fermentation
• multi substrate kinetic model
• Runge-Kutta numerical method
• sensitivity analysis

Introduction

In biotechnology, most genetic engineering uses metabolic techniques as a powerful tool for optimising beneficial products from microbiological metabolism. The ultimate goal is to develop optimal cellular metabolism to produce biofuels through regulation of the conversion of renewable plant biomass sources into liquid fuels [1–6]. Metabolic engineering with intent to enhance cellular activities of a microbiology organism is one of the challenging problems due to the complexity of the organism’s metabolic system. Most of researchers partially studied a complex metabolic system by considering the problem with theoretical and practical aspects of metabolic engineering [7–20]. For the theoretical aspects, kinetic modelling is mainly used as a tool to approach the complex problem since mathematical modelling allows us to study a complex system involving multi-enzymes and multi-metabolites that can be considered as an engineering tool to increase yield and productivity of a microorganism. As a metabolic engineering tool, enzymes can be regulated through other molecules that either increase or decrease their activity. The abundant biochemical information with free access [21] supports the theoretical study of a complex system with regulatory purposes [15–18,22].

As a cellular metabolism with beneficial products, fermentation has been intensively studied by many researchers to find its optimal performances [23–29]. Some studies were performed in term of theoretical studies using modelling approach [23,24,26–39] with Saccharomyces cerevisiae as the most studied fermentation microorganism. Some aspects were focused to study such as investigation of glucose transport, understanding the glycolysis process, probability the appearance of oscillatory behaviour in the yeast glycolytic, study the effect of dilution rate to the dynamic of metabolites, etc. All of these theoretical studies lead to the understanding the behaviour of the complex system that probably cannot be captured through experiment. In this study, we focus on analysing the central metabolic process of a yeast cell to find the optimal regulation to enhance its metabolic product such as ethanol as much as possible. Since fermentation consists of a multiple branch metabolic pathway that interact biochemically, enzymes together with its co-enzyme became a key point in regulating the metabolic network. Here, we investigate the involvement of co-enzyme/co-factor in pyruvate and acetaldehyde branch points to predict how fluxes through microbial metabolic pathways will respond the perturbation of cellular system. As shown in several literature sources [29,33,34], some enzymatic reactions require certain substrates and produce some products. For this type of reactions, all substrates are bound to the enzyme active site before the reaction catalysis takes place to release the products. The binding process consists of sequential reactions that can be ordered or random. Therefore, multi-substrate reactions followed by complex rate equations will be used to describe how the substrates bind and in what sequence. By investigating the existence of the second substrates as variables in the system, we numerically analyse how to increase ethanol flux by altering the maximal activity of enzymes and the total concentration of co-enzyme/co-factor in the system. Our numerical study is divided into two parts, i.e. investigate the sensitivity of ethanol production to the alteration of enzyme activity and investigate the sensitivity of ethanol production to the alteration of total the second substrates (co-enzymes/co-factors) as the new variables.

Materials and methods

Multi-substrate kinetic modelling

The glycolytic model of Lei et al. [23] and Kasbawati et al. [30–31] became the starting point of this study. It is well known that chemical reactions are basically a multi-substrate reaction in which enzymes or enzyme complexes require several cofactors or coenzymes to enhance their activity as a catalyst. A coenzyme is a substance that can help enzyme and enhance the action of enzyme. Similar to a coenzyme, a cofactor is also a substance or a non-protein chemical compound that is required by the enzyme to increase the rate of a chemical reaction. It can be considered as a helper molecule that assist the enzyme in biochemical transformation. In the central pathway of yeast cell metabolism (Figure 1), some coenzymes and/or cofactors involve in each chemical reaction a phosphate group (ATP, ADP, AMP) and nicotinamide adenine dinucleotide (NAD⁺ and NADH). Then, it is interesting to approach the chemical reaction of each enzyme by using multi-substrate kinetic model to involve the enzyme companions.

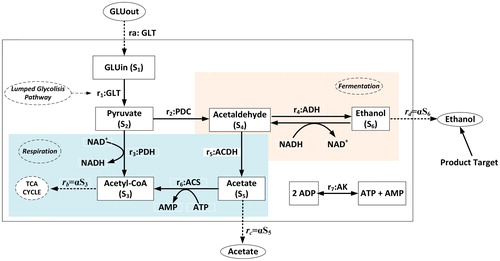
Figure 1. Central metabolism of S. cerevisiae.

Note: Reaction r₁ is a lumped process of glucose conversion to become pyruvate and reaction r_i, i = 2,…,7 is a chemical conversion catalysed by: (2) pyruvate decarboxylase, (3) pyruvate dehydrogenase complex, (4) alcohol dehydrogenase, (5) acetaldehyde dehydrogenase, (6) acetyl-CoA synthetase, (7) adenylate kinase. Glucose transport (GLT) becomes the input and some products flow out of the system with dilution rate $\alpha .$

In this study, we present ATP ($S_9$), ADP ($S_{10}$), and AMP ($S_{11}$) as variables in the system to monitor their dynamics instead of using a variable for the energy-rich phosphate bond as used in [34]. By using the mass action rate law, we derive the mathematical modelling of the metabolites in the central metabolism of the yeast cell as follows, $$\dot{S_1}\left(t\right)=\mathrm{ }\alpha G-\mathrm{ }{r}_1,$$ $$\dot{S_2}\left(t\right)=\mathrm{ }{r}_1-(r_2+r_3),$$ $$\dot{S_3}\left(t\right)=\mathrm{ }{r}_3+r_6-\mathrm{ }\alpha S_3,\mathrm{ }$$ $$\dot{S_4}\left(t\right)=\mathrm{ }{r}_2-(r_4+r_5),$$ $$\dot{S_5}\left(t\right)=\mathrm{ }{r}_5-r_6-\mathrm{ }\alpha S_5,\mathrm{ }$$ $$\dot{S_6}\left(t\right)=\mathrm{ }{r}_4-\mathrm{ }\alpha S_6,$$ $$\dot{S_7}\left(t\right)=\mathrm{ }-\mathrm{ }{r}_3+r_4-r_5,$$ $$\dot{S_8}\left(t\right)= -\dot{S_7},$$ $$\dot{S_9}\left(t\right)= -r_6+r_7,$$ $$\dot{S_{10}}\left(t\right)= {-2r}_7,$$ (1) $$\dot{S_{11}}\left(t\right)= r_6+r_7.$$(1) with initial conditions, $$S_1\left(0\right)=S_{a1}{,\mathrm{ }S}_2\left(0\right)=S_{a2},\mathrm{ }{S}_3\left(0\right)=S_{a3},S_4\left(0\right)=S_{a4},S_5\left(0\right)=S_{a5},S_6\left(0\right)=S_{a6},S_7\left(0\right)=S_{a7}{,\mathrm{ }S}_8\left(0\right)=S_{a8},\mathrm{ }{S}_9\left(0\right)=S_{a9},S_{10}\left(0\right)=S_{a10},S_{11}\left(0\right)=S_{a11},$$ where $S_{ai}, i=1,\dots ,11$ is the initial concentration of metabolites which is greater than or equal to zero. All branch outputs are considered as a linear output, $\alpha S_{\mathrm{i}},i=3,5,6,$ which are proportional to the concentration of S_i in the output branch i with dilution rate $\alpha .$ The kinetic of each reaction is derived as follow.

As seen in Figure 1, the carbon metabolism of the yeast cell is started with the transport of glucose across the cell membrane through facilitated diffusion [34–38]. The transport process is modelled as [34]: (2) $$r_a=V_{\mathit{GLT}}\frac{(\mathit{GLUo}-S_1)}{K_{\mathrm{GLT}}+\mathit{GLUo}+S_1+\frac{K_{\mathrm{i}}}{K_{\mathrm{GLT}}}\left(\mathit{GLUo}{S}_1\right)},$$(2) where GLUo and $S_1,$ respectively, refer to the concentration of the extracellular and intracellular glucose. A lumped reaction ($r_1$) describes the glucose uptake in the glycolysis pathway. Following the kinetic model of Kasbawati et al. [30–31], the kinetic of the lumped glycolysis pathway is given as (3) $$r_1=V_1\frac{S_1}{S_1+K_1},$$(3) where the maximum reaction of the lumped glucose transport is $V_1$ with Michaelis constant K₁. As the last product of glycolysis pathway, pyruvate ($S_2)$ becomes the branching point between the respiratory pathway through acetyl-CoA ($S_3)$ and the fermentation pathway through acetaldehyde $(S_4$). Conversion of pyruvate to acetaldehyde by pyruvate decarboxylase ($r_2$) did not involve any coenzyme or cofactor such that single substrate Michaelis-Menten kinetic model is used as follows, (4) $$r_2=V_2\frac{S_2}{S_2+K_2},$$(4) with maximum reaction rate $V_2$ and Michaelis constants $K_2.$ Different from reaction$r_2,$ reaction $r_3$ catalysed by pyruvate dehydrogenase complex needs NAD⁺ ($S_7$) as a cofactor. Using multi-substrate Michaelis-Mente kinetic equation, reaction $r_3$ is modelled as: (5) $$r_3=V_3\frac{S_2{S}_7}{{L_{1}S}_2+K_3{S}_7+S_2{S}_7},$$(5) with maximum reaction rate $V_3,$ Michaelis constants $K_3$ for pyruvate, and Michaelis constants $L_1$ for NAD⁺ ($S_7$). At the second branching point, acetaldehyde (S₄) is converted to become acetate (S₅) and ethanol (S₆). Conversion of acetaldehyde by alcohol dehydrogenase also requires cofactor nicotinamide adenine dinucleotide in form NADH ($S_8$). According to Ganzhorn et al. [40], alcohol dehydrogenase follows ordered bi-bi kinetics, with the cofactor binding first,

(6) $$r_4=\mathrm{ }\frac{V_f\frac{S_4{S}_8}{K_{ia}{K}_b}\mathrm{ }-\mathrm{ }{V}_b\frac{S_6{S}_7}{K_{iq}{K}_p}}{{\mathrm{\Delta }}_1},$$(6)

with ${\mathrm{\Delta }}_1=1+\frac{S_4}{K_{ia}}+\frac{\left(K_a{S}_8+S_4{S}_8\right)}{K_{ia}{K}_b}+\frac{\left(K_q{S}_6+S_6{S}_7\right)}{K_{iq}{K}_p}+\frac{S_7}{K_{iq}}+\frac{K_q{S}_4{S}_6}{K_{ia}{K}_{iq}{K}_p}+\frac{\left(K_a{S}_8{S}_7+S_8{S}_6{S}_7\right)}{K_{ia}{K}_b{K}_{iq}}+\frac{S_4{S}_8{S}_6}{K_{ia}{K}_b{K}_{ip}}.$ For acetaldehyde dehydrogenase ($r_5$) and acetyl-CoA synthetase ($r_6$), we use the ordered bi-bi irreversible kinetic equation to include NAD⁺($S_7$) and NADH($S_8$) as the second substrate for both enzymes, respectively. The kinetic equations are (7) $${\mathrm{r}}_5={\mathrm{V}}_5\frac{{\mathrm{S}}_4{S}_7}{{\mathrm{S}}_4{S}_7+{\mathrm{K}}_5{\mathrm{S}}_4+{\mathrm{L}}_2{S}_7},$$(7) (8) $$r_6=V_6\frac{S_5{S}_9}{S_5{S}_9+K_6{S}_5+L_3{S}_9}.$$(8)

The adenylate kinase reaction (r₇), which is assumed to be in equilibrium is simulated using the rapid mass action kinetics. The kinetic of adenylate kinase reaction follows the kinetic of du Preez et al. [33], (9) $$r_7=V_7\left(S_{10}^2-\frac{S_9{S}_{11}}{K_e}\right).$$(9)

A conservation relationship for the nicotinamide nucleotides and the adenine nucleotides fulfils,

$S_7$+$S_8=P_1$ and $S_9$+$S_{10}$+$S_{11}=P_2,$(10)

where P₁ and P₂ are total of adenine nucleotide and nicotinamide nucleotide in the system, respectively. We assume that all model parameters are positive. Therefore, we have the mathematical model of metabolites in the central metabolism of yeast cell which takes into account effect of cofactor. The model is given in Equation (1)(1) $$\dot{S_{11}}\left(t\right)= r_6+r_7.$$(1) with kinetic Equations (2)–(9) that fulfil (10). Before proceeding to the optimization of ethanol flux, first of all, we studied the sensitivity of ethanol flux with respect to all enzymatic reactions.

Sensitivity of steady-state ethanol production

Sensitivity of ethanol flux for reaction rates at steady state is examined to determine the extent to which a reaction in the pathway controls the steady-state of ethanol flux within the pathway. Sensitivity of ethanol flux (r_d) with respect to reaction rate i is measured by (11) $${\mathrm{\delta }}_i=\frac{r_{\mathrm{i}}}{r_{\mathrm{d}}}\frac{\partial r_{\mathrm{d}}}{\partial r_{\mathrm{i}}}, i=2,\dots ,7,$$(11) where ${\mathrm{\delta }}_i$ refers to the relatively change of r_d with respect to the change of reaction rate i. We use V_i as an adjusting parameter for changing the activities of individual enzymes such that we have (12) $$r_i^{\mathit{new}}=r_{\mathrm{i}}\left(V_{\mathit{new}}\right),$$(12) with $V_{\mathit{new}}=V_{\mathit{max}}[1\pm p_i]$ and $0\le p_i\le 1.$ Here, the non-dimensional parameter $p_{\mathrm{i}}$ can be considered as the percentage of interference of the maximal activity of enzyme i and $V_{\max }$ is the maximal reaction rate of the adjusted enzyme. Plus or minus sign in (12) refers to the increasing or decreasing p% of V_max, respectively. So the adjustment of V_max of enzyme i leads to the alteration of the i^th reaction rate.

Results and discussion

Sensitivity of ethanol flux to the enzyme maximal activity

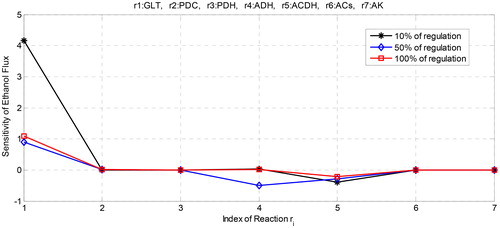
In our study, we supposed that 10% of V_max of all enzymes are increased. Using parameter values in Table 1, we have the sensitivity results as depicted in Figure 2. We can observe that glucose transport (GLT) is a reaction with the highest positive sensitivity in increasing the flux of ethanol with ${\mathrm{\delta }}_1=4.16,$ followed by the second and the third reactions which are catalysed by alcohol dehydrogenase (ADH) and pyruvate decarboxylase (PDC), with ${\mathrm{\delta }}_4=0.033$ and ${\mathrm{\delta }}_2=0.005,$ respectively. On the other hand, acetaldehyde dehydrogenase (ACDH) is a reaction with the highest negative sensitivity which decreases ethanol flux with ${\mathrm{\delta }}_5=-0.382,$ followed by pyruvate dehydrogenase complex (PDH) and adenylate kinase (AK) with ${\mathrm{\delta }}_3=-0.0007$ and ${\mathrm{\delta }}_7=-0.00003,$ respectively. However, although the ${\mathrm{\delta }}_i$ of PDH and AK are negative, the values are quite small to give negative effect to the ethanol production meaning that the effects are not significant in decreasing the flux of ethanol. Therefore, for 10% of enzyme regulation, ACDH is the only enzyme which gives significant effect in decreasing the flux of ethanol. This observation was also found in previous research [30].

Figure 2. Sensitivity of ethanol flux to the regulation of the maximal activity of enzymes.

Table 1. Kinetic parameters of the model.

Par.	Val.	Ref.	Par.	Val.	Ref.	Par.	Val.	Ref.
${\mathit{GLU}}_{\mathrm{o}}$	50	[34]	${\mathrm{V}}_1$	0.584	[23]	${\mathrm{V}}_{\mathrm{f}}$	810	[34]
$\mathrm{\alpha }$	0.02	[23,32]	${\mathrm{K}}_1$	0.0116	[23]	${\mathrm{V}}_b$	810	[34]
$V_{\mathrm{GLT}}$	97.264	[34]	${\mathrm{V}}_5$	0.98*60	[34]	${\mathrm{K}}_{\mathrm{p}}$	17	[34]
$K_{\mathrm{GLT}}$	1	[34]	${\mathrm{K}}_5$	0.17	[19]	${\mathrm{K}}_{\mathrm{ip}}$	90	[34]
$K_{\mathrm{i}}$	1.1918	[34]	${\mathrm{L}}_2$	0.17	[19]	${\mathrm{K}}_q$	0.17	[34]
${\mathrm{V}}_2$	174.194	[34]	${\mathrm{V}}_6$	1.241*60	[19]	${\mathrm{K}}_{iq}$	0.92	[34]
${\mathrm{K}}_2$	4.33	[34]	${\mathrm{K}}_6$	0.28	[19]	${\mathrm{K}}_{\mathrm{b}}$	0.11	[34]
${\mathrm{V}}_3$	6.32*60	[34]	${\mathrm{L}}_3$	1.2	[19]	${\mathrm{K}}_a$	1.11	[34]
${\mathrm{K}}_3$	70	[34]	${\mathrm{V}}_7$	133.333	[34]	${\mathrm{K}}_{ia}$	1.1	[34]
${\mathrm{L}}_1$	160	[34]	${\mathrm{K}}_{\mathrm{e}}$	0.45	[34]

Then, we supposed that the maximal reaction of all enzymes is increased to 50%. We can observe that the highest positive effect still resides on the GLT with ${\mathrm{\delta }}_1=0.89$ (Figure 2). However, increasing the maximal reaction of GLT makes the sensitivity value decreases compared with the first regulation. If we extremely increase the maximal activity of GLT until 100% then we get the sensitivity that also increases but still below the value of the first regulation. It is interesting to find that increasing GLT does not directly increase the flux of ethanol although the glucose is the main carbo for life-supporting of the yeast cell. Figure 3(a) gives the profile of the effect of regulation of GLT to the ethanol flux. Therefore, the percentage of increasing glucose transport should be properly chosen for increasing the production of ethanol.

Figure 3. Profile of sensitivity of ethanol flux with respect to the regulation of the maximal activity of enzymes.

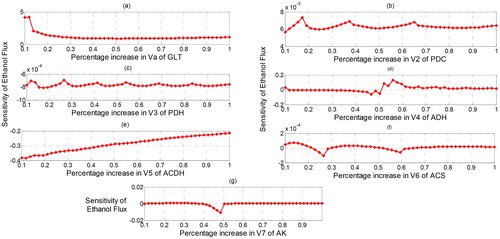
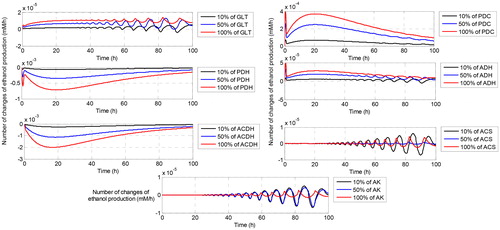
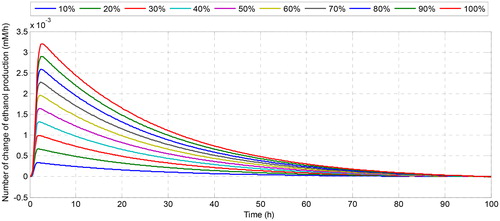
On the other hand, reaction with the highest negative effect changes from ACDH to ADH when the regulation increases to 50%. When the percentage of regulation is extremely increased to 100%, ACDH returns to be the reaction with the highest negative effect. This is probably due to ACDH is the enzyme that catalyzes the formation of acetate and ADH is the enzyme that catalyses the formation of ethanol where both reactions involve cofactor NAD + and NADH as the second metabolite. Both cofactors have different roles in which NAD + is produced by ADH, while ACDH needs NAD + as the second substrate for activated its reaction. So does for NADH where it becomes second substrate for ADH and at the same time, NADH is produced by ACDH as the second product besides ethanol. This inverse role certainly generates the fluctuation effects of both reactions to the sensitivity of the ethanol flux. As a result, controlling both reactions is an interesting challenge due to the inverse role of NAD + and NADH in both reactions. For the other reactions, the profile of their effects on the ethanol flux is shown in Figure 3 where PDC, PDH and ACS (Figure 3(b,c,f)) have sensitivity that is quite small to the increasing or decreasing of ethanol flux. All three reactions also show fluctuation at the negative and positive small intervals of the sensitivity of ethanol flux. This is probably due to the involvement of NADH and NAD in the PDH reaction and involvement of ATP and AMP at the ACS reactions. The existence of cofactors has controlled the change of the sensitivity of ethanol flux. Figure 4 shows the number of changes of ethanol flux after regulation by increasing the maximal reaction of each enzyme. We can observe that some oscillations occur at the end of time observation. The oscillation refers to the ups and down the flux of ethanol due to the existence of cofactor that also influences the dynamic of ethanol flux.

Figure 4. Number of change of ethanol production after increasing the maximal activity of all enzymes.

Sensitivity of ethanol flux to the total of cofactor

In this section, we numerically investigate the effect of the existence of cofactor in controlling the flux of ethanol. As we have shown in the previous section, NAD + and NADH have an inverse role in several reactions affecting the fluctuation of the number of changes in ethanol flux and the sensitivity value. Since the cofactors have controlled the dynamic of the system, it is interesting to find the effect of the total cofactor to the production of ethanol flux. Therefore, some simulations are presented by changing the initial concentration of NAD⁺, NADH and ATP. The initial concentrations of these three cofactors are varied due to the involvement of NAD + as the second substrate in the reaction catalysed by PDH and ACDH, the involvement of NADH also as the second substrate in the reaction catalysed by ADH, and the involvement of ATP in ACS reaction as a second substrate.

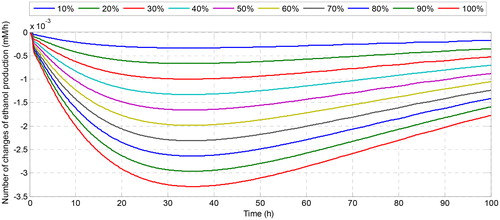
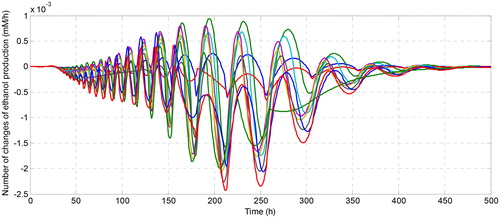
Figures 5–7 shows how the flux of ethanol is changed due to the changes in the number of the cofactor in the system. Although the number of changes in ethanol flux is quite small, their dynamic behaviour with respect to the change of time is interesting to be investigated. For instance, when we increase the concentration of NADH at the initial observation (Figure 5), ethanol flux grows at the beginning of fermentation. With time, the number of change of ethanol flux coincides with the zero changes meaning that all solutions converge to the same steady-state solution even though it is started at different conditions. Conversely, when we regulate the initial concentration of NAD+, it affects the decreasing of ethanol flux even in a small magnitude. The greater the number of initial NAD+, the smaller the number of changes in ethanol flux. This is caused by the role of NADH as a substrate in the reaction that produces ethanol, while NAD + becomes the substrate in the acetate production that affects the decreasing of ethanol concentration. For the effect of the increase of the initial concentration of ATP, it can be seen in Figure 7 that the dynamic of the change of ethanol flux is very fluctuating in a small magnitude of flux ethanol changes. Although ATP has an effect on reducing or increasing the concentration of ethanol, the effect is not too significant due to the small effect on the change of ethanol flux. Therefore, among the involved cofactors, nicotinamide nucleotides are the cofactors that have a significant effect on the change of ethanol flux and recommended to be the target of regulation for increasing the production of ethanol as the candidate of renewable biofuel.

Figure 5. Number of change of ethanol production after increasing the initial concentration of NADH.

Figure 6. Number of change of ethanol production after increasing the initial concentration of NAD⁺.

Figure 7. Number of change of ethanol production after increasing the initial concentration of ATP.

Conclusions

A numerical study was conducted by investigating the numerical solutions of a biochemically structured model of the central metabolism of the yeast cell. The structured model was formulated based on the multi-substrate kinetic model for some enzymatic reactions with sequential processes such as an ordered bi-bi for irreversible and reversible mechanisms. A regulation rule was applied to observe the sensitivity of enzymes to ethanol production and ethanol flux. It was observed that when a certain maximal activity of an enzyme was disturbed, the other reactions were affected due to the coupling of the system through the involvement of co-enzymes/co-factors from adenine nucleotide and nicotinamide nucleotide. For nicotinamide nucleotide, NAD + and NADH have a different role at the different metabolic parts. At the ADH reaction, NADH acted as a substrate that also was produced in the ACDH reaction. Conversely, NAD + acted as a substrate in ACDH reaction and at the same time, it also was produced by ADH reaction. This inverse role generated a fluctuation effect on the ethanol flux when the maximal activity of all enzymes was disturbed. As a result, controlling ADH and ACDH became an interesting challenge due to the inverse role of NAD + and NADH in both reactions. The inverse role of NADH and NAD + also generated some oscillations at the end of time observation of ethanol production. The oscillations referred to the ups and downs of the production of ethanol due to the existence of cofactor that also influenced the dynamic of ethanol flux. These observations could then be used to explore the boundaries of metabolic engineering involving orders of magnitude changes in enzyme activities and level concentration of cofactor in the system. It also guided future work to an improvement of our ability to understand the in vivo behaviour of glycolysis and fermentation on the basis of the properties of the glycolytic enzymes and the important role of the existence of the cofactors/coenzymes as the second substrate in a reaction.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The authors would like to thank DIKTI via Institute for Research and Community Services Hasanuddin University that supported this research through Penelitian Dasar Unggulan Perguruan Tinggi (PDUPT) under grant number 1740/UN4.21/PL.00.00/2019.