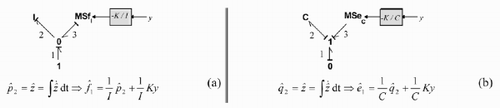Luenberger observers for linear time-invariant systems modelled by bond graphs

Abstract

This paper shows how to build Luenberger observers for linear time-invariant systems modelled by bond graph. The methods are based on Luenberger's algebraic methods to design both full-order and reduced-order observers. The procedure for reduced-order observers uses the bicausality concept to simplify some classical matrix calculations (the calculation of matrix inverses is not needed), which is an important improvement mainly for large-scale systems. The calculation of the observer gains is based on the pole-placement techniques for linear systems modelled by bond graphs. As an application, both observers are designed for a vehicle suspension modelled by bond graphs.

Keywords:

• Bond graph
• Luenberger observers
• Linear systems

1 Introduction

In some applications of automatic control, it is assumed that the entire state vector is available for feedback. Often, however, this is not the case; it is either impractical to measure some or all of the states, or the quality of the measurement, in terms of the signal-to-noise ratio, is poor enough to reduce the utility of the compensator. In these instances, we must estimate the unavailable state variables, using an observer. This approach normally allows implementation of the compensator with an acceptable performance. If an observer is used to provide estimates of all state variables, it is referred to as a full-order state observer. Sometimes, however, it is possible to obtain a satisfactory measurement of some, but not all, states. In these instances, a reduced-order state observer may be used to estimate only the non-accessible states.

Considering an observable model, Luenberger observers [1] can be designed in such a way that the difference between the actual system states and the states of the observer can be reduced to zero. Luenberger's methods consider a system modelled by a linear time-invariant state equation:

where A ∈ ℜ ^n × n , B ∈ ℜ ^n × p , C ∈ ℜ ^m × n , y are the measured outputs of the model.

1.1 Full-order observer

Under observability assumptions on the pair [A, C] and the non-existence of redundant outputs, a full-order observer for equation (1) can be readily constructed as:

The observer gives the following dynamics for the estimation error,

:

1.2 Reduced-order observers

The principal advantage of implementing a reduced-order observer is that it will estimate only those state variables that cannot be accessible by the measurements; the order of the observer model will be lower than the order of a complete order observer, and thus the computational cost to estimate these variables decreases.

Luenberger's method for building reduced-order observers [2 –  4] divides the state variables of the model into accessible variables and non-accessible variables.

Definition 1

The accessible variables are the state variables that can be directly measured from a sensor or can be calculated directly from the measurement.

With this classification, the state equation of the system can be written as a function of the accessible (x_a ∈ ℜ ^m ) and non-accessible (x_b ∈ ℜ ^n-m ) variables as follows:

Afterwards, with a linear transformation, the state equation is written as a function of the output and the non-accessible state:

where:

Equation (6) needs the inversion of a C_a submatrix. Because of this, x_a must be selected such that rank(C_a ) = m to guarantee the existence of

.

Remark

One special type of accessible state variable is the measurable state variable. This variable is a state variable that can be measured directly from a sensor; if all outputs are measurable state variables, then C_a is equal to the identity matrix, C_b is equal to zero, and thus the equation (6) is simplified.

From the state equation (4) Luenberger's method proposes the estimated state as:

with K ∈ ℜ(n-m) × m. Thus, the dimension of the observer is equal to (n – m), where n is the total number of state variables, and m is the number of outputs of the system.

As x_b is non-accessible, in equation (7) the term

must be substituted by an expression derived from equation (4), which is a function of y and u (equation (8)):

Afterwards, to avoid the time derivation of the output, defining an auxiliary variable

, the state equation for the estimated states is:

where

This observer gives the following dynamics for the estimation error,

:

1.3 Design of the observer: calculation of the gain matrix K

The pole assignment method is a classical technique to design linear observers. When a full-order observer is designed, the observability of the pair (A, C) is needed to fix the eigenvalues of (A – KC), as shown in Theorem 1:

Theorem 1

The eigenvalues of (A – KC) can be fixed arbitrarily if and only if the pair (A, C) is observable. Then, for asymptotically stable error dynamics the gain vector K should be chosen such that the eigenvalues of (A – KC) lie strictly in the left half plane. For designing reduced-order observers, Luenberger [3] showed the result of Theorem 2.

Theorem 2

If the pair (A, C) is observable, the pair

is also observable; therefore, the eigenvalues of

an be arbitrarily selected to define the error dynamics.

According to Theorems 1 and 2, selecting the eigenvalues of the observer, the calculation of K may be based on the characteristic polynomial coefficients obtained for the observer. Many authors have studied this problem using algebraic, geometric and graphical approaches. In particular, Pichardo-Almarza et al. [5, 6] used the results of Rahmani et al. [7] to calculate the gain of reduced-order observers directly from a bond-graph model.

The main objective of the present work is to provide a bond-graph approach to build and design Luenberger observers for linear time-invariant systems. As an application, the observers are designed for a 1/2 vehicle passive mechanical suspension, which has two measurements that depend on several states variables.

This paper is organized as follows: Section 2 shows the bond-graph implementation of Luenberger observers. Section 3 shows the principles to design the observer starting from a bond-graph model. Section 4 proposes the implementation of the observers on an example. Finally, Section 5 presents the conclusions of this work.

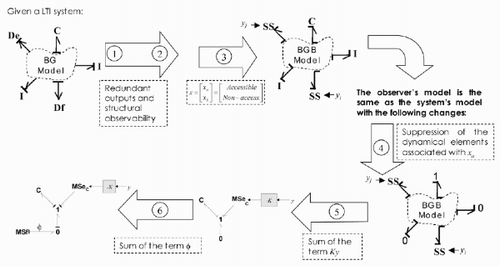
2 Bond-graph approach to build the observers

The bond-graph implementation is based on Luenberger's methods detailed in the previous section. The observer bond graphs are equivalent to equations (2) and (9), and thus, the system's bond-graph model must be equivalent to equation (1). For the sake of clarity, it is supposed that in the bond-graph model, there are no causal loops between R-elements or derivative causalities that could generate an implicit state equation. In a bond-graph model, there may be derivative causalities or causal loops between R-elements that generate an implicit state equation, which means that the state equation has the following form:

where the E matrix is a singular matrix. Since the inverse E ⁻¹ does not exist, the state equation cannot be expressed as equation (1); thus, Luenberger's methods shown in this paper cannot be used properly.

The use of bond graphs allows techniques of structural analysis to be used to determine several different properties of a model. In this paper, the results shown by Sueur and Dauphin-Tanguy [8] will be used to analyse the model of the system before building the linear observer. The first two steps of the procedure to build both observers (full-order and reduced-order) are the same. The first step is related to the verification of the non-existence of redundant outputs for observability purpose, and the second is related to the verification of the structural observability of the model.

Step 1. Verification of the non-existence of redundant outputs

From a bond-graph point of view, the definition of bond-graph rank (bg-rank) can be used to confirm the rank of the model's matrices. The bg-rank is a structural rank in the sense of graph theory but corresponds in fact to the numerical rank because it takes into account parameter dependency through the causality. Sueur and Dauphin-Tanguy [8] have shown the following property for the bg-rank[C]:

Property 1

The bg-rank[C] is equal to the number of detectors in a bond-graph model that can be dualized without creating causality conflicts at the junctions while accepting the change in causality in the dynamical elements. This property provides information about the existence of redundant outputs. Some redundant outputs might exist and might be neglected; thus, taking only the outputs in the detectors that can be dualized without any causality conflict, the bg-rank[C] will be equal to the number of non-redundant outputs: bg-rank[C] = m.

Step 2. Verification of the structural observability

The verification of structural observability of the bond-graph model is made using the technique proposed by Sueur and Dauphin-Tanguy [8]. They have shown that if all dynamical elements in integral causality are causally connected with a detector, and all the I-C elements in integral causality are in derivative causality when a derivative assignment is performed over the initial bond graph (with an eventual dualization of some detectors), then the model is structurally state-observable by the detectors.

2.1 Procedure to build full-order observers

Karnopp [9] proposed a method for bond-graph models to build both complete-order observers and reduced-order observers for linear systems. In his work, the method used the bond-graph model basically for the architecture of the observer. The observer gain is calculated using classical algebraic methods. In the present work, the architecture of full-order observers shown by Karnopp is used.

After applying Step 1 to select only the non-redundant outputs and Step 2 to confirm the structural observability, there is only one additional step to be added for building full-order observers. Thus, the procedure can be summarized as follows:

1.	Step 1 and Step 2. See above.
2.	Step 3. Linear output injection: addition of the term in the dynamical elements of the observer model (figure 1).

After the construction of the observer, the gain matrix K can be calculated by means of the method presented in Section 3.

Figure 1. Addition of the term to the dynamic element of the observer model.

2.2 Procedure to build reduced-order observers

The bond-graph implementation will calculate the estimated state using the auxiliary variable,

(equation (9)). The bond-graph approach to build a reduced-order observer can be summarized as shown in figure 2.

Figure 2. Procedure to build the reduced order observer.

The relevant steps in this procedure are 3 and 5, because they show how to use the bicausality concept in the bond-graph implementation of the observer. Step 3 shows how to avoid the calculation of

, whereas in step 5, two lemmas are proposed to facilitate the observer building. A brief description of each step is now given.

1.	Step 3. Selection of xa , verification of rank (Ca ) = m and calculation of Ca and Cb .
2.	Step 3.1. Selection of xa.

Definition 2 allows the accessible state variables to be identified in a bond-graph model.

Definition 2

The accessible states in the bond-graph model are the state variables causally connected with the outputs. This means that x_a are state variables associated with the dynamical elements that have a direct causal path (or an indirect causal path through a R-element) with a detector.

The first condition that x_a must satisfy is: dim(x_a ) = bg-rank[C] = m. Afterwards, x_a must be selected such that the C_a submatrix is invertible.

Step 3.2. Verification of bg-rank of C_a submatrix: Invertibility

Taking only the outputs in the detectors that can be dualized without any causality conflict, Property 1 implies that there exists an invertible submatrix of C with dimensions m × m, called C_a , corresponding to a selection of components x_a .

After applying Property 1 to select the non-redundant outputs, the bicausality concept can be used to select the x_a vector guaranteeing the existence of C_a ⁻¹.

The computational capabilities of the bicausality concept have shown that this is an adequate tool for solving the problem of inverse systems [10]. The bicausality allows a variable to be fixed or imposed at the same time, and its conjugate as bicausal bonds decouples the effort and flow causalities. In the context of the inversion problem, imposing the output variable without modifying the energy structure (or constraint equations) of the system can be carried out by an SS element having a flow source/effort source causality [11].

From Property 1, it is possible to determine bg-rank[C] by means of the dualization of detectors. When this procedure is carried out, the conjugate variable equals zero, because the detector is supposed to be ideal (with no power being dissipated or stored). Then, to obtain information on

, the detectors can be substituted by SS elements leading to a null power flow on that bond. This analysis yields Theorem 3.

Theorem 3

The inverse of C_a submatrix exists (or the bg-rank[C_a ] = m), if the following operations can be made in the bond-graph model without introducing any causality conflict:

1.	All detectors are substituted by SS elements (figure 3a).
2.	The integral causality of the dynamical elements associated with xa change into a bicausality (figure 3b).
3.	The dynamical elements associated with xb stay in integral causality.

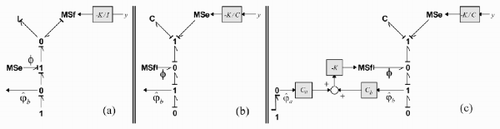
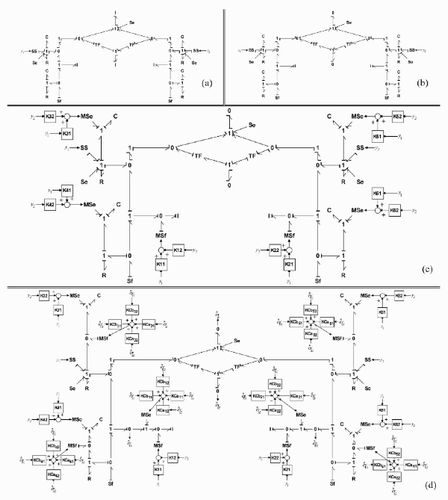
Figure 3. (a) Substitution of detectors by SS elements. (b) Bicausality of elements associated with x_a .

Proof

Consider the junction structure equation of the initial bond-graph model:

This structure is equivalent to the state equation (1), because S ₃₄ = 0. However, Luenberger's methods can be extended to build observer for linear systems written as:

Performing a bicausality assignment in the storage elements and changing the detectors by SS elements is equivalent to inverting some terms in equation (12); then a new output structure vector

can be built, as shown in equation (13):

If equation (13) is solvable, that is if (I – M ₁₀  L ^*) is invertible, where I is an identity matrix and L ^* is such that

, it follows, with Z_a = F_a x_a and Z_b = F_b x_b ,

On the other hand, to calculate x_a from equation (4), the condition bg-rank[C_a ] = m has to be satisfied; thus:

Obviously, there are two possible ways to invert the output equation in equation (4), directly with the inverse of C_a submatrix, or using the bicausality assignment. The same equation has to be obtained, so equation (14) has to be equal to equation (15), meaning that the bg-rank[C_a ] = m and the inverse of C_a exists.

Step 3.3. Calculation of C_a and C_b

Once x_a has been selected (considering the conditions of Theorem 3 to confirm bg-rank(C_a ) = m), the calculation of C_a (or C_b respectively) is derived from the initial bond-graph model by calculating the gain of the causal path of length one (1) from the I or C-elements associated with x_a (or x_b respectively) to the output y. With this operation, Step 3 is completed. Afterwards, the observer model is built from the bond-graph model with bicausality generated to analyse the invertibility of C_a . Steps 4 – 6 specify the changes needed to conclude the construction of the observer.

Step 4. Suppression of the dynamical elements associated with x_a

When the causality of the dynamical elements associated with x_a changes to a bicausality (figure 3b) and the detectors are substituted by SS elements (figure 3a), the complementary variables Z_a and the derivative of the state variables

can be calculated if the output y is known. Then, in the observer model, these dynamical elements are removed and substituted by 0-junctions or 1-junctions, as shown in figure 4. (The dynamical elements are substited by junctions because the effort in the new 0-junction or the flow in the new 1-junction will be used as new auxiliary variables

for the construction of the observer—see Step 6 of this procedure.) With the suppression of these elements, the order of the system’s model and the calculation of

is not needed.

Figure 4. Suppression of dynamical elements in the bond graph model of the observer.

Step 5. Sum of the term Ky

The term Ky has to be summed to calculate the state

. This operation is equivalent to changing in the observer the I or C-elements associated with

by the bond graph shown in figure 5a and 5b, respectively.

Figure 5. Sum of Ky: (a) in an I-element; (b) in a C-element.

Step 6. Sum of the term ϕ

The term ϕ is required to calculate

(equation (9)). Using equation (4), this term is:

where:

According to equation (16), variables ϕ and

(

respectively) will be flows when the state variable x_b (x_a respectively) is associated with a C-element. In the same way, ϕ and

(

respectively) will be efforts when the state variable x_b (x_a respectively) is associated with an I-element. Lemmas 1 and 2 are proposed to identify the variables

and

directly in the observer's bond-graph model.

Lemma 1

The variables

are equal to the output variables in the junctions (0 or 1) with bicausality that substitute the dynamical elements associated with x_a (figure 6).

Figure 6. Variable in the observer bond graph associated with: (a) I-element; (b) C-element.

Lemma 2

In the bond-graph model of the observer, when x_b is associated with a C-element,

is the flow before the addition of ϕ (when the dynamical element associated with x_b is an I-element,

is the effort before the addition of ϕ).

Figure 7c shows the addition of the term ϕ in the observer bond graph. In this figure, ϕ is added using a modulated flow source (because x_b is associated with a C-element); according to Lemmas 1 and 2,

is the effort in the 0-junction associated with x_a ; and

is the flow before the addition of ϕ. With Step 6, the procedure is concluded, and the observer model is complete.

Figure 7. (a) Variable with an I-element; (b) Variable with a C-element; (c) Addition of term ϕ.

If the designer does not want to use the bicausality concept to implement a reduced-order observer, another bond-graph approach for building reduced-order observer can be used (as proposed by Pichardo-Almarza et al. [5]).

In that case, not using the bicausality concept in the implementation of the observer will have the following consequences:

1.	Calculation of will be necessary (a new step must be added in the procedure).
2.	The architecture of the observer model will be more complex because the order reduction is made substituting the dynamical elements associated with xa by modulated sources.
3.	Lemma 1 must be modified to identify in the observer model.

In conclusion, the designer has two options to build a Luenberger observer from a bond-graph model. The first is the construction of a full-order observer, which will estimate all the state variables. The procedure is simpler than the procedure for the reduced-order observers, but the estimation may have a larger computational cost.

If the designer decides to implement a reduced-order observer, the graphical manipulations in the bond graph increase, but the estimation will have a smaller computational cost.

Once the designer has selected the type of observer, they are ready to calculate the gain from the observer bond-graph model. Next section proposes the technique used to design the observers.

3 Bond-graph approach to design the observer

The observer design is based on the pole placement techniques proposed by Rahmani et al. [7] as in the approach proposed by Pichardo-Almarza et al. [5, 6]. In this case, the characteristic polynomial of the full-order observer (P _{( A−KC )} (s)) or the characteristic polynomial of the reduced observer

is selected, and then the calculation of K is based on the polynomial coefficients. This calculation is possible, considering the information signals associated with K and applying the proposed Theorem 4. Although it is possible for the observer bond graph to contain bicausalities, Theorem 4 can be applied.

Theorem 4

The value of each coefficient of the characteristic polynomial P_(A−KC) (s) or

is equal to the total gain of the ith-order families of causal cycles in the bond-graph model:

The gain of each involved family of causal cycles must be multiplied by (−1) ^d if the family is constituted by d disjoint causal cycles.

Thus, the causal analysis to calculate K is made only with the family of causal cycles in the observer's bond graph.

Remark

The calculation of causal cycles in the observer model may be an arduous task if the designer does not have efficient bond-graph software. Ideally, the designer should dispose of bond-graph software that can calculate the observer gain applying a graphical analysis in the bond-graph model. Bond-graph software such as ARCHER [12] or MS1 [13] allows the causal loops and paths between variables in a model to be identified. These software suites are good tools for control analysis, but they need some improvements to be useful for the observer design.

In this paper, 20-sim® software [14] was used as simulation tool. This software allows easy implementation of the observer bond graph, but symbolic calculations are not possible from the graphical model. For this reason, the authors had to use mathematical software (MATLAB®) to facilitate the symbolic and numerical calculations associated with observer gain.

4 Example

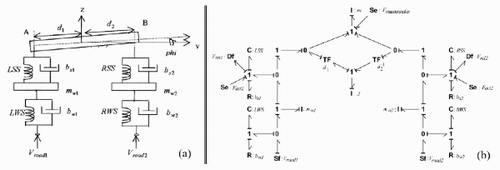
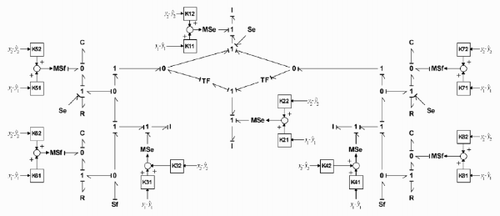
This example considers the 1/2 vehicle passive mechanical suspension (figure 8a) used by Dauphin-Tanguy et al. [15]. The motions considered are heave and pitch. The disturbance inputs are road motion (on the left and right wheels), the gravity and the mass-transfer force due to braking or accelerating effects applied on the car's inertia centre G. Figure 8b shows the bond-graph model in the integral causality of the system. Only relative velocities are measurable, which are represented by Df-sensors in the BG model. These measures will be used to design the state observers for a future state feedback control law implementation.

Figure 8. Bicycle suspension in vertical motion: (a) physical model; (b) bond graph model.

From figure 8b, it is possible to define four states as accessible: p_m, p_J, p_mw1 and p_mw2 because the I-elements I_m, I_J, I_mw1 and I_mw2 have a direct causal path with a detector. As there are only two measurements, it is possible to define six different pairs of accessible state variables (x_a ):

Using 20-sim software, it is possible to find the poles of the model (figure 8b):

To build both types of Luenberger observers, Steps 1 and 2 should be applied.

Step 1. Verification of the non-existence of redundant outputs.

In the model of figure 8b, the detectors can be dualized without creating any causality conflict; thus, from Property 1: bg-rank[C] = 2. Thus, the measurements in the Df-sensors are non-redundant outputs.

Step 2. Verification of the structural observability

Applying the technique proposed by Sueur and Dauphin-Tanguy [8], after assigning a preferred derivative causality on the model, it is possible to conclude that the model is structurally observable by these detectors.

4.1 Full-order observer

The construction of the full-order observer is based on procedure 2.1. Thus, only Step 3 should be applied to finish the construction.

Step 3

The term

is added in the dynamical elements of the observer model with modulated sources, as shown in figure 9.

Figure 9. Bond graph model of the full-order observer.

4.2 Design of the full-order observer

The poles of the observer have been selected slightly more rapid than the poles of the model:

From the observer bond-graph model (figure 9), it is possible to find hundreds of families of causal cycles associated with each polynomial coefficient. MATLAB® software has been used to calculate numerically the gain matrix of the observer. Then, with the desired poles, s_d , the gain of the observer is:

4.3 Reduced-order observer

The construction of the reduced-order observer is based on the procedure 2.2. Then, step 3, 4, 5 and 6 can be applied.

Step 3. Selection of x_a

As mentioned before, to build the reduced-order observer there are four states variables that can be defined as accessible: p_m, p_J, p_mw1 and p_mw2 ; then, there exist six possible pairs of x_a to build a reduced-order observer. In this example, only one observer is designed, considering p_m and p_J as accessible state variables; then:

Step 3.1. Verification of rank (C_a ) = m

In the bond-graph model, the detectors are substituted by SS elements, and the causality of the dynamical elements associated with x_a is changed to a bicausality (figure 10a). This operation can be made in the BG-model, thus: bg-rank (C_a ) = m.

Figure 10. (a) Step 3: Verification of bg-rank (C_a ); (b) Step 4: Suppression of dynamical elements; (c) Step 5: Sum of the term Ky; (d) Step 6: Bond graph model of the reduced order observer.

Step 4. Suppression of the dynamical elements associated with x_a

From the bond-graph model with bicausalities obtained in the previous step, the I-elements with bicausalities are substituted by 1-junctions (figure 10b).

Step 5. Sum of the term Ky

The term Ky is added in each dynamical element (associated with x_b ) with modulated sources as shown in figure 10c.

Step 6. Sum of the term ϕ

The term ϕ is added with modulated sources. With this last operation, the observer model is complete (figure 10d). In figure 10d, the terms KCa_ij are the components of – KC_a , and KCb_ij are the components of – KC_b (according to equation (16)).

4.4 Design of the reduced-order observer

The poles of the observer have been selected slightly more rapidly than the poles of the model:

In this case, hundreds of families of causal cycles are found, too. Again, MATLAB® software has been used to calculate the gain of the observer. Then, with the desired poles, s_d , the gain of the observer is:

4.5 Simulations

For the simulations, the parameters have the following numerical values: m = 761 kg, m_{w 1} = m_{w 2} = 35 kg, b_{w 1} = b_{w 2} = 1000 Ns m⁻¹, b_{s 1} = b_{s 2} = 1900 Ns m⁻¹, d ₁ = d ₂ = 1.495 m k _LSS = k _RSS = 12 000 N m⁻¹, k _LWS = k _RWS = 120,000 N m⁻¹, J = 850 kgm⁻².

The mass transfer, supposed to be due to a braking action, is modelled by the response of a first-order model 1 / (1 + 0.1s) to a pulse input (amplitude – 800 N, t ₀ = 0.1 s, t ₁ = 0.2 s). The observer behaviour is evaluated considering that there exist uncertainties in the vehicle mass; the mass was incremented up to 1000 kg (which might represent the mass of three additional passengers in the car).

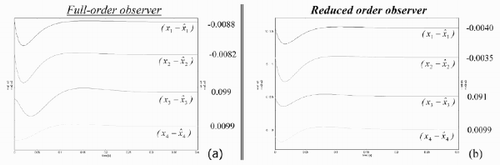
Figure 11 shows the dynamics of absolute errors (for some state variables [x1 x2 x3 x4] ^T = [p _{mw 1} p _{mw 2} p _LSS p _LRS ] ^T ), and table 1 shows the relative estimation error in the steady state when both observers are used. These results show the sensitivity of the estimation error with respect to the variation in vehicle mass. When the parameters of the Luenberger observers are equal to the parameters of the original model the estimation error always converges to zero. However, the state estimation error does not always converge to zero if a Luenberger observer is used to estimate the states in linear uncertain systems [16].

Figure 11. Estimation error: (a) full-order observer; (b) reduced-order observer.

Table 1. Relative estimation error in steady state*.

Full-order observer	_ (%) = 13	_ (%) = 8	_ (%) = 24	_ (%) = 20
Reduced order observer	_ (%) = 6	_ (%) = 4	_ (%) = 22	_ (%) = 20

*Relative estimation error = 

Remark

When the bond-graph approach to build the reduced-order observer without bicausalities is applied in this example, the same K matrix is obtained, and the simulation results are equal to those shown in figure 11.

5 Conclusions

In this paper, two methods have been shown to build and design Luenberger observers. Although the full-order observers are simpler in their construction, the reduced-order observers represent a good estimator, since these yield a computational cost decrease. With the advantages of the bicausality concept, the bond-graph approach to build the reduced-order observers does not need an explicit calculation of C_a ⁻¹. The approaches shown in this paper represent a control tool for those developing a bond-graph model. The matrix calculations are substituted by causal manipulations applied in the observer bond graph.

Although, with the development of computers, the inversion of matrices is an operation that can be easily handled (even for relatively large matrices), besides saving on computational costs associated with matrix inversion, it is useful for a bond-graph modeller to have graphical control tools (based on bond graphs) for which state equations do not need to be written and which simplify the matrix calculations as soon as possible. Finally, the methods for designing linear observers shown in this paper would be less arduous if the graphical operations related to the calculation of the K matrix could be implemented directly in the existing bond-graph software.