Mathematical modelling of a domestic heating system with stratified storage tank

Revised and expanded version of a paper presented at the 5^th Vienna International Conference on Mathematical Modelling (5^th Mathmod), Vienna, Austria, 2006.

Abstract

A hybrid distributed parameter model of a heating system for domestic hot water is presented in this paper. This heating system comprises a condensing boiler (burner), a counter current heat exchanger, and a so-called stratified storage tank which is the state of the art domestic hot water storage unit. The paper presents the model for the different operational modes of the plant which are described by a finite state automaton representing the discrete-event dynamics and driving the underlying continuous-time dynamics of the storage tank, the heat exchanger, and the burner. These interconnected components are modelled by a system of six coupled, quasi-linear partial differential equations (PDEs) comprising diffusion-, convection-, and source terms. In order to perform numerical simulations, the set of PDEs is spatially discretized using the method of lines. Thereby, the influence of various discretization schemes on the temporal evolution of the traveling temperature profiles in the single components is investigated. A high resolution slope limiter scheme for the stratified storage tank and a higher order up–/downwind scheme for the heat exchanger and the burner are found to be an appropriate choice for the spatial discretization of the model equations in order to adequately cover the plant dynamics. Simulation results fortify the effectiveness of the chosen discretization schemes and show the excellent performance of the suggested model representing the measurement data.

Keywords:

• stratified storage tank
• hybrid distributed parameter system
• diffusion-convection system
• counter current heat exchanger

1. Introduction

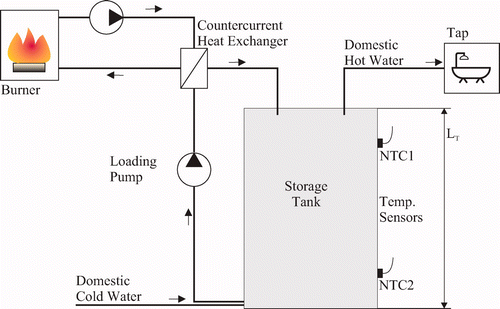
The use of storage tanks for domestic hot water in contemporary heating systems, as shown in Figure 1, has proven great potential to save energy and increase comfort and availability. For solar heating systems, it is even indispensable, since in most cases there is a significant time gap between energy gain and consumption. Although storage of hot water is common practice in most households, the efficiency of ordinary storage systems is not satisfactory. Therefore, in the heating systems community, the state-of-the-art system for domestic hot water storage is the so-called stratified storage tank 1. In general, the fluid in the storage vessel has a certain temperature profile and thus a density gradient which assures the physical principle of stratification. To maintain this stratification, the storage tank in Figure 2 is driven with relatively low mass flows and equipped with baffle plates to ensure that the mixing and excitation of agitation flows in the in- and outflow regions of the tank are minimized. Due to the characteristic stratification of the water in the tank, i.e. hot water at the top part and cold water at the bottom part, domestic hot water (e.g. for shower, bath, kitchen) is always taken from the uppermost fluid layer. During tapping, equal amounts of cold fluid are introduced at the very bottom of the tank such that the vessel is always entirely filled with water. During loading, the storage tank is connected to the secondary side of a counter current heat exchanger and filled with the desired amount of hot water. Thereby, cold water is pumped from the bottom part over the heat exchanger and introduced back up into the top part of the tank. To feed the corresponding primary side with hot water, the heat exchanger is connected to a condensing boiler, referred to as the burner. The interconnection of the components of interest, i.e. burner, heat exchanger, and storage tank, can be inferred from Figure 2. The system considered here is referred to as the Cerasmart Module and commercially available from Robert Bosch GmbH.

Figure 1. Heating unit with stratified storage tank, control unit, loading pump, burner, counter current heat exchanger, and temperature sensors (NTC 1 and NTC 2).

Figure 2. Sketch of the plant.

The dynamics of the plant is characterized by discrete-time events due to e.g. tapping or loading events as well as continuous time-varying spatial temperature profiles, which occur in the storage tank, the heat exchanger, and the burner. These components are represented by the respective distributed parameter models which are then coupled according to the flowsheet in Figure 2. In detail, the models are given as a diffusion–convection system (DCS) with heat loss to the ambiance for the storage tank and as two counter current transport systems with heat exchange between the primary and secondary side for the heat exchanger and the burner. Thus, the entire model consists of a finite state automaton interacting with a continuous-time model of six underlying coupled quasi-linear partial differential equations. Consequently, the entire plant can be interpreted as a hybrid distributed parameter system 2.

Due to the rapid increase of the cost of energy, consumers require that process control schemes operate the plant in such a manner that energy consumption is minimized. However, today's standard is that the loading cycle is driven by a two-point controller that activates the loading pump and the burner if a predefined temperature threshold at the temperature sensor NTC1 is detected and correspondingly stops the loading after detecting a respective temperature threshold at NTC2. To develop a process control system which minimizes the consumed energy of the heating system, the set-up of a model-based process control scheme 3 is mandatory. Even though complex 3D finite element models exist for similar applications 4, the contribution of this paper is to provide a reduced-order model of the plant which is suitable for the development of a process control scheme for energy efficient, optimal loading of the storage tank. The tasks therefore are the design of a state observer 5, a control algorithm based e.g. on a flatness approach 6,7, or on the method of characteristics 8,9 and a dynamic real-time optimization scheme for the design of an economically optimal loading strategy 10.

The first part of the paper outlines the derivation of the hybrid plant model. Here, the finite state automaton with its five discrete states and its corresponding transitions is presented. Furthermore, the partial differential equations (PDEs) for the storage tank, the heat exchanger and the burner are derived. To perform numerical simulations, the spatial discretization of the PDEs is investigated in the second part of the paper. Thereby, the temporal evolution of the traveling temperature profiles in dependence of the discretization approach for the convection terms is analysed. For the tank model, a finite volume approach switching between an up – and a downwind scheme in dependence of the flow direction is compared to a switching high resolution slope limiter scheme. For the heat exchanger and the burner, a finite volume first order up- and downwind approach is compared to respective third- and fourth-order discretization approaches. In the last part of the paper, the suggested plant model is identified and compared to measurement data.

2 Hybrid plant model

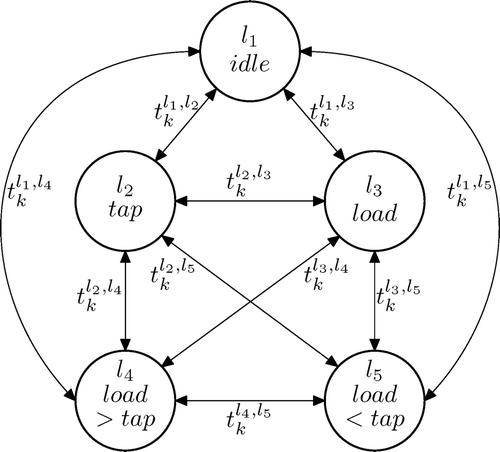
The discrete plant dynamics is characterized by switching events due to tapping and loading, which drive the underlying dynamical behaviour of the heat exchanger, the burner, and the storage tank 11. The discrete-event dynamics is fully described by a finite state automaton of five discrete states and their respective transitions. These states represent the operational modes of the plant and are distinguished as follows: idle state, loading state, tapping state, and the combined state of tapping and loading. Thereby, the operational mode where tapping and loading occurs simultaneously has to be divided into two discrete states depending on the resulting direction of the plug flow in the tank. The underlying continuous-time dynamics is characterized by time-varying spatial temperature profiles in the storage tank, the heat exchanger, and the burner. These components are modelled by six quasi-linear PDEs for the six state variables, namely the temperature T(z,t) in the storage tank, the primary and secondary side temperatures Θ_pr(x,t) and Θ_sec(x,t) in the heat exchanger, and the primary side, wall, and secondary side temperatures τ_pr(ζ, t), τ_w(ζ, t), and τ_sec(ζ, t) in the burner. These temperature profiles depend on the spatial coordinates z, x, and ζ as well as on time t. In the subsequent section (2.1), the finite state automaton is introduced, followed by a description of the distributed energy balances for the heat exchanger, the burner, and the storage tank in Sections 2.2–2.4.

2.1 Discrete state automaton

A finite state automaton can be denoted as a labelled transition system, described by a triple (L,A,E), where L is the finite state space, A is a finite set called alphabet, and E is the corresponding transition rule 2. A sequence (l ₀, a ₀, l ₁, a ₁, … , l _N−1, a _N−1, l _N ) with (l _m , a _m , l _m+1) ∈ E for m = 1, 2, … is called a trajectory on the state space 2. Using this notation, the state space of the finite state automaton of the storage tank is given by

The graph of the resulting finite state automaton is depicted in Figure 3. Note that depending on the tapping and loading mass flows during the states l ₄ and l ₅, the resulting plug flow in the storage tank is either positive, i.e. directed from top to bottom, or negative, i.e. from bottom to top. For an appropriate choice of the numerical approach, the separation of these two states is of great relevance. The alphabet of the finite state automaton 2 is labelled by implicitly caused discrete switching times (due to a tapping or loading event) denoting the transitions from one state l _m to another state l _n , i.e.

Figure 3. Graph of the finite state automaton describing the operational modes of the plant. For the sake of simplicity, transitions are labeled only unidirectionally, i.e. for each there exists a corresponding transition .

With Equations (1) and (2), the general transition rule can be derived to be 2, i.e. is an example for a possible trajectory on the discrete state space L in dependence of the events occurring.

2.2 Distributed parameter model of the heat exchanger

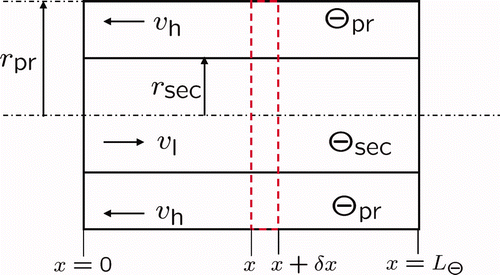
The counter current heat exchanger is modelled by a set of two coupled first-order partial differential equations 8,12, each comprising a convection and a source term accounting for the heat exchange between the primary and the secondary side of the system. Therefore, a pipe-in-pipe system with length L _Θ is used to model the primary (outer pipe) and the secondary side (inner pipe) of the heat exchanger (see Figure 4). The separating wall between the two pipes is assumed to be negligibly thin, such that heat conduction along and through the wall is neglected. Setting up the energy balance for an infinitesimally small volume element with length δx and applying a Taylor series expansion for the element bound at x + δx yields the model equations of the heat exchanger for δx → 0. The resulting equation for the primary side is

Figure 4. Sketch of the counter current heat exchanger with primary and secondary side temperature profiles Θ_pr(x,t) and Θ_sec(x,t) as well as the respective flow velocities v _h(t) and v _l(t).

Accordingly, the energy balance of the secondary side is given by

As shown in Section 4, the heat transfer coefficient α between the two heat exchanger pipes in Equations (3) and (4) is obtained by minimizing the least squares error between model and measurement data. Therefore, the geometry of the pipes is chosen to match the transfer area and the primary and secondary side volumes of the heat exchanger. The Dirichlet boundary condition (BC) at x = 0 reads as

and analogously at x = L _Θ as

The initial conditions (ICs) in the pipes are

Here, , which means that the heat exchanger model is activated during the discrete states l ₃, l ₄ and l ₅.

2.3 Distributed parameter model of the burner

This section first summarizes the operating principle of the condensing boiler, followed by the presentation of the distributed parameter model of the burner. A fan feeds the combustion chamber of the burner with an air mass flow proportional to the fan speed (n _F(t)) (see Figure 5). The respective gas mass flow is adjusted by a mechanical λ – control, which guarantees optimal combustion in the burner. Here, the combustion chamber is referred to as the primary side of the burner. The burning gas is then used to heat up the water in the secondary side of the burner. The model of the burner is therefore set up in accordance to the counter current principle used for the heat exchanger in Section 2.2. Due to the thickness of the walls in the burner, i.e. the separating wall between the primary and secondary side, the structure in Equations (3) and (4) has to be extended by an additional PDE for the wall. As depicted in the sketch in Figure 5, the actual model of the burner is split up into two parts. The first part consists of two algebraic relations to determine the flow velocity v _g(t) and the primary side feed-flow temperature as a function of the fan speed n _F(t) according to

and

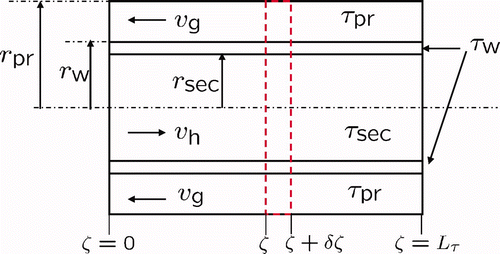
Figure 5. Setup of the burner composed of the fan with the fan speed n _F and the heat exchanging unit (pipe system) with the primary and secondary side temperatures τ_pr(ζ, t) and τ_sec(ζ, t) as well as the respective flow velocities v _g(t) and v _h(t).

The parameters v _g,max and p _{1, … ,4} are determined by minimizing the least squares error between simulations and measurement data, i.e. all effects of combustion are summarized in . Equations (8) and (9) are employed to calculate the respective primary side inputs of the second part of the burner model, i.e. the dynamical part (the pipe system) which can be interpreted as a counter current heat exchanger with a dividing wall, as depicted in Figure 6. Setting up the energy balance for the volume element δζ and following the procedure in Section 2.2 yields the model equations for the primary side,

the wall,

and the secondary side,

Figure 6. Sketch of the heat exchanging part of the burner with the primary side, wall, and secondary side temperatures τ_pr, τ_w, and τ_sec as well as the respective flow velocities v _g(t) and v _h(t).

The boundary conditions at the inlets of the primary and secondary side are

The ICs read as

In the sequel, the IC of the wall τ_w(ζ, ) is chosen to be the arithmetic mean between the temperatures of the primary and secondary side. Note that due to the significant length of the pipe system in the burner, heat conduction within the wall is negligible. The coefficients of the exchange terms in Equations (10)– (12), i.e. γ_pr, γ_sec, q _pr and q _sec, are also obtained by an optimization-based parameter identification. The optimization result is presented in Section (4).

2.4 Distributed parameter model of the stratified storage tank

The governing model equations of the storage tank can be obtained following the derivation of the heat exchanger and burner equations. Due to the large diameter of the storage vessel, flow velocities are significantly smaller than in the heat exchanger. Therefore, it is necessary to extend the partial differential equation by a conductive component which is set up according to Fourier's heat conduction 13. Further, the BCs have to be expanded to Cauchy BCs to model the heat loss through the ceiling and bottom of the storage tank. The resulting temperature distribution in the stratified storage tank can be described by the following PDE with BCs and a respective IC according to

with ΔT = T – T _amp, the density and heat capacity of water ρ(T) and c(T) as well as the loading and tapping velocities v ₁(t) and v _d(t). Note that due to the high Peclet numbers of about 5 · 10⁶, the temperature dependency of ρ, c and λw is negligibly small in the considered range of operation. The respective starting and end times are defined as . Equations (15)– (18) hold for the discrete states l ₂ – l ₅. Further note that due to the occurrence of complex free convection phenomena in the state l ₁, this case is not analysed further in this contribution. The notation for the loading and tapping velocities and the resulting plug flow velocity v(t) = (v(t) – v _d(t))/ā can be inferred from Figure 7, where the parameter ā describes the ratio between the cross-sectional areas of the storage tank and the heat exchanger pipes. For the presented model, the parameter λ_w(T) only covers the heat conduction due to intermolecular transport, i.e. λ_w = λ_w,mol. Note, however, that due to the forced convection, macroscopic back-mixing phenomena are present at the storage wall and contribute to the heat conduction coefficient such that the actual λ_w > λ_w,mol 14.

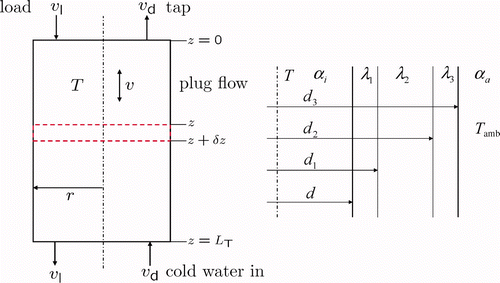
Figure 7. Left: labeled scheme of the storage tank with respective in- and outflow velocities v _l,d(t) and the resulting plug flow velocity v(t). Right: cross section of the storage wall with corresponding diameters d _m , m = 1,2,3, heat conduction coefficients λ _m , and heat transfer coefficients α _n , n∈{i, a}.

The general hybrid I/O-behaviour of the plant is on the one hand dominated by uncertain tapping events driven by the consumer and on the other hand based on the loading events initiated by a respective process control strategy. These events determine the in- and outflows of the storage tank. Consequently, the model equations depend on the corresponding discrete states in L and may furthermore be simplified significantly. This concerns especially the BCs (16)–(17) of the stratified storage tank. The reduction for the relevant discrete states in L is summarized below and can be easily incorporated in the respective equations according to

2.4.1 Model parameters

In the sequel, the derivation of the heat transfer coefficient of the storage tank is outlined. The derivation of the respective coefficient is hereby based on physical relations. As shown in Figure 7, the storage wall consists of three material layers with different heat conductivity. The coefficient k _w is therefore composed of the convective heat transfer in water and air, the heat conduction in each of the three wall layers and the radiative heat at the outside wall of the tank. According to 13, the equation for the heat transfer coefficient k _w of a wall with various layers and an inner wall diameter d is given by

with d _m and λ _m denoting the m‐th diameter and the m‐th conductivity, see Figure 7, right. Inside the tank, the heat transfer coefficient reads as α_i(T,v) = Nu λ_w/d, with the corresponding Nusselt number Nu(T,v) = (49,028 + 4,173Pr v(t) d ²/(νL _T ))^0,333 for water, assuming laminar flow and sufficient friction between the fluid and inside wall of the tank 15,16. The heat transfer coefficient at the outside wall of the tank is composed of a convective and a radiant part yielding α_a = α_convection + α_radiation. The convective part can be calculated by α_convection = Nu λ_air/LT with the Nusselt number

at the ambient and the Rayleigh number 13

The radiative heat transfer is governed by

with the emission ratio ϵ 15. The derivation of these equations assumes that the outside wall temperature is approximately equal to the ambient temperature. This can easily be affirmed for sufficiently good isolation. For a profound discussion on the appropriate choice of parameters for different materials and geometries, the reader is referred to 16.

3 Numerical simulation of the hybrid plant model

This section illustrates the numerical setup of the hybrid plant model for the discrete states l ₂ – l ₅. Due to the hyperbolic nature of the PDEs during tapping and loading, the discretization of the convection terms plays a major role for numerical simulation studies. Hence, different discretization schemes are investigated in terms of accuracy and resulting model dimension of the discretized lumped model. The first part of this section considers the discretization of the storage tank model. Here, the reconstruction of sharp spatial transitions, as they are present in the stratified storage tank, is of great interest. Therefore, a finite volume up- and downwind scheme in dependence of the flow direction as well as a high resolution scheme, a so-called slope limiter scheme 17, are investigated. The second part of the section gives a brief discussion on the discretization of the heat exchanger and burner model where up- and downwind schemes of different approximation orders are used.

3.1 Discretization of the storage tank equation

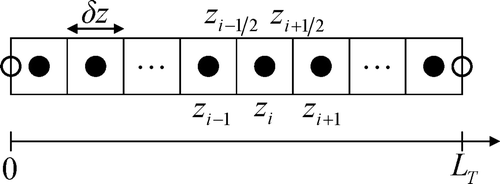
A method of lines (MOL) approach 18 is employed for the spatial discretization of the model Equation (15). The temperature distribution in z – direction is approximated by clustering the spatial domain in N _T finite volumes, see Figure 8. The centre of the i‐th volume is denoted by z _i and the volume bounds as , respectively. Integration of (15) over a control volume yields

Figure 8. Finite volumes of discretized boundaries (ˆ) and PDE (•).

For the evaluation of the integral (23), certain assumptions are made. Choosing the coefficients λ_w, ρ, c, k _w and the temperature T to be constant within the interval z  ∈ [z _i−1/2, z _i+1/2] and with δz = z _i+1/2 – z _i−1/2 = const, entails the discretized version of the storage PDE (15), i.e.

As mentioned before, special effort has to be spent to find an appropriate approximation of the convective terms. The various approaches mentioned previously are generally represented by the following substitution for the control volume bounds T ^i±1/2 according to

where Φ denotes the so-called limiter function 17,19. Consequently, for v > 0, the spatially discretized PDE (15) results as

In Equation (29), the well-known upwind scheme is obtained by setting the limiter function Φ ^i+1/2 = Φ ^i−1/2 = 0, whereas the corresponding downwind scheme can be obtained for Φ ^i+1/2 = Φ ^i−1/2 = 2 18. Since the plug flow velocity in the storage tank changes sign, Gibb's phenomenon 20 has to be avoided by employing the upwind scheme for v > 0 and the downwind scheme for v < 0, i.e. the choice of the numerical scheme depends on the flow direction and therefore also on the discrete state of the finite state automaton. The so-called central difference scheme (CDS) is obtained by setting Φ ^i+1/2 = Φ ^i−1/2 = 1. The performance of the previously named approaches changes significantly for different spatial resolutions, especially for the upwind scheme. However, due to numerical diffusion, this approach is not feasible for the reconstruction of sharp spatial transitions. As opposed to the upwind scheme, the CDS perfectly reconstructs sharp transitions of the spatial profile. Unfortunately, this discretization method leads to the occurrence of spatial oscillations and therefore to an unsatisfactory result. The idea of a high resolution slope limiter scheme is now to combine the benefits of the previously named methods, i.e. oscillation-free reconstruction of sharp transitions. This can be realized by defining Φ as a nonlinear function of the so-called smoothness , which in turn is defined as

for the corresponding flow directions. In the literature, many limiter functions can be found 19,21. Numerical tests were performed for a number of limiter functions, such as the monotonized centred, Van Leer, Koren, and Superbee limiters 17,19,21. For the purpose of reconstructing sharp spatial transitions, the Superbee limiter with the limiter function

yields the most promising results (see Section 4). It is furthermore worth noting that the presented discretization schemes are conservative 19.

3.2 Discretization of the heat exchanger and burner equations

Similar to the spatial discretization of the stratified storage tank, a MOL approach is used for the discretization of the heat exchanger and the burner. Due to the similarity of the system structure and the occurring spatial temperature profiles in the heat exchanger and the burner, the subsequent considerations are outlined on the basis of the heat exchanger model in Equations (3) and (4) but are then used for the discretization of both the heat exchanger and the burner. The following three discretization approaches adopted from 18 are investigated:

Hereby, a classical first-order up/downwind scheme is used for the calculation of the boundary values in Equations (33) and (34), while the forth-order approach is based on a special higher order up- and downwind approximation of the boundary conditions (referred to as “Subroutine DSS020” in 18).

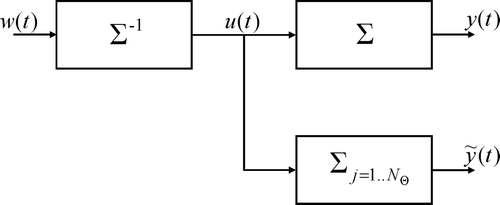
To classify the transient and stationary performance of the different discretization orders, a respective reference trajectory has to be specified. This can be done using an analytical solution of the PDE. However, the analytical solution is generally not known or difficult to evaluate. For the special case of the heat exchanger, the analytical solution includes infinite sums of Bessel functions 22. Their evaluation is costly and only possible to a certain accuracy. Hence, an alternative approach is suggested for cases, where an exact inversion of the PDE considered is available 6. The procedure is then as follows: a desired trajectory w(t) which is dynamically feasible on one hand and which covers the transient and the stationary behaviour of the process on the other hand has to be chosen. With the use of an exact inversion Σ⁻¹ of the system Σ, a feedforward control u(t) can be calculated, i.e. u(t) = Σ⁻¹ w(t) 15. Then w(t) can be used as the respective reference trajectory when the calculated feedforward control is applied to the system Σ, i.e. y(t) = Σu(t) = ΣΣ⁻¹ w(t) and therefore (see Figure 9). 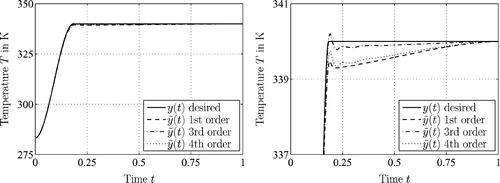Substituting the distributed system Σ by its discretized counterpart yields the distorted output trajectory , which is then used for the assessment of the discretization scheme. For the explicit case of the heat exchanger model, the performance is depicted in Figure 10. The inversion of the heat exchanger model is hereby obtained according to the methodology described in 6. Figure 10 further shows that the minimum variation between the desired and distorted trajectory can be obtained using the 3rd order discretization scheme. This means that for the considered range of operation, the different approximation of the boundary values in Equation (35) leads to an overall degradation of the 4th order scheme compared to the 1st and 3rd order approach. Hence, the 3rd order scheme according to Equation (34) is used for the spatial discretization of both, the heat exchanger and the burner model.

Figure 9. Structure for the classification of discretization schemes using exact system inversion of the distributed parameter system Σ.

Figure 10. Left: transient and stationary distortion due to spatial discretization of the heat exchanger PDE using N _Θ = 50 compartments. Right: magnified version showing the transition between the transient and stationary region.

3.3 Simulation results of the hybrid plant model

The discretized plant model, i.e. burner, heat exchanger, and stratified storage tank, is implemented in a MATLAB/SIMULINK environment 23, allowing for the numerical simulation of the plant and the examination of its hybrid behaviour. The implementation is set up in a flexible manner, such that all types of scenarios which can possibly occur in the course of the plant operation may be studied. 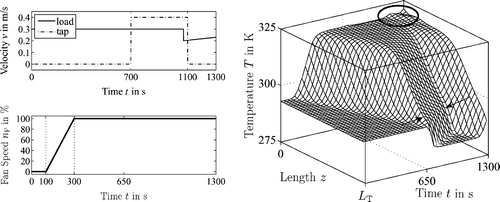1 Figure 11 shows the simulation result of the temperature profile T(z,t) in the storage tank for various variations of the flow velocities v _l,d and the fan speed n _F. Hereby, the simulation scenario covers the following effects: at t = 0 s the storage tank has an initial temperature profile with T(z,0) = 293 K. During the time interval 0 s ≤ t < 700 s, the storage tank is operated in the discrete state l ₃ with a ramp-like rise of the fan speed n _F for 100 s ≤ t ≤ 300 s and a loading velocity v _l = 0.3 m/s, according to the solid lines in Figure 11. It can be seen that due to the wall and the circular setup of the heat exchanger and the burner, the ramp-like increase of the fan speed results in a smooth rise of the feed flow temperature at z = 0. Due to the tapping event occurring during the time interval 700 s ≤ t ≤ 1100 s, cold water is introduced at z = L _T . Note that in this case, the discrete state automaton is in state l ₅, where the tapping flow velocity v _d exceeds the loading flow velocity v _l, i.e. the plug flow reverses and the tank discharges. Hereby, the transitions between the discrete states l ₃ and l ₅ are denoted by the arrows in Figure 11. At t = 1100 s, the state automaton switches back to the state l ₃ and the storage tank gets refilled. For this latter case, the variation of the loading velocity for t ≥ 1070 s is chosen such that the variation of the feed flow temperature at the top of the storage tank is kept inside a certain band. The respective region is marked by a circle in Figure 11.

Figure 11. Simulation results of the plant model for loading and tapping scenarios. Top left: tapping and loading velocities v _d and v _l. Bottom left: variation of the fan speed n _F. Right: 3D temperature profile T(z,t) of the storage tank.

4 Model identification

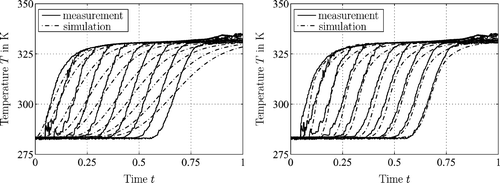
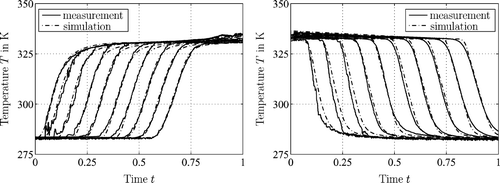
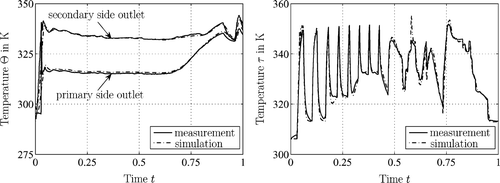
In this section, the hybrid plant model is identified via least squares optimization using measurement data obtained for the operational modes l ₂ and l ₃. The datasets of the heat exchanger, the burner, and the storage tank are presented and compared to the respective simulation results. Thereby, the discretization scheme and the required number of grid points for the storage tank model are furthermore discussed and determined. It shall be emphasized that the subsequent plots rely on a normalized time scale. Figure 12 shows the identification results for the heat exchanger and the burner. It can be inferred from the plots that the heat exchanger and the burner model are feasible to track the measurement data very well for both, the stationary and the transient regions. To identify the storage tank model, ten equidistantly distributed thermocouples are attached from top to bottom on the inside wall of the tank. The numerical simulations of the upwind scheme (Figure 13) and the slope limiter scheme using a Superbee limiter (Figure 14) are compared to corresponding measurement data. In the case of the upwind scheme with a spatial discretization of 20 nodes, the model reconstructs the measured values very poorly. However, by increasing the spatial discretization up to 300 nodes, a far better fit can be achieved. Even though better results are attained by increasing the spatial resolution of the upwind scheme, numerical diffusion is still present, see Figure 13. As illustrated in Figure 14, the slope limiter scheme bears significant improvements for the loading scenario. It is furthermore shown that applying the high resolution scheme with Superbee limiter to the tapping state where hot water is taken from an entirely filled storage cell, the measured and simulated values agree very well. Note that for the high resolution scheme, a spatial discretization of only 21 grid nodes is sufficient.

Figure 12. Left: plot of the measured and simulated outlet temperatures of the primary and secondary side of the counter current heat exchanger. Right: measured and simulated temperature profiles at the secondary outlet of the condensing boiler.

Figure 13. Measured and simulated temperature profiles for a loading scenario, using an upwind difference scheme for discretization of the PDE with N _T  = 20 grid points (left) and N _T  = 300 grid points (right).

Figure 14. Plot of the measurements and simulations using the Superbee limiter and N _T  = 21 grid points for the discretization of the PDE. Left: loading scenario l ₃. Right: tapping scenario l ₂.

5 Conclusion and outlook

In this paper, the derivation of a hybrid model of a domestic heating system comprising a condensing boiler (burner), a heat exchanger, and a stratified storage tank is outlined. Thereby, the model parameters of the burner and the heat exchanger are obtained by minimizing the least squares error between the simulation results and measurement data. The derivation of the storage tank parameters are based on physical considerations. To perform numerical simulations, different discretization schemes according to the method of lines approach are investigated in terms of feasibility and numerical performance. It is hereby shown that for the storage tank, where sharp spatial temperature gradients are present, the high resolution slope limiter scheme with Superbee limiter outperformed the up-/downwind scheme and the CDS. It is further found that a third-order up-/downwind scheme is well suited for the discretization of the heat exchanger and the burner. The good agreement between the measurement data and simulation results for stationary and transient scenarios justifies the suitability of the suggested models of the burner, the heat exchanger, and the stratified storage tank. Consequently, this model can be used to study the challenging task of advanced process control design for domestic heating systems with stratified storage tank as an example for a hybrid distributed parameter system 24. Future research is necessary to model the free convection phenomena occurring in the course of the discrete state l ₂ of cooling.

Notes

Revised and expanded version of a paper presented at the 5^th Vienna International Conference on Mathematical Modelling (5^th Mathmod), Vienna, Austria, 2006.

1. The MATLAB - ode23tb solver is used for the time-integration of the discretized PDEs.