To what extent are students expected to participate in specialised mathematical discourse? Change over time in school mathematics in England

ABSTRACT

From a discursive perspective, differences in the language in which mathematics questions are posed change the nature of the mathematics with which students are expected to engage. The project The Evolution of the Discourse of School Mathematics (EDSM) analysed the discourse of mathematics examination papers set in the UK between 1980 and 2011. In this article we address the issue of how students over this period have been expected to engage with the specialised discourse of school mathematics. We explain our analytic methods and present some outcomes of the analysis. We identify changes in engagement with algebraic manipulation, proving, relating mathematics to non-mathematical contexts and making connections between specialised mathematical objects. These changes are discussed in the light of public and policy domain debates about ‘standards’ of examinations.

KEYWORDS:

• specialised discourse
• mathematical discourse
• examinations

Introduction

Politicians, university mathematicians and the media in many countries are prone to make pronouncements about changes in the quality of school mathematics. These claims are often based on anecdotal evidence or upon the basis of uncritical or flawed interpretation of changes in success rates in national examinations or rankings in international surveys such as the Programme for International Student Assessment (PISA). It is, however, notoriously difficult to make comparisons over time of the quality of student experience and learning as curricula, forms of pedagogy and the assessment instruments themselves have all changed, while the students themselves and the classrooms in which they have learnt are no longer available for us to study. The project The Evolution of the Discourse of School Mathematics (EDSM) has sought to investigate change in school mathematics in England over the last three decades of curriculum and assessment reforms, developing a methodology that uses high-stakes public examinations taken by students at the end of compulsory schooling as a window onto school mathematics. These examinations are taken to represent the nature of the mathematics that school students are expected to participate in. The assumption that examinations provide us with a valid window onto students’ curricular experience is justified by the strong influence that such high-stakes examinations are known to have on the classroom implementation of curriculum (Broadfoot, 1996). In this article we will present some of the findings of the EDSM project, focusing on changes in the ways in which examinations set at different times have expected students to engage with specialised mathematical forms of discourse. The first year of examinations included in our study is 1980; the ‘Ordinary Level’ examinations in this year have been taken as a base line immediately before the publication of the Cockcroft report (DES, 1982) and the subsequent reforms to the curriculum and assessment in England that resulted in the introduction of the General Certificate of Secondary Education (GCSE) examinations in 1988. Other years were chosen in order to attempt to capture the effects of changes in policy and practice during the period. Details and explanation of our data set, including the reasons for selecting eight specific years from 1980 to 2011, are given in Morgan and Sfard (this issue).

Mathematics in general and school mathematics in particular are specialised practices with ways of communicating, including ways of reasoning, that are distinctive. It is thus possible to speak of mathematical discourse as the forms of communication used in mathematical practices. In the EDSM project, we have adopted a discursive perspective established by Sfard (2008) that identifies doing mathematics with participating in mathematical discourse. Learning mathematics is conceptualised as learning to communicate in ways that are recognisably mathematical. By studying the forms of discourse in high stakes examinations taken at the end of compulsory schooling, we thus gain insight into the nature of the participation in mathematical practices that is expected of school students. A fuller discussion of the theoretical foundations of the project is given in Morgan and Sfard (this issue).

This discursive perspective is opposed to that found in most research related to the language of examinations, which tends to conceive of language as an obstacle or barrier that prevents some students from accessing the mathematics. For example, researchers have attempted to identify how the presence of various linguistic and other textual features affect the difficulty of mathematics test questions. The features studied have included: specialised vocabulary and complex grammatical structure (Abedi & Lord, 2001; Barbu & Beal, 2010; Shaftel, Belton-Kocher, Glasnapp, & Poggio, 2006); use of passive verb forms and impersonal presentation of problems (Abedi & Lord, 2001); item structure (Fisher-Hoch, Hughes, & Bramley, 1997); interactions between vocabulary, context and cultural aspects (Pollitt, Marriott, & Ahmed, 2000); spatial lay-out of questions (Crisp & Sweiry, 2003). Such research and the use made of it by the examination boards in designing examination questions tends to be based on the assumption that simplifying the language makes it easier for students to access a question but leaves the mathematics essentially unchanged, although studies investigating performance of second language learners and students with learning difficulties suggest that the assumption that simplifying the language improves access is not universally valid. For example, Shaftel et al. (2006) report that these groups are not disproportionately affected by the presence of linguistic features such as passive voice in mathematics tests. While accepting that simplifying the language (or changing it in other ways) may make a question more accessible, we reject the dualism that separates mathematics and language. The notion that some linguistic difficulties can be removed because they are ‘construct-irrelevant’ is flawed. Instead we argue that, however carefully linguistic changes are made by those designing examination questions, changing the language inherently changes the nature of the mathematics that the student is expected to engage with. The aim of our analysis is not, therefore, to determine whether examinations have changed in difficulty (either linguistic or mathematical) but to understand how the practice of school mathematics itself may have changed.

Sfard (2008) characterises mathematical discourse as comprising four aspects: vocabulary and syntax; visual mediators; routines; endorsed narratives. We have taken these four aspects as a starting point for structuring our scheme for analysing the nature of the mathematics in examination papers. In this article we present a part of the analysis, focusing in particular on the extent to which the examinations make use of specialised school mathematical discourse as opposed to colloquial or everyday discourse. In the next section we define the components of specialisation included in this analysis and outline the analytical tools used and the overall approach to analysis. We then present some of the results of the analysis, addressing the question of whether expectations about student participation in specialised school mathematical discourse have changed over the period of our study and, if so, in what ways. Finally, we discuss the implications of these results and consider how they contribute to debates about changing standards in school mathematics.

Method of analysis

According to social semiotics, the way in which language and other modes of communication is used functions to construe our experience of the world. This construal is what Halliday (1978) terms the ideational metafunction of language. A fundamental way in which the ideational metafunction is realised in the lexicogrammar¹ of texts is through the system of transitivity, that is, through the processes and the actors (both human and non-human) in those processes (Halliday, 1985). By investigating the nature of the processes included in a school mathematics text and the objects and/or people that are actors in those processes we may construct a picture of how that text construes the nature of mathematics: What are the objects of mathematics? What activities are considered to be mathematical? In what ways may humans be actors in mathematical activities? (Morgan, 2006).

Our investigation of the lexicogrammar of the discourse of mathematics examinations focuses on the extent to which the objects and processes present in examination texts are specialised objects and processes, defined and used in ways distinctive to school mathematical practices, hence construing school mathematics as a specialised practice. Conversely, we also consider the extent of extra-mathematical content in the form of non-mathematical contextualisation of examination questions.

A further significant characteristic of specialised mathematical discourse is objectification. Objectification is described by Sfard (2008) as a process by which speaking about our experience creates metaphorical objects (such as conception or learning disability or function) that then appear to have an independent existence akin to that of material objects. Sfard identifies two components of the objectification of mathematical discourse: reification, a term that refers to the movement from speaking about processes to speaking about objects, and alienation, the presentation of phenomena as if they occur independent of human action. Within the EDSM project we have considered alienation to contribute to the construal of the origin of mathematical knowledge (addressing the place of human beings in mathematical activity). This characteristic is therefore included in a different section of the analytic scheme, discussed in Morgan (this issue). In this article, our analysis of objectification includes attention only to the reification component. We have identified instances of reification as specialised words that encapsulate processes into an object. One way in which reification occurs is through use of nominalisation, identified by Halliday (1993) as a phenomenon used extensively in scientific discourse. Nominalisation is a ‘grammatical metaphor’ by which a process word is transformed into an object word. For example, the active process reflect is reframed as the object reflection. Additionally, Sfard (2008) points out that many specialised mathematical objects, such as function, sequence and even number words, also contribute to the reification of mathematical discourse.

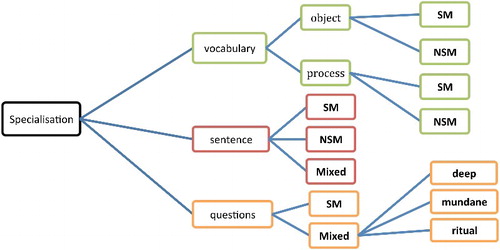
Table 1 shows the part of the analytic scheme developed in the EDSM project that was used to investigate these aspects of specialised mathematical discourse in the examination papers. We will discuss these properties of specialised mathematical lexicogrammar further in the following sections of this article, together with some of the results of the analysis. The extract in Table 1 illustrates the structure of the complete scheme: for each discourse property, one or more subsidiary research question is posed to guide the analysis and textual indicators are identified that enable us to identify instances of the property in the examination texts. (See Morgan and Sfard in this issue for the complete analytic scheme.)

Table 1. Extract of the EDSM analytic scheme: specialisation and objectification.

Property of the discourse	Subsidiary research questions	Textual indicators
Specialisation	To what extent is specialised vocabulary used?	lexical items used in accordance with mathematical definitions or in ways distinctive to school mathematics, considered at the level of: vocabulary sentence text unit (question) extra-mathematical context depth of engagement with context
Reification of the discourse	To what extent does the discourse speak of properties of objects and relations between them rather than of processes?	nominalisation: use of a ‘grammatical metaphor,’ converting a process (verb, e.g. rotate) into an object (noun, e.g. rotation) the use of specialised mathematical nouns such as function, sequence which encapsulate processes into an object

Codes were developed for each of the textual indicators. For example, considering the property of specialisation at the level of vocabulary, nouns and verbs within each examination paper were allocated to one of the codes School Mathematics (SM) or Non-School Mathematics (NSM). At the levels of sentence and question, an additional code Mixed was introduced to account for longer pieces of text that incorporated both specialised and non-mathematical aspects. The definitions of these codes are elaborated in the next section. The depth of engagement with the non-mathematical context at the level of question was then additionally coded as deep, mundane or ritual (see section 4 for definition of these terms). The coding tree for specialisation of the discourse was thus as shown in Figure 1.

Figure 1. Coding tree for specialisation.

Initially, one of the authors coded the full data set. A sub-sample was then coded independently by the second author. Inter-rater reliability was not computed because discrepancies were discussed and resolved, resulting in redefinition of some codes in order to tighten the descriptions; review and recoding of the data set was then done by the two authors in consultation with one another. Using NVivo, we were able to interrogate the data, both obtaining quantitative summaries (e.g. How many specialised SM nouns occurred in the examinations in each year?) and extracting sub-sets allocated to particular codes (e.g. the set of all verbs coded as specialised to School Mathematics). In the next section, we discuss the definition and application of the coding at the level of vocabulary, then present some of the results of the analysis.

Specialised vocabulary

The use of specialised vocabulary is probably the most obvious characteristic of mathematical discourse. While we have argued that over-emphasis on vocabulary results in an impoverished view of mathematical discourse (Morgan, 2005), nevertheless the use of specialised vocabulary is an essential component of specialised mathematical activity. When an object or a process is named, that object or process becomes available for our mathematical thinking. The first measure of specialisation of the language is thus taken to be the objects and processes present in the text, coded at the level of vocabulary as specialised to the discourse of school mathematics or non-specialised. A word is coded as specialised to the discourse of school mathematics (SM) if:

1. it has a mathematical definition and is used in accordance with that definition; for example, in the statement The centre of the hexagon is O, the terms centre and hexagon are both coded as SM.

   or

2. it is widely used in mathematics classrooms and learning materials and is located in a segment of text distinctive to school mathematics; for example, the process find in the text segment find the value of … is coded as SM.

Symbolic expressions for objects (e.g. algebraic expressions, equations and names for geometric objects such as O in the example given in a) above) were also coded as SM. An equation may be considered either as a single object or as a complete sentence in its own right. We have chosen to consider all equations only as objects for the purposes of this part of the analysis. Other objects and processes were coded as non-specialised (NSM). Non-specialised vocabulary mainly included terms used in colloquial or everyday ways, generally found in questions involving non-mathematical contexts. For example, a question on statistics started with the sentence:

The table gives some information about the delays, in minutes, of 80 flights. (Edexcel GCSE Mathematics (Linear), Paper 3 Higher Tier, June 2010, question 22)

In this sentence the objects delays and flights were coded as NSM, while table, information and minutes were coded as SM. Clearly in this example each of the object words coded as SM may also occur in everyday discourse. However, we would argue that the way they are used in the context of this examination question is distinctive to school mathematics. In particular, there is an expectation that students will make use of these objects to perform mathematical actions: extracting numerical information from the table and calculating with it, giving answers in minutes.

In a small number of questions there were also words from other specialised discourses. For example, a question involving calculating upper and lower bounds started:

The voltage V of an electronic circuit is given by the formula V = I R where I is the current in amps and R is the resistance in ohms. (Edexcel GCSE Mathematics (Linear), Paper 4 Higher Tier, June 2010, question 26)

In this question, the words voltage, circuit, current, resistance and ohm may be considered part of a specialised scientific discourse but they are not part of school mathematics discourse and knowledge of them is not essential to successful engagement with the question. Although not part of everyday discourse, for the purposes of this study we have coded these scientific terms as non-specialised (NSM).

Although we used NVivo to support the coding and interrogation of the data, the process of coding was done almost entirely manually as in many cases decisions about whether a particular word may be considered specialised or non-specialised can only be made within the context of its use. For example, the object line is considered specialised in the following text:

The line passes through the point (2,4).

but not here:

John passed the finish line in 12.2 seconds.

Specialised words do not stand by themselves but may be incorporated into sentences and into whole questions that may be characterised as specialised school mathematical or mixed, involving both specialised and non-specialised discursive features. There are also sentences that are entirely non-specialised, containing no specialised vocabulary. In this section, we present some results of the analysis of specialisation at the level of vocabulary. In section 4 we look at the extent of specialisation at the level of whole questions.

The charts in Figure 2 show the extent of specialisation of the vocabulary in the examination papers for each year in our data set. They are based on a simple categorisation of objects (nouns and nominal groups) and of processes (verbs) as specialised to school mathematics (SM) or non-specialised (NSM). The specialised objects also included those given in symbolic mode such as variable names, algebraic expressions and equations. The earliest examinations in our data set, sat in 1980 before the major reform of the examination system, stand out with a higher proportion of SM vocabulary: 63% of objects and 55% of processes. Apart from this pre-reform year, the proportions show relatively little variation with specialised vocabulary comprising between 44% and 53% of the objects and between 39% and 45% of the processes. The results of a two-tailed Z-test, shown in Table 2, were used to compare the proportions of specialised objects and processes in 1980 to those in each other year. The proportions of both specialised objects and specialised processes in 1980 were significantly greater than in each of the other years (p < 0.01 in every case). The year with the lowest proportion of specialised vocabulary (both objects and processes) was 1991, the first year in our data set after the full implementation of the National Curriculum and GCSE examination system. The Z-test results in Table 2 confirm that the proportion of specialised objects in 1991 was significantly lower than 1980, 1987, 1999 and 2004 (p < 0.01 in each case). Other comparisons were not significant at the 1% level.

Figure 2. Proportions of specialised school mathematics and non-specialised objects and processes: (a) Proportions of object words specialised to school mathematics and non-specialised objects; (b) Proportions of process words specialised to school mathematics and non-specialised processes.

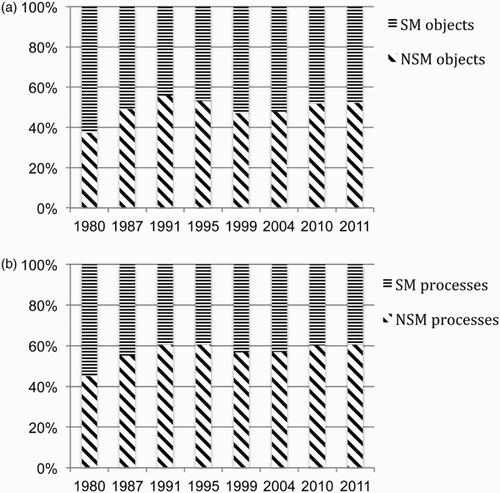
Table 2. Proportions of specialised vocabulary – objects and processes.

	1980	1987	1991	1995	1999	2004	2010	2011
proportion of specialised objects	0.63	0.51	0.44	0.47	0.53	0.52	0.48	0.48
Z-score comparing each year to 1980	…	5.48	8.43	7.58	4.35	4.71	6.40	6.54
Z-score comparing each year to 1991	-8.43	-3.52	…	-1.39	-4.31	-3.93	-1.88	-1.73
proportion of specialised processes	0.55	0.45	0.39	0.39	0.43	0.43	0.40	0.39
Z-score comparing each year to 1980	…	2.76	4.15	4.40	2.99	3.04	3.90	4.05

In order to understand better what changes may have taken place in the nature of specialised school mathematics discourse, a more detailed comparison of the nature of the specialised vocabulary was conducted for a sub-set of three years taken from the data set: 1980 (pre-reform and most highly specialised), 1991 (least specialised) and 2011 (the most recent year in our data set). Lists of specialised objects and specialised processes for each of these years were extracted from the database. We consider each of these in more detail.

Specialised objects

The list of objects was first separated into those presented in purely symbolic form (including algebraic variables, expressions and equations and geometric objects named by labelled vertices) and those presented as words. The object words were then examined to identify distinct ‘school mathematics’ object words, some of which were modified in several ways (e.g. acute angle, right angle, angle of depression have all been included in the single distinct category angle).

As may be seen in Table 3, examination papers in 1991 contained a lower proportion of objects in symbolic form as well as having a lower proportion of specialised school mathematics objects as a whole compared to the other years. It might be thought that this indicated a lower expectation of student engagement in specialised mathematical discourse in this year. Indeed, the analysis of specialisation at the level of whole questions tends to support this conclusion, as a very high proportion of questions in 1991 were set in a non-mathematical context (see Figure 6 and the discussion of contextualised questions in section 4). However, it is also notable that students taking the examination in 1991 were expected to engage with a wider variety of mathematical objects. As may be seen in the final row of Table 3, the number of distinct specialised objects in 1991 exceeded the totals in each of 1980 and 2011 by more than 20%. In interpreting these figures, it is important to take into account the different length and structure of examination papers. Although the time allowed for each examination has remained relatively constant, more recent papers contain many more separate questions. In 2011, the number of distinct specialised objects per question was considerably lower than in the other two years considered here. Although the extent of distinct specialised objects that students were expected to deal with was similar in 1980 and in 2011, the density of such objects within individual questions (the number of distinct specialised objects per question) was lower, meaning that students were required to coordinate fewer distinct objects in order to engage with the question. The consequences of such lower density of specialised vocabulary are discussed in section 5 in the context of the analysis of objectification.

Table 3. Specialised objects – symbolic and verbal.

	1980	1991	2011
All SM objects (% of all objects)	553 (63%)	570 (44%)	507 (48%)
Objects in symbols (% of SM objects)	246 (44.5%)	179 (31.4%)	193 (38%)
Distinct SM non-symbolic object words (rate per question)	115 (3.19)	143 (3.11)	118 (1.30)

Of the distinct SM object words found in 1980, 1991 and 2011, only 41 were found in all three years. In each year, approximately 20% of the distinct objects were found only in that year. Of course, examinations inevitably contain only a sample of the content of the curriculum so we would expect there to be some variation in the specialised vocabulary. It is, however, clear that the variation between the two extreme dates also represents a change in the emphasis of the curriculum. Of those 39 objects found in 1980 but not in 2011, 17 were related to geometry (base, bisector, chord, corner, diagonal, elevation, hexagon, mid-point, pentagon, plan, point, rhombus, segment, six-pointed star, tangent, vertex) and two were related to statistics (bar chart, pie chart), while of the 35 objects found in 2011 but not in 1980, just two were related to geometry (polygon, prism) and 13 to statistics (class, distribution, histogram, interval, key, mean, median, mode, plots, probability, questionnaire, sample, survey). This is consistent with the inclusion of Handling Data in the National Curriculum from 1988 (DES/WO, 1988), which greatly increased the emphasis on statistics. Although the revised version of the National Curriculum introduced in 2000 (DfEE, 1999) attempted to reinstate some of the Euclidian geometry content omitted from earlier versions, it appears that this has not resulted in a return to the same level of expectation of student engagement with the specialised discourse of geometry.

Specialised processes

The lists of specialised processes in each of the three years were also compared. These included processes involving manipulation of mathematical objects (e.g. calculate, simplify, rotate) and processes involved in mathematical problem-solving, reasoning and communication (e.g. explain, prove, describe). The numbers of distinct specialised processes were very similar across the three years: 31 distinct words in 1980 and 30 in each of 1991 and 2011. In all three years, the majority of these words are imperatives, instructing students to carry out mathematical processes. A notable exception is the process give. Apart from a small number of instances of imperatives in which students are instructed to ‘give’ an answer, this verb was mainly found in the non-finite forms given that … , given by … , and giving … , used as a form of connective between mathematical statements. This usage was found extensively in the examination papers from 1980 (23 instances) and 1991 (11 instances), but only in three instances in 2011. The almost complete eradication of the use of give as a connective is consistent with a more general simplification of the complexity of the syntax of more recent examination papers. Although some forms of complexity are typical of mathematical discourse, the section of the EDSM analytic scheme dealing with specialisation focuses only on vocabulary. Syntactic and logical complexity are included in a separate section of the analytic scheme; some preliminary results were reported in Morgan, Tang, and Sfard (2011).

Across the three years considered here, 15 SM processes were found in all three years: calculate, construct, describe, estimate, express, factorise, find, give, make, represent, show, simplify, solve, take, work out. The frequencies of the most common of these are shown in Table 4.

Table 4. Frequency of the most common school mathematics processes found in 1980, 1991 and 2011.

	1980	1991	2011
Calculate	30	55	12
Find	31	36	14
Show	10	7	7
Simplify	5	1	8
Give	23	19	3
Prove	8	1	1
Solve	3	6	13
Work out	1	1	30

Although instructions such as find or work out do not specify the specialised nature of the mathematical processes expected, we have included them in this analysis because their use is characteristic of school mathematics discourse and the mark schemes for the examinations indicate that they are expected to prompt specialised mathematical activity by students. For example, of the four marks allocated for the question shown in Figure 3, one was given for demonstrating use of the calculation 1–(0.2 + 0.1 + 0.5) ‘or equivalent’ for part (a) and another for showing the calculation 800 × 0.2 for part (b) (Edexcel, Mark Scheme, June 2011, GCSE Mathematics (1380), Paper 4H).

Figure 3. Edexcel GCSE Mathematics (Linear) – 1380, June 2011, Paper 4 Higher Tier, question 1.

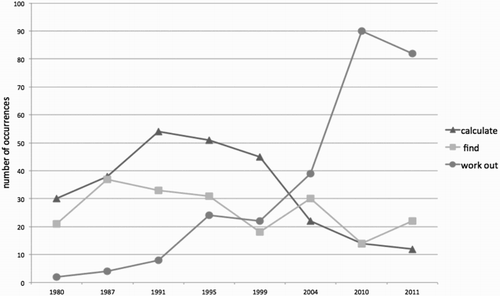
It is interesting to note the emergence of work out by 2011 as the dominant instruction to students, taking over much of the functions of calculate and find, more commonly used in the earlier years. Figure 4 shows how these instructions have varied across all the years in the data set.

Figure 4. Variation in instructions to students to calculate, find or work out.

Work out seems to indicate a less specialised discourse than calculate, which specifies a particular kind of mathematical activity. Yet it is simultaneously more directive than find in that it indicates that some “work” needs to be done. Indeed, a common hint we have heard teachers give when preparing students in GCSE examination techniques is that the instruction to “find” means that you can just write down the answer, whereas, if instructed to “work out”, you need to show the steps in your working. A tendency to be more directive is apparent in the higher occurrence of simplify and solve in 2011. All years included some explicit instructions to perform algebraic manipulations, though sometimes using instructions such as “calculate the value of x” or simply “find x”, rather than “solve”. The examination papers set in 2011 included 18 questions involving such explicit instructions, sometimes with several separate explicit tasks within a single question. The examinations in 1980 and 1991 included only seven and eight such questions respectively but also included several questions that implicitly expected students to perform algebraic manipulations in the course of finding the required answer. An example of such an implicit expectation to use algebraic manipulation is shown in Figure 5.

Figure 5. Implicit expectation of algebraic manipulation. University of London GCE Ordinary Level Mathematics Syllabus B Paper 2, June 1980.

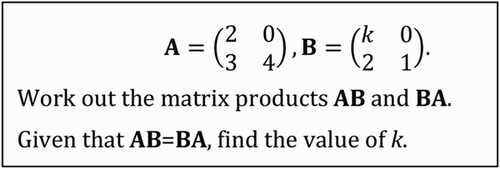
An increase in the explicitness of instructions to use specific mathematical methods may contribute to reduction in student participation in independent decision-making.

One important change in the frequency of specialised mathematical processes is the almost complete disappearance of prove, with only one instance of this process in each of the years 1991 and 2011. The decrease of prove is in part, but by no means completely, mitigated by some uses of show. Show is used in several ways in the examination papers, two of which (show that and show how), involve a request for justification of a solution, either a solution offered within the examination question itself (e.g. “Show that is parallel to the vector a + b”) or a solution demanded of the student (e.g. “Show how you decide”).

Investigation of the occurrence of prove and these uses of show across all the years in our data set, shown in Table 5, suggests that there has been a change in the nature of the specialised mathematical discourse of examinations and increasing distance between what is expected of school students at the end of compulsory schooling and this crucial component of the practice of mathematicians. There is a large discontinuity between 1980, when there were 0.44 occurrences of prove or show that/how per question, and the later years, when the rate ranged from 0.03 to 0.16. Moreover, apart from a slight anomaly in 2004, Table 5 suggests a further downward trend in both the absolute number of occurrences and the rate of occurrence per question.

Table 5. Occurrence of prove and show that/show how.

	1980	1987	1991	1995	1999	2004	2010	2011
prove	8	0	1	4	2	7	0	1
show that/how	8	6	5	4	2	5	3	2
total	16	6	6	8	4	12	3	3
occurrences per question of prove and show that/how	0.44	0.11	0.13	0.09	0.06	0.16	0.03	0.03

Although we have argued that asking students to ‘show that’ or to ‘show how you decide’ is close to a request to ‘prove’, as show is more widely used in non-mathematical discourse, it may function to allow students more scope to provide a range of mathematical or non-mathematical justifications (which may or may not be considered legitimate answers in the examination context). This discursive openness or ambiguity was demonstrated by some student responses in a later phase of the EDSM project when students were given a test containing questions involving a variety of discursive characteristics. One question asked students to calculate the volume of a cylindrical glass, state whether it would hold the contents of a ½ litre bottle of water, then “Show how you decide”. Several students drew on non-mathematical discourses to explain their decision. For example, one used informal “remembering” of everyday experience, writing:

The volume of the glass and size is big enough for ½ a litre of water to fit in. Worked it out by using my ruler to work out how big the glass would actually be and then remembering the size of ½ litre bottles and 1 litre cartons and comparing it. (student Y8/114)

In this case, the student’s response would certainly not have been considered acceptable, although, from reading the examiners’ report following the original examination, the level of reasoning demanded by the assessment criteria does not appear very sophisticated:

To gain the mark in part (b) candidates needed to state both “1⁄2 litre = 500” (ml or cm³) and give the conclusion “No”. (OCR, 2011)

The difference between the discourse in 1980 and that since 1987 must be seen in the light of the different student populations expected to take these examinations. The ‘O’ level examination in 1980 examined a syllabus designed specifically for the highest attaining students and it seems likely that those not deemed capable of attempting this examination experienced a curriculum discourse that contained less emphasis on proving. The 1987 examinations included in our data set were a ‘joint’ syllabus, intended for students with a wider range of attainment, and from 1988 all students followed a common GCSE syllabus, albeit examined at different levels. The target population for all the examinations in our data set included the highest attaining group so we can conclude that, at least for this group, the expectation that they should engage in a discourse of proving decreased with the change to a unified syllabus and appears to have continued to decrease since then.

Summary: specialisation at the level of vocabulary

The quantitative analysis suggests that the vocabulary found in the earliest examination papers in our data set, taken from before the major developments in curriculum and examinations following the Cockcroft report, was more highly specialised, as well as involving a slightly higher proportion of symbolic objects. The examination papers from 1991 show a distinctly smaller proportion of specialised vocabulary and this is associated with a high proportion of contextualised questions. Differences in proportions of specialised vocabulary across the years of the rest of the data set were small, showing no overall trend. When we look more closely at the data, however, it suggests changes in the ways that students appear to be expected to engage in mathematical discourse. In particular, there seem to be changes in how students are directed to engage in algebraic manipulation as well as a downward trend in the extent to which students are expected to engage in proving.

Contextualisation: specialisation at the level of whole questions

Some of the examination questions involved only specialised (SM) objects and processes. These questions were coded as abstract. However, many of the examination questions in all years involve some kind of non-mathematical context. This is a widespread characteristic of much of school mathematics in England, especially since the reforms of the late 1980s; the National Curriculum emphasises the utility of mathematics and the need for students to learn to apply mathematics. The curricular emphasis on application of mathematics in context is clearly represented in the examinations studied in the EDSM project, although contextualisation has been demonstrated to cause problems with the validity of assessment (Cooper & Dunne, 2000). While some questions appear to demand mathematical modelling of a novel situation, others suggest more routine application of familiar techniques to familiar situations. We consider the relationship between the mathematics and the context to be a further aspect of the degree of specialisation, so developed a categorisation to enable us to characterise the nature of contextualisation and to investigate it across the years of our study.

The categorisation is based on that used by Nyabanyaba (2002), though the specific definitions of the categories and their application have been adapted. At the lowest level, we identify what Nyabanyaba calls ritual context. Questions coded as ritual are those which follow a pattern widely used in textbooks and other resource materials, often as part of a repetitive exercise for practicing a particular skill.² Many traditional word problems are of this type, for example:

60% of the members of a youth club are girls. There are 12 boys in the youth club.

How many members are there in the youth club altogether? (OCR GCSE Mathematics Syllabus A, Paper 3 Higher Tier, June 2010, question 4)

A student who is well prepared for the examination will have done many questions with similar structures (including, in particular, comparisons of numbers of boys and girls in a group) and is likely to recognise the mathematics demanded and pick out the relevant quantities and operations without any need to consider the reality of the context.

Questions coded as mundane are those which, while containing some element that is unlikely to be familiar to students from repetitive exercises, nevertheless require minimal engagement with the context in order to work out what mathematics needs to be done. This category is wide, including: questions which give some novel contextual information and then state explicitly the mathematics that needs to be applied to this information; questions that are posed entirely in non-mathematical terms but involve a familiar context that can be modelled in a straightforward way with a familiar routine mathematical procedure; and questions that may on the surface resemble ritual word problems but demand some engagement with the context in order to give a ‘reasonable’ answer. The following example includes a non-routine context but states explicitly the mathematical techniques required:

Martin won the 400 metre race in the school sports with a time of 1 minute. The distance was correct to the nearest centimetre. The time was correct to the nearest tenth of a second.

(a) Work out the upper bound and the lower bound of Martin’s speed in km/h. Give your answers correct to 5 significant figures.

Upper bound …  …  …  …  …  …  …  …  …  …  …  …  …  km/h

Lower bound …  …  …  …  …  …  …  …  …  …  …  …  … . km/h

(b) Write down an appropriate value for Martin’s speed in km/h. Explain your answer. (Edexcel GCSE Mathematics Syllabus A, Paper 6 Higher Tier, June 2004, question 20)

Questions coded as deep demand more extensive engagement with the context in order to determine how specialised mathematical discourse should be used. This may be because the context itself is unfamiliar, because the area of mathematics students are expected to use is not routinely applied to similar contexts in school mathematics, or because the student is expected to make a non-routine judgement about how the results of mathematical computation relate to the context, for example:

David is investigating weekly earnings. The earnings in pounds at one company are listed below.

60 60 60 65 70 70 75

80 80 90 90 100 120 130

130 145 145 150 300 410 650

(a) David does not know which one of the mode, mean or median he should use to represent the employees’ earnings.

State which you would use, giving your reasons for rejecting the other two.

(b) Find the inter-quartile range and state why this is a better measurement than the range to represent the spread of earnings at this company. (OCR GCSE Mathematics Syllabus A, Paper 5 Higher Tier, June 1999, question 8)

The application of the categories is clearly dependent on the researchers’ knowledge and judgements about the usual curriculum experience of students taking these examinations. The two authors have extensive experience of school mathematics practices and learning resources in England, supporting our judgements of the likely familiarity of contexts and question types. As described in Section 2 above, the coding process included discussion and resolution of any discrepancies between our initial judgements leading to tighter definition of the categories. The reliance of the definition of these categories on knowledge of a particular curricular context means that it remains likely that other researchers with different experiences of the curriculum would allocate questions to the categories in slightly different ways. Moreover, similar questions, appearing in texts originating in different educational systems are likely to be coded differently, depending on the common content of curriculum resources in those systems. Nevertheless, we are confident that our analysis has sufficient validity to highlight variation in the nature of contextualisation of examination questions over time. The proportions of questions coded in each category are shown in Figure 6.

Figure 6. Degree of contextualisation (all questions).

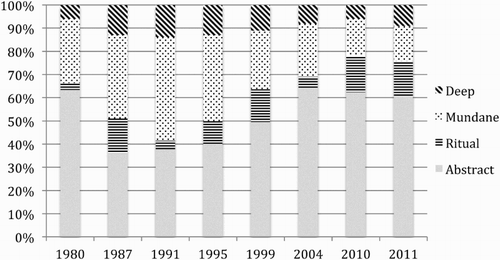
The first point to note is that the proportion of context-free ‘abstract’ questions fell substantially between 1980 (64%) and 1987 (36%) (two-tailed Z-score = 2.5718, p = 0.0102) but has since recovered to approximately the 1980 level (between 60% and 64% in 2004, 2010 and 2011). While the initial drop was an immediate consequence of the curricular emphasis on utility described above, the resurgence of abstract questions can be explained as a response to concern expressed by university mathematicians and others about students’ lack of skills in algebraic manipulation (e.g. London Mathematical Society, 1995). A report by the School Curriculum and Assessment Authority following the examination in 1995 called for increased emphasis on algebra in GCSE examinations (SCAA, 1996). As seen in the discussion of explicit processes above, this call has been followed by the inclusion of non-contextualised questions instructing students to solve equations or simplify algebraic expressions.

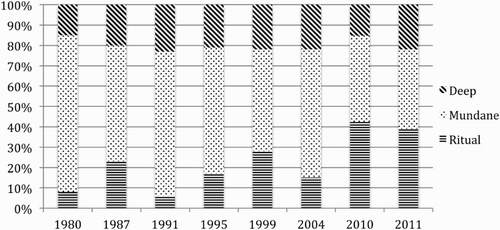
Considering just the questions involving contextualisation, Figure 7 shows the proportions of each degree of contextualisation within these questions. The proportion of contextualised questions involving ‘deep’ context has remained consistently low throughout the period, varying between 15% and 23%. The proportion of contextualised questions in which the context is categorised as ritual, however, rose substantially in the most recent years of the data set from just 8% in 1980 to 42% and 39% in 2010 and 2011 respectively. Thus in 2010 and 2011, not only had the proportion of completely specialised context-free questions almost returned to the pre-GCSE level of 1980 but the degree of depth to which students were expected to engage with context had fallen far below that expected in earlier years. The curricular rhetoric about the importance of use of mathematics was not reflected in the discourse of these examinations. More recent changes in examination specifications since the end of the EDSM study, in particular the emphasis on ‘functional mathematics’ (which “requires learners to use mathematics in ways that make them effective and involved as citizens, to operate confidently in life and to convey their ideas and opinions clearly in a wide range of contexts.” QCA, 2007, p. 19) may have reversed this trend, though the discontinuity between official rhetoric and practice seen within our data set suggests that such change cannot be taken for granted.

Figure 7. Degree of contextualisation (contextualised questions only).

Objectification

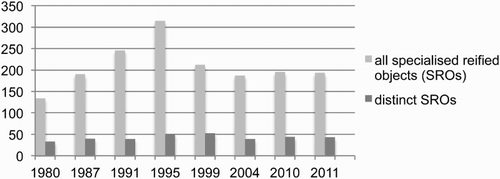
As discussed in section 2 above, an important characteristic of specialised mathematical discourse is the fact that it is highly objectified. In particular, many mathematical objects are reifications of processes, formed either by grammatical metaphors (transforming process words into object words) or by coining specialised words to refer to the reified objects. The specialised objects identified by the process described in section 3 were further examined and, where relevant, coded as reifications. Figure 8 shows the number of such objects found in each year.

Figure 8. Specialised reified objects.

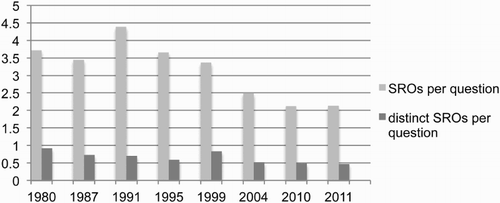
As was the case with specialised objects generally (see section 3), the number of distinct reified objects has not varied enormously, though there was a slightly higher number found in the 1990s than in either earlier or later years. It may thus be concluded that students are expected to be able to engage with a broadly similar variety of such reified mathematical objects. However, it is worth noting that the number of questions in each examination paper has increased substantially over the years. Figure 9 shows a decreasing trend in the mean number of specialised reified objects per question and in the mean number of distinct specialised reified objects per question.

Figure 9. Density of specialised reified objects per question.

Of course, the examinations in the earlier years comprised fewer questions but had similar duration to those in more recent years. They thus expected students to spend more time on a single question. It may not, therefore, be surprising that they should be expected to engage with a greater variety of specialised objects in general and reified objects in particular within the scope of a single question. In Figures 10 and 11, questions from 1980 and 2011 are shown, addressing similar topics. Even though the 1980 question is divided into shorter sub-questions, these sub-questions are related and there is an expectation that the student should be able to make use of and form relations between the reified objects: graph, function, equation and root as well as the objects f(x) and g(x), given in symbolic mode. (Symbols used for objects such as functions and equations may also be considered to be reifications but have not been coded as such in our analysis so far.) The 2011 question involves only graph and equation together with two objects in symbols. The process of solution is construed purely as a process solve rather than as involving the reified object root. Clearly, both questions involve objectified discourse. The number of specialised reified objects in the 1980 question is not disproportionately higher, given the number of marks allocated (12 marks compared to 4 marks for the 2011 question). However, we would argue that the intensity of the objectification is higher in the 1980 question, given the need to make more connections between specialised reified objects (a possible ⁴ C₂ = 6 connections between graph, function, equation and root, compared to just 1 connection between graph and equation).

Figure 10. University of London, GCE Examination Ordinary Level, Mathematics Syllabus B (361), Paper 2, June 1980.

Figure 11. OCR GCSE Mathematics Syllabus A, Paper 4 (Higher Tier), June 2011.

Conclusion

The outcomes of the analysis that we have reported in this article illustrate the complexity of the issue we have sought to address. Specialised mathematical discourse is a multi-faceted phenomenon and it is difficult to formulate a simple answer to the question of how its presence in school mathematics examinations has changed over the three decades covered by our study. Rather than attempt to summarise our findings once again, in this section we reflect first on methodological issues raised by the work reported here and then on how the EDSM study of specialised discourse addresses two of the key concerns raised in the public and policy domains during the period in relation to the ‘standards’ of examinations.

Methodological reflection

This article has taken the specialised nature of the discourse of school mathematics as its focus, contrasting specialisation of vocabulary and of whole questions with everyday discourse and non-mathematical contexts and investigating the degree of objectification. We have discussed just this one section of the EDSM analytic scheme, defining its terms and illustrating the results of its application. In the course of doing so, however, it has been necessary to draw on other parts of the analytic scheme in order to interpret the findings. For example, in order to make sense of changes in the occurrence and use of the school mathematical process give, discussed in section 3.2, it has been necessary to consider how its use contributes to the syntactic and logical complexity of questions. Similarly, interpretation of changes in the intensity of objectification (section 5), demanding that students make more connections between specialised reified objects, needed to draw on findings related to the length and structuring of examination questions.

It is perhaps inevitable that we have needed to consider a wider range of textual characteristics in order to form interpretations of an analysis undertaken at the level of vocabulary. Words (and symbolic expressions and graphical objects) do not stand alone, but are integrated into sentences, questions, and whole examination papers. It is only by considering the place of a word within its immediate and wider contexts that we can seek to understand its place within school mathematics discourse. Nevertheless, by focusing initially on words in isolation, our analytic scheme has enabled us to handle a large amount of textual data and to achieve a quantitative overview of variation in expectations about student engagement with specialised vocabulary. Such an overview – of vocabulary and of other specific linguistic features identified within our analytic scheme – was an important step towards achieving our objective of addressing the question of how the discourse of examinations has changed over time. For example, the results of the analysis of vocabulary allow us to report that examinations from 1987 to 2011 have demanded generally similar levels of engagement with specialised vocabulary, though these are markedly lower than the pre-reform examinations of 1980.

However, supplementing the initial quantitative approach with more detailed analyses and consideration of longer segments of text has enabled subtler insights into how the discourse has changed. For example, extracting the specialised process words and looking at the distribution of specific processes brought to our attention differences in the ways that students were instructed to perform algebraic manipulations. This led us to return to the original examination papers in order to scrutinise the place of algebraic manipulation more deeply. Looking in a qualitative way at all the questions involving algebraic manipulation allowed us to see that recent examinations have made their expectations about use of algebra more explicit. Again, this finding relates to another part of the analytic scheme, contributing to our understanding of how opportunities for students to make autonomous decisions about their mathematical activity have varied through the years.

The interconnectedness of our analytic categories and the movement between quantitative and qualitative approaches present a challenge for us in communicating outcomes of our study and for our readers in making sense of the methods and reported findings. We hope that the current article presents a coherent narrative about specialisation and refer our readers to other articles in this Special Issue for further details of the full analytic scheme and the application of other parts of it.

Engaging with the ‘standards’ discourse

Finally, we reflect on how the findings we have reported here address issues raised in the public and policy discourse of ‘standards’. As mentioned earlier, concern was expressed in the mid-1990s by, among others, university mathematicians (London Mathematical Society, 1995) about a supposed decline in algebraic manipulative skills. This seems to have resulted in a subsequent increase in completely abstract questions in the examinations. However, our analysis suggests that recent expectations about student engagement with algebra are nevertheless different from those in pre-GCSE days. In particular, the role played by purely symbolic objects has changed: the specialised discourse still involves a smaller proportion of objects in symbolic form than in the 1980s and there is increased explicitness about the nature of the algebraic manipulation required. This suggests that, although the amount of manipulation may have returned to close to 1980s levels, students tend to be asked to perform specific manipulations in isolation, rather than to make use of algebra in the course of solving a problem. While university mathematicians will find that the examinations have addressed their concern about students’ manipulation skills, they may still be disappointed by students’ participation in mathematical discourse that involves use of algebra.

A second concern has related to the extent to which students are expected to engage in independent problem-solving. The use of structured questions was raised as an issue by the regulatory bodies at least as early as 1996 (SCAA, 1996). The number of questions set in each examination paper has increased over the time period, although the time allocated to the examinations as a whole has not changed substantially. Moreover, longer questions have tended to be broken into steps. This affects the extent to which students are expected to engage independently, an issue dealt with elsewhere in the EDSM project. There are, however, other aspects of mathematical thinking that are associated with problem-solving. In particular, we might expect that, when problems are divided into shorter steps, there may be fewer opportunities to engage in some forms of reasoning. From the data presented in this article, it appears that the expectation that students should engage in proving has decreased substantially. At the same time, the disappearance of the use of given that and a general reduction in use of logical connectives have changed the nature of the logical reasoning expected.

By 2009 examination boards were required to include some ‘longer and unstructured’ questions (QCA, 2009). The examinations in the most recent years of our data set (2010 and 2011) involve more problems that have not been broken into steps, demonstrating the response by the examination boards to concerns about lack of independent problem solving. However, this does not appear to have reversed the changes in expectations about reasoning. The reduction in the rate of specialised reified objects per question may also be a consequence of shorter questions, although again this trend has continued in 2010 and 2011 in spite of the inclusion of more unstructured questions. As suggested above, mathematical discourse that includes a higher density of such objects provides more opportunities for students to make connections between specialised objects and more expectation that they should be able to do so.

A theme emerging from this discussion is that responses by the examination boards to public debates and pressure from policymakers have effects that are not necessarily those that are intended or desired. The increase in algebraic manipulation desired by university mathematicians has made manipulation an end in itself rather than a tool for problem-solving. The return to unstructured questions may have introduced more opportunities for students to make independent decisions but it has not been accompanied by increased expectations that students should engage in proving or making mathematical connections. Similarly, the rhetoric about the importance of being able to use mathematics in real world contexts, by 2011, seemed only to have resulted in an increase in the shallowest level of engagement with context.

A possible explanation for this apparent mismatch between intention and practice is the continuing wish to make mathematics examinations accessible to the widest possible population of students. As we identified in section 1, previous research on the language of mathematics examinations has tended to focus on factors that affect the difficulty of items, as measured by success in achieving the required answers, and the examination boards have systematically attempted to avoid forms of language that they consider to ‘obscure’ the mathematics. Some of the textual characteristics that we have identified as tending to decrease are among those likely to be considered linguistically challenging, including:

• complex grammatical constructions such as given that … ;

• density of specialised reified objects;

• extensive contextual information.

If consideration of the effects of language focuses primarily on difficulty, then avoiding these characteristics is likely to enable more students to access ‘the mathematics’. From a discursive perspective, however, we have argued that such linguistic changes actually alter the nature of the mathematics with which students are expected to engage. We would certainly not wish to dispute the political desire to enable students to gain access to success in high-stakes examinations. However, we hope that the EDSM analysis of the changing nature of school mathematics discourse can help those responsible for writing examination papers and for developing the curriculum and assessment system understand better how changes to the language of examinations affect the possibilities for student engagement in mathematical discourse.

Acknowledgements

The examination questions shown in Figures 3, 5 and 10 are included by kind permission of Pearson Education Ltd.

The examination question shown in Figure 11 is included by kind permission of Oxford Cambridge and RSA (OCR) Examinations.

Additional information

Funding

The EDSM project was funded by the Economic and Social Research Council grant reference: ES/1007911/1.

Notes

1. The term lexicogrammar is used in systemic functional linguistics, indicating the continuity between lexis and grammar.

2. Note that this use of the term ritual is different from that used in Sfard’s discursive approach to refer to a particular type of routine (Sfard, 2008).