Exploring the relationship between metacognitive and collaborative talk during group mathematical problem-solving – what do we mean by collaborative metacognition?

ABSTRACT

The purpose of this study was to enhance our understanding of the relationship between collaborative talk and metacognitive talk during group mathematical problem-solving. Research suggests that collaborative talk may mediate the use of metacognitive talk, which in turn is associated with improved learning outcomes. However, our understanding of the role of group work on the individual use of metacognition during problem-solving has been limited because research has focused on either the individual or the group as a collective. Here, primary students (aged nine to 10) were video-recorded in a naturalistic classroom setting during group mathematical problem-solving sessions. Student talk was coded for metacognitive, cognitive and social content, and also for collaborative content. Compared with cognitive talk, we found that metacognitive talk was more likely to meet the criteria to be considered collaborative, with a higher probability of being both preceded by and followed by collaborative talk. Our results suggest that collaborative metacognition arises from combined individual and group processes.

KEYWORDS:

• collaborative metacognition
• problem-solving
• mathematics

Introduction

Mathematical problem-solving ability constitutes an important component of applied mathematical knowledge. Although students encounter various difficulties with problem-solving (e.g. Boonen, van Der Schoot, van Wesel, de Vries, & Jolles, 2013; Verschaffel et al., 1999) there is evidence to suggest that effective use of metacognition can be an important factor associated with successful outcomes (Stillman & Mevarech, 2010). Researchers propose a facilitative role for metacognition during mathematical problem-solving (e.g. Garofalo & Lester, 1985; Lester, 2013; Schoenfeld, 1992; Stillman & Mevarech, 2010). Learning mathematics can be viewed as a social activity requiring students to acknowledge and discuss their mathematical understanding and strategy use (Ginsburg, Labrecque, Carpenter, & Pagar, 2015; Schoenfeld, 1992; Sfard, 2012). In group-work environments, students need the skills to make known to others their procedural and declarative knowledge of mathematics while simultaneously understanding that of their peers (Schoenfeld, 1992). They must also regulate their own cognitive processes (Garofalo & Lester, 1985), and to some extent, also those of the group. A broader understanding of these metacognitive processes could serve to inform teaching and learning practices (Schraw, Crippen, & Hartley, 2006).

Although our understanding of the relative roles of metacognitive processes in group learning environments is incomplete, the relationship between metacognition and mathematical achievement is well established. Metacognitive knowledge (Özsoy, 2011; Schneider & Artelt, 2010) and cognitive regulation (Morosanova, Fomina, Kovas, & Bogdanova, 2016) are both associated with higher levels of mathematical achievement. Numerical metacognitive knowledge in young children (aged five) can predict levels of mathematical knowledge at school (Vo, Li, Kornell, Pouget, & Cantlon, 2014). Metacognitive beliefs and monitoring are also associated with mathematical problem-solving performance in primary school students (Cornoldi, Carretti, Drusi, & Tencati, 2015). Similarly, metacognitive ability has been shown to predict mathematical achievement in high school (Van der Stel, Veenman, Deelen, & Haenen, 2010; Veenman, Kok, & Blote, 2005).

Although there is considerable evidence suggesting a positive influence of metacognition on mathematics achievement, much of this is from research designs which do not incorporate the influence of a group environment on individual use of metacognition. Metacognition is often conceptualised as an individual process, based on understandings developed by Flavell (e.g. 1979), grounded in Piaget’s individual-based stage theory of cognitive development (Inhelder & Piaget, 1958). A rich body of research has developed since Flavell’s early work and although there is no universally accepted definition of the term, it is generally accepted that individual metacognition comprises two main components: knowledge of cognition and control (or regulation) of cognition (Larkin, 2009; Schneider & Artelt, 2010).

Research on metacognition in group situations is less well developed, despite group learning being commonplace in schools and other learning environments, especially in mathematics. As a pedagogical approach, collaboration is deemed so significant that the OECD has published the PISA Collaborative Problem Solving Framework (OECD, 2015), acknowledging it as a key skill assessed alongside science, reading and mathematics. Because research suggests metacognition is an important factor in effective learning, both in general and in mathematical problem-solving, it is vital that researchers develop appropriate definitions and methods to develop our understanding of the construction and mediation of metacognition that are appropriate for naturalistic group learning environments.

Within the mathematical problem-solving literature, a range of definitions and research methods have been employed to understand the role of metacognition in group learning environments. It is therefore difficult to compare and thus consolidate empirical findings, and to link them consistently with the theoretical literature. The following section discusses current empirical research on the contribution of metacognition to effective learning, and understandings of its role during group mathematical problem-solving. It highlights methodological progress and limitations, with a focus on our limited understanding of the role of group work on the individual use of metacognition during mathematical problem-solving.

Current understanding of the use of metacognition in mathematical problem-solving

Empirical evidence for the role of metacognition

Research on metacognition during mathematical problem-solving has two main directions: understanding student use of metacognition; and the use of metacognitive interventions to improve learning. Outcome measures are generally individual achievement, either in group settings (e.g. Mevarech & Kramarski, 2003) or during individual working (e.g. Cardelle-Elawar, 1992; Teong, 2003).

Much empirical evidence for the role of metacognition in enhancing learning in mathematics and other areas comes from intervention studies. Interventions which aim to improve metacognitive ability have typically been shown to result in improved learning outcomes, across a range of subject areas. For example, empirical research considering metacognitive interventions has covered areas such as science education (Adey & Shayer, 1993; Georghiades, 2000; Zohar & David, 2008), mathematics (Desoete, Roeyers, & Buysse, 2001; Kramarski, 2004; Mevarech & Fridkin, 2006; Mevarech & Kramarski, 1997, 2003; Teong, 2003), chemical engineering (Case & Gunstone, 2006), reading (McElvany & Artelt, 2009; Michalsky, Mevarech, & Haibi, 2009) and teacher education (Kramarski, 2008).

One intervention applied in a number of empirical studies in mathematics education is Introducing new concepts, Metacognitive questioning, Practicing, Reviewing and reducing difficulties, Obtaining mastery, Verification and Enrichment (IMPROVE) (Mevarech & Kramarski, 1997). Derived from theories of social cognition and metacognition, the IMPROVE intervention is designed specifically for teaching mathematics in heterogeneous classrooms. There are three interdependent components of the intervention: metacognitive activities, peer interaction and systematic provision of feedback-corrective-enrichment. Mevarech and Kramarski (1997) propose that the use of peer interaction produces a situation of varying background knowledge, which should generally be advantageous to all pupils. The authors designed metacognitive questions to encourage students to produce elaborate explanations regarding the structure of the problem, connections between new and existing knowledge and specific strategies that might be appropriate for solving the problem.

In their initial work, Mevarech and Kramarski (1997) employed a quasi-experimental design and focused on Israeli children in the 7th grade (aged 12–13). The intervention group worked collaboratively, whist the control group worked individually. The study focus was to measure information processing ability and mathematical reasoning ability. Results showed that pupils who underwent the intervention achieved higher scores in post-intervention tests. However, positive results were not seen across all measures and low achievers were not consistent in their improvement. In a follow-up study, Mevarech and Kramarski (2003) compared two groups working collaboratively. The authors found that the group which underwent the intervention performed better than the control. Whilst the authors suggested that the intervention had brought a qualitatively different kind of interaction between the group members, they did not directly investigate the qualitative differences in interactions in an attempt to ascertain why achievement improved.

Another key series of studies providing convincing evidence for the efficacy of metacognitive interventions in enhancing learning is the Cognitive Acceleration in Mathematics Education programme ([CAME] Adhami, Johnson, & Shayer, 1998). Metacognition constitutes one component of the CAME programme, which incorporates Inhelder and Piaget’s (1958) stage theory of development, and the acceleration of students’ thinking skills from the concrete to the formal operational stage. Using this programme, Shayer, Johnson, and Adhami (1999) found significant improvements in mathematical achievement measured through school tests.

Metacognitive interventions can also be effective when they target teachers rather than pupils. Gillies and Khan (2009) gave teachers systematic training on promoting metacognitive thinking with children, in a study using some mathematically-based problems. Pupils who were exposed to metacognitive questioning provided more information regarding justifications and reasons for their answers than those who did not receive the intervention.

However, the benefits of metacognitive interventions may be influenced by the task and the metacognitive ability of the students prior to the intervention. Following a metacognitive intervention during mathematical problem-solving, Mevarech and Kramarski (1997) concluded that the type of problem can influence the outcome of the intervention and metacognitive instruction is more useful when the problem requires higher levels of metacognitive reasoning. Metacognitive interventions have also been shown to be more beneficial to lower achieving students. Pennequin, Sorel, Nanty, and Fontaine (2010) found that the mathematical problem-solving skills and metacognitive ability of lower achieving students improved to a greater degree than for those who were high achieving, allowing them to solve problems at a similar level.

Research shows the use of interventions in mathematical problem-solving can have differential outcomes in terms of the development of skills. For example, after a metacognitive intervention, low achieving students have been shown to increase their use of appropriate problem-solving strategies (Cardelle-Elawar, 1992), while in other studies, students have also been show to increase their use of metacognitive talk (e.g. Teong, 2003) and metacognitive skills (e.g. Veenman et al., 2005) during problem-solving.

More recently, researchers have considered the mediation of metacognitive skills during mathematical problem-solving. Evidence suggests that the use of metacognitive prompts during problem-solving improves both understanding and the use of appropriate strategies (e.g. Jacobse & Harskamp, 2009). Furthermore, giving students the option of using prompts may support them in developing self-regulation skills by allowing them to become more aware of points when they require further assistance (Kramarksi & Friedman, 2014).

Taken together, these studies suggest that in the domain of mathematics education, metacognitive interventions may have a positive effect on metacognitive skills or achievement. Although the evidence is consistent with the explanation that these improvements result from the interventions used, it is difficult to ascertain the precise nature of the metacognitive development. Nonetheless, these studies support the idea that metacognitive skills can be taught and are beneficial to students during problem-solving.

The role of metacognition during group mathematical problem-solving

Suggestions regarding the role of metacognition during group mathematical problem-solving can be found in both theoretical work and empirical studies concerned with collaborative learning. From a theoretical perspective, metacognition fits well with cognitive constructivist and social constructivist views of learning (Carr & Biddlecomb, 1998). When children work with peers to solve problems, metacognitive awareness may be enhanced through children explaining their reasoning to peers, or critiquing a suggestion made by a peer (e.g. Schraw et al., 2006). From a methodological perspective, it may also be easier to assess the types of interactions children use when solving problems, when they are verbalised during problem-solving with peers (Veenman, Van Hout-Walters, & Afflerbach, 2006).

Empirically, research evidence suggests higher levels of metacognition are displayed by more successful individuals during collaborative mathematical problem-solving. For example, Artz and Armour-Thomas (1992) studied several groups of students during their mathematical problem-solving class. Utilising protocol analysis, utterances were coded as cognitive or metacognitive. Students who successfully solved problems demonstrated higher levels of metacognitive interactions than those who did not.

There is also evidence that levels of metacognitive talk may influence the interaction patterns of group members. Hurme, Palonen, and Jarvela (2006) considered the role of metacognition during networked discussions in mathematics with 13-year-old students. Data were collected from three computer-supported collaborative learning lessons. Utilising correspondence analysis, social network analysis and content analysis, they found that students showing more advanced patterns of metacognitive processes had greater involvement in discussions and subsequent solutions. This suggests that students with higher metacognitive awareness had more influence during the problem-solving exercise. A similar relationship between use of metacognition and collaborative input was also studied by Goos, Galbraith, and Renshaw (2002). They argued it was important to look beyond the individual, and particularly to consider whether students played any part in their partners’ metacognitive development. In a three-year study, 15- and 16-year-old pupils engaged in group mathematical problem-solving. Their verbal interactions were coded for metacognitive and collaborative content. The authors suggested that students mediate the use of metacognitive talk through the use of transactive interactions.

Collaborative metacognition: methodological progress and limitations

Although existing work represents important progress in developing our understanding of the role of metacognition in group settings, even in the most rigorous studies, methodological difficulties remain. For example, one limitation of the study by Goos et al. (2002) is that when coding utterances as metacognitive, the authors only included those that provided “potentially useful information or an alternative approach” (p. 199). If a student presented a strategy or approach that was inappropriate for solving the problem, it was not coded as metacognition. Flavell (1979) noted that metacognitive knowledge could be technically wrong, a point that is important within a mathematical problem.solving situation. For example, if a group of students was working toward a solution of a mathematical problem with an incorrect understanding of some aspect of it, it is crucial that this be corrected in order to progress. Therefore, when coding for metacognitive knowledge, it is important to code both accurate and inaccurate knowledge in order to gain a full understanding of the role of metacognition in the group situation, or the role of the group on the use of metacognition.

Nonetheless, the work by Goos et al. (2002) made a major contribution to the work on collaborative metacognition through distinguishing a key feature of collaboration, that of mutuality. Mutuality occurs when each student explores their own and others’ ideas in order to construct a shared understanding of the mathematical problem. To produce solutions which are agreeable to all, students must propose and justify suggested approaches to solving the problem. To assess this aspect of collaboration, Goos et al. (2002) employed Teasley and Rochelle’s (1993, p. 235) definition of collaboration as “a coordinated, synchronous activity that is the result of a continued attempt to construct and maintain a shared conception of the problem”. Students’ interactions were viewed from the perspective of their potential to contribute to the shared understanding and solution of the problem. Interactions that corresponded to the definition of collaboration were termed transactive (Teasley & Rochelle, 1993). Goos et al. (2002) developed a coding scheme according to which data could be coded both for their metacognitive content and their transactive (or collaborative) content.

The notion of transactive interaction was first described by Berkowitz and Gibbs (1983) studying children’s reasoning abilities. They suggested that transactive discussion was “reasoning that operates on the reasoning of another” (Berkowitz & Gibbs, 1983, p. 402). This notion was developed by Kruger and Tomasello (1986) who suggested distinguishing between three types of transacts: transactive statements, transactive questions and transactive responses. Transactive statements were statements representing a critique, refinement or extension of an idea. Transactive questions were requests for clarification, justification, or elaboration of the partner’s ideas. Both transactive questions and statements were spontaneously produced. Transactive responses, however, were those following a transactive question in which an individual would justify their ideas or proposals (Berkowitz & Gibbs, 1983). Furthermore, these transacts could be self-oriented or other-oriented.

Research in the area of transactive reasoning was initially conducted from a Piagetian perspective and sought to understand the relationship between transactive discussion and learning through the notion of cognitive conflict (e.g. Kruger, 1993). However, a parallel field of research has followed conducted from a socio-cultural perspective in order to understand social learning processes (e.g. Teasley, 1997). Although these theoretical perspectives have differed, the concept of transactive discussion has remained. Teasley’s (1997) conceptualisation of transactive discussion was similar to that proposed by Berkowitz and Gibbs (1983), in which a child would use their conversational turn to operate on the reasoning of others or themselves. Nucci (2006) refers to the attempt of the speaker to extend the logic of or critique the prior speaker’s argument. Finally, Wahlstedt and Lindkvist (2007) suggested “a turn is considered transactive if it extends, paraphrases, refines, completes, critiques an other’s reasoning or the speaker’s own reasoning” (p. 1078). Wahlstedt and Lindkvist (2007) proposed a development in understanding the role of transactive discussion. When individuals work collaboratively towards a goal, Wahlstedt and Lindkvist (2007) suggest that it is important that individuals are able to “support and use each other in a way that contributes to goal fulfilment” (p. 1078) and further that within the collaborative environment there is a social obligation to engage in a way that encourages collaboration.

Whilst Goos et al. (2002) highlighted the mediating roles of group members in supporting one another’s thinking, they did not investigate the potential mediating properties of metacognitive talk in drawing group members into the discussion. The authors made specific reference to the term collaborative metacognitive activity and defined it as utterances which were simultaneously metacognitive and transactive in nature. Although these researchers highlighted the reciprocal nature of collaborative metacognitive activity, their operationalisation allowed for an utterance to be coded as such when only one person was involved in the process. For example, a student might say “what am I doing wrong – can someone tell me?” This would be classed as collaborative metacognition even if no one replied. It is difficult in such cases to argue that the requirement for feedback, or indeed the metacognitive knowledge that the adopted process is not correct, would not have been displayed if the student was working alone. In their analysis, Goos et al. (2002) found that around half of all collaborative metacognitive utterances were self-oriented, such as this one where students questioned their own thinking in the group situation, and invited others to question it. However, the interactive nature of the metacognitive questioning was not explored to ascertain if a response was produced.

Goos et al. (2002) considered the proportions of metacognitive utterances which were either followed or preceded by a collaborative utterance, and these were termed nodes. They found that, in successful problem-solving sessions, there were about twice as many nodes as during unsuccessful sessions. This suggests that interaction between students is an important factor in successful sessions. However, the authors did not consider further the relationship between collaborative, metacognitive and other types of interactions such as cognitive or social.

The work of Goos et al. (2002) suggests the level of metacognitive input is related to successful problem-solving and levels of collaborative interaction. However, the precise relationship between metacognitive talk and collaborative talk is not clear. Whilst Goos et al. (2002) found that collaborative and metacognitive talk were clustered during successful problem-solving, they did not investigate this pattern further.

Because the use of metacognition and effective group work skills in mathematical problem-solving rarely develop automatically (e.g. Sfard & Kieran, 2001), it is important that researchers are able to understand the nature of group interactions, together with mediating factors. Research in the area of collaborative problem-solving suggests that there is a relationship between metacognitive talk and collaborative talk, but this relationship has not been fully explored. We therefore sought to develop our understanding of the relationship between collaborative talk and metacognitive talk in order to consider further the extent to which these interactions may be mutually mediating. The research questions addressed in our study were:

1. Is there a positive association between metacognitive utterances and transactive talk in mathematics group work?

2. How might we operationalise collaborative metacognition in order to understand the reciprocal collaborative interaction between learners?

The study

The data in this article were drawn from a wider investigation into the use of collaborative metacognition during mathematical problem-solving with primary school children in a naturalistic context. Twelve primary students in Scotland (aged nine to 10) were observed and video-recorded during group problem-solving sessions. They worked weekly in groups of four for one full school term lasting 15 weeks. As one of the main purposes of the study was to understand metacognition in a natural group setting in a classroom, it was left to the teacher to choose how to group students. The teacher was aware of the aims of the study and that student interactions would be recorded. Alongside standard pedagogical considerations, this influenced her decision to avoid putting two students who were not working well together in the same group. Students were allocated to mixed-gender groups (two boys and two girls) – which also reflected the mixed ability of the class and were maintained across the sessions.

Problem-solving sessions lasted approximately 90 minutes. Lessons began with a short, whole-class introduction to the problem led by the teacher. Students were provided with a paper copy of the problem and joined their groups to develop a solution. During problem-solving sessions, the teacher joined the groups at various points to monitor progress. Students were video-recorded during three sessions: one session near the beginning of the study period, one in the middle and one near the end of the study.

The mathematical problems

Care was taken to ensure the problem types were congruent with metacognitive requirements, as previous studies have noted the impact of different problem types on metacognitive use (e.g. Mevarech & Kramarski, 1997). The problems were also assessed against Garofalo and Lester’s (1985) problem-solving framework to ensure metacognitive input would be required. Each problem required identification of the problem type, organisation of information, regulation of behaviour in order to execute the solution, and evaluation of the solution. Problems were designed collaboratively with the teacher to ensure they were applicable to the curriculum being taught and at the appropriate academic level for the students. The teacher’s assessment of the problems was that students would find them reasonably difficult but should be able to complete them with effective collaborative input. The requirement for collaborative input was considered carefully for each problem. Previous research has identified differential effects that the problem type might have on collaboration, suggesting that when students think there is only one solution they are more likely to work individually (Cohen, Lotan, Abram, Scarloss, & Schultz, 2002; Cohen, Lotan, Scarloss & Arellano 1999). Each problem therefore consisted of several different components which had to be brought together in order to find suitable solution. The problems covered mathematical concepts such as length, area and sequencing. An example problem on length used the context of the Winter Olympics (which were currently underway). The wording of the problem was:

The American skier jumped 2 cm. The Canadian jumped twice as far as the American. The Brit jumped 3 times as far as the American. The Australian jumped one-and-a-half times as far as the American and the Swiss jumped two-and-a-half times as far as the American.

1.	How far did each skier jump?
2.	Who won gold, silver and bronze medals?1

We note that, in this problem, the measurements provided were deliberately unrealistic, but were chosen for two reasons: (1) centimetres were familiar to the students because they had previously used them in class; and (2) the teacher wanted students to be able to use rulers to help with the problem, so units were selected to be consistent with this. The teacher explained to the students that the measurements were unrealistic, and it was clear from student discussions and laughter that they understood this. Furthermore, it was important for student motivation that the problems were realistic enough to engage them in learning but not so detailed or beyond their current understanding to make them think it was beyond their capabilities (Boonen, de Koning, Jolles, & van Der Schoot, 2016). On the basis of this rationale, the teacher decided that the introduction of new units could have been off-putting, and would have detracted from the mathematical essence of the problem. Although the units were unrealistic, the problem remained consistent with our study design in that it was a mathematical word problem, presented in textual format rather than mathematical notation (Timmermans, Van Lieshout, & Verhoeven, 2007), making it a requirement to understand the text as well as to perform the mathematical operations required to solve it (Jitendra & Star, 2012; Van der Schoot, Bakker Arkema, Horsley, & Van Lieshout, 2009). Of the three problems that the students worked on during the study, this was the only one in which units were simplified.

Development of the coding schemes

In order to fully operationalise collaborative metacognition, two coding schemes were developed. The first was developed to identify the metacognitive content of student interactions. The second was used to code the collaborative quality of the interactions.

(Meta)cognitive coding scheme

The purpose of the (Meta)cognitive coding scheme was to separate talk with a metacognitive content from talk with other content. Accordingly, the (Meta)cognitive coding scheme contained options to code talk under five categories. The categories of metacognitive, cognitive or social talk allowed a distinction to be made regarding the type of information the students were conveying. At points throughout the sessions, the teacher would join the groups and therefore a category of teacher talk was added. Finally, to ensure that all talk was included in the final analysis, a category of other talk was developed to acknowledge that at some points, the student contributions could not be heard clearly. The coding scheme can be found in Appendix 1. We drew on previously published coding schemes to provide continuity and allow comparison between studies, as described below.

In relation to metacognitive talk, three papers provided direction in developing the coding scheme: Artz and Armour-Thomas (1992), Goos et al. (2002) and Hurme et al. (2006). To identify cognitive talk, Artz and Armour-Thomas (1992) cognitive coding scheme was applied. During data analysis, the distinction between metacognitive and cognitive talk was not always clear. To avoid the arbitrary use of inferences regarding what the student meant or how a student understood a situation, Teong’s (2003, p. 141) distinction was used during the coding process: “metacognitive behaviours could be exhibited by statements made about the problem or about the problem-solving process while cognitive behaviours could be exhibited by verbal actions that indicated actual processing of information”.

Acknowledging that students working in groups might go off-task, the category of social talk was included. In addition, two further categories were used: teacher talk (drawing mainly on the work of Anderson, Rourke, Garrison, & Archer, 2001) and other (when verbalisations were indistinguishable).

Together, these categories formed a scheme that we refer to as the (Meta)cognitive coding scheme, an illustration of the application of which is provided in Table 1, focusing on the cognitive/metacognitive/social distinctions among utterances in which students were discussing a problem on length.

Table 1. Examples of the application of the (Meta)cognitive coding scheme.

Metacognitive talk
No, you said three and a half. The Swiss jumped two and a half.	Here, the student is using the metacognitive skill of monitoring the interactions of another student.
Well, what you could do. … Get a ruler, check if they’re the same.	In this excerpt, the student is displaying metacognitive knowledge about the problem, and presenting a strategy.
Cognitive talk
I think the Brit came first.	The student is providing a solution without an explanation. This statement implies that the student may have an explanation for their answer, but they have not shared the processes they have gone through to reach the conclusion.
No wait, three times, so that’s four, four, eight, twelve. Twelve centimetres. Twelve, twelve centimetres.	In this example, the student is calculating the answer out loud, and is processing information.
Social talk
I’ve got that, eh, key ring that you gave me in my pencil case. Do you want it back?	Social statements were interactions which occurred during the problem-solving processes but which were unrelated to the problem.

Collaborative talk coding scheme

The coding scheme used to operationalise collaborative talk was adapted from the work of Goos et al. (2002) which used the transactive nature of interaction as an operationalisation of collaboration. This previously published scheme was chosen because it provided a clear conceptualisation of the term collaboration. The coding scheme incorporates the concept of transacts as suggested by Kruger and Tomasello (1986). Transacts can be statements, questions and responses, and constitute the type of verbal data which can be classified as transactive. To qualify as transactive, they can consist of clarification, elaboration or justification of another utterance, and may focus on a critique of one’s own reasoning or the reasoning of another within the group (see Appendix 2). An example of the application of the coding scheme can be found in Table 2.

Table 2. Examples of application of the collaborative talk coding scheme.

How do you get four and a half?	In this Quother utterance, one student is questioning another’s thinking and inviting them to justify their answer.
They’re not allowed to move to the left so they have to keep going that way. They can only move to the right.	In this STother utterance, the student is responding to another student’s suggestion that the sequencing of moves can go in a specific order.
Who won the gold? The Brit won, yeah the Brit won.	Here a student is trying to work out the solution to the problem, and answers her own question, constituting a Resown.

Data and coding

Data were in the form of verbal utterances from three groups of students over the three sessions, providing a total of nine video-recorded sessions. Data were first coded for their metacognitive content and then coded for their collaborative (or transactive) content. This double coding of the data meant metacognitive talk could also be coded as transactive talk and transactive talk could also be metacognitive. However, the term collaborative metacognition was reserved for instances in which transactive talk was followed by metacognitive talk or when metacognitive talk was followed by transactive talk.

Our approach differs from the definition used by Goos et al. (2002) who included as collaborative metacognition talk by an individual which was both transactive and metacognitive in nature. We rejected the notion of this being collaborative as there was no guarantee that another group member would interact – or collaborate – in response to an utterance coded as both transactive and metacognitive. Rather, our notion of collaborative metacognition is reserved for instances where there is collaborative talk between students regarding the problem. Some of these utterances could have been coded both transactive and metacognitive, but if so, this is incidental: our notion of collaborative metacognition is operationalised in the transition between transactive and metacognitive utterances.

To ensure coding reliability, two authors independently coded approximately 10% of the transcripts, agreeing on over 80% of segments. A process of consensus seeking was then used to clarify and finalise the coding scheme, until 100% agreement was achieved. The first author then proceeded to code the full data set. In order to determine the correct coding, the primary data were the words that students used. In the main coding, data from the video were also used, especially when coding for transactive talk. For example, it was sometimes necessary to consider eye gaze to determine if a student was speaking to someone specific or the group as a whole, and body positioning was also helpful in this regard. Applications of the (Meta)cognitive coding scheme and the collaborative talk coding scheme are illustrated in Table 3 which provides examples of collaborative metacognition and metacognition which was not deemed collaborative in nature.

Table 3. Example of collaborative metacognition.

In the following short excerpt, which constitutes collaborative metacognition, the students are trying to create a ruler to measure the lengths presented in the problem:
Student 1: Right, where do you think the quarters are? There? Just about there? Student 2: Just in the middle of the half	Student 1 is questioning the other members of the group (QUother) and inviting them to make suggestions. Student 2 responds with a display of metacognitive knowledge regarding the position of quarters in relation to a half.
In the following excerpt, which does not constitute collaborative metacognition, the students are trying to determine the length of the different jumps:
Student 1: Do we add it on to the American’s? Student 2: The Australian is one and a half times as long as the American	Student one is displaying metacognitive monitoring by seeking clarification through QUother. The student is inviting the others in the group to engage in discussion regarding their strategy use. However, the other students do not respond to the questioning and instead continue with the strategy they are currently employing.

Data analysis

Once the coding schemes were applied, analysis was performed to produce an understanding of the type of utterances (Social, Cognitive, Metacognitive, Teacher teaching, or other) which followed from each type of talk (Transactive or Non-transactive). For ease of interpretation, a Transactive code was only applied in the case of on-task (Cognitive, Metacognitive and Teacher teaching) utterance types. Counts were produced for the number of transactive utterances which led to other utterance types, and also for the number of each utterance type which led to a transactive utterance, to identify collaborative talk.

Results

Focusing on those utterances with both a preceding and a following utterance (i.e. excluding the first and last utterance of each session), 3196 utterances were analysed. Table 4 shows that the majority of these (54%) were social in nature and not related to the problem-solving activity, demonstrating that students engaged in a large portion of off-task talk during the problem-solving sessions. Metacognitive talk accounted for 9% (302) and cognitive talk for 28% (904). The large proportion of social talk during the sessions meant that only a small proportion (12%) of talk was considered transactive in nature (Table 5). Results for each research question are now discussed separately.

Table 4. Breakdown of talk types according to the (Meta)cognitive coding scheme.

Utterance type	Count	Proportion of utterances
Social	1718	54%
Cognitive	904	28%
Metacognitive	302	9%
Teacher teaching	150	5%
Other	122	4%
	3196	100%

Table 5. Breakdown of types of talk according to the collaborative talk coding scheme.

Type of talk	Count	Proportion of overall talk
Transactive	372	12%
Non-transactive	2824	88%
	3196	100%

Is there a positive association between metacognitive talk and transactive talk in mathematics group work?

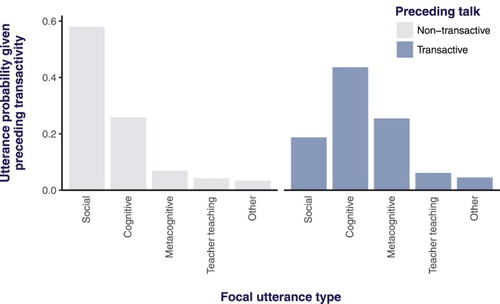
To explore possible influences of collaborative talk on downstream utterance types, we compared the distribution of utterance types following transactive talk and non-transactive talk (Figure 1). Our findings showed that after non-transactive talk, social talk was dominant, as observed overall. However, following transactive talk, the probability of social talk fell threefold and there was a shift towards on-task talk types, with the difference being strongest for metacognitive talk. Specifically, whereas the probability of cognitive talk was around one-and-a-half times higher after transactive talk than non-transactive talk, the probability of metacognitive talk increased more than threefold. Conversely, although the majority of talk following all utterance types was non-transactive, the probability of observing transactive talk was higher after metacognitive talk than following any other utterance type.

Figure 1. Distribution of focal utterance types following non-transactive and transactive talk.

These findings suggested a positive association between metacognitive talk and transactive talk and, to further explore this phenomenon, we examined the proportion of metacognitive talk that was also collaborative, that is, that constituted collaborative metacognition. Talk was considered to be collaborative if it was preceded by transactive talk or followed by transactive talk, or both. We then compared the proportion of metacognitive talk that was collaborative with the proportion of other types of talk that were collaborative. The height of the central blue bar in Figure 2 shows that, overall, around half of all metacognitive talk was collaborative, and this proportion was higher than for any other type of talk (Figure 2).² Furthermore, proportionally, more metacognitive talk was preceded by and followed by transactive talk than were other types of talk, as shown by height of the central blue shaded bars in Figure 3(a) and 3(b) relative to other bars. Interestingly, an utterance had the same probability of being considered collaborative due to upstream or downstream talk being transactive (96 out of 206 utterances; approximately 30%).

Figure 2. Proportion of utterances coded as collaborative, by utterance type. N indicates the total raw count of utterances of each type. The bar corresponding to utterances meeting the criteria for collaborative metacognition is marked with an asterisk.

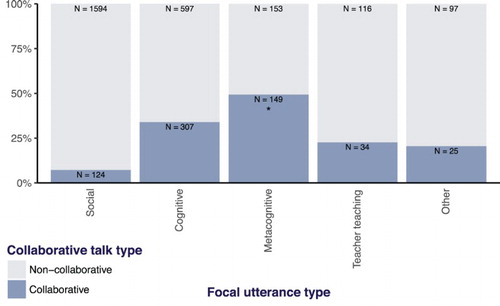
Figure 3. Proportion of each utterance type: (a) preceded by; and (b) followed by transactive talk. N indicates the total raw count of utterances of each type. Utterances meeting the criteria for collaborative metacognition are marked with an asterisk.

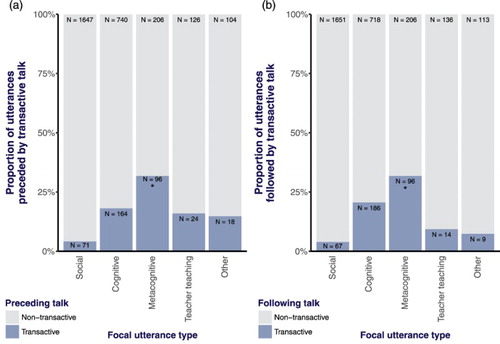
To test whether the proportion of talk considered collaborative differed between utterance types, we conducted chi-square tests. For collaborative criteria based on both the transactive nature of the preceding and following utterances, chi-squared tests showed that this proportion was not independent of utterance type (for preceding utterances, χ² (4, N = 3196) = 253.83, p < 0.001; for following utterances, χ² (4, N = 3196) = 292.38, p < 0.001; df = 4, N = 3196). We were particularly interested in whether metacognitive utterances were more likely to be collaborative than cognitive utterances, and performed additional chi-squared tests, limiting analysis to these two utterance categories. These tests also showed a significant difference in the proportion of metacognitive utterances meeting the collaborative criteria relative to the proportion of cognitive utterances meeting the criteria (for preceding utterances, χ² (1, N = 1206) = 24.93, p < 0.001; for following utterances, χ² (1, N = 1206) = 15.89, p < 0.001). In summary, a higher proportion of metacognitive utterances was collaborative (either because they were preceded by or followed by transactive talk) than other utterance types, and the difference between the proportion of metacognitive collaborative and cognitive collaborative utterances was statistically significant.

How might we operationalise collaborative metacognition in order to understand the reciprocal collaborative interaction between learners?

Overall, our results support the existence of a relationship between collaborative and metacognitive talk displayed during problem-solving. Firstly, metacognitive talk was more likely to meet the criteria for collaboration than any other type of talk (because it was preceded by or followed by transactive talk, or both; Figures 2 and 3). Secondly, when the preceding talk was transactive, the subsequent talk was more likely to be metacognitive compared to when the preceding talk was non-transactive (Figure 1). We therefore suggest that a conceptual understanding of collaborative metacognition should acknowledge this. Given the sample size, it is hard to know whether this relationship generalises. Nonetheless, our findings provide a protocol for further developing this work in order to produce generalisable findings and to more fully understand the nature of this relationship.

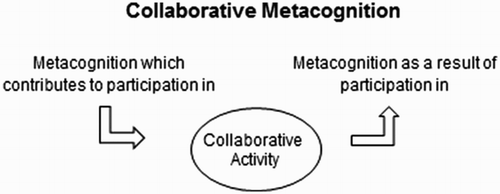
As illustrated in Figure 4, we propose that the term collaborative metacognition can be defined as:

Collaborative metacognition is metacognition which can be identified as having contributed to, or arisen as a result of, group processes (or collaborative talk).

Figure 4. Proposed conceptualisation of collaborative metacognition.

Our refined definition allows for individual metacognition to be displayed in a group setting, but emphasises the potential value of this metacognitive activity in encouraging or resulting from participation in collaborative activity. Although we claim no theoretical or conceptual originality in relation to this definition that draws heavily on the work of other authors, we believe that this clarification provides an opportunity to further develop our understanding of collaborative metacognition. This is the case because it allows us to examine the importance of the use of collaborative talk for mediating metacognitive talk, as well as the importance of metacognitive talk for the mediation of collaborative talk. Further understanding of the extent to which these processes are “mutually mediating” in a social environment (sensu Goos et al., 2002) can underpin new understanding of the types of talk which are more likely to result in positive outcomes of collaborative problem-solving.

Discussion and conclusion

The purpose of this research was to develop our understanding of the relationship between collaborative and metacognitive talk, and to begin to explore the potential that they could be mutually mediating. Through the use of a small-scale case study we found that metacognitive talk was more likely to meet the criteria for collaboration than any other type of talk. In addition, the probability of subsequent metacognitive talk was most strongly influenced by whether the preceding talk was transactive or non-transactive.

We have proposed a definition of collaborative metacognition and its operationalisation in the form of joint coding schemes that we hope can allow researchers to further examine the interactions which occur between students whilst working on a problem-solving task in mathematics or similar domains of learning.

The definition presented in this article represents a development of the work of Goos et al. (2002), who use the term collaborative metacognitive activity. They defined this as talk with both transactive and metacognitive qualities. Our definition builds on their work by proposing a reciprocity in the communicative process produced by transactive talk. We have also provided some tentative evidence of the mutually mediating qualities of metacognitive talk and transactive talk. We propose that this theoretical understanding of the term collaborative metacognition may be a useful starting point for the development of a coherent research base for those interested in the social mediation of metacognition.

By employing a conceptualisation of collaborative metacognition that clearly distinguishes collaborative and metacognitive aspects, we are able to highlight when we are talking about collaborative metacognition as distinct from similar concepts in the mathematical literature, such as group metacognition (e.g. Chalmers, 2009) and socially mediated metacognition (e.g. Goos et al., 2002). This brings much needed conceptual clarity to the field and aids consolidation of findings.

Lester (2013) notes that there is relatively little empirical evidence regarding how best to support the development of students’ metacognitive use during mathematical problem-solving. Our research has provided exploratory evidence for a relationship between collaborative and metacognitive talk. Developing our understanding of this relationship should help us develop strategies to fully maximise the use of metacognitive interventions in group mathematical problem-solving. This is particularly relevant within the teaching and learning of mathematics (Sfard & Kieran, 2001) because the verbal interaction skills required for successful mathematical problem-solving in collaborative settings rarely develop alone.

In order to develop our understanding of the relationship between metacognitive and transactive talk, we suggest that further research be conducted. A larger sample size would enable results to be applied in a more general way. Similarly, a more diverse population in the sample, for example comparing different age groups, would provide evidence of its applicability across stages of learning. To understand the mediating factors involved, qualitative data would be valuable. For example, the use of the Critical Incident Technique (e.g. Kain, 2004) would allow researchers to pinpoint specific instances of collaborative metacognition and engage students in discussion regarding their thought processes at that time. An alternative approach would be the use of in vivo recording of thought processes (e.g. via a think-aloud protocol) which would allow the researcher to question students during problem-solving sessions.

Overall, our contribution is threefold: Firstly, we provide a definition that makes explicit the influence of group interactions on metacognitive processes, while situating metacognition itself at the individual level. This allows us to answer new research questions focusing on the individual within the social situation. Secondly, our empirical case study shows that this definition, operationalised via dual coding of talk according to its metacognitive and collaborative nature, can function as a useful research tool. We show that the application of this definition allows us to identify new relationships between metacognitive talk and group interactions that were previously only suggested on theoretical grounds. Thirdly, although our small sample size means that we have not been able to answer the question of the relationship between metacognition and transactive utterances in a general way, we provide a protocol to show how this might be achieved in future research.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Julie M. Smith http://orcid.org/0000-0002-2927-9514

Additional information

Funding

This work was supported by Engineering and Physical Sciences Research Council [Grant Number EP/P505534/1].

Notes

1 To answer this part of the problem, one needs to assume that all participants are mentioned in the problem. Analysis of student transcripts showed that this was transparent for them.

2 Although there were higher raw counts of collaborative cognitive talk than collaborative metacognitive talk overall, this was due to the larger total number of cognitive talk.

Appendices

Appendix 1. (Meta)cognitive Coding Scheme

Metacognitive Talk

Table

Code	Description	Example	Reference
Monitoring Instructions or plans	It will be clear that a pupil is monitoring what is being said or done in relation to the solution of the problem or instructions they have received	“No, you said three and a half. The Swiss jumped two and a half.”	Artz Armour-Thomas exploring (monitoring) Veldhuis-Diermanse (2002) Hurme, Palonen & Jarvela Metacognitive Skills, monitoring
Presenting a strategy or approach	A pupil provides a strategy which could be used to solve the problem.	“Well, what you could do. … Get a ruler, check if they’re the same.”	Artz Armour-Thomas planning Veldhuis-Diermanse Hurme, Palonen & Jarvela Metacognitive knowledge, strategy variable
Refocusing attention	A pupil draws others back, or give instructions as to what they are supposed to be doing	“Yes but that’s not the problem is it?”	Artz and Armour-Thomas exploring (monitoring) Hurme, Palonen & Jarvela Metacognitive Skills, monitoring
Evaluating	A pupil gives an evaluation of their progress with an explanation.		Goos et al. (2002) Assessing
Clarifying or understanding	Pupils answer the teacher or question the teacher about the problem in order to aid their understanding (this is more of a questioning but shows their understanding through it)	“Do you, is it like, do you have to draw a line in the middle of the ruler to, em, figure out what side to do the halves and quarters on?”	Artz & Armour-Thomas analyzing Goos, Galbraith & Renshaw New Idea or Assessment
Disagreement with explanation	A pupil critiques another’s suggestion and provide a reason for it		Goos, Galbraith & Renshaw Assessment

Cognitive Talk

Table

Code	Description	Example	Reference
Instruction relevant to solution	Pupil gives to another pupil an instruction to do something which is directly linked to solving the problem	“Now we’ve got to discuss.”	Artz & Armour-Thomas implementing AND Veldhuis-Diermanse
Instruction not relevant to solution	Pupil gives to another pupil an instruction to do something which is not directly linked to solving the problem	' “Talk.”
Step or solution without explanation	A pupil provides a step towards the solution or a possible solution without explaining why it is relevant	“I think the Brit came first.”	Veldhuis-Diermanse and Artz & Armour-Thomas Exploring (cognitive)
Agrees without explanation	A pupil agrees with a previous suggestion but doesn't explain why		Veldhuis-Diermanse
Disagrees without explanation	A pupil disagrees with a previous suggestion but doesn't explain why	“Nah, nah, nah, nah, nah. No.”	Veldhuis-Diermanse
Reading	Pupil reads the problem from the sheet provided	“The Canadian jumped twice as long as the American.”	Artz Armour-Thomas Reading
Content directed question	A pupil asks another pupil a question related to the content of the problem		Veldhuis-Diermanse
Evaluating	A pupil gives an evaluation of their progress without reasoning.		I am using this because there is a difference between metacognitive evaluation and reflection and a quick one-word answer!

Teacher Talk

Table

Code	Description	Example	Reference
Facilitating discourse	Teacher draws pupils into a discussion	“What do you think the problem’s about?”	Anderson et al. facilitating discourse
Giving instructions	Teacher gives specific instructions regarding the task	“Uh uh [taking ruler away], those aren't your tools.”	Anderson et al instructional design
Encouraging or Reinforcing student contributions	Teacher gives positive feedback to a contribution by a pupil	“Brilliant.”	Anderson et al. facilitating discourse
Seeking clarification or understanding	Teacher asks pupils if they all agree or understand	“So, there was a specific order that you had to follow? And did you all agree?”	Anderson et al facilitating discourse
Instructions not related	Teacher gives instructions not directly related to the task	“You’ll need to speak up because they can't hear you on.”

Social Talk

Table

Code	Description	Example	Reference
Negative about other group members	Pupils interact in a negative way towards one another	“I’ll scream in your ear again when we go out to break.”	These codes are general headings which are derived from the data.
Negative to other people/things	Pupils talk negatively about other things or people out with the group	[“Do you like her?”] “No. She’s a show off.”
Positive/neutral about other group members	Pupils interact in a positive or neutral way towards one another	“So, if you draw that you’ll get a tan?”
Positive / neutral to other people/things	Pupils talk positively or in a neutral way about other things or people out with the group	“Do you know Donald in the other class? He sent Ben a picture from Facebook and I was round at Ben’s house.”

Other Talk

Table

Code	Description	Example	Reference
Indistinguishable talk	Talk which can't be made out because it is cross talk or because of unclear speech by an individual
Silly noises or singing
Nonsensical utterances	When an utterance cannot be classified as making sense on its own.	“Two, twelve, right wait right.”

Appendix 2 Collaborative Talk Coding Scheme

Table

Clarification Elaboration Justification	Statements	Questions	Response to transactive question
Own thinking	Stown	Quown	Resown
Other’s thinking	Stother	Quother	Resother