Melnikov analysis of chaos in a simple SIR model with periodically or stochastically modulated nonlinear incidence rate

Abstract

In this paper, Melnikov analysis of chaos in a simple SIR model with periodically or stochastically modulated nonlinear incidence rate and the effect of periodic and bounded noise on the chaotic motion of SIR model possessing homoclinic orbits are detailed investigated. Based on homoclinic bifurcation, necessary conditions for possible chaotic motion as well as sufficient condition are derived by the random Melnikov theorem, and to establish the threshold of bounded noise amplitude for the onset of chaos.

Keywords:

• SIR model
• Melnikov theorem
• chaos
• homoclinic orbit

2010 Mathematics Subject Classifications:

• 34C28
• 34C23
• 34F05
• 37N25
• 65P20

1. Introduction

A classical SIR model is considered and the model postulates a constant population which is divided into three classes: susceptible individuals (S), infected individuals (I) and recovered individuals (R). The assumption of constant population size is therefore mathematically expressed by S+I+R=1. Vital dynamics are taken into account by considering a natural mortality rate per capita $\mu >0,$ and a number μ of births per time unit. Let $\beta (t)>0$ denote the rate of transmission per infective so that a number $\beta (t)I^{2}S$ of individuals leave the susceptible compartment to pass into the infective one. We assume that $\beta (t)$ is periodic or stochastic, with period $T_t$ and an infected individual may recover at the rate $\gamma >0$.

Dynamics are therefore described by the following system (1) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mu (1-S)-\beta (t)I^{2}S,\\ \frac{\mathrm{d}I}{\mathrm{d}t}& =\beta (t)I^{2}S-(\gamma +\mu )I,\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\mu R.\end{array}$(1) which has been extensively studied [22,23,27]. More complicated forms of the incidence function have been studied. Liu et al. studied the codimension-1 bifurcation for SEIRS and SIRS models with the incidence rate $\beta I^p{S}^q$ in [20,21]. Derrick and van den Driessche [8] studied saddle-node bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation of SIRS or SIR models with the incidence rate of $\beta I^p{S}^q$. Ruan and Wang [30] studied saddle-node bifurcation, Hopf bifurcation, Bogdanov–Takens bifurcation and the existence of none, one and two limit cycles of an SIRS model with an incidence rate of $k{I}^{2}S/(1+a{I}^2)$, which was also proposed by Liu et al. [21]. Van den Driessche and Watmough [33,34] studied an incidence rate of the form $\beta I(1+\nu I^{k-1})S$, where $\beta >0,\nu ⩾0$ and $k>0$. When $\nu =0$ this incidence rate is the bilinear incidence rate $\beta IS$ [6]. In [34], they studied an SIS model with this incidence rate for $\nu >0$ and k=2, showing the backward bifurcation, local stability and global stability of equilibria. In [33], they further introduced the same incidence rate in an SIRS model. Alexander and Moghadas [1] analysed an SIV model with a generalized nonlinear incidence rate $f(I;\nu )$ and showed the existence of bistability and various Hopf bifurcation, especially for the incidence rate $\beta I(1+\nu I^q)S$ with $\beta >0,\nu >0$ and $0<q⩽1$. Jin et al. [16] give a detailed theoretical analysis of the SIRS model with the incidence rate $\beta I(1+\nu I^{k-1})S$, clearly show the effect of this nonlinear incidence rate on the transmission dynamics of epidemics, not only theoretically obtained backward bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation for this SIRS model, but also shown bistable steady states and explicit conditions for asymptotic stability of equilibria, even for globally asymptotic stability, and especially found stability switches for one of the endemic equilibria.

In (1(1) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mu (1-S)-\beta (t)I^{2}S,\\ \frac{\mathrm{d}I}{\mathrm{d}t}& =\beta (t)I^{2}S-(\gamma +\mu )I,\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\mu R.\end{array}$(1) ), $\beta (t)$ (called the transmission rate) is either constant or a periodic modulation about a constant value, for example: (2) $\beta (t)={\beta }_0(1+{\beta }_1\sin \omega t).$(2) Greenman et al. [14] understand the structure of possible modes of ecological and epidemiological system oscillation with the simplest case of seasonality supposed that $\beta ={\beta }_0(1+\delta \cos (2\pi t))$, in particular, the conditions under which they appear and disappear that the multiplicity, typically created by a hierarchy of subcritical subharmonics can lead to high amplification of the forcing signal and complex switching under chaos and stochastic externalities. Yi et al. [37] studied the periodic, chaotic and hyperchaotic dynamical behavior of an SEIR epidemic system governed by differential and algebraic equations with seasonal forcing in transmission form $\beta ={\beta }_0(1+{\beta }_1\cos 2\pi t)$. Nakata and Kuniya [26] studied a class of periodic SEIR epidemic models and it is shown that the global dynamics is determined by the basic reproduction number $R_0$. Best [4] used bifurcation analysis to investigate the effects of seasonal forcing in the form $\beta (t)={\beta }_0(1+\delta \sin (\omega t))$ on the already complex epidemiological dynamics of the SPI model. More recent models, motivated by biological realism, rather than mathematical simplicity, have taken the contact rate to be governed by the school terms (3) $\beta (t)={\beta }_0(1+{\beta }_{1}Term(t)),$(3) where $\mathit{T}\mathit{e}\mathit{r}\mathit{m}\mathit{(}\mathit{t}\mathit{)}$ is a periodic function which is $+1$ during school terms and $-1$ during school holidays [5,11]. However, throughout this paper, an alternative and more natural, form will be used (4) $\beta (t)={\beta }_0(1+{\beta }_1{)}^{Term(t)}.$(4) Although these two forms are equivalent after rescaling parameters, the second form is far more convenient as we do not have to place an upper bound on ${\beta }_1$. Augeraud-Veron and Sari [3] consider a seasonally forced SIR epidemic model where periodicity occurs in the contact rate of the form $\beta (\tau )=\{\begin{array}{ll}{\beta }_{+}={\beta }_0(1+\delta )& \mathrm{for}\tau \in [n{T}_{\tau },n{T}_{\tau }+\theta T_{\tau }),\\ {\beta }_{-}={\beta }_0(1-\delta )& \mathrm{for}\tau \in [n{T}_{\tau }+\theta T_{\tau },(n+1)T_{\tau }),\end{array}$ where $\delta \in (0,1)$ and $\theta \in (0,1)$. Olinky et al. [28] provide new insights into the dynamics of recurrent diseases and specific predictions about individual outbreaks using the seasonally forced SIR epidemic model, the contact rate is same as [3].

It is in particular well-known that when ${\beta }_1$ is sufficiently large in (2(2) $\beta (t)={\beta }_0(1+{\beta }_1\sin \omega t).$(2) ), it is possible to obtain strong numerical evidence of chaotic motion in these examples [2,17,29]. As ${\beta }_1$ was varied, a period-doubling route to chaos was observed [13], this generated much excitement and prompted many researchers to look for chaos in epidemiological time series [12,31,32]. Chaotic behaviour has been observed numerically in many numerical simulations of forced SIR models, and in slightly more complicated models which take into account the time delay between being infected and becoming infective (SEIR models). The arguments, for example in the context of measles, tend to concentrate on the relatively large values of necessary to observe chaotic trajectories. Glendinning and Perry [13] have utilized a periodically forced nonlinear incidence rate to prove that there are SIR models with chaotic trajectories. The choice of the incidence function used is $\beta (t)I^2$ with the transmission rate (5) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ\mathrm{\Omega }t)),$(5) where ε is a small positive parameter and Ω is the frequency of harmonic excitation. Diallo and Kon [9] establishes mathematically the existence of chaotic motion of the SIR models by Melnikov's method through a series of coordinate transformations to bring the equations into amenable to Melnikov analysis. The choice of the incidence function used is $\beta (t)I^p$ with the transmission rate (6) $\beta (t)=\frac{p^{2p}}{(p-1{)}^{2p-1}}\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ\mathrm{\Omega }t)),$(6) where $ϵ,\mathrm{\Omega }$ are same as (5(5) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ\mathrm{\Omega }t)),$(5) ), and $\sin (\mu ϵ\mathrm{\Omega }t)$ is a periodic function. Diallo et al. [10] studied the well-known SIR model of epidemic dynamics with an almost periodic incidence rate in the form $\beta (t)I^p$ with the transmission rate (7) $\beta (t)=\frac{p^{2p}}{(p-1{)}^{2p-1}}\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3(\sin (\mu ϵ\mathrm{\Omega }t)+\sin (\sqrt{2}\mu ϵ\mathrm{\Omega }t))),$(7) where $ϵ,\mathrm{\Omega }$ are same as above, and $\sin t+\sin \sqrt{2}t$ is a (possibly not periodic) almost periodic function. It maked the use of similar techniques utilized in recent work to establish the existence of chaotic motions.

In this paper, we will consider the incidence function $\beta (t)I^2$, which may vary periodically and stochastically with time and the transmission rate is (8) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t)),$(8) where $b_1,b_2,b_3,b_4$ and ${\mathrm{\Omega }}_1$ are order one constants such that (9) $4b_2-b_1^2>0$(9) is also of order one. If p=2, $\frac{p^{2p}}{(p-1{)}^{2p-1}}$ in (7(7) $\beta (t)=\frac{p^{2p}}{(p-1{)}^{2p-1}}\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3(\sin (\mu ϵ\mathrm{\Omega }t)+\sin (\sqrt{2}\mu ϵ\mathrm{\Omega }t))),$(7) ) can be transformed into 16 in (8(8) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t)),$(8) ). Nevertheless, there is an almost periodically in (7(7) $\beta (t)=\frac{p^{2p}}{(p-1{)}^{2p-1}}\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3(\sin (\mu ϵ\mathrm{\Omega }t)+\sin (\sqrt{2}\mu ϵ\mathrm{\Omega }t))),$(7) ) and periodically and stochastically in (8(8) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t)),$(8) ) forced nonlinear incidence rate. The latter is more complex which be unaware of any work for proving mathematically that can be chaotic.

We will also assume that (10) $\gamma =\mu (1+{ϵ}^2{b}_1).$(10) Thus we are dealing with a disease for which the timescales for infection, recovery and reproduction are all of the same order of magnitude and such that the transmission rate varies very slowly (assuming that μ is bounded as ε tends to zero). $\xi (t)$ is belong to stochastic excitation and called bounded noise to be described that is a harmonic function with constant amplitude and random frequency and phase. The mathematical expression for the bounded noise is (11) $\xi (t)=b_4\sin ({\mathrm{\Omega }}_{2}t+\mathrm{\Psi }),\mathrm{\Psi }=\sigma B(t)+\mathrm{\Gamma },$(11) where ${\mathrm{\Omega }}_2$ and σ are positive constant. $\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)$ is harmonic excitation, and $b_3$ and $b_4$ represent the amplitude or level of the harmonic and stochastic (bounded noise) excitation, respectively. ${\mathrm{\Omega }}_1$ is the frequency of harmonic and ${\mathrm{\Omega }}_2$ is average frequency of bounded noise. σ is the strength of the noise. $B(t)$ is a standard Wiener process, Γ is a random variable uniformly distributed in $[0,2\pi )$ representing a random phase angle. $\xi (t)$ is a broad-band stationary bounded stochastic process in a wide sense with zero mean which is non-Gaussian distribution [19]. Its covariance function is (12) $C_{\xi }(\tau )=\frac{b_4^2}{2}\exp (-\frac{{\sigma }^2|\tau |}{2})\cos ({\mathrm{\Omega }}_2\tau ).$(12) The variance of the bounded noise is $C_{\xi }(0)=b_4^2/2$ which implies that the bounded noise has finite power. Its spectral density is (13) $\begin{array}{rl}{S}_{\xi }(\omega )& =\frac{(b_4\sigma {)}^2}{2\pi }(\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4})\\ & =\frac{b_4^2{\sigma }^2}{4\pi }\frac{{\omega }^2+{\mathrm{\Omega }}_2^2+\frac{{\sigma }^4}{4}}{({\omega }^2-{\mathrm{\Omega }}_2^2-\frac{{\sigma }^4}{4})+{\sigma }^4{\omega }^2}.\end{array}$(13) The spectral density of bounded noise for several sets of parameters is shown in Figure 1. The position of peak of the spectral density depends on ${\mathrm{\Omega }}_2$, and the bandwidth of the bounded noise depends mainly on σ. It has density function $p(\xi )=\frac{1}{\pi \sqrt{b_4^2-{\xi }^2}}.$ For $|\xi (t)|⩽b_4$, $\xi (t)$ is a bounded stochastic process, it is still a continuous process which satisfies the conditions which can deduce the Melnikov function [35,36]. Modifying the value of $b_4$ and σ one can obtain different band width.When $\sigma \to 0,\xi (t)$ will be narrow band process and if $\sigma \to \mathrm{\infty },\xi (t)$ will approach a white noise which has constant power. Choosing proper values for $b_4$ and $\sigma ,\xi (t)$ may represent the turbulent flow in the wind and the motion of seismic floor. So it is reasonable to add the bounded noise as a stochastic excitation. It can be shown that the sample functions of the noise are continuous and bounded which are required in the derivation of the random Melnikov process [18,24,25].

Figure 1. The spectral density of bounded noise for $b_4=1,{\mathrm{\Omega }}_2=1$. (a) $\sigma =0.1$. (b) $\sigma =0.5$. (c) $\sigma =1$ and (d) $\sigma =2$.

In this paper, our aim is to explore the effect of periodic and bounded noise excitation on the chaotic motion of system (1(1) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mu (1-S)-\beta (t)I^{2}S,\\ \frac{\mathrm{d}I}{\mathrm{d}t}& =\beta (t)I^{2}S-(\gamma +\mu )I,\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\mu R.\end{array}$(1) ) by using the stochastic Melnikov method. The paper is organized as follows. In Section 2, the random Melnikov process for Hamiltonian system subject to light damping and external or parametric perturbation of bounded noise is derived. We describe the scaling of the SIR variables which will allow us to use Melnikov's method in Section 3. The crucial step here is to identify a doubly degenerate stationary point close to which the equations can be seen as a perturbation of a nearly Hamiltonian system, and then to determine the appropriate scaling of the variables which allow Melnikov's method to be applied. In Section 4, this method is used to prove the existence of chaotic solutions in the SIR model with periodic and random transmission rates. Conclusions are made in Section 5.

2. Random Melnikov process

Consider a single degree-of-freedom Hamiltonian system subject to light damping and weakly external and (or) parametric excitations of bounded noise. The equation of motion of the system is of the form (14) $\begin{array}{rl}\dot{x}& =\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y},\\ \dot{y}& =-\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }x}-ϵg(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+ϵf(x,y)\xi (t),\end{array}$(14) where x and y are generalized displacement and momentum, respectively; $H_a=H_a(x,y)$ is Hamiltonian with continuous first-order derivatives; ε is a small positive parameter; $g(x,y)$ denotes the coefficient of quasi-linear damping; $f(x,y)$ denotes the amplitude of excitation. $f\xi (t)$ is an external excitation of bounded noise if f is a constant. Otherwise, it is a parametric excitation. It is assumed that the Hamiltonian system associated with Equation (14(14) $\begin{array}{rl}\dot{x}& =\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y},\\ \dot{y}& =-\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }x}-ϵg(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+ϵf(x,y)\xi (t),\end{array}$(14) ) possesses a hyperbolic fixed point connected to itself by homoclinic orbits $(x_0(t),y_0(t))$.

A bounded noise with spectral density (13(13) $\begin{array}{rl}{S}_{\xi }(\omega )& =\frac{(b_4\sigma {)}^2}{2\pi }(\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4})\\ & =\frac{b_4^2{\sigma }^2}{4\pi }\frac{{\omega }^2+{\mathrm{\Omega }}_2^2+\frac{{\sigma }^4}{4}}{({\omega }^2-{\mathrm{\Omega }}_2^2-\frac{{\sigma }^4}{4})+{\sigma }^4{\omega }^2}.\end{array}$(13) ) can be approximated by a sum of many harmonic functions with different frequency and random phases. As in [25], the random Melnikov process for system (14(14) $\begin{array}{rl}\dot{x}& =\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y},\\ \dot{y}& =-\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }x}-ϵg(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+ϵf(x,y)\xi (t),\end{array}$(14) ) is (15) $M(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}[-g(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+f(x,y)\xi (t+t_0)]\mathrm{d}t=M_d+Z(t_0),$(15) where $M_d$ is the component of Melnikov process due to damping and $Z(t_0)$ is that due to bounded noise excitation. Note that $x(t)$ and $y(t)$ in the integrand of Equation (15(15) $M(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}[-g(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+f(x,y)\xi (t+t_0)]\mathrm{d}t=M_d+Z(t_0),$(15) ) are taken as $x_0(t)$ and $y_0(t)$ of homoclinic orbit. Obviously, the mean of random Melnikov process is (16) $E[M(t_0)]=M_d=-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(x,y){\left(\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}\right)}^2\mathrm{d}t,$(16) where $E[\bullet ]$ denotes the expectation operator. For positive damping, Equation (16(16) $E[M(t_0)]=M_d=-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(x,y){\left(\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}\right)}^2\mathrm{d}t,$(16) ) always yields a negative value, which implies that system (14(14) $\begin{array}{rl}\dot{x}& =\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y},\\ \dot{y}& =-\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }x}-ϵg(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+ϵf(x,y)\xi (t),\end{array}$(14) ) cannot be chaotic in mean sense. The mean-square values of the two components of random Melnikov process (15(15) $M(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}[-g(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+f(x,y)\xi (t+t_0)]\mathrm{d}t=M_d+Z(t_0),$(15) ) are (17) $\begin{array}{rl}{M}_d^2& ={({\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(x,y){\left(\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}\right)}^2\mathrm{d}t)}^2,\end{array}$(17) (18) $\begin{array}{rl}{\sigma }_Z^2& =E(Z^2(t_0))=E\left[{({\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}f(x,y)\xi (t+t_0)\mathrm{d}t)}^2\right].\end{array}$(18) To calculate ${\sigma }_Z^2$, $Z(t_0)$ in Equation (15(15) $M(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}[-g(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+f(x,y)\xi (t+t_0)]\mathrm{d}t=M_d+Z(t_0),$(15) ) is rewritten as a convolution integral (19) $Z(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}f(x,y)\xi (t+t_0)\mathrm{d}t=h(t)\ast \xi (t),$(19) where $h(t)=(\mathrm{\partial }{H}_a/\mathrm{\partial }y)f(x,y){|}_{x=x_0(t),y=y_0(t)}$ can be regarded as the impulse response function of a time-invariant linear system while $\xi (t)$ as an input to the system. Thus, the variance of the system can be obtained in the frequency domain as follows: (20) ${\sigma }_Z^2={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}|H(\omega ){|}^2{S}_{\xi }(\omega )\mathrm{d}\omega ,$(20) where $H(\omega )$ is the frequency response function of the system, which is the Fourier transformation of the impulse response function $h(t)$.

Random Melnikov process (15(15) $M(t_0)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}[-g(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+f(x,y)\xi (t+t_0)]\mathrm{d}t=M_d+Z(t_0),$(15) ) has a simple zero in the the mean-square sense when (21) $M_d^2={\sigma }_Z^2,$(21) which yield the threshold amplitude of bounded noise excitation for the onset of chaos in the system (14(14) $\begin{array}{rl}\dot{x}& =\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y},\\ \dot{y}& =-\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }x}-ϵg(x,y)\frac{\mathrm{\partial }{H}_a}{\mathrm{\partial }y}+ϵf(x,y)\xi (t),\end{array}$(14) ).

3. Scaling the equations

Since S=1−I−R the basic SIR model, (1(1) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mu (1-S)-\beta (t)I^{2}S,\\ \frac{\mathrm{d}I}{\mathrm{d}t}& =\beta (t)I^{2}S-(\gamma +\mu )I,\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\mu R.\end{array}$(1) ) can be written as (22) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}t}& =\beta (t)I^2(1-I-R)-(\gamma +\mu )I,\\ \frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\mu R.\end{array}$(22) Define a new timescale $t^{\prime }=\mu t$ with respect to which the equations are independent of μ, so (23) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}{t}^{\prime }}& ={\beta }^{\prime }(t^{\prime })I^2(1-I-R)-({\gamma }^{\prime }+1)I,\\ \frac{\mathrm{d}R}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }I-R.\end{array}$(23) where $\beta =\mu {\beta }^{\prime }$ and $\gamma =\mu {\gamma }^{\prime }$.

We need to change coordinates in such a way that the system is able to use the Melnikov method. We will make a succession of changes of coordinates to bring the equation into a standard form, based around the fact that near certain degenerate stationary points it is, typically, possible to write the equations as perturbations of a Hamiltonian system. Link in [9], our first aim is to make some changes of coordinates in order to adapt the system (23(23) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}{t}^{\prime }}& ={\beta }^{\prime }(t^{\prime })I^2(1-I-R)-({\gamma }^{\prime }+1)I,\\ \frac{\mathrm{d}R}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }I-R.\end{array}$(23) ) to the Melnikov analysis.

We shall work with (23(23) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}{t}^{\prime }}& ={\beta }^{\prime }(t^{\prime })I^2(1-I-R)-({\gamma }^{\prime }+1)I,\\ \frac{\mathrm{d}R}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }I-R.\end{array}$(23) ), and for the remainder of this section we shall drop the primes to avoid making the equations look worse than they are. Begin by defining a new variable $z=\gamma I-R$, so (23(23) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}{t}^{\prime }}& ={\beta }^{\prime }(t^{\prime })I^2(1-I-R)-({\gamma }^{\prime }+1)I,\\ \frac{\mathrm{d}R}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }I-R.\end{array}$(23) ) becomes (24) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =\gamma \dot{I}-\dot{R}=P_2(R,z),\end{array}$(24) where the dots denote differentiation with respect to the rescaled time. After a little manipulation, substituting (23(23) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}{t}^{\prime }}& ={\beta }^{\prime }(t^{\prime })I^2(1-I-R)-({\gamma }^{\prime }+1)I,\\ \frac{\mathrm{d}R}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }I-R.\end{array}$(23) ) into the second equation of (24(24) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =\gamma \dot{I}-\dot{R}=P_2(R,z),\end{array}$(24) ) and using $I={\gamma }^{-1}(R+z)$, so (24(24) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =\gamma \dot{I}-\dot{R}=P_2(R,z),\end{array}$(24) ) becomes (25) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =-(1+\gamma )R+\beta (t)\frac{1}{\gamma }{R}^2-\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^3-(2+\gamma )z+\beta (t)\frac{1}{\gamma }{z}^2-\beta (t)\frac{1}{{\gamma }^2}{z}^3\\ & +2\beta (t)\frac{1}{\gamma }Rz-\beta (t)\frac{1}{\gamma }(1+\frac{3}{\gamma })R{z}^2-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^{2}z=P_2(R,z).\end{array}$(25) Stationary points of (25(25) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =-(1+\gamma )R+\beta (t)\frac{1}{\gamma }{R}^2-\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^3-(2+\gamma )z+\beta (t)\frac{1}{\gamma }{z}^2-\beta (t)\frac{1}{{\gamma }^2}{z}^3\\ & +2\beta (t)\frac{1}{\gamma }Rz-\beta (t)\frac{1}{\gamma }(1+\frac{3}{\gamma })R{z}^2-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^{2}z=P_2(R,z).\end{array}$(25) ) clear have z=0 and either R=0 which corresponds to the disease-free equilibrium, or z=0 and R satisfies (26) $\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^2-\beta (t)\frac{1}{\gamma }R+(1+\gamma )=0,R\ne 0.$(26) This quadratic (26(26) $\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^2-\beta (t)\frac{1}{\gamma }R+(1+\gamma )=0,R\ne 0.$(26) ) has two real roots if $\mathrm{△}>0,$ that is $(\beta (t)1/\gamma {)}^2-4\beta (t)1/\gamma (1+(1/\gamma ))(1+\gamma )>0.$ We obtain by simplifying $\beta >4(1+\gamma {)}^2.$ So the system (25(25) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =-(1+\gamma )R+\beta (t)\frac{1}{\gamma }{R}^2-\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^3-(2+\gamma )z+\beta (t)\frac{1}{\gamma }{z}^2-\beta (t)\frac{1}{{\gamma }^2}{z}^3\\ & +2\beta (t)\frac{1}{\gamma }Rz-\beta (t)\frac{1}{\gamma }(1+\frac{3}{\gamma })R{z}^2-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^{2}z=P_2(R,z).\end{array}$(25) ) has a saddle-node bifurcation if $\beta (t)={\beta }_{sn}(t)=4(1+\gamma {)}^2.$ At this value, the equilibrium, supporting an endemic level of the disease, is $S_{sn}=\frac{1}{2},I_{sn}=\frac{1}{2(1+\gamma )},R_{sn}=\frac{r}{2(1+\gamma )}.$ The Jacobian matrix of the system (25(25) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =-(1+\gamma )R+\beta (t)\frac{1}{\gamma }{R}^2-\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^3-(2+\gamma )z+\beta (t)\frac{1}{\gamma }{z}^2-\beta (t)\frac{1}{{\gamma }^2}{z}^3\\ & +2\beta (t)\frac{1}{\gamma }Rz-\beta (t)\frac{1}{\gamma }(1+\frac{3}{\gamma })R{z}^2-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^{2}z=P_2(R,z).\end{array}$(25) ) at z=0 is $A=\left(\begin{array}{cc}{\displaystyle \frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }R}}& {\displaystyle \frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }z}}\\ {\displaystyle \frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }R}}& {\displaystyle \frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }z}}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ J_{21}& J_{22}\end{array}\right),$ where $\begin{array}{rl}{J}_{21}& =-(1+\gamma )+2\beta (t)\frac{1}{\gamma }R-3\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^2,\\ J_{22}& =-(2+\gamma )+2\beta (t)\frac{1}{\gamma }R-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^2.\end{array}$ The determinant of this matrix $(-J_{21})$ equals to 0 at $\beta (t)=4(1+\gamma {)}^2$, but if, in addition, the trace $(J_{22})$ also equals to 0, then we have a more degenerate situation, Known as a Takens–Bogdanov point and near this point it should be possible to write the equations in nearly Hamiltonian form as required if the Melnikov method is to be applied [15]. The trace of the Jacobian matrix equals to 0 at the saddle-node point (where $\beta =4(1+\gamma {)}^2,R=\gamma /2(1+\gamma )$) if (27) $\gamma =1,\beta =16.$(27) For these values of parameters, the degenerate equilibrium is $S_{tb}=\frac{1}{2},I_{tb}=\frac{1}{4},R_{tb}=\frac{1}{4}.$ Note that a curve of Hopf bifurcation also terminates at this point. This curve is given by $J_{22}=0,J_{21}<0.$

To perturb about this degenerate equilibrium point we define new variables and parameters by $R=\frac{1}{4}+\theta ,\gamma =1+g,\beta (t)=16(1+b(t)),$ where $\theta ,g$ and b are to be thought of as small (they will be chosen in accordance with (8(8) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t)),$(8) )–(10(10) $\gamma =\mu (1+{ϵ}^2{b}_1).$(10) ) in Section 1, but for the moment it is instructive to think of them as arbitrary small numbers, so that the scaling of Section 1 are demystified. Substituting into (25(25) $\begin{array}{rl}\dot{R}& =z=P_1(R,z),\\ \dot{z}& =-(1+\gamma )R+\beta (t)\frac{1}{\gamma }{R}^2-\beta (t)\frac{1}{\gamma }(1+\frac{1}{\gamma })R^3-(2+\gamma )z+\beta (t)\frac{1}{\gamma }{z}^2-\beta (t)\frac{1}{{\gamma }^2}{z}^3\\ & +2\beta (t)\frac{1}{\gamma }Rz-\beta (t)\frac{1}{\gamma }(1+\frac{3}{\gamma })R{z}^2-\beta (t)\frac{1}{\gamma }(2+\frac{3}{\gamma })R^{2}z=P_2(R,z).\end{array}$(25) ) and ignoring cubic order and higher we find (28) $\begin{array}{rl}\dot{\theta }& =z,\\ \dot{z}& =(\frac{1}{2}b(t)-\frac{1}{2}g-\frac{1}{4}b(t)g)+(2b(t))\theta -8{\theta }^2+(3b(t)-g)z-8\theta z\\ & +O((|\theta |+|z|+|g|+|b(t)|{)}^3).\end{array}$(28) We introduce the small parameter ε by setting (29) $b(t)={ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t),g={ϵ}^2{b}_1.$(29) In accordance with (8(8) $\beta (t)=16\mu (1+{ϵ}^2{b}_1+{ϵ}^4{b}_2+{ϵ}^5{b}_3\sin (\mu ϵ{\mathrm{\Omega }}_{1}t)+{ϵ}^5{b}_4\xi (t)),$(8) ), so $\begin{array}{rl}\frac{1}{2}b(t)-\frac{1}{2}g-\frac{1}{4}b(t)g& =(\frac{1}{2}{b}_2-\frac{1}{4}{b}_1^2){ϵ}^4+\frac{1}{2}{b}_3{ϵ}^5\sin (ϵ{\mathrm{\Omega }}_{1}t)+\frac{1}{2}{b}_4{ϵ}^5\xi (t)+o({ϵ}^6),\\ 2b(t)& =2b_1{ϵ}^2+o({ϵ}^4),\\ 3b(t)-g& =2b_1{ϵ}^2+o({ϵ}^4).\end{array}$ Defining new coordinates and time by $\theta ={ϵ}^{2}u,z={ϵ}^{3}v,\tau =ϵt,$ gives $\begin{array}{rl}\frac{\mathrm{d}u}{\mathrm{d}\tau }& =v,\\ \frac{\mathrm{d}v}{\mathrm{d}\tau }& =(\frac{1}{2}{b}_2-\frac{1}{4}{b}_1^2)+2b_{1}u-8u^2\\ & +ϵ(2b_{1}v-8uv+\frac{1}{2}{b}_3\sin ({\mathrm{\Omega }}_1\tau )+\frac{1}{2}{b}_4\xi (\tau ))+o({ϵ}^2)\\ & =(\frac{1}{2}{b}_2-\frac{1}{8}{b}_1^2)-8{(u-\frac{1}{8}{b}_1)}^2\\ & +ϵ(2b_{1}v-8uv+\frac{1}{2}{b}_3\sin ({\mathrm{\Omega }}_1\tau )+\frac{1}{2}{b}_4\xi (\tau ))+o({ϵ}^2).\end{array}$ and so, setting $\eta =u-\frac{1}{8}{b}_1$, we obtain (30) $\begin{array}{rl}\frac{\mathrm{d}\eta }{\mathrm{d}\tau }& =v,\\ \frac{\mathrm{d}v}{\mathrm{d}\tau }& =(\frac{1}{2}{b}_2-\frac{1}{8}{b}_1^2)-8{\eta }^2+ϵ(b_{1}v-8\eta v+\frac{1}{2}{b}_3\sin ({\mathrm{\Omega }}_1\tau )+\frac{1}{2}{b}_4\xi (\tau ))+o({ϵ}^2).\end{array}$(30) On further rescaling brings this equation into a standard form [37]: let $x=-8\eta ,y=-8v,$ then Equations (30(30) $\begin{array}{rl}\frac{\mathrm{d}\eta }{\mathrm{d}\tau }& =v,\\ \frac{\mathrm{d}v}{\mathrm{d}\tau }& =(\frac{1}{2}{b}_2-\frac{1}{8}{b}_1^2)-8{\eta }^2+ϵ(b_{1}v-8\eta v+\frac{1}{2}{b}_3\sin ({\mathrm{\Omega }}_1\tau )+\frac{1}{2}{b}_4\xi (\tau ))+o({ϵ}^2).\end{array}$(30) ) become (31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) where $c^2=4b_2-b_1^2$, where is a strictly positive order one constant by assumption (9(9) $4b_2-b_1^2>0$(9) ). In the following we suppose that c>0.

Equation (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with $b_3=0$ and $b_4=0$ is a standard normal form for the Takens–Bogdanov bifurcation, and an extensive analysis can be found in Chow et al. [7]. The dynamics is boring if $b_1<0,$ so assume that $b_1>0,c^2=4b_2-b^2>0,b_3=0$ and $b_4=0$. Then there are two stationary points: $S_{\pm }=(\pm c,0)$, $S_{+}$ is a saddle and

1. if $2b_1^2>4b_2>b_1^2$ then $S_{-}$ is an unstable focus;

2. if $l(b_1)>4b_2>2b_1^2$, where $l(b_1)\approx (74/25)b_1^2$, then $S_{-}$ is a stable focus and is surrounded by an unstable periodic orbit;

3. if $4b_2>l(b_1)$ then $S_{-}$ is a stable focus, and there are no periodic orbits encircling it.

The bifurcation at $b_1^2=2b_2$ is a standard (subcritical) hopf bifurcation, and the bifurcation which destroys the periodic orbit at $l(b_1)=4b_2$ is a homoclinic (global) bifurcation.

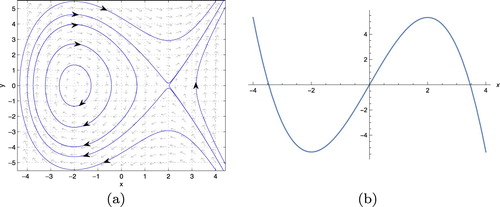
The phase portraits are shown in Figure 2(a–c) for $b_3=0,b_4=0$. (a): $b_1=2,b_2=3/2$, (b): $b_1=2,b_2=5/2$, (c): $b_1=2,b_2=3$, respectively. In Figure 2(a), $S_{+}(\sqrt{2},0)$ is a saddle, and $S_{-}(-\sqrt{2},0)$ is an unstable focus. In Figure 2(b), $S_{+}(\sqrt{6},0)$ is a saddle, and $S_{-}(-\sqrt{6},0)$ is a stable focus and is surrounded by an unstable periodic orbit. In Figure 2(c), $S_{+}(2\sqrt{2},0)$ is a saddle, and $S_{-}(-2\sqrt{2},0)$ is a stable focus, and there are no periodic orbits encircling it.

Figure 2. Phase portraits of the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) for $b_3=0,b_4=0$.(a) $b_1=2,b_2=3/2$. (b) $b_1=2,b_2=5/2$ and (c) $b_1=2,b_2=3$

4. Chaos in the SIR model with periodically or stochastically modulated nonlinear incidence rate

We can apply Melnikov method to the SIR model in the form (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) for sufficiently small ε. If $ϵ=0$, Equation (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) is considered as an unperturbed system and can be written as (32) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2=-(4b_2-b_1^2)+x^2,\end{array}$(32) where dots now denote differentiation with respect to the rescaled time τ and c>0. Equation (32(32) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2=-(4b_2-b_1^2)+x^2,\end{array}$(32) ) is a Hamiltonian system with Hamiltonian function (33) $H(x,y)=\frac{1}{2}{y}^2+c^{2}x-\frac{1}{3}{x}^3=\frac{1}{2}{y}^2+(4b_2-b_1^2)x-\frac{1}{3}{x}^3.$(33) and so solution lie on curves of constant H. The function $V(x)=c^{2}x-\frac{1}{3}{x}^3=(4b_2-b_1^2)x-\frac{1}{3}{x}^3$ is called the potential function. The Jacobian matrix is $\left(\begin{array}{cc}cc0& 1\\ 2x& 0\end{array}\right)$. The characteristic polynomial is ${\lambda }^2-2x=0$. Equation (32(32) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2=-(4b_2-b_1^2)+x^2,\end{array}$(32) ) is well- known in the literature [15]. It has two stationary points: $S(c,0)$, which is a saddle and $C(-c,0)$, which is a centre. The centre is surrounded by a continuous family of periodic orbits, $(x_T(\tau ),y_T(\tau ))$ and these are bounded by a homoclinic orbit ${\mathrm{\Gamma }}_{hom}:((x_h(\tau ),y_h(\tau ))$ such that $\underset{\tau \to \pm \mathrm{\infty }}{lim}(x_h(\tau ),y_h(\tau ))=(c,0).$ The explicit form of the homoclinic solution [15] is (34) $\begin{array}{rl}{x}_h(\tau )& =c-3c{\cosh }^{-2}\left(\tau \sqrt{\frac{c}{2}}\right),\\ y_h(\tau )& =3c\sqrt{2c}{\cosh }^{-2}\left(\tau \sqrt{\frac{c}{2}}\right)\tanh \left(\tau \sqrt{\frac{c}{2}}\right),\end{array}$(34) The phase portrait and potential diagram are shown in Figure 3(a,b) for $b_1=0,b_2=1$, respectively. In Figure 3(a), $C(-2,0)$ is a centre and $S(2,0)$ is a saddle, which is connected itself by homoclinic orbits ${\mathrm{\Gamma }}_{hom}$.

Figure 3. Phase portrait and potential of the system (32(32) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2=-(4b_2-b_1^2)+x^2,\end{array}$(32) ) for $b_1=0,b_2=1$. (a) Phase portrait. (b) Potential.

In the following, three cases are considered and $t_0$ is the cross-section time of the Pioncar$\acute{e}$ map and $t_0$ can be interpreted as the initial time of the forcing term.

Case 1: Now we can find the Melnikov function of system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) without stochastic excitation $(b_4=0)$ as follows: (35) $\begin{array}{rl}M(t_0)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{y}_h(t)(b_1{y}_h(t)+x_h(t)y_h(t)-4b_3\sin {\mathrm{\Omega }}_1(t+t_0))\mathrm{d}t\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-\frac{24\pi {\mathrm{\Omega }}_1^2{b}_3}{\sinh (\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}})}\cos ({\mathrm{\Omega }}_1{t}_0),\end{array}$(35) If the Melnikov function has simple zero point, the stable manifolds and the unstable manifolds intersect transversally, chaos in the sense of Smale horseshoe transform will occur. So let $M(t_0)=0$, the criterion for the existence of a zero of this Melnikov function is easy to obtain from $|\cos ({\mathrm{\Omega }}_1{t}_0)|<1$. $|b_3|>b_c$, where (36) $b_c\approx \frac{\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}}{24\pi {\mathrm{\Omega }}_1^2}\sinh \left(\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}}\right),$(36) and the following theorem can be obtained.

Theorem 4.1

If $|b_3|>b_c$, the stable and unstable manifolds of the fixed point in the Poincar$\acute{e}$ map intersect transversely and there is chaos in the model, whilst if $|b_3|<b_c$, there is no intersection between the stable and unstable manifolds. At $|b_3|=b_c$ there is a tangential intersection between the stable and unstable manifolds.

If $b_1=0$, then $c^2=4b_2$, it takes a particularly simple form: $|b_3|>b_c$, where $b_c\approx \frac{(2c{)}^{7/2}}{56\pi {\mathrm{\Omega }}_1^2}\sinh \left(\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}}\right).$The homoclinic bifurcation curve for Smale chaos in the $({\mathrm{\Omega }}_1,b_3)$ plane for $b_1=0,b_2=1$ and $b_1=0,b_2=2$ in Figure 4(a,b), respectively. In the parameter region below the bifurcation curve, no transverse intersection of stable and unstable manifolds of saddle occurs and above the bifurcation curve, the transverse intersections of stable and unstable manifolds of the saddle occur. Just above the homoclinic bifurcation curve onset of cross-well chaos is expected.

The phase portraits of the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) for $b_1=0,b_2=1,b_3=3,{\mathrm{\Omega }}_1=2,ϵ=0.00001$ and $b_1=0,b_2=2,b_3=5,{\mathrm{\Omega }}_1=2,ϵ=0.00001$ are plotted in Figure 5(a,b). By simple calculating with (36(36) $b_c\approx \frac{\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}}{24\pi {\mathrm{\Omega }}_1^2}\sinh \left(\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}}\right),$(36) ), $b_c\approx 2.10062$ and 4.27242, respectively. We can see that the motion of system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) are chaotic from Figure 5.

Figure 4. The homoclinic bifurcation curve for Smale chaos in the $({\mathrm{\Omega }}_1,b_3)$ plane. (a) $b_1=0,b_2=1$ and (b) $b_1=0,b_2=2$.

Figure 5. Phase portrait with $b_1=0,{\mathrm{\Omega }}_1=2,ϵ=0.00001$ and initial value: $x(0)=0.1,y(0)=0.2$. (a) $b_2=1,b_3=3$ and (b) $b_2=2,b_3=5$.

Case 2: Now we can find the Melnikov function of system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with two periodic excitation $(\mathrm{\Psi }=0)$ as follows: (37) $\begin{array}{rl}M(t_0)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{y}_h(t)(b_1{y}_h(t)+x_h(t)y_h(t)-4b_3\sin {\mathrm{\Omega }}_1(t+t_0)-4b_4\sin {\mathrm{\Omega }}_2(t+t_0))\mathrm{d}t\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-\frac{24\pi {\mathrm{\Omega }}_1^2{b}_3}{\sinh (\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}})}\cos ({\mathrm{\Omega }}_1{t}_0)-\frac{24\pi {\mathrm{\Omega }}_2^2{b}_4}{\sinh \left(\frac{{\mathrm{\Omega }}_2\pi }{(2c{)}^{1/2}}\right)}\cos ({\mathrm{\Omega }}_2{t}_0)\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-24\pi (\frac{{\mathrm{\Omega }}_1^2{b}_3}{\sinh (\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}})}\cos ({\mathrm{\Omega }}_1{t}_0)\\ & +\frac{{\mathrm{\Omega }}_2^2{b}_4}{\sinh \left(\frac{{\mathrm{\Omega }}_2\pi }{(2c{)}^{1/2}}\right)}\cos ({\mathrm{\Omega }}_2{t}_0)),\\ & =C_0+C_1\cos ({\mathrm{\Omega }}_1{t}_0)+C_2\cos ({\mathrm{\Omega }}_2{t}_0),\end{array}$(37) where $C_0=\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2},C_1=-\frac{24\pi {\mathrm{\Omega }}_1^2{b}_3}{\sinh (\frac{{\mathrm{\Omega }}_1\pi }{(2c{)}^{1/2}})},C_2=-\frac{24\pi {\mathrm{\Omega }}_2^2{b}_4}{\sinh (\frac{{\mathrm{\Omega }}_2\pi }{(2c{)}^{1/2}})}.$ The criterion for the existence of a zero of this Melnikov function is obtained from $|\cos ({\mathrm{\Omega }}_1{t}_0)|<1$ and $|\cos ({\mathrm{\Omega }}_2{t}_0)|<1$. Therefore we obtain criteria for the existence of chaos in two periodic forced system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) if (38) $|C_0|<\sqrt{C_1^2+C_2^2}.$(38)

Theorem 4.2

Suppose the condition (38(38) $|C_0|<\sqrt{C_1^2+C_2^2}.$(38) ) is satisfied, then a homoclinic bifurcation occurs, then the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) may exhibits chaotic motion.

The upper bound of possible chaotic domain due to the homoclinic bifurcation for the cases without noise perturbation of system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) is obtained by equating the expressions in (38(38) $|C_0|<\sqrt{C_1^2+C_2^2}.$(38) ) and portrayed in Figure 6(a). It depict the domains of possible occurrence of chaotic motion in $(b_3,b_4,b_1)$ space. 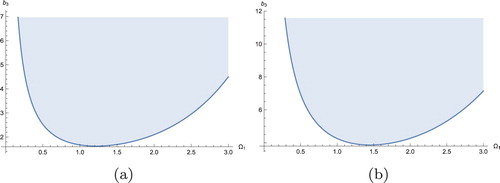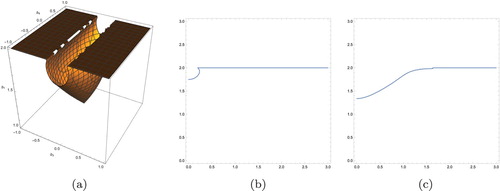The upper bounds are also presented in Figure 6(b,c) with $b_4=1$ and $b_3=0.2$ for the case without noise perturbation in $(b_3,b_1)$ and $(b_4,b_1)$ plane, respectively. From Figure 6 one can see that the presence of two periodic excitation enlarges the threshold amplitude and reduces the possible chaotic domain in small parameter space.

Figure 6. Upper bound for possible chaotic domain due to homoclinic bifurcation $(\mathrm{\Psi }=0)$ with ${\mathrm{\Omega }}_1=1,{\mathrm{\Omega }}_2=2,b_2=1$. (a) Upper surface in $(b_3,b_4,b_1)$ space. (b) Upper bound in $(b_3,b_1)$ plane with $b_4=1$ and (c) Upper bound in $(b_4,b_1)$ plane with $b_3=0.2$.

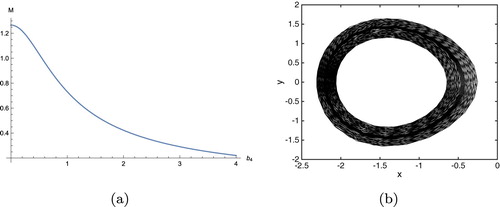
Let $M=\frac{|C_0|}{\sqrt{C_1^2+C_2^2}},$ then the condition (38(38) $|C_0|<\sqrt{C_1^2+C_2^2}.$(38) ) is written as (38′) $\begin{array}{}\text{(}{38}^{\prime }\text{)}& M<1.\end{array}$(38′) The bifurcation curve (38′(38′) $\begin{array}{}\text{(}{38}^{\prime }\text{)}& M<1.\end{array}$(38′) ) for the homoclinic orbit ${\mathrm{\Gamma }}_{hom}$ covering the range $0<b_4<4$ are plotted in Figure 7(a). From it we can see that when the value of $b_4$ increases, the value of M decreases. It is easy to know that if the parameter values are chosen from the region M<1, the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) can exist chaotic dynamics. For example, for the fixed parameter values $b_1=2,b_2=3/2,b_3=1,{\mathrm{\Omega }}_1=1/3$ and ${\mathrm{\Omega }}_2=\sqrt{3}$, when $b_4=2$, there is M<1. The chaotic trajectory at $b_4=2$ are shown in Figure 7(b).

Figure 7. (a) Bifurcation curve $({38}^{\prime })$ for the homoclinic orbits ${\mathrm{\Gamma }}_{hom}$. Here $b_1=2,b_2=3/2,b_3=1,{\mathrm{\Omega }}_1=1/3$ and ${\mathrm{\Omega }}_2=\sqrt{3}$; (b) Phase portrait for (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with $b_1=2,b_2=3/2,b_3=1,b_4=2,{\mathrm{\Omega }}_1=1/3,{\mathrm{\Omega }}_2=\sqrt{3},ϵ=0.00001$ and initial value: $x(0)=0.1,y(0)=0.2$.

Case 3: Now we can find the Melnikov function of system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) just with stochastic excitation ($b_3=0$).

The random Melnikov function for this problem is therefore (from (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) )) (39) $\begin{array}{rl}M(t_0)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{y}_h(t)(b_1{y}_h(t)+x_h(t)y_h(t)-4b_4\xi (t+t_0))\mathrm{d}t\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}4b_4{y}_h(t)\xi (t+t_0)\mathrm{d}t=I_1+Z(t_0),\end{array}$(39) where (40) $I_1=\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2},$(40) and (41) $Z(t_0)=-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}4b_4{y}_h(t)\xi (t+t_0)\mathrm{d}t.$(41) The first two integral in (39(39) $\begin{array}{rl}M(t_0)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{y}_h(t)(b_1{y}_h(t)+x_h(t)y_h(t)-4b_4\xi (t+t_0))\mathrm{d}t\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}4b_4{y}_h(t)\xi (t+t_0)\mathrm{d}t=I_1+Z(t_0),\end{array}$(39) ) represent the mean of the Melnikov process due to damping force, and the last integral denotes the random portion of the Melnikov process due to bounded noise $\xi (t)$. We can analyse the simple zero point of $M(t_0)$ in probability or statistics sense. Consider the mean of random process $E(Z(t_0))$ is zero, one can get $E[M(t_0)]=I_1=\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}$. If it gives a non-zero constant, that is to say in mean sense chaos never occurs in system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ). If it equals to zero, in the mean-value sense the condition for the occurrence of chaotic motion in the sense of Smale horseshoe transform is $\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}=0$. 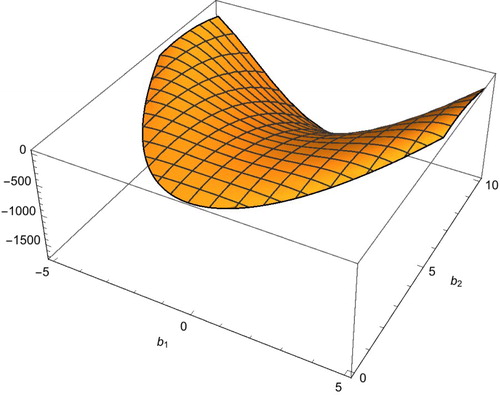The surface $I_1=0$ in $(b_1,b_2,t_0)$ plane is shown in Figure 8.

Figure 8. The surface in $(b_1,b_2,t_0)$ plane for $I_1=0$.

Now, let us consider if random Melnikov process (39(39) $\begin{array}{rl}M(t_0)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{y}_h(t)(b_1{y}_h(t)+x_h(t)y_h(t)-4b_4\xi (t+t_0))\mathrm{d}t\\ & =\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}4b_4{y}_h(t)\xi (t+t_0)\mathrm{d}t=I_1+Z(t_0),\end{array}$(39) ) has simple zeros on mean-square sense. In this case, the impulse response function is (42) $h(t)=y_h(t)=3c\sqrt{2c}{\cosh }^{-2}\left(t\sqrt{\frac{c}{2}}\right)\tanh \left(t\sqrt{\frac{c}{2}}\right),$(42) and the associated frequency response function of the system is (43) $\begin{array}{rl}H(\omega )& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}h(t)\exp (-j\omega t)\mathrm{d}t\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}3c\sqrt{2c}{\cosh }^{-2}\left(t\sqrt{\frac{c}{2}}\right)\tanh \left(t\sqrt{\frac{c}{2}}\right)\exp (-j\omega t)\mathrm{d}t\\ & =\frac{j\pi {\omega }^2}{2(-\frac{1}{3\sqrt{2c}})\sinh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)\cosh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)}.\end{array}$(43) i.e. the Fourier transformation of the impulse response function $h(t)$. Note that $\xi (t)$ has zero mean. We can also consider whether the mean value of $(M(t_0)-E[M(t_0)]{)}^2$ and $(0-E[M(t_0)]{)}^2$ may be equal. Since that (44) $\begin{array}{rl}E(M(t_0)-E[M(t_0)]{)}^2& =E[Z(t_0){]}^2={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}|H(\omega ){|}^2{S}_{\xi }(\omega )\mathrm{d}\omega ={\sigma }_Z^2,\end{array}$(44) (45) $\begin{array}{rl}E(0-E[M(t_0)]{)}^2& =E^2[M(t_0)]=I_1^2.\end{array}$(45) $S_{\xi }(\omega )$ is the spectral density of $\xi (t)$. Random Melnikov process has simple zeros in mean-square sense if (46) $I_1^2={\sigma }_Z^2.$(46) The variance of $Z(t_0)$ as the output of the system can be expressed as follows. (47) $\begin{array}{rl}{\sigma }_Z^2& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}|H(\omega ){|}^2{S}_{\xi }(\omega )\mathrm{d}\omega \\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}|H(\omega ){|}^2\frac{(b_4\sigma {)}^2}{2\pi }(\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4})\mathrm{d}\omega .\end{array}$(47)

Theorem 4.3

The criterion for possible chaotic motion based on Melnikov process is performed in mean-square representation $I_1^2={\sigma }_Z^2$, i.e. (48) $\begin{array}{rl}{[\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}]}^2& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\left[\frac{j\pi {\omega }^2}{2(-\frac{1}{3\sqrt{2c}})\sinh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)\cosh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)}\right]}^2\\ & \times \frac{(b_4\sigma {)}^2}{2\pi }[\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}]\mathrm{d}\omega ,\\ & =\frac{9\pi b_4^{2}c}{4}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\sigma }^2{\omega }^4}{{\sinh }^2\left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right){\cosh }^2\left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)}\\ & \times [\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}]\mathrm{d}\omega .\end{array}$(48)

The integral in (48(48) $\begin{array}{rl}{[\frac{6}{5}(2c{)}^{5/2}{b}_1-\frac{3}{7}(2c{)}^{7/2}]}^2& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\left[\frac{j\pi {\omega }^2}{2(-\frac{1}{3\sqrt{2c}})\sinh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)\cosh \left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)}\right]}^2\\ & \times \frac{(b_4\sigma {)}^2}{2\pi }[\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}]\mathrm{d}\omega ,\\ & =\frac{9\pi b_4^{2}c}{4}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\sigma }^2{\omega }^4}{{\sinh }^2\left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right){\cosh }^2\left(\frac{\pi \omega }{4\sqrt{\frac{c}{2}}}\right)}\\ & \times [\frac{1}{4(\omega -{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}+\frac{1}{4(\omega +{\mathrm{\Omega }}_2{)}^2+{\sigma }^4}]\mathrm{d}\omega .\end{array}$(48) ) can be calculated by numerical method. Numerical computation has been made for the following parameter values: $b_1=2,b_2=3/2,{\mathrm{\Omega }}_2=2$. The mean-square criterion in (46(46) $I_1^2={\sigma }_Z^2.$(46) ) yields the threshold of bounded noise amplitude for the onset of chaos in the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) by numerical computation, which is shown in Figure 9(a,b).

Figure 9. The threshold amplitude $b_4$ of bounded noise excitation for the onset of chaos in system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with $b_3=0,b_1=2,b_2=3/2,{\mathrm{\Omega }}_2=2$. (a) $\sigma \in [0,3];(b)\sigma \in [0,1]$.

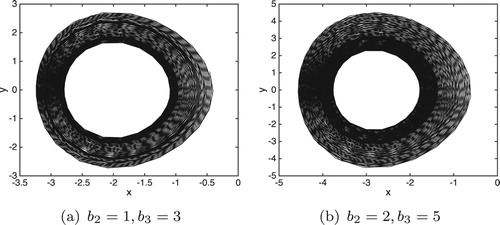
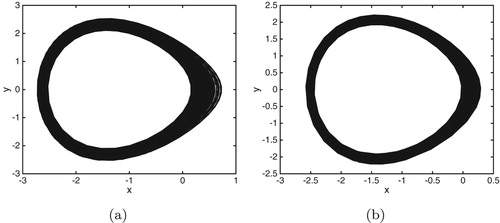
The phase portraits of the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) for $b_4=7.5,\sigma =0.5$ and $b_4=10,\sigma =2$ are shown in from Figure 10(a,b). We can see the chaos orbits.

Figure 10. Phase portraits of the system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with $b_3=0,b_1=2,b_2=3/2,{\mathrm{\Omega }}_2=2$ and $ϵ=0.00001$. (a) $b_4=7.5,\sigma =0.5$ with initial value: $x(0)=0.1,y(0)=0.2$. (b) $b_4=10,\sigma =2$ with initial value: $x(0)=-0.1,y(0)=0.2$.

5. Conclusion

In this paper, the effect of periodic and bounded noise on the chaotic motion of SIR model possessing homoclinic orbits is detailed investigated. Based on homoclinic bifurcation, necessary conditions for possible chaotic motion as well as sufficient condition are derived by the random Melnikov theorem, and to establish the threshold of bounded noise amplitude for onset of chaos. The results indicate that the presence of larger noise enhances the threshold amplitude $b_4$ and reduces the possible chaotic domain in parameter space. Numerical calculation of the phase portraits of the original system also validates that the threshold amplitude $b_4$ for onset of chaos will move upwards as the noise intensity increases for larger noise intensity. The results reveal chaotic attractor is diffused by bounded noise, and the larger the noise intensity results in the more diffused attractor.

However, for chaos in model with periodically and stochastically modulated nonlinear incidence rate, further investigation is needed to clarify the inconsistency between the two kinds of thresholds given by the random Melnikov method with the associated mean-square criterion and by the numerical simulation of the Pioncar$\acute{e}$ maps. In addition, the criterion for possible chaotic motion in system (31(31) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}\tau }& =y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }& =-c^2+x^2+ϵ(b_{1}y+xy-4b_3\sin ({\mathrm{\Omega }}_1\tau )-4b_4\xi (\tau ))+o({ϵ}^2),\end{array}$(31) ) with periodic and stochastic excitation is performed analytically and further numerical validation is needed.

Acknowledgments

The author is very thankful to the referee for careful reading of the paper and valuable suggestions and useful comments that improved the presentation of the paper.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

Yanxiang Shi http://orcid.org/0000-0002-6134-200X

Additional information

Funding

This work is supported by the National Natural Science Foundation of China (No. 11972019), the Natural Science Foundation of Shanxi Province (Nos. 201901D111041 and 201601D202002).