Fuzzy fractional-order PID control for two-wheeled self-balancing robots on inclined road surface

Abstract

Two-wheeled self-balancing robots (TWSBR) is a highly nonlinear and inherently unstable under-driving system. When controlling its movement on an inclined surface, it is more difficult than when it is on a level road. This paper proposes a fuzzy fractional-order PID (FFOPID) controller for the motion control of a TWSBR system in an inclined environment. The control goal of TWSBR is to realize the wheel position control and to stabilize the non-vertical direction of intermediate body (IB). Finally, we compare the control effect of the proposed FFOPID controller with that of the integer-order PID controller, the fuzzy PID (FPID) controller, and the fractional-order PID (FOPID) controller when TWSBR moving on the inclined plane. The simulation results show that the FFOPID controller has better control performance and anti-interference ability.

Keywords:

• Fuzzy fractional-order PID controller (FFOPID)
• two-wheeled self-balancing robots (TWSBR)
• balance control
• slope surface

1. Introduction

TWSBR is usually composed of two wheels and the intermediate body (IB). Comparing with multiwheeled robot, TWSBR has some advantages, such as turning in place, small structure, flexible movement and so on Wang et al. (2018). TWSBR system is a typical nonlinear system, which has many factors, such as multi-variable, inherent instability, under-actuated and non-holonomic constraints. Therefore, TWSBR has become an ideal platform to verify advanced control algorithms. The goal of the controller is to realize the position control of the robot and the balance control of the IB.

In view of the stability control problem of TWSBR on the horizontal ground, the existing literature has proposed many types of controller design schemes. The traditional PID controller is proposed in Lee and Lee (2012) and Juang and Lum (2013). Linear quadratic regulator (LQR) (Prasad et al., 2012) controller and pole assignment method (Siradjuddin et al., 2017) can control the position of robot or the vertical stability of IB without steady-state error. Due to the poor control effect of PID controller on the system with high order and extra noise, in these literatures (Bingul & Karahan, 2011; Kumar & Dinesh, 2014; Paliwal, 2017; Singh, 2015), based on the integer-order PID controller, the FOPID controller is designed for TWSBR system. Comparing with the former, the latter adds two adjustable parameters, which expand the parameter tuning range and improves the control ability. In view of the good nonlinear approximation ability of fuzzy controller, it is often used alone or combined with other controllers to form a composite controller, and then applied to TWSBR system to improve the control ability of the controller, just to take a few examples (Jian et al., 2018; Paliwal et al., 2016; Qiu, 2015; Shi et al., 2020; Wu & Zhang, 2011; Wu et al., 2012).

The above methods are only for balancing robots moving on horizontal plane. However, in reality, TWSBR's motion environment is more on uneven road, including sloping road, undulating road and irregular road. The research in this paper is to control the position and balance of the robot in a sloping road environment. When TWSBR is stable on the inclined road, there is a fixed angle between the IB and the vertical axis, which is related to the ground inclination angle, and the wheel torque is not equal to zero (Kausar et al., 2012). In Liang et al. (2017) and Peng et al. (2012), they established the dynamic model of the robot on the inclined road with Lagrange method and designed the linear controller with LQR method after getting the equilibrium state, while the overshoot is very large at the beginning. In Huang et al. (2010), a sliding mode controller is designed for the speed tracking problem of TWSBR system, which basically realizes the speed tracking control under the condition of unknown ground inclination. A new Takagi-Sugeno fuzzy logic controller is designed in Xu et al. (2013), which implements TWSBR position control and verifies the effectiveness of the controller through experiments. It is worth noting that the control effect of type-1 fuzzy controller is not particularly prominent when the system is uncertainty. Therefore, on the basis of the previous robot model, the authors of Dian et al. (2019) are designed and applied a generalized type-2 T-S fuzzy balance controller to achieve the balance control of TWSBR and designed a generalized type-2 Mamdani fuzzy position controller to make TWSBR reach the set position. The simulation results show that the controller has good control effect.

Due to the new λ and µ two adjustable parameters, FOPID controller increases the parameter tuning range, and thus the control performance is better than the integer-order PID controller (Paliwal, 2017). According to the investigation of the existing literature, FFOPID controller is superior to the traditional controller in the control performance and robustness in the field of power control and manipulator control (Barbosa & Jesus, 2013a; George et al., 2021; Sharma et al., 2018). According to the literature survey, FFOPID controller has not been used in position and balance control of TWSBR. In this paper, combining the advantages of Fuzzy Logic Controller (FLC) and FOPID controller, a FFOPID controller suitable for TWSBR control of slope roads is designed. By adding new parameters in the fractional-order controller and increasing the parameter tuning range, FLC can adjust the fractional-order parameters online and improve the control quality and anti-interference ability. The contributions of the current work are described below:

• Combining the advantages of FOPID and FLC, the FFOPID controller is designed to achieve dual control of the position and balance of TWSBR when it moves on a sloping road.

• The FLC in the FPID and FFOPID controllers is one of the difficult points in the design. Based on the control experience of the self-balancing robot, the fuzzy rule library and the membership function are redesigned.

• The PID, FPID, FOPID and FFOPID controllers are studied, respectively, and these controllers are used to control the position and stability of the TWSBR moving on the slope.

• In the simulation experiment, two slope environments with different inclination and two disturbance conditions are designed to compare the performance of the four controllers. The results show that the FFOPID controller has good control effect and anti-disturbance ability.

The other parts of this paper are as follows. In Section 2, the dynamic model of TWSBR on the inclined plane is introduced. Section 3 mainly introduces the design process of FFOPID controller, briefly explain the other three controllers. In Section 4, the simulation tests on the controller are performed to verify the effectiveness of the FFOPID controller. The conclusions and future work are drawn in Section 5.

2. Dynamic model on the slopes

2.1. TWSBR model

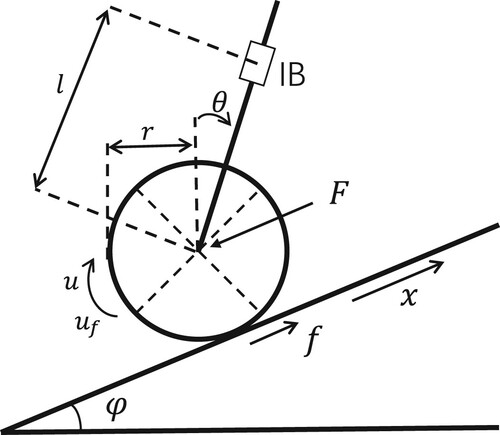
Figure 1 is a sectional view of the TWSBR dynamic model on an inclined road surface (Xu et al., 2014). In this paper, the wheel is always in contact with the inclined plane, and there is no sliding phenomenon. The displacement and velocity of the robot are defined as x and $\dot{x}$. θ is the inclination angle of the IB, with the vertical direction as the zero point, and the angle is positive when rotating clockwise. $\dot{\theta }$ is the angular velocity of rotation. φ indicates the angle between the inclined road surface and the horizontal plane. u is the output torque of the drive motor and the input of TWSBR system. When u is positive, it means that the motor rotates clockwise; when the number is negative, it means that the motor rotates counterclockwise. f is the friction between the wheel and the ground. $u_f$ refers to the rolling resistance between the wheel and the road surface. F is the interaction force between the IB and the wheel in the inclined plane component. The direction indicated by a single arrow indicates the direction of motion when the relevant parameter is positive. In this paper, the system is regarded as an ideal state temporarily, that is, $u_f$ and f are both zero. Due to the small mass and volume of the robot, there is no requirement for the characteristics of the inclined road surface in the simulation experiment. The parameters of the robot are shown in Table 1.

Figure 1. Model of the TWSBR.

Table 1. Robot parameters.

Parameter	Definition	Numerical value
$m_w$	Mass of wheels	1.551 kg
$m_p$	Mass of the IB	1.6 kg
$I_w$	Moment of inertia of wheel	0.005 kg.m${}^2$
$I_p$	Moment of inertia of IB	0.0027 kg.m${}^2$
l	Distance between centre of IB and chassis	0.13 m
r	The radius of the road	0.08 m
g	Acceleration of gravity	9.81 m/s${}^2$

Lagrange method is used to establish the dynamic model of the two-wheeled self-balancing robot. The following formula is derived, the Lagrange function scalar is defined as the difference between the kinetic energy and potential energy of the system (Liang et al., 2017): (1) $\mathcal{L}=T-V$(1) where T, V are the total kinetic and potential energy of the TWSBR, respectively. T consists of four parts: the wheel moving kinetic energy, the wheel rotating kinetic energy, the kinetic energy of movement of IB and the kinetic energy of rotation of IB; V contains the potential energy of body and wheel. The kinetic energy of the IB is expressed as follows: (2) $\frac{1}{2}{m}_p\left({\left(\dot{x}+\dot{\theta }l\cos (\theta +\phi )\right)}^2+{\left(-\dot{\theta }l\sin (\theta +\phi )\right)}^2\right)$(2) The rotational kinetic energy of the IB is $\frac{1}{2}{I}_p{\dot{\theta }}^2$, the kinetic energy of the wheel is $\frac{1}{2}{m}_w\left({{\dot{x}}_L}^2+{{\dot{x}}_R}^2\right)$, the rotational kinetic energy of the wheel are as follows (${\dot{x}}_L$, ${\dot{x}}_R$ is the speed of the left and right wheels) : (3) $\frac{1}{2}{I}_w\left({\left(\frac{{\dot{x}}_L}{r}\right)}^2+{\left(\frac{{\dot{x}}_R}{r}\right)}^2\right)$(3) The total potential energy V: (4) $m_{w}gx\sin \phi +m_{p}g(l\cos \theta +x\sin \phi )$(4) Substitute Equations (2(2) $\frac{1}{2}{m}_p\left({\left(\dot{x}+\dot{\theta }l\cos (\theta +\phi )\right)}^2+{\left(-\dot{\theta }l\sin (\theta +\phi )\right)}^2\right)$(2) )–(4(4) $m_{w}gx\sin \phi +m_{p}g(l\cos \theta +x\sin \phi )$(4) ) into Equation (1(1) $\mathcal{L}=T-V$(1) ) yields: (5) $\begin{array}{rl}\mathcal{L}& =\frac{1}{2}{m}_p{\dot{x}}^2+\frac{1}{2}(m_w+\frac{I_w}{r^2})({\dot{x}}_L+{\dot{x}}_R)\\ & +\frac{1}{2}(m_p{l}^2+I_p){\dot{\theta }}^2\\ & +m_p\dot{x}l\dot{\theta }\cos (\theta +\phi )-m_{w}gx\sin \phi \\ & -m_{p}g(l\cos \theta +x\sin \phi )\end{array}$(5) According to the force relationship shown in Figure 1, the differential equations for wheel displacement and vehicle body inclination can be obtained by taking the derivative of the Lagrangian equation, as shown below: (6) $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{\dot{x}}_L}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{x}_L}& =\frac{u}{r}-F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{\dot{x}}_R}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{x}_R}& =\frac{u}{r}-F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\dot{x}}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }x}& =F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\dot{\theta }}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\theta }& =-u\end{array}$(6) Substituting Equations (5(5) $\begin{array}{rl}\mathcal{L}& =\frac{1}{2}{m}_p{\dot{x}}^2+\frac{1}{2}(m_w+\frac{I_w}{r^2})({\dot{x}}_L+{\dot{x}}_R)\\ & +\frac{1}{2}(m_p{l}^2+I_p){\dot{\theta }}^2\\ & +m_p\dot{x}l\dot{\theta }\cos (\theta +\phi )-m_{w}gx\sin \phi \\ & -m_{p}g(l\cos \theta +x\sin \phi )\end{array}$(5) ) into (6(6) $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{\dot{x}}_L}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{x}_L}& =\frac{u}{r}-F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{\dot{x}}_R}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{x}_R}& =\frac{u}{r}-F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\dot{x}}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }x}& =F\\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\dot{\theta }}-\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }\theta }& =-u\end{array}$(6) ) to obtain the second-order nonlinear model of TWSBR on the inclined plane: (7) $\begin{array}{rl}& (m_p+m_w+\frac{I_w}{r^2})\ddot{x}+m_{p}l\ddot{\theta }\cos (\theta +\phi )=\frac{u}{r}\\ & +m_{p}l{\dot{\theta }}^2\sin (\theta +\phi )-(m_p+m_w)g\sin \phi \end{array}$(7) (8) $\begin{array}{rl}& m_p\ddot{x}l\cos (\theta +\phi )+(m_p{l}^2+I_p)\ddot{\theta }=-u+m_{p}gl\sin \theta \end{array}$(8) Define the state variable vector: (9) $z=[z_1{z}_2{z}_3{z}_4{]}^T=[x\dot{\phantom{a}}x\theta \dot{\phantom{a}}\theta {]}^T$(9) According to Equations (7(7) $\begin{array}{rl}& (m_p+m_w+\frac{I_w}{r^2})\ddot{x}+m_{p}l\ddot{\theta }\cos (\theta +\phi )=\frac{u}{r}\\ & +m_{p}l{\dot{\theta }}^2\sin (\theta +\phi )-(m_p+m_w)g\sin \phi \end{array}$(7) )–(9(9) $z=[z_1{z}_2{z}_3{z}_4{]}^T=[x\dot{\phantom{a}}x\theta \dot{\phantom{a}}\theta {]}^T$(9) ), the state space expression of TWSBR is derived: (10) $\begin{array}{rl}\dot{z_1}& =z_2\\ \dot{z_2}& =\frac{\begin{array}{c}-\left(\frac{c}{r}+b\cos \left(z_3+\phi \right)\right)u\\ +m_{p}glb\sin z_3\cos \left(z_3+\phi \right)\\ -m_{p}lc\sin \left(z_3+\phi \right)z_4^2+\left(m_p+m_w\right)gc\sin \left(\phi \right)\end{array}}{{\left(b\cos \left(z_3+\phi \right)\right)}^2-ac}\\ \dot{\phantom{a}}{z}_3& =z_4\\ \dot{z_4}& =\frac{\begin{array}{c}\left(\frac{b\cos \left(z_3+\phi \right)}{r}+a\right)u\\ +\frac{1}{2}{m}_{p}glb\sin \left(2z_3+2\phi \right)z_4^2\\ -m_{p}gla\sin z_3+\left(m_p+m_w\right)\\ gb\cos \left(z_3+\phi \right)\sin \phi \end{array}}{{\left(b\cos \left(z_3+\phi \right)\right)}^2-ac}\end{array}$(10) where $a=m_p+m_w+\frac{I_w}{r^2},b=m_{p}l$ and $c=m_p{l}^2+I_p$.

2.2. Systematic analysis in steady state

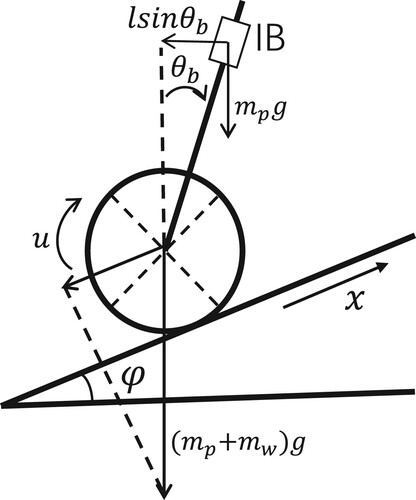
When TWSBR is stable on an inclined road surface, as shown in Figure 2, $\ddot{x}$=0, $\ddot{\theta }$=0 and $\dot{\theta }$=0, substituting in the formula (7(7) $\begin{array}{rl}& (m_p+m_w+\frac{I_w}{r^2})\ddot{x}+m_{p}l\ddot{\theta }\cos (\theta +\phi )=\frac{u}{r}\\ & +m_{p}l{\dot{\theta }}^2\sin (\theta +\phi )-(m_p+m_w)g\sin \phi \end{array}$(7) ) (8(8) $\begin{array}{rl}& m_p\ddot{x}l\cos (\theta +\phi )+(m_p{l}^2+I_p)\ddot{\theta }=-u+m_{p}gl\sin \theta \end{array}$(8) ), the following equation are obtained: (11) $\begin{array}{rl}& (m_p+m_w)gr\sin \phi =u\end{array}$(11) (12) $\begin{array}{rl}& m_{p}gl\sin {\theta }_b=u\end{array}$(12) From the above equation, it can be concluded that: (13) ${\theta }_b=\arcsin \left(\frac{r(m_p+m_w)\sin \phi }{m_{p}l}\right)$(13) where ${\theta }_b$ is the inclination angle of the robot when it is stable on the inclined road, the inclination angle is only determined by the ground tilt angle, and the other parameters are the robot's own parameters. Equation (11(11) $\begin{array}{rl}& (m_p+m_w)gr\sin \phi =u\end{array}$(11) ) is the torque provided by the wheels when the robot is stabilized to counteract the effect of gravity.

Figure 2. Diagram of balance state.

3. Controller design

This section will introduce the design and implementation of the FFOPID controller in detail. Briefly introduce the design of FOPID, PID and FPID controller.

3.1. FOPID controller

FOPID was first proposed by professor Podlubny (1999). Compared with the integer-order PID controller, it adds two variable parameters, λ-order integral and µ-order derivative. The general form is denoted as $P{I}^{\lambda }{D}^{\mu }$, and the control action can be described by Equation (14(14) $\begin{array}{rl}u\left(t\right)& =K_{P}e\left(t\right)+K_I\frac{{\mathrm{d}}^{-\lambda }}{\mathrm{d}{t}^{-\lambda }}e\left(t\right)+K_D\frac{{\mathrm{d}}^u}{\mathrm{d}{t}^u}e\left(t\right)(\lambda ,\mu >0)\\ G\left(s\right)& =K_P+K_I\frac{1}{s^{\lambda }}+K_D{s}^{\mu }\end{array}$(14) ). (14) $\begin{array}{rl}u\left(t\right)& =K_{P}e\left(t\right)+K_I\frac{{\mathrm{d}}^{-\lambda }}{\mathrm{d}{t}^{-\lambda }}e\left(t\right)+K_D\frac{{\mathrm{d}}^u}{\mathrm{d}{t}^u}e\left(t\right)(\lambda ,\mu >0)\\ G\left(s\right)& =K_P+K_I\frac{1}{s^{\lambda }}+K_D{s}^{\mu }\end{array}$(14) In this paper, $\frac{{\mathrm{d}}^{\alpha }}{\mathrm{d}{t}^{\alpha }}=D^{\alpha }$ (α = -λ, µ) is used to represent the component number order operator, and a simple G-L definition is used to solve the fractional-order operator (Barbosa & Jesus, 2013b): (15) $\begin{array}{rl}{D}^{\alpha }f\left(t\right)& =\underset{h\to 0}{lim}\frac{1}{h^{\alpha }}\sum _{j=0}^{\left[t/h\right]}(-1{)}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)f(t-jh)\end{array}$(15) (16) $\begin{array}{rl}{D}^{\alpha }f\left(k\right)& \approx \frac{1}{T^{\alpha }}\sum _{j=0}^k(-1{)}^j\left(\begin{array}{l}\alpha \\ j\end{array}\right)f(k-j)\end{array}$(16) The output equation of discrete FOPID controller is as follows: (17) $u\left(k\right)=K_{P}e\left(k\right)+K_I{D}^{-\lambda }e\left(k\right)+K_D{D}^{u}e\left(k\right)$(17) where $c_j^{\alpha }=(-1{)}^j(\begin{array}{c}\alpha \\ j\end{array}\left)\right(\alpha =-\lambda ,\mu )$ is binomial coefficient, the simplified expression is as follows: (18) $\begin{array}{rl}u\left(k\right)& =K_{P}e\left(k\right)+\frac{K_I}{T^{-\lambda }}\sum _{j=0}^k{c}_j^{(-\lambda )}e(k-j)\\ & +\frac{K_D}{T^{\mu }}\sum _{j=0}^k{c}_j^{\mu }e(k-j)\end{array}$(18) The recurrence formula is as follows: (19) $c_0^{\alpha }=1,c_j^{\alpha }=(1-\frac{1+\alpha }{j})c_{j-1}^{\alpha },j=1,2,\dots$(19) when the step size T is very small, the approximate value of fractional calculus can be obtained directly according to the recursive formula.

3.2. PID controller

The standard PID control equations and traditional functions are expressed as follows: (20) $\begin{array}{rl}u\left(t\right)& =K_{P}e\left(t\right)+K_I{\int }_0^{t}e\left(\tau \right)\mathrm{d}\tau +K_D\frac{\mathrm{d}}{\mathrm{d}t}e\left(t\right)\\ G\left(s\right)& =K_P+K_I\frac{1}{s}+K_{D}s\end{array}$(20) Comparing the transfer functions of the two controllers, it can be seen that the four common types of PID controllers (P, PI, PD, PID) are all special cases of FOPID controllers. For example, when $\lambda =\mu =1$, the FOPID controller degenerates into a regular integer-order PID controller.

3.3. FPID controller

The principle of converting FFOPID to FPID is the same as that of degenerating FOPID to PID. As shown in Figure 3, if the fractional integral operator $\lambda =1$ and the differential operator $\mu =1$ in the FFOPID controller, then the FPID controller is obtained.

Figure 3. Schematic diagram of FFOPID controller.

3.4. Design of FFOPID controller

Figure 3 is the structure block diagram of the FFOPID controller. In this paper, the integrator/differentiator is set to a fractional-order form based on the relatively simple fuzzy PD and fuzzy PI parallel FPID controller structure to obtain the FFOPID controller. Taking the error and fractional-order error as the input of the FLC. $G_E$ and $G_{EC}$ are the input scaling factor, $G_{PD}$ and $G_{PI}$ are the output scaling factor, λ and µ are fractional orders. They are all optimization variables in particle swarm optimization (PSO) algorithm.

According to the schematic diagram, the controller output u can be expressed by Equation (21(21) $\begin{array}{rl}u\left(t\right)& =G_{PD}{U}_{FLC}+G_{PI}\frac{{\mathrm{d}}^{-\lambda }}{\mathrm{d}{t}^{-\lambda }}{U}_{FLC}\\ U_{FLC}& =f\left(G_{E}e\right(t)+G_{EC}\frac{{\mathrm{d}}^{\mu }}{\mathrm{d}{t}^{\mu }}e\left(t\right))\end{array}$(21) ): (21) $\begin{array}{rl}u\left(t\right)& =G_{PD}{U}_{FLC}+G_{PI}\frac{{\mathrm{d}}^{-\lambda }}{\mathrm{d}{t}^{-\lambda }}{U}_{FLC}\\ U_{FLC}& =f\left(G_{E}e\right(t)+G_{EC}\frac{{\mathrm{d}}^{\mu }}{\mathrm{d}{t}^{\mu }}e\left(t\right))\end{array}$(21) Due to the characteristics of the fuzzy controller, it can be concluded that the control law $U_{FLC}$ of the fuzzy logic controller is a nonlinear function of the error and the fractional derivative of the error. The input and output of the FLC are usually a nonlinear complex mapping relationship, where the function f represents a nonlinear function. Use the linear approximation method (Jantzen, 1998) to process f into a linear function. Then the control rate u is expressed as: (22) $\begin{array}{rl}u\left(t\right)& =\left[G_E{G}_{PD}\right]e\left(t\right)+\left[G_{EC}{G}_{PD}\right]\frac{{\mathrm{d}}^{\mu }e\left(t\right)}{\mathrm{d}{t}^{\mu }}\\ & +\left[G_E{G}_{PI}\right]\frac{{\mathrm{d}}^{-\lambda }e\left(t\right)}{\mathrm{d}{t}^{-\lambda }}+\left[G_{EC}{G}_{PI}\right]\frac{{\mathrm{d}}^{\mu -\lambda }e\left(t\right)}{\mathrm{d}{t}^{\mu -\lambda }}\end{array}$(22) Compared with (14(14) $\begin{array}{rl}u\left(t\right)& =K_{P}e\left(t\right)+K_I\frac{{\mathrm{d}}^{-\lambda }}{\mathrm{d}{t}^{-\lambda }}e\left(t\right)+K_D\frac{{\mathrm{d}}^u}{\mathrm{d}{t}^u}e\left(t\right)(\lambda ,\mu >0)\\ G\left(s\right)& =K_P+K_I\frac{1}{s^{\lambda }}+K_D{s}^{\mu }\end{array}$(14) ), the scaling factor in FFOPID controller is defined as follows: $G_E{G}_{PD}$ is the proportional term, $G_{EC}{G}_{PD}$ is a fractional differential term, $G_E{G}_{PI}$ is a fractional integral term, $G_{EC}{G}_{PI}$ is a fractional-order action term. Whether it is a fractional integral term or a fractional differential term depends on the size of λ and µ.

There is an information fusion link in the structure diagram. Since TWSBR system has four variables, in order to prevent the explosion of designing multiple FLC and fuzzy rules, the information fusion method is used to fuse the four state variables into two variables, which reduces the difficulty of controller design. The specific process of information fusion is as follows:

• A state feedback gain matrix $K_{1\times 4}$ is constructed. In the previous section, the state space model of the self-balancing robot nonlinear system has been derived, and the state feedback matrix $K_{1\times 4}$ is designed by using the linear quadratic optimal control theory.

• The fusion matrix $K_{2\times 4}^{\prime }$ is constructed by state feedback gain matrix. In this paper, the fusion matrix is designed as follows: (23) $K_{2\times 4}^{\mathrm{\prime }}=[\frac{K(1,1)}{d},0,\frac{K(1,3)}{d},0;0,\frac{K(1,2)}{d},0,\frac{K(1,4)}{d}]$(23) Where $d=\sqrt{K(1,1{)}^2+K(1,2{)}^2+K(1,3{)}^2+K(1,4{)}^2}$.

• Error e and error change rate ec are obtained by parameter fusion. (24) $\left[\begin{array}{c}e\\ ec\end{array}\right]=-K_{2\times 4}^{\mathrm{\prime }}\ast [z_1{z}_2{z}_3{z}_4{]}^T$(24)

According to the structure of the controller, only the error e is used in the input. After fusion, the input of the controller still contains all the information of position and tilt angle, which reduces the variable dimension and the difficulty of controller design.

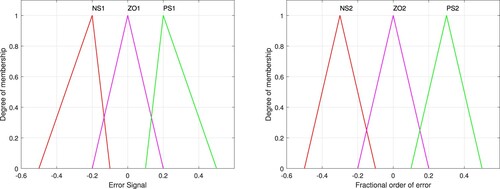
The error (e) and fractional derivative of error ($\frac{{\mathrm{d}}^{\mu }}{\mathrm{d}{t}^{\mu }}e$) are selected as the inputs of the controller. Figure 4 shows the membership function of input, which is divided into three linguistic variables, namely, negative small (NS), zero (ZO) and positive small (PS). Fuzzy logic rules are usually set according to expert knowledge and practical experience. In this paper, the logic rules are summarized through practical experience. For example, at the beginning, there is a big difference between the set value and the target value, which needs to produce a large control output. At this time, $K_P$ and $K_I$ choose the larger value, $K_D$ select the smaller value. When moving to the target value, in order to reduce the steady-state error, $K_P$ and $K_I$ choose the smaller value, $K_D$ select the larger value. Therefore, the fuzzy rule table is shown in Table 2.

Figure 4. Membership function – error signal, fractional order of error.

Table 2. Rule based for $K_P$/ $K_I$/ $K_D$.

	$K_P$/ $K_I$/ $K_D$
	e
$\frac{{\mathrm{d}}^{\mu }}{\mathrm{d}{t}^{\mu }}e$	NS1	ZO1	PS1
NS2	M1/B2/M3	S1/S2/B3	M1/B2/M3
ZO2	B1/M2/S3	M1/M2/B3	B1/B2/S3
PS2	M1/M2/M3	S1/S2/B3	M1/M2/M3

The next section applies the FFOPID controller into the TWSBR system to realizes the position and balance control and gives the corresponding numerical simulation.

4. Simulation results and analysis

The proposed FFOPID controller is simulated on the MATLAB platform and applied to the position and stability control of the TWSBR. The control effect and robustness are compared with those of FOPID, PID and FPID controllers. In order to quantitatively compare the performance index parameters of the four controllers, three evaluation functions ISE, IAE and ITAE are used in this section to comprehensively evaluate the control performance of the controller. Definition of evaluation function index (Lin et al., 2010): (25) $\begin{array}{rl}IAE& ={\int }_0^{\mathrm{\infty }}e(t{)}^2\mathrm{d}t\\ ISE& ={\int }_0^{\mathrm{\infty }}|e\left(t\right)|\mathrm{d}t\\ ITAE& ={\int }_0^{\mathrm{\infty }}t|e\left(t\right)|\mathrm{d}t\end{array}$(25) The weighting matrix Q, R and state feedback matrix K (Xu et al., 2013) and fusion matrix $K_{2\times 4}^{\prime }$ are used in the simulation experiment are as follows: (26) $\begin{array}{rl}Q& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[1000.19001\right],R=1\\ K& =\left[-10-13.2218-35.3382-3.4504\right]\\ {K^{\prime }}_{2\times 4}& =\left[\begin{array}{cccc}-0.2552& 0& -0.9018& 0\\ 0& -0.3374& 0& -0.0881\end{array}\right]\end{array}$(26) The initial value of the TWSBR is set as $z=[0.500.30{]}^T$, and the function of the controller is to control the robot to move to the target balance point $z=[00{\theta }_{b}0{]}^T$(${\theta }_b$ refers to the self-inclination angle of the balancing robot when it moves stably on the inclined plane). Particle swarm optimization (PSO) algorithm is used to optimize the parameters of FFOPID, FOPID, FPID and PID controller, including $G_E$, $G_{EC}$, $G_{PD}$, $G_{PI}$, λ and µ. The optimized parameters in shown Table 3.

Table 3. Optimal parameters of controller.

	Parameters
Controller Type	$G_E$/$K_P$	$G_{EC}$/$K_I$	$G_{PD}$/$K_D$	$G_{PI}$	λ	µ
FFOPID	1.9718	0.5059	0.7009	0.5949	0.9983	0.8021
FPID	1.4431	1.9718	0.5057	0.4190	1	1
FOPID	0.4829	0.4011	2.5947	2.6722	0.9843	0.3001
PID	2.2566	1.6125	0.2663	–	–	–

4.1. Position and balance control

In the first case, we first set the slope angle $\phi =5^{\circ }$, according to Equation (11(11) $\begin{array}{rl}& (m_p+m_w)gr\sin \phi =u\end{array}$(11) ) and (13(13) ${\theta }_b=\arcsin \left(\frac{r(m_p+m_w)\sin \phi }{m_{p}l}\right)$(13) ), when the robot tends to be stable, ${\theta }_{\mathrm{b}}=0.1058$ rad, control rate $u=0.2156$ N.m. The simulation results are shown in Figure 5; Figure 5(a,b) show the changes of x and θ of the system with the participation of four controllers, and Figure 5(c) shows the output of the FFOPID controller. In Figure 5(a), the reason why the robot moves in the opposite direction at the beginning is that the torque is too large at the beginning. In order to prevent the IB from falling, the robot moves in the opposite direction to the target until the IB tilts to the target again. The four controllers can realize the position and balance control of TWSBR, but the stabilization time is different. The tilt angle of $\theta$ approaches 0.1058 rad, and the control rate is close to 0.2156 N.m, which is consistent with the theoretical calculation.

Figure 5. When $\phi =5^{\circ }$, the robot's position and balance performance on the inclined plane. (a) Position control of the robot. (b) Balance control of the robot and (c) The output of the FFOPID controller.

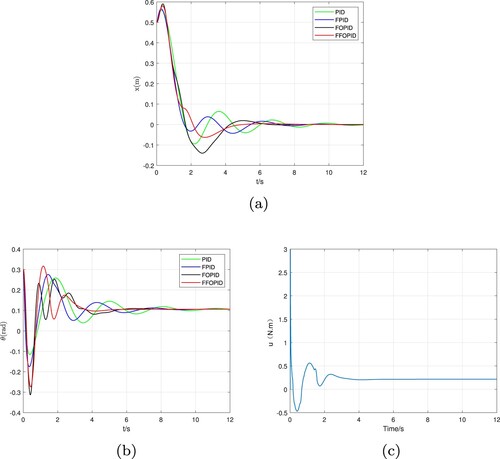
According to Figure 5 and Table 4, the performance of the PID controller is the worst, which is characterized by the largest oscillation during the motion process and a longer stabilization time; secondly, the system reduces the oscillation under the parameters of the FPID controller and stabilizes earlier time; The FOPID controller has good performance, but the overshoot is larger in position control; Compared with the FOPID controller, FFOPID has the same settling time, but the oscillation is smaller and the performance is the best.

Table 4. The performance index result under the condition of $\phi =5^{\circ }$.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	0.8001	0.2698	1.3073	0.4658	0.0497	1.1616
FPID	0.6788	0.2385	0.9788	0.4507	0.0603	0.9183
FOPID	0.8047	0.2745	1.0615	0.3713	0.0669	0.5498
FFOPID	0.6666	0.3589	0.7166	0.2147	0.0112	0.5303

In the second case, we change the tilt angle and set $\phi ={10}^{\circ }$. When TWSBR stabilizes, at this time ${\theta }_{\mathrm{b}}=0.2120$ rad, control rate u = 0.4156 N.m. It can be seen from the Figure 6 that when TWSBR stabilizes on the slope, the inclination angle $\theta$ tends to 0.2120 rad, and the control rate tends to 0.4156 N.m, which is consistent with the theoretical calculation.

Figure 6. When $\phi ={10}^{\circ }$, the robot's position and balance performance on the inclined plane. (a) Position control of the robot. (b) Balance control of the robot and (c) The output of the FFOPID controller.

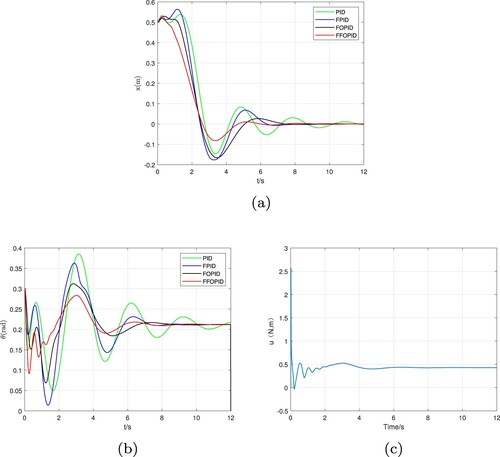
Figure 6(a,b) shows the changes of x and θ of the system with the participation of four controllers, and Figure 6(c) shows the output of the FFOPID controller. In Figure 6(a), the movement in the opposite direction at the beginning is caused by the excessive torque at the beginning. Compared with the former case, the angle of the inclined road is larger, and the movement in the opposite direction is more obvious. Combined with Figure 6 and Table 5, the system has a large oscillation phenomenon in the whole dynamic motion process with the participation of the other three controllers. With the participation of the FFOPID controller, TWSBR is superior to the other three controllers in terms of position movement and time to stabilize.

Table 5. The performance index result under the condition of $\phi ={10}^{\circ }$.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	1.4647	0.5687	2.9777	0.5553	0.0535	2.0755
FPID	1.3569	0.5459	2.3036	0.4513	0.0490	1.2590
FOPID	1.2563	0.4734	2.1013	0.3027	0.0226	0.8019
FFOPID	0.9665	0.3589	1.2566	0.2147	0.0112	0.5303

4.2. Anti-disturbance performance

To verify the anti-random disturbance performance of the proposed controller, a random disturbance of $0.05\ast randn$ is added to the TWSBR system to simulate the internal disturbance caused by inaccurate derivation of the system dynamic model. Figure 7 shows the performance of the four controllers in position and balance control in the case of two inclined planes. Since the random disturbance is added to the state space model of the system, the stability value changes with the disturbance. The system manifests that the robot oscillates in a certain range above and below the theoretical position and the balance tilt angle to maintain dynamic stability. In the case of disturbance, the control performance of the four controllers for TWSBR system is compared.

Figure 7. After adding $0.05\ast randn$ disturbance, the robot's position and balance performance on the inclined plane. (a) $\phi =5^{\circ }$ and (b) $\phi ={10}^{\circ }$.

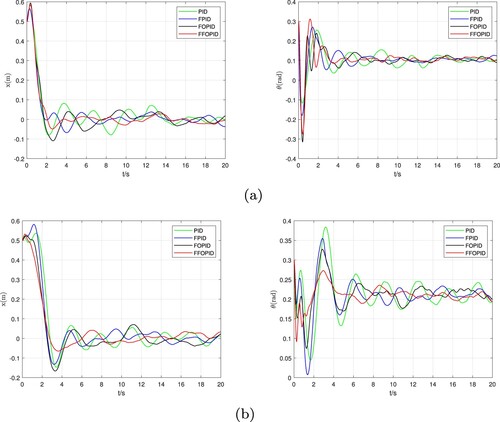
In the experiment, in order to avoid the incompatibility of performance between controllers caused by random numbers, after adding random interference, various controllers are tested for 10 times, and the best result is the final result. Combined with Figure 7 and the Tables 6 and 7, since the input of the PID controller is directly an error, it is most affected by the disturbance, and the system shows a great shock. Because of the addition of two adjustable parameters, the FOPID controller is better than the traditional PID controller in terms of disturbance performance. The FPID controller uses manual control experience to fuzzify the error within a certain range, so as to effectively adjust the system output. The result also proves that its controller effect is better than the previous two controllers. The FFOPID controller mentioned in this article combines the advantages of the FPID and FOPID controllers. It is mainly manifested in the smallest dynamic swing amplitude of the robot, especially in the case of a large tilt angle, the swing amplitude is significantly smaller than that of the other three controllers. The system also shows that the controller has good anti-random disturbance ability.

Table 6. When $\phi =5^{\circ }$, performance index under the condition of $0.05\ast randn$ disturbance.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	1.0929	0.2822	5.5358	0.6265	0.0523	3.7875
FPID	0.8351	0.2473	3.1351	0.5170	0.0575	2.1137
FOPID	1.0628	0.2844	4.2739	0.5128	0.0681	2.2224
FFOPID	0.8073	0.2522	3.0071	0.4665	0.0725	1.7539

Table 7. When $\phi ={10}^{\circ }$, performance index under the condition of $0.05\ast randn$ disturbance.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	1.8066	0.5382	7.8453	0.8121	0.0629	5.4014
FPID	1.5587	0.5344	5.4277	0.5664	0.0545	2.8683
FOPID	1.4492	0.4983	4.5960	0.4137	0.0276	2.0727
FFOPID	1.2576	0.3850	4.3972	0.2875	0.0112	1.6375

Next, we consider another kind of interference, adding a signal of 0.5 rad to the state variable $z_3$ in the ninth second to simulate when the robot is in a stable state, its tilt angle state quantity $z_3$ suddenly receives an amplitude magnitude pulse interference of 0.5 rad. Figure 8 shows the control performance of the four controllers under disturbance interference when $\phi =5^{\circ }$ and $\phi ={10}^{\circ }$. Tables 8 and 9 shows the performance index results of the four controllers under two disturbance conditions.

Figure 8. After adding 0.5 rad interference, the robot's position and balance performance on the inclined plane. (a) $\phi =5^{\circ }$ and (b) $\phi ={10}^{\circ }$.

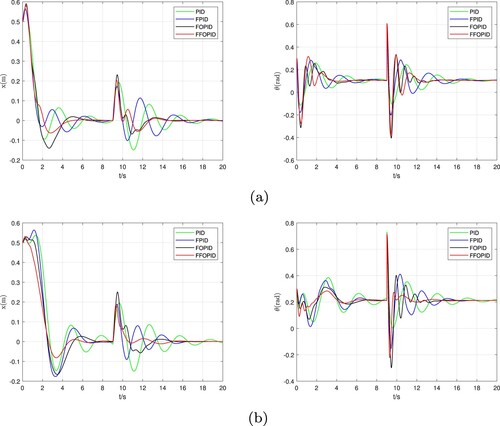
Table 8. When $\phi =5^{\circ }$, performance index under the condition of 0.5 rad disturbance.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	1.2806	0.3201	6.9639	0.9494	0.1116	6.8602
FPID	1.0893	0.2736	5.8265	0.9681	0.1377	6.7171
FOPID	1.5340	0.5055	5.0775	0.7816	0.1783	4.6738
FFOPID	0.8612	0.2649	2.7833	0.7715	0.1699	4.5413

Table 9. When $\phi ={10}^{\circ }$, performance index under the condition of 0.5 rad disturbance.

	x			θ
	IAE	ISE	ITAE	IAE	ISE	ITAE
PID	1.9452	0.6204	8.7103	1.0598	0.1203	8.0035
FPID	1.6506	0.5711	5.5636	0.9582	0.1390	6.7372
FOPID	1.5340	0.5055	5.0393	0.7160	0.1336	4.9672
FFOPID	1.1202	0.3731	2.8652	0.4385	0.0662	2.7836

When the system is affected by instantaneous disturbance, the performance of the traditional PID controller is obviously insufficient. It can be seen that the position changes greatly, and the time to stabilize is the longest. With the participation of FPID and FOPID controllers, the system will produce a larger oscillation process when it is disturbed, but the overall performance of the controller is better than that of the PID controller. Combined with the controller performance indicators, with the participation of the FFOPID controller, the robot displacement change is small, the dynamic process vibration is small, and the system performs better in the case of instantaneous disturbances, indicating that the FFOPID controller participates in the system's anti-interference ability better.

5. Conclusion

Based on the derivation of TWSBR dynamic equation on inclined surface, the fusion function is used to reduce the input parameters of the system and prevent the explosion of fuzzy rules. The FFOPID controller is designed to achieve the position and balance control of TWSBR when it moves on inclined pavement. The simulation results show that the TWSBR system with the participation of FFOPID controller has smaller overshoot, shorter motion time and better anti-interference performance. The future work is to apply the controller proposed in this article to the Arduino self-balancing robot to verify the actual control effect of the controller. Secondly, for more complex and more realistic terrain conditions, the fuzzy rules, membership functions and controller parameters in the FFOPID controller are designed to realize the position and balance control of the TWSBR system in a complex road environment.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Additional information

Funding

This work is supported by the Sichuan Science and Technology Program [grant number 2020YFG0115] and Chengdu Science and Technology Program [grant number 2019-YF05-00958-SN].