Output feedback model predictive control of spacecrafts based on proportional-integral observer

Abstract

A novel attitude control algorithm is developed for spacecrafts based on the model predictive control and proportional-integral observer (PIO) in the presence of constraints. The high dimensional nonlinear dynamics are firstly transformed into three single-input single-output linear structural subsystems with coupled actions. Then these actions are viewed as disturbances estimated by the PIOs, and their values are embedded into the models to improve the accuracy of prediction. The predictive controller is composed of the analytical solution and the heuristic constraint handling. In addition, the angular position information is only needed for implementation. Finally, several simulations are used to verify the effectiveness of the developed algorithm. The results show that the designed system compensates the coupled actions well and makes the attitude control performance good.

KEYWORDS:

• Spacecraft attitude control
• nonlinearity
• decoupling
• model predictive control
• proportional-integral observer

1 Introduction

Attitude control system plays a very important role in the space missions, providing spacecrafts with capabilities of maneuvering, tracking and pointing. As we know, the motion equation of a spacecraft is highly nonlinear, and there is coupling between the channels. Especially, the nonlinearity and coupling are more serious in the case of large attitude angles, which makes it very difficult to apply the linear control theory to controller design directly. Up to now, various nonlinear control algorithms have been applied to spacecrafts, such as sliding mode control (Pukdeboon, 2016; Pukdeboon & Kumam, 2015), finite time control (Du et al., 2011; Zou et al., 2017), robust control (Wang & Xue, 2017) and backstepping control (Sun et al., 2017). Generally, the nonlinear design is more complicated than the linear design. In order to make the linear design for spacecrafts, a feasible way is to apply the feedback linearization technique to the nonlinear dynamics (Liu et al., 2016; Yin et al., 2016). However, the linearization procedure involves a lot of calculations, such as the Lie derivative operation.

It should be pointed out that many algorithms used for spacecraft attitude control do not have the ability to handle hard constraints. Meeting the constraint requirements, for example the limited amplitude and rate of change, is a key issue. If not, the practical control performance may be heavily degraded even the closed-loop systems become unstable (Li et al., 2017). Till now, plenty of techniques are used to deal with constraints for spacecrafts. Xia and Huo (2016) introduced a virtual control signal to compensate the input saturation using anti-windup technique. In the work (Li et al., 2016), the second-order command filters were used to handle constraints on the control input and angular velocity. For a spacecraft with assigned velocity and control constraints, the Lyapunov function and least-square method were utilized to treat them (Hu et al., 2013).

However, only the amplitude constraints were considered in the above three works. As a matter of fact, the rate constraints are also critical to the control performance. Moreover, the rate constraints of spacecrafts can be used to limit the possible excitation of high frequency unmodeled dynamics (Wallsgrove & Akella, 2005). In the reference (Long et al., 2016), both the amplitude and rate constraints were respected through inserting a saturation compensator into the feedback controller. Whereas, designing such a controller is not an easy task because it involves the selection of many parameters.

Model predictive control (MPC), also called receding horizon control, provides a reliable way to handle system constraints (Li et al., 2017; Tang & Cai, 2012). In the work (Kalabić et al., 2017), a MPC method was applied to spacecraft attitude control in the presence of state and control constraints. An optimal maneuvering control with state and input constraints was considered by Zhang et al. (2015), in which a sequential quadratic programming method was used to solve the constrained problem. In order to reduce the computational complexity, Guiggiani et al. (2015) developed a MPC scheme based on low-order spacecraft dynamics. A compound double layer structure was proposed by Bayat (2019), this structure makes full use of features of sliding mode control and MPC to address the robust attitude tracking problem.

Although the model predictive control systems have certain robustness，the control performance will be greatly reduced when the systems are seriously disturbed. It is due to the fact that these systems only rely on the self-regulating functions of algorithms and hence have limited disturbance rejection ability (Chen et al., 2016; Roman et al., 2021). To enhance the robustness of spacecraft attitude tracking control systems, the influence of disturbances on the systems needs to be actively considered, namely disturbance active control (DAC). In the DAC framework, a targeted feedforward compensation will be designed based on the value of disturbance measurement or estimation. In most cases, a special technique is needed to estimate the disturbance, such as the observer (Fu et al., 2018), the adaptive technology (Ren et al., 2021a, 2021b).

In addition, traditional attitude control usually requires angle and angular velocity measurement information, but angular velocity information is not always available during spacecraft operating if the rate gyroscope fails or is not installed at all. Moreover, modern spacecrafts have put forward higher and higher requirements for low cost and miniaturization, and gradually show the trend of gyroscope-free. Therefore, the design of efficient and practical attitude controller without angular velocity measurement information feedback has attracted more and more attention (Gao et al., 2021; Zhao et al., 2022).

Based on the above statement, a novel output feedback control algorithm via MPC and PIO is presented for a spacecraft attitude system. Specifically, the high-order nonlinear dynamics are transformed into three low-order subsystems with coupled actions according to the three-axis control principle. For each subsystem, the coupled action is considered as a disturbance which is estimated by the PIO and used in the design of model predictive controller. Besides, using the limited measurement information, the full state is also estimated by the PIO. To the best knowledge of the authors, this control strategy has not yet been applied to attitude control of spacecrafts. The main contributions of this study relative to other works are as follows.

1. Three low-order control design models are derived according to the characteristics of spacecraft dynamics, which are convenient for engineering applications.

2. The disturbance is compensated in the prediction model, and a unique constraint treatment method is used to ensure the efficient implementation of the algorithm while making the control law have integral function.

3. The active disturbance control without angular velocity information feedback can be achieved using the observer to estimate the state/disturbance at the same time, which meets the development trend of modern spacecraft control.

The rest of paper is organized as follows. Section 2 states a spacecraft mathematical model and subsystems. In Section 3, the controllers for the subsystems are designed using model predictive control technique. Several simulations are carried out to demonstrate the effectiveness of the presented algorithm in Section 4. The final Section 5 summarizes the paper with a few remarks.

2. Spacecraft mathematical model

Consider a rotating rigid body spacecraft described by kinematic and dynamic equations in terms of Euler’s equation form (Tsiotras et al., 1995). The dynamic equation can be written as (1) $J\dot{\omega }=S\left(\omega \right)J\omega +M,$(1) where $J=\left[\begin{array}{ccc}{J}_x& 0& 0\\ 0& J_y& 0\\ 0& 0& J_z\end{array}\right]$ is the inertia matrix, $S\left(\omega \right)=\left[\begin{array}{ccc}0& {\omega }_z& -{\omega }_y\\ -{\omega }_z& 0& {\omega }_x\\ {\omega }_y& -{\omega }_x& 0\end{array}\right]$ is a skew- symmetric matrix, $\omega ={\left[\begin{array}{ccc}{\omega }_x& {\omega }_y& {\omega }_z\end{array}\right]}^{\text{T}}$ is the vector of angular velocities and $M={\left[\begin{array}{ccc}{M}_x& M_y& M_z\end{array}\right]}^{\text{T}}$ is the vector of external torques. And the kinematic equation can be given by (2) $\omega =J\left(q\right)\dot{q},$(2) where $J\left(q\right)=\left[\begin{array}{ccc}1& \sin \theta & 0\\ 0& \cos \theta \cos \gamma & \sin \gamma \\ 0& -\cos \theta \sin \gamma & \cos \gamma \end{array}\right]$, $q=\left[\begin{array}{c}\gamma \\ \psi \\ \theta \end{array}\right]$. $\gamma$, $\psi$, $\theta$ are roll, yaw and pitch attitude angles, respectively. It is commonly known that the Equations (1) and (2) are strongly nonlinear and coupled between three channels.

Obviously, directly taking the Equations (1) and (2) as a prediction model is a big challenge for an embedded MPC controller. On one hand, it will greatly increase the difficulty of controller design. On the other hand, it will greatly increase computational loads. Hence, the spacecraft model (1) and (2) need to be simplified while preserving significant dynamics. To this end, the model (1) and (2) will be divided into three subsystems according to the three-channel control principle, i.e. the yaw, the pitch and the roll subsystems as stated in the sequel.

Assumption 1: Suppose that the $\gamma$ equals to zero. This is due to the fact that the spacecraft does not need to roll around the longitudinal axis even when it is maneuvering at a large angle.

Denote $x_{1z}=\theta$, $x_{2z}=\dot{\theta }$, then a second-order pitch subsystem can be described as (3) $\begin{array}{rl}\left[\begin{array}{c}{\dot{x}}_{1z}\\ {\dot{x}}_{2z}\end{array}\right]& =\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_{1z}\\ x_{2z}\end{array}\right]+\left[\begin{array}{c}0\\ 1/J_z\end{array}\right]M_z+\left[\begin{array}{c}0\\ f_z\end{array}\right],\end{array}$(3) (4) $\begin{array}{rl}{y}_z& =\theta ,\end{array}$(4) with $f_z=\frac{J_x-J_y}{J_z}{\omega }_x{\omega }_y+{\omega }_y\dot{\gamma }$. Similarly, denote $x_{1y}=\psi$, $x_{2y}=\dot{\psi }$, $x_{1x}=\gamma$, $x_{2x}=\dot{\gamma }$, then other two subsystems can be described as (5) $\begin{array}{rl}\left[\begin{array}{c}{\dot{x}}_{1y}\\ {\dot{x}}_{2y}\end{array}\right]& =\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_{1y}\\ x_{2y}\end{array}\right]+\left[\begin{array}{c}0\\ 1/\left(J_y\cos \theta \right)\end{array}\right]M_y+\left[\begin{array}{c}0\\ f_y\end{array}\right],\end{array}$(5) (6) $\begin{array}{rl}{y}_y& =\psi ,\end{array}$(6) (7) $\begin{array}{rl}\left[\begin{array}{c}{\dot{x}}_{1x}\\ {\dot{x}}_{2x}\end{array}\right]& =\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_{1x}\\ x_{2x}\end{array}\right]+\left[\begin{array}{c}0\\ 1/J_x\end{array}\right]M_x+\left[\begin{array}{c}0\\ f_x\end{array}\right],\end{array}$(7) (8) $\begin{array}{rl}{y}_x& =\gamma ,\end{array}$(8)

with $f_y=\frac{\left(J_z-J_x\right)}{J_y\cos \theta }{\omega }_x{\omega }_z+\frac{\dot{\theta }\sin \theta }{{\cos }^2\theta }{\omega }_y-\frac{\dot{\gamma }\cos \theta }{{\cos }^2\theta }{\omega }_z$, $f_x=\frac{J_y-J_z}{J_z}{\omega }_y{\omega }_z-{\sec }^2\theta {\omega }_y-\tan \theta \left({\dot{\omega }}_y-\dot{\gamma }{\omega }_z\right)$.

Remark 1: As depicted in (5)–(8), the singularity will be occur at $\theta =\pm {90}^{\circ }$, which can be avoided by changing the representation $J\left(q\right)$, for details, please refer to the work (Bayat, 2019).

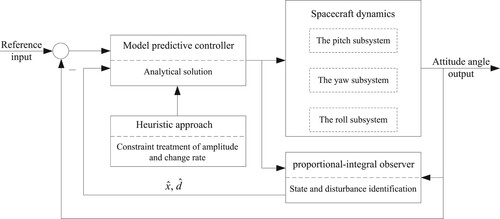
As shown in (3)–(8), if the terms $f_x$, $f_y$, $f_z$ are viewed as disturbances, the pitch and roll subsystems are linear, while the yaw subsystem is linear-like. Moreover, these subsystems are decoupled. The control block diagram is shown in Figure 1, including the dynamics, the observer and the controller three parts. The control objective is to make the pitch and yaw angles track the desired signals, and the roll angle is stabilized to zero.

Figure 1. Block diagram of the designed spacecraft attitude control.

Figure 2. Response to step pitch angle command.

Figure 3. Response to step yaw angle command.

3. Model predictive controller design

The predictive controllers for the three subsystems are designed in this section. The general state-space descriptions of these subsystems are firstly given and analysed. And then the coupled actions are estimated by the PIOs. Finally, the predictive controllers are designed based on these estimations. According to the descriptions of (3)–(8), these subsystems can be further expressed as (9) $\begin{array}{rl}{\dot{x}}_z& =A{x}_z+B_z{M}_z+d_z\\ y_z& =C{x}_z,\end{array}$(9) (10) $\begin{array}{rl}{\dot{x}}_y& =A{x}_y+B_y{M}_y+d_y\\ y_y& =C{x}_y,\end{array}$(10) (11) $\begin{array}{rl}{\dot{x}}_x& =A{x}_x+B_x{M}_x+d_x\\ y_x& =C{x}_x,\end{array}$(11) with $x_z=\left[\begin{array}{c}\theta \\ \dot{\theta }\end{array}\right]$, $x_y=\left[\begin{array}{c}\psi \\ \dot{\psi }\end{array}\right]$, $x_x=\left[\begin{array}{c}\gamma \\ \dot{\gamma }\end{array}\right]$, $A=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$, $B_z=\left[\begin{array}{c}0\\ 1/J_z\end{array}\right]$, $B_y=\left[\begin{array}{c}0\\ 1/\left(J_y\cos \theta \right)\end{array}\right]$, $B_x=\left[\begin{array}{c}0\\ 1/J_x\end{array}\right]$, $d_z=\left[\begin{array}{c}0\\ f_z\end{array}\right]$, $d_z=\left[\begin{array}{c}0\\ f_y\end{array}\right]$, $d_x=\left[\begin{array}{c}0\\ f_x\end{array}\right]$, $C=\left[\begin{array}{cc}1& 0\end{array}\right]$.

It can be proved that these above subsystems (9)-(11) are observable and controllable in the absence of disturbances, which provides a basis for the design of controllers and observers. It should be pointed out that the yaw subsystem is a linear-like uncertain structure that can be found in the state-dependent Riccati equation method (Batmani et al., 2017), the others are two linear time-invariant uncertain systems.

3.1 Disturbance identification

The PIO is an extension of the Luenberger observer which can estimate unmeasurable states via available measurements for linear, time-invariant and deterministic plants (Luenberger, 1971). However, both the current and the past information are adopted in the PIO, which can enhance the system robustness against uncertainties. Herein, a PIO proposed in the work (Söffker et al., 1995) is used to identify the coupled action $d_i$ $\left(i=x,y,z\right)$.

Take the pitch subsystem (9) as an example, the dynamics of PIO can be given by (12) $\begin{array}{rl}\left[\begin{array}{c}{\dot{\hat{x}}}_z\\ {\dot{\hat{d}}}_z\end{array}\right]& =\left[\begin{array}{cc}A-L_{1z}C& L_{3z}\\ -L_{2z}C& 0\end{array}\right]\left[\begin{array}{c}{\hat{x}}_z\\ {\hat{d}}_z\end{array}\right]+\left[\begin{array}{c}{B}_z\\ 0\end{array}\right]M_z\\ & +\left[\begin{array}{c}{L}_{1z}\\ L_{2z}\end{array}\right]y_z,\end{array}$(12) where $L_{1z}$, $L_{2z}$ and $L_{3z}$ are gain matrices which can be determined by the pole-placement. Similarly, the other two PIOs can be designed.

Remark 2: Note that the gain matrices $L_{1z}$, $L_{2z}$, $L_{3z}$, $L_{1x}$, $L_{2x}$ and $L_{3x}$ can be determined in advance, while the gain matrices $L_{1y}$, $L_{2y}$ and $L_{3y}$ are calculated on line at each sampling instant because the yaw channel is a time-varying system.

3.2 Controller design

Likewise, take the pitch subsystem as an example to illustrate the controller design. By discretizing the system (9), the prediction model can be depicted as (13) $\begin{array}{rl}{x}_{mz}\left(k+1\right)& =A_{mz}{x}_{mz}\left(k\right)+B_{mz}{M}_z\left(k\right)+N_{mz}{d}_z\left(k\right)\\ y_{mz}\left(k\right)& =C_{mz}{x}_{mz}\left(k\right),\end{array}$(13) where $A_{mz}$, $B_{mz}$, $N_{mz}$, $C_{mz}$ are the system matrices, expressed by $A_{mz}=e^{A_z{T}_s}$, $B_{mz}={\int }_0^{T_s}{e}^{A\left(x\right)T_s}{B}_{z}dt$, $N_{mz}={\int }_0^{T_s}{e}^{A\left(x\right)T_s}dt$, $C_{mz}=C$, respectively. And $T_s$ is the sample period. In order to obtain the future output, the state prediction should be done at first. By iterative operations of the state equation in (13), the state at the future instant $k+i$ can be written as (14) $\begin{array}{rl}{x}_{mz}\left(k+i\right)& =A_{mz}^i{x}_{mz}\left(k\right)+\sum _{l=0}^{i-1}{A}_{mz}^l{B}_{mz}{M}_z\left(k+i-1-l\right)\\ & +\sum _{l=0}^{i-1}{A}_{mz}^l{N}_{mz}{d}_z\left(k+i-1-l\right).\end{array}$(14)

However, the future $d_z\left(k+i-1-l\right)\left(i-1-l>1\right)$ is not available. Therefore, $d_z\left(k+i-1-l\right)\left(i-1-l>1\right)$ is replaced by the $d_z\left(k\right)$, then the (14) can be rewritten as (15) $\begin{array}{rl}{x}_{mz}\left(k+i\right)& =A_{mz}^i{x}_{mz}\left(k\right)+\sum _{l=0}^{i-1}{A}_{mz}^l{B}_{mz}{M}_z\left(k+i-1-l\right)\\ & +\sum _{l=0}^{i-1}{A}_{mz}^l{N}_{mz}{d}_z\left(k\right).\end{array}$(15)

Using the output equation in (13), the output at time $k+i$ can be obtained as (16) $\begin{array}{rl}{y}_{mz}\left(k+i\right)& =C_{mz}{A}_{mz}^i{x}_{mz}\left(k\right)\\ & +\sum _{l=0}^{i-1}{C}_{mz}{A}_{mz}^l{B}_{mz}{M}_z\left(k+i-1-l\right)\\ & +\sum _{l=0}^{i-1}{C}_{mz}{A}_{mz}^l{N}_{mz}{d}_z\left(k\right).\end{array}$(16)

Furthermore, the (16) can be expressed in a concise way, as (17) $Y\left(k\right)=\mathrm{\Phi }{x}_{mz}\left(k\right)+\mathrm{\Theta }U\left(k\right)+\mathrm{\Gamma }{d}_z\left(k\right),$(17) with $Y\left(k\right)=\left[\begin{array}{c}{y}_{mz}\left(k+1\right)\\ ⋮\\ y_{mz}\left(H_u+1\right)\\ ⋮\\ y_{mz}\left(H_p+1\right)\end{array}\right]$, $U\left(k\right)=\left[\begin{array}{c}{M}_z\left(k\right)\\ ⋮\\ M_z\left(k+1\right)\\ ⋮\\ M_z\left(k+H_u-1\right)\end{array}\right]$, $\mathrm{\Gamma }=\left[\begin{array}{c}{C}_{mz}{N}_{mz}\\ ⋮\\ \sum _{l=0}^{H_u-1}{C}_{mz}{A}_{mz}^l{N}_{mz}\\ ⋮\\ \sum _{l=0}^{H_p-1}{C}_{mz}{A}_{mz}^l{N}_{mz}\end{array}\right]$, $\mathrm{\Phi }=\left[\begin{array}{c}{C}_{mz}{A}_{mz}\\ ⋮\\ C_{mz}{A}_{mz}^{H_u}\\ ⋮\\ C_{mz}{A}_{mz}^{H_p}\end{array}\right]$, $\mathrm{\Theta }=\left[\begin{array}{ccc}{C}_{mz}{B}_{mz}& \cdots & 0\\ ⋮& \cdots & ⋮\\ C_{mz}{A}_{mz}^{H_u-1}{B}_{mz}& \cdots & C_{mz}{B}_{mz}\\ ⋮& ⋮& ⋮\\ C_{mz}{A}_{mz}^{H_p-1}{B}_{mz}& \cdots & \sum _{i=0}^{H_p-H_u}{C}_{mz}{A}_{mz}^i{B}_{mz}\end{array}\right]$. Herein, the $H_p$, $H_u$ are the prediction and control horizons, respectively. As shown in (17), the output prediction consists of three parts, namely the free one $\mathrm{\Phi }{x}_{mz}\left(k\right)$ caused by the present state, the controlled one $\mathrm{\Theta }U\left(k\right)$ caused by the control input and last one $\mathrm{\Gamma }d\left(k\right)$ caused by the disturbance. Compared to the conventional MPC, the last part in (17) can improve the prediction accuracy and hence raise the system performance.

What’s more, there is an error between the model output in (13) and the actual output due to modelling simplifications. So it is necessary to use this error to compensate for the prediction. Here, this error prediction can be defined as (18) $e_z\left(k+i\right)=y_{pz}\left(k\right)-y_{mz}\left(k\right),$(18) where the $y_{pz}\left(k\right)$ is the actual output. The MPC is an optimization algorithm, and the control input is obtained by minimizing a performance index. Take the quadratic performance index as (19) $\begin{array}{rl}{J}_z& =\sum _{i=1}^{H_p}||y_{mz}(k+i)+e_z(k+i)-r_z(k+i)|{|}_{Q\left(i\right)}^2\\ & +\sum _{i=0}^{H_u-1}||M_z(k+i)|{|}_{R\left(i\right)}^2,\end{array}$(19) where $r_z(k+i)$ is the expected output, $Q(\cdot )$ and $R(\cdot )$ is the weighting matrices, $||\cdot ||$ denotes the Euclidean norm. After arranging, the index (19) can be rewritten as (20) $J_z=||Y\left(k\right)+E\left(k\right)-\mathrm{T}\left(k\right)|{|}_Q^2+||U\left(k\right)|{|}_R^2,$(20) with $E\left(k\right)={\left[\begin{array}{ccc}e\left(k+1\right)& \cdots & e\left(k+H_p\right)\end{array}\right]}^{\text{T}}$, $Q=\text{diag}\left[\begin{array}{ccc}Q\left(1\right)& \cdots & Q\left(H_p\right)\end{array}\right]$, $R=\text{diag}[R\left(1\right)\begin{array}{cc}\cdots & R\left(H_u\right)\end{array}]$, $\mathrm{T}\left(k\right)={\left[\begin{array}{ccc}{r}_z\left(k+1\right)& \cdots & r_z\left(k+H_p\right)\end{array}\right]}^{\text{T}}$.

Define a symbol as (21) $\xi \left(k\right)=T\left(k\right)-\mathrm{\Phi }{x}_{mz}\left(k\right)-E\left(k\right)-\mathrm{\Gamma }{d}_z\left(k\right).$(21) Substituting (21) into (20) yields (22) $J_z=||\mathrm{\Theta }U\left(k\right)-\xi \left(k\right)|{|}_Q^2+||U\left(k\right)|{|}_R^2.$(22)

Expand (22) according to the definition of norm, getting (23) $J_z={\xi }^{\text{T}}\left(k\right)Q\xi \left(k\right)-U^{\text{T}}\left(k\right)G+U^{\text{T}}\left(k\right)HU\left(k\right),$(23) where $G=2{\mathrm{\Theta }}^{\text{T}}Q\xi \left(k\right)$, $H={\mathrm{\Theta }}^{\text{T}}Q\mathrm{\Theta }+R$. For the unconstrained problem, the optimal control can be obtained by finding that the derivative of $J_z$ with respect to $U\left(k\right)$ is equal to zero, that is (24) $U\left(k\right)=\frac{1}{2}{H}^{-1}G.$(24)

It should be noted that the current control applied to the plant is the first element of (24). For the constrained problem, the spacecraft control input and its change rate limits are considered here, that is $u_{min}\le u\left(k\right)\le u_{max}$, $\mathrm{\Delta }{u}_{min}\le \mathrm{\Delta }u\left(k\right)\le \mathrm{\Delta }{u}_{max}$, a heuristic approach is used to deal with them (Tang & Cai, 2012). Using the heuristic approach to handle constraints gets the incremental form of control, as (25) $\mathrm{\Delta }u\left(k\right)=\{\begin{array}{l}min\left[\begin{array}{ccc}\mathrm{\Delta }\overline{u}\left(k\right),& \mathrm{\Delta }{u}_{max},& u_{max}-u(k-1)\end{array}\right],\\ \mathrm{\Delta }\overline{u}\left(k\right)>0\\ max\left[\begin{array}{ccc}\mathrm{\Delta }\overline{u}\left(k\right),& \mathrm{\Delta }{u}_{min},& u_{min}-u(k-1)\end{array}\right],\\ \mathrm{\Delta }\overline{u}\left(k\right)<0\end{array}.$(25) where $\mathrm{\Delta }\overline{u}\left(k\right)$ is the unconstrained control increment calculated by (24), i.e. $\mathrm{\Delta }\overline{u}\left(k\right)=u\left(k\right)-u(k-1)$. In actual implementation, the current control $u\left(k\right)$ is the sum of (25) plus $u(k-1)$.

Remark 3: Clearly, the optimal constrained solution can not be obtained by using (25), but very similar results will be got. Compared with the quadratic programming approach, the heuristic approach can greatly reduce the computational burdens, which is of great significance for spacecrafts. Moreover, such a constraint handling approach enables the control $u\left(k\right)$ to have an integral function, which is beneficial to the steady-state performance.

Remark 4: In order to perform this controller, the $x_z$, $d_z$ used in above expressions should be replaced by the ${\hat{x}}_z$, ${\hat{d}}_z$ defined in (12).

Remark 5: It should be noted that the design concept used in this paper is the same as that used in the work (Mohammadkhani et al., 2017), dividing the output feedback predictive control into the model predictive control and the observer design two subproblems. However, the solving process is different. In this paper, the state/disturbance observer is designed first, and then the controller is designed. In addition, the heuristic approach is used for constraint treatment (obtaining an approximate optimal solution) to meet the high efficiency of algorithm implementation. While in the work (Mohammadkhani et al., 2017), the model predictive controller and the observer are designed simultaneously (obtaining an optimal solution). Moreover, the offline design combined with the online search is used to achieve efficient operation of the algorithm.

Remark 6: The main parameters involved in the designed control algorithm are prediction $H_p$ horizon and control horizon $H_u$, weighting matrices $Q(\cdot )$ and $R(\cdot )$ in (19), and poles of the PI observer in (12). The prediction and control horizons are related to the stability of the system and cannot be selected too small (Morato et al., 2020). The effects of the weighting matrices on the algorithm can refer to the general optimal control (Zhang et al., 2019). The poles are directly related to the convergence speed of the observer system, so it has great effects on the system performance, which can be reflected in the analysis of Figure 5 later. Although each parameter has its own unique function, the selections of these parameters needs to be comprehensively considered to obtain better control performance.

To sum up, the proposed control algorithm comprises the following steps (illustrated by the pitch subsystem).

1. Step 1. Select appropriate poles and calculate the gain matrices $L_{1z}$, $L_{2z}$ and $L_{3z}$ of the observer.

2. Step 2. Calculate the state ${\hat{x}}_z$ and the disturbance ${\hat{d}}_z$ based on the observer (12).

3. Step 3. Use (24) to calculate the control sequence $U\left(k\right)$.

4. Step 4. Deal with the constraints based on (25), and calculate the current control $u\left(k\right)$.

5. Step 5. Next sampling period, go to the Step 2.

4. Simulation results and analysis

The parameters of a spacecraft are $J_x=0.1\text{kg}\cdot {\text{m}}^{\text{2}}$ and $J_y=J_z=1\text{kg}\cdot {\text{m}}^{\text{2}}$. The constraints on the external torques ($\text{N}\cdot \text{m}$) are $-0.5\le M_n\le 0.5$, $-2\le \mathrm{\Delta }{M}_n\le 2$, $\left(n=z,y\right)$, $-0.3\le M_x\le 0.3$, $-2\le \mathrm{\Delta }{M}_x\le 2$. The prediction and control horizons are selected as $H_{pn}=100$, $H_{un}=30$ $\left(n=z,y\right)$ for the pitch and yaw subsystems, and $H_{px}=70$, $H_{ux}=20$ for the roll subsystem. The eigenvalues of the observers are selected as $-3$, $-4$, $-5$ for the pitch and yaw subsystems, and $-1$, $-2$, $-3$ for the roll subsystem. Additionally, the sampling time is 0.01s. The initial positions of attitude angles are $\theta \left(0\right)=0^{\text{o}}$, $\psi \left(0\right)=0^{\text{o}}$ and $\gamma \left(0\right)={30}^{\text{o}}$, the expected positions are ${\theta }_r={60}^{\text{o}}$, ${\psi }_r={30}^{\text{o}}$ and ${\gamma }_r=0^{\text{o}}$.

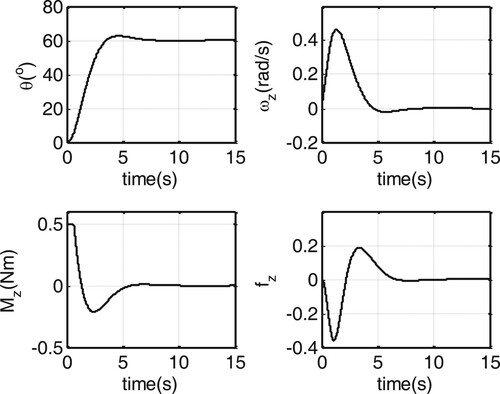
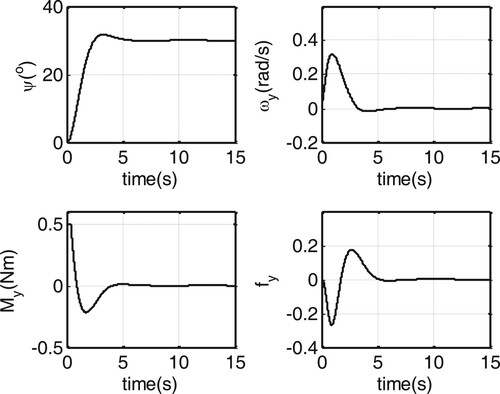
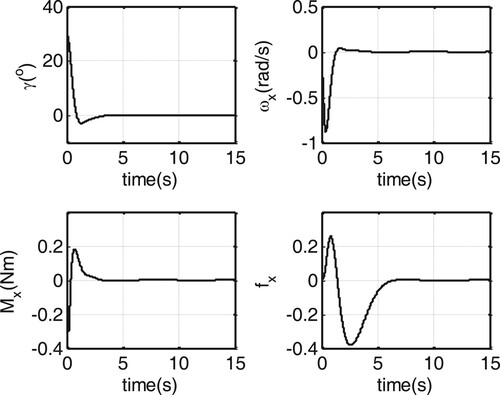
The simulation results are shown in Figures 2–4. It is observed that the pitch and yaw angles converge to the expected positions quickly, and the roll angle achieves quick convergence to zero. In the beginning, the control inputs $M_z$ and $M_y$ reach their limits for obtaining fast response speeds. Besides, the angular velocities ${\omega }_z$, ${\omega }_y$ and ${\omega }_x$ are eventually stabilized to zero. 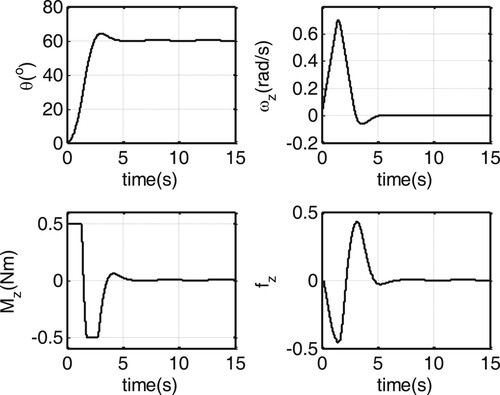In concern of the coupled actions $f_x$, $f_y$ and $f_z$, it can be seen that there exist strong coupled actions among channels in the beginning. Therefore, these actions aren’t be neglected in the controller design otherwise the control performance may be seriously degraded by them. In short, the proposed control algorithm can well compensate the coupled actions between the channels, thus achieving good attitude tracking performance (Figure 4).

Figure 4. Response to initial roll angle.

In order to illustrate the effects of observer convergence on the system performance, the poles of the observer of the pitch subsystem are all selected as −6.5, while the poles of the other observers remain unchanged. The results indicate that the performance of the pitch subsystem varies significantly, as shown in Figure 5, whereas the performance of the others varies slightly. It can be seen from Figure 5 that the dynamic performance of the tracking is improved, that is, the rise time and settling time are shortened. Better performance requires more control efforts, so more time for the control input to go into saturation. More control efforts make the other two variables ${\omega }_z$ and $f_z$, vary more widely. The above results reveal that the observer have an important effect on the whole system performance, and the performance can be improved by modifying it.

Figure 5. Response to step pitch angle command using a faster convergent observer.

5. Conclusions

According to the theoretical analysis and simulation results, the following conclusions can be made:

1. Considering the couplings between channels as disturbances helps the system analysis and simplify the controller design;

2. The coupled actions can be effectively identified by the PIOs, which can be used to improve the prediction accuracy of the system's future behaviour;

3. The control framework based on output feedback is more convenient for practical applications;

4. Compared with the online quadratic programming technique, the heuristic approach can greatly improve the real time performance of constrained systems.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability

All data generated or analysed during this study are included in this study.

Additional information

Funding

This work was supported by the Fujian Natural Science Foundation Project: [Grant Number 2019J01868 and 2020J01281]; the Open Fund of the Key Laboratory of Advanced Industrial Process Control: [Grant Number 2019KFJJ06]; the Science and Technology Program of Gansu Province: [Grant Number 20JR10RA150 and 21JR7RA204]; the Gansu Provincial Higher Education Industry Support and Guidance Project: [Grant Number 2019C-05].