An accelerating approach of designing ferromagnetic materials via machine learning modeling of magnetic ground state and Curie temperature

ABSTRACT

Magnetic materials have a plethora of applications from information technologies to energy harvesting. However, their functionalities are often limited by the magnetic ordering temperature. In this work, we performed random forest on the magnetic ground state and the Curie temperature (T_C) to classify ferromagnetic and antiferromagnetic compounds and to predict the T_C of the ferromagnets. The resulting accuracy is about 87% for classification and 91% for regression. When the trained model is applied to magnetic intermetallic materials in Materials Project, the accuracy is comparable. Our work paves the way to accelerate the discovery of new magnetic compounds for technological applications.

GRAPHICAL ABSTRACT

KEYWORDS:

• Magnetic ground state
• Curie temperature
• machine learning
• random forest

Introduction

Magnetic materials have a wide spectrum of applications, particularly in efficient energy utilization [1]. Specifically, permanent magnets (PMs) are the key components for energy related technologies, such as conventional generators, e-mobility, automatization and refrigeration [2]. Moreover, ferromagnetic (FM) materials have been widely applied in spintronics, such as sensing, memory and logic, whereas the emerging antiferromagnetic (AFM) spintronics have recently drawn intense attention [3]. Three fundamental intrinsic properties desired for promising candidate magnetic materials are a FM ground state, a high Curie temperature (T_C) and the magnetocrystalline anisotropy (MCA). These properties are also important for magnetic refrigeration which promises enhanced energy efficiency over the conventional cooling technologies [4]. In this work, we focus on the machine learning modeling of the magnetic ground state and the T_C, as both the magnetization and MCA can be obtained via density functional theory (DFT) calculations for most compounds even in a high-throughput manner [5] and using machine learning [6], though evaluation of MCA is numerically expensive.

Although T_C is experimentally measurable, synthesis, characterization and optimization of a wide range of real materials are time-consuming and costly. Thus, a methodology to accelerate the development of magnetic materials with a theoretical pre-screening is of obvious interest. Typical theoretical approaches to evaluate T_C rely on the parameterization of DFT electronic structure to construct a Heisenberg Hamiltonian. This approach has good accuracy in predicting the Curie temperature of magnetic compounds in the localized limit (e.g. bcc Fe), but may fail for systems with tricky origin of magnetism (e.g. fcc Ni) [7–9]. Moreover, DFT is insufficient in describing the strong-correlated 4f electrons in rare-earths [10], while the orbital dependent functional (e.g. DFT + U) treatment is often chosen to fit to experiments. The state-of-the-art DFT plus dynamical mean field theory (DMFT) method can be applied to tackle the electronic correlation problem, which is one of the most sophisticated methods to evaluate the magnetic properties. It provided many successful predictions, [11] but the T_C evaluated for bcc Fe based on DFT + DMFT ranges from 840 K to 1800 K, due to different ways to treat the Coulomb interactions, and the selection the U and J parameters [12,13]. Besides, DFT + DMFT is numerically expensive, thus it cannot be used for extensive predictions. Therefore, there is a great impetus for a predictive approach to obtain T_C, which is applicable to compounds with arbitrary compositions and crystal structures.

Machine learning is an emerging tool in materials science, being applied successfully to model the thermodynamic stability [14], band gap [15], inter-atomic potentials [16] and in predicting potential high temperature superconductors [17]. However, regression models to predict ordering temperature of magnetic materials have only been reported in a limited scope while classification models to distinguish AFM and FM are absent in literature to the best of our knowledge. Sanvito et al. trained a linear regression model using 40 intermetallic Heusler alloys (with experimental T_C), and made predictions for another 20 compounds. Through experimental validation, they discovered Co₂MnTi with a remarkably high T_C of 900 K [18]. Dam et al. focused on selecting the best features for fitting T_C of binary 3d-4f intermetallic compounds by applying Gaussian kernel regression on 108 compounds. The add-one-in test accuracy can reach above 95% when only eight descriptors are used, with the rare-earth concentration being the most relevant [19]. Nelson et al. demonstrated that only chemistry is required to model the T_C, where the accuracy is about 88% with a MAE of 50 K [20].

In this work, we develop a FM/AFM classification model along with a regression model to predict the T_C for intermetallic FM compounds, using the random forest method. These models are then used to identify the magnetic ground state of 5193 magnetic intermetallic compounds from the Materials Project database and to predict the T_C of those classified as FM. It is demonstrated that our machine learning framework is efficient and predictive, and can be used to accelerate the screening for FM compounds which are promising for spintronics and permanent magnets applications. Please find the workflow of our machine learning modelling in Figure S1.

Materials and methods

Data

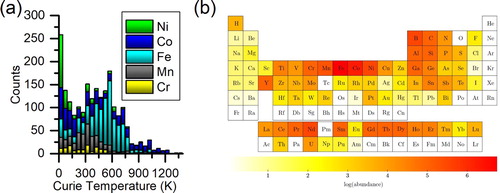
1749 FM and 1056 AFM inter-metallic compounds are collected from the AtomWork database [21], which contains experimental structures and properties of magnetic materials. By excluding oxides, along with compounds without either Cr, Mn, Fe, Co, and Ni atoms, which are the typical magnetic atoms in transition metal based intermetallic magnetic materials. The distribution of experimental FM ordering temperatures is shown in Figure 1(a). The periodic table in Figure 1(b) highlights the distribution of the chemical elements for the FM compounds in our database, covering a large compositional phase space that includes not only the typical magnetic elements (3d and 4f) but also the s and p blocks.

Figure 1. Distribution of T_C. (a) Histogram of T_C for 1749 FM materials in the database. (b) Distribution of the elements for compounds in the FM database.

Descriptors

The Materials Agnostic Platform for Informatics and Exploration (MAGPIE) [22] proposed by Ward et al. is used to obtain the chemical descriptors, labeled as CHEM. As for structural descriptors (labeled as STR), Smooth Overlap of Atomic Positions (SOAP) is used to describe the local crystalline environment such as coordination and distance between atoms [23]. Space group number and volume of the unit cell are considered as a structural descriptor as well. In total, 139 (26) CHEM (STR) descriptors for each compound are considered.

Random forest

The random forest method is used both for identifying magnetic ground state of intermetallic compounds as well as predicting T_C for FM. The AtomWork database is spitted into training/validation set by the ratio of 80%/20%, the MP database is used to demonstrate the prediction ability. It can capture complicated relationship, analyze feature importance and is insensitive to extreme data compared with other machine learning methods (like neural network) [24].

Results

Classification

To enable the prediction of the magnetic ordering in a computationally inexpensive fashion, we perform a classification of the AFM or FM ground state. The training set consisted of 80% of the database and 20% are used for validation. The confusion matrix (CM) is a table that represents the instances in a predicted class versus the ones in the actual class, as shown in Figure 2(a), together with the resulting metrics for 10 cross-validation sets plotted in Figure 2(b). The best accuracy for a model trained with all CHEM and STR features is found to be 87.3% as demonstrated in Figure S6. When the number of features used is reduced to 15, by considering the feature correlation and SHARP analysis, the accuracy drops slightly to 86.8%, with 91.1% FM and 78.5% AFM compounds being correctly classified (Figure 2(a)). This combined with an F1 score of 90.1% indicates good predictability, with a slight bias towards predicting compounds as FM, which might be due to the unbalanced number of FM/AFM compounds in the database. By performing 10-fold cross validation (Figure 2(b)), the average accuracy is about 81.1%, meaning the random forest model has neither overfitting nor biased sampling.

Figure 2. Performance of the classification model. (a): Confusion matrix of FM and AFM classification test set (b): Line graph represents the accuracy, precision, recall and F₁ score of the 10-folder cross validation of classification data, and the pie chart denotes the most important features in classification model (cf. Supplementary for detailed explanation).

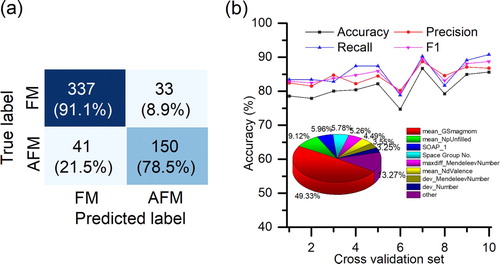
Interestingly, the descriptor ‘mean GSmagmom’ (the average of magnetic moment of the elemental solids for atoms in a given compound) is selected as the most important feature, contributing 49% of feature importance. In this regard, it suggests that ‘mean GSmagmom’ is critical, which accounts for the number of 3d/4f electrons and the elemental properties of corresponding atoms. It is noted that the STR features contribute almost 15%, which proves its significance in determining the magnetic ground state. This is unsurprising given that it is known that interatomic distance is a determining factor for the nature of the AFM/FM exchange interaction following the Bethe-Slater curve [25]. The STR descriptors (especially the volume of the unit cell) could then be expected to be more important when the FM and AFM states are competing. However, it is noted that the relative importance of the STR feature depends also on the contents of our database. By replacing 682 experiment crystal structures in the training set with the DFT relaxed structures based on GGA from MP, the features importance of the model has change slightly, indicating our model is robust against the subtle changes in the crystal structures.

Regression

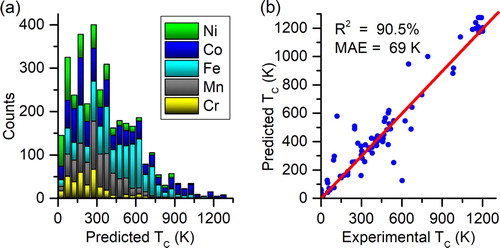
Turning now to modeling the T_C, we construct and compare three random forest models with different feature combinations, using a 80%/20% partition for training/validation of the 1749 FM compounds. For the first two models we proceed in the same way as for the classification. The first model is trained with all CHEM and STR features, giving a R² of 91.24% and mean absolute error (MAE) of 54.99 K (Figure S7). The second model is trained using the reduced number of features as obtained by the dimensional reduction, with a comparable R² and MAE of 90.4% and 58 K, respectively (Figure S8). The last one is a two-step random forest model, intended to better describe the compounds with isomers (i.e. compounds with the same composition but different crystal structures). In the first step, we train a model using a reduced set of 17 CHEM features to predict the T_C, and in a second step, we train a new model using only the T_C predicted in the first step and 6 STR features as descriptors. The best R² obtained from the validation is as high as 91.2%, indicating very good agreement between the experimental and predicted values. As shown in Figure 3(a), the corresponding MAE is 55 K. It is noted that, compared to the accuracy of 90% for the T_C of Heusler compounds obtained based on DFT calculations [26], the accuracy (about 91.2%) of our machine learning model is improved, which can be applied on intermetallic compounds with various crystal structures.

Figure 3. Regression model performance and feature importance. (a) Predicted vs. experimental T_C for test set. (b) Line graph represents the MAE and R² score of the 10-folder cross validation of our database, and the pie chart denotes the most important features in two-step regression model (cf. Supplementary for detailed explanation).

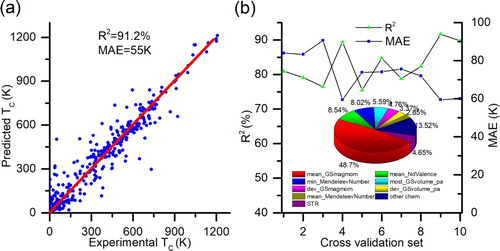
The two-step random forest model generates comparable results to the one-step models but uses fewer features, so we choose to adopt the two-step random forest model for the regression of T_C and discuss the most important features selected in each step. In the first step, ‘mean GSmagmom’ is assigned with the highest importance of 52%, which highlights the relationship between electronic structure and magnetic properties of the elements and those of the compounds, as in the case of classification. For the second step, the T_C predicted by only CHEM contributes the most around 95%, which leaves the contribution of STR to be 5%, where ‘Space Group No.’ is the most important feature among them. Though the absolute contribution of the STR descriptors is not high, they are crucial in distinguishing the T_C of isomers. Even though, the CHEM descriptors alone can already provide good accuracy (90%, 60 K), T_C of isomers are not distinguishable without considering structure descriptors. For example, the experimental T_C for DyMn₂ with space group number 227 and 194 are 40 K and 37 K, respectively. By excluding all isomers in the training set to train the model, when using only CHEM descriptors both structures have the same (as expected) T_C of 62.37 K, however the values after considering the STR descriptors are 40.43 K and 36.37 K (Table S6). In general, considering STR descriptors increase the prediction accuracy of isomers from 90% to 91% and decrease the MAE from 74 K to 67 K (Figure S9), the average T_C difference between structures is only 18.7 K making it a reasonable improvement.

Prediction

Having established the predictive power of our models we now turn to its application on establishing the ground state and T_C of compounds in an existing database. We perform AFM/FM classification of 5193 magnetic intermetallic compounds from Materials Project, leading to 3002 (2191) FM (AFM) (see Data file S1 in the Supplementary). Figure 4(a) shows the predicted T_C for the classified FM compounds, ranging from 5 K to 1280 K. Obviously, the compounds with T_C higher than 600 K are again mostly Co and Fe based, and the element-wise distribution is comparable to that of our training set as shown in Figure S11. Furthermore, we randomly select 548 compounds from 3002 FM materials, and find that 85 among them have experimentally reported T_C. As shown in Figure 4(b), comparing the predicted T_C with the experimental values reveals that the accuracy of our prediction reaches as high as 90.5% with a corresponding MAE of 69 K. For example, despite that the calculation of compounds containing rare earth element has been a well-known trouble, GdCo₄B (space group P6/mmm) and Gd₃Co₁₁B₄ (space group P6/mmm) have been predicted to be FM with a T_C of 490 K and 333 K, which are quite close to the experimental values of 517 K and 303 K, respectively. This is in line with the results obtained via the construction of the machine learning models, validating the workflow that we propose. Detailed values of all predicted and the experimental values are presented in Data file S2 and Table S1, respectively.

Figure 4. T_C prediction. (a) Histogram of predicted T_C for 3002 FM materials in the database. (b) Scatter plot of predicted vs. experimental T_C for 85 compounds with experimental T_C.

Discussion

It is demonstrated that machine learning using the random forest algorithm is able to distinguish materials with FM and AFM ordering, and further to predict the T_C of FM compounds, solving two critical problems in designing magnetic materials. For classification, the accuracy reaches 87%, outperforming the DFT calculations [27], which are applied on a selected set of compounds. For the resulting FM compounds, the magnetization can be straightforwardly evaluated using DFT. Furthermore, the T_C can be accurately modeled with R² about 91% and MAE about 55 K. This enables us to reduce the number of candidates for further computational and experimental characterizations. For instance, the MCA can be evaluated in a high throughput way [5], which sets an upper limit for the coercivity. Thus, the machine learning model developed in this work in conjunction with DFT calculations enables us to get all three essential intrinsic magnetic properties evaluated.

This paves the way to develop FM materials with systematic characterization of the intrinsic magnetic properties, with the help of further high throughput DFT calculations.

Acknowledgements

We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG - German Research Foundation) and the Open Access Publishing Fund of Technical University of Darmstadt.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

Teng Long thanks the financial support from the China Scholarship Council. Part of this work was supported by the European Research Council under the European Union’s Horizon 2020 research and innovation program [grant number 743116 – project Cool Innov] and the Deutsche Forschungsgemeinschaft [grant number 405553726 – TRR 270].