Teacher positioning, student mathematics identity and the mediating effects of problem-solving flexibility

Abstract

The students’ perception of how they are positioned by their teachers offer valuable insights into how teachers might engage students in the act of learning, construct themselves and acts in ways desirable to students, and how they might make the learning process a more enjoyable one for students. Teacher positioning is an important factor in developing the student mathematics identity. It is through positioning that a teacher communicates a set of rights, duties, and obligations that are linked to the position. In this study, we explore the relationships between students’ perception of teacher positioning and student mathematics identity and how problem-solving flexibility mediates this relationship. The study employed a mixed-methods research design. A sample of 12 mathematics teachers responded to the Teachers’ Perception of Mathematics Identity Survey while their corresponding students, with a total of 508 Grade 11 students responded to the Students’ Perception of Teacher Positioning Survey, Student Mathematics Identity Scale, and Problem-Solving Flexibility Test. The correlational statistics and mediation analysis employing a structural equation model were used to investigate the relationships among the variables of the study. In-depth interviews of the teachers and focus group discussions with students were conducted and subjected to qualitative content analysis. Results of the mediation analysis showed that problem-solving flexibility partially mediated the relationship between students“ perception of teacher positioning and student mathematics identity. Knowing that students” perception of how they are positioned by their teachers influences students’ problem-solving flexibility and student mathematics identity, mathematics instruction that promotes flexibility is encouraged.

Keywords:

• identity
• positioning
• teachers’ practice
• problem-solving flexibility

1. Introduction

Learning mathematics involves the development of an identity as an individual member of the mathematics classroom community (Alexander, 2015; Andersen & Ward, 2014). In a community of learners, it is important to see the interaction among its members of the community because it may help us understand how student mathematics identity is developed. An important part of the interaction is teacher positioning. How a teacher assigns a position to themselves and their students is very crucial to the development of student mathematics identity (Yamakawa, 2014). It is through positioning moves that a teacher implicitly communicates a set of rights, duties, and obligations that are linked to the position (Harré, 2012; Wood, 2013). The students’ views of how they are being positioned by their teachers offer valuable insights into how teachers might engage students in the act of learning, construct themselves and acts in ways desirable to students, and how they might make the learning process a more enjoyable one for students.

Looking the students’ perception of how they are positioned by their teachers and student mathematics identity within classroom interactions would provide useful information on their interactions in terms of discursive positions that they take up, what they do with their talk and storylines which they develop during interactions, all of which are constitutive elements of conversations (Wagner & Herbel-Eisenmann, 2015). Positioning creates interactions that may impact learning and identity that brings attention to the effects of teachers’ and students’ actions and utterances in claiming and assigning identities (Norton, 2013).

Looking at the big picture, teacher positioning is influential in the development of student mathematics identity. This is based on the findings of the study conducted by Yamakawa (2014) which suggest that students made use of positioning to be recognized as good mathematics learners, and that social comparisons appeared when students need to negotiate multiple positions to construct a positive future identity as a learner. On the other hand, the consideration of problem-solving flexibility in this study addressed Jorgensen’s (2014) critique of social theories of learning in general which argues that mathematics educators drawing on social theories and identity often render mathematics content invisible.

Thus, the objective of this study is to explore the relationship of students’ perception of teacher positioning and student mathematics identity and how this relationship is mediated by problem-solving flexibility. Specifically, this study investigated the relationship between students’ perception of teacher positioning and student mathematics identity and the mediating effect of problem-solving flexibility. Specifically, this study sought to answer the following questions: (1) How do teachers describe their practice and what do they consider to be mathematics persons? (2) How do students describe their performance and what do they consider in describing a mathematics person? (3) How does students’ perception of teacher positioning relate to problem-solving flexibility and student mathematics identity? (4) How does problem-solving flexibility mediate students’ perception of how they are positioned by their teacher and student mathematics identity?

2. Literature review

2.1. Understanding student mathematics identity

From a social practice perspective, it is through cultural practices as people do life that social identities are constructed (Black & Hernandez-Martinez, 2016). This means that this involves a relationship between the individual and the social and cultural environments in which each is inherently involved in the other’s definition and none exists separately. Identity is a complex and abstract notion that has been explored theoretically across a variety of disciplines. Previous studies highlighted several ideas from theory central to the view of identity, namely, (a) identity as individual attributes (Andersen & Ward, 2014; Axelson, 2009); (b) identity as narratives (Black et al., 2010; Solomon, 2012); (c) identity as a relationship with practice (Darragh, 2013); (d) identity as ways of acting (Turner et al., 2013); (e) identity as afforded and constrained by local practices (Hodges & Hodge, 2017).

Boaler and Selling (2017) define identity as a set of ideas, beliefs, and behaviors that may be performed in specific domains, such as the learning of mathematics. They claim that “Mathematics identity involves how students think about themselves concerning mathematics and the extent to which they have developed a commitment to, are engaged in, and see value in mathematics and themselves as learners of mathematics” (p. 82). This definition includes ideas, beliefs, “ways in which the students think about themselves”, commitment, engagement and seeing values” all of which are difficult concepts to operationalize. The work of Sfard and Prusak (2005) is one of the few papers that provided operationalized definitions of identity by drawing on identity as a narrative (Heyd-Metzuyanim & Graven, 2016; Heyd-Metzuyanim et al., 2016). (Lutovac and Kaasila 2018) rely on the definition of identity as a narrative taken from other sources. Some, such as Oppland-Cordell and Martin (2015), relied on Wenger’s (1998) theorizing of identity, not defining the term identity itself, but rather defining the concepts related to identity according to his theory, namely engagement, imagination, and alignment. In an attempt to define identity, some previous works drew its definition from the social learning theories of Gee (2000) and Wenger’s (1998) that serve as a basis for the discussion of identity: namely; engagement, imagination, alignment, and nature.

In this paper, student mathematics identity is built upon the interplay between the core and normative identities. This interplay is seen to produce personal identity which impacts a person’s actions. On the other hand, it also takes into account the following faces of identity namely, engagement, imagination, nature, and alignment (Anderson, 2007). This means that core identity is who one thinks he or she is (nature) and who one would like to be (imagination), and normative identity is who one thinks one would need to become (engagement) to belong in a certain context (alignment). The interplay between the core and normative identities produces personal identities which impact a person’s actions.

2.2. Teacher positioning

The concept of positioning has appeared so frequently in educational research (Kayi-Aydar & Miller, 2018) and socio-cultural we think that the concept would help to explain a variety of students’ participation in classroom discourse and how such participation is associated with the production of students’ identities as learners. Even though positions emerge dynamically in social interactions, they are not freely constructed (Harré & van Langenhove, 1999). Simply stated, positioning is an act in which people assign or are assigned particular positions within a conversation, that is, a joint action by conversation participants to locate each other in a particular storyline (Harré & van Langenhove, 1999). Examining positioning means a close look at what people are doing with their talk or speech act, from what perspective they are speaking or position, and what story they are producing or storyline within interactions.

Although we did not find any study that investigates students’ perception of how they are positioned by their teachers, a related study on students’ perception of teachers’ performance and behavior (Dalley-Trim, 2007) showed that students pick up on and read particular embodied actions or visual clues as apparent in their teacher’s performance. It was mentioned in this study that students viewed favorably those teachers who smile, laugh, have a sense of humor, are active, enthusiastic, dramatic and who are seen to enjoy what they do. In contrast, students viewed negatively those teachers who frown, sit inactively at the desk, and who indicate a visible lack of enjoyment of teaching by “the expression on [their] face”. It is also noted in this study that students favorably judged teachers who positioned them like adults; not putting them down; showing a genuine interest in the students as individuals; fostering relationships of equity and respect with and between students; being fair and helpful; and caring about, understanding and encouraging students which reinforced appropriate students’ behavior in the classroom. It can be seen that the application of positioning to investigations of classroom discourse would help understand the complexity of interactions. However, in this study, as identified by Yamakawa (2014), teacher positioning can be validating, interrupting, or comparing. On the other hand, teacher positioning on students is based on Bossér and Lindahl (2019) which classify student position as independent learners, legitimate contributors, dependent learners, and recipients of information. This construct includes indicators based on the work of Yamakawa (2014) and Bossér and Lindahl (2019), modified and put together in a survey questionnaire

2.3. Problem-solving flexibility

Flexibility in problem-solving is defined as knowledge of (a) multiple strategies and (b) the relative efficiency of these strategies (Star & Rittle-Johnson, 2008). A strategy is defined here as a step-by-step procedure for solving a problem (Siegler, 1996). First, a key feature of flexibility is the knowledge of multiple strategies. Flexible problem solvers know more than one way to complete tasks. For example, young children have a variety of strategies they use to add, ranging from counting objects to counting up from the larger addend on their fingers to retrieving an answer from memory (Siegler, 1995). Variability in strategy use has clear benefits for learning and performance. For example, learners with knowledge of multiple strategies at the pretest are more likely to learn from instructional interventions (Alibali et al., 2019; Siegler, 1995). More generally, the presence and benefits of multiple strategies among learners have been well documented in a variety of domains, including elementary school mathematics (Rittle-Johnson & Star, 2007; Star & Seifert, 2006; Star et al., 2016). Second, flexibility involves knowledge of strategy efficiency. Flexible problem solvers know which strategies are more efficient than others under particular circumstances. Arslan and Yazgan (2015) pointed out that students usually can select the most appropriate strategy, and use multiple strategies in one problem. Students were comfortable using “look for a pattern” and “make a drawing” strategies. However, according to them, the most unfavorable strategy for them was to “simplify the problem” (Arslan & Yazgan, 2015). Additionally, there were enterprises to use the “write an equation” strategy. Besides, it was observed that students did not need to make a significant change in their thinking ways when their first attempts were wrong and they rarely change their strategies between problems.

3. Method

This study employed a survey research design using the convergent parallel mixed-method (Schoonenboom & Johnson, 2017) in which we concurrently conducted the quantitative and qualitative elements in the same phase of the research process, weighed the methods equally, analysed the two components independently, and interpreted the results together (Creswell & Plano Clark, 2011).

3.1. Participants of the study

A two-stage random sampling procedure was employed in this study. The sample of the study included 12 senior high school mathematics teachers and 508 senior high school students coming from different public schools in urban areas. The students were handled by the teachers of the study. Interview sessions were conducted separately for 12 teachers and 24 students. The said sample size was already sufficient for this study which utilized structural equation modeling with three latent variables (Hair et al., 2019; Kyriazos, 2018; MacCallum et al., 1996; Schumacker & Lomax, 2016).

3.2. Instruments of the study

The researcher-made instruments intended to measure student mathematics identity, problem-solving flexibility, and students’ perception of teacher positioning were developed based on the existing instruments and related literature, we developed all the instruments based on existing literature and were subjected to face, content, and construct validity testing and were pilot-tested to other group of grade 11 students to ensure comprehensibility. The aforementioned instruments were subjected to internal reliability testing for which Cronbach’s coefficient alpha was used. The student’s perception of the teacher positioning survey scale and the student mathematics identity scale were subjected to the following process: (1) identifying the scope of the content based on literature, (2) writing the items, (3) reviewing by a panel of experts for content validation and clarity, (4) revising of the items based on experts’ recommendation, (5) pilot testing and analysis, (6) reliability testing, and (7) identifying the final number of items based on confirmatory factor analysis. On the other hand, the problem-solving flexibility test was adopted from existing work (Arslan & Yazgan, 2015) and tried out on another group of grade 11 students.

Since the questionnaires were adapted and modified from previous studies and additional indicators were added, there was a need to validate the constructs and questionnaire items. For this purpose, a multivariate statistical approach and confirmatory factor analysis were used (Williams et al., 2010). These statistical approaches were used to interpret self-reporting questionnaires in educational psychology (Thompson, 2004). Exploratory factor analysis (EFA) was used when the researcher has no prediction of the number of indicators to be measured (Costello & Osborne, 2005). The primary objective was to reduce many indicators to a smaller set of factors. This process tested whether there was a relationship between student-related variables and latent constructs. Confirmatory factor analysis (CFA) was used by the researcher to propose a priori factor structure based on theory and preliminary analyses, and it provided valid evidence for the scales used in the questionnaire. Both EFA and CFA helped to refine a proposed theory (Costello & Osborne, 2005).

3.2.1. Students’ perception of teacher positioning survey

This was measured using a questionnaire inventory modified based on the work of Yamakawa (2014) which students perceived their teacher as validating, interrupting, or comparing. On the other hand, students’ perception of how they are being by their teacher was based on Bossér and Lindahl (2019) which classified student position as independent learners, legitimate contributors, dependent learners, and recipients of information, and other statements that positioned them as mathematics person or not. This construct includes indicators based on the work of Yamakawa (2014) and Bossér and Lindahl (2019), modified and put together in a survey questionnaire This study adopted a four-point Likert scale, ranging from almost always (4) to never (1). The students’ perception of teacher positioning is classified into high or low positioning based on the classification of perception and expectations provided by Rubie Davies (2010). The average score of 2.5 and above were classified as high TP and those who scored 2 and below were classified as low TP. Those students whose scores range between 2 and 2.5 were not included in this study.

3.2.2. Student mathematics identity scale

To measure student mathematics identity, an instrument composed of questions using a 4-point Likert scale was used ranging from 1 which is “not at all true to me” to 4 which is exactly true to me.” The items of this scale were based on the four faces of mathematics as identified by Anderson (2007). This four faces includes: who one thinks he or she is (nature); who one would like to be (imagination), who one thinks one would need to become (engagement); and to belong in a certain context (alignment)

3.2.3. Problem-solving flexibility test

Problem-solving flexibility was measured using an instrument composed of four routine problems taken from the work of Xu et al. (2017) and three non-routine problems taken from the work of Arslan and Yazgan (2015). The routine problems were composed of four linear equations which were designed so that each could be solved using a standard algorithm but where a more innovative strategy also existed. The four problems were divided into two problem types, with two instances of each problem type. On the other hand, the non-routine problems were used because students who develop flexibility in problem-solving are more likely to use existing strategies when faced with unfamiliar transfer problems (Star & Rittle-Johnson, 2008). According to Arslan and Yazgan (2015), the strategy flexibility of students could be more observable while they are solving nonroutine problems since they do not know a direct way of reaching the solutions to these problems.

3.2.4. Interview questionnaires

Two questionnaires were used in this study: (1) an interview questionnaire for students and (2) a teacher interview questionnaire

3.2.4.1. Interview questionnaire for students

Previous research in the area of identity has examined the development of self-beliefs predominantly from the results of structured surveys. To allow for the unique narratives that emerge when individuals reflect on their own mathematics identity, an open-ended interview protocol was designed. The interview protocol was semi-structured, allowing both the standardization needed to acquire similar information from the participant as well as the flexibility required during individual administration. The protocol was structured so that the same questions were asked to each participant in a similar order to remain focused on student mathematics identity.

3.2.4.2. Teacher interview questionnaire (TIQ)

The TIQ was used to interview mathematics teachers after the administration of the survey questionnaires to the students. The interview probed how the level of teacher positioning influenced student mathematics identity and other student-related variables. The questionnaire covered how the teacher felt and what they believed about themselves in relation to the teaching of mathematics and to the learners, their main considerations in selecting activities for the mathematics classes, and how their views about themselves and their students influence their choice of strategies, activities, and approaches to teach mathematics.

3.3. Data collection and analysis

We coordinated with the schools where the sample from the accessible population belonged and asked for approval from the respective schools. Soon after the approval and endorsement, a meeting with each of the school heads or teachers in charge of the senior high school was held to orient them on the purpose of the study and to discuss the process of administering the instruments. Schedules of the administration of the questionnaires and the conduct of the interview were obtained from the school samples. A total of twelve Grade 11 Mathematics teachers situated in different schools were the teacher-respondents of the study. On the other hand, their respective Grade 11 students were the student respondents of the study. The data collection procedure was done in two parts. The first part was the administration of students’ perception of teacher positioning survey (TPS), problem-solving flexibility test (PSFT), and the student mathematics identity scale (SMIS) were administered to the students. The second part consisted of the interview with teachers using the teacher interview questionnaire (TIQ) and the group interview with selected students using the Interview questionnaire for students (IQS).

3.3.1. Quantitative data collection and analysis

In the analysis of the quantitative data, this study employed variable-oriented analyses (Onwuegbuzie & Combs, 2015) which involved identifying relationships—typically probabilistic—among constructs that were treated as variables in a way that facilitated research that often is conceptual and theory-centered from the onset, and has a tendency toward external generalizations. As such, variable-oriented analyses, whose “‘building blocks’ are variables and their intercorrelations, rather than cases” (Miles & Huberman, 1994, p. 174), are more applicable for quantitative research in general and quantitative analyses in particular. Furthermore, descriptive statistics such as the mean, median, standard deviation, percentages, and minimum and maximum scores were computed to summarize the data obtained. This was useful in examining the general characteristics of the data gathered from the samples. For the preliminary analysis, a test for normality using the Shapiro-Wilk test and the d’Agostino-Pearson test was conducted. Mann-Whitney test was conducted to test whether there was a significant difference in mathematics identity (SMI) of students with low scores in their perception of how they were positioned by their teacher (low TP) to those of students with high scores in their perception of how they were positioned by their teachers (high TP). To determine the mediating effects of problem-solving flexibility, the mediation analysis using structural equation modelling (SEM) was employed in this study.

3.3.2. Qualitative data collection and analysis

The teacher-participants who accomplished the questionnaires were also the same respondents who were requested for an interview. The researcher provided the teachers with the interview questions. During the interview, the researcher asked the teacher-respondents based on these questions: 1) What is to them a mathematics person? 2) Do they identify their students as mathematics persons? Why? Or Why not? 3.) How do they describe themselves as mathematics teachers? During the interview, we asked probing questions about their practice as mathematics teachers. All of the respondents requested that the interview would not be recorded. The researcher took notes while the teachers responded to the questions. After the interview, the researcher spent a few minutes with the teacher for clarification and validation of the teacher’s responses. The teacher-respondents also provided the researcher with their written responses to the interview questions. The interview session took an average of 20 minutes per teacher. On the other hand, male and female students were selected from each of the student samples handled by the teacher-respondents. In all cases, the teachers provided the researcher with two students for the interview. The researcher explained first to the students the purpose of the interview. The interview session with the students was conducted as a group and was audio recorded. The researcher also took notes of the keywords of the students’ utterances. Overall, the group interview with the students took a maximum of 30 minutes.

In summary, the participants reflected upon their prior experiences and narrated their personal stories. “The process of forming, recounting, and revising stories allows people to maintain a sense of continuity between their past, present, and future selves” (Edwards, 2010, p. 39). Recollection played an important role in this process because rather than displacing objectivity, recollection can facilitate it. When people tell their own stories, they often uncover the information they did not consciously know themselves (Bell, 2002), which sheds light on the identities of individuals (Creswell, 2015). The data source for this study was constructed narratives created from transcripts from semi-structured interviews. Recollection provided

…distance and perspective needed for a more comprehensive appraisal of what has actually happened. If the task is to understand how the shape and subjective meaning of a person’s life is created out of unfolding events, recollections may be best. (Freeman et al., 1986, p. 183)

In the collection of the qualitative data, the analysis of the interview with the students was conducted based on the following questions: (a) What kind of experiences did students recall having with their junior high school mathematics teachers? (b) What made students perceive that the said experiences influenced their mathematics identities? and (c) What common student experiences positively or negatively affecting mathematics identity emerged from the data?

3.3.3. Mediation analysis

In the mediation analysis, this paper utilized the measurement-of-mediation design which was conceptualized as a statistical approach (Bullock & Shang, 2011). This design was used by taking the measures of the proposed mediating variables and then used statistical analyses to establish mediation. This approach did not involve manipulation of the hypothesized mediating variable, but only involved measurement. Based on the guidelines for mediation analysis in SEM proposed by Hair et al. (2014), the researcher evaluated the significance of a direct path. If the direct effect was not significant, there would be no mediation. If the direct path was significant, the researcher included the mediating variable and used the bootstrapping procedure again. If the indirect path was not significant after bootstrapping, there would be no mediation; if it was significant, the variance accounted for (VAF) would be calculated. According to Hair et al. (2014), a VAF value of greater than 80% indicated a full mediation and a value between 20% and 80% indicated a partial mediation, while a value less than 20% indicated no mediation. Further tests of significance were applied using the Sobel and the Aroian test statistics. The mediation effect built on the process by which students’ perception of teacher positioning (TP) influenced student mathematics identity (SMI), was twofold: the direct effect on SMI and the indirect effect on SMI through the mediator variables (Preacher et al., 2007). The total effect is the degree to which a change in TP has an effect on SMI. A direct effect is a degree to which a change in TP produces a change in SMI without going through any other variable. In contrast, an indirect effect is the degree to which a change in a TP produces a change in SMI by means of the mediator variables.

Assuming that mediation occurs, the relationship between students’ perception of teacher positioning and student mathematics identity could be partly explained by a mediator variable. A theoretical framework was developed to confirm possible mediating factor of problem-solving flexibility between students’ perception of teacher positioning and student mathematics identity. The mediation pathways were explored based on this theoretical framework. To assess and test the indirect effects, different sets of techniques were available (Little, 2013). In this study, the researcher employed the Product coefficient approach using the Sobel and Aroian test equations and the Bootstrapping approach (Turnes & Ernst, 2015).

4. Results and discussion

4.1. The results are presented based on the research questions of the study

4.1.1. Research question 1: How do teachers describe their practice and what do they consider to be mathematics persons?

We asked the teachers to describe their practice as mathematics teachers and to describe mathematics persons and their students in their mathematics classroom. Mathematics teachers’ descriptions of their classroom practices and their students revealed how they position themselves and their students in their mathematics classroom.

4.1.2. Teachers’ description of their practice

The result of the content analysis showed that teachers in the low TP group considered themselves to be authorities in the classroom and viewed students as dependent learners and recipients of information. On the other hand, teachers in the high TP group considered themselves facilitators of student learning and their students as independent learners and legitimate contributors to classroom discussion.

Teachers in the low TP group generally have high regard for teacher preparation and mathematics content. Most of them believed that mathematics teachers who are the authorities in the classroom should prove to be knowledgeable of the content. This view is also mentioned by Wagner and Herbel-Eisenmann (2013), who said that teachers could be “an authority in mathematics” and they could be “in authority” (p. 491) if they are knowledgeable and skilled in the subjects they are teaching. However, most of the teachers in the low TP group considered their students as dependent learners and recipients of information.

Teachers as authorities in the classroom. The teacher as the authority in the classroom is a traditional view and has been a held belief for so many years. Teachers in the low TP group believed that a mathematics teacher should have a robust knowledge of the content of mathematics as an authority in the classroom. Teacher A mentioned that “students should have confidence in their teachers … this can only happen if teachers are knowledgeable.” This was also mentioned by Teacher E, that she “was trying [her] best to make students learn.” She mentioned that it was “difficult for her and [she] did most of the talking.” She rarely asked students to explain, because she said that she “might get disappointed” for a “wrong answer.” On the other hand, Teacher B who is from school G said:

As a teacher, I do not have control over my students … if they do not want to learn, then that’s it. I observed them working and tried to help them as much as possible. [If they [students] don’t want it, I do not discuss difficult examples. I made it simpler. If they do not know, I just repeat the example … sometimes I give them another example for them to understand. If they still don’t … I just asked them to study at home …

Teachers who are an authority should have the required content knowledge to facilitate learning; teachers in authority have the power within the lesson to decide what happens, when, and how (Tait McCutcheon, 2014).

On the other hand, teachers in the high TP group generally considered themselves facilitators of student learning. They also believed that students were capable of learning mathematics. They mentioned that “students could be independent learners and could contribute to the discussion”. Based on the result of the content analysis, two themes were generated.

Teachers as facilitators of student learning. Teachers in the high TP group believed that teachers have to be patient and may intervene only when students are at a loss. The teachers’ role was more on guiding students and facilitating student learning. Teacher F, a teacher in the high TP group said:

As a mathematics teacher, I see to it that I am prepared for the day’s lesson. I want my students to cooperate and do their part for them to learn. I believe that my students should take an effort … I do not believe in “spoon-feeding” which is why I let them do or perform activities in class or solve problems either individually or in a group.

Teachers in the high TP group such as “Teacher K” and “Teacher N” believed that “students” activities are important … because this is one way of giving them the opportunities to work in groups and to share ideas”. “Teacher I” said, “at least in groups, they can talk. I listened and I just intervened when they were lost … I asked them to explain why they were doing it.

4.1.3. Teachers’ description of mathematics persons

Based on teachers’ interview transcripts, we identified four major themes that described a mathematics person. Teachers pointed out four dimensions that identified students to be mathematics persons. The results of the qualitative analysis identified four themes that were the bases of teachers’ description of a mathematics person and these are: (a) students’ performance and competence in mathematics; (b) students’ confidence in doing mathematics; (c) students’ disposition towards mathematics and; (d) students’ participation and engagement in mathematics activities.

Students’ performance and competence in mathematics. Based on the interview transcripts and the questionnaires given to teachers suggested that beliefs about the competence and performance of the students were pronounced, indicating an important indicator of SMI. According to “Teacher K”, a mathematics person is “one who knows how to organize ideas, think critically and solve problems in a rational and creative way.” Other teachers handling STEM classes also agreed that a mathematics person is one who “has competence in mathematics”, one “who understands the concept of Mathematics” and “who knows its applications and the reason behind its theories and ideas.” On the other hand, teachers in the low TP group said that their students are not mathematics persons because students “have difficulty in problem-solving”, “unable to explain answers and solutions”, “basically their performance in mathematics is poor”, and students are “struggling with most of the mathematics problems.” Teacher B (low TP teacher handling HUMSS class) narrated:

I don’t consider my students as mathematics persons because most of them have difficulties in mathematics, especially in problem-solving. Most of them lacked understanding of the basic mathematics concepts and they do not know how to explain their answers … their grades in junior high school were very low and it was evident during their General Mathematics class … [their] grades were not good.”

Based on the results of the analysis of the qualitative data, it is evident that teachers considered competence and performance as key indicators of whether a student is a mathematics person or not. Cribbs et al. (2015) found that competence and performance are filtered through recognition and interest, thus having an indirect effect on student mathematics identity.

Students’ confidence in doing mathematics. Confidence in doing mathematics when students are working in groups affected the improvement of problem-solving skills and the motivation to learn mathematics which indirectly affected the development of the student mathematics identity (Hima et al., 2019). This finding is consistent with the qualitative result of this study. Teacher F (who was perceived by students to have high TP handling STEM class) articulated that “a mathematics person is [someone] who is confident in doing mathematics.” There seemed to have an agreement among teachers in this study who said that a “student who is confident in doing mathematics is [usually] a mathematics person”, “who is not afraid when called to answer”, and “one who confidently volunteers to solve problems when everyone else seemed hiding.”

Students’ disposition towards mathematics. Disposition is a tendency to behave consciously, frequently, and voluntarily to achieve certain goals. These behaviors include self-confidence, persistence, curiosity, and flexible thinking. In the context of mathematics, the mathematics disposition regarding how students complete a mathematics problem: whether confident, diligent, interested, and flexible thinking to explore various alternative resolutions. In the context of learning, mathematics dispositions are related to how students ask, answer questions, communicate mathematics ideas, work in groups, and solve problems. Mathematics disposition is a tendency to think and act positively. This trend reflected the students’ interest and confidence in learning mathematics and a willingness to reflect on their thinking (Anku, 1996). Mathematics disposition is the desire, consciousness, and a strong dedication to students to learn mathematics and implement a variety of mathematics activities. This study revealed that students’ disposition towards mathematics is an indicator of being a mathematics person. Teacher L (high TP) believed that a mathematics person is someone who “sees mathematics as a useful practice” and was seconded by Teacher E (high TP), who said that a mathematics person is someone who “sees the importance of mathematics in choosing college courses”, one who “feels comfortable and excited about mathematics.” According to Teacher H (high TP handling STEM class):

A mathematics person is someone who likes mathematics and treats mathematics as a useful subject. He must be a person with a heart for numbers. I believe that a person does not only have the brain or the talent but he or she has to have the right attitude toward mathematics. I think being a mathematics person is being a whole person.

Students’ participation and engagement in mathematics activities. Engagement refers to persons’ direct experience of the world and their active involvement with others (Wenger, 1998). Much of what students know about learning mathematics comes from their engagement in mathematics classrooms. Through varying degrees of engagement with mathematics, their teachers, and their peers, students see themselves and are seen by others, as one who has or has not learned mathematics. Based on the data, teachers considered “students” participation and engagement in mathematics as indicators of being a mathematics person”. “Teacher H” (handling STEM class), said:

For me, most of my students were ‘mathematics persons’ since they could easily comprehend mathematics and were able to participate and easily engaged themselves in the discussion and in answering the problems. They were very participative and were always ready with their assignments.

According to Anderson (2007), engaging in a particular mathematics learning environment aids students in their development of an identity as capable mathematics learners. Other students, however, may not identify with this environment and may come to see themselves as only marginally part of the mathematics learning community. In traditional mathematics classrooms where students work independently on short, single-answer exercises and an emphasis is placed on getting the right answers, students not only learn mathematics concepts and skills, but they also discover something about themselves as learners (Anderson, 2007; Boaler & Greeno, 2000). Students may learn that they are capable of learning mathematics if they can fit together the small pieces of the “mathematics puzzle” delivered by the teacher.

4.2. Research question 2: How do students describe their performance and what do they consider in describing a mathematics person?

On the other hand, analysis of qualitative data from students’ interviews, has generated different themes that are consistent with the literature and the review of related studies presented in this paper. The themes generated different constructs which have been influential in the development of student mathematics identity. Based on students’ utterances, constructs that are evident to have been influential to student mathematics identity include (a) personal competence beliefs, interest, and confidence in doing mathematics; (b) personal and others’ recognition of mathematics ability; (c) perception of mathematics; and (d) perceived usefulness of mathematics.

Beliefs, interests, and confidence in doing mathematics. Interest is a vital component of student mathematics identity development. An individual’s interests defined as a “person’s likes, preferences, favorites, affinity toward, or attraction to a subject, topic, or activity (Dunst & Raab, 2012), have a rich theoretical basis as a fundamental construct in models for human learning (Hidi et al., 1992). Vygotsky claimed as mentioned by Dipardo and Potter (2003) that thought is engendered by motivation, desires and needs, interests, and emotions. For these reasons, interest in mathematics as a subject has been an important part of behavioral research within mathematics education. Interest plays a key role in whether or not students want to take an identity in mathematics.

Student H-1 recalled that when he was in elementary, he never had an interest in mathematics and he never had good grades. He said:

When I hear the term mathematics, at first I think that it is hard because it takes time to solve a question[problem] and you need to have [a bigger] knowledge when it comes to mathematics. I never had an interest in mathematics when I was in elementary. When I was in high school, I became interested in mathematics and I realized that I needed to have good background to have confidence in mathematics. That is why I became interested and I decided to take STEM.

Student K-2, whose parents are both engineers decided to take STEM because of his interest in mathematics. He mentioned that his father was instrumental in making him interested in mathematics and eventually decided to pursue a course related to mathematics.

For my love for mathematics, I always attribute it to my father… it’s always my father who is involved, introducing me to many wonderful things in mathematics, that made me interested in mathematics… and until now I always look for algorithms or shortcuts in solving problems, interested in learning concepts in higher mathematics… not only for the sake of my interest but also gaining knowledge for mathematics.

Personal competence beliefs are broader than self-efficacy, which has been traditionally measured as task-specific attainment (Goldstein, 2018). Students’ beliefs about their ability to perform the practices of their discipline and understand the content of their discipline—whether science or mathematics—has an impact on their ability to see themselves as the kind of person who can legitimately participate in these areas.

Student L-1, a student in the STEM strand showed an alternating level of perceived competence: solid confidence at primary school and some hardships with mathematics during junior high school. Student L-1 said:

When I was in grade one until grade 4, I like math compared to other subjects. As if math was easy…I helped my classmates with their assignments. But when I was in grade 9…I had difficulty. I did not know why. I think I could not do it. Sometimes I feel bad about my teachers…I know you know what I mean. Ah, because…they did not explain well to us.]

As for Student L-1, it seemed that his pattern somewhat matches that of Student A-2 showing confidence in her primary school and some problems in her junior high school. Student A-2 who is from the HUMSS strand said that she “had difficulty in solving mathematics problems when she was in junior high school.” And because of this experience, she decided to take HUMSS.

During the interview, the researcher did not ask direct questions about the student’s mathematics competence. However, an analysis of the transcripts revealed it as a very small detail, yet showing significant variations in this area. This was manifested by the responses of Student J-1 when he said:

I like Mathematics and I do not have a hard time understanding mathematics. I think I will pursue engineering and… yes I need math for it. They said that I am diligent that’s why I made it.

Personal and others’ recognition of mathematics ability. Recognition plays a significant part in identity development and has more recently become a focus in science identity research. A student’s perception of how others view him or her is vitally important to how that student sees himself or herself. According to Strayhorn (2010), these recognition messages are important early on in students’ careers from parents and teachers. This idea is related to students’ self-efficacy beliefs, which have been shown to be a significant positive predictor of mathematics persistence (Bandura, 1986).

A student, Student J-2 who is in the STEM strand admitted that she never had high grades in mathematics when she was in junior high school. She also admitted that she never consider herself better than others in mathematics. She also said that when she was in elementary school, her “parents encouraged her and believed and expected her to do good in mathematics”. She further mentioned that her teachers told her that she is good at mathematics. She said:

I feel responsible [for] my studies. Although I never see myself as better than others in mathematics, I work hard because my parents expected me to do well in mathematics and they believe that I can do well in mathematics… I am a hardworking student and I always try to challenge myself and I try to do my best and always develop my study habit. My teacher once told me that I could do better in mathematics if I just focus on my studies. Since then, I take extra effort in doing my homework and I feel that I am successful. That is the reason that I never doubted why I am enrolled in STEM.

When others recognize students’ ability in mathematics, they build their confidence and this motivates them to do better in mathematics. Student K-1 was elated because his classmates recognized him and look up to him when he was in junior high school. Although he no longer felt that confident in his senior high school because his grades are not that high, he still believed he could and it was affirmed by his teacher in General Mathematics. He said:

I feel I was being looked up to. But that was before I thought I was good at math. However, during my senior high school, it was already difficult. But my grade in Gen Math was ok. I felt that I just need to review. Math is my favorite subject until now though my grade was a bit lower. My teacher also expected me to do better. My teacher told me that I could do better to increase my grade. I was inspired. I like solving problems… it is my priority because I enjoy it.

Beliefs about personal competence are highly influenced by others’ recognition. This is also true for Student H-2. He said that “my teacher and my parents wanted me to compete in a quiz bee and other competitions. I think I can do it… I won a few of the competitions in mathematics before.” Many authors (Anderson, 2007; Gee, 2001; Wenger, 1998) stress the main role of self-recognized and socially acknowledged competence as learners of mathematics in the construction of mathematics identity for students. DiMartino and Zan (2010) observe patterns in the essays of students that lowly perceived competence is often correlated with an instrumental vision of mathematics. Similar patterns are noticed in the interviews: those students whose answers revealed competence perceived comparatively lower focused their narratives on an instrumental vision of mathematics to a larger extent.

Perception of mathematics due to experience. It has been pointed out in the literature that perceptions and beliefs about mathematics originate from past experiences which comprised both cognitive and affective dimensions (Mutodi & Ngirande, 2014). Schoenfeld (2008) also pointed out that students’ perception of mathematics and mathematics teaching has been considered to be a very significant factor underlying their school experience and achievement. Thus, students’ perceptions of mathematics play an important role in developing student mathematics identity. This is also a factor in students’ consideration of their choice of SHS strand. Student B-2 narrated:

In my elementary [school], I had a teacher who was very clear in her instructions. I got the highest scores most of the time. The teacher explained mathematics to us, and, probably, I can still remember all that she discussed. Then in high school, it changed. I had a teacher in math who was strict and did not explain all to us. Since then, I hated math. But now, it is fine. I am no longer anxious. I wish that STEM was my choice because I want to be an engineer. However, I am afraid that mathematics is still difficult.

Furthermore, Student J-2 clearly articulated that her elementary teacher made her like mathematics. She said:

My most memorable in mathematics was when I was in the elementary school. My teacher in mathematics was so approachable. She gave us some problems to answer then when my answer was wrong she provided correction and … I was never disappointed with my teacher. For me, mathematics was easy… I felt that I enjoyed it.

Perceived usefulness of mathematics. Following the study by DiMartino and Zan (2010), relationships with mathematics are analyzed in a broader life context, highlighting their properties and emotional tone. For students who were interviewed in this study, these relationships differed to some extent. In one case, it is observed that those students who admitted that they are not good in mathematics viewed mathematics as important for their college course, and some viewed mathematics as a lifebuoy in practical life situations. In the case of H-1, his positive view of mathematics as a unique exclusive subject, positive relationships as well as instrumental relationships are apparent, though not so much as to help in daily hassles, but as to developing the entire personality and, especially, cognitive processes. Student H-1 narrated:

I believe that mathematics is important in developing myself to be disciplined and becoming a good person as a good problem solver and as a critical thinker. I need to study mathematics because I always wanted to be an engineer.

Although mathematics is not her favorite subject, Student D-2, who is a student in the HUMSS strand, mentioned that mathematics is different and very challenging and she believed that mathematics is important. She said:

My favorite subject is history because I want to know those who have been in our country for a long time. However, I see to it that I work on my assignment in mathematics because I want to improve myself in solving a problem or any situation… Math is everywhere so mathematics is important to us. But the other subject is really good. But math is different. It is very challenging.

Furthermore, Student G-1, a student in the STEM strand, admitted that mathematics is difficult but because of his belief that mathematics is important in college, he took extra effort in mathematics as compared to other subjects. He said:

I never had good grades in mathematics, and I wish I could do better this time because I would be taking a course that needs mathematics. Mathematics is difficult…but important not only in school but also in life. That is why I always spend more time studying mathematics and working on my homework.

These perspectives coincide with the conclusions drawn by Kaasila et al. (2008) that different views about mathematics may be explained by the socially emotional orientation and coping strategies of research participants. Hence, the common theme for all three students was their view of mathematics as an instrument, although using it for different purposes: to solve personal and life situations, to develop cognitive skills and the entire personality, or to aid as a psychological coping strategy. None of the interviewed students had a negative view of mathematics regardless of the mentioned hardships while learning.

4.3. Research question 3: How do students’ perception of teacher positioning, students problem-solving flexibility, and student mathematics identity relate to each other?

4.3.1. Students’ perception of teacher positioning and student mathematics identity

A one-way between-subjects ANOVA was conducted to compare the effect of students’ perception of teacher positioning on student mathematics identity. There was a significant effect of students’ perception of teacher positioning on student mathematics identity at p < 0.001 for both groups [F (1, 506) = 745.835, p < 0.001]. The result of the analysis of variance indicated that 59.6% of the variability of SMI could be explained by students’ perception of TP. Post hoc comparisons using the Tukey HSD test indicated that the mean score for Low TP (M = 2.479, SD = 0.535) was significantly different than the mean score for High TP (M = 3.534, SD = 0.304). Moreover, using the Tukey test, the mean difference of Low TP and High TP [mean difference = 1.055, t = 27.310, p < 0.001] was significant.

4.3.2. Students’ perception of teacher positioning and problem-solving flexibility

A one-way between-subjects ANOVA was conducted to compare the effect of TP (Low TP and High TP) on problem-solving flexibility. There was a significant effect of teacher positioning on problem-solving flexibility at p < 0.001 for both groups [F (1, 506) = 584. 879, p < 0.001]. Based on the result of the analysis of variance, it showed that 53.6% of the variability of PSF is explained by students’ perception of teacher positioning. Post hoc comparisons using the Tukey HSD test indicated that the mean score for low teacher positioning (M = 5.663, SD = 1.075) was significantly different than the mean score for high teacher positioning (M = 3.645, SD = 0.785). Moreover, using the Tukey test, the mean difference of low TP and High TP [mean difference = 2.015, t = 24.1841, p < 0.01] was significant.

4.3.3. Problem-solving flexibility and student mathematics identity

There was a positive correlation between problem-solving flexibility and student mathematics identity, r = 0.55, p < 0.01. Students in problem-solving settings developed identities of competence that included mathematics as part of their envisioned future, while students in lecture-based settings did not. Cobb and his colleagues (e.g., Cobb et al. 2009) corroborated these findings by showing how students in a problem-solving setting aligned themselves to the new norms of participation in ways that could positively influence their mathematics identity.

In view of the above findings, thinking about teachers’ perceptions of students, Aaron & Herbst (2015) revealed that when teachers talk about their students within the context of instruction, they describe their students in terms that can be understood to relate to the task; and that teachers might talk about their students differently depending on if students are engaged in working independently or if students are engaged in sharing and discussing ideas. In particular, how teachers see their students is an important factor in determining SMI. Aguirre et al. (2013) state that mathematics identity is “how students see themselves and how they are seen by others” (p. 13).

4.4. Research question 4: How does problem-solving flexibility mediate students’ perception of how they are positioned by their teacher and student mathematics identity?

4.4.1. Mediation analysis

The mediation model with problem-solving flexibility as a mediator of the relationship between students’ perception of teacher positioning (TP) and student mathematics identity (SMI) is shown in Figure 1. The figure indicates both unstandardized and standardized (in parentheses) path coefficients. The model shows that PSF mediated the relationship between TP and SMI.

Figure 1. Mediation Model Showing TP and SMI Mediated by PSF.

Note: The Mediation Model shows the relationship between students’ perception on teacher positioning (TP) and student mathematics identity (SMI) with problem-solving flexibility (PSF) as mediator. The direction of the relationship is indicated by the direction of the arrow.

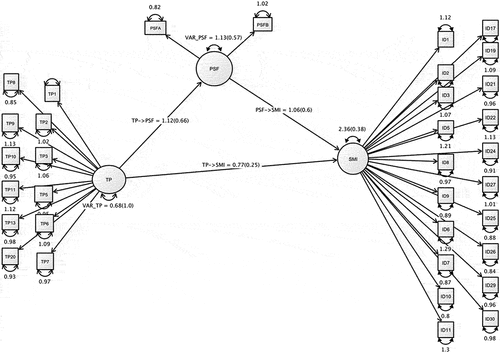
The mediation model showing students’ perception of how their were positioned by their teacher (TP) and student mathematics identity (SMI) mediated by problem-solving flexibility (PSF) shows that the model fit indices are highly acceptable with $X^2=600.9$ and df = 590, with CMIN = 1.0186, p > 0.05; TLI = 1.0, CFI = 1.0, SRMR = 0.006; RMSEA = 0.001. The path coefficients were all significant at p-value = 0.05 as shown in Table 1. The direct effect of TP on SMI (0.7692, p < .01) was significant. The indirect effect of TP in SMI (1.1897, p < .01) with 95% CI [0.8611, 1.520], and the total effect of TP on SMI (1.959, p < .01) were significant. The variance accounted for (VAF) of 60.73%, indicating a partial mediation means that 60.73% of the effect of TP on SMI was mediated by PSF. This indicated further that PSF as the mediator partially mediated the relationship between TP and SMI. When PSF mediated the relationship between TP and SMI, the direct effect was significant which indicated that the direct effect measured the extent to which SMI changes when TP is increased by one unit and PSF, the mediator variable remains unaltered.

Table 1. Path coefficients of the model with PSF as a mediator

Path	Estimate	Standard Error	z-value	Indirect effect	95% Confidence Interval	Total Effect	VAF (%)
TP ➔ SMI	0.7692	0.0324	23.74*	1.1897*	[0.861, 1.52]	1.959*	60.73%
PSF ➔ SMI	1.0597	0.0194	54.62*
TP ➔ PSF	1.1227	0.0168	66.83*

*Significant at p = 0.05

The significance of direct and indirect effects was further tested using the Sobel test and the Aroian test. Sobel test statistic (42.293), with standard error (0.0281), was significant (p < 0.01). On the other hand, the Aroian test statistic (42.290), with a standard error (0.0281), was also significant (p-value<0.01). In this case, the mediation model again indicated a significant effect of PSF on the relationship between TP and SMI.

In relation to these results, it has been noted that in traditional mathematics classrooms where students work independently on short, single- answer exercises and an emphasis is placed on getting the right answers, students not only learn mathematics concepts and skills, but they also discover something about themselves as learners (Anderson, 2006). In the same manner, students who are asked to follow procedures on repetitive exercises without being able to make meaning on their own may not see themselves as mathematics learners but rather as those who do not learn mathematics (Boaler & Greeno, 2000).

Furthermore, Boaler and Greeno (2000) showed that students in problem-solving settings developed identities of competence that included mathematics as part of their envisioned future, while students in lecture-based settings did not. Cobb et al., (2009) corroborated these findings by showing how students in a problem-solving setting aligned themselves with the new norms of participation in ways that could positively influence their mathematics identity.

Since problem-solving flexibility mediated the relationship between teacher positioning and student mathematics identity, the use of open-ended mathematics tasks, questions, or projects that have multiple responses or one response with multiple solution paths can be beneficial in engaging students and supporting the development of student mathematics identity (NCTM, 2000). Hence, mathematics tasks that engage students in doing mathematics, making meaning, and generating their solutions to complex mathematics problems are important in developing students’ problem- solving flexibility. Furthermore, to develop students’ problem-solving flexibility, the mathematics classroom can be organized to encourage discussion, sharing, and collaboration (Boaler & Greeno, 2000). In this type of classroom setting, teachers “pull knowledge out” (Ladson-Billings, 1995, p. 479) of students and make the construction of knowledge part of the learning experience. In addition, Hima et al. (2019), mention that for many students mathematics lessons can be scary, but when students were allowed to solve problems with other strategies, they were able to call mathematics into something positive. They also contend that there was a significant increase in understanding the mathematics concepts that directly affected the improvement of problem-solving skills and the motivation to learn mathematics. Therefore, the increase of these two components indirectly affected the development of the mathematics identity that students have.

From this finding that problem-solving flexibility partially mediated the relationship between teacher positioning and student mathematics identity. Furthermore, students’ perception of how they are being positioned by their teachers and how they position their teachers is influential in the development of student mathematics identity even with the presence of the mediator variables such as problem-solving flexibility. This means that teachers can tap into problem-solving flexibility which can be tapped through teacher positioning.

5. Summary and conclusion

In summary, teachers who are perceived by students to have high regard for their students in terms of positioning their students considered themselves facilitators of student learning and believed that students were capable of learning mathematics. They also mentioned that in considering a mathematics person, they look at students’ performance and competence in mathematics, students’ confidence in doing mathematics, students’ disposition towards mathematics and students’ participation and engagement in mathematics activities. They mentioned that students who are mathematics persons are independent learners and contribute to the discussion. On the other hand, students who have high mathematics identity explicitly believed that they are mathematics persons because they have personal competence, interest, and confidence in doing mathematics, and that others’ such as their teachers, parents, and classmates recognized their mathematics ability, and they also perceived mathematics to be useful in life and in their college studies.

Students’ perception of how they are positioned by their teachers may result to students liking or disliking mathematics. Disliking mathematics may eventually lead them to leave mathematics, not because of the cognitive demand, but because they did not want to be positioned as the receiver, engaging in practices that left no room for their interpretation or agency (Boaler & Greeno, 2000). Furthermore, this perception of how they are being positioned by their teachers influenced problem-solving flexibility and in turn influences student mathematics identity. Problem-solving flexibility has been shown to have a strong influence on the construction of student mathematics identity. Since a substantial portion of students’ direct experience with mathematics happens within the classroom, a teacher has to provide mathematics tasks and structure teaching and learning structures that enhance the development of problem-solving flexibility for this in turn can contribute significantly to the development of students mathematics identity. Thus, it is good that teaching and learning should be aligned to this finding to help develop students problem-flexibility which is a constitutive element in the construction of student mathematics identity.

As a mediator between the relationship of student’ perception of teacher positioning and student mathematics identity implies that we should advocate for problem-solving flexibility. Problem-solving flexibility contributes to the construction of student mathematics identity and since students’ perception of how they are positioned by their teachers affects problem-solving flexibility, therefore, teaching and learning of mathematics in the classroom must be mindful of the importance of teacher positioning and therefore problem-solving focusing on flexibility so that a positive mathematics identity among students is developed.

6. Recommendations

In constantly seeking to help develop mathematics teachers might as well consider teacher positioning as one of the aspects of developing teachers becoming better teachers specifically in times when face-to-face interaction is not possible. Taking into consideration the context of every student, teacher, and family, those pathways need to address their teaching and learning needs. In helping students—in both subtle and explicit ways—as they navigate their paths, empowering students to realize their mathematics identity is as important as helping them to learn key mathematics concepts. Everyone plays a role in empowering students to see themselves as mathematics learners and develop their mathematics identity. With the varying approaches to delivering learning, educators and school leaders should also be open to modifying and framing mathematics instruction in the view of how teacher positioning should be enacted in the new normal to have a positive influence on the development of student mathematics identity Also, teacher discourse should be leaning towards flexibility, because the result implied that the way to tap mathematics identity is through enriching flexibility, which can be tapped through teacher positioning. Finally, future studies should include a comparison between students’ perception of teacher positioning in the face-to-face context and in a flexible learning context toward framing effective mathematics instruction responsive to the demands of the new normal.

Acknowledgments

The authors acknowledge the OVCRD of the University of the Philippines Diliman for the research grant and the Science Education Institute of the Department of Science and Technology for the scholarship grant.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The work was supported by the Department of Science and Technology, Republic of the Philippines University of the Philippines Diliman .

Notes on contributors

Allan M. Canonigo

Allan M. Canonigo is a Mathematics Education Specialist IV at the National Institute for Science and Mathematics Education Development at the University of the Philippines in Diliman, where he is involved in teacher training, research on teaching and learning mathematics, developing curriculum materials, writing resource books both for teachers and students and doing extension services for the university. He has been active in conducting research in mathematics education and has published book chapter articles in few of the NISMED publications and has published a research article in an international journal.