An optimal inventory policy under certainty distributed demand for cutting tools with stochastically distributed lifespan

Abstract

Traditional inventory policy was deeply investigated for various kinds of demand in different industrial sectors. More extensive explorations on inventory policy, including the combination with manufacturing process, detailed attributes of the purchased products, etc. was conducted by many researchers. During manufacturing process, lifespan of cutting tools have significant impact on both the quantity of inventory and production cost. In this paper, the impact of maximum allowable stopping time for cutting tools on production-inventory policy under general production demands was investigated. An optimal inventory policy with general demand (OIPGD) was developed with which the allowable stopping time for tools, order-up-to-level inventory, and order cycle can be optimally determined by an exhaustive searching algorithm. Examples with different distributions on tool lifespan and production demand is presented to show the implementation of the OIPGD model. The results and the sensitivity analysis about the parameters show that optimized combination of selection for tool allowable stopping time, order-up-to-level, and order cycle time can dramatically minimize the total cost of the whole inventory activity.

Keywords:

• inventory policy
• general demand
• lifespan assessment
• cutting tools

Public Interest Statement

This paper aims at putting up with an optimizing inventory policy, and its purpose is to determine the lowest inventory cost model. In this cost model, three most important parameters order-up-to-level R, the length of time between placement of replenishment orders, and maximum allowable usage time of cutting tools are taken into consideration and the cutting tools’ lifespan is stochastically distributed. Before deriving such a cost model, the authors present a lifespan analysis of cutting tools and various compound cost related to the total inventory cost and then a few examples are showed to illustrate the model. By employing this theory, enterprise can minimize their total supply chain cost and cutting tools’ usage cost.

1. Introduction

Under most conditions with inventory policy, more extensive explorations on inventory, including the combination with manufacturing process, detailed attributes of the purchased products, etc. were conducted by many researchers for a better manipulation of the supply chain system. If the tools inventory is not enough when the failure of cutting tools occurs, it will result in loss of production which will also influence the production schedule. On the other hand, if the tools inventory is too much, it will cause higher holding cost, which is also not permitted. However, some factors in manufacturing process may also be taken more into consideration, since they may have impact on inventory policy because of their influences on cutting tool lifespan. In manufacturing system, the demand of production usually follows some distributions. The tool lifespan and general distributed demand sometimes convoluted together and have concurrent impact on the total cost of the supply chain system for a company. As a result, research on the convolution problem of inventory policy for cutting tools has a great significance accordingly. The goal of this paper is to develop an optimal inventory policy with general demand (OIPGD) as the lifespan of cutting tools is random under general distributed production demand.

1.1. Procurement and inventory policy

Moritz and Roelof (2003) had analyzed the impact of this inbound flow on inventory and presented the usage of results on Markvo decision process which showed average cost optimality of an order policy. Mungan, Yu, and Sarker (2010) studied the manufacturing lot-sizing, procurement and delivery schedules for technology-connected companies with their products facing continuous price decrease problem during the life cycle. Timothy (2005) researched two types of inventory control model through the use of a simple periodic review model and also an alternative approach to sensitivity analysis of the model. Unlike traditional inventory research, Ben-Daya and Raouf (1994)and Hariga and Ben-Daya (1999))dealt lead time as a decision variable which gave a new model about inventory. Sarkar, Ghosh, and Chaudhuri (2012) and Chung and Lin (2001) had done a research about optimal inventory replenishment policy for a deteriorating item and discussed it with numerical analysis. Banerjee and Sharma considered a deterministic inventory model that incorporated price and time and conditions of the net profit function and then illustrated it with examples and sensitivity analysis. Yu, Mungan, and Sarker (2011) and Sarker, Duan, and Wu (2012) discussed a highly improved approach on consignment and inventory policy with generalized demand distributions of retailers. The above literatures have done extensive researches on procurement and inventory; however, when considering the lifespan of a product in a whole supply chain, only a few of those researches could be involved.

1.2. Inventory policy and demands

About the optimization of supply chain, various kinds of researches have been done with different aspects taken into consideration. Kamath and Pakkala (2002) proposed an optimal policy for an inventory model which allows stock disposal and shows a solution of a dynamic programming backward recursion. A commonly used inventory policy for dealing with demands with different penalty costs is the critical-level inventory policy. Hwang and Hahn (2000) investigated an optimal procurement policy for items with an inventory-level-developed demand rate and fixed lifetime based on the demand rate of a function of current inventory level, and each unit having its fixed expiry date. Toktay and Wein (2001) show a production stage that produces a single item in make-to-stock and demand for finished goods in detail, such as accurate condition in a simulation study, safety stock, stochastic correlated demand, etc. in forecasting–production–inventory systems. Zequrira, Valdes, and Berenguer (2007) study the optimal buffer inventory to satisfy the demand during the interruption period due to maintenance action considering the possibility of imperfect production and opportunities for the fabrication of the buffer inventory.

1.3. Lifespan assessment of cutting tools

From the well-known F. W. Taylor’s formula (see Shaw, 2005) V = A/T_m (where V represent the cutting speed, T is the lifespan of the cutting tools, and m means different influence of T and A in different cutting condition), is described the relationship of cutting tools’ lifespan, which is related to the cutting parameters; however, when the penalty of cutting tools’ failure is taken into consideration, the way to determine the maximum allowable lifespan will be different.

Traditional research on lifespan of cutting tools is concentrated only on the materials’ performance, while it is not enough. Axinte, Belluco, and De Chiffre (2001) proposed a method to acquire reliable measurements of tool lifespan in turning and provided a basis for the quantification of tool lifespan measurement uncertainty. Arsecularatne (2003) used Oxley’s machining theory to predict cutting forces and cutting temperature which can be used to estimate the tool lifespan under RC conditions and further predicted tool deformation by accounting for the rake face temperature. Non-linear regression analysis techniques are used by Oraby and Hayhurst (2004) to establish models for wear and tool life determination in terms of the variation of a ratio of force, rather than absolute values of force components acting at the tool tip. Serra, Ouahabi, and Rmili (2012) presented a new criterion for the detection of cutting tool end of life from cutting tool vibration, the study aiming at the development of a cutting tool wear monitoring strategy applicable to the particular issues of turning process. Li and Sarker (2013) discussed how the parameters influence the lifespan and put forward an evaluation method; however, they have not taken the inventory policy into consideration.

As discussed above, there are very fewer researches concentrated on the lifespan distribution of cutting tools in supply chain. But in fact, the lifespan has great impact on the inventory policy. At the same time, the optimal order-up-to-level can minimize the total cost of the manufacturing process and also lacks investigation. There are so many factors that have influence on cutting tools, such as the tool type, the tool size, the tool materials, the working condition and even the machining angle. The tools’ inventory has much influence on the holding cost and the penalty cost that have impact on the total cost. As a result, it is quite important to find an appropriate order-up-to-level which is determined by the lifespan of cutting tools to minimize the cost. Thus, this paper has formulated an inventory model which takes the lifespan distribution, order-up-to-level, and order cycle into consideration to make optimal decision about minimizing the total cost and give examples to show its application.

2. Model formulation

Lifespan and order-up-to-level of cutting tools have significant impacts on the minimization of inventory total cost. In this section, an attempt is made to formulate the objective function (total cost) which needs to be minimized to find the optimal lifespan, order cycle, and order-up-to-level for the manufacturing process.

2.1. Assumptions and notations

As the inventory issue of cutting tools is quite complex, in order to realize the aim of this paper, a few assumptions will be taken into consideration during the formulation of the process.

2.1.1. Assumptions

To simplify the research, the following assumptions are necessary to model in this paper:

1. In order to avoid complication, only one type of machining tool is considered for model formulation.

2. Total products for machining in a period are fixed.

3. A penalty cost will be existed when the failure of a machining tool causes potential damage of work piece.

4. Tool vendors are located nearby and result in negligible tool supplying time.

5. Tool shortage results in downtime with machine and is not back ordered.

6. The tool demand rate for production follow a general distribution, g(x).

2.1.2. Notations and definitions summary

The definitions used in this paper are list as below:

Decision variables
R	=	order-up-to-level (tools)
Tc	=	Cycle length, the length of time between placement (or receipt) of replenishment orders
Tm	=	Maximum allowable usage time of cutting tools (in time unit)

Parameters
Tu	=	Average unit processing time per product (time unit/product)
Dp	=	Demand rate of products (products/year)
T	=	Lifespan of cutting tools (in time units)
Cf	=	Fixed cost for every order ($/order)
cx	=	Unit replacement cost of a tool ($/tool)
ch	=	Unit holding cost of a tool ($/tool/year)
cp	=	Unit penalty cost of tool failure ($/tool)
Dp	=	Demand rate of product (products/year)
π	=	Unit shortage cost ($/tool)

Cost function components and intermediate variables
Co	=	Annual ordering cost
Cp	=	Expected total penalty cost
Cs	=	Expected annual total shortage cost
Ch	=	Expected annual holding cost
xd	=	Random demand of production per month
xt	=	Random demand of cutting tools depending on xd and Tm
DT	=	Demand of tools required per year
Tw	=	Total working time needed per year
TC	=	Total cost ($/year)

2.2. Expected lifespan estimation for pre-empt cutting tools

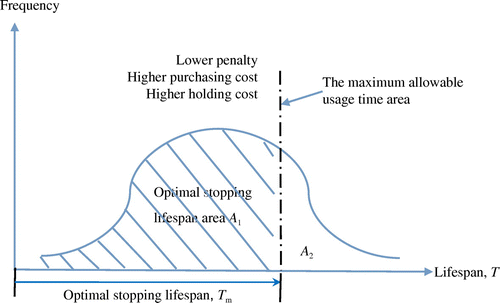
The lifespan of a machining tool, T, is discussed by Li and Sarker (2013), which follows a distribution f(T) that is mainly affected by three main parameters V (machining speed), f (cutting feed), and d (machining depth), other factors(such as cutting angle) which are insignificant for practical usage are ignored. As depicted in Figure 1, the horizontal axis T means the usage time distribution and the vertical axis means the usage frequency of the cutting tools, from Figure 1 it is obvious that most of the cutting tools’ lifespan is in the maximum allowable usage time area and only a few cutting tools failure outside the range. So the optimal lifespan of a machining tool is absolutely in that area and through discussion it can be defined as T_m. When the lifespan is shorter than T_m, it means lower penalty but more tools will be used, thus causes higher purchasing cost and higher holding cost. On the other hand, if the lifespan is longer than that, the penalty will be higher, while the purchasing and holding cost lower. Under this condition, it is important to find an optimal lifespan of cutting tools to make decisions about the inventory policy and then reach the purpose of minimizing the total cost.

Figure 1. General distribution of cutting tools’ lifespan.

If a stopping policy is implemented, the distribution, f(T) with $-\infty \le T\le \infty$ is modified to f(T) with $-\infty \le T\le T_m$. It is obvious that if the cutting tools lasted less than T_m, the order-up-to-level will increase and the order cycle will decrease. Now the key point is to find this most optimal stopping time T_m of tool lifespan which will minimize the total cost TC. So in order to make a good decision about procurement policy for the revised situation, the optimal stopping time T_m needs to be based on the expected lifespan E(T) of the revised distribution.

For the part with $T\le T_m$, marked as area A₁, as shown in Figure 1, the expected lifespan of all tools can be defined as(1) $$E{(T)}_{T\le T_m}={\int }_0^{T_m}Tf(T)dT$$(1)

For the other part marked as area A₂ in Figure 1, where T > T_m, which means the lifespan of the tools exceeds the maximum allowable usage time; thus the lifespan of all these tools is practically T_m. So, the expected lifespan for these pre-empted tools (in area A₂) is defined as(2) $$E{(T_m)}_{T\succ T_m}=T_m{\int }_{T_m}^{\infty }f(T)dT=T_m\left[1-F(T_m)\right]$$(2)

where f(T) follows the same generic distribution.

Thus, $F(T_m)=P(T\le T_m)$ is the probability of a tool failure earlier than T_m and $1-F(T_m)=P(T>T_m)$ is the probability of a tool exceeding the maximum allowable usage time T_m when the tool can be replenished before any natural failure which result in no cost to the whole system.

Since the total distribution of the tools contains two different groups, A₁ and A₂ as represented above, each group has different weight in the expected lifespan. Now the total expected lifespan of both groups can be defined as(3) $$E{(T)}_{A_1+A_2}=E{(T)}_{T\le T_m}+E{(T_m)}_{T\succ T_m}$$(3)

2.3. Demand of cutting tools with generally distributed demand of production

In practical manufacturing process, the total demand for a production within a relative long period is steady, which makes an approximately constant demand. However, the demand usually varies due to the requirements of terminal user and sometimes follows a kind of distribution.

It is assumed that the product has a demand of D_p products/year. The average unit processing time is T_u per product (time unit/product). Thus, the total manufacturing working time T_w required per year for the product can be expressed as T_w = T_u D_p time unit/year. For an expected pre-empt lifespan (in time units/tool) of a machining tool, $E{(T)}_{A_1+A_2}$, the total demand of cutting tools per year, D_T (tools/year), can be computed as(4) $$D_T=T_u{D}_p/E{(T)}_{A_1+A_2}$$(4)

where the tool lifespan T follows a generic distribution f(T).

It is assumed that the demand within an order cycle, T_c, is a continuous variable with stationary probability distribution. Units demanded out of stock are at high expense and the average shortages are not negligible relative to the on-hand inventory.

Assume that random variable x_d has a density function g(x_d) with a mean ${\mathit{\mu }}_d$ and standard deviation ${\mathit{\sigma }}_d$, and this is for the demand of production. Considering the density function g(x_d) depends on the ordering cycle T_c, and the demand of tools for the period x_d is also a function of T_m, so for the period of T_c, the expected demand of tools, x_t, can be expressed as $x_t=T_u{x}_d/E{(T)}_{A_1+A_2}$, combined with Equation 3, x_t can also be rewritten as(5) $$x_t=\frac{T_u{x}_d}{{\left.E(T)\right|}_{T=T_m}+E(T_m)}$$(5)

where T follows a generic distribution of f(T), x_d follows a distribution g(x_d).

2.4. Analysis of OIPGD model

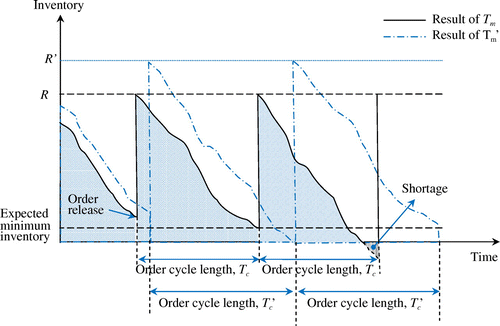
In this paper, the cost components of OIPGD consists of annual ordering cost C_o, expected total penalty cost C_p, expected annual total replacement cost C_r, expected annual total shortage cost C_s, and expected annual holding cost C_h. This section will discuss each of the components, respectively, because the selection of optimal lifespan with the allowable maximum stopping time for cutting tools incurs change of total tool requirements, D_T, and eventually has impact on the order-up-to-level quantity, R, and review interval (i.e. ordering cycle), T_c. This relation is illustrated in Figure 2.

1. Annual ordering cost, C_o

   Since the demand has a continuous density function, the inventory level will always fall from the maximum possible inventory level, R, to zero. The practical inventory will decide another order with every ordering review. As a result, there are 1/T_c orders per year and the expected annual cost of ordering, C_o, (only for purchasing) can be expressed as(6) $$C_o=C_f/T_c$$(6)

2. Expected total penalty cost, C_p

   Penalty cost depends on the allowable maximum stopping time T_m. As shown in Figure 1, the tool fails in group A₁ will result in penalty cost. For a single machining tool, the probability of fail before T_m is F(T_m), which is the cumulative probability while the tool life $T\le T_m$. The expected penalty cost can be obviously expressed as $c_{p}F(T_m)=c_p{\int }_{-\infty }^{T_m}f(T)dT$. Equation 4 gives the expected total demand of cutting tools, thus the yearly total penalty cost is(7) $$C_p=D_T{c}_{p}F(T_m)=\frac{T_u{D}_p{c}_p}{E{(T)}_{A_1+A_2}}{\int }_{-\infty }^{T_m}f(T)dT$$(7)

3. Expected annual total replacement cost, C_r

   Since a lot of cutting tools will be replaced each year and replacement takes time and effort, the replacement cost should be taken into consideration. As the lifespan of cutting tools gets longer, the replacement of cutting tools gets less. c_x is the cost of replacement per unit and Equation 4 gives the expected total demand of cutting tools, So the expected replacement cost can be easily expressed as(8) $$C_r=c_x{T}_u{D}_p/E{(T)}_{A_1+A_2}$$(8)

4. Expected annual total shortage cost, C_s

   From the distribution of production demand x_d in the ordering cycle, $x_d\sim g(x_d)$, the distribution of tools demand, x_t can be deducted as (see Appendix A)

Figure 2. Illustration of influence of stopping time T_m on review cycle T_c and order-up-to-level R.

(9) $$x_t\sim g_{x_t}(x_t)=\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)$$(9)

Obviously, x_t is a stochastic demand of cutting tools for a review period T_c, if x_t > R, a shortage of tools occurs (which is shown in Figure 2). This will result in downtime of production and consequently shortage cost. Under this circumstance, for an ordering (review) period, the expected shortage of tools, Q_s, is given by(10) $$Q_s={\int }_R^{\infty }[(x_t-R)g_{x_t}(x_t)]d{x}_t={\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t$$(10)

Thus, the expected annual total shortage cost C_s can be expressed as(11) $$C_s=\frac{\mathit{\pi }}{T_c}{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t$$(11)

1. Expected annual holding cost, C_h

With expected annual holding cost C_h, it compromises to two sub components, (1) regular expected inventory, $\overline{I}$, and (2) the non-back ordered inventory (there is no need to fill the shortage of previous review period when a shortage occurs in previous period).

Once the allowable maximum stopping time, T_m, is determined, the demand for cutting tools has a constant mean and the inventory varies on the average linearly between the minimum and maximum inventory. Here the expected minimum inventory is $R-u_t$ combined with Equation 5, that is,(12) $${\overline{I}}_{min}=R-\frac{T_u{\mathit{\mu }}_d}{E{(T)}_{A_1+A_2}}$$(12)

The expected maximum inventory, that occurs at the arrival of the replenishment, is given by $R-{\mathit{\mu }}_t+D_T{T}_c$. Combined with Equations 4 and 5, this sub component can be rewritten as(13) $${\overline{I}}_{max}=R+\frac{T_c{T}_u{D}_p-T_u{\mathit{\mu }}_d}{E{(T)}_{A_1+A_2}}$$(13)

Because the inventory varies approximately in a linear way, the average inventory for sub component $\overline{I}$ is halfway between expected maximum inventory, ${\overline{I}}_{max}$ and expected minimum inventory, ${\overline{I}}_{min}$. Thus, the average inventory for this sub component is easily computed as(14) $$\overline{I}=\frac{{\overline{I}}_{min}+{\overline{I}}_{max}}{2}=R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}$$(14)

Adding up the inventories expressed in Equations 10 and 14, the expected annual holding cost, C_h, can be expressed as(15) $$C_h=c_h\left\{R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}+{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}$$(15)

The total cost objective function $TC(T_m,T_c,R)$ consists of five components of C_o, C_p, C_r, C_s, and C_h, and is given by $TC(T_m,T_c,R)=C_o+C_p+C_s+C_h+C_r$. With Equations 6, 7, 11, and 15, the total cost objective function can be concluded as(16) $$TC(T_m,T_c,R)=\frac{\mathit{\pi }}{T_c}{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t+\frac{C_f}{T_c}+\frac{T_u{D}_p{c}_p}{E{(T)}_{A_1+A_2}}{\int }_{-\infty }^{T_m}f(T)dT+c_h\left\{R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}+{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}+c_x{T}_u{D}_p/E{(T)}_{A_1+A_2}$$(16)

By merging the similar items, function (16) can be rewritten as(17) $$TC(T_m,T_c,R)=\frac{C_f}{T_c}+\frac{T_u{D}_p{c}_p}{E{(T)}_{A_1+A_2}}{\int }_{-\infty }^{T_m}f(T)dT+c_h\left(R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}\right)+\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t+c_x{T}_u{D}_p/E{(T)}_{A_1+A_2}$$(17)

where tool life, T ~ f(T), $E{(T)}_{A_1+A_2}={\left.E(T)\right|}_{T=T_m}+E(T_m)$, ${\left.E(T)\right|}_{T=T_m}={\int }_0^{T_m}Tf(T)dT$, $E(T_m)=T_m\left[1-F(T_m)\right]$.

3. Solution methodology and computation results

Total cost objective function $TC(T_m,T_c,R)$ in Equation 17 for the replenishment policy consists of three decision variables. T_u, D_p, c_f, c_u, c_p, c_x, and c_h are the system characteristic parameters. Variables T_m (optimal stopping time of cutting tools), ordering cycle time T_c, and order-up-to-level R are required to be solved to satisfy the minimum total cost.

3.1. Exhaustive search algorithm for OIPGD model

In order to find the optimal order-up-to quantity, R, review time, T_c, and tool allowable maximum stopping time, T_m, partial derivative approach can be employed to calculate the stationary points.

With decision variable T_c, by differentiation, $\mathit{\partial }TC/\mathit{\partial }{T}_c$ = 0 leads to $\frac{c_h{T}_u{D}_p}{2E{(T)}_{A_1+A_2}}-\frac{C_f+\mathit{\pi }{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t}{T_c^2}=0$, which yields(18) $$T_c=\sqrt{\frac{2E{(T)}_{A_1+A_2}\left\{C_{+}\mathit{\pi }{\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}}{c_h{T}_u{D}_p}}$$(18)

For decision variable T_m, by differentiation, $\mathit{\partial }TC/\mathit{\partial }{T}_m$ = 0 leads to(19) $$\frac{T_u{D}_p{c}_{p}f(T_m)}{E{(T)}_{A_1+A_2}}-\frac{T_u{D}_p{c}_p[1-F(T_m)]}{{[E{(T)}_{A_1+A_2}]}^2}{\int }_{-\infty }^{T_m}f(T)dT-\frac{c_h(T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d)[1-F(T_m)]}{2{[E{(T)}_{A_1+A_2}]}^2}+\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left\{(x_t-R)\left[\left(\frac{1-F(T_m)}{T_u}\right)g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)+\left(\frac{E{(T)}_{A_1+A_2}}{T_u}\right)g^{\prime }\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\left(\frac{1-F(T_m)}{T_u}\right)x_t\right]\right\}d{x}_t-c_x{T}_u{D}_p[1-F(T_m)]/2{\left[E{(T)}_{A_1+A_2}\right]}^2=0$$(19)

which is too complicated to yield a mathematical expression for T_m. (Appendix B)

Similar to the above differential method, $\mathit{\partial }TC/\mathit{\partial }R$ = 0 leads to the following expression (see Equation C4 in Appendix C):(20) $$c_h+\left(\frac{\mathit{\pi }}{T_c}+c_h\right)\frac{E{(T)}_{A_1+A_2}}{T_u}{\int }_R^{\infty }g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)d{x}_t=0$$(20)

which is also too complex to be simplified further.

3.2. Exhaustive search algorithm method for OIPGD model

Equations 19 and 20 cannot be transformed into a simplified expression, and it is also too complicated to delaminate two of the three decision variables R, T_c, and T_m through Equations 18, 19, and 20. However, with Equation 18, by using exhaustive search method, only two dimensions R and T_m can be searched in their feasible domain, then the result of T_c computed. With R, T_m, and dependent variable T_c, a result of total cost can be computed. In this section, an exhaustive search algorithm (ESA) method is developed to find the optimal solution of R, T_c, and T_m by satisfying the minimum total cost TC.

Equation 19 is a mathematical expression of T_m. And numerical algorithms can be used to solve the value of T_m and then the variable R can be solved by Equation 20. Eventually, total cost TC can be worked out by using Equation 17. This computational algorithm is given as follows. In this algorithm, g(T_m) will be defined to indicate the left-hand side of Equation 19 in terms of T_m. If g(T_m) equals or is close to 0, the corresponding value of T_m is determined to be the optimal solution.

3.2.1. ESA method

Step 1: Initialize C_f, c_p, c_u, c_h, c_x, T_u, D_p, ${\mathrm{\Delta }}_T$ (step-size lifespan of T), ${\mathrm{\Delta }}_{T_c}$ (step-size lifespan of T_c), ${\mathrm{\Delta }}_R$ (an arbitrary value of R) and define the distribution of T, the length of time between placement T_c, and the range of R. Specify the parametric values for distribution of T and express f(T) and E(T).

Step 2: Set the starting values ${\mathrm{\Delta }}_R$, ${\mathrm{\Delta }}_T$, ${\mathrm{\Delta }}_{T_c}$, and evaluate the cost function $T{C}^{\ast }(T_c,T_m,R)\leftarrow \infty$.

Step 3: (a) Calculate cumulative distribution probability F(T),

(b) Compute expected lifespan $E{(T)}_{A_1+A_2}$ with stopping time $T_m\leftarrow T$ using Equation 3.

(c) Compute the cycle length T_c with Equations 3 and 18.

Step 4: (a) Compute $TC(T_c,T_m,R)$ using Equation 17.

(b) If $TC(T_c,T_m,R)<T{C}^{\ast }(T_c,T_m,R)\leftarrow \infty$,

 Set $T{C}^{\ast }(T_c,T_m,R)\leftarrow TC(T_c,T_m,R)$, $R^{\ast }=R$, ${T_m}^{\ast }=T_m$, set . $T_c^{\ast }=T_c+\mathrm{\Delta }{T}_c$

 If $TC(T_c,T_m,R)\leftarrow T{C}^{\ast }(T_c,T_m,R)$, go to Step 4(a)

Else set $T_m=T_m+\mathrm{\Delta }T$,

  If $TC(T_c,T_m,R)<T{C}^{\ast }(T_c,T_m,R)$, go to Step 4(a)

 Else set $R=R+\mathrm{\Delta }R$,

   If $TC(T_c,T_m,R)<T{C}^{\ast }(T_c,T_m,R)$, go to Step 4(a)

  Else set $R^{\ast }=R$, ${T_m}^{\ast }=T_m$, $T_c^{\ast }=T_c$.

Step 6: Stop and current values of $T_m^{\ast }$, $T_c^{\ast }$ and R^* are the best solution and $T{C}^{\ast }(R^{\ast },T_m^{\ast },T_c)$ is the minimum total cost.

3.3. Numerical analysis

The following example illustrates the simulation results obtained from the algorithm of ESA. In real machining process for a mechanical manufacturing enterprise, a milling cutter named as “S-NA2T030” is used to proceed with their own product. When the product is with material hardness value of HRC45~50, the lifespan of the cutter follows a normal distributed with mean ${\mathit{\mu }}_T$ = 4.5 h and standard deviation of $\mathit{\sigma }$ = 0.2 h. This company processes approximately $D_p$ = 72,800 products per year by using this tool. For every product, an average of $T_u$ = 0.1 h machining time is required. The fixed purchasing cost for each order C_f = $30.00/order, the penalty cost for each failure of the tool is c_p = $0.50/tool, the replacement cost per tool is c_x = $6.00/tool, the holding cost per tool per year is c_h = $6/tool/year, and the tool unit shortage cost $\mathit{\pi }$ = $20.00/tool. Under this situation, the objective of this practical problem is to minimize the total cost TC by determining the optimal values of order cycle T_c, optimal stopping time T_m, and order-up-to-level R.

By running the ESA program, the optimal decision variables, search result can be concluded of this vulnerable parts changing and procurement problem. The optimal decision variables, T_m = 3.70 h, an order cycle T_c = 0.12 years ≈ 44 days (about one and a half months), an order-up-to-level R = 1,020 tools, and the minimized total cost TC = $19,322.

Above is the example of when the cutting tools’ lifespan follows normal distribution and the theoretical results with the ESA method. For further discussion, two different lifespan distributions will be used here to demonstrate the generic solution methodology with the ESA method.

Assume that the lifespan of the cutting tools is uniform (a, b), the distribution of which is shown below in Table 1.

Table 1. Expected lifespan $E(T){\left.\right|}_{T=T_m}$ of tools for uniform distribution

Distribution	f(T)	F(Tm)	${\left.E(T)\right|}_{T=T_m}$
Uniform (a, b)	$\frac{1}{b-a}$	$\frac{T_m-a}{b-a}$	$\left(\frac{T_m-a}{b-a}\right)\left(\frac{T_m+a}{2}\right)$

With f(T) following the uniform distribution, from the data above, the range of the lifespan of cutting tools can be assumed as a = 4 and b = 5, by running the ESA method, the optimal result is T_m = 4.7 h, an order cycle T_c = 0.08 years ≈ 29 days (about one-and-a-half months), an order-up-to-level R = 2,000 tools, and the minimized total cost TC = $23,143.

A detailed comparison of the two distributions about the function and the result through the usage of ESA method are listed in Table 2. Using the ESA method, all the possibilities are compared and the most optimal solution is obtained which is shown below, and as the distribution changes the optimal solution will be different. In the table below, a generic solution methodology is demonstrated that can be applied accordingly for other types of demand distributions.

Table 2. Optimal solution for different distributions

Distributions	f(T) (a = 4, b = 5)	Tm (h)	Tc (years)	R (tools)	TC ($)
Uniform (a, b)	$\frac{1}{b-a}$	4.7	0.08	2,000	23, 143
Normal (μ, σ^2)	$\frac{1}{\sqrt{2\mathit{\pi }}\mathit{\sigma }}{e}^{-{\left(T-\mathit{\mu }\right)}^2/2{\mathit{\sigma }}^2}$	3.7	0.12	1,020	19, 322

4. Sensitivity analysis

In this research, the maximum allowable usage time of cutting tools T_m, the length of time between placement (or receipt) of replenishment orders T_c, and the order-up-to-level of tools R are interacted. If one of the parameters changes, the other two are influenced, and the total cost TC is absolutely changed. Since there are three variables, it is hard to clearly depict all the variables as to how they influence the object function. In order to investigate which one is the most influential, one of the variables is fixed and then analysed.

4.1. Impact analysis of T_m and T_c on TC while R is fixed

This paper has established the model of TC, therefore, when individually inspecting after T_m, T_c, R effects on the cutting tools reliability lifespan, reviewed parameter changes in a reasonable range, and the other parameters respectively take typical values.

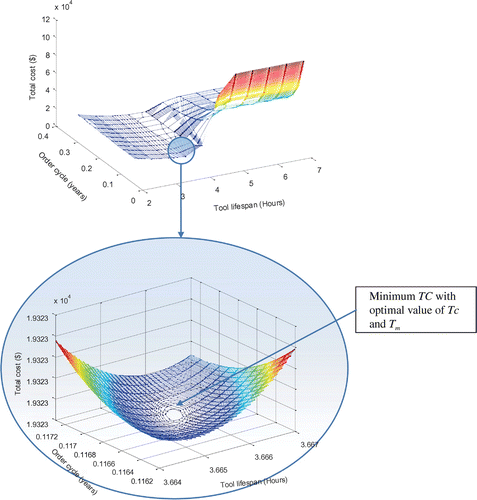
While R = 1,000, the relationship between T_m, T_c, and TC is shown in Figure 3. As the unit of time is hour, accuracy to two decimal places is sufficient, while for the unit of T_c, three decimal places is sufficient. The result is limited to the accuracy and it can be seen from figure that the total cost TC = $19,323, T_c = 0.117 years ≈ 44 days, T_m = 3.66 h.

Figure 3. Fluctuation of TC according to changing of T_m and T_c.

It is easy to see that T_m is more influential than T_c from Figure 3. When T_m and T_c are smaller than the optimal solution, the total cost changes slightly and when T_m is bigger than 3.67, it starts to change sharply.

4.2. Influence analysis of T_m and R on TC while T_c is fixed

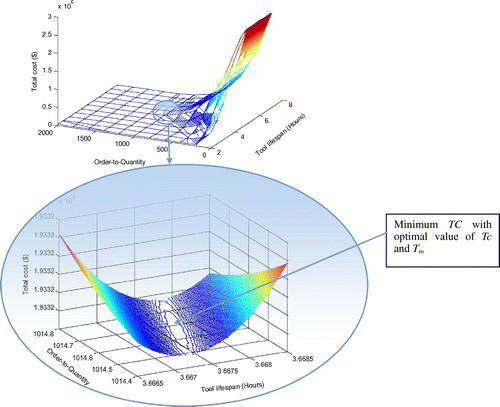
While T_c = 0.1, the relationship between T_m, R, and TC is shown in Figure 4. And with the accuracy fixed, it can be seen from Figure 4 that the total cost TC = 19,332$, R = 1,015, T_m = 3.67 h.

Figure 4. Fluctuation of TC according to changing of T_m and R.

From Figure 4, it is easy to see the optimal solution. As the total machining time T_w = T_u × D_p = 7,280, while the average lifespan is around 4.5, the cutting tools needed per year is around 1,617 products, so when the order-to-quality is bigger than that, the total cost will not change much.

In addition, through analysis of the two pictures above, it can be concluded that the lifespan of cutting tools T_m has the greatest influence on the total cost, the length of time between placement (or receipt) of replenishment orders T_c and order-up-to-level R have relatively small effects on total cost.

5. Conclusions

In this paper, the author has depicted an interactive relationship among three important factors which influence the inventory policy under certainty distribution demand for cutting tools with stochastically distributed lifespan. They are the maximum allowable usage time of cutting tools, the length of time between placement (or receipt) of replenishment orders, and order-up-to quantity. An optimal ESA method was found to solve this problem, with two commonly used lifespan distribution of cutting tools to make a comparison and come to a conclusion that the ESA method is useful for general distribution. Because with three variables, the analysis is four-dimensional and is too complicated to express, the research fixed one variable and depicted the object function with the other two variables to see the relationship and compare the different results. From the research above it is easy to find that “T_m” is the most influential factor of the total cost. But in this paper, the author only considered one kind of machining tool and ignored the compound influence of the manufacturing system. For future work, it is necessary to study different cutting tools, which follow various lifespan distribution and compound influence.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Cun Rong Li

Cun Rong Li received his PhD degree from Wuhan University of Technology (WHUT) majored in Mechanical Design & Theory. He is now an associate professor in Industrial Engineering Department in WHUT. His research interests are supply chain, enterprise information system, and manufacturing automation. He visited the Advanced Manufacturing Center, Liverpool University in 2005, Mechanical and Industrial Engineering Department, Louisiana University in 2013 as a visiting scholar. He published more than 20 research papers and engaged in more than 10 research projects from government and enterprise. He is also a reviewer of several international journals.

Appendix A.

Proof of distributed demand for tools

Demand of production in a review period x_d follows a generic distribution of g(x_d). There exists a relation expressed in Equation 5. Thus, for demand of cutting tools, let us note that x_t follows a distribution $g_{x_t}(y)$, from the definition of cumulative probability, $G_{x_t}(y)$ is given by(A1) $$G_{x_t}(y)=P(x_t\le y)$$(A1)

Combined with Equation 5, Equation A1 is given by(A2) $$G_{x_t}(y)=P\left(\frac{T_u{x}_d}{{\left.E(T)\right|}_{T=T_m}+E(T_m)}\le y\right)$$(A2)

Because $T_u{x}_d/{\left.[E(T)\right|}_{T=T_m}+E(T_m)]>0$, Equation A2 can be rewritten as(A3) $$G_{x_t}(y)=P\left(x_d\le \frac{{\left.E(T)\right|}_{T=T_m}+E(T_m)}{T_u}y\right)=G\left(\frac{{\left.E(T)\right|}_{T=T_m}+E(T_m)}{T_u}y\right)$$(A3)

A differentiation on both sides of Equation A3 yields(A4) $$g_{x_t}(y)=\frac{{\left.E(T)\right|}_{T=T_m}+E(T_m)}{T_u}f\left(\frac{{\left.E(T)\right|}_{T=T_m}+E(T_m)}{T_u}y\right)$$(A4)

Appendix B.

Differential process on $\mathit{\partial }TC/\mathit{\partial }{T}_m=0$

The total cost objective function is expressed as follows:(B1) $$TC(T_m,T_c,R)=\frac{C_f}{T_c}+\frac{T_u{D}_p{c}_p}{E{(T)}_{A_1+A_2}}{\int }_{-\infty }^{T_m}f(T)dT+c_h\left(R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}\right)+\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t$$(B1)

By differentiation on T_m, $\mathit{\partial }TC/\mathit{\partial }{T}_m$ = 0 yields(B2) $$\frac{T_u{D}_p{c}_{p}f(T_m)}{E{(T)}_{A_1+A_2}}-\frac{T_u{D}_p{c}_p[1-F(T_m)]}{{[E{(T)}_{A_1+A_2}]}^2}{\int }_{-\infty }^{T_m}f(T)dT-\frac{c_h(T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d)[1-F(T_m)]}{2{[E{(T)}_{A_1+A_2}]}^2}+\left(\frac{\mathit{\pi }}{T_c}+c_h\right)\frac{\mathit{\partial }}{\mathit{\partial }{T}_m}\left\{{\int }_R^{\infty }\left[(x_t-R)\left(\frac{E{(T)}_{A_1+A_2}}{T_u}\right)g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}=0$$(B2)

because(B3) $$\mathit{\partial }E{(T)}_{A_1+A_2}/\mathit{\partial }{T}_m=\mathit{\partial }E{(T)}_{A_1+A_2}/\mathit{\partial }{T}_m=\frac{\mathit{\partial }}{\mathit{\partial }{T}_m}\left({\int }_0^{T_m}Tf(T)dT+T_m[1-F(T_m)]\right)=1-F(T_m)$$(B3)

the differential part within Equation B2(B4) $$\frac{\mathit{\partial }}{\mathit{\partial }{T}_m}\left\{{\int }_R^{\infty }\left[(x_t-R)\left(\frac{E{(T)}_{A_1+A_2}}{T_u}\right)g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}={\int }_R^{\infty }\left\{(x_t-R)\left[\left(\frac{1-F(T_m)}{T_u}\right)g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)+\left(\frac{E{(T)}_{A_1+A_2}}{T_u}\right)g^{\prime }\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\left(\frac{1-F(T_m)}{T_u}\right)x_t\right]\right\}d{x}_t$$(B4)

Appendix C.

Differential process on $\mathit{\partial }TC/\mathit{\partial }R$ = 0

The total cost objective function is expressed as follows:(C1) $$TC(T_m,T_c,R)=\frac{C_f}{T_c}+\frac{T_u{D}_p{c}_p}{E{(T)}_{A_1+A_2}}{\int }_{-\infty }^{T_m}f(T)dT+c_h\left(R+\frac{T_c{T}_u{D}_p-2T_u{\mathit{\mu }}_d}{2E{(T)}_{A_1+A_2}}\right)+\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left[(x_t-R)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t$$(C1)

Let us differentiate on R, $\mathit{\partial }TC/\mathit{\partial }R$ = 0 yields(C2) $$\mathit{\partial }TC/\mathit{\partial }R=c_h+\mathit{\partial }\left\{\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left[x_t\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}/\mathit{\partial }R-\mathit{\partial }\left\{\left(\frac{\mathit{\pi }}{T_c}+c_h\right){\int }_R^{\infty }\left[R\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)\right]d{x}_t\right\}/\mathit{\partial }R=0$$(C2)

which leads to(C3) $$c_h-\left(\frac{\mathit{\pi }}{T_c}+c_h\right)\frac{E{(T)}_{A_1+A_2}}{T_u}g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}R\right)R+\left(\frac{\mathit{\pi }}{T_c}+c_h\right)\frac{E{(T)}_{A_1+A_2}}{T_u}\left[{\int }_R^{\infty }g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)d{x}_t+g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}R\right)R\right]=0$$(C3)

Thus,(C4) $$c_h+\left(\frac{\mathit{\pi }}{T_c}+c_h\right)\frac{E{(T)}_{A_1+A_2}}{T_u}{\int }_R^{\infty }g\left(\frac{E{(T)}_{A_1+A_2}}{T_u}{x}_t\right)d{x}_t=0$$(C4)