Designing sparse sensing matrix for compressive sensing to reconstruct high resolution medical images

Abstract

Compressive sensing theory enables faithful reconstruction of signals, sparse in domain $\mathrm{\Psi }$, at sampling rate lesser than Nyquist criterion, while using sampling or sensing matrix $\mathrm{\Phi }$ which satisfies restricted isometric property. The role played by sensing matrix $\mathrm{\Phi }$ and sparsity matrix $\mathrm{\Psi }$ is vital in faithful reconstruction. If the sensing matrix is dense then it takes large storage space and leads to high computational cost. In this paper, effort is made to design sparse sensing matrix with least incurred computational cost while maintaining quality of reconstructed image. The design approach followed is based on sparse block circulant matrix (SBCM) with few modifications. The other used sparse sensing matrix consists of 15 ones in each column. The medical images used are acquired from US, MRI and CT modalities. The image quality measurement parameters are used to compare the performance of reconstructed medical images using various sensing matrices. It is observed that, since Gram matrix of dictionary matrix ($\mathrm{\Phi }\mathrm{\Psi })$ is closed to identity matrix in case of proposed modified SBCM, therefore, it helps to reconstruct the medical images of very good quality.

Keywords:

• compressive sensing
• telemedicine
• sensing matrix design
• medical image reconstruction

Public Interest Statement

The article titled ‘DESIGNING SPARSE SENSING MATRIX FOR COMPRESSIVE SENSING TO RECONSTRUCT HIGH RESOLUTION MEDICAL IMAGES’. This article aims to give contribution to global Health Care system.

In case of intricate disease, patient located at another place from where his ultrasound, computed tomography or any other related modality images may be taken and transmitted remotely where more specialized doctors are located for better consultation at affordable cost.

Generally, medical images are of huge size, occupies huge space and bandwidth to transmit remotely. So, if low resolution images are captured then radiation dosage given to patient will reduce and it will take lesser bandwidth for transmission. This low resolution image is then used to reconstruct high resolution image using sparse recovery algorithms in which sensing matrix design plays a vital role. The sensing matrix is designed in this paper for reconstructing high resolution images.

1. Introduction

Technological growth has reduced the gap between domestic and global Health Care system. Telemedicine is one such field which promises to provide affordable and quality health care facilities to people at large. The successful deployment of Telemedicine depends heavily on storage and transfer of huge size clinical image/video. Various compression techniques have been developed which transforms the signal in some suitable domain and then achieve compression by discarding less significant coefficients. For reconstruction, signal must be sampled at the Nyquist rate. However, compressive sensing (CS) technique can recover signals from lesser number of samples or measurements of sparse signal (Donoho, 2006). Generally, real time signals are sparse in transform domain $\mathrm{\Psi }$such as wavelet or discrete cosine transform. Work done by Candes, Tao and Romberg (2006) proves that if the sparse sensing matrix $\mathrm{\Phi }$ consists of small number ($k$) of non-zero elements drawn from iid Gaussian or Bernoulli random variables then it is possible to recover the k-sparse signal of length $N$, from lesser number of $M$ measurements, using linear program, on condition that $k\lesssim \frac{M}{\log (\frac{N}{M})}$ (Candes & Romberg, 2007; Candes, Romberg, & Tao, 2006a). However, computational cost and storage space of using such dense sensing matrix is very high. Therefore, lot of work is going on to design efficient sensing matrix.

Toeplitz and circulant structure sensing matrix was used in Xu, Yin, and Osher (2014), Rauhut (2009), Haupt, Waheed, Bajwa, Raz, and Nowak (2010), Sebert, Yi, and Leslie (2008), Yin, Morgan, Yang, and Zhang (2010), to sucessfully recover original signal and at the same time it reduces the storage space and computational time. Various authors have proposed to use deterministic instead of random sensing matrix, consisting of elements based on binary (0, 1), bipolar$(\pm 1)$, ternary (0, 1, -1) values (Arash & Farokh, 2011) and codes such as Walsh Hadamard, Low Density Parity Check (LDPC) codes, BCH and Reed Solomon (Calderbank, Howard, & Jafarpour, 2010; Gan, Do, & Tran, 2008; Lu, Kpalma, & Ronsin, 2012). It has been proved that if matrices satisfy restricted isometry property (RIP) then signal of good quality may be reconstructed (Baraniuk, Davenport, DeVore, & Wakin, 2008). A sensing matrix which satisfies RIP has minimum mutual coherence between sensing $\mathrm{\Phi }$ and sparsity $\mathrm{\Psi }$ matrix. Considering equivalent dictionary matrix $A=\mathrm{\Phi }\mathrm{\Psi }$, then the coherence between the columns of dictionary matrix must be small (Duarte, Davenport, Wakin, & Baraniuk, 2006). Elad proposes to minimize mutual coherence of equivalent dictionary matrix by minimizing average of off-diagonal elements of the Gram matrix (Elad, 2007). Duarte-Carvajalino and Sapiro (2006) have simultaneously optimized sensing matrix and dictionary matrix for specific set of signals using algorithm based on K-SVD approach.

In Zelnik-Manor and Eldar (2011), sensing matrix is optimized by minimizing a weighted sum of the interblock coherence and subblock coherence of the equivalent dictionary. The nearly orthonormal blocks of equivalent dictionary is obtained by minimizing mostly the subblock coherence resulting in slight increase in total interblock coherence. Equiangular tight frame (ETF) approach to Gram matrix of equivalent dictionary matrix is used in Shuang, Zhihui, Li, Chang, and Li (2013) to minimize weighted sum of both interblock and subblock coherence. In Shuang et al. (2013), best recovery results were obtained when total subblock coherence is minimized in contrast to Zelnik-Manor and Eldar (2011).

Statistical restricted isometry property (STRIP) is used in Gan, Cong, Thong, and Trac (2009) to prove that deterministic matrices reconstructs signal better comparative to random matrices. The deterministic sensing matrices used were partial FFT matrix, partial Walsh-Hadamard matrix and matrix constructed from kasami code. Deterministic sensing matrix was also used in Lorne, Stephen, Stephen, and Calderbank (2009), which was based on chirp signal. The validity of sensing matrix was proved empirically and by bounding the eigenvalues of submatrices. In Iwen (2014), compressed sensing and recovery algorithm were proposed which performs recovery in O((k log k) logN)-time and provides error bounds as well. The sensing matrix is constructed by randomly subsampling rows from incoherent matrix.

The goal of this paper is to design sensing matrix which will help in reconstructing the image faithfully based on SBCM (Sun, Shu, & Dong, 2013). In this paper, low resolution medical images: Ultrasound (US), Computed Tomography (CT) and Magnetic Resonance Imaging (MRI) of size $128\times 256$ have been considered for simulation and analysis. Block Sparse Bayesian Learning Bounded Optimization (BSBL_BO) (Zhang & Rao, 2013) and Smooth approximation to $L_0$ norm (SL0) (Mohimani, Babaie-Zadeh, & Jutten, 2007) CS algorithms are used for high resolution image reconstruction.

The rest of the paper is organized as follows. In Section 2, design of sparse sensing matrix is discussed. Simulation and results are discussed in Section 3.

2. Sparse sensing matrix for CS

Real time signals/images are sparse in transform domain. Considering k-sparse signal s $\in R^N$ sparse in $\mathrm{\Psi }$ basis matrix, then a sensing matrix $\mathrm{\Phi }\in R^{M\times N}$ can recover the signal with high probability if it satisfies restricted isometric property (RIP) given as Xu and Xu (2013),(1) $$\begin{array}{c}\hfill \left(1-{\mathit{\delta }}_k\right){∥s∥}_2\le {∥\mathrm{\Phi }\mathrm{\Psi }s∥}_2\le \left(1+{\mathit{\delta }}_k\right){∥s∥}_2\end{array}$$(1)

where ${\mathit{\delta }}_k$is restricted isometric constant (RIC) which should be very much smaller than 1.

Defining,(2) $$\begin{array}{c}\hfill A=\mathrm{\Phi }\mathrm{\Psi }\end{array}$$(2)

Equivalently (1) can be stated as Candes, Romberg, and Tao (2006b),(3) $$\begin{array}{c}\hfill \left(1-{\mathit{\delta }}_k\right){∥s∥}_2\le {∥{\mathrm{A}}_{\mathrm{T}}s∥}_2\le \left(1+{\mathit{\delta }}_k\right){∥s∥}_2\end{array}$$(3)

for every subset $T\subset \left\{1,\dots ,p\right\}$, having no more than $k$ indices, ${\mathrm{A}}_{\mathrm{T}}$ a submatrix of size $M\times \left|T\right|$obtained from matrix $A$ by considering number of columns corresponding to indices in $T$. However, evaluating RIP is impractical. The alternative way to find sensing matrix which satisfy RIP and hence guarantee to reconstruct signal is to obtain coherence value between sensing and sparsifying matrix. The two matrices should be incoherent for perfect reconstruction, so the value of coherence should be very small (Ben-Haim, Eldar, & Elad, 2010). The coherence can be obtained by taking inner product between two distinct normalized columns of matrix $A$ as Duarte et al. (2006),(4) $$\begin{array}{c}\hfill \mathit{\mu }\left(A\right)=\underset{i\ne j}{max}\frac{〈A_i,A_j〉}{∥A_i∥∥A_j∥}\end{array}$$(4)

Figure 1. Flowchart of proposed method to generate sensing matrix.

Since $A$ is obtained after normalizing columns, so its Gram matrix, given as $G=A^{T}A$ , should have diagonal elements close to one. Further analysis of sensing matrix can be done by obtaining average value of the off-diagonal element of $G$, which is given as Abolghasemi, Ferdowsi, Makkiabadi, and Sanei (2010),(5) $$\begin{array}{c}\hfill {\mathit{\mu }}_{av}\left(A\right)=\frac{{\sum }_{i\ne j}|G_{ij}|}{N(N-1)}\end{array}$$(5)

Ideally, $G$ should be close to identity matrix of size $N\times N$ and coherence and average absolute off-diagonal value must be zero (Abolghasemi et al., 2010). According to Gershgorin’s disc theorem, Gram matrix of sub-matrix ${\mathrm{A}}_{\mathrm{T}}$ given as, $G={A_T}^T{A}_T$, should have eigenvalues bounded in magnitude $\left(1-{\mathit{\delta }}_k,1+{\mathit{\delta }}_k\right)$ for A to satisfy RIP${(k,\mathit{\delta }}_k).$ However, RIP is a satisfactory condition but not necessary condition for perfect reconstruction.

Mamaghanian, Khaled, Atienza, and Vandergheynst (2011) proposed three alternatives to design $k-$sparse sensing matrix satisfying RIP1 property. The non-zero elements consisted of entries equal to $\pm \sqrt{k}$ , $\sqrt{k}$ or k number of ones in each row. The location of non-zero entries was randomly chosen. Sensing matrix having k number of ones had lower coherence value with Daubechies db10 wavelet sparsity matrix; therefore, it is used in this paper.

In order to achieve lower computational cost, SBCM for CS, was proposed by Sun et al. (2013). The sensing matrix $\mathrm{\Phi }\in R^{M\times N}$ considered was a sparse block circulant matrix. The matrix $\mathrm{\Phi }$, was divided into sub-matrices. There were $L$ number of columns ($L=N/d)$ and $D$ number of rows $(D=L\times \frac{M}{N})$ where $NmodL=0$. The sensing matrix $\mathrm{\Phi }$ was divided into number of blocks ${\mathrm{\Phi }}_{\mathrm{ij}}$, given as,$$\mathrm{\Phi }=\left[\begin{array}{ccc}{\mathrm{\Phi }}_{11}& \cdots & {\mathrm{\Phi }}_{1\mathrm{L}}\\ ⋮& \ddots & ⋮\\ {\mathrm{\Phi }}_{\mathrm{D}1}& \cdots & {\mathrm{\Phi }}_{\mathrm{DL}}\end{array}\right]$$

where ${\mathrm{\Phi }}_{\mathrm{ij}}$ is inherently circulant sub-matrix $(i=1,\dots ,D;j=1,\dots ,L)$. The circulant nature of matrix is given as,$${\mathrm{\Phi }}_{\mathrm{ij}}=\left[\begin{array}{ccc}{b}_0& b_1& \cdots b_d\\ b_{\begin{array}{c}d\\ ⋮\end{array}}& b_{\begin{array}{c}0\\ ⋮\end{array}}& {\cdots b}_{\begin{array}{c}d-1\\ ⋮\end{array}}\\ b_1& b_2& \cdots b_0\end{array}\right]$$${\mathrm{\Phi }}_{\mathrm{ij}}$ is a sparse matrix having elements denoted by $b_q(q=1,\dots ,d$). Each row and column of ${\mathrm{\Phi }}_{\mathrm{ij}}$ had one non-zero element which belong to $L$ set of iid Gaussian random variables. Each row and column of $\mathrm{\Phi }$ had different non-zero elements. Thus in a row there were $L$ number of coefficients and in a column $D$ number of coefficients. It had been proved that the diagonal elements of Gram matrix of $\mathrm{\Phi }(\mathrm{G}=\mathrm{\Phi }{}^{\prime }\mathrm{\Phi })$ is close to 1 and off-diagonal elements are bounded in magnitude with high probability and hence satisfies RIP.

Table 1. Analysis of $\mathrm{\Phi }$.

Type of $\mathrm{\Phi }$	Mutual coherence	${\mathit{\mu }}_{av}$	Max eigenvalue
Bin_Phi	0.5610	0.0989	26.33
SBCM	0.4889	0.0588	4.45
SBCM_Mod (8)	0.7561	0.0932	20.08
SBCM_Mod (16)	0.7385	0.0756	10.49
SBCM_Mod (32)	0.7024	0.0638	5.50
SBCM_Mod (64)	0.6820	0.0470	3.56
SBCM_Mod (128)	0.7246	0.0105	2.08

Figure 2. Distribution of elements in Gram matrix G for various sensing matrix.

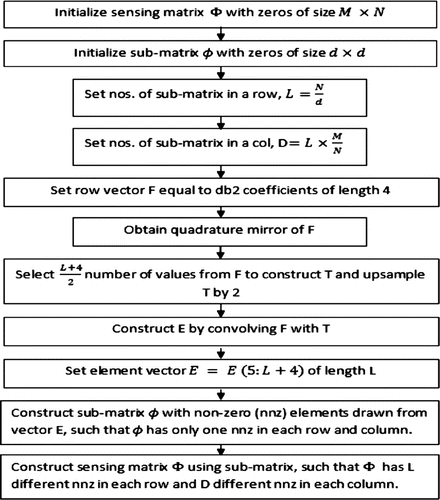
The SBCM approach for designing sensing matrix is further modified in the paper to reduce computational load without degrading reconstructed image quality. Instead of using iid Gaussian random variables, non-zero elements are generated by using inverse Daubechies db2 wavelet coefficients. Since random matrices are completely unstructured, so they increase computation complexity as well as memory requirement for storage, hence costly to implement in practical applications (Do, Gan, & Tran, 2012). Therefore, deterministic approach is followed in choosing the elements of sensing matrix, using this approach further reduces the off-diagonal elements of matrix $G$. The structure of sensing matrix is maintained as earlier and the location of non-zero elements in sensing matrix is kept random. The flowchart of proposed design of sensing matrix is shown in Figure 1. Image matrix of size $N\times N$ is transformed using Daubechies db10 wavelet basis matrix, from which the sparse column vector $s\in {\mathrm{R}}^{\mathrm{N}}$ is extracted. The measurement vector $y\in R^M$ is obtained by multiplying $\mathrm{\Phi }$ with sparse vector $s$ as,(6) $$\begin{array}{c}\hfill y=\mathrm{\Phi }s\end{array}$$(6)

The reduced $M$ number of samples of $s$ are scaled, to bound the magnitude, before giving it as an input to the CS algorithm for reconstruction. The CS algorithm used is SL0. Here, N is set to 256 and M to 128. The sensing matrix $\mathrm{\Phi }$ of size $128\times 256$, is divided into sub-matrices each of size $d\times d$, where $d$ is varied from $8,16,32,64$ and $128$. The mutual coherence value obtained for different sub-matrix size is tabulated in Table 1. As evident from table the coherence value is lowest for sub-matrix size $128\times 128$, therefore this is used as a sensing matrix for modified SBCM case.

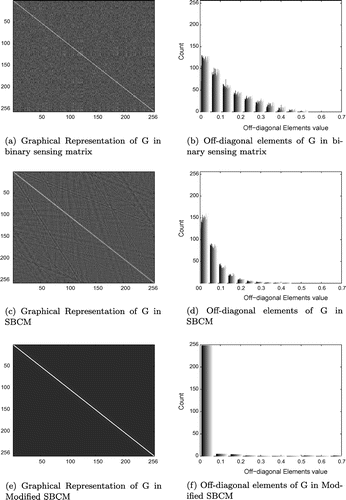
To analyse the sensing matrix further, Gram matrix G is obtained for three different sensing matrix containing non-zero elements as: (i) fifteen ones in each column present at random locations; (ii) sparse block circulant matrix with iid Gaussian random values, with block-size $32\times 32$; and (iii) modified sparse block circulant matrix with sub-matrix size of $128\times 128$. The three cases selected are the ones which gave the best results in the respective sensing matrix design method discussed above.

Gram matrix G, of size $256\times 256$, is given as, $G={\widehat{A}}^T\widehat{A}$, where $\widehat{A}$ is a normalized column version of matrix A and ${\widehat{A}}^T$ is the transpose. The mutual coherence, average value of absolute off-diagonal elements (${\mathit{\mu }}_{av}$) and maximum eigenvalue of G for different sensing matrix is tabulated in Table 1. The sensing matrix with 15 ones is denoted by Bin_Phi, SBCM and modified SBCM by SBCM and SBCM_Mod respectively in the table.

Table 2. Recovered US image quality parameters for different sensing matrix $\mathrm{\Phi }$.

Type of $\mathrm{\Phi }$	Time	MSE	SSIM	PSNR	NAE	NKR
SBCM_Mod	1.21	0.0206	0.913	32.86	0.13	0.9737
SBCM	1.44	0.5953	0.663	23.46	0.58	0.5158
Bin_Phi(BSBL_BO)	26.73	0.0481	0.703	35.57	0.24	0.9448
Bin_Phi(SL0)	7.97	0.0687	0.685	35.17	0.26	0.9176

Binary sensing matrix has least coherence value and modified SBCM with $128\times 128$ block size has least ${\mathit{\mu }}_{av}$ and its eigenvalue is bounded to 2.08. The histogram of off-diagonal elements of G is shown in Figure 2(b), (d) and (f). It shows that in case of (a) sensing matrix having 15 ones, 60% of elements are below 0.1, (b) SBCM matrix has 83% elements below 0.1 and (c) modified SBCM has 97% of elements lying below 0.1. The distribution of matrix G of size $256\times 256$, is shown in Figure 2(a), (c) and (e) which indicates that for modified SBCM, G has non-zero elements close to unity present in diagonal and just off-diagonal position and the rest elements are close to zero. So G, in case of modified SBCM, closely resembles identity matrix and this feature is useful for faithful reconstruction of images.

3. Simulation and results

Medical images of US, MRI and CT available online in DICOM format are used for simulation (Barre, 2014; DICOM, 2014; DICOM Test Images, 2014; Sample DataSet, 2014). Sparsifying matrix is generated from Daubechies db10 wavelet coefficients. Simulation is performed on 50 different images acquired from each type of modality using three different sensing matrices as defined in Section 2. SL0 and BSBL_BO CS algorithms are used for reconstruction of medical images. In BSBL_BO, input parameters are set to the default values as threshold set for pruning $\mathit{\gamma }$ is 1e-4, noise variance $\mathit{\lambda }$ is given by $std{(y)}^2/1e2$, block size is set to 16 and stopping criterion $\mathit{\delta }$ is set to 1e-8. The input parameter of SL0 algorithm is set to default values as ${\mathit{\sigma }}_{min}=0.001$ and ${\mathit{\sigma }}_{decrease\_factor}=0.5$.

The quality of reconstructed images is evaluated using parameters like Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR), Structural Similarity Index (SSIM), Normalized Cross-Correlation (NKR) and Normalized Absolute Error (NAE). The formula used to calculate performance metrices are as given below (Grgic, Grgic, & Mrak, 2004).

MSE is obtained by using relation,(7) $$\begin{array}{c}\hfill MSE=\frac{1}{N^2}\sum _{i,j=0}^{N-1}{||x\left(i,j\right)-y(i,j)||}^2\end{array}$$(7)

where $x\left(i,j\right)$ and $y(i,j)$ are original and reconstructed images, respectively, of size $N\times N$ and $i$ and $j$ are the pixel indices. PSNR is obtained as,(8) $$\begin{array}{c}\hfill PSNR=10log\frac{{(2^n-1)}^2}{MSE}\end{array}$$(8)

where $n$ is the number of bits used to represent a pixel. SSIM can be given as,(9) $$\begin{array}{c}\hfill SSIM\left(x,y\right)=\frac{\left(2{\mathit{\mu }}_x{\mathit{\mu }}_y+C_1\right)\left(2{\mathit{\sigma }}_{xy}+C_2\right)}{\left({\mathit{\mu }}_x^2+{\mathit{\mu }}_y^2+C_1\right)\left({\mathit{\sigma }}_x^2+{\mathit{\sigma }}_y^2+C_2\right)}\end{array}$$(9)

where mean values of the two images are represented by ${\mathit{\mu }}_x$, ${\mathit{\mu }}_y$, standard deviation as ${\mathit{\sigma }}_x$, ${\mathit{\sigma }}_y$ respectively, $C_1$ and $C_2$ are the two constants used to avoid instability. NKR is obtained as,(10) $$\begin{array}{c}\hfill NKR=\frac{{\sum }_{i,j=0}^{N-1}x(i,j)y(i,j)}{{\sum }_{i,j=0}^{N-1}x{(i,j)}^2}\end{array}$$(10)

and NAE is obtained by using formula,(11) $$\begin{array}{c}\hfill NAE=\frac{{\sum }_{i,j=0}^{N-1}|x(i,j)-y(i,j)|}{{\sum }_{i,j=0}^{N-1}|x(i,j)|}\end{array}$$(11)

The vital parameters amongst these are PSNR, MSE and SSIM. PSNR gives the ratio between maximum possible power of original image to the power of error introduced while reconstruction. MSE measures pixel wise distortion and SSIM is used to compute similarity between the original and reconstructed images based on luminance, contrast and structure. Since in medical images, structure of images should not be distorted, therefore SSIM plays a very important role in deciding the quality of reconstructed images. Computational load is calculated based upon CPU processing time. The simulation tool used is Matlab running on a PC with Intel core i3 processor and 4 GB RAM.

Column vectors of sparse medical image in wavelet domain are multiplied by sensing matrix of size $128\times 256$. Thus, lesser number of measurements of image of size $128\times 256$ are obtained. This low resolution image is given as input to CS algorithm for reconstruction of $256\times 256$ size image. The mean values of different quality indicator parameters are obtained after running simulation over 50 images of each modality. The values obtained for SBCM sensing matrix is obtained over 50 trials. The sensing matrix with 15 ones is denoted by Bin_Phi and the CS algorithm used is mentioned within the brackets in the table. In case of SBCM and modified SBCM sensing matrix SL0 CS algorithm is used.

Figure 3. US original and recovered images.

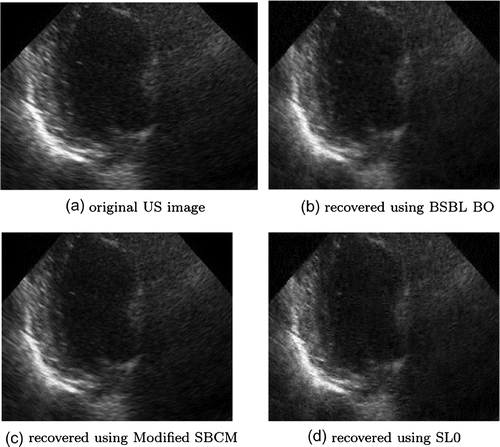
US images of resolution $128\times 256$ are given as input to CS algorithms SL0 and BSBL_BO which reconstructs $256\times 256$ size images. The mean values of quality indicator parameters for US image are given in Table 2. PSNR values indicate that the sensing matrix consisting of 15 ones with BSBL_BO CS algorithm performs better. However, mean values of other parameters like SSIM, MSE and NKR values are far better in case of modified SBCM. Lower value of MSE and NAE with very good SSIM value of about 0.913 and NKR of about 0.9737 indicates that good quality US images are reconstructed using modified SBCM, as also evident from Figure 3.

CPU processing time with SL0 algorithm is least as compared to BSBL_BO. Total number of non-zero elements in modified SBCM is 128, in SBCM 1024 and 3840 elements in binary sparse sensing matrix, therefore, this is one of the cause of increased CPU processing time in case of binary sparse sensing matrix and reduced timing in modified SBCM, as also shown in Figure 6(a). In typically 1.21 s US image is reconstructed using modified SBCM sensing matrix.

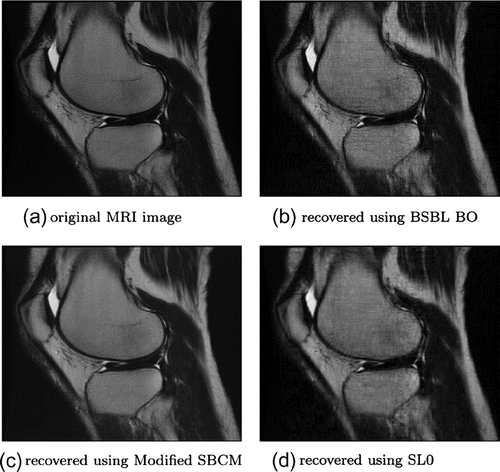
MRI images of low resolution $128\times 256$ are reconstructed very well using modified SBCM as indicated by mean values of quality indicator parameters tabulated in Table 3. Good quality MRI images are reconstructed as shown in Figure 4, with highest PSNR of about 37.44 , 0.9948 NKR, very good SSIM value of about 0.8447 and lowest MSE and NAE values in typically 1.23 s.

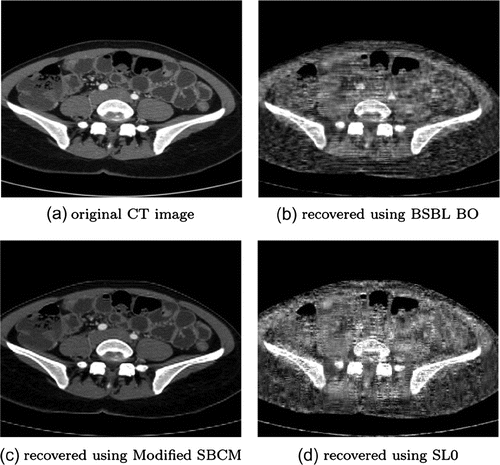
CT images of resolution $128\times 256$ are very difficult to reconstruct. As shown in Figure 5, both BSBL_BO and SL0 with sparse binary sensing matrix are unable to reconstruct the low resolution images. The quality indicator parameter values are shown in Table 4. The reconstruction done using SBCM sensing matrix generates poorer results as evident from the table. Modified SBCM out performs in this case also, reconstructing CT images of good quality having PSNR of about 32.93 dB, 0.9921 NKR, lowest MSE and NAE values and comparatively good SSIM value of about 0.7556. The CPU processing time taken is typically about 1.25 s.

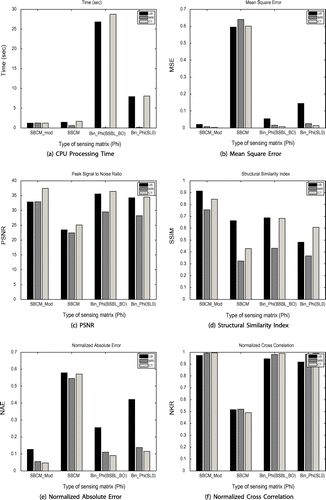
Overall performance of sensing matrices can be evaluated from graphs of Figure 6. CPU processing time taken is highest for binary sparse sensing matrix and least for modified SBCM as shown in Figure 6(a). MSE and NAE values are high (Figure 6(b) and (e)), PSNR (Figure 6(c)), SSIM (Figure 6(d)) and NKR (Figure 6(f)) values are comparatively lower for SBCM sensing matrix for all type of images. Modified SBCM sensing matrix allows reconstruction of images having lowest MSE and NAE values with comparatively highest PSNR, SSIM and NKR values.

Sampling images in appropriate manner is essential for faithful reconstruction of images. Thus, sampling or sensing matrix plays a significant role in CS. Since Gram matrix G of modified SBCM is closest to identity matrix and then is the G of sparse binary sensing matrix and last is G of SBCM so accordingly sensing matrices reconstructs images having quality in similar order.

Table 3. Recovered MRI image quality parameters for different sensing matrix $\mathrm{\Phi }$.

Type of $\mathrm{\Phi }$	Time	MSE	SSIM	PSNR	NAE	NKR
SBCM_Mod	1.23	0.0035	0.8447	37.44	0.05	0.9948
SBCM	1.67	0.6006	0.4282	25.10	0.57	0.4910
Bin_Phi(BSBL_BO)	28.75	0.0077	0.6830	36.43	0.09	0.9901
Bin_Phi(SL0)	8.07	0.0138	0.6079	34.47	0.11	0.9905

Table 4. Recovered CT image quality parameters for different sensing matrix $\mathrm{\Phi }$.

Type of $\mathrm{\Phi }$	Time	MSE	SSIM	PSNR	NAE	NKR
SBCM_Mod	1.25	0.0079	0.7556	32.93	0.05	0.9921
SBCM	1.66	0.6399	0.3241	22.45	0.55	0.5199
Bin_Phi(BSBL_BO)	19.25	0.0157	0.4314	29.52	0.11	0.9814
Bin_Phi(SL0)	7.60	0.0252	0.3670	28.21	0.13	0.9828

Figure 4. MRI-ankle original and recovered images of size $256\times 256$.

Figure 5. CT-abdomen original and recovered images of size $256\times 256$.

Figure 6. US, CT, MRI image quality measure for various sensing matrix.

Further quality of reconstructed images can be enhanced by using image denoising filters or by developing algorithms based on optimization techniques such as particle swarm optimization method or fuzzy logic method (Shibin, Qingsong, & Yaoqin, 2013). Speckle noise prominent in US images can be removed by performing adaptive homomorphic or non-homomorphic wavelet filtering (Rizi, Ahmadi, & Setarehdan, 2011), Yuvarani and Kumarasamy (2012). MRI images are affected by noise having RICIAN distribution which is difficult to remove, since it is dependent on signal. Adaptive wavelet domain filter may be used for CT and MRI image denoising.

The proposed method can be applied to colour images as well. The luminance (Y) and chrominance (${\mathrm{C}}_b$ and ${\mathrm{C}}_r$) parts of image may be extracted and then the method may be adopted on the Y, ${\mathrm{C}}_b$ and ${\mathrm{C}}_b$ - ${\mathrm{C}}_r$ transformed parts. The designed sensing matrix may be used to reduce the luminance and chrominance information. At receiver, ${\mathrm{YC}}_b{\mathrm{C}}_r$ components can be recovered back by applying CS algorithm and then performing inverse transformation. ${\mathrm{C}}_r$ part can be obtained by adding the recovered chrominance information. The ${\mathrm{YC}}_b{\mathrm{C}}_r$ components are then converted back to RGB domain to recover transmitted colour image. In future, the applicability of this technique may be tested on colour images by evaluating reconstructed image quality measurement parameters.

4. Conclusion

Sparse block circulant matrix of size $128\times 256$ is constructed with an aim to reduce mutual coherence between sensing and sparsity matrix. After doing modifications in SBCM matrix, the number of non-zero elements in matrix is only 128 so it takes lesser storage space and reduces computational time. Since the Gram matrix $G$ of dictionary matrix closely resembles with the identity matrix so it is guaranteed that the images are reconstructed with more accuracy. The low resolution medical images of size $128\times 256$ acquired from US, MRI and CT modalities are reconstructed using SL0 algorithm to generate good quality $256\times 256$ size images. The quality indicator parameters used are PSNR, MSE, SSIM, NAE and NKR. With modified SBCM sensing matrix very good results are obtained which are as follows. US images are reconstructed with mean value of PSNR of about 32.86 dB, MSE around 0.0206, very good SSIM value of about 0.913 and 0.9737 NKR. US image is reconstructed in typically 1.21 s. In case of MRI images, mean value of PSNR is about 37.44 dB. NKR is 0.9948, very good SSIM value of about 0.8447 and lowest MSE and NAE values are obtained. MRI image is reconstructed typically in 1.28 s. CT images of size $128\times 256$ could not be recovered using other sensing matrices. Using modified SBCM, CT images are very well reconstructed with PSNR of about 32.93 dB, 0.9921 NKR, lowest MSE and NAE values and comparatively good SSIM value of about 0.7556. CT image is reconstructed in typically 1.25 s.

Thus, low resolution images can be obtained in clinical settings with lesser storage and in lesser time. This enables the medical image/signals to be sent to distant diagnostic centre over low data rate transmission channels. At remote end, high resolution image/signals can be recovered for better clinical assessment by specialized doctors. The proposed method is applied on grey images; the method may be tested with colour images.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Vibha Tiwari

Vibha Tiwari received BE and ME degree in 1999 and 2002, respectively. She is currently pursuing PhD. Her current research interests include medical image compression, super-resolution image processing, colourization, image restoration and enhancement. The work presented in the paper aims to design sensing matrix so as to transfer low size medical image requiring less storage space and low transmission bandwidth and at remote end reconstruct high fidelity image