Stabilization of nonlinear inverted pendulum system using MOGA and APSO tuned nonlinear PID controller

Abstract

An inverted pendulum system (IPS) is a highly nonlinear dynamical open loop unstable system, typically used as a benchmark to verify the performance of controllers. The IPS emulates the behaviour of an altitude control of a space booster or rocket on take-off. The problem is to develop suitable controllers to maintain the stabilization and swing up of an inverted pendulum on a cart. This paper presents the evolutionary tuning methods of nonlinear PID (NL-PID) controller for IPS with the multi-objective genetic algorithm (MOGA) and adaptive particle swarm optimization (APSO) algorithm. The function of NL-PID controllers is to keep the pendulum in an upright position by maintaining the pendulum at same state and angle at zero degrees. The comparison of responses and performance of MOGA tuned NL-PID and APSO tuned NL-PID controllers for an IPS are described. The mathematical modeling and simulation analysis of the IPS is presented in detail to test the effectiveness of controller tuning algorithm. The APSO based tuning of the NL-PID controller has lesser chattering, noise and fast settling time than MOGA based tuning of the controller.

Keywords:

• inverted pendulum system
• NL-PID controller
• tuning
• multi-objective genetic algorithm
• adaptive particle swarm optimization algorithm

Public Interest Statement

It is interesting to watch the rocket launching at the space center, many of us watching on television the launching process of the rocket/satellites and their establishment in the orbit of the earth. Sometimes our mind stuck on certain aspects while watching the scenario of rocket flight. The aspects include what force is controlling the launching rocket which is carrying the satellite, how the rocket of such huge weight is projected upright, how the satellite is placed into the space orbit. All these aspects for a budding control engineer are hard to understand initially, but once we start embracing the results obtained from control engineering, to learn and design dynamic controllers are becoming inevitable nowadays. The nonlinear inverted pendulum system(IPS) is a challenging benchmark control problem to design and test such new dynamic controllers. It resembles the many real-world dynamical systems, such as self-erecting rocket, missile launchers, Segway robotic platforms.

1. Introduction

Most of the physical systems are nonlinear dynamic systems which exhibit multiple equilibrium points. The stability analysis of the nonlinear system in the presence of unknown disturbances, uncertainties in system model and system parameter variations are more complex when compared to the linear systems (Sastry, 1999; Vidyasagar, 1993). The inverted pendulum system (IPS) is one of the established benchmark problems in control literature as well as one of the most complicated dynamical systems according to report of the International Federation of Automatic Control (IFAC) theory committee. It is a standard benchmark problem (Davison, 1990; How, 2015) to test controllers and their tuning algorithms due to the presence of higher order nonlinearities and instability problem (Aracil & Gordillo, 2004; Geva & Sitte, 1993). It has a resemblance to many complex practical engineering systems such as helicopter control, ballistic missile or space flight launching control and humanoid mobile robots, etc.

The IPS is an upright pendulum with its fulcrum fixed at the top of the cart that can move horizontally and controlled such that the pendulum is always balanced and upright. The cart is free to move in the horizontal plane in response to an externally applied force. Consider a situation that the pendulum is in an upright position on the cart without control action, now a slight position change of cart would destabilize the pendulum causing instability in the system. The objective of the controller is to regulate control input i.e. the torque on the cart and keep the pendulum in an upright position by maintaining pendulum angle at same state and zero degrees. Extensive research work on control of dynamical systems have been reported and available in three subgroups such as classical, adaptive and artificial intelligence based controllers. PI, PID, and LQR controllers are classical controllers and suggested for linear systems control. The classification of sliding mode and model predictive controllers belongs to adaptive controllers for nonlinear regimes. The artificial intelligence based controllers such as fuzzy controllers, neuro-controllers, hybrid neuro-fuzzy controllers and metaheuristic algorithm tuned PID controllers (Astrom & Kumar, 2014) are more suitable for nonlinear dynamical systems. Despite the advent of many controllers, PID controller is still one of the most simple and easy to implement in the stabilization of IPS. It offers simple structure, practicability, robustness, cost-effective solution with good performance and simple tuning methods. Most of the conventional tuning methods require tedious numerical computations to get appropriate PID parameters. Tuning of PID parameters are very critical, and it is anticipated to find optimal parameters to give satisfactory response for an inverted pendulum. In Recent past, besides the conventional tuning methods, several researchers have attempted for optimisation of PID gain parameters exclusively based on metaheuristic algorithms. The genetic algorithm (GA) (Liu & Daley, 1999; Shen, 2002) and particle swarm optimisation algorithm (Banks, Vincent, & Anyakoha, 2007, 2008; Oi, Nakazawa, & Matsui, 2008; Zhao, Li, & Qian, 2005) tuning methods yields optimal results than conventional tuning techniques. These metaheuristic algorithms are highly robust since the efficiency does not depend upon the characteristics of the IPS. The application of GA and standard PSO for tuning of linear PID controller in the linear dynamical system has emerged significantly in last few decades.

Chinichian and Kashani (1989) presented design and analysis of state variable feedback controller for a state space linear model of IPS mounted on a motor driven cart. Murata, Matsuno, Moran, and Hayase (1995) presented the dynamical modeling and nonlinear observer based controller with linear feedback gains to stabilize the inverted pendulum mounted on cart system. Tuning of PID controller is difficult due to parameters variations. Deris, Omatu, and Kitagawa (1995) and Omatu and Yoshioka (1998) have applied genetic algorithm tuned neuro PID controller to stabilize the pendulum mounted cart system. Medrano-Cersa (1999) illustrates the design of a robust digital controller with a blend of state space and frequency methods to balance the IPS on moving cart. An energy based control strategy is described by Åström and Furuta (2000) to control and swing up of an IPS on the cart. Patnaik and Behera (2008) have reported the design and implementation of a multi-objective genetic algorithm (MOGA) based classic quadratic regulator, standard H_∞ and mixed H₂/H_∞ controllers for the inverted pendulum. The response of PID plus LQR has been compared to that of simple PID on a pendulum cart system by Prasad, Tyagi, and Gupta (2011). Aouaouda, Chadli, Khadir, and Bouarar (2012) consider the tracking problem of uncertain Takagi-Sugeno fuzzy continuous systems subject to unknown inputs. Bououden, Chadli, and Fouad Allouani (2013) introduced a new approach for designing an adaptive fuzzy model predictive control using standard particle swarm optimization algorithm. Durand, Guerrero-castellanos, and Marchand (2013) proposed energy control and event-based state feedback control strategies for unstable IPS on cart system and demonstrated the computational cost efficiency on real-time test bed. Chadli, Aouaouda, Karimi, and Shi (2013) presented a fault-tolerant tracking controller for a verticle take-off and landing aircraft flight in uncertain conditions. Aouaouda, Chadli, and Karimi (2014) described the design of a robust fault estimation and fault tolerant control for the vehicle lateral dynamics subject to external disturbance and unknown faults. Bououden, Chadli, and Karimi (2015) proposed ant colony optimization for designing an adaptive fuzzy model predictive control. Aouaouda, Chadli, Shi, and Karimi (2015) have designed a multi-objective H₋/H_∞ sensor fault detection observer for a discrete-time nonlinear system subject to parameter uncertainties. An output feedback controller is proposed by Lee, Mukherjee, and Khalil (2015) to stabilize and trajectory control for inverted pendulum on cart system. Korkmaz, Aydoğdu, and Doğan (2012) disfavor the classical tuning of PID besides this, they proposed the design of nonlinear PID (NL-PID) and compared with GA tuned PID controller. Different PSO algorithms are stated by Menhas, Wang, Fei, and Pan (2012) to design optimal PI and PID controllers for a MIMO system. Valluru, Singh, Bhushan, and Sreevidya (2015) have made a comparative study of untuned PID, NARMA L-2, and standard PSO tuned linear PID for a nonlinear dynamical system.

This paper presents a performance evaluation of the IPS with MOGA tuned NL-PID, and APSO tuned, NL-PID controllers instead of routine GA and standard PSO tuning of linear PID controller. The present study focuses on detailed investigations, and performance evaluation of the NL-PID controlled IPS for optimal gain tuning by new variants of metaheuristics i.e. MOGA and APSO based optimization of controller parameters. The simulation results validate the system performance index regarding chattering, noise and settling time.

The paper is organized in five sections commencing with the introduction followed by Section 2, which analyzes mathematical modeling of IPS and its control strategies. In Section 3 the design of NL-PID controller for an IPS is presented. Section 4 discusses pseudo codes of the MOGA, APSO algorithms and pendulum angle response of IPS is investigated with NL-PID controller. Section 5 presents the conclusion.

2. Mathematical modeling of IPS

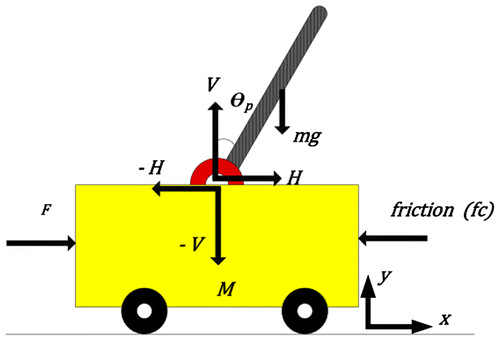
The IPS (Chatterjee, Patra, & Joglekar, 2002) involves a cart which is capable of moving backward and forward with a pendulum fulcrum at the bottom of its limited length such that the pendulum can move along with cart in the same plane. The pendulum attached to the cart is free to fall along the cart axis of motion. The pendulum movement is constrained in a vertical plane while the cart can move only in the horizontal plane. The control input force F is used to control the motion and hence the displacement x of the cart in the horizontal plane while indirectly controlling the angular position of the pendulum angle θ_p. The value of the input force depends upon control voltage (u) applied to DC motor, which drives the cart. The cart position and pendulum angle are monitored and used to change control signal so that the pendulum remains in stable region and upright at zero angles and does not affect even by small disturbance on the cart. A schematic representation combined with free body diagram is shown in the Figure 1.

Figure 1. Schematic of inverted pendulum.

The modeling of the IPS is challenging due to its inherent nonlinearities and instability. The mathematical modeling is based on the motion patterns through physical and mechanical means to set up the input-output relationship in the system.

2.1. IPS model equations

The nomenclature of the parameters and variables used in modeling of IPS are given in Table 1.

Table 1. Parameters and variables of IPS

F	Force applied to the cart by motor
M	Mass of the cart
fc	Frictional force of the cart wheels on the track
m	Mass of the pendulum or pole
2l	Length of the pendulum or pole
I	Moment of inertia of the pendulum or pole at the center of gravity
x	Cart position coordinate
y	Pendulum or pole position coordinate
θp	Pendulum or pole angle measured from vertical axis
H	Horizontal component of the reaction force at the fulcrum
V	Vertical component of the reaction force at the fulcrum

The dynamic equations (Guida, Nilvetti, & Pappalardo, 2010; Teixeira & Zak, 1999) of the system using Newton’s second law described as:(1) $$\ddot{x}=-\text{mal}{\ddot{\mathit{\theta }}}_{\text{p}}cos{\mathit{\theta }}_{\text{p}}+\text{mal}{\dot{\mathit{\theta }}}^{2}sin{\mathit{\theta }}_{\text{p}}-a{f}_{\text{c}}+aF$$(1) (2) $${\ddot{\mathit{\theta }}}_{\text{p}}=\frac{\text{mgl}sin{\mathit{\theta }}_{\text{p}}+{\text{m}}^2{\text{l}}^{2}a{\dot{\mathit{\theta }}}_{\text{p}}^{2}sin{\mathit{\theta }}_{\text{p}}cos{\mathit{\theta }}_{\text{p}}}{I-m^2{l}^{2}a{\text{cos}}_2{\mathit{\theta }}_{\text{p}}+{\text{ml}}^2}$$(2)

where $a=\frac{1}{\left(m+M\right)}$

The Equations (1) and (2) denotes the nonlinear dynamic model of the IPS.

2.2. Control strategy and stability analysis

The nonlinear dynamic equations for $\ddot{x}$ and ${\ddot{\mathit{\theta }}}_{\text{p}}$ may be represented into a state space form by considering the four state variables as:

x₁ = θ_p = pendulum angle measured from vertical.

$x_2={\dot{\mathit{\theta }}}_{\text{p}}$ = pendulum angular velocity.

$x_3=x$ = cart position.

$x_4=\dot{x}$ = cart velocity.

Therefore the nonlinear dynamic equations in the state space form rewritten as follows(3) $${\dot{x}}_1=x_2$$(3)

(4) $$\dot{x_2}=\frac{gsin{x}_1-{\text{mlax}}_2^2\text{sin}{x}_{1}cos{x}_1}{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}-\frac{\text{mla}cos{x}_1(F-f_{\text{c}})}{\frac{4{\text{ml}}^2}{3}-{\text{m}}^2{\text{l}}^{2}a{cos}^2{x}_1}$$(4) (5) $$\dot{x_3}=x_4$$(5) (6) $$\dot{x_4}=\frac{\frac{-\text{mag}\text{sin}(2x_1)}{2}+\frac{4\text{ml}}{3}a{x}_2^2\text{sin}{x}_1+\frac{4a(F-f_{\text{c}})}{3}}{\frac{4}{3}-{\text{macos}}^2{x}_1}$$(6)

(7) $$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\end{array}\right]=\left[\begin{array}{c}{x}_2\\ \frac{gsin{x}_1-{\text{mlax}}_2^2\text{sin}{x}_{1}cos{x}_1}{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}\\ x_4\\ \\ \frac{\frac{-\text{mag}\text{sin}(2x_1)}{2}+\frac{4\text{ml}}{3}a{x}_2^2\text{sin}{x}_1}{\frac{4}{3}-{\text{macos}}^2{x}_1}\end{array}\right]+\left[\begin{array}{c}0\\ \frac{acos{x}_1}{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}\\ 0\\ \\ \frac{\frac{4a}{3}}{\frac{4}{3}-{\text{macos}}^2{x}_1}\end{array}\right]\left(F-f_{\text{c}}\right)$$(7)

Applying the first order Taylor series approximations, nonlinear dynamics of the IPS shall be linearized around (Prasad et al., 2011) the equilibrium point $x={\left[\begin{array}{cccc}{x}_1\hfill & x_2\hfill & x_3\hfill & x_4\hfill \end{array}\right]}^{\text{T}}={\left[\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]}^{\text{T}}$.(8) $$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{3\text{g}}{4\text{l}-3\text{mla}}& 0& 0& 0\\ 0& 0& 1& 0\\ \frac{-3\text{mag}}{4-3\text{ma}}& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\hfill \\ x_2\hfill \\ x_3\hfill \\ x_4\hfill \end{array}\right]+\left[\begin{array}{c}0\\ \frac{3a}{3\text{mla}-4\text{l}}\\ 0\\ \frac{4a}{4-3\text{ma}}\end{array}\right]F$$(8)

The parameters of the system chosen as l = 0.3 m, M = 0.5 Kg, m = 0.2 Kg, $a=1.428{\text{kg}}^{-1}$, $I=0.006\text{kg}{\text{m}}^2$. The system matrices are$$\left[A\right]=\left[\begin{array}{cccc}0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 31.18\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ -2.67\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right];\left[B\right]=\left[\begin{array}{c}0\\ -4.547\\ 0\\ 1.8172\end{array}\right];\left[C\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right];\left[D\right]=\left[\begin{array}{c}0\hfill \\ 0\hfill \end{array}\right]$$

According to direct Lyapunov method (Chadli & Borne, 2013; Khalil, 2002), the controller state can define as ${\mathit{\theta }}_{\text{p}}\left(x_1,x_2\right)$ which is a function of the control is input $\left(F-f_{\text{c}}\right)$. Now by assuming the system equilibrium at origin i.e. ${\mathit{\theta }}_{\text{p}}\left(0,0\right)$ and choosing positive definite matrix P as $\left[\begin{array}{cc}1/2& 0\\ 0& 1/2\end{array}\right]$ the energy equation is(9) $$V\left(x\right)=\frac{1}{2}{X}^{\text{T}}PX$$(9)

where $X=\left[\begin{array}{c}{x}_1\hfill \\ x_2\hfill \end{array}\right]$(10) $$\dot{V}=\left[x_1{x}_2\right]\left[\begin{array}{c}{x}_2\\ \frac{gsin{x}_1-{\text{mlax}}_2^{2}sin{x}_{1}cos{x}_1}{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}-\frac{\text{mla}cos{x}_1\left(F-f_{\text{c}}\right)}{\frac{4{\text{ml}}^2}{3}-{\text{m}}^2{\text{l}}^{2}a{cos}^2{x}_1}\end{array}\right]$$(10)

Let $V:\mathcal{D}\to \mathbb{R}$ be a continuously differential function such that $\dot{V}<0$ verify the asymptotic stability. To prove this there exists a scalar $\mathit{\beta }>0$ (Khalil, 2002), then the asymptotic stability of the system satisfies the control input.(11) $${\mathit{\theta }}_{\text{p}}\left(x_1,x_2\right)>\left[\frac{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}{\text{mla}cos{x}_1}\right]\left[\frac{\mathit{\beta }}{x_2}+x_1-\left(\frac{gsin{x}_1-\frac{\text{mla}}{2}{x}_2^{2}sin2x_1}{\frac{4\text{l}}{3}-\text{mla}{cos}^2{x}_1}\right)\right]$$(11)

To ensure asymptotic stability, the control input of IPS must be as follows(12) $${\mathit{\theta }}_{\text{p}}\left(x_1,x_2\right)>\left[\frac{0.4-0.08568{cos}^2{x}_1}{0.08568cos{x}_1}\right]\left[\frac{\mathit{\beta }}{x_2}+x_1-\left(\frac{9.81sin{x}_1-0.04284x_2^{2}sin2x_1}{0.4-0.08568{cos}^2{x}_1}\right)\right]$$(12)

3. Design of NL-PID controllers for IPS

The PID controllers are widely used to stabilize the unstable systems. The PID controllers for unstable systems are having the capability of self-tuning by either conventional or intelligent technique to attain the stability in the neighborhood of operating envelope. However, the conventional tuning requires tedious numerical computation to achieve best possible controller gains, during the change of parameter variations. Therefore, the PID controller may perform poorly if the unstable system operates at different operating points, which need that the controller to be repeatedly re-tuned. The system may lose the stability at that operating point if the re-tuning made through complex and slow tuning methods. In these situations, an alternate approach to eliminate the problem is to use NL-PID with intelligent tuning techniques such as bio-inspired meta-heuristics, which are suitable to achieve faster and precise computation with best controller gains. However, when the system structure is complex with parameter variations, the linear PID do not exhibit good efficacy compared to that of the NL-PID. The NL-PID controller changes its parameters quickly over time according to system error and can provide an additional degree of freedom to achieve improved performance. Currently, different variants of GA and PSO algorithms tuned PID controllers have shown renewed interest among the researchers to automate the tuning process in the design of the controller.

3.1. NL-PID controller design

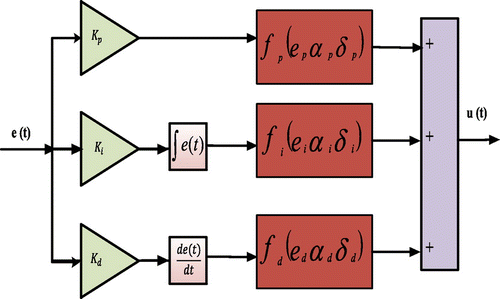
Mostly the PID controllers are employed to control unstable systems. While linear PID controllers are often sufficient for stabilizing unstable systems during small linear operating envelope, however for more high precision control, the competency and robustness of linear PID remained insufficient. The major failure of linear PID controller comes due to the constraints in the mathematical model i.e. contradiction between increased gain and the faster response of the system. If a suitable law is formulated for the system, which removes this limitation leading to a better control action for the system (Han, 1994). A general NL-PID module is introduced (Chen, Ballance, Gawthrop, Gribble, & O'Reilly, 1999; Su & Dong Sun, 2005) as in Equation (13)(13) $$f\left(e,\mathit{\alpha },\mathit{\delta }\right)=\left\{\begin{array}{cc}{\left|e\right|}^{\mathit{\alpha }}\text{sign}\left(e\right)\hfill & \left|\mathit{\gamma }\right|\ge \mathit{\delta }\hfill \\ \frac{e}{{\mathit{\delta }}^{1-\mathit{\alpha }}}\hfill & \left|\mathit{\gamma }\right|<\mathit{\delta }\hfill \end{array}\right.$$(13)

where $\text{sign}\left(e\right)=\left\{\begin{array}{cc}1,\hfill & e\ge 0\hfill \\ -1,\hfill & e<0\hfill \end{array}\right.$

where e is the error signal, δ describes the linear range of the function f, here function f can accommodate a greater range of nonlinear characteristics which is determined by α. Hence now control signal being generated by the NL-PID is given in Equation (14)(14) $$u\left(t\right)=K_{\text{p}}e{f}_{\text{p}}\left(e_{\text{p}},{\mathit{\alpha }}_{\text{p}},{\mathit{\delta }}_{\text{p}}\right)+K_{\text{i}}{f}_{\text{i}}\left(e_{\text{i}},{\mathit{\alpha }}_{\text{i}},{\mathit{\delta }}_{\text{i}}\right)\int e\text{d}t+K_{\text{d}}{f}_{\text{d}}\left(e_{\text{d}},{\mathit{\alpha }}_{\text{d}},{\mathit{\delta }}_{\text{d}}\right)\frac{\text{d}e}{\text{d}t}$$(14)

The function f(e, α, δ) denotes the rate of error feedback, to compensate the nonlinearity of the systems considered the value of α_p is taken in the range of ${\mathit{\alpha }}_{\text{p}}\in [0,1]$ since it needs lower gain when the error is high and vice versa. The integral saturation problem of the integral term can be rectified by using α_i in the range of ${\mathit{\alpha }}_{\text{i}}\in [-1,0]$. The value of differential term is chosen as α_d > 1 so that when the steady state is reached the effect of the differential term is reduced. The systematic structure design of NL-PID is shown in Figure 2.

Figure 2. Structure design of NL-PID.

4. Metaheuristics tuned NL-PID controllers for IPS

Bio-inspired metaheuristic algorithms are dissimilar as compared to the traditional algorithms regarding a multi solid solution while later have a single point solution; metaheuristic algorithms can all together evaluate some points in the search space with lesser convergence time and converge to global optima rather than local optima. Further, the metaheuristic algorithms reproduce offspring to progress the search space in addition to solution. Many metaheuristic algorithms such as Genetic Algorithm, Ant colony algorithm, particle swarm optimizer algorithm, firefly algorithm, and artificial bee colony algorithm (Yang, 2010) and their advanced variants have been developed in recent past. These algorithms differ from each other by variables to be tuned, offspring generation, and replacement mechanism. Out of all these algorithms, the most familiar is a genetic algorithm and particle swarm optimization algorithm for PID tuning of several systems. The variants of MOGA and Adaptive Particle Swarm Optimization Algorithm (APSO) have been considered here for the tuning of NL-PID controllers for IPS. The advantage of these algorithms is a shortfall of system matrix eigenvalues.

4.1. MOGA tuned NL-PID controllers

The MOGAs were one type of combinatory optimized search algorithm, which require discretized search space to solve real decision variables of system optimization problems for both single objective and multi- objective functions. The MOGA selects individuals based on random selection from the population and consists of genetic transformations such as crossover, mutation to create a new set population. Hence initially there is no clue, regarding the best answer for an optimization problem. Over the successive generations, the best among the lot are selecting, operators are worked upon on them and evaluated again until they evolve to the global optimal or suboptimal solution. The objective of using MOGA (Valluru, 2011) here is to determine the optimal value of NL-PID parameters (K_p, K_i and K_d) such that the objective functions J(x) is minimized. The overall result of the finding of the optimal parameters would lead to fine tuning of the PID controller and simultaneously improvement in the transient as well as steady state response of the system under consideration. The objective function $J(x)$ becomes an instrument to evaluate the performance of NL-PID controller with the determined value of gain parameters, resulting in an optimized controller with the best individual is given in Equation (15)(15) $$J(x)={(r\left(n\right)-y\left(n\right))}^2+{(max[r]-max[y])}^2$$(15)

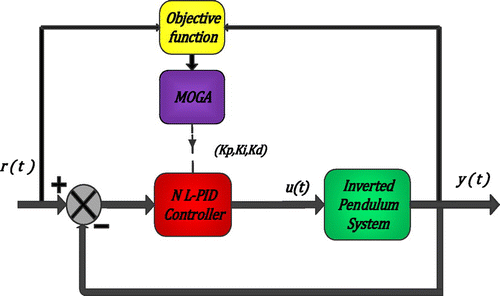
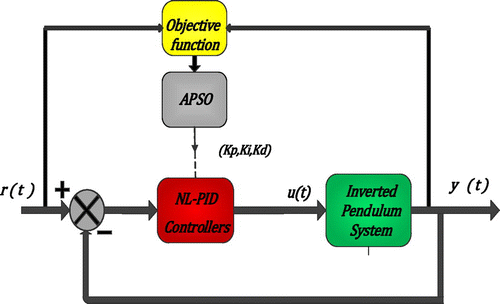
where $r\left(n\right)$ is nth input of the system and $y\left(n\right)$ the nth output of the system. A general block diagram of MOGA tuned NL-PID is shown in Figure 3 which uses the torque as reference signal to the inverted pendulum, the error between actual output and the reference signal along with proportional (K_p) integral (K_i) derivative (K_d) gains generate the control signal.

Figure 3. MOGA tuned NL-PID controller for inverted pendulum.

The pseudo code of MOGA employing to tune NL-PID controllers for IPS can be summarized as follows:

1.	Set the range of PID controller parameters as objective function $J\left(x\right),x={(K_{\text{p}},K_{\text{i}},K_{\text{d}})}^{\text{T}}$.
2.	Encode the solution into chromosomes as binary strings.
3.	Define the fitness F ∝ J(x) for maximization.
4.	Generate the initial population of size N for the NL-PID controller parameters.
5.	Initial probabilities of crossover (pc) and mutation (pm).
6.	Evaluate the initial population.
7.	While (t < Max. number of generations) Generate new solution by crossover and mutation If pc >  rand, Crossover; end if If pm >  rand, Mutation; end if The new solutions are accepted if fitness increases. Select the current best for new generation end while.
8.	Decode the binary strings and visualize the new values of Kp, Ki, Kd.

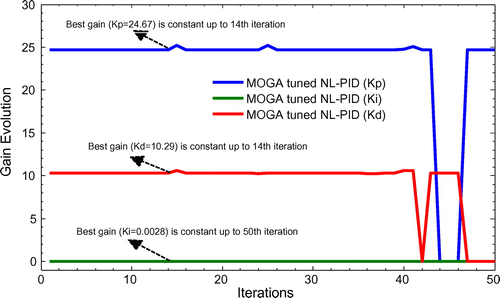
The size of the population, dimension, mutation rate, selection rate, maximum iterations used in the MOGA process to find best optimizing tuning parameters of NL-PID controllers for IPS taken as 10, 3, 0.2, 0.3, 100 respectively. The estimated NL-PID controller gain parameters by MOGA, which is tabulated in Table 2 and shown in Figure 4.

Table 2. MOGA tuned NL- PID controller best gain parameters

Controller	Time elapsed for MOGA (s)	Kp	Ki	Kd
NL-PID	295.7	24.67	0.0028	10.29

Figure 4. Best gain evolution by MOGA tuned NL-PID controlled inverted pendulum.

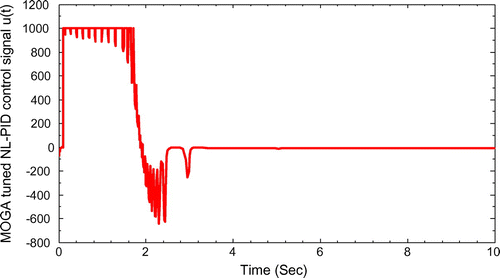
The control signal u(t) for MOGA tuned NL-PID as shown in Figure 5. The pendulum angle response of IPS with MOGA tuned NL-PID as shown in Figure 6.

Figure 5. Control signal of MOGA tuned NL-PID controller.

Figure 6. Pendulum angle response of IPS with MOGA tuned NL-PID controller.

4.2. APSO tuned NL-PID controllers

APSO algorithm is effective for optimizing a broad range of objective functions, inspired from the swarming phenomena of fish schooling and bird flocking. The multiple agents known as particles, swarm around the search space starting from an initial guess. APSO has some similarities with MOGA, but APSO is much simpler because it uses real number randomness and global communications instead of mutation/crossover. The APSO algorithm starts with the initialization of group of arbitrary particles in the search space, and each particle represents a potential solution for the optimization of an objective function.

During each iteration, all the particles in the search space discover a feasible solution. After, the particle updates its position according to the present velocity vector which contains its previous value and decides to take into account the past local and global best solutions. By keeping the best solutions, the particle moves towards local best solution attained by its fellow particles but also the global best. Hence if a particle has discovered a new best solution, then all other particles would try to move toward it. The four important terms in APSO (Chen, Hu, Wang, Gao, & Li, 2016; Li, Zhan, Lin, & Zhang, 2015; Zhan, Zhang, Li, & Chung, 2009) for the particles in the swarm are p_i position v_i, (current velocity), Pb_i (local best position), Gb_j (global best position). Each particle is updated according to the above four features in each iteration, assuming an cost function J to be minimized. The innovative velocity of a particle is determined by the Equation (16)(16) $$v_{i,j}\left(n+1\right)=C\times \left\{w{v}_{i,j}(n)+c_1{r}_1\left[{\text{Pb}}_{i,j}\left(n\right)-p_{i,j}\left(n\right)\right]+c_2{r}_2\left[{\text{Gb}}_j\left(\text{n}\right)-p_{i,j}\left(n\right)\right]\right\}$$(16)

where n is the number of iterations, w is inertia weight, c₁, and c₂ are the acceleration co-efficients (called cognitive and social component respectively) and r₁ and r₂ are two quasi uniform random numbers between (0, 1). v_i,j is the velocity of the jth dimension of the ith particle. The new position of the particle is updated by using Equation (17)(17) $$p_{i,j}\left(n+1\right)=p_{i,j}\left(n\right)+v_{i,j}\left(n+1\right)$$(17)

The local best of every particle is updated by the Equation (18)(18) $$\text{Pb}\left(n+1\right)=\left\{\begin{array}{cc}\text{Pb}\left(n\right),\hfill & J\left(p\left(n+1\right)\right)\ge J\left(\text{Pb}\left(n\right)\right)\hfill \\ \text{Pb}\left(n+1\right),\hfill & \text{otherwise}\hfill \end{array}\right.$$(18)

Here the population size is denoted by s; then the optimized global best can be found by the Equation (19)(19) $$\text{Gb}\left(n+1\right)=\underset{\text{Pb}}{min}J\left({\text{Pb}}_i\left(n+1\right)\right),1\le i\le s$$(19)

Tuning of NL-PID can be done efficiently by using particle swarm optimizer to find the values of optimal gain parameters (K_p, K_i and K_d) which will minimize the objective function (J). The block diagram of APSO tuned NL-PID for cart pendulum system is shown in Figure 7 which uses the step reference signal to the IPS, the error between actual output and the reference signal along with proportional (K_p), integral (K_i), derivative (K_d) gains generated the control signal u(t).

Figure 7. APSO tuned NL-PID controller for IPS.

The APSO pseudo code to tune the L-PID and NL-PID controllers for IPS is summarized as follows:

1.	Set the range of PID controller parameters $J\left(x\right),x={(K_{\text{p}},K_{\text{i}},K_{\text{d}})}^{\text{T}}$
2.	Initialize the locations of pi and velocity vi for swarm size n, acceleration factors c1 and c2 to the controller parameters Kp, Ki, Kd each representing dimensions of particle position vector in real parameter space.
3.	for each particle, i do, by testing each particle for fitness by evaluating the objective function $J\left(x\right)$
4.	Set the initial local best (Pbi), and global best (Gbj).
5.	While stopping criteria is not reached do for every particle i do Generate innovative velocity $v_{i,j}\left(n+1\right)$ according to Equation (16) Generate new positions $p_{i,j}\left(n+1\right)$ according to Equation (17) Evaluate objective functions at new positions Renew the current best of each particle end for Find the current global best end while
6.	Output the final results of optimized global best

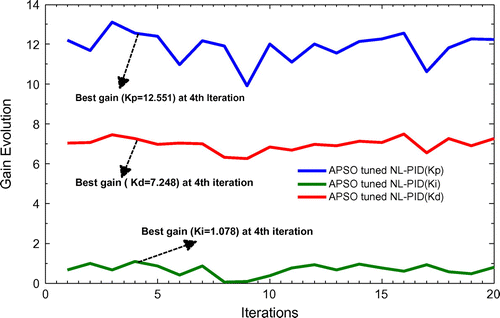
The size of the swarm, dimension, maximum iterations, cognitive factor, social factor, constriction factor used in the adaptive particle swarm optimizer to find the best-optimized parameters for NL-PID controller for the IPS are 10, 3, 50, 2.05, 2.05, and 2 respectively. The best gain parameters of APSO tuned NL-PID controllers are given in Table 3 and gained evolution is shown in Figure 8.

Table 3. APSO tuned NL-PID controller best gain parameters

Controller	Time elapsed for APSO algorithm (s)	Kp	Ki	Kd
NL-PID	46.85	12.551	1.078	7.248

Figure 8. Best gain evolution by APSO tuned NL-PID controlled IPS.

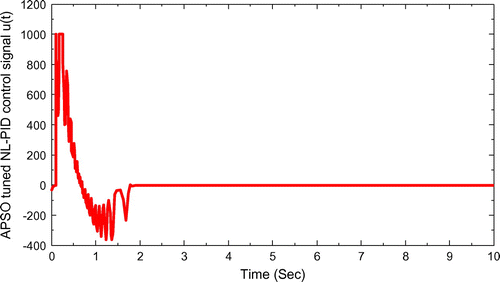
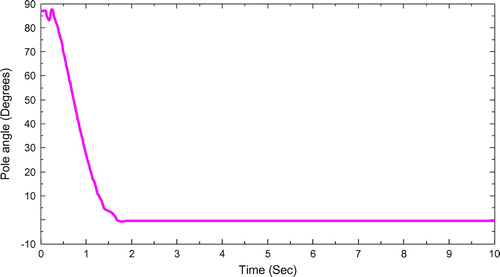
The control signal u(t) for APSO tuned NL-PID as shown in Figure 9. The pendulum angle response of IPS with APSO tuned NL-PID as shown in Figure 10.

Figure 9. Control signal of APSO tuned NL-PID controller.

Figure 10. Response of IPS with APSO tuned NL-PID controller.

4.3. Performance comparison of MOGA and APSO tuned NL-PID controller for IPS

A comparison performance of the IPS for pendulum angle response using MOGA and APSO algorithm tuned NL-PID controllers are carried out through simulation studies in MATLAB and summarized in Table 4.

Table 4. Performance indices of L-PID and NL-PID

Performance Index	MOGA tuned NL-PID controller	APSO tuned NL-PID controller
Chattering time (s)	0.752	0.328
Settling time (s)	2.5	1.7

5. Conclusion

This investigation presents comprehensive tuning strategy and performance evolution of NL-PID controller in conjunction with MOGA and APSO to stabilize the pendulum angle of IPS. APSO based tuning of NL-PID gives lesser settling time, and lesser chattering in response than MOGA tuned NL-PID controller. In addition to this, it is observed that the utilization of an NL-PID controller improves the dynamic performance of IPS. The APSO tuned NL-PID controller provides the optimum performance of the IPS and stabilize the system in operating state quickly with less chattering in the initial response. In the present scope of work, efforts are made to validate the performance and stabilization of IPS with MOGA and APSO based tuning of NL-PID controllers. However, the authors are motivated to implement these control algorithms on real-time prototype IPS in the laboratory.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Sudarshan K. Valluru

Sudarshan K. Valluru has been an associate professor of Electrical Engineering since 2009 at Delhi Technological University, New Delhi, India. His area of interests is Meta-Algorithms Applications to Control of Dynamical Systems, Intelligent, and Soft Computing Techniques. He is Fellow Member of Institution of Electronics and Telecommunication Engineers, Life Member of Institution of Engineers (I), and Life Member of Indian Society for Technical Education and also a member of IEEE (USA).

Madhusudan Singh

Madhusudan Singh has been working as Professor of Electrical Engineering since 2007 at Delhi Technological University, New Delhi, India. His research interests are in the area of modeling and analysis of Electrical Machines and Dynamical Systems, Voltage control aspects of Self-Excited Asynchronous Generator, Power Electronics, and Drives. He is a Fellow Member of Institution of Electronics and Telecommunication Engineers, Fellow Member of Institution of Engineers (I), and Life Member of Indian Society for Technical Education and also a Senior member of IEEE (USA).