Partially coherent light beam shaping via complex spatial coherence structure engineering

ABSTRACT

The techniques of optical beam shaping have enabled progress in a broad range of interdisciplinary science and engineering, owing to the unique properties and promising applications of their created structured light. However, the conventional methods, which are based on fully coherent optics approaches, introduce several adverse effects such as speckles noise in the generated beams and susceptible to be disturbed in complex environment (e.g. turbulent atmospheres), because of the sensitive coherent light-matter interaction. To overcome those side effects, a new protocol relied on the partially coherent beam shaping has been developed. By elaborately tailoring the complex spatial coherence structure of a partially coherent beam, the desired beam profile and trajectory with high beam quality and robust propagation feature in complex environment can be generated. In this review, we present an overview of such unconventional partially coherent beam shaping with a focus on the important role of the complex spatial coherence structure engineering. Partially coherent beam shaping not only provides an efficient means for resisting the disadvantages in coherent optics methods but also enables new applications in novel optical imaging and tweezers.

Graphical abstract

KEYWORDS:

• Optical beam shaping
• structured light
• partially coherent light
• optical coherence
• spatial coherence engineering

1. Introduction

Light beam shaping refers to the modulation of the light characteristics in spatial, temporal, frequency, or spatiotemporal domains. The shaped beams [1,2] have shown extraordinary physical properties during the propagation and light-matter interactions, and therefore, have been widely used in a broad range of applications, including industrial manufacturing, optical communications, particle trapping, imaging, nanoscience, and quantum technology. Tools such as optical free-form surfaces [3], liquid-crystal spatial light modulators [4], digital micromirror devices [5,6], novel fibers [7,8], geometric phase elements such as q-plate [9] and metamaterial [10], nonlinear elements [11,12], and even specially designed laser cavities [13] have been well developed to reshape the profile of light beam for particular applications. The physical mechanism behind the beam shaping is relied on the optical phase modulation, either the phase of a scalar wavefront or the phase between the orthogonal field components. Thus, the beam shaping is typically performed with fully coherent light.

Unfortunately, the fully coherent approaches for light beam shaping induce coherent artefacts such as speckle noise due to the phase-sensitive of the fully coherent light-matter interaction [14]. Furthermore, when the shaped fully coherent beam propagates through a complex environment, e.g. turbulent atmosphere, the distortion, scintillation, and beam wander will be introduced in the beam [15]. These adverse effects, therefore, limit not only the quality of the beam shaping but also the applications such as in high-quality optical imaging and optical communication through complex media. Reducing the spatial coherence of the beam is an efficient way to suppress the coherent artefacts induced by the fully coherent beam shaping. In addition, the optical beam with low spatial coherence provides more controllable (statistical) degrees of freedom for light beam shaping, compared to the fully coherent beam with deterministic characteristics.

In this review, we discuss the principle and technique of the unconventional partially coherent light beam shaping. We mainly focus on the effect of the recently introduced spatial coherence structure engineering on the modulation of the statistical properties of the partially coherent beam during propagation. We show the advantages of the partially coherent beam shaping over the fully coherent ones. We also discuss some of the applications for which such partially coherent beam shaping protocol is used.

2. Partially coherent light fields

All optical fields, whether encountered in nature or created in a laboratory, have more or less random fluctuations within their physical properties. For example, the fluctuations of the thermal light are mainly due to the random and uncorrelated spontaneous emission from atoms, while the fluctuations of the laser light are from the uncontrollable mechanical vibrations and temperature fluctuations in the laser cavity as well as the omnipresent spontaneous emission mixed in the stimulated radiation. These fluctuations within the light fields, however, are too rapid to be directly detected. Thus, it is necessary to use the statistical approach to describe the (observable) average quantities for the random light fields [16,17]. As the most successful framework to describe the classical, electromagnetic, and quantum statistical features of random light fields, optical coherence theory [18–29] has been well established by several distinguished physicists, including Frits Zernike, Emil Wolf, Roy Glauber, Leonard Mandel, Franco Gori, Ari Friberg, and others.

Optical coherence has nowadays been viewed as one of the most fundamental properties of light fields. It has played an important role in understanding interference, propagation, light-matter interactions, and other fundamental characteristics of classical and quantum wave fields. The random light field displays partial coherence in its space-time domain or space-frequency domain. Thus, the random light is also named as partially coherent light field. All the (second-order) statistical properties of the (stationary) partially coherent light are involved in a two-point electric coherence matrix $\mathbf{W}({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )=⟨{\mathbf{E}}^{\ast }({\mathbf{r}}_1,\omega ){\mathbf{E}}^{\mathrm{T}}({\mathbf{r}}_2,\omega )⟩$, where ${\mathbf{r}}_1$, ${\mathbf{r}}_2$ are two arbitrary spatial position vectors, $\omega$ denotes the (angular) frequency, $\mathbf{E}(\mathbf{r},\omega )$ is one of the random electric-field realizations, the angle brackets stand for the ensemble averaging over all the realizations, and the asterisk and the superscript T denote the complex conjugate and the matrix transpose, respectively. We remark in this review that the coherence matrix is considered only in the space-frequency domain because the formulation in such domain yields insight into the inner spectral structure of light and shows advantages in the study of light-matter interactions, i.e. the material responses such as the refractive index in optics are typically frequency-dependent.

Several statistical average quantities can be obtained from the coherence matrix. Firstly, the spectral density (or average intensity at frequency $\omega$) can be obtained by $S(\mathbf{r},\omega )=\mathrm{t}\mathrm{r}\mathbf{W}(\mathbf{r},\mathbf{r},\omega )$, where $\mathrm{t}\mathrm{r}$ denotes the matrix trace. Secondly, the polarization property of the partially coherent field is characterized by the polarization matrix, which is obtained by $\mathbf{\Phi }(\mathbf{r},\omega )=\mathbf{W}(\mathbf{r},\mathbf{r},\omega )$. The polarization state and the degree of polarization can be obtained from the polarization matrix if we decompose it into completely unpolarized and fully polarized parts [29]. We remark the decomposition can be realized only for the two-dimensional (2D) optical fields such as a paraxial beam-like field considered in this review. For a genuine 3D random field, a 3D nonregular polarization component must be considered [30–35].

Polarization and coherence of light fields had been treated separately for historical reasons. Today it is well understood that polarization and coherence are closely connected. From the statistical point of view, polarization can be viewed as a manifestation of the correlation involving the components of the fluctuating electric field at a single point [36], while coherence for a random light field may be regarded as the correlation involving the components of the fluctuating electric field between pairs (or more) of space-time or space-frequency points [20,29]. The partial coherence can be quantitatively measured by the normalized spatial correlation functions among the field components at two spatial positions, i.e. ${\mu }_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2)=W_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2)/\sqrt{S({\mathbf{r}}_1,\omega )S({\mathbf{r}}_2,\omega )}$, where $\alpha ,\beta =x,y$, and $W_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2)$ are the elements of the coherence matrix. We name the spatial distribution of the complex degree of correlation as the complex spatial coherence structure. In this review, we mainly discuss the shaping of the statistical properties of the partially coherent beam through engineering the spatial coherence structure of the partially coherent source.

3. Complex spatial coherence structure engineering

3.1. Structure of partially coherent field

To show how to control the complex spatial coherence structure of a partially coherent source, we first introduce the way to see the inner structure of the partially coherent beam. One way is to express the coherence matrix as the integral form [37,38], i.e. $W_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )=\int \int p_{\alpha \beta }(\mathbf{v})H_{\alpha }^{\ast }({\mathbf{r}}_1,\mathbf{v})H_{\beta }({\mathbf{r}}_2,\mathbf{v}){\mathrm{d}}^2\mathbf{v}$. The functions $H_x(\mathbf{r},\mathbf{v})$ and $H_y(\mathbf{r},\mathbf{v})$ are two arbitrary kernels that connect the function $p_{\alpha \beta }(\mathbf{v})$ in $\mathbf{v}$-space and $W_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )$ in $\mathbf{r}$-space. $p_{\alpha \beta }(\mathbf{v})$ are the elements of the weighting matrix $\mathbf{p}(\mathbf{v})$. To obtain the genuine coherence matrix, $\mathbf{p}(\mathbf{v})$ must obey the nonnegative condition for any $\mathbf{v}$. From the above integral, it is found that by controlling the distributions of the weighting matrix and the kernel functions, partially coherent sources with various spatial coherence structures can be constructed [39].

3.1.1. Schell-model-correlated sources

The partially coherent beams with Schell-model-correlated spatial coherence structure are the most popular ones. The spatial coherence structure of such beams depends only on the separation of two spatial positions, i.e. ${\mu }_{\alpha \beta }({\mathbf{r}}_1,{\mathbf{r}}_2)={\mu }_{\alpha \beta }({\mathbf{r}}_1-{\mathbf{r}}_2)$. To construct the Schell-model-correlated beams, the kernel function $H_{\alpha }(\mathbf{r},\mathbf{v})$ has a Fourier transform form as $H_{\alpha }(\mathbf{r},\mathbf{v})=T_{\alpha }(\mathbf{r})exp(\mathrm{i}{a}_0\mathbf{r}\cdot \mathbf{v})$, where $T_{\alpha }(\mathbf{r})$ is the initial amplitude of the constructed partially coherent source and $a_0$ is a factor that controls the beam’s initial spatial coherence width. The spatial coherence structure thus has the relation ${\mu }_{\alpha \beta }({\mathbf{r}}_1-{\mathbf{r}}_2)\propto \mathcal{F}[p_{\alpha \beta }(\mathbf{v})]$, where $\mathcal{F}$ denotes the Fourier transform operator. We remark that when both $\mathbf{p}(\mathbf{v})$ and $T_{\alpha }(\mathbf{r})$ have Gaussian shape, the partially coherent source becomes the classic Gaussian Schell-model (GSM) source [40–43].

Under the scalar circumstance [i.e. $\mathbf{p}(\mathbf{v})$ reduces to a scalar function $p(\mathbf{v})$], by modulating the spatial distribution of the $p(\mathbf{v})$ function, the Bessel-correlated [44–50], multi-Gaussian-correlated [51–53], Bessel-Gaussian correlated [54–56], Laguerre-Gaussian-correlated [54,57–62], Cosine-Gaussian-correlated [63–69], and Hermite-Gaussian-correlated Schell-model [70–73] sources have been introduced. The distributions of $p(\mathbf{v})$ functions and the corresponding spatial coherence structure are shown in Figure 1. These non-Gaussian-correlated spatial coherence structures embedded in the partially coherent source induce nontrivial propagation properties such as the self-splitting and self-shaping effects in free space.

Figure 1. Spatial distributions for $p(\mathbf{v})$ function (a–f) and for the corresponding spatial coherence structure (g–l) for the Gaussian-correlated, Laguerre-Gaussian-correlated, multi-Gaussian-correlated, Hermite-Gaussian-correlated, Cosine-Gaussian-correlated, and rectangular multi-Gaussian-correlated Schell-model sources. (m–o) Spatial distributions for $p(\mathbf{v})$ function and for the amplitude and phase of the spatial coherence structure for the self-steering partially coherent source. (p–r) Spatial distributions for $p(\mathbf{v})$ function and for the amplitude and phase of the spatial coherence structure for the Airy-correlated partially coherent source

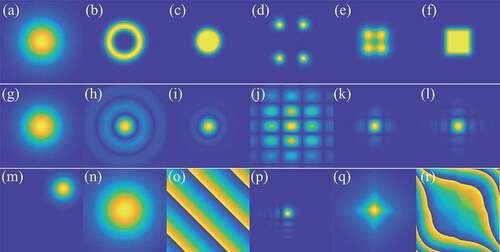
3.1.2. Phase structuring of Schell-model-correlated sources

Because the distributions of $p(\mathbf{v})$ in the above models have circular or rectangular symmetry, only the amplitude of the spatial coherence structure can be modulated. To modulate the phase distribution of the spatial coherence structure, the symmetry of the $p(\mathbf{v})$ function must be broken [74–79]. For a simple example, when we introduce a linear spatial shift ${\mathbf{v}}_0$ in $p(\mathbf{v})$, a linear phase $exp[\mathrm{i}{a}_0{\mathbf{v}}_0\cdot ({\mathbf{r}}_1-{\mathbf{r}}_2)]$ will be added in the spatial coherence structure (Figure 1) [80,81]. The source embedded with such phase shows a self-steering property in the free-space propagation and can be used in dynamic particle manipulations. When the $p(\mathbf{v})$ function has an Airy beam distribution, a second-order cubic phase will be introduced in the spatial coherence structure (Figure 1) and induce the self-acceleration of the beam during propagation in free space [82]. More general, the $p(\mathbf{v})$ function can be the amplitude of an optical image [83,84]. In such a case, the spatial coherence structure may have no analytic expression but has important application in coherence-based optical encryption and image transmission [85]. The requisite symmetry condition for the phase distribution of the spatial coherence structure can be obtained by representing the spatial coherence function as an auto-convolution of a Fourier-transformable sliding function [74,76].

3.1.3. Vectorial Schell-model-correlated sources

The spatial coherence structure including ${\mu }_{xx}({\mathbf{r}}_1,{\mathbf{r}}_2)$, ${\mu }_{yy}({\mathbf{r}}_1,{\mathbf{r}}_2)$, ${\mu }_{xy}({\mathbf{r}}_1,{\mathbf{r}}_2)$, and ${\mu }_{yx}({\mathbf{r}}_1,{\mathbf{r}}_2)$ of a vectorial partially coherent Schell-model-correlated beam can be engineered by governing the $\mathbf{p}(\mathbf{v})$ matrix. Compared with the scalar case, the vectorial spatial coherence structure includes an additional degree of freedom, i.e. the correlation among the orthogonal field components that play a key role in shaping the polarization properties such as the degree of polarization and the polarization state of the beam during propagation [86–96]. For instance, by letting $\mathbf{p}(\mathbf{v})$ have the structure of a radial polarization state [97], the created vectorial partially coherent source will become unpolarized at source and generally become more and more polarized during propagation. This phenomenon is quite different from that for the partially coherent vector beam with conventional spatial coherence structure, for which depolarization happens during propagation [98].

3.1.4. Nonuniformly correlated sources

In addition to the Schell-model-correlated spatial coherence structures, the integral form of the partially coherent structure can also be used to construct partially coherent sources having other types of spatial coherence structures. Due to the position difference dependence, the spatial coherence structures for the Schell-model correlations are spatially uniform. By modulating the kernel function $H_{\alpha }(\mathbf{r},\mathbf{v})$ into the forms that are different from the Fourier transform kernel, such as in one-dimensional situation $H(x,v)=T(x)exp[\mathrm{i}{a}_0(x-x_0{)}^{m}v]$ with the positive factor $m\ge 2$, the partially coherent sources with nonuniform spatial coherence structures can be created [99–106]. The spatially varying correlation properties lead to partially coherent fields with extraordinary free-space propagation characteristics, such as locally sharpened and laterally shifted intensity maxima [107–110]. It is interesting to find that the famous twisted partially coherent source [111–116] can also be constructed by modulating $H_{\alpha }(\mathbf{r},\mathbf{v})$ function into the form of $H_{\alpha }(\mathbf{r},\mathbf{v})=exp[-a(\mathbf{r}-\mathbf{v}{)}^2-\mathrm{i}b(v_{x}y-v_{y}x)]$ with $a>0$ and $b$ being a real parameter [117]. At the same time, by modulating the $p(\mathbf{v})$ distribution, new types of twisted partially coherent sources such as the high-order twisted Gaussian-correlated, twisted Laguerre-Gaussian-correlated, and twisted multi-Gaussian-correlated sources can be created [118–128]. More recently, Gori and Santarsiero showed that the spatial coherence structure can be controlled by the Laplace transform of $p(\mathbf{v})$ function by modulating $H_{\alpha }(\mathbf{r},\mathbf{v})=exp[a_0\mathbf{r}\cdot \mathbf{v}]$, where $a_0$ is a real factor [129,130].

3.2. Coherent-mode representation

With the aid of the coherent-mode representation, we can also see the inner structure of the partially coherent field. The coherent-mode representation is a milestone result in optical coherence theory [20]. The essence of the representation is that a partially coherent field can be decomposed as a sum of elementary modes that are fully coherent and mutually uncorrelated, i.e. $\mathbf{W}({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )={\sum }_n{\beta }_n(\omega ){\varphi }_n^{\ast }({\mathbf{r}}_1,\omega ){\varphi }_n^{\mathrm{T}}({\mathbf{r}}_2,\omega )$, where ${\varphi }_n(\mathbf{r},\omega )$ and ${\beta }_n(\omega )$ are the coherent-mode vectors and their corresponding modal weights, respectively. Thus, we can find that the spatial coherence structure of the partially coherent source can be tailored by controlling the distributions of ${\varphi }_n(\mathbf{r},\omega )$ and ${\beta }_n(\omega )$. Different types of novel partially coherent vortex fields have been created with such method. However, in order to obtain the desired spatial coherence structure, ${\varphi }_n(\mathbf{r},\omega )$ and ${\beta }_n(\omega )$ must be extracted from the calculation of the eigenfunctions and eigenvalues of the Fredholm integral equations. Unfortunately, only a few models of partially coherent sources including GSM source and twisted GSM source can find the modes and weights analytically [131]. However, if one release the orthogonal condition among the coherent modes, the problem will become much easier. The coherent pseudo-mode representation and the random-mode representation have been proposed to synthesize the partially coherent sources with desired spatial coherence structures [132–140]. The details regarding the representations will be discussed in Sec. 6.

4. Partially coherent beam shaping

We now turn to discuss the effects of spatial coherence structure engineering on the partially coherent beam shaping during propagation. The propagation problem of a partially coherent field can be solved with the help of the Green’s function formulation [141], i.e. $\mathbf{W}({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )=\int \int {\mathbf{G}}^{\ast }({\mathbf{r}}_1,{\mathbf{r}}_1^{\prime },\omega )\cdot {\mathbf{W}}^{(0)}({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega )\cdot {\mathbf{G}}^{\mathrm{T}}({\mathbf{r}}_2,{\mathbf{r}}_2^{\prime },\omega ){\mathrm{d}}^2{\mathbf{r}}_1^{\prime }{\mathrm{d}}^2{\mathbf{r}}_2^{\prime }$, where the Green tensor $\mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime },\omega )$ is a spatial transfer function between the coherence matrix ${\mathbf{W}}^{(0)}({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega )$ in the source plane and the coherence matrix $\mathbf{W}({\mathbf{r}}_1,{\mathbf{r}}_2,\omega )$ in the output plane. The Green’s function formulation can be used to solve not only the propagation problem but also the light-matter interactions such as partially coherent light scattering [20,142–145]. Within the validity of the paraxial approximation, the Green’s function formulation reduces to the extended Collins formula [146,147], which is quite useful for studying the propagation properties of a partially coherent beam in a stigmatic ABCD optical system.

By using the Fourier transform and the convolution operators in the propagation formula, the polarization matrix of a Schell-model-correlated source in the output plane can be obtained by ${\mathrm{\Phi }}_{\alpha \beta }(\mathbf{r})\propto {\tilde{A}}_{\alpha }^{\ast }(\mathbf{r}){\tilde{A}}_{\beta }(\mathbf{r})\otimes {\tilde{\mu }}_{\alpha \beta }({\mathbf{r}}_1-{\mathbf{r}}_2)$ [148], where the superscript tilde denotes the Fourier transform, $\otimes$ denotes the convolution operator, and $A_{\alpha }(\mathbf{r})=T_{\alpha }(\mathbf{r})exp(\mathrm{i}kA{\mathbf{r}}^2/2B)$. It is found that in general the average intensity and polarization of a partially coherent beam during propagation are controlled by both the initial source’s (complex) amplitude $T_{\alpha }(\mathbf{r})$ and spatial coherence structure ${\mu }_{\alpha \beta }({\mathbf{r}}_1-{\mathbf{r}}_2)$. The propagation properties of the classic GSM sources with customized intensity, polarization, and phase have been studied extensively [98,149–154]. It has been shown the flat-topped, dark-hollow, and other beam profiles can be obtained in the propagation.

However, we see from the convolution relation above that when the spatial coherence of the source is very low, i.e. the Fourier transform of beam amplitude is a much faster function compared to the Fourier transform of the spatial coherence structure, the effect from the source’s amplitude then can be neglected. In such situation, the average intensity and polarization properties of a partially coherent beam during propagation can be shaped effectively by the source’s spatial coherence structure. The spatial coherence structure and the polarization matrix during propagation, thus, form the Fourier transform pair and the $\mathbf{p}(\mathbf{v})$ can be mapped into the polarization matrix of the partially coherent beam during propagation. It has been shown that not only the beam spot can be controlled, but also the propagation trajectory can be shaped by spatial coherence structure engineering. For example, see in Figure 2, the Hermite-Gaussian-correlated beam displays an intensity self-splitting feature [70] and the phase-controlled GSM beam shows a self-steering property during propagation in free space [80,93]. By focusing a Laguerre-Gaussian-correlated beam with a thin lens, a controllable optical cage can be formed in the focal area [155].

Figure 2. Partially coherent beam shaping with spatial coherence structure engineering. (a) Self-splitting and self-combining of a focused Hermite-Gaussian-correlated beam [70]. (b) Self-steering of a phase-engineered partially coherent beam [80]. (c) Optical cage formation with a focused Laguerre-Gaussian-correlated beam [155]. (d) Evolution of the intensity and the degree of polarization for the specially correlated partially coherent vector beam during propagation [97]

We remark that the modulations by the initial beam amplitude and the spatial coherence structure have different effects on the propagation properties. For example, when the radial polarization modulation is in the initial beam amplitude, the beam is fully polarized in the source plane and gradually becomes unpolarized during propagation [98]. While when the same modulation is in the spatial coherence structure [97], the generated beam becomes completely unpolarized at source and generally increases its degree of polarization on propagation (Figure 2). When the modulation appears both in the beam amplitude and spatial coherence structure, the joint effect must be considered in the beam shaping [57], unless the spatial coherence is very low or relatively high since in the former case the effect from the modulation of spatial coherence structure is dominant and in the latter situation the effect from the initial beam amplitude becomes dominant. It is typically difficult to calculate the propagation properties of the partially coherent beam with nonuniform spatial coherence structure because the generalized Collins formula dealt with the four-dimensional integral. To solve this problem, the coherent-mode or coherent pseudo-mode representation method has been successfully applied in the paraxial and nonparaxial propagation of partially coherent field [156–160]. In such a manner, the propagation problem can be solved with the coherent optics methods such as fast Fourier transform algorithm. Furthermore, as we have discussed in Sec. 3.2, with the help of the coherent-mode or pseudo-mode superposition, the spatial coherence structure can be engineered. Thus, the beam shaping can also be realized by mode superposition methods. It has been shown that by modulating the complex amplitude and modal weight of each mode, the nonuniformly correlated beams with controllable intensity profile, polarization property, and self-focusing propagation feature can be created [102,103].

5. Advantages of partially coherent beam shaping

As we have discuss above, when the spatial coherence of the source is sufficiently low, the statistical properties such as the average intensity and the polarization features are determined by the distribution of spatial coherence structure. Thus, the beam shaping is performed in the lowly spatially coherent environment. In such environment, the coherent artefacts such as speckle noise in the output beam profile can be suppressed [161] because of the weak first-order interference effect [16,17]. Therefore, high quality beam shaping can be realized with the spatial coherence engineering of the partially coherent light, e.g. see in (Figure 3). At the same time, by engineering the spatial coherence structure into spatial periodic structure, the high quality partially coherent beam arrays such as Bessel vortex array (Figure 3) and cylindrical polarization state array (Figure 3) can be created [162–164].

Figure 3. High quality beam shaping with low spatial coherence. (a) The images formed by passing the beams with different spatial coherence widths through four pinholes [80]. (b) High-quality Bessel beam array generation by spatial coherence structure engineering [162]. (c) High-quality radially polarized beam array generated by focusing the specially correlated partially coherent vector beam though lens array [163]

In addition, because of the low spatial coherence property, the partially coherent light beam shows a super-strong self-healing effect during propagation in the path within the obstacles [163,165–167]. Such effect is similar to that for the fully coherent diffraction-free beam. However, their physical interpretations are different. The self-reconstruction capacity of a partially coherent beam is closely related to its small spatial coherence area. When the condition $A_c\ll A_a$ holds, it is found in the far-field or focal plane the average intensity and polarization of the partially coherent beam can be well reconstructed (Figure 4). Above, $A_c$ denotes the beam’s initial spatial coherence area and $A_a$ stands for the obstacle area. The self-healing effect of a fully coherent beam relies on special properties of diffraction-free complex amplitude profiles [168]. For the case when the obstacle has a large size, the nonnegligible diffraction effects will distort the fully coherent beam’s spatial distribution, while the partially coherent beam’s spatial profile can be well recovered.

Figure 4. Self-reconstruction and robustness of a partially coherent beam with engineered spatial coherence structure propagation through the complex media. (a) Physical interpretation of the self-reconstruction capacity when the relation ${\sigma }_c<{\sigma }_a<{\sigma }_I$ holds, where ${\sigma }_c,{\sigma }_a$, and ${\sigma }_I$ are the widths for the spatial coherence, obstacle size, and beam intensity. (b)–(c) Intensity distribution of the specially correlated partially coherent vector beam at several propagation distances (b) without obstructed, (c) and (d) with sector-shaped opaque object of center angle $\phi =7\pi /4$ and $\phi =71\pi /36$ placed in the source plane. (e) Experimental setup for analyzing fully coherent radially polarized beam and specially correlated partially coherent vector beam transmission through a turbid medium with random refractive index fluctuations. (f) Experimental intensity profile self-reconstruction of the fully coherent radially polarized beam passing through diluted milk at different instances of time $t$. (g) Experimental intensity profile for the specially correlated partially coherent vector beam [163]

Moreover, when the propagation link is filled with atmospheric turbulence, the absorption, scattering, and refractive-index fluctuation of the turbulence will affect the propagation of the beam and introduce the distortion, beam wander, and intensity scintillation in the beam profile [15]. While the partially coherent beam, due to its low spatial coherence property and multimode nature, has shown to be robust in atmospheric turbulence [169,170]. By modulating the spatial coherence structure, the turbulence-induced adverse effects can be efficiently resisted [50,55,59,64,66,69,101,105,126]. Thus, the coherence-based beam shaping has the advantage in complex environment compared to the coherent-based ones. By passing a fully coherent radially polarized beam and a specially correlated partially coherent beam through the diluted milk [163], the output intensities for two beams at different time instances, shown in (Figure 4), indicate that the coherent transmitted beam is strongly affected by the medium resulting in poor beam profile and stability, while the partially coherent beam possess a smooth spatial intensity distribution in the output plane.

6. Experimental approaches for spatial coherence structure engineering

In this section, we discuss two strategies to experimentally control the spatial coherence structure for the light beam shaping. The comparison of the two strategies is also given.

6.1. From incoherent light to partially coherent light

In the first strategy, the spatial coherence structure is controlled during the conversion of spatially incoherent light into partially coherent light beam. The physics behind is based on the famous van Cittert–Zernike theorem [19], which states that under certain conditions the Fourier transform of the intensity distribution function of a distant, incoherent source is equal to the complex visibility of the created wavefront. The complex visibility stated above denotes the complex spatial degree of coherence, also named spatial coherence structure of the generated partially coherent beam. The certain conditions in van Cittert-Zernike theorem can be implemented, for example, by an optical Fourier transform system [171]. Thus, the intensity distribution of the incoherent source and the spatial coherence structure of the secondary partially coherent beam generated in the Fourier plane compose the Fourier transform pair. Conveniently, by modulating the intensity distribution of the incoherent source, the complex spatial coherence structure of the generated partially coherent beam can be governed [39,172]. At the same time, the spatial coherence width of the secondary partially coherent source is determined by the beam width of the incoherent source and the focal distance of the Fourier transform lens. Typically, the spatial coherence width decreases with the increase of the beam width and the decrease of the focal distance.

6.2. From coherent modes to partially coherent light

The second strategy we discussed is an ‘inverse’ method compared to the first one. The partially coherent beams with customized complex spatial coherence structures can be synthesized from the full coherent modes rather than the incoherent source. The physical behind relies on the theory of coherent-mode representation for partially coherent fields, in which the partially coherent field is viewed as a superposition of spatially coherent but mutually uncorrelated modes. In the principle, by controlling the complex profile and the weight of each mode as well as the acting mode number, the partially coherent beam with any desired spatial coherence structure and spatial coherence width can be synthesized (Figure 5). However, in the classical coherent-mode representation only a few partially coherent models can find analytical expressions for their coherent modes and the corresponding weights. This is because the modes and weights are the (orthonormalized) eigenmodes and eigenvalues of a linear Fredholm integral equation that is generally difficult to be solved. Thus, the spatial coherence structure cannot be modulated arbitrarily with the coherent-mode superposition. If the orthogonal condition for each mode in the superposition is released, the (approximate) coherent modes and weights can be obtained conveniently. The coherent pseudo-mode and random-mode superpositions have been proposed to synthesize partially coherent sources with different coherence properties [173–183]. In the experiment, the modes can be generated with the help of a single spatial light modulator (SLM) and the mode weight can be controlled by the probability of the appearance of modes in the SLM (Figure 5). However, due to the low refresh speed of an SLM ($\sim 60$ Hz), the synthesis is time consuming. To overcome such limitation, the digital micro-mirror device have been used to replace the SLM. The modulation speed can be up to 17 kHz [184,185].

Figure 5. Experimental realization of the spatial coherence structure engineering by coherent-mode superposition. (a) Schematic diagram for the coherent-mode representation (CMR), pseudo-mode representation (PMR), and random-mode representation (RMR) [188]. (b) Experimental setup for the spatial coherence structure engineering by coherent-mode superposition. (c) The computer generated holograms and their probability loaded on the digital micro-mirror device (DMD) [184]

6.3. Comparison of strategies

Because the high energy loss within the conversion of incoherent light into partially coherent light, the light efficiency for the first strategy is typically low and the generated partially coherent sources cannot be used in high power light beam shaping applications. The second strategy based on the fully coherent modes superposition, on the other hand, has a high light efficiency and can find potential applications in high power beam shaping. In the first strategy, the incoherent light can be viewed as a superposition of lots of independent random processes, the generated secondary source obeys Gaussian statistics according to the central limit theorem [16]. Thus, the generated partially coherent sources can be used in high-order correlation images, e.g. ghost imaging [186,187]. The random-mode superposition in the second strategy has a similar high-order statistical property. However, the fields generated by the coherent-mode and coherent pseudo-mode superposition method do not obey Gaussian statistics although their second-order statistical properties are the same as the fields generated by the random-mode superposition [188]. This indicates that by using the coherent-mode superposition, not only the ‘local’ second-order statistical properties, but also the ‘global’ high-order statistical properties can be modulated.

7. Applications of partially coherent beam shaping

Due to the unique properties of the spatial coherence structure engineering and the advantages of partially coherent beam shaping, various novel applications including coherence-based optical encryption, moving targets tracking through scattering media, robust optical imaging, and optical trapping have been proposed.

7.1. Optical encryption

Information encryption with the aid of optical technologies has been studied extensively in the past decade due to remarkable multidimensional capabilities and ultrafast modulation speed afforded by the light fields. Similar as other first-order deterministic field characteristics (like optical phase, intensity, and polarization), the second-order statistical spatial coherence structure can also be viewed as an efficient degree of freedom to realize the optical encryption. The coherence-based optical encryption protocol has been recently developed (Figure 6) [85]. It has been shown that the coherence-based approach has two key advantages over the conventional ones. First, the complexity of measuring the spatial coherence structure of light enhances the encryption protocol security. Second, the relative insensitivity of the second-order statistical characteristics of light to environmental noise makes the protocol robust against the environmental fluctuations, e.g. the atmospheric turbulence (Figure 6). This circumstance bestows certain advantages on the protocol over the alternatives in the application scenarios where an attacker aims to deliberately destroy the ciphertext rather than temper with it.

Figure 6. Application in optical encryption. (a) Encoding of an optical image into the spatial coherence structure of a random light beam through a generalized van Cittert-Zernike theorem formed by a dynamic diffuser and an encoding system with the encryption keys embedded inside. (b) The experimental results for the measured spatial coherence structure and the corresponding recovered image in the turbulence free situation. (c) The experimental results in the presence of thermally induced turbulence with the temperature $T$ of hot graphitic plate being 250°C [85]

7.2. Moving targets tracking through scattering media

In the process of spatial coherence structure engineering through van Cittert-Zernike theorem, it is found the image information before the dynamic scatterer can be encoded into the spatial coherence structure of the created partially coherent source [171]. When the optical system between the dynamic scatterer and the source is a Fourier transform system, the image information and the complex spatial coherence structure form the Fourier transform pair. It has been shown that by the complex spatial coherence measurement, not only the spatial shape, but also the position of the object hidden behind the scattering media can be tracked [189]. By extending into the vector case, the complex vectorial spatial coherence structure measurement can also be used in polarization information tracking through scattering media [190]. Dogariu’s group demonstrated that spatial coherence measurement can also been used in non-line-of-sight imaging through highly scattering wall (Figure 7) [191].

Figure 7. Application in moving targets tracking through scattering media. (a) Schematic diagram for non-line-of-sight imaging using spatial coherence. (b) Measured complex spatial coherence distribution. (c) 1D projection of the intensity of the recovered images [191]

7.3. Robust optical imaging

It is well known that light field modulation in the frequency domain of a $4f$ imaging system is quite important in novel optical imaging applications such as the edge enhanced imaging [192]. However, when an obstacle is introduced into the Fourier plane (frequency domain) to partially block light transmission, distortions inevitable arise in image plane even for low-coherence light illumination [193,194]. Recently, it has been found that the distortions originate from the source pseudo-modes whose maxima are located at the edge of the obstacle when a suitable coherent pseudo-mode representation is employed. By engineering the spatial coherence structure of the light source to ensure that all the coherent modes circumnavigate the obstacle, the same output image as if the obstacle were absent from the system has been obtained, see in Figure 8 [195].

Figure 8. Application in robust optical imaging. (a)Schematics of the experimental setup for a $4f$ optical imaging system with its Fourier plane partially blocked by a sector-shaped opaque obstacle and the input plane is illuminated by a partially coherent light. (b) The output images by the fully coherent, partially coherent GSM, and partially coherent special correlated illuminations [195]

7.4. Optical trapping

In optical trapping, it was demonstrated that a simplest type of partially coherent beam, i.e. a GSM beam, can produce the same optical force as a fully coherent laser beam in any ABCD optical system in the condition that even the peak intensity is much lower than the fully coherent one [196]. This indicates a great advantage in the application of trapping biological samples that are sensitive to thermal heating induced by high intensities. The lowly coherent beams with structured spatial coherence structures, on the other hand, provide more opportunities for novel optical trapping. For example, it has been shown that the cosine-Gaussian correlated Schell-model beam [197], multi- and generalized multi-Gaussian correlated Schell-model beams [198,199], Laguerre–Gaussian correlated Schell-model beam [200], and Bessel-Gaussian correlated Schell-model beam [201] can be used to trap two types of Rayleigh particles with different refractive indices simultaneously in the trapping areas. Furthermore, based on the reciprocity theorem for the partially coherent light, the far-field intensity (or the focused intensity) will display the same symmetry as the coherence structure in the source plane [22]. Therefore, the distribution of the radiation forces related with the focused intensity will show different symmetries and thus the particles can be trapped in the areas with desired symmetry with the help of spatial coherence structure engineering [202].

8. Conclusions and outlook

The spatial coherence structure, as a unique statistical characteristic of partially coherent light, describes the correlations among the random field components at two spatial positions or in general the correlations within two optical modes. It has nowadays became an important degree of freedom to govern the statistical properties of a partially coherent beam during propagation in different media. We show that the far-field (or focal-plane) intensity distribution and polarization property of the partially coherent beam are determined, in general, by the joint effect of the complex amplitude and the spatial coherence structure. However, when the spatial coherence of the source is sufficiently low, the propagation properties of the beam is solely determined by the spatial coherence structure, which indicates that the partially coherent beam shaping based on spatial coherence structure engineering is performed in the low-coherence environment. Thus, such beam shaping can overcome the adverse effect induced by the coherent artefacts such as the speckle noise. Furthermore, the partially coherent beam shaping shows super-strong self-healing and robustness effects in complex environment such as atmospheric turbulence. The extraordinary features of such coherence-based light beam shaping have found advantages in various applications such as in the novel optical encryption, robust optical imaging, and optical trapping.

The spatial coherence structure engineering and the partially coherent beam shaping discussed in this review are carried out outside the laser cavity due to the flexibility of the performance. However, the direct output of a partially coherent beam with engineered spatial coherence structure from a laser is important in specific applications where high-power and low-coherence laser are required, e.g. in inertial confinement fusion [203,204] and free-space telecommunication [205] applications. The spatial coherence engineering inside the laser cavity may be realized with the help of unconventional, complex cavities [206] or modified pumping conditions [207]. In addition, the spatial coherence structure engineering and the partially coherent beam shaping discussed in this review are limited in the two-dimensional paraxial propagation beams. The coherence-based beam shaping for nonparaxial three-dimensional optical fields such as the highly focused fields [60,160,208–210] and electromagnetic surface waves [211–219] has potential novel applications in nanophotonics. Finally, the spatial beam shaping for the statistical stationary partially coherent beam can be extended into the temporal and even spatiotemporal beam shaping [220–222] with the help of temporal or spatiotemporal coherence structure engineering of a nonstationary partially coherent light [223–227].

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the National Key Research and Development Program of China [2019YFA0705000]; National Natural Science Foundation of China [91750201, 11874046, 11974218, and 11904247]; Innovation Group of Jinan [2018GXRC010]; Local Science and Technology Development Project of the Central Government [YDZX20203700001766]; China Postdoctoral Science Foundation [2019M661915]; and Natural Science Foundation of the Jiangsu Higher Education Institutions of China [19KJB140017].