Influence of the preparation processes on the residual stresses in PCD and PcBN tools

Abstract

Ultra-hard cutting materials such as polycrystalline diamond (PCD) and cubic boron nitride (PcBN) are increasingly being used as cutting tools in machining. The finishing of cutting tools is challenging due to their mechanical and thermal properties. Both mechanical preparation processes such as grinding and brushing are used to prepare the final contour of the tools. All processes affect the subsurface of the cutting edge, thermally, mechanically, or both. In addition to influencing the cutting edge microgeometry and topography, it is also to be expected that the residual stress state is influenced. In particular for the highly loaded cutting edge, the residual stress state is of major interest, since high cyclic load stresses occur during cutting. A measurement using conventional X-ray diffraction to determine the residual stress state in the cutting edge is not possible due to the very small surface and the strong curvature. For this reason, the influence of the cutting edge preparation methods grinding and brushing for PCD and PcBN on the residual stress state is determined in this work using Raman spectroscopy. For this purpose, the preparation-induced peak shift in the Raman spectrum is determined. This is then converted into absolute residual stresses using previously determined conversion factors.

Keywords:

• Polycrystalline diamond
• polycrystalline cubic boron nitride
• residual stresses
• grinding
• brushing

1. Introduction

The ultra-hard cutting material phase leads to a high hardness of the composites PcBN and PCD. However, it also makes it very difficult to machine with mechanical manufacturing processes. One possibility of machining these cutting materials in a mechanically and geometrically defined way is to grind them with diamond grains (Behrens, 2016; Tso & Liu, 2002). The disadvantage of this method is the high level of grinding wheel wear, which in case of PcBN can be many times the removed material volume from the tool (Leahy, 2013) and can be considerably higher when machining PCD (Friemuth, 2002). If this process is examined in more detail, it can be seen that the removal mechanism is not entirely mechanical. At high temperatures, the diamond in the PCD graphitizes and can subsequently be removed as the mechanically less demanding graphite (Schindler, Brocker, Klocke, & Mattfeld, 2016). It becomes clear here that the subsurface of the finished tool has been subjected to additional thermal stress due to mechanical processing. Grinding PcBN is much easier to implement due to its lower hardness and therefore also differs in terms of its material separation mechanisms which is described as microdestruction of the surface by the grinding wheel (Mamalis, Horvath, & Grabchenko, 2000). Due to the higher thermal stability of PcBN, a thermal influence on the subsurface is less probable (Xikun et al., 2007).

PCD machining is already completed after grinding, as the sharpest possible cutting edge is necessary for use in aluminium machining, see for example (Brinksmeier, Fangmann, & Rentsch, 2011; Tsao & Hocheng, 2007). In PcBN machining, a ground chamfer is necessary to stabilize the cutting edge, which optimises chip formation and increases tool life (Fang & Wu, 2005; Klocke, Brinksmeier, & Weinert, 2005; Kress, 2007). Furthermore, a cutting edge rounding is used to protect the cutting edge from micro chipping (Özel, Karpat, & Srivastava, 2008). For this purpose, the cutting edge is machined by means of diamond brushes and is thus abrasively rounded. The influence of the machining process on the residual stress state has already been investigated for PCD for the EDM process. Rahim et al. show high tensile residual stresses in the cutting edge area measured by Raman spectroscopy (Rahim, Pourmoslemi, Ding, & Mo, 2013). Furthermore, Sotillo et al. found an influence of laser machining on the compressive residual stresses determined by Raman spectroscopy, which can be reduced (Sotillo et al., 2017). According to Li et al., the grinding of PCD tools leads to compressive residual stresses or low tensile residual stresses (Li, Rahim, Ding, & Sun, 2016).

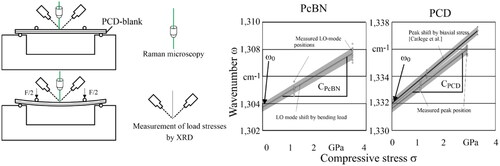
For the measurement of load or residual stresses, the sensitivity of the peak position of the transverse-optical (TO) or logitunial-optical (LO) modes of cubic boron nitride and the first mode of diamond can be used. All modes shift to higher wavenumbers when a compressive load stresses is applied (Boppart, Silvera, & van Straaten J, 1985; Mitra, Brafman, Daniels, & Crawford, 1969; Ono, Mibe, Hirao, & Ohishi, 2015). On the basis of known conversion factors, the resulting residual stresses can be calculated (Catledge, Yogesh, Ladi, & Rai, 1996; Sanjurjo, López-Cruz, Vogl, & Cardona, 1983). The measurability of residual stresses in coatings by Raman spectroscopy has already been demonstrated on coatings (Breidenstein, Vogel, Behrens, Dietrich, & Andersson, 2022).

It is evident that the influence of different preparation methods on the subsurface of PCD and PcBN has been investigated and basic influences have been identified. However, the influence of the process parameters during grinding or brushing has not yet been extensively investigated and is the subject of this paper.

2. Materials and methods

2.1. Cutting materials

PCD and PcBN cutting materials were used for the investigations. PCD has diamond grains with a diameter of d_g = 4 µm and a diamond content of 90%. Due to the manufacturing process, the 0.5 mm thick PCD layer is soldered on a 1.1 mm thick tungsten carbide substrate (data sheet information). The PCD grade is characterized by a good measurability by means of Raman spectroscopy and the later machining of highly eutectic aluminium alloys with a high silicon content. PcBN with a cBN content of 85% was used, which has an AlWCoB binder and a cBN grain diameter of d_g = 2 µm (data sheet information). Due to the high cBN content, reproducible Raman spectroscopy measurements are possible. For the grinding process, indexable insert bodies of type CNGA 120408 were previously provided with tips made of the above-mentioned cutting materials to enable machining on a tool grinding machine.

2.2. Preparation processes

2.2.1. Grinding process

A Wendt WAC Centro 715 CBN tool grinding machine, specialized in the machining of indexable inserts, was utilized for grinding PCD and PcBN cutting materials. The grinding tool used was a Saint Gobain D15A PCX-PRIME grinding wheel, possessing a diamond grain diameter of d_g = 15 µm and a ceramic bonding. On this machine, two process parameters can be varied: the cutting speed v_c and the feed rate f, which acts orthogonal to the machined surface.

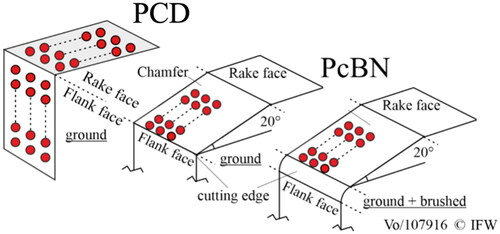
When machining PcBN tools, the feed rate was varied in two steps (f = 6 and 8 mm/min) and the cutting speed in three steps (v_c = 10, 15, and 20 m/s). Both, the flank face and a chamfer with an angle of 20° and a length of l = 200 µm were produced by grinding.

Due to strong graphitization of the grinding wheel during PCD machining, reduced cutting speeds were applied (v_c = 10/12.5/15 m/s). For the same reason, the feed rate was fixed at f = 6 mm/min. As PCD tools do not have a protective chamber as it is common with PcBN tools, only the flank face was ground.

2.2.2. Brushing process

In addition to the grinding process, PcBN tools were rounded using a brushing process to stabilize the cutting edge. An in-house development, based on an industrial robot, was employed for this purpose, ensuring reproducible brushing (Rehe, 2015). In this process, the tool is moved into the diamond brushes using an industrial robot and is thus brushed in a defined orientation. The brushing speed v_b was varied in 3 steps (v_b = 11.8/21.6/31.4 m/s). Tools were brushed that have been ground at both cutting speeds.

2.3. Raman spectroscopy

Raman spectra were obtained using a Bruker Santerra II spectrometer on an Olympus BX51 microscope with a green laser (λ = 532 nm) and a 100× magnification objective lens. The measurements followed the settings from Table 1.

Table 1. Measurement settings for Raman spectroscopy

Parameter	PCD	PcBN
Laserpower PL	5 mW	10 mW
Accumulation time t	15 s	20 s
Coaddition	2x

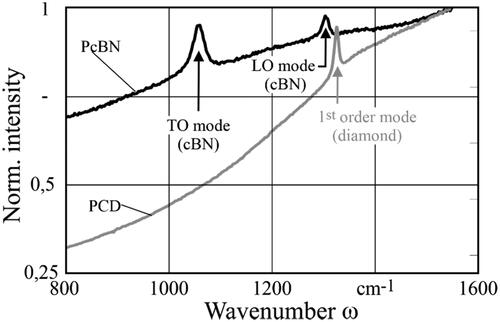
For the PcBN tools machined by grinding, 30 measurements were performed on the chamfer near the cutting edge. The first 3 measurements were taken directly at the transition to the cutting edge with a distance of 2 µm parallel to the cutting edge, the other measurements with a distance of 2 µm from each other on the chamfer (Figure 1). The same procedure was also carried out for the PCD tools machined by grinding. Here, however, the machined flank and the unmachined rake face were measured 30 times for each grinding process parameter variation. After brushing, the measurements were repeated as shown in Figure 1. The measuring point diameter d_M was approx. 2 µm. The peak positions in the diamond (ω ≈ 1,330 cm⁻¹) and the cBN (ω ≈ 1305 cm⁻¹) spectra were then determined using the Fityk program after adjusting the background using a polynomial baseline correction (Wojdyr, 2010).

Figure 1. Measuring positions Raman spectroscopy.

3. Results

3.1. Raman-Spectroscopy

3.1.1. Ground and brushed tools

After the machining of PCD tools, Raman measurements were performed on the rake and flank surfaces as described and the spectra were evaluated accordingly. The spectra of the two cutting materials are shown as an example in Figure 2.

Figure 2. Raman-spectra of cBN and diamond.

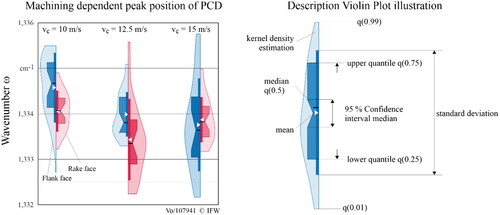
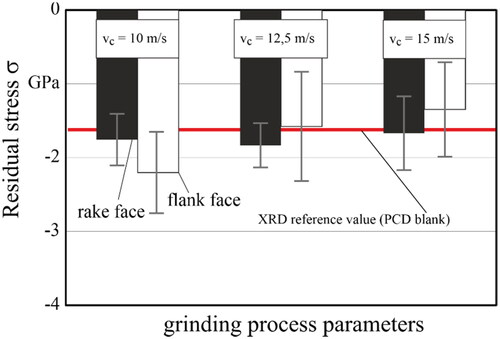
The results of the measurements described in Section 2.2 are shown in Figure 3 as violin plots. Violin plots are used because of the high spread of the measurements. The explanation of a vioin plot is shown on the right in the same figure. The peak position on the non-machined rake face shows a change to lower wavenumbers at v_c = 12.5 m/s in relation to the mean value, with a high standard deviation at the same time. At a higher cutting speed, however, the shift normalizes again towards a wavenumber close to ω = 1,334 cm⁻¹. If, however, the flank face finished by grinding is considered, there is a clear trend from a peak position significantly at higher wavenumbers than the peak position on the rake face at v_c = 10 m/s, moving towards a comparable peak position at v_c = 15 m/s. If the cutting speed is increased further, the mean value tends to shift further towards lower wavenumbers, while at the same time the standard deviation increases sharply and thus the trend can only be estimated.

Figure 3. Influence of grinding on PCD peak position.

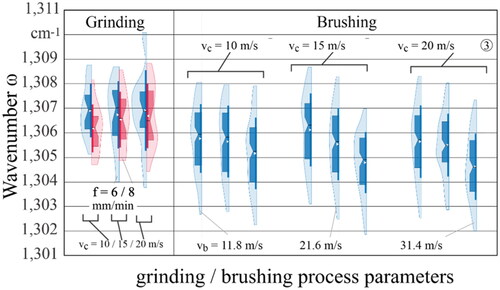
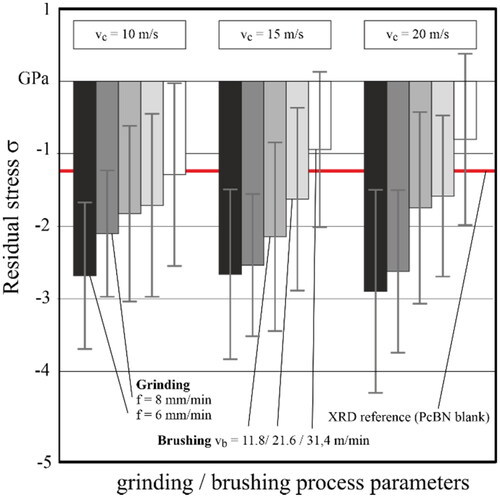
After grinding, 30 measurements were carried out on the ground chamfer of the PcBN tools at different cutting speeds and feed rates as described. If the mean value in Figure 4 is considered, there is no visible influence with regard to the cutting speed. The peak position of the LO (transversal optical) mode remains in the range between ω = 1,306.7 and 1,307 cm⁻¹. However, increasing the feed rate from f = 6 to 8 mm/min shows a trend towards lower wavenumbers across all cutting speeds.

Figure 4. Influence of grinding on cBN peak position LO-Mode.

The tools, which were previously produced with a feed rate of f = 6 mm/min, are now machined at a low brushing speed of v_b = 11.8 m/s, which shows a further shift of the peak position to lower wavenumbers. A trend with regard to the initial grinding processing is not recognizable. With increasing brushing speed to v_b = 21.6 m/s and finally to 31.4 m/s the trend of shifting the peak position to lower wavenumbers continues. The peak thus shifts to a mean value between ω = 1,304.6 and 1,305.2 cm⁻¹. The variation range of the determined peak positions follows this trend. It should be noted, however, that the mean values at the different brushing speeds are within the standard deviations of the other brushing speeds. Only at high brushing speeds a clear difference to the unbrushed tool can be seen in Figure 4 on the right, where the mean value lies outside the standard deviation of the unbrushed tools.

In order to establish a direct relationship between the peak shifts determined and the residual stresses causing them, the cutting materials were exposed to a load stress. This was done with the use of a 4-point bending device as shown schematically in Figure 5. The load stresses on the surface were determined using XRD (X-ray diffraction). In parallel, the Raman spectrum was recorded and the peak position of the LO mode of cBN and the first mode of diamond were determined as described above. If the peak positions are plotted over the measured load stresses, the correlation shown in Figure 5 emerges. Compressive load stresses at the surface lead to a shift to higher wavenumbers.

Figure 5. Setup and determination of the conversion factors.

Based on the slope of the linear interpolation, a conversion factor C_PcBN for PcBN and C_PCD for PCD can be determined. Furthermore, a stress-free wavenumber ω₀ can be determined for both cutting materials by extrapolation, in other words, a wavenumber ω that would be present in an ideally stress-free cutting material. If the shift of the peak and thus the slope of the linear regression is compared with literature values from Catledge et al., an almost parallel course is shown (Catledge et al., 1996). The deviation can be explained both by measurement-device deviations and by a deviating peak detection by means of Gauss-fit. The determined conversion factors and extrapolated peak positions of a stress-free state are shown in Table 2.

Table 2. Conversion parameters C and stress-free wavenumber ω₀.

Cutting material	Conversion factor C	stress-free wavenumber ω0
PcBN	1.14 GPa/cm^−1	1,303.7 cm^−1
PCD	1.36 GPa/cm^−1	1,331.6 cm^−1

A detailed explanation of the procedure for determining the conversion factor and a detailed comparison with existing conversion factors from the literature can be found in (Breidenstein & Vogel, 2024)

4. Discussion

The analysis of high hardness cutting materials by Raman spectroscopy has been able to show influences of the tool preparation processes grinding and brushing on peakpositions. As shown in the previous evaluation of the results, clear tendencies of both the preparation process and most of the process parameters are recognizable. However, this influence is covered by the high standard deviation of the determined peak positions. Each stress value σ in the cutting material can be assigned to a peak position ω_s in the Raman spectrum. Using the stress-free peak position ω₀ and the stress-dependent conversion factor C, the resulting residual stress value σ_RS can be calculated according to the following Equations (1)(1) $${\sigma }_{\mathit{\text{RS}}}=\frac{{\Delta \omega }_G}{C}$$(1) and (2)(2) $${\Delta \omega }_G={\omega }_s-{\omega }_0$$(2) adapted from (Catledge et al., 1996): (1) $${\sigma }_{\mathit{\text{RS}}}=\frac{{\Delta \omega }_G}{C}$$(1) (2) $${\Delta \omega }_G={\omega }_s-{\omega }_0$$(2)

If the averaged peak positions from the previously performed measurements are converted into absolute residual stress values using the conversion factors, the residual stress values for the ground PcBN tools in Figure 6 are obtained. As it can already be seen directly from the peak positions, there is no clear influence of the cutting speed when grinding PcBN. However, at all cutting speeds, strong compressive residual stresses between σ_RS = −2.6 and −2.9 GPa are present after machining. The reason for this is that a higher feed rate leads to an increase in the single grain chip thickness, and this, in turn, increases the temperature in the contact zone due to friction. This increased thermal effect induced by friction overlays the mechanical effect of the grinding process, which essentially causes compressive residual stresses.

Figure 6. Residual stresses converted from Raman spectra after grinding and brushing PcBN.

If the tools that were ground at a low feed rate and therefore have high initial compressive residual stresses are also machined using the brushing process, a decrease in compressive residual stresses is already seen at low brushing speeds (v_b = 11.8 m/s) at all initial cutting speeds. If the brushing speed is increased to v_b = 21.6 or 31.4 m/s, this trend continues and leads to residual stresses between σ_RS = −0.8 and −1.3 GPa. This is almost one third of the previously present compressive residual stresses. Originally, the mechanical process of brushing was expected to increase compressive residual stresses as it is kinematically similar to abrasive blasting, which has been shown to increase the residual stress state in PVD coatings in previous studies (Breidenstein et al., 2022). However, it should be noted that brushing is machining with a bonded grain and blasting with a non-bonded grain. This leads to cutting material with high compressive residual stresses being removed near the surfaces and unaffected cutting material being exposed. Raman measurements on samples prepared by manual polishing for the bending test and thus only minimally influenced by the preparation process show peak positions in the range ω_s = 1,305.1 ± 0.34 cm⁻¹ and residual stresses of σ_RS = −1.35 GPa determined by XRD. The subsurface properties of the brushed tools thus converge with the unprepared cutting material. Furthermore, it can be stated that the brushing process cannot mechanically induce any further compressive residual stresses into the cutting material. This can be explained by the high hardness of cBN, which does not allow any plastic deformation caused by the brushing process.

Considering the ground PCD tools and using the peak positions determined from Figure 3, absolute residual stress values were obtained by applying the conversion factor C and shown in Figure 7. As already seen in the peak positions in Figure 7, grinding of the PCD tools does not influence the residual stress state on the rake face. Regardless of the cutting speed, measurements near the cutting edge show no influence of the cutting speed. However, if the machined flank face is considered, the converted residual stresses show a dependency. With increasing cutting speed v_c, the compressive residual stresses σ decrease. The reason for this can be found in the increasing temperature in the contact zone between the PCD tool and the diamond grinding wheel at increased cutting speed, especially since the removal mechanism in grinding PCD tools is fundamentally related to the thermally induced diamond graphitization (Schindler, 2015; Schindler et al., 2016). The graphite formed was completely removed mechanically by the grinding wheel and could not be detected in the Raman spectrum.

Figure 7. Mean residual stresses converted from Raman spectra after grinding PCD.

In brief, the mechanical preparation methods involving grinding and brushing of PcBN tools show a trend towards influencing the peak positions, which correlate with the induced compressive residual stress state. Thermal influences encountered during grinding tend to reduce the compressive residual stresses within the machined area. On the other hand, the brushing process, being entirely mechanical, serves to remove stressed material without significantly reinducing compressive residual stresses. Comparisons between these transformed residual stresses and the initial residual stress states determined by XRD suggest that the resultant residual stress values are plausible.

5. Conclusion

The investigations have shown that the cutting-edge preparation processes of grinding and brushing have an influence on peak positions within the Raman spectrum and thus on the residual stress state. When considering both the peak shifts in the spectrum and the converted residual stress states, it is apparent that the grinding process increases the compressive residual stresses in the PcBN tools compared to the initial state of the unprocessed and non-separated cutting material blank. However, an influence of the cutting speed on the Raman spectrum and thus on the residual stresses could not be demonstrated in the context of this investigation. Nevertheless, when considering the mechanical process of brushing, it is evident that there is a decrease in the resulting compressive residual stresses, which can be explained removing material from the tool surface, thus exposing material unaffected by the grinding process.

The machining of PCD by grinding further shows that the cutting speed tends to have an influence on the residual stresses on the machined flank face, especially when compared with the non-machined rake face. The reduced compressive residual stresses at higher cutting speeds v_c can be explained by thermal effects during machining. Lower cutting speeds increase the compressive residual stresses compared to the non-machined rake face. This suggests that a variation in cutting speed allows for the targeted adjustment of the residual stress state, which can be used to influence the tool life of PcBN and PCD tools.

The aim of further research is to produce tools with significantly different compressive residual stress states and to use these in the machining of hardened 100Cr6 and AlSi10Mg to demonstrate the influence of residual stresses on the wear behaviour of cutting tools.

Acknowledgments

The authors would like to thank the German Research Foundation (DFG) for funding research project BR 2967/22-1 “Influence of preparation-induced residual stresses in the cutting edge of cutting tools on the wear behavior of extremely hard cutting materials.”

Disclosure statement

No potential conflict of interest was reported by the authors.