Abstract
The HIV-1 reverse transcriptase (RT) inhibitory activity of benzyl/benzoylpyridinones is modeled with molecular features identified in combinatorial protocol in multiple linear regression (CP-MLR) and genetic algorithm (GA). Among the features, nDB and LogP are found to be the most influential descriptors to modulate the activity. Although the coefficient of nDB suggested in favor of benzylpyridinones skeleton, the coefficient of LogP suggested the favorability of hydrophilic nature in compounds for better activity. The partial least squares analysis of the descriptors common to CP-MLR and GA has displayed their predictivity over the total descriptors identified in both the approaches. The back-propagation artificial neural networks model from the five most significant common descriptors (nDB, T(O..O), MATS8e, LogP, and BELp4) has explained 93.2% variance in the HIV-1 RT activity of the training set compounds and showed a test set r2 of 0.89. The results suggest that the descriptors have the ability to identify the patterns in the compounds to predict potential analogues.
Introduction
HIV-1 reverse transcriptase (HIV-1 RT) is a key enzyme in the progression of infection by HIV retrovirus. It has been widely explored as a drug targetCitation1,Citation2. Two classes of compounds have gained attention as potential inhibitors of this enzyme. They are termed as nucleoside/nucleotide reverse transcriptase inhibitors (NRTIs) and non-nucleoside reverse transcriptase inhibitors (NNRTIs)Citation3. Between them, NNRTIs have received a great deal of attention because of low toxicity and favorable pharmacokinetic propertiesCitation4,Citation5. The low toxicity of NNRTIs is attributed to their interaction with an allosteric site on the enzymeCitation6. Since the introduction of NNRTIs, >30 different structure classes are shown to bind with the allosteric site of the enzyme and elicit the desired responseCitation7. Also, some of these compounds have been put to clinical useCitation8. The flexibility of HIV-1 RT in accommodating diverse NNRTIs has been subjugated by the development of quick resistance to different compoundsCitation9,Citation10. This has necessitated continued efforts to discover new ways to modify the chemical space of compounds and/or alternative targets for the HIV chemotherapy.
In medicinal chemistry, structure–activity relationships pave way to notional insight of the activity (or receptor space) against the chemical space. The application of quantification protocols to this paradigm fine tunes the notional insight of the activity in terms of properties of the chemical space and gives an opportunity to understand and modulate the variations around the scaffold on a broad canvas of diverse structures. Among the different NNRTIs, pyridinone derivativesCitation11 represent simple structure space. They bear some structure space resemblance with the 7-chloro-1-(2,6-difluorophenyl)-1H,3H-thiazolo[3,4-a] benzimidazole (7-Cl-TBZ) and thiazolidinones ().
Figure 1. (A) 7-Chloro-1-(2,6-difluorophenyl)-1H,3H-thiazolo[3,4-a] benzimidazole (7-Cl-TBZ), (B) 2,3-diaryl-thiazolidin-4-ones, and (C) 4-benzyl/benzoyl-pyridin-2-ones benzylpyridinones.
![Figure 1. (A) 7-Chloro-1-(2,6-difluorophenyl)-1H,3H-thiazolo[3,4-a] benzimidazole (7-Cl-TBZ), (B) 2,3-diaryl-thiazolidin-4-ones, and (C) 4-benzyl/benzoyl-pyridin-2-ones benzylpyridinones.](/cms/asset/ac582be8-514e-4a23-a3ff-dc77a66117a9/ienz_a_548328_f0001_b.gif)
Since all the NNRTIs are reported to interact with the HIV-1 RT allosteric site, it is of interest to investigate the important structural features of pyridinones for the HIV-1 RT inhibitory activity. Earlier, we had investigated the quantitative structure–activity relationships (QSARs) of HIV-1 RT inhibitory activity of 2,3-diaryl thiazolidin-4-one class of NNRTIs with different physicochemical and topological indicesCitation12–14. These studies while confirming the importance of compounds attaining “butterfly-like” conformation for the activity also indicated the prospects of 3-heteroaryl moiety (of thiazolidinones) in modulating the activity. Also, the QSAR of HIV-1 RT inhibitory activity of 2-arylsulfonyl-6-substituted benzonitriles was investigated using Fujita-Ban and Hansch approachesCitation15. This has led to suggest the importance of sulfonyl and amine moieties for the activity. In this milieu to explore the scope of chemical space of 4-benzyl/benzoyl-3-dimethylaminopyridin-2(1H)-ones (; )Citation16 as HIV-1 RT inhibitors, an attempt has made to rationalize their activity with 0D-2D descriptors from DRAGON softwareCitation17.
Table 1. Observed and predicted HIV-1 RT inhibitory activity 4-benzyl/benzoylpyridin-2-ones ().
Feature selection procedures are essential components of modeling studies wherever the number of descriptors involved is very large. It is known in modeling studies that different feature selection approaches show different “bias” in the selection of features from a pool of descriptors to model the phenomenon. Earlier, a hybrid-genetic algorithm (GA)-based descriptor optimization was used in QSAR to model the HIV protease inhibition of tipranavir analogsCitation18. Apart from this, weights and biases of neural network were also used in developing highly significant QSAR models from descriptor poolsCitation19. Additionally, the descriptors consensus to different feature selection approaches may be more promising to pursue in modeling and lead optimization studies. With this in view, two feature selection approaches namely combinatorial protocol in multiple linear regression (CP-MLR) and GA have been used to identify the descriptors for modeling the activity of 4-benzyl/benzoyl-3-dimethylaminopyridin-2(1H)-ones. In this, CP-MLR is a filter-based feature selection procedureCitation20–22. It involves a systematic search for the identification of influential features to model the activity. In contrast to CP-MLR, the GA is a stochastic procedureCitation23. Being multi-model approaches, both CP-MLR and GA identify different structural features across molecular frame to explain the activity and provide a holistic view to the structure–activity relationsCitation24. As both these approaches involve different search algorithms, the consensus features evolved from them may be highly significant to model the activity. Furthermore, in QSAR studies, artificial neural networks (ANN) have a special place to develop highly significant predictive modelsCitation25–28. The consensus features of the CP-MLR and GA may serve as good input variables for the ANN to develop predictive models. The results are presented below.
Materials and methods
Chemical structure database and biological activity
The study has involved a series of 55 4-benzyl/benzoyl-pyridin-2-ones () from the literature (hereafter referred as benzylpyridinones) along with their anti-HIV activity (concentration to achieve 50% inhibition (IC50) of wild-type HIV-1 RT in LAI cell line) ()Citation16. For modeling study, the activity has been expressed in the form of logarithm of inverse of inhibitory concentration (−logIC50). Adopting the standard procedure, the structure files of the compounds were generated in the ChemDrawCitation29. In DRAGON softwareCitation17, these structures have resulted in 475 descriptors representing the 0D to 2D characteristics of the molecules. Here, all those descriptors showing a correlation of less than 0.1 with the dependent variable (descriptor vs. activity r < 0.1) and descriptor–descriptor intercorrelation ≥0.9 (r ≥ 0.9) were excluded. It has resulted in 99 descriptors for the investigation. Apart from these, LogP of compounds calculated from the Chem3D UltraCitation29 is also incorporated as a descriptor. This makes total descriptors used in analysis as 100. Before proceeding with model development, using the descriptors in single linkage hierarchical cluster analysisCitation30, all 55 compounds were partitioned into training (35 compounds) and test (20 compounds) sets. Only the training set compounds were used for the development of models.
Descriptors consensus to different feature selection approaches may be more promising to pursue in modeling and lead optimization studies. With this view, two different feature selection approaches namely CP-MLR (a filter directed approach)Citation20 and GA (a stochastic approach)Citation23 have been separately used to identify potential features to model the HIV-1 RT inhibitory activity of benzylpyridinones. The descriptors surfaced from these feature selection approaches were pooled together and utilized in partial least squares (PLS) analysisCitation31,Citation32 to develop single-window structure–activity models. In PLS, the normalized regression coefficients of descriptors provide estimate of each descriptor’s fraction contribution to the explained activity. Hence, it is used to rank the descriptors’ significance in the PLS model. The high-ranked descriptors of PLS analysis were used in back-propagation ANNCitation25–28 to develop the predictive models. Since 35 compounds were considered for training the QSAR models, equations containing up to five descriptors were explored (ratio of number of molecules to number of descriptors is >1:5). The computational procedure is briefly described.
Feature selections
CP-MLR
CP-MLR is a filter-based feature selection procedureCitation20–22. The thrust of this procedure is in the embedded “filters”. Briefly, filter-1 seeds the variables by limiting inter-parameter correlations to predefined level (default value 0.3); filter-2 controls the seeds through t values of variables’ coefficients in regression (default threshold value ≥2.0); filter-3 provides comparability of equations of seeds with different numbers of variables in terms of square-root of adjusted multiple correlation coefficient of regression equation, r-bar (default value 0.74); and filter-4 estimates the consistency of the equation in terms of cross-validated r2 or Q2 with leave-one-out (LOO) cross-validation as a default option (default threshold value 0.3 ≤ Q2 ≤ 1.0). In CP-MLR, the filters operate in tandem and process the seeds (a string of variables as a bundle) leading to their selection or rejection. Since the principle of combinatorics work in the formation of seeds, the number of seeds result from a set of variables are much more than the individual variables participating in their (seeds) formation. The limits of number of descriptors per seed are the model search perimeter. The models were reassessed for the chance correlations through 100 simulation runs with the randomized biological responseCitation12–14,Citation33 and were also validated with test set compounds.
The selection in CP-MLR proceeded with an initial threshold of filter-1 as 0.3 and subsequently liberated it to 0.79 to boost the formation of different seeds. Considering the degree of correlation of individual descriptors of the dataset with the activity, the search was started with two-variable seeds and an initial filter-3 value of 0.71. The information-rich descriptors were collected by successively incrementing the number of variables per seed as well as the threshold of filter-3 to the optimum r-bar value of the preceding generation.
Genetic algorithm
The GA variable subset selection routine as implemented in MOBY DIGSCitation23,Citation34 was used for the selection of GA features. It has proceeded with an initial population of 100 solutions (chromosomes) with maximum allowed variables in a solution as five. The fitness for each chromosome was calculated based on LOO cross-validation (Q2). The reproduction/mutation trade-off (T) value was set to 0.5. Based on the T value, the crossover and mutation values of GA were automatically fixed in situ in the computation. The optimum solutions were identified at the end of 100 generations of GA evolution process (selection, crossover and mutation).
Back-propagation ANN
The training set (35 compounds) of CP-MLR/GA analysis was considered as such for the training set of ANN. The test set (20 compounds) of CP-MLR/GA analysis was randomly divided into ANNs validation (10 compounds) and test (10 compounds) sets. The compounds from the training set were used for the model generation whereas the compounds from the validation set were used to stop the overtraining of network. And the compounds from the test set were used to verify the predictivity of the generated model. Coinciding with the number of descriptors in individual feature selection models, for ANN also five descriptors were considered in the input. Before training the networks, the input and output values were normalized with autoscaling of all data. The initial weights were selected randomly between (−0.3) and (0.3). In a standard evaluation procedure with different numbers of hidden layer nodes, the optimum number of nodes for hidden layer was found as fourCitation25–28,Citation35. The optimization of number of nodes necessary for hidden layer has proceeded by starting with two hidden nodes followed by training the network for best possible output (minimum root mean square error of prediction as a fitness function for training and validation sets). The process has been repeated with incremented hidden layer nodes followed by training the network for assessing output. Using this trial-and-error procedure, the optimum number of hidden nodes necessary for minimizing the error in output is estimated as four. The goal of training the network is to minimize the output errors by changing the weights between the layers. Equation 1 gives the changes in the values of the weights in the network in the optimization of the output.
In this, Δwij is the change in the weight factor for each network node, α is the momentum factor, and F is a weight update function, which indicates how weights are changed during the learning process. The weights of hidden layer were optimized using the second derivative optimization method namely Levenberg–Marquardt algorithmCitation36,Citation37.
Levenberg–Marquardt algorithm
In this algorithm, the update function, Fn, is calculated using equations.
where g is gradient and J is the Jacobian matrix that contains first derivatives of the network errors with respect to the weights, and e is a vector of network errors. The parameter µ is multiplied by some factor (λ) whenever a step would result in an increased e and when a step reduces e, µ is divided by λ.
Statistical parameters
In training the network, the over fitting of data was controlled by comparing the root-mean-square errors (RMSEs) of training and validation sets. It measures the goodness of the output and is useful for the comparison of the target values. The training of the network for the prediction of target value was stopped when the RMSE of the validation set began to increase while that of training set continues to decrease. The goodness-of-fit of activity of the test set compounds was used to further validate the developed models. The predictive ability of the constructed models were assessed using different statistical measures namely, the training, validation and test sets’ correlation coefficients (r2), and corresponding root mean square error of prediction (RMSEP), relative standard error of prediction (RSEP) and mean absolute error (MAE) values. They are calculated using the following equations.
where yobs is the observed activity, ymean is the mean of observed activity and ypred is the predicted activity of the compound in the sample, and n is the number of samples in the concerned set. The ANN computations were carried out using the MATLAB 7.6 for windowsCitation38.
Results and discussion
In CP-MLR, at the end of a search, 18 descriptors () were identified as significant ones to model the HIV-1 RT inhibitory activity of benzylpyridinones (). They are constituent features of several overlapping five-parameter models surfaced for the activity of the compounds (). Many of these models have explained >78% variance (r2 ≥ 0.78) in the activity of training set compounds. They have also accounted for >50% variance (r2t ≥ 0.50) in the activity of test set compounds. Equation 9 is a regression model from among them.
Table 2. Information content of descriptors identified from CP-MLR and GA approaches.
Table 3. Five parameter models for HIV-1 RT inhibitory activity of 4-benzyl/benzoylpyridin-2-ones () from CP-MLR and GA along with statistics.
In this and in all other regression equations, n is the number of compounds, r2 is the squared correlation coefficient, Q2 and Q2G5 are cross-validated R2 from LOO and leave group of five out, respectively, s is the standard error of the estimate and F is the F-ratio between the variances of calculated and observed activities. The values given in the parentheses are the standard errors of the regression coefficients. In the randomization study involving 100 simulations per model, none of the identified models has shown any chance correlation. Furthermore, the models were validated through a test set of 20 analogues listed in . The predictions of all the test set compounds are within the reasonable limits of their actual values (). Equation 9s is a derivative of Equation 9, derived using the scaled X (XS) in place of X as shown.
where XMIN and XMAX are minimum and maximum values of the training set feature X. This transforms the descriptor values between “0” and “1”, and provides an opportunity for direct comparison of the regression coefficients within the equation. The scaled descriptors are identified with subscript “S” suffixed to the abbreviated names.
Furthermore, the analysis of molecular features in GA has resulted in 14 descriptors as important ones to explain the activity of the compounds (). They are part of several overlapping five-descriptor models () emerged from this approach. These models have explained >83% variance (r2 ≥ 0.83) in the activity of training set compounds and showed test set r2 values ≥0.50. Equation 11 is one among them. Equation 11s is a variant of Equation 11 derived using scaled descriptors.
The activity predictions from this and other GA equations are within the acceptable limits of their actual values (). Jointly, the QSAR equations from CP-MLR and GA approaches have led to 21 descriptors as information rich features to model the activity (). They have come from six descriptor classes namely, constitutional, topological, BCUT, Galvez, 2D-Autocorrelations and atom-centered fragments. The physical meaning of these descriptors in terms of structural features is described in . They provide composite property map of the compounds for the HIV-1 RT inhibitory activity. Several of these descriptors have shown their significance in the QSAR models of HIV-1 RT inhibitory activity of thiazolidin-4-onesCitation12–14. From this list of descriptors, LogP and nDB are found to be the most influential to modulate the activity of these compounds. Among the 21 descriptors, 11 are common to both CP-MLR and GA approaches. shows some CP-MLR and GA models emerged from the descriptors for the activity. Also, both feature selection approaches have shared some common models between them ().
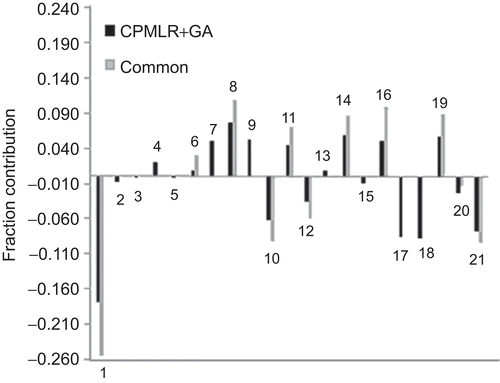
The 21 descriptors of CP-MLR and GA, and the 11 common descriptors of both these approaches are further analyzed in PLS to facilitate the development of single-window structure–activity models comprising these features. For PLS analysis, the descriptors have been autoscaled (zero mean and unit SD) to give each one of them equal weight in the study. In the cross-validation procedure of the PLS analysisCitation31,Citation32, four components are found to be the optimum to explain the activity of the compounds. The PLS model from the 21 descriptors of CP-MLR and GA has explained 89.0% variance (r2 = 0.890, Q2 = 0.848, s = 0.515, F = 60.91) in the HIV-1 RT inhibitory activity of the training set compounds and showed a test set r2 value 0.569. On the other hand, the PLS model from the 11 common descriptors of CP-MLR and GA has explained 88.8% variance (r2 = 0.888, Q2 = 0.834, s = 0.520, F = 59.46) in the HIV-1 RT inhibitory activity of the training set compounds and showed 0.607 as test set r2 value. As the PLS, models emerged from 21 and 11 descriptors have shown almost same level of statistical significance, under principle of parsimony the later may be regarded as better model to explain the activity. The MLR-like PLS coefficients of these two feature sets are shown in . The plot of fraction contribution of these descriptors to the activity is shown in . In both PLS equations, the descriptors nDB, LogP, T(O..O), MATS8e and BELp4 are found to be significant to modulate the activity. Here, nDB accounts for the non-conjugate double bonds, including functional groups, in the molecule. In these compounds, they are due to carbonyl and thionyl functions. In a majority of the analogues of this dataset, it can be attributed to the variation in the bridge carbon between A and B rings (). In regression as well as PLS models, the coefficient of nDB suggested in favor of lesser number (or absence) of these double bonds for better activity. It may be viewed as that between A and B rings, a CH2 bridge is more favorable than a carbonyl bridge () for the activity. Also in all models, the sign of regression coefficient LogP is negative. Even though LogP is a parameter for hydrophobicity, it suggests the molecular polarity as well. In these analogues, the negative coefficient of LogP may be viewed as favorability of hydrophilic or polar compounds for better activity. The earlier modeling study on these analogues has suggested that –NH–CO-portion of pyridinone moiety offers polar interactions with the receptorCitation16,Citation39. This may be satisfying one polar interaction site of the enzyme. The descriptor T(O..O), sum of topological distances between oxygen atoms, has participated in the models with positive regression coefficient. This suggested that in these compounds increasing separation between oxygen atoms as well as their number favor the activity. This may be viewed as the importance of electronegative oxygen in different parts of the structure for the activity. Also, the 2D-autocorrelation descriptor MATS8e with positive regression coefficient suggested the importance of lag 8 autocorrelation weighted by atomic electronegativities for the activity. In these analogues, a small value for BELp4, the 4th lowest eigenvalue of Burden matrix weighted by atomic polarizabilities, would be beneficial for the activity. Galvez topological charge index of orders 4 and 6 (JGI4, GGI4, and GGI6) and Geary autocorrelation of lag 4 weighted by atomic polarizabilities (GATS4p) are the other charge and polarizability indices showed significance in the models ( and ). All these descriptors signify the importance of specific path lengths (in the molecules) weighted by atomic charges and polarizabilities for the activity.
Table 4. MLR-like PLS models from the combined as well as common descriptors of CP-MLR and GA approaches () for the HIV-1 RT inhibitory activity (−logIC50) of 4-benzyl/benzoylpyridin-2-ones ().
Figure 2. Plots of fraction contribution of MLR-like PLS coefficients (normalized) of the combined and common descriptors of CP-MLR and GA for the HIV-1 RT inhibitory activity of 4-benzyl/benzoyl-pyridin-2-ones; the numbers on the bars refer to the descriptors’ numbers ().
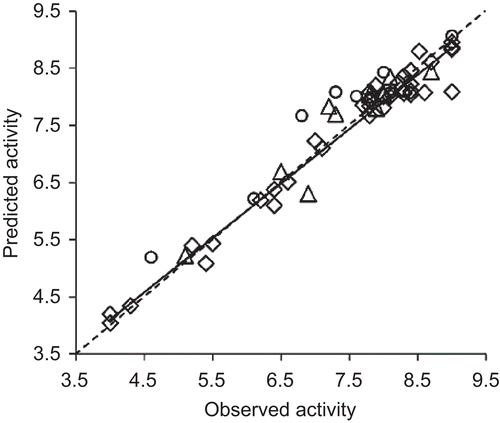
ANN is a powerful tool to identify the patterns in the data. Also, ANN models are difficult to interpret due to the complex computations embedded in the neural networks in deriving the models. In this background, application of well-selected features to ANN input leads to meaningful outputs in terms of rationale behind the input variablesCitation40. In this scenario, the features from the selection approaches suggest the direction of modification of the chemical space for the activity modulation. Since the number of descriptors in each model of CP-MLR and GA approaches is five, for ANN also five descriptors are considered as input features. In PLS analysis, among the 11 common features of CP-MLR and GA, nDB, T(O..O), BELp4, MATS8e and LogP are more significant ones. Hence, they have been used as input for the development of BP-ANN model for the activity. The architecture and network parameters of ANN are shown in . In model development, the over fitting of training set has been controlled by the RMSE values of training and test set compounds. The training of the network for the prediction of target value (−logEC50) has been stopped when the RMSE of the validation set has began to increase while that of training set continues to decrease. The developed model has been further evaluated for the goodness-of-fit with the test set. The statistics of ANN model are shown in . In ANN, these descriptors have well explained the HIV-1 RT activity of the compounds (training, validation and test sets r2 are 0.932, 0.925, and 0. 890, respectively) (). The plots of observed versus ANN predicted activities are shown in . Attempts are also made to develop ANN model with 11 common features of CP-MLR and GA as input features. This has resulted in excellent predictions for training set but showed relatively less significant predictions in case of validation and test sets (training, validation and test sets r2 are 0.989, 0.774, and 0.681, respectively). There may be several reasons for this kind of behavior: one is too many input variables for a relatively small dataset. However, in view of the magnitude of test set r2 value (0.681) the 11 descriptors ANN model still qualifies as predictive model. The results clearly suggested that these descriptors have the ability to identify the patterns in the data and predict the activity of potential analogues.
Table 5. ANN Architecture and goodness of fit of HIV-1 RT inhibitory activity of 4-benzyl/benzoylpyridin-2-ones () in training, validation and test sets with five most significant features from PLS in BP-ANN model*.
Figure 3. The plots of observed versus predicted activities of 4-benzyl/benzoyl-pyridin-2-ones’ training (open diamonds), validation (open citrcles) and test (open triangles) sets from BP-ANN. The solid line indicates the best fit. The dashed line passing through the origin, making an angle of 45° with the axis, bisects the plot area.
Conclusions
The feature selection approaches CP-MLR and GA have led to the identification of 21 descriptors to model the HIV-1 RT inhibitory activity of benzylpyridinones. Several of these descriptors have shown significance in explaining the HIV-1 RT inhibitory activity of thiazolidin-4-ones as well. Among the 21 descriptors identified in this exploration, 11 are common to both CP-MLR and GA approaches. Of all the descriptors, LogP and nDB are found to be the most influential to modulate the activity of the benzylpyridinones. In regression as well as PLS models the coefficient of nDB suggested in favor of a CH2 bridge in between A and B rings of these analogues () for the activity. The regression coefficient of LogP suggested the favorability of hydrophilic or polar compounds for better activity. In BP-ANN, the five most significant descriptors of PLS analysis (nDB, T(O..O), MATS8e, LogP and BELp4) have explained 93.2% variance in the HIV-1 RT activity of the training set compounds and showed a test set r2 of 0.890. These results suggest that the descriptors emerged from this study have the ability to identify the patterns in the compounds and can predict the activity of potential analogues.
Supplementary Material
Download PDF (213.3 KB)Acknowledgement
One of the authors (S.D.) thanks CSIR, New Delhi, India, for the financial support in the form of Senior Research Fellowship. CDRI Communication No.7902.
Declaration of interest
The authors report no conflicts of interest in this work.
References
- Pauwels R. New non-nucleoside reverse transcriptase inhibitors (NNRTIs) in development for the treatment of HIV infections. Curr Opin Pharmacol 2004;4:437–446.
- Clercq ED. The design of drugs for HIV and HCV. Nat Rev Drug Discov 2007;6:1001–1018.
- Safadi YE, Boudou VV, Marquet R. HIV-1 reverse transcriptase inhibitors. Appl Microbiol Biotechnol 2007;75:723–737.
- Clercq ED. Non-nucleoside reverse transcriptase inhibitors (NNRTIs): past, present and future. Chem Biodivers 2004;1:44–64.
- Prajapati DG, Ramajayam R, Yadav MR, Giridhar R. The search for potent, small molecule NNRTIs: A review. Bioorg Med Chem 2009;17:5744–5762.
- Esnouf R, Ren J, Ross C, Jones Y, Stammers D, Stuart D. Mechanism of inhibition of HIV-1 reverse transcriptase by non-nucleoside inhibitors. Nat Struct Biol 1995;2:303–308.
- Ragno R, Frasca S, Manetti F, Brizzi A, Massa S. HIV-reverse transcriptase inhibition: inclusion of ligand-induced fit by cross-docking studies. J Med Chem 2005;48:200–212.
- Clercq ED. Emerging antiHIV drugs. Expert Opin Emerg Drugs 2005;10: 241–274.
- Buckheit RW, Fliakas-Boltz V, Yeagy-Bargo S, Weislow O, Mayers DL, Boyer PL, Hughes SH, Pan BC, Chu SH, Bader JP. Resistance to 1-[(2-hydroxyethoxy)methyl]-6-(phenylthio)thymine derivatives is generated by mutations at multiple sites in the HIV-1 reverse transcriptase. Virology 1995;210:186–193.
- Richman D, Shih CK, Lowy I, Rose J, Prodanovich P, Goff S, Griffin J. Human immunodeficiency virus type 1 mutants resistant to nonnucleoside inhibitors of reverse transcriptase arise in tissue culture. Proc Natl Acad Sci (USA) 1991;88:11241–11245.
- Franco JLM, Mayorga KM, Gordiano CJ, Castillo R. Pyridin-2(1H)-ones: a promising class of HIV-1 non-nucleoside reverse transcriptase inhibitors. Chem Med Chem 2007;2:1141–1147.
- Prabhakar YS, Solomon VR, Rawal RK, Gupta MK, Katti SB. CP-MLR/PLS Directed Structure–Activity Modeling of the HIV-1 RT Inhibitory Activity of 2,3-Diaryl-1,3-thiazolidin-4-ones. QSAR Comb Sci 2004;23:234–244.
- Prabhakar YS, Rawal RK, Gupta MK, Solomon VR, Katti SB. Topological descriptors in modeling the HIV inhibitory activity of 2-aryl-3-pyridyl-thiazolidin-4-ones. Comb Chem High T Scr 2005;5:431–437.
- Rawal RK, Prabhakar YS, Katti SB. Molecular surface features in modeling the HIV-1 RT inhibitory activity of 2-(2,6-disubstituted phenyl)-3-(substituted pyrimidin-2-yl)-thiazolidin-4-ones. QSAR Comb Sci 2007;26:398–406.
- Sharma BK, Kumar R, Singh P. Quantitative structure–activity relationship study of 2-arylsulfonyl-6-substituted benzonitriles as non-nucleoside reverse transcriptase inhibitors of HIV-1. J Enzyme Inhib Med Chem 2002;17:219–225.
- Benjahad A, Croisy M, Monneret C, Bisagni E, Mabire D, Coupa S et al. 4-Benzyl and 4-benzoyl-3-dimethylaminopyridin-2(1H)-ones: in vitro evaluation of new C-3-amino-substituted and C-5,6-alkyl-substituted analogues against clinically important HIV mutant strains. J Med Chem 2005;48:1948–1964.
- DRAGON software version 5.0-2005. By Todeschini R, Consonni V, Mauri A, Pavan M. Milano, Italy. http://disat.unimib.it/chm/Dragon.htm.
- Reddy AS, Kumar S, Garg R. Hybrid-genetic algorithm based descriptor optimization and QSAR models for predicting the biological activity of Tipranavir analogs for HIV protease inhibition. J Mol Graph Model 2010;28:852–862.
- Guha R, Stanton DT, Jurs PC. Interpreting computational neural network quantitative structure–activity relationship models: a detailed interpretation of the weights and biases. J Chem Inf Model 2005;45:1109–1121.
- Prabhakar YS. A combinatorial approach to the variable selection in multiple linear regression analysis of Selwood et al. data set – a case study. QSAR Comb Sci 2003;22:583–595.
- Prabhakar YS, Gupta MK, Roy N, Venkateswarlu Y. A high dimensional QSAR study on the aldose reductase inhibitory activity of some flavones: topological descriptors in modeling the activity. J Chem Inf Model 2006;46:86–92.
- Saquib M, Gupta MK, Sagar R, Prabhakar YS, Shaw AK, Kumar R, Maulik PR, Gaikwad AN, Sinha S, Srivastava AK, Chaturvedi V, Srivastava R, Srivastava BS. C-3 Alkyl/Arylalkyl-2,3-dideoxy Hex-2-enopyranosides as antitubercular agents: synthesis, biological evaluation, and QSAR study. J Med Chem 2007;50:2942–2950.
- Pavan M, Mauri A, Todeschini R. Total ranking models by the genetic algorithm variable subset selection (GA-VSS) approach for environmental priority settings. Anal Bioanal Chem 2004;380:430–444.
- Deshpande S, Gupta MK, Prabhakar YS. Multi-model environment as a rational approach for drug design: an experience with CP-MLR. IUP J Chem 2010; 3:1–33.
- Rumelhart DE, Hinton GE, Williams RJ. Learning representations by backpropagating errors. Nature, 1986;323:533–536.
- Gasteiger J, Zupan J. Neural networks in chemistry. Angew Chem Intl Ed Engl 1993;32:503–527.
- Bishop CM. Neural Networks for Pattern Recognition. Clarendon Press: Oxford, 1995. P 116–163 and 253–294.
- Graupe D. Principles of Artificial Neural Networks, 2nd ed. World Scientific Publishing Co.: Singapore; 2007. P 59–111.
- ChemDraw Ultra 6.0 and Chem 3D Ultra, Cambridge Soft Corporation, Cambridge, USA.
- SYSTAT, Version 7.0: SPSS Inc., 444 North Michigan Avenue, Chicago, IL 60611.
- Wold S. Cross validatory estimation of the number of components in factor and principal components analysis. Technometrics 1978;20:397–406.
- Stahle L, Wold S, in: Eillis GP, West WB. ggEds., Progress in Medicinal Chemistry, vol. 25, Elsevier Science Publishers, B.V. Amsterdam, 1988. P 291–338 (Chapter 6).
- So SS, Karplus M. Three-dimensional quantitative structure–activity relationships from molecular similarity matrices and genetic neural networks. 1. Method and validations. J Med Chem 1997;40:4347–4359.
- Todeschini R, Consonni V, Pavan M. MOBYDIGS software (Version 1.2) for Windows, Talete Srl, Milan, Italy, 2002. http://www.talete.mi.it/mobydigs.htm.
- Marini F, Bucci R, Magrì AL, Magrì AD. Artificial neural networks in chemometrics: History, examples and perspectives. Microchem J 2008;88:178–185.
- Marquardt DW. An algorithm for leastsquares estimation of nonlinear parameters. J Soc Ind Appl Math 1963;11:431–441.
- Hagan MT, Menhaj MB. Training Feedforward Networks with the Marquardt Algorithm. IEEE T Neural Net 1994;5:989–993.
- MATLAB, Version 7.6: <http://www.mathworks.com/products/matlab/>.
- Carlsson J, Boukharta L, Aqvist J. Combining docking, molecular dynamics and the linear interaction energy method to predict binding modes and affinities for non-nucleoside inhibitors to HIV-1 reverse transcriptase. J Med Chem 2008;51:2648–2656.
- Goodarzi M, Deshpande S, Murugesan V, Katti SB, Prabhakar YS. Is Feature Selection Essential for ANN Modeling? QSAR Comb Sci 2009; 28: 1487–1499.