Structural analysis of structurally diverse α-glucosidase inhibitors for active site feature analysis

Abstract

In the present investigation, a QSAR analysis on structurally diverse α-glucosidase inhibitors (andrographolide, chromenone, triazole derivatives) was performed and the developed models were validated by various validation methods (LMO, LOO, LSO, bootstrapping, Y-randomization and test set). The statistical parameters calculated for the models show that the developed models are statistically significant and have predicted the activities with small residual errors. The crossvalidated correlation coefficient (Q²) values obtained from different validation methods show >0.7 for both the models. Other correlations coefficient statistical parameters (R²_pred and R²_m) show that the developed models are reliable and robust. The leave-series-out (LSO) results reveal that the developed models can predict the activity of new compounds and its crossvalidated correlation coefficients’ values are comparable with the Q² values obtained from other validation methods. The descriptors contributed in the selected models are suggested that the lower/reduced polarizability on the vdW surface area of the molecules and the presence of flexible bonds allow the substituents/side chains in the molecules with free movement and with lesser stretching energy which are favourable for the α-glucosidase inhibitory activity. These results reveal that the developed models are statistically significant and can be used with other molecular modelling works for designing novel α-glucosidase inhibitors with multiple activities (HIV, diabetics, cancer, etc).

Keywords::

• α-glucosidases
• QSAR
• validation methods
• polarizability

Introduction

The glycosidase family enzymes such as glucosidases, glucotransferases, mannoses, galactosidases, etc cleave the glycosidic bond of the oligosaccharides and liberate glucose which retard the carbohydrate digestion and/or inhibit the biosynthesis of the N-linked oligosaccharides on the HIV envelope glycoproteins (gp120 and gp41) from their precursor (gp160). Biogenesis of viral coat glycoproteins depends on the host cell glycosylation machinery and a key intermediate (a mono-glucosylated N-linked oligosaccharide), which is required for chaperone recognitions to assist glycoprotein folding^1–3. The glycosylation pathway (including the transfer of the glycon precursor onto the nascent protein and the subsequent glucose trimming) is needed for processing, folding and routing of the precursor gene (Env). α-Glucosidases (EC 3.2.1.20) are involved in the synthesis and breakdown of α-linked di-, oligo-, and polysaccharides, playing a crucial role in metabolic processes such as food storage and utilization and in cellular communication through modification of the glycosylation state of proteins^4,5. The effective α-glucosidase inhibitors may serve as chemotherapeutic agents for clinical use in the treatment of diabetes, hypertension, dyslipidemia, obesity, antiviral (HIV, HCV, HBV, influenza, SARS, etc.) and cardiovascular diseases in patients with metabolic syndrome^1–7. Hence, α-glucosidase has drawn a special interest of the pharmaceutical research community because of its multiple actions.

The mechanistic, the catalytic and the pharmacological studies of the of the α-glucosidases enzyme and its inhibitors are lacking due to the structural information on α-glucosidase, which has been limited to those of a few bacterial strains only in ligand free forms. Hence, it is a difficult task to discover good lead compounds based on the structure-based inhibitors design. Literature shows that some homology modelled α-glucosidase and other glycosidase family enzymes were used to study the binding mode analysis of the inhibitors for novel molecule design^4,8–12.

Since last two years, research work on α-glucosidase inhibitors design (ligand/analogues-based drug design techniques) has been undergoing in our laboratory. The structural feature analysis of the existing α-glucosidase inhibitors may provide more insights into the interaction with α-glucosidase whose crystal structure remains unclear. Quantitative structure activity relationship (QSAR) analysis is one of the techniques used to investigate the correlation between activities, generally, the biological activity and the physicochemical properties of a set of molecules^13,14. This provides information on the feature of the ligands that needed to interact with the active site residues. Earlier, our group have performed structural analysis of some series of compounds exhibiting α-glucosidase inhibitory activity^15–18. In continuation to the earlier studies, in the present study we have performed QSAR analysis on a data set comprised of structurally diverse series of compounds reported as α-glucosidase inhibitors for the structural analysis in order to design novel inhibitors with multiple activities (HIV, diabetics, cancer, etc).

Experimental

Data set

The reliability and robustness of the QSAR analysis is depending on the data set, the method of analysis and the validations of the developed models. In the present analysis, structurally different compounds such as andrographolides, chromenone and triazole derivatives having α-glucosidase inhibitory activity^19–22 were considered to perform the QSAR analysis (Table S1). α-Glucosidase inhibitory activity of the compounds were reported as percentage inhibition was converted as pIC₅₀ by log (P/100 − P), where P is the percentage inhibition^16,18.

The Molecular Operating Environment (MOE) software (Chemical Computing Group Inc. Montreal, H3A 2R7 Canada, 2007) was used to sketch the structure of the molecules and to optimise the energy of the molecules. The semi-empirical MOPAC program with Hamiltonian Austin Model 1 (AM1) force field with 0.05 RMS gradients of MOE software was used to optimise the molecules. A large number of theoretical molecular descriptors such as physical, subdivided surface area, atom and bond counts, connectivity, adjacency and distance matrix, pharmacophore feature, partial charge, potential energy, MOPAC, vsurf (surface area, volume and shape) and conformation dependent charge descriptors are available in the package to define the structural property of the molecules explicitly²³ and these descriptors were used for the present QSAR analysis. The data set which contains 78 compounds (with defined activity) was divided randomly as training (2 sets having 60% and 50% of total compounds) and test sets (2 sets having 40% and 50% total compounds) for the correlation analysis using the Statistica 8.0 software (StatSoft Inc. Tulsa, OK, USA, 2008).

In order to investigate the correlation, QSAR models were developed using the observed α-glucosidase inhibitory activity as dependent variables and the calculated physicochemical descriptors as independent variables by multiple linear regression (MLR) analysis method. In order to reduce the descriptors’ pool, those descriptors possessed zero correlation to the dependent variable (biological activity) as well as those descriptors showed intercorrelation superior to 0.5 were discarded (Table S2a and S2b). The significant models were selected for further validation study by internal (LOO, LMO, LSO, bootstrapping and Y-randomisation) and external (test set) methods^24,25. Multicollinearity and serial correlations of the descriptors and the models were tested with variance inflation factor (VIF) and Durbin–Watson (DW) values.

The leave-many-out (LMO) validation analysis was carried out as LOO (leave-one-out) method but in this method, the training set compounds were divided into groups (blocks) of N compounds. These groups were constructed in a way that the number of blocks is the integer of the ratio of the total compounds in the training set/number of compounds in a block. In this study, each block has 5 compounds (9 blocks for training set 1 and 7 blocks for training set 2, the blocks have at least one compound from each parent structure) and the remaining compounds made the last block (10^th and 8^th block for training sets 1 and 2, respectively). The activities of the excluded compounds were predicted from their corresponding MLR models and its statistical parameters were calculated to examine their predictive capacity. The Y-randomization test ensures the robustness of a QSAR model. The Y-randomization test was performed by (1) repeatedly permuting the activity values of the data set, (2) using the permuted values to generate QSAR models and (3) comparing the resulting scores with the score of the original QSAR model generated from non-randomized activity values. To confirm robustness and reliability of the developed QSAR models, 20 trials were made with randomly shuffled dependent variable vectors. Finally, the resulting R² values were compared with their corresponding R² values of the original QSAR models generated from non-randomiszd activity values.

LSO is leave-series-out, which is same as the test set method, but in this method the activity of a particular series of compounds (derivatives has same parent structure) were predicted from the training set models developed with remaining series of compounds to examine the reliability of the selected models. The bootstrapping validation was carried out by randomly splitting the data set into several times (5 times) as training and test sets (each set has 6 compounds), the MLR models developed with the training set (excluded test set) were used to predict the activity of the test set compounds. The statistical parameter (Q²) was calculated and was compared with the real set models. In this validation study, each sample has been excluded 5 times in different test set and the average statistical parameters values were calculated.

The predictability, reliability and robustness of the developed models are also quantified in terms of their corresponding Q² (LOO, LMO, LSO, BS, test), R², PRESS, S_PRESS, SDEP and other correlation coefficients (R²₀, R²_pred, R²_m, k or k′, etc) values obtained from the validation studies.

Results and discussions

The present QSAR analysis was performed on structurally diverse compounds (training set contains 60% (model 1) and 50% (model 2) of total compounds) by MLR analysis method. The significant models derived from the analysis are given as model 1 and model 2. In this analysis, we have also tried to develop other significant models with additional descriptors to explain the inhibitory activity of the compounds elaborately. Unfortunately, the other developed models did not provide statistically significant results as the selected models to discuss the inhibitory activity. Hence, we have rejected those models for further validation studies and discussion.

Model 1

#1Model 2

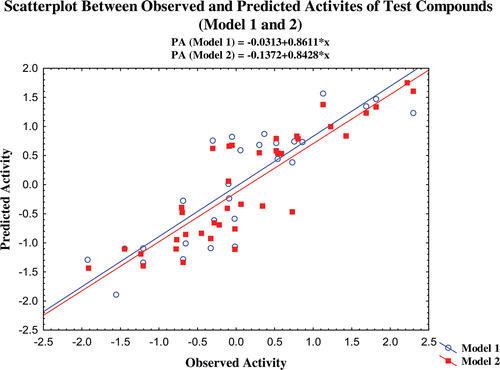
In these models, N is the number of compounds used to develop the corresponding QSAR models. Models 1 and 2 were developed with 48 (60%) and 39 (50%) compounds, respectively, and the remaining compounds were used as test set. The values within the parenthesis that follow the regression coefficient terms are the standard errors of the regression terms and the constants. R and R² are correlation coefficients of the models and in the present models, the correlation coefficients values are >0.92 (R) or >0.85 (R²). These correlation coefficients describe the relative measure of the quality of fit by the regression equations. It explains the variation in the observed data (experimental) and its value varies from−1 to +1. This reveals that the selected models possessed significant fit for activity prediction.

The F and the t_test values are used to examine the confidence level in which the regression models are significant. The values within the parentheses that follow the calculated F values are the tabulated values at 99% significance. The F value indicates that the regression relations are not a chance fit but are a significant occurrence. t is the student t_test and the value within the parenthesis after the calculated value, is the tabulated t value at 0.0005 confidence level. The F statistics and the t value of all the models have a large margin of difference from their limiting values at 0.01 (99%) and 0.0005 (99.95%), respectively, which shows that the models are statistically significant for further validation study to confirm its reliability and robustness.

The significant QSAR models derived by MLR analysis were selected for further validation study by taking into account of high correlation coefficients (R or R²), F, t_test values and the significance of the descriptors included in the model building.

The statistically significant QSAR models (1 and 2) derived by MLR analysis were validated by LOO, LMO, LSO, Y-randomisation, bootstrapping and test set validation methods. These methods examine the self consistency and reliability of the models, which imply a quantitative assessment of the model robustness and its predictive power. The results derived from various validation methods are provided in Table 1.

Table 1.  Summary of the validation results.

Model no	Statistical parameters	Training set	Test set
Model 1	R^2	0.8630	0.7452
	Q^2(LOO)	0.8397	0.7258
	Q^2(LMO)	0.8318
	Q^2(BS)	0.8286
	Q^2(LSO)	0.792
	PRESS	7.5528	7.7864
	SPRESS	0.4143
	SDEP	0.3967	0.5182
	R^20	0.4595	0.7442
	R^2pred		0.7315
	(R^2 − R^20)/R^2		0.0013
	Rm		0.7216
	k	1.0000	0.9037
	k′	0.8646	0.8243
	D^2 (avg)	2.9375
	Cooks (avg)	0.0204
Model 2	R^2	0.8548	0.7657
	Q^2(LOO)	0.8233	0.7318
	Q^2(LMO)	0.8293
	Q^2(BS)	0.8133
	Q^2(LSO)	0.7669
	PRESS	6.5830	9.6864
	SPRESS	0.4337
	SDEP	0.4108	0.5049
	R^20	0.4653	0.7449
	R^2pred		0.7641
	(R^2 − R^20)/R^2		0.0272
	Rm		0.6553
	k	1.0000	0.8654
	k′	0.8625	0.8599
	D^2 (avg)	2.9231
	Cooks (avg)	0.0259

The QSAR model 1 developed against the α-glucosidase inhibitory activity shows low S_PRESS (0.4143) and SDEP (0.3967 for training set and 0.5182 for test set) values which reveal that model 1 provides small residual values between observed and predicted activities. Model 2 also provides significant low S_PRESS and SDEP values for the training and test set, which is closer to the values obtained from model 1. Hence, models 1 and 2 predicted the activity of the training set and the test set compounds with small residual errors. Other statistical parameter used to find out the residual error between the observed and the predicted activity of the models is PRESS. This value has significant effect on the crossvalidated correlation coefficient (Q²) of the models. The training set models 1 and 2 have the PRESS values of 7.5528 and 6.5830, respectively and the test set compounds have comparatively equal and higher (9.6864) values for model 1 model 2, respectively, than the training set compounds. It shows that model 2 has predicted the activity with little higher residual error than model 1. The Q² values of the models are one of the important parameters that explain the predictive capacity of the models and are calculated from the PRESS values as 1 − (PRESS/Y_obs−Y_avg) (Table S3–S5).

The crossvalidated correlation coefficients (Q²_LOO, Q²_LMO, Q²_LSO and Q²_BS) of the derived models are >0.7669 for the training set compounds. The test set compounds also provided the significant Q² value of 0.7258 and 0.7318 for models 1 and 2, respectively. It is interesting that the PRESS value of the test set compounds in model 2 is higher than model 1, but the Q² value of model 2 (test set) is better than model 1. The crossvalidated correlation coefficient values of the training set models 1 and 2 in different validation techniques provided significant values, which are graphically represented in Figure S1. It may be considered that a high Q² (for instance Q² > 0.5) is one of the indicators, that the model is significantly predictive^25,26. This reveals that the selected models have sufficient predictive power and self consistency. The predictive capacity of the models is also confirmed by other correlation coefficient parameters. The correlation coefficient between the predicted activity of the compounds by the validation methods and the observed activity is significant and which are graphically provided in Figure S2. Furthermore, at least one slope of regression lines (k or k′) through the origin should be close to 1. The slope of regression lines (k and k′ were calculated and are given in Table 1), which shows that both the training set models have the k values of 1 and the k′ value for the models are 0.86. But, the test set compounds give the k and k′ values between 0.86 and 0.90. It shows that the slope of the regression lines of the models passes through the origin. The QSAR models are considered acceptable^25–27, if they satisfy all of the following conditions: (i) Q² > 0.5, (ii) R² > 0.6, (iii) R²₀ or R′²₀ is close to R², such that [(R²− R²₀)/R²] or [(R²− R′²₀)/R²] < 0.1 and 0.85 ≤ k ≤1.15 or 0.85 ≤ k′ ≤1.15.

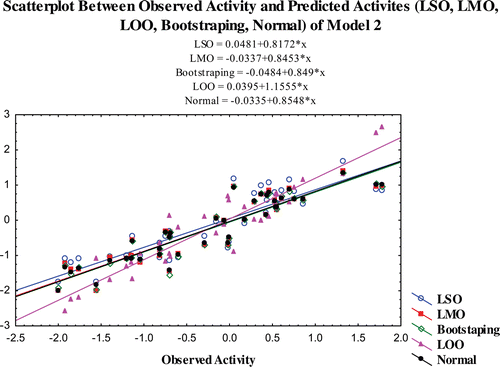
The predictability of the models is also confirmed by additional validation parameters R²₀. The R²₀ values of the test compounds are nearest to their corresponding R² values and the calculated (R²−R²₀)/R² values for both the models are <0.1. The R²_pred and R²_m values of the models are also higher than 0.7 and 0.65 for models 1 and 2, respectively. The results obtained from the validation studies show that the statistical parameters of the of the models satisfy the conditions stated as above and it illustrates that the predicted activity of the compounds through the selected models are comparable with the observed activity with small prediction errors (Table S3–S5). The scatter plot between the observed and predicted activities of the compounds by various validation methods are graphically represented in Figures 1–3.

Figure 1.  Scatterplot between observed activity and predicted activites (LSO, LOO, LMO, bootstraping and normal) of model 1.

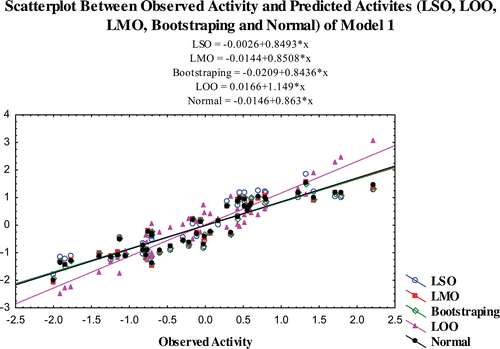
Figure 2.  Scatterplot between observed activity and predicted activites (LSO, LMO, LOO, bootstraping, normal) of model 2.

Figure 3.  Scatterplot between observed and predicted activites of test compounds (model 1 and 2).

The models were further validated by applying the Y-randomisation test. Thus, for each original model, randomisation experiments yield R² values for possible comparison with the original R². If the original QSAR model is statistically significant, its score should be significantly better than those from permuted data. The R² values for 20 trials based on permuted data are shown in Figure 4. The R² value of the original model was higher than any of the trials using permuted data. Hence, the models are statistically significant and robust. The validation results obtained from various validation studies reveal that models 1 and 2 are statistically significant and have significant predictive capacity and robust.

Figure 4.  Y-randomization test.

Distance-based approaches are also a way of validation of the QSAR models. They represent the distance from each point to a particular point. Cook’s distances indicate the distances between the computed B values (standard coefficient values) and the values one would have obtained if the respective case has been excluded (LOO). All distances should be of about equal magnitude, otherwise there is reason to believe that the respective case (s) biased the estimation of the regression coefficients²⁸.

The maximum Cook’s distance value of the models are <0.12 which is <1 (squared Cook’s distances²⁸) and the Cook’s distances of all the compounds have almost equal magnitude (<1), showing that the equation has significant predictive ability for α-glucosidase inhibitory activity.

Mahalanobis distances methods (D²) identify the interpolation region by assuming that the data have a normal distribution. Mahalanobis distances improve the prediction accuracy and speed up a solution for QSAR. The higher the Mahalanobis distances for a case (molecule), the more the independent variables diverge from the average values. That compounds may be considered as outlier in the series or biases in the model building and activity prediction. The maximum and the average D² values of the models are <10 and <3, respectively, which shows that the activity data points in the models are not widely deviated from the average observed activity values.

The multicollinearity and the autocorrelation of the models and the descriptors provide information on the stability, reliability and robustness of the models. Multicollinearity is a statistical phenomenon used in multiple regression models in which two or more predictor descriptors are highly correlated. In this situation, the regression coefficients of the descriptors may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole; it only affects calculations regarding individual predictors.

To confirm the absence of multicollinearity, the variance inflation factor (VIF) was calculated for each parameter in the regression equations. The VIF is based on the proportion of variance, the i^th independent variable shares with the other independent variable in the model. More precisely, the VIF is an index which measures the collinearity of i^th independent variable with the other variables in the analysis and is connected directly to the variance of a coefficient (square of the standard deviation) associated with this independent variable. VIF denotes the fact that the variance of the standardised regression coefficients can be computed as the product of the residual variance (for the correlation transformed model) and it can be calculated as follows (eq. 1).

1

where R² is the multiple correlation coefficient of one parameter’s effect regressed on the remaining parameters. If R equals to zero (i.e. no correlation between X and the remaining independent variables) then VIF equals 1, the minimum value. A value greater than 10 is an indication of potential multicollinearity problems (inflated standard errors of regression coefficients), and also it is possible to have no independent variable that is statistically significant even though R² is relatively large. Not uncommonly, a VIF of 10 or even one as low as 4 (equivalent to a tolerance level of 0.10 or 0.25) have been used as rules of thumb to indicate excessive or serious multicollinearity²⁹. In the selected models (training and complete set), the VIF value is less than 2.3 for model 1 and VIF < 3 for model 2 shows that the descriptors in the selected models are free from multicollinearity, i.e. none of the independent variables in the models are collinear with other independent variables in the mode^27,29. The results are provided in Table 2.

Table 2.  VIF and Durban–Watson values for the models.

Models no	Descriptors	Tolerance	R^2	VIF	Durbin–Watson
					Calc.	Tab
Model 1	E_str	0.4536	0.5462	2.2046	2.0440	1.2450–1.4910
	SMR_VSA0	0.4610	0.5390	2.1692
	vsurf_Wp4	0.4411	0.5589	2.2671
Model 2	E_str	0.4038	0.5962	2.4765	1.7361	1.1370–1.4520
	SMR_VSA0	0.3399	0.6601	2.9420
	vsurf_Wp4	0.4101	0.5899	2.4384

A Durbin–Watson (DW) test was employed to check the serial correlation of residuals (correlation of adjacent residuals). The DW statistics is useful for evaluating the presence or absence of a serial correlation of residuals (i.e. whether or not residual for adjacent cases are correlated, indicating that the observations or cases in the data file are not independent) or the regression models assume that the error deviations are uncorrelated.

2

where e_t is the residual associated with the observation at time t, since d is approximately equal to 2(1− r), where r is the sample autocorrelation of the residuals, d = 2 indicates no autocorrelation. The value of d always lies between 0 and 4. If the DW statistic is substantially less than 2, there is evidence of positive serial correlation and a value toward 4 indicates negative autocorrelation^27,29–31.

The tabulated upper and lower bound values of Durbin–Watson were considered to test the hypothesis of zero autocorrelation against the positive and negative autocorrelations. In the present study, the DW values for both the models are higher than the tabulated upper and lower bound value at 5% significance level (Table 2) and the values are closer to 2, and also show that the models are not having any serious autocorrelation problem.

The validation results obtained from the study and other statistical parameters obtained from the stability studies (multicollinearity and autocorrelation) show that the developed (selected) models are robust, reliable and statistically significant.

Applicability of the descriptors

The QSAR models derived from the studies are triparameteric, which comprises the potential energy (E_str), the subdivided surface area (SMR_VSA0) and the surface area, volume and shape (vsurf_Wp4) descriptors. The statistical parameters calculated for the models are significant and were discussed earlier. The potential energy descriptor (E_str) is a 3D descriptor that represents the bond stretch potential energy of the molecules²³. The negative coefficient of this descriptor reveals that the stretching energy of the molecule is detrimental for the α-glucosidase inhibitory activity, if the energy value is higher. It explains that the stretching energy of the molecule should be lower, which can be possible when the molecules posses flexible bonds (or functional groups) in their structure. These flexible bonds are also important for the free/flexible movement of the molecule in the active site of the enzyme. Earlier structural feature analysis results on the α-glucosidase inhibitors performed by our laboratory and it also showed the importance of the flexible bonds for the α-glucosidase inhibitory activity^15–18. Hence, it confirms that the flexible bonds (with less stretching energy) in the molecule are important for the α-glucosidase inhibitory activity of the molecules.

The vsurf descriptors calculations depend on the structure connectivity and conformation (dimensions are measured in Å). The vsurf_ descriptors similar to the Volsurf descriptors and these descriptors have been shown to be useful in pharmacokinetic property prediction by the vdW surface properties of the molecules. The vsurf_Wp descriptors describe the polar volume of the molecule and are calculated at eight different energy levels (−0.2, −0.5, −1.0, −2.0, −3.0, −4.0, −5.0 and −6.0 kcal/mol) and may be defined as the molecular envelope accessible by solvent water molecules. The volume of this envelope varies with the level of interaction energies between water and the solute molecule. In general, W1–4 account for polarisability and dispersion forces, while W5–8 account for polar and hydrogen bond donor–acceptor regions^14,32. In the present model, the vsurf_Wp4 has contributed with negative sign suggesting that the molecule should have less polarisable properties on the vdW surface for interaction with the target or water molecules in the target. This descriptor suggests that the molecular vdW surface should not have more hydrophilic property but may have balanced polar (hydrophilic) and non-polar (hydrophobic) property for better activity. It illustrates that the active site environment of the enzyme may have balanced hydrophilic and hydrophobic properties for interaction with the molecules.

SMR_VSA0 is defined to be the sum of the v_i over all atoms i. p_i denotes the contribution to molar refractivity for atom i as calculated in the SMR descriptor, which was calculated in a specified range from 0.00 to 0.11. This descriptor intends to reflect the polarizability and the atomic contribution to the molar refractivity^23,27,29. The negative sign of the regression coefficient in this descriptor suggests that the polarizability property on the van der Waals surface area of the molecule should be decreased for the favourable inhibitory activity. This reveals that the active site of the enzyme may have some low polarisable groups on the surface for better interaction.

The vsurf_Wp4 and SMR_VSA0 descriptors explain the importance of polarisable groups on the vdW surface of the molecules. Both the descriptors contributed negatively for the α-glucosidase inhibitory activity prediction and suggest that the active region of the enzyme should have distributed hydrophobic and hydrophilic environment for interaction with the molecules. The vdW surface property of the aligned structure of the data base and the individual series (compounds have same parent structures) of compounds were performed and are shown in Figure S3. The vdW surface of the molecule has the distribution of the hydrophobic (green) and the hydrophilic properties (pink and blue) and it reveals that these properties are important for the α-glucosidase inhibitory activity of the compounds. The reported literatures reveal that the binding mode of the enzyme has histidine, tyrosine, aspartic acid and glutamic acid residues, which provide distributed (balanced) hydrophilic and hydrophobic properties in the active site environment analysis^8–12. This confirms that the descriptors contributed in these models explain the active site environment of the enzyme significantly.

Conclusion

The QSAR analysis was carried out to interpret the structural relationship between physicochemical descriptors and α-glucosidase inhibitory activity of structurally diverse compounds. The models developed were triparameteric and were validated by various methods. The descriptors, vsurf_Wp4 and the VSA_SMR0 are illustrating the vdW surface property of the molecules and suggest that the polarizable property on the surface should be lower for better α-glucosidase inhibitory activity. These results clearly suggest that the hydrophobic and hydrophilic properties of the molecules should be balanced on the vdW surface area. It reveals that the active site of the enzyme should have polar, aromatic/hydrophobic residues for the interactions. It is evidenced from the homology models and other glycosidase family enzymes^8–12, and the active site residues of α-glucosidase enzyme of different species. This shows that the active site has aspartic acid, histidine and glutamic acid residues. Hence, it is possible that the polar, aromatic groups in the molecule can interact with the active site residues (aspartic acid, glutamic acid, tyrosine and histidine) by hydrogen bonding or other electrostatic interaction. The flexibility of the bonds in the molecules can allow the pharmacophore groups on the molecules to interact with the active residue with less stretching energy. The results obtained from this analysis will be useful for designing novel molecules having multiple actions (HIV, diabetics, cancer, etc) with earlier studies results in our laboratory^15–18.

Declaration of interest

One of the authors N.S.H.N. Moorthy is grateful to the Fundaçao para a Ciencia e Technologia (FCT), Portugal for a Postdoctoral Grant (SFRH/BPD/44469/2008). The authors gratefully acknowledge FCT for financial support for project PTDC/QUI/68302/2006. The authors declare no conflicts of interest.