Computation for biomechanical analysis of aortic aneurysms: the importance of computational grid

Figures & data

Figure 1. Example of patient-specific abdominal aortic aneurysm (AAA) geometry (Patient 1): (a) AAA model segmented from CTA image – sagittal view, and (b) a cross-section of AAA geometry showing the intraluminal thrombus (ILT), lumen, and AAA external wall (blue color) created automatically using BioPARR (Joldes et al. 2017).

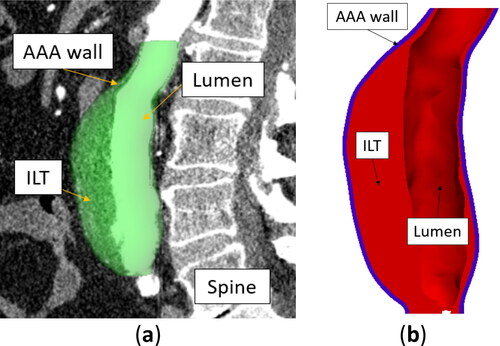
Table 1. Tetrahedral and hexahedral finite elements from ABAQUS finite element code library (Abaqus 2018) analysed in this study.

Element name in ABAQUS	Element description	No. of nodes	No. of integration (Gauss) points	Finite element formulation
C3D10	10-node quadratic tetrahedron	10	4	Displacement-based
C3D10H	10-node quadratic tetrahedron, hybrid with constant pressure	10	4	Hybrid (Displacement/pressure-based)
C3D20	20-node quadratic hexahedron	20	27	Displacement-based
C3D20H	20-node quadratic hexahedron, hybrid with linear pressure	20	27	Hybrid (Displacement/pressure-based)
C3D20R	20-node quadratic hexahedron, reduced integration	20	8	Displacement-based
C3D20RH	20-node quadratic hexahedron, reduced integration, hybrid with linear pressure	20	8	Hybrid (Displacement/pressure-based)
C3D8	8-node linear hexahedron	8	8	Displacement-based
C3D8H	8-node linear hexahedron, hybrid with linear pressure	8	8	Hybrid (Displacement/pressure-based)
C3D8R	8-node linear hexahedron, reduced integration with hourglass control	8	1	Displacement-based
C3D8RH	8-node linear hexahedron, reduced integration with hourglass control, hybrid with constant pressure	8	1	Hybrid (Displacement/pressure-based)

Figure 2. Example of finite element meshes generated in this study (Patient 3). Blue color: aneurysm wall (with a constant wall thickness of 1.5 mm). Red color: intraluminal thrombus (ILT) meshed using tetrahedral elements. (a) Tetrahedral meshes of aneurysm wall, and (b) hexahedral meshes of aneurysm wall. Both meshes have two layers of elements through the wall thickness.

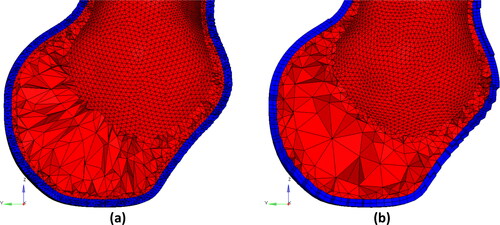
Figure 3. Histograms of the maximum principal stress in the aneurysm wall (Patient 1) calculated using tetrahedral and hexahedral finite element meshes with different number of elements through the wall thickness (1 layer, 2 layers, 4 layers and 8 layers of elements) and for different element type/formulation (a) Quadratic tetrahedra with displacement formulation (C3D10); (b) Quadratic tetrahedra with hybrid formulation (C3D10H); (c) Linear hexahedra with displacement (C3D8) and hybrid (C3D8H) formulations. Only three histograms are visible as the results for C3D8 and C3D8H overlap; (d) Linear hexahedra with reduced integration, and displacement (C3D8R) and hybrid (C3D8RH) formulations. Only three histograms are visible as the results for C3D8R and C3D8RH overlap; (e) Quadratic hexahedra with displacement formulation (C3D20); (f) Quadratic hexahedra with hybrid formulation (C3D20H), (g) Quadratic hexahedra with reduced integration and displacement formulation (C3D20R), and (h) Quadratic hexahedra with reduced integration and hybrid formulation (C3D20RH).

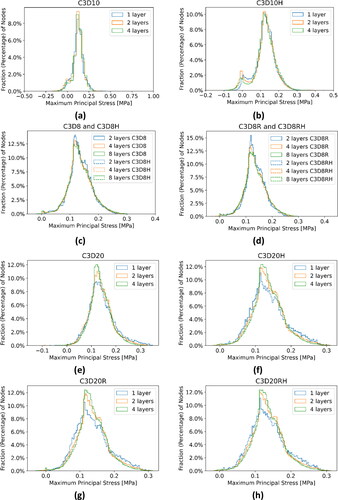
Figure 4. (a) Contour plots of the maximum principal stress (MPS) including residual stress (RS) obtained using C3D10H 10-noded quadratic tetrahedral hybrid elements (left-hand-side figures) and C3D20RH 20-noded quadratic hexahedral hybrid elements with reduced integration (right-hand-side figures) for the aneurysm wall; and (b) percentile plots of MPS for the studied AAA patients.

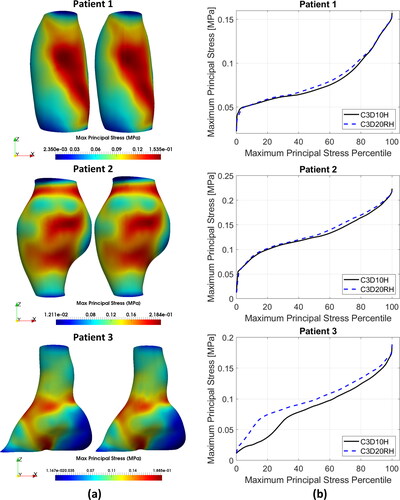
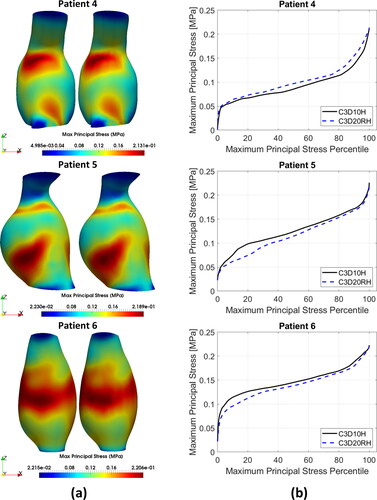
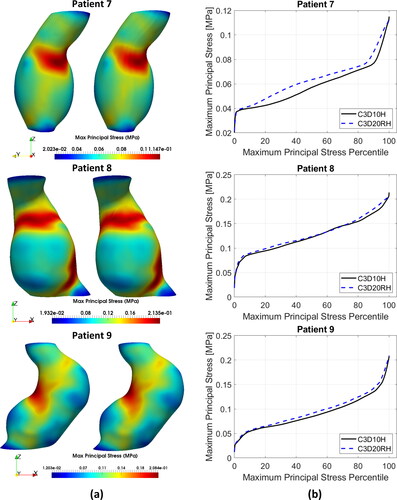
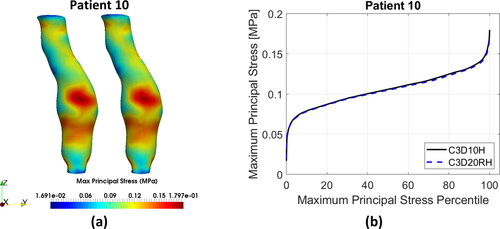
Figure A1. AAA biomechanical analysis (the figure shows the pressure distribution in MPa) for Patient 1 using finite element mesh constructed with 10-noded quadratic displacement-based tetrahedral elements (element type C3D10 in ABAQUS finite element code). Volumetric locking, as indicated by nonphysical chess-board-like pattern of the pressure distribution, is clearly visible.

Table A1. Summary of the patient-specific computational biomechanics finite element (FE) models of AAA created and used in this study; a total of 60 models. The number of elements through the wall thickness determines the AAA mesh density. ILT is the intraluminal thrombus. The symbol ✗ indicates that ILT was not included in the model.

Patient no.	Applied MAP (kPa)	Model no.	Finite Element type (from ABAQUS)		No. of elements across AAA wall thickness
			AAA Wall	ILT
1	12	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
		4	C3D10	✗	1
		5	C3D10H	✗	1
		6	C3D10	✗	2
		7	C3D10H	✗	2
		8	C3D10	✗	4
		9	C3D10H	✗	4
		10	C3D20	✗	1
		11	C3D20H	✗	1
		12	C3D20R	✗	1
		13	C3D20RH	✗	1
		14	C3D8	✗	2
		15	C3D8H	✗	2
		16	C3D8R	✗	2
		17	C3D8RH	✗	2
		18	C3D20	✗	2
		19	C3D20H	✗	2
		20	C3D20R	✗	2
		21	C3D20RH	✗	2
		22	C3D8	✗	4
		23	C3D8H	✗	4
		24	C3D8R	✗	4
		25	C3D8RH	✗	4
		26	C3D20	✗	4
		27	C3D20H	✗	4
		28	C3D20R	✗	4
		29	C3D20RH	✗	4
		30	C3D8	✗	8
		31	C3D8H	✗	8
		32	C3D8R	✗	8
		33	C3D8RH	✗	8
2	13	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
3	13	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
4	14	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
5	14	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
6	15	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
7	9	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
8	13	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
9	12	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2
10	13	1	C3D10H	C3D10H	2
		2	C3D20H	C3D10H	2
		3	C3D20RH	C3D10H	2

Table A2. Tetrahedral (tetra) and hexahedral (hexa) AAA wall mesh with two layers of elements through the wall thickness generated in this study: number of elements, percentage of poor-quality elements with respect to the total number of elements for each part, and values of mesh quality measures.

Patient no.	Wall mesh topology	No. of elements	Poor-quality elements (%)	Min. interior element angle	Max. interior element angle	Max. volumetric skew	Min. Jacobin ratio
1	Tetra	718,738	0%	3.32	173.37	1.00 (1 element)	–
	Hexa	21,090	0%	49.73	131.16	–	0.86
2	Tetra	849,479	0%	1.47	177.05	1.00 (16 elements)	–
	Hexa	35,616	0%	45.31	140.64	–	0.73
3	Tetra	662,876	0%	15.29	144.15	0.97	–
	Hexa	27,072	0.25%	25.92	162.42	–	0.57 (5 elements)
4	Tetra	855,299	0.01%	0.50	179.00	1.00 (48 elements)	–
	Hexa	46,472	0.11%	37.21	146.44	–	0.72
5	Tetra	527,213	0%	2.15	175.70	1.00 (8 elements)	–
	Hexa	25,894	0.06%	43.65	143.47	–	0.75
6	Tetra	624,894	0%	16.42	139.88	0.96	–
	Hexa	26,578	0%	58.70	126.16	–	0.84
7	Tetra	656,219	0%	6.15	142.29	0.97	–
	Hexa	32,200	0%	52.94	130.73	–	0.87
8	Tetra	863,937	0%	0.63	178.75	1.00 (25 elements)	–
	Hexa	44,968	0.02%	43.19	140.19	–	0.74
9	Tetra	745,591	0%	17.16	139.80	0.95	–
	Hexa	49,720	0.19%	38.91	146.40	–	0.67
10	Tetra	864,558	0%	16.35	138.73	0.96	–
	Hexa	52,884	0%	47.97	136.25	–	0.86

Table A3. Solution convergence and computation time for displacement-based (elements C3D10, C3D8, C3D8R, C3D20, and C3D20R) and hybrid (elements C3D10H, C3D8H, C3D8RH, C3D20H, and C3D20RH) finite element (FE) formulations. MPS = maximum principal stress, GCI=grid convergence index (Equation 2), p=order of convergence (Equation 3), and f_estimated= estimated asymptotic solution. Refer to Table A1 for more information about the models. For models 4, 6, 8, 12, 20, and 28, p, GCI and f_estimated could not be obtained due to the solution inconsistency.

Model no.	FE formulation	No. of elements across AAA wall thickness	No. of elements	No. of nodes	Peak MPS (MPa)	Computation time (sec)	p	GCI	festimated
4	C3D10	1	72,507	137,862	1.194662	13	–	–	–
6		2	718,738	1,117,412	1.923035	259
8		4	2,164,776	3,462,038	1.916670	2512
5	C3D10H	1	72,507	137,862	0.555902	17	2.227	0.0433	0.6923
7		2	718,738	1,117,412	0.575515	287
9		4	2,164,776	3,462,038	0.667334	2825
14	C3D8	2	27,972	42,291	0.267113	4	0.748	0.0613	0.3192
22		4	225,676	283,210	0.288184	36
30		8	1,801,840	2,031,084	0.300730	991
15	C3D8H	2	27,972	42,291	0.267113	4	0.748	0.0613	0.3192
23		4	225,676	283,210	0.288184	45
31		8	1,801,840	2,031,084	0.300730	4084
16	C3D8R	2	27,972	42,291	0.264955	3	0.608	0.0831	0.3224
24		4	225,676	283,210	0.284721	30
32		8	1,801,840	2,031,084	0.297690	893
17	C3D8RH	2	27,972	42,291	0.264955	4	0.608	0.0831	0.3224
25		4	225,676	283,210	0.284721	41
33		8	1,801,840	2,031,084	0.297690	4277
10	C3D20	1	3,465	45,095	0.349787	3	0.226	0.2580	0.23529
18		2	27,972	154,734	0.337121	20
26		4	225,676	1,075,083	0.322297	401
11	C3D20H	1	3,465	45,095	0.307018	3	1.950	0.0012	0.3129
19		2	27,972	154,734	0.311382	26
27		4	225,676	1,075,083	0.312511	520
12	C3D20R	1	3,465	45,095	0.312899	3	–	–	–
20		2	27,972	154,734	0.311790	17
28		4	225,676	1,075,083	0.312540	308
13	C3D20RH	1	3,465	45,095	0.311511	3	3.574	0.0003	0.3127
21		2	27,972	154,734	0.311593	23
29		4	225,676	1,075,083	0.312570	568

Table A4. Computation time, peak maximum principal stress (MPS), relative absolute difference in the peak value of MPS between tetrahedral and hexahedral meshes for the studied AAAs. C3D10H is fully integrated quadratic tetrahedron using hybrid formulation. C3D20RH is quadratic hexahedron using hybrid formulation and reduced integration. Relative absolute difference was calculated as the absolute difference between the peak MPS obtained using C3D10H (MPS_C3D10H) and C3D20RH (MPS_C3D20RH) elements divided by the peak MPS obtained using C3D20RH elements: $\frac{\left|{\mathrm{\text{MPS}}}_{\mathrm{C}3\mathrm{D}10\mathrm{H}}-{\mathrm{\text{MPS}}}_{\mathrm{C}3\mathrm{D}20\mathrm{H}\mathrm{R}}\right|}{{\mathrm{\text{MPS}}}_{\mathrm{C}3\mathrm{D}20\mathrm{H}\mathrm{R}}}·100\mathrm{\%}.$

Patient ID	Model no.	Element type of AAA wall	Computation time (sec)	Peak MPS (MPa)	Peak MPS relative absolute difference (%)
1	1	C3D10H	880	0.1574	2.5%
	3	C3D20RH	157	0.1535
2	1	C3D10H	1641	0.2237	2.4%
	3	C3D20RH	296	0.2184
3	1	C3D10H	1196	0.1888	0.1%
	3	C3D20RH	133	0.1886
4	1	C3D10H	3048	0.2141	0.5%
	3	C3D20RH	1355	0.2130
5	1	C3D10H	503	0.2265	3.4%
	3	C3D20RH	152	0.2188
6	1	C3D10H	753	0.2230	1.1%
	3	C3D20RH	181	0.2206
7	1	C3D10H	823	0.1154	1.1%
	3	C3D20RH	221	0.1141
8	1	C3D10H	1795	0.2145	2.4%
	3	C3D20RH	519	0.2094
9	1	C3D10H	1415	0.2087	0.1%
	3	C3D20RH	373	0.2090
10	1	C3D10H	2139	0.1803	4.0%
	3	C3D20RH	501	0.1731

Joldes GR, Miller K, Wittek A, Forsythe RO, Newby DE, Doyle BJ. 2017. BioPARR: a software system for estimating the rupture potential index for abdominal aortic aneurysms. Sci Rep. 7(1):4641.

 PubMedGoogle Scholar

Abaqus. 2018. Abaqus 6.14 Documentation. 2018. Dassault Systèmes Simulia Corp. [accessed 2022 June]. https://www.3ds.com/support/documentation/.

 Google Scholar