Exploring evolutionary-tuned autoencoder-based architectures for fault diagnosis in a wind turbine gearbox

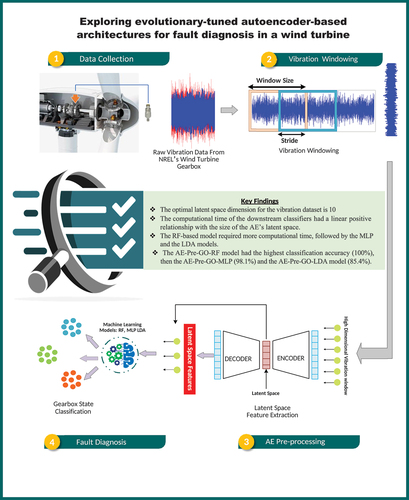
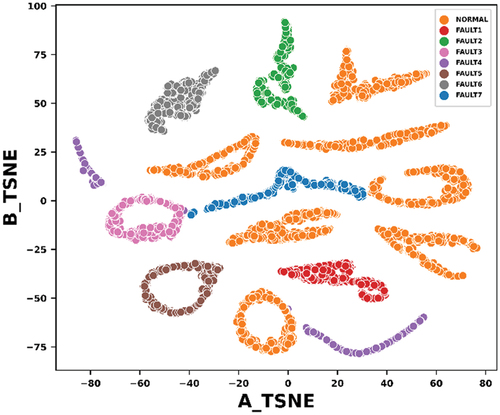
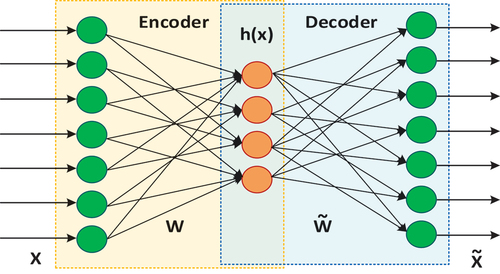
Figures & data

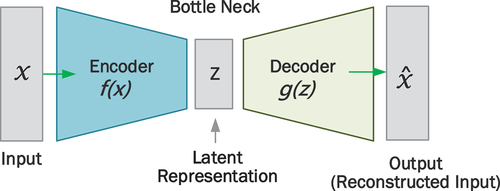
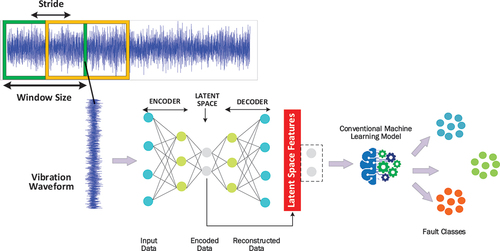
Figure 1. Wind turbine gearbox vibration-based fault diagnosis: (a) Traditional vibration pre-processing framework (b) Autoencoder vibration pre-processing framework.

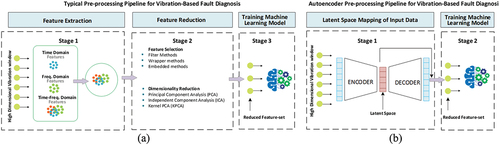
Figure 2. Vibration waveform of the intermediate speed shaft bearing: (a) Damaged signal (b) Normal signal.

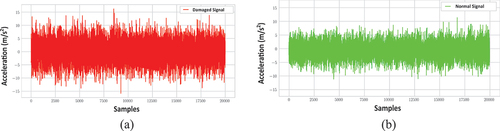
Figure 3. Vibration spectrum of the intermediate speed shaft bearing: (a) Damaged signal (b) Normal signal.

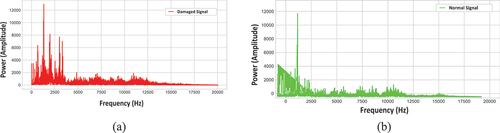
Figure 4. The waveform (a) and spectrum (b) of the intermediate speed shaft bearing’s normal vibration signals superimposed upon the damaged.

Figure 5. Schematic representation of a standard autoencoder model.

Figure 6. Autoencoder latent space feature extraction process.

Figure 7. Two-dimensional t-TSNE scatter plot of a window of the vibration data.

Figure 8. Architecture of a typical autoencoder model.

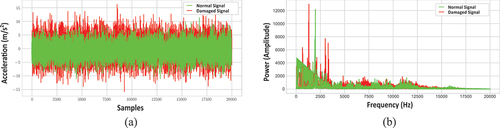
Table 1. The experimented Autoencoder model architectures.

Layer type	Dense
Activation function	Rectified Linear Unit (ReLU)
Model	Latent space dimension	Numbers of Neuron
1	2	500	250	100	50	20	10	2	10	20	50	100	250	500
2	3	500	250	100	50	20	10	3	10	20	50	100	250	500
3	5	500	250	100	50	20	10	5	10	20	50	100	250	500
4	7	500	250	100	50	20	10	7	10	20	50	100	250	500
5	10	500	250	100	50	20	10			20	50	100	250	500
6	15	500	250	100	50	20	15			20	50	100	250	500
7	20	500	250	100	50	20					50	100	250	500

Table 2. The Autoencoder model training hyperparameters.

Parameter Name	Value
Number of epochs	5
Batch size	100
Optimizer	Adam
Loss	Mean absolute error (MAE)
Learning rate	0.001

Figure 9. Genetic algorithm optimization process.

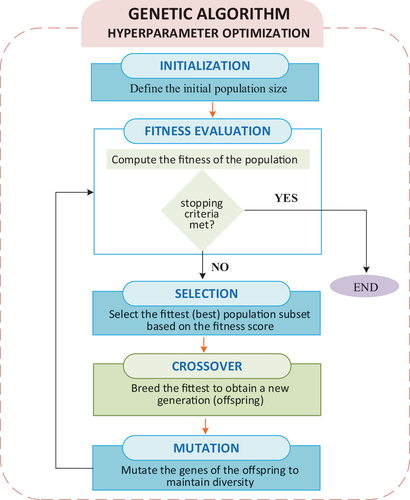
Table 3. Parameters of the genetic algorithm.

Hyperparameter	Value
Number of generations (N)	5
Population size	24
Offspring size	12
Number of cross-validations	5
Scoring metric	Accuracy

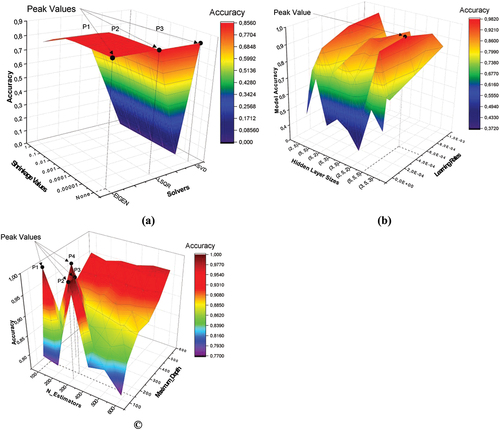
Figure 10. (a) Impact of the autoencoder latent space dimension size on the LDA model’s (a) performance metrics (b) accuracy and computational time.

Figure 11. (a) Impact of the autoencoder latent space dimension size on the MLP model’s (a) performance metrics (b) accuracy and computational time.

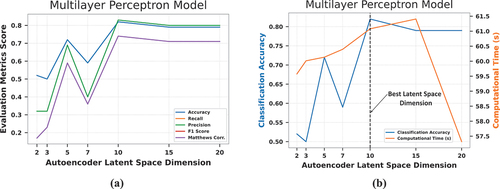
Figure 12. (a) Impact of the autoencoder latent space dimension size on the RF model’s (a) performance metrics (b) accuracy and computational time.

Figure 13. Hyperparameter optimization plot for (a) the LDA model (b) MLP model (c) RF model.

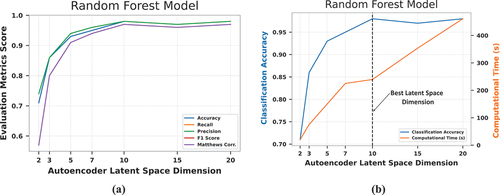
Figure 14. (a) Confusion matrix of the AE-Pre-GO-LDA model (b) confusion matrix of the AE-Pre-GO-MLP model (c) confusion matrix of the AE-Pre-GO-RF model (d) comparison of the computation time of the AE-Pre-GO-LDA, AE-Pre-GO-MLP and AE-Pre-GO-RF.

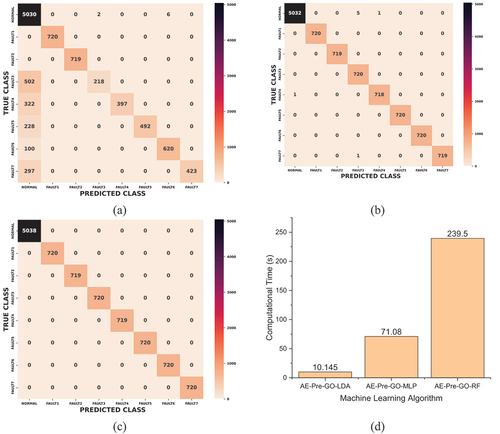
Table 4. Performance of the LDA, MLP and RF models based on the optimized hyperparameters.

Model	Accuracy (%)	Recall or Sensitivity (%)	Precision or Specificity (%)	F1-Score (%)	Matthew’s Correlation (%)	Training Time (s)
AE-Pre-GO-LDA	85.4	85.0	85.6	86.0	80.0	10.14
AE-Pre-GO-MLP	98.1	98.7	97.8	97.7	96.8	71.08
AE-Pre-GO-RF	100.0	100.0	100.0	100.0	100.0	239.50

Table 5. Comparison of wind turbine studies employing conventional methods for pre-processing gearbox vibration signals.

	Vibration Pre-processing Strategies
Reference	Features extraction strategy	Feature reduction technique	Machine learning algorithms	Classification accuracy (%)
[82]	Statistical feature extraction after empirical model decomposition	Decision tree feature selection	Support vector machine (SVM)	92.80
[83]	Time domain statistical feature extraction	Dynamic principal component analysis (DPCA)	Support vector machine (SVM)	82.0
[84]	Discrete wavelet transform followed by extraction of statistical features	Sequential feature selection	Artificial neural network (ANN) and support vector machine (SVM)	100.0
[85]	Histogram feature extraction	Feature selection using J48 decision tree algorithm.	K-nearest neighbour (KNN)	93.8
[27]	Time domain statistical feature extraction after empirical mode decomposition with adaptive noise. Frequency domain feature extraction after fast Fourier transform (FFT)	Recursive feature elimination (RFE) combined with chi-square test	Extreme learning machine (ELM) and support vector machine (SVM)	99.6
[86]	Feature extraction after discrete wavelet transforms (DWT)	Dimensionality reduction using singular value decomposition	Extreme learning machine (ELM)	99.9
This study	Manifold learning with AE		AE-Pre-GO-LDA	80
This study	Manifold learning with AE		AE-Pre-GO-MLP	96
This study	Manifold learning with AE		AE-Pre-GO-RF	100

Inturi V, Sabareesh GR, Sharma V. Integrated vibro-acoustic analysis and empirical mode decomposition for fault diagnosis of gears in a wind turbine. Procedia Struct Integr. 2019;14(2018):937–944. doi: 10.1016/j.prostr.2019.07.074

 Google Scholar

Kordestani M, Rezamand M, Orchard M, et al. Planetary gear faults detection in wind turbine gearbox based on a ten years historical data from three wind farms. IFAC-Papersonline. 2020;53(2):10318–10323. doi: 10.1016/j.ifacol.2020.12.2767

 Google Scholar

Biswal S, George JD, Sabareesh GR. Fault size estimation using vibration signatures in a wind turbine test-rig. Procedia Eng. 2016;144:305–311. doi:10.1016/j.proeng.2016.05.137

 Google Scholar

Joshuva A, Sugumaran V. A lazy learning approach for condition monitoring of wind turbine blade using vibration signals and histogram features. Measurement. 2020;152:107295. doi:10.1016/j.measurement.2019.107295

 Web of Science ®Google Scholar

Tang Z, Wang M, Ouyang T, et al. A wind turbine bearing fault diagnosis method based on fused depth features in time–frequency domain. Energy Rep. 2022;8:12727–12739. doi:10.1016/j.egyr.2022.09.113

 Web of Science ®Google Scholar

Pang Y, Jia L, Zhang X, et al. Design and implementation of automatic fault diagnosis system for wind turbine. Comput Electr Eng. 2020;87:106754. doi: 10.1016/j.compeleceng.2020.106754

 Web of Science ®Google Scholar