Constrained intermittent model predictive control

Abstract

The generalised hold formulation of intermittent control is re-examined and shown to have some useful theoretical and practical properties. It is shown that this provides a foundation for constrained model predictive control in an intermittent context. The method is illustrated using an example and verified with experimental results.

Keywords:

• model-predictive control
• constrained control
• intermittent control
• ball and hoop
• quadratic programming

1. Introduction

As discussed by Gawthrop and Wang (2007) intermittent control is based on a sequence of open-loop trajectories punctuated by intermittent feedback; each open-loop trajectory is, in turn related to an underlying closed-loop control. There are at least three areas where intermittent control may be relevant:

• Continuous-time model-based predictive control (MPC) where the intermittency provides the time within which on-line optimisation occurs (Ronco, Arsan, and Gawthrop 1999; Gawthrop 2002, 2004; Gawthrop and Wang 2006).

• Control over low-bandwidth channels where there is a finite rate at which feedback information can be received and transmitted (Nair and Evans 2003).

• Physiological control systems which may, in some cases, have an intermittent character (see Loram, Gawthrop, and Lakie (2006) and the references therein). This intermittency may be due to the ‘computation’ in the central nervous system.

The key result of Gawthrop and Wang (2007) is that the basis function (Wang 2001; Gawthrop and Ronco 2002) approach to intermittent control (Ronco et al. 1999) can be replaced by a generalised hold. The purpose of this article is to explore that result further and, in particular show that a particularly simple formulation of constrained intermittent control is possible. As discussed by Gawthrop and Wang (2006), although MPC was developed with process control applications in mind, it has been shown to be applicable to mechanical systems (Giorgetti, Bemporad, Tseng, and Hrovat 2006; Cairano, Bemporad, Kolmanovsky, and Hrovat 2007; Gawthrop and Wang 2007). A key feature of MPC is the ability to handle state constraints via quadratic programming (QP) but the high speed of mechanical systems as compared to process systems means that computational time is an issue. As discussed by Gawthrop and Wang (2006), the combination of the use of basis functions, efficient QP and intermittent control allows the successful application of MPC to mechanical systems. This article makes use of the generalised hold formulation of Gawthrop and Wang (2007) to provide a new approach to constrained MPC.

Section 2 briefly summarises the unconstrained approach of Gawthrop and Wang (2007) but with some simplifications and additions. Section 3 builds on § 2 and derives an explicit equation giving the combined trajectories of system and generalised hold which is then used to re-derive prediction equations, constraint equations and optimisation equations leading to a new formulation of constrained intermittent control. Section 4 illustrates the result with a simple example, § 5 gives some experimental results and § 6 concludes the article.

2. Unconstrained intermittent control

This article considers single-input–single-output (SISO) systems given in state space form as:

A is an n × n matrix, B an n × 1 column vector and C a 1 × n row vector. The n × 1 column vector x is the system state. y and u are scalar functions of time and x ₀ is the system initial condition. For the theoretical development, it is assumed that the state x is available; in practice, a state observer (Kwakernaak and Sivan 1972) is used to provide and estimate of x; this is discussed further in § 4. As discussed by Gawthrop and Wang (2007), (1) can be regarded as representing the perturbation of a system about a steady-state operating point and thus, by changing the steady state, setpoint following can be readily incorporated–this is not discussed further here but is used in § 4.

Intermittent control makes use of three time frames:

1. continuous-time, within which the controlled system (1) evolves, which is denoted by t.

2. discrete-time points at which feedback occurs indexed by i. Thus, for example, the discrete-time time instants are denoted t _i and the corresponding system state is x _i = x(t _i ). The i-th intermittent interval is defined as

   Δ _i will be assumed to have a constant value of Δ for the rest of this article.

3. intermittent-time is a continuous-time variable, denoted by τ, restarting at each intermittent interval. Thus, within the i-th intermittent interval, τ = t − t _i .

Following Gawthrop and Wang (2007) a set of n (continuous-time) basis functions are defined as the state transient response of the linear time-invariant system evolving within intermittent time τ:

where A _u is an n × n matrix and x _u is an n × 1 column vector containing the n basis functions.

In conjunction with these basis functions, the n × 1 intermittent control vector U _i is defined at the discrete-time instants t _i so that the (scalar) intermittent control signal u(t) is given by:

The linear (unconstrained) intermittent feedback control law intermittently generating U _i is of the form:

where K is an n × n matrix. The use of the future state is discussed in § 3.1. Equations (4) and (5) thus give intermittent feedback control where periods of continuous-time open-loop control are punctuated with feedback at the discrete-time points t _i .

The key result of Gawthrop and Wang (2007) is that the basis function generator (3) and intermittent control signal (4) can be replaced by the generalised hold

where x _h is the n-dimensional state of the system dual to that formed by (3) and (4). The system (6) is a generalised hold in the sense that the intermittent control U _i is the initial state of the system in an analogous fashion to the zero-order hold where the discrete-time control signal becomes the initial state of an integrator.

Following Gawthrop and Ronco (2002), this article uses the predictive pole-placement (PPP) approach for designing the intermittent feedback gain K of (5). In particular, K is chosen so that the intermittent closed-loop system formed by (1), (4) and (5) matches the continuous-time closed-loop system given by (1) and the conventional continuous-time state-feedback controller with gain k given by:

The corresponding closed-loop system is:

where A _c = A − Bk. There are many ways to choose k. One is linear-quadratic regulator (LQR) design (Kwakernaak and Sivan 1972; Jacobs 1974; Goodwin, Graebe, and Salgado 2001) which chooses the control u to minimise the infinite-horizon linear-quadratic cost function:

The solution to this optimisation is of the form of (7) where:

and P is the positive-definite solution of the Algebraic Riccati Equation (ARE):

This article presents a new approach to PPP design which is simpler than that given by Gawthrop and Ronco (2002) or Gawthrop and Wang (2007). Following Gawthrop and Wang (2007), the basic idea is to make the generalised hold formulation of (6) similar to the closed-loop system (8). In particular, following Kailath (1980) and Polderman and Willems (1997), (6) and (8) can be made similar as follows:

1. Choose A _u to have the same eigenvalues as A _c .

2. Choose x _uo such that is observable (which is the same as [A _u x _uo ] being controllable).

3. Define the observability matrices 𝒪 _c and 𝒪 _d

It follows that the PPP intermittent feedback gain K (5) is given by:

This approach differs from Gawthrop and Wang (2007) insofar as the observability matrix rather than the controllability matrix is used.

In the particular case that and , K = 1, (8) and (6) are identical and x _h = x _c . This possibility has the nice consequence that the generalised hold acts as a ‘model’ of the desired closed-loop system. However, as discussed in § 4, the choice of A _u has a significant effect on the numerical properties of constrained MPC and so this particular choice may not be good from the numerical point of view. Other possible choices of A _u include the companion matrix with the same characteristic polynomial as that of A _c ; this choice is used in the examples of § 4.

An important aim of this article is to replace the linear intermittent feedback controller (5) by an on-line optimisation procedure so that both state and input hard constraints can be obeyed by the control law. This is considered in § 3.

3. Constrained intermittent control

Using the linear time-invariant feedback (5) may cause state or input constraints to be violated over the intermittent interval. The aim of this section is to derive a controller which corresponds to (5) when constraints are not violated but otherwise chooses U _i to avoid violation.

The first step is to construct a set of equations describing the evolution of the system state x and the generalised hold state x _h that does not rely on (5). Combining (1) and (6) gives such a set of equations:

where

The differential Equation (16) has the explicit solution

where τ is the intermittent continuous-time variable based on t _i .

The explicit solution (18) (which relies on the generalised hold interpretation of intermittent control) simplifies both analysis and implementation. In particular, it is now used for three purposes: prediction, constraint mapping and optimisation.

3.1 Prediction

As discussed in more detail elsewhere (Ronco et al. 1999; Gawthrop and Wang 2006), the intermittent interval can be used to provide the time needed to execute the QP needed to handle constraints in the context of MPC. This means that the intermittent control vector U _i+1 is computed between time i and time i + 1 based on the prediction of x _i+1 = x(t _i+1). Partitioning the 2n × 2n matrix E(τ) (19) into four n × n sub-matrices:

it follows that the prediction can be written as:

3.2 Constraints

The vector X (17) contains the system state and the state of the generalised hold; Equation (18) explicitly give X in terms of the system state x _i and the intermittent control vector U _i at time t _i . Therefore, any constraint expressed at a future time τ as a linear combination of X can be re-expressed in terms of U _i and x _i . In particular if the constraint at time τ is expressed as:

where Γ_τ is a 2n-dimensional row vector and γ_τ a scalar then the constraint can be re-expressed using (18) in terms of the intermittent control vector U _i as:

where E has been partitioned into the two 2n × n sub-matrices E _x and E _u as:

If there are n _c such constraints, they can be combined as:

where each row of Γ is Γ_τ E _u (τ), each row of Γ _x is Γ_τ E _x (τ) and each (scalar) row of γ is γ_τ.

Following standard MPC practice, constraints beyond the intermittent interval can be included by assuming that the control strategy will be open-loop in the future.

3.3 Optimisation

Following, for example, Chen and Gawthrop (2006), a modified version of the infinite-horizon LQR cost (9) is used:

where the weighting matrices Q and R are as used in (9) and P is the positive-definite solution of the ARE (11). There are an number of differences between our approach to minimising J _ic (27) and the LQR approach to minimising J _LQR (9).

1. Following the standard MPC approach (Maciejowski 2002), this is a receding-horizon optimisation in the time frame of τ not t.

2. The integral is over a finite time τ₁.

3. A terminal cost is added based on the steady-state ARE (11). In the discrete-time context, this idea is due to Rawlings and Muske (1993).

4. The minimisation is with respect to the intermittent control vector U _i generating the the control signal u (4) through the generalised hold (6).

Using X from (18), (27) can be rewritten as

Using (18), Equation (28) can be rewritten as:

Using integration by parts, J ₁ can be shown to be the solution of the singular ARE:

The 2n × 2n matrix J _XX can be partitioned into four n × n matrices as:

The value of U _i minimising (28) is then given by (5) with

Given the inverse of J _UU in (36), it is clearly important that J _UU is well conditioned to avoid numerical problems. As mentioned in § 2, the choice of generalised hold matrix A _u does affect the conditioning of J _UU ; from (27), so does τ₁. This point is examined further in § 4.

3.4 Quadratic programme

Lemma 3.1 Constrained optimisation

The minimisation of the cost function J _ic of Equation (27) subject to the constraints (26) is equivalent to the solution of the QP:

subject to ΓU _i ≤ γ − Γ _x x _i where J _UU and J _Ux are given by (35) and Γ, Γ _x and γ as described in § 3.2.

Proof

See Chen and Gawthrop (2006).□

4. Example

A unit double integrator has the transfer function and has a state-space representation of the form of (1) where:

A constant input disturbance corresponds to the transfer function which when the state-space equivalent is combined with (38) gives (39) with:

Following § 3, the LQR cost function with

This gives a state-feedback gain

with closed-loop poles at .

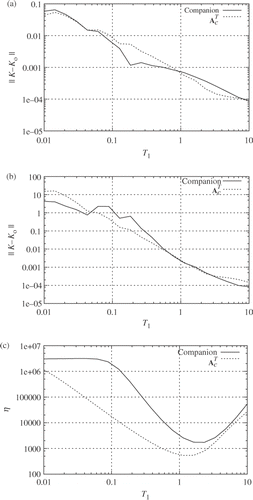
The controller was designed as in §§ 2 and 3 using Octave (Eaton 2002) and simulated using Scilab (Campbell, Chancelier, and Nikoukhah 2006). To test the numerical properties of the cost (28) with respect to the time horizon τ₁, three functions were evaluated:

1. the norm of the difference between the LQR gain k _LQR (10) and the derived gain (Figure 1(a)).

2. the norm of the difference between K computed from (15) and from the cost function (36) (Figure 1(b)).

3. the condition number η of J _UU (35) (Figure 1(c)).

In this example, the companion form gives a better conditioned problem; and in both cases τ₁ (27) gives the smallest condition number. This suggests the need for theoretical results on conditioning.

Figure 1. Numerical properties. The three measures are plotted against optimisation horizon τ₁ for two cases A _u is the companion matrix with the same eigenvalues as A _c and . (a) ‖k − k _LQR‖; (b) ‖k − k _LQR‖; (c) Condition number η.

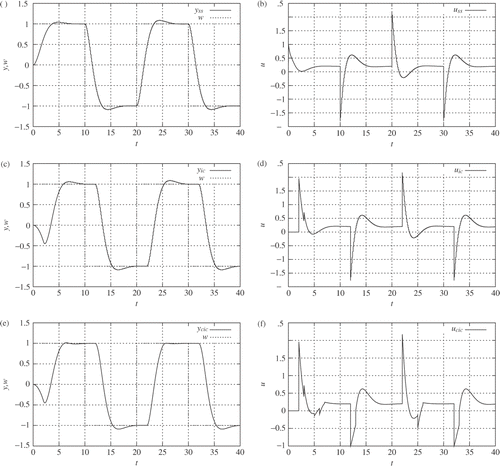
Three different controllers were simulated:

1. the state-space controller with feedback gain (41)

2. the corresponding unconstrained intermittent controller with a fixed intermittent interval Δ = 1 s

3. the corresponding constrained intermittent controller (CIC) with constraints y ≤ 1 at τ = 1 and u ≥ −1 at τ = 0.01.

In each case, a unit square-wave setpoint with period 20 s and a constant input disturbance of −0.2 was applied and the initial observer state was zero. Figure 2(a), (c) and (e) shows the system output y for the three controllers and Figure 2(b), (d) and (f) the corresponding control signals.

• The (unconstrained) intermittent and continuous controls differ initially due to the initial observer error caused by the constant offset disturbance. The intermittent control is worse because of the initial open-loop control generated with incorrect state information.

• The disturbance is eliminated eventually because the controlled system contains an integrator.

• The constrained intermittent control differs from the unconstrained intermittent control at the setpoint changes. At times t = 5 and 25 this is due to the constraint that y ≤ 1; at times t = 12.5 and 32.5 this is due to the constraint that u ≥ −1.

• The constraint that y ≤ 1 is violated around time t = 5 due to the initial observer error; otherwise both constraints are satisfied.

Figure 2. Simple example double integrator with input disturbance. (a) y: state-space controller; (b) u: state-space controller; (c) y: intermittent controller; (d) u: intermittent controller; (e) y: CIC; (f) u: CIC.

5. Experimental verification

A series of experiments, based on the ‘Ball and Hoop’ (Wellstead 1979) apparatus, was conducted to verify the approach. Section 5.1 provides a mathematical model; § 5.2 discussed the controller implementation and § 5.3 describes the experimental results.

5.1 System modelling

Figure 3 is a photograph of the ball and hoop laboratory experiment (Wellstead 1979) where a spherical ball bearing rolls without slipping within a metal hoop and the hoop rotates about its centre driven by a DC motor. The angle of an arbitrary point on the hoop from vertical is denoted by θ _h and the angle subtended by the ball centre by θ _b , the corresponding angular velocities are Ω _h and Ω _b , respectively. The hoop radius is r _h . The hoop has a velocity feedback loop with setpoint Ω₀ designed so that:

This inner loop not only gives a well-defined setpoint response but also practically eliminates the effect of the ball motion on the hoop; this simplifies both modelling and control.

Figure 3. Ball and hoop.

Assuming that the angle θ _b is small, the translational velocity v _b = r _h Ω _b of the ball along the hoop can be written in terms of the distance x _b = r _h θ _b as:

where f _b is the force acting on the ball at the ball–hoop interface and the gravitational spring constant k _g is defined as

The rotational motion of the ball is given in terms of its angular velocity ω _b as:

where r _b is the ball radius and is the moment of inertia of the ball about the mass centre. Because of the non-slip condition, the two differential Equations (43) and (45) are not independent and thus from a differential–algebraic equation. As will now be shown, this differential–algebraic equation can be reduced to an ordinary differential equation but with an acceleration appearing on the right-hand side.

Defining the relative velocities and as

and substituting f _b from (43), (45) becomes:

Rearranging and dividing by the hoop radius r _h gives:

where the equivalent mass m _e is given by:

It is always difficult to include an accurate friction model in such systems; here, we have chosen to add a linear coulomb friction term to the right-hand side of (48). With this addition, and substituting from the ordinary differential equation equivalent of (42) finally gives:

Using Equation (50) the state equations are of the form of (1) where:

and

Numerical values appear in Table 1. The friction coefficient was estimated, the rest were taken from data sheets for the experiment. Without the friction coefficient, this system would have four poles at s = 0, and s = ±jω₀ where . The first two reflect the hoop dynamics and the last two reflect the ball dynamics. With the friction included, the ball exhibits lightly damped oscillations.

Table 1. System numerical values.

Parameter	Value
g ms^−2	9.81
m b kg	0.032
r b m	0.0091
r h m	0.085
b b Nm rad^−1 s^−1	2.0
τ h s	1.0
ω0 rad s^−1	9.08
f 0 Hz	1.45

5.2 Control design and implementation

The purpose of this experiment is to control the hoop position without moving the ball excessively. One approach to this is to set up a linear-quadratic cost function with weighting on both hoop and ball position. However, this linear approach gives rise to ball motion proportional to hoop motion.

On the other hand, a fixed constraint on ball motion can be imposed using the CIC of this article. In particular, hoop angle θ _h is to be controlled with a hard constraint on the ball angle θ _b .

The controller was designed off-line as in §§ 2 and 3 using Octave (Eaton 2002). The controller was implemented on a computer with an Intel core 2 duo processor running at 1.4 GHz running the Ubuntu 7.1 32bit distribution with an RTAI kernel compiled from a standard Linux 2.6.23.14 kernel patched with RTAI-3.6. The controller was implemented using RTAI-lab (Bucher and Balemi 2006) which is in turn based on Scilab 4.2 (Campbell et al. 2006); in particular, the generalised hold was implemented using the Scilab ‘jump’ block. A special Scilab block was used to implement the QP using Hildreth's method Luenberger (1984). Matlab code used previously by Gawthrop and Wang (2007) was translated into C++ using the mat2cpp, BLAS and ATLAS libraries. This C++ code was then incorporated into the Scilab block using a C wrapper function.

5.3 Experimental results

Two controllers were evaluated in separate experiments at a base sample interval of 2 ms. A conventional linear-quadratic state-feedback/observer with parameters from Table 2 and the corresponding constrained intermittent control with the state constraint θ _b ≤0.2 rad and intermittent interval 10 ms. For the purposes of comparison, a numerical simulation of the hoop with corresponding controller was run in real-time and in parallel with the control of the real system. To demonstrate the non-linear nature of the constrained control, the hoop was subject to a square-wave setpoint of increasing amplitude.

Table 2. Controller numerical values.

Parameter	Value
Control weight R	10^−4
Observer weight R o	10^−6
Intermittent interval Δ	10 ms
Cost horizon τ1	1s
State constraint	θ b ≤ 0.2 rad

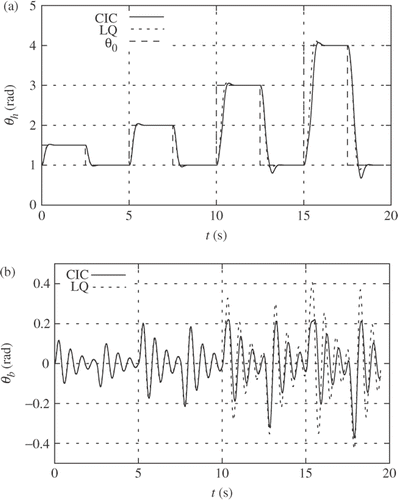
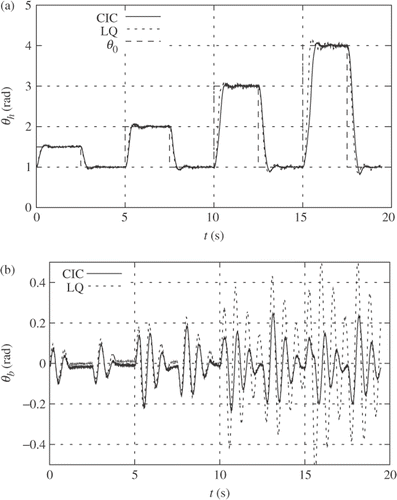
Figure 4 gives the simulation results and Figure 5 gives the corresponding experimental results. Each figure has two parts:

1. The hoop angle θ _h resulting from the experiment corresponding to each controller CIC, and linear quadratic (LQ)) together with the setpoint θ₀.

2. The ball angle θ _b .

Figure 4. Ball & hoop Experiment: real-time simulation. (a) y: simulation; (b) y_b : simulation.

Figure 5. Ball & hoop experiment: real-time experiment. (a) y: real; (b) y_b : real.

Both the simulation and experimental results are quite similar thus verifying the system modelling and controller implementation. As expected, the linear quadratic controller gives a ball angle motion which increases with hoop angle setpoint. In contrast, the CIC keeps the ball angle within the constraint except for two cases. For small setpoint changes, the LQ and CIC behave in the same way, but for larger angles, the constraint on ball angle implies a corresponding change in the hoop motion which is evident from the figures. As in the example of § 4, the integrator inherent in the system leads to zero steady-state error.

The two cases of constraint violation are due to amplifier saturation, and this was verified by including this saturation into the simulation.

6. Conclusion

The generalised hold reformulation of intermittent control, first given by Gawthrop and Wang (2007), has been restated in a form that is more convenient for analysis and implementation. In particular, explicit compact equations suitable for prediction, constraint formulation and optimisation are given. A simulated example illustrates the approach which is verified using a real-time implementation to control a mechanical system.

The issue of stability in the constrained case is, as is well known (Mayne, Rawlings, Rao, and Scokaert 2000), tied to the issue of feasibility. In particular, feasibility is a key issue for mechanical systems which typically have poles on the imaginary axis and often have poles in the right-half complex plane. As discussed in this article, constraint handling is coupled to choice of basis function. This article uses a particular set of basis functions matched to the desired closed-loop system. This has the advantage of using a few basis functions and giving good off-constraint performance; however, it is not clear that this is the best choice for constraint handling in more complicated situations than treated in § 5.

For these reasons, future work will combine the matched basis functions with Laguerre functions in the form of Kautz functions which have been previously used in the context of system identification (Wahlberg and Makila 1996; Bokor and Schipp 1998). We believe that this will combine good off-constraint performance with accurate handling of complicated constraints and lead to a theory of how to design basis functions for feasibility.

The control-system properties of intermittent control have yet to be investigated. In the unconstrained case, the article of Goodwin and Salgado (1994) and the book of Feuer and Goodwin (1996) provide a possible way forward.

Acknowledgements

Peter Gawthrop is a Leverhulme Emeritus Research Fellow and gratefully acknowledges the support of the Leverhulme Trust. Some of the work reported here was accomplished whilst the first author was a Visiting Professor at RMIT University, Melbourne supported by the RMIT Professorial fund and the Royal Academy of Engineering grant ITG C7-292. The work reported here is related to EPSRC Grant EP/F069022/1 ‘Intermittent control of man and machine’.