Adaptive tracking of switched nonlinear systems with prescribed performance using a reference-dependent reparametrisation approach

ABSTRACT

In this paper, adaptive tracking control of switched nonlinear systems in the parametric strict-feedback form is investigated. After defining a reparametrisation lemma in the presence of a non-zero reference signal, we propose a new adaptive backstepping design of the virtual controllers that can handle the extra terms arising from the reparametrisation (and that the state-of-the-art backstepping designs cannot dominate). The proposed adaptive design guarantees, under arbitrarily fast switching, an a priori bound for the steady-state performance of the tracking error and a tunable bound for the transient error. Finally, the proposed method, by overcoming the need for subsystems with common sign of the input vector field, enlarges the class of uncertain switched nonlinear systems for which the adaptive tracking problem can be solved. A numerical example is provided to illustrate the proposed control scheme.

KEYWORDS:

• Adaptive tracking control
• switched nonlinear systems
• global ultimate boundedness
• arbitrarily fast switching

1. Introduction

Uncertainties and nonlinearities are ubiquitous when controlling complex systems. As an effective method to cope with uncertainties and nonlinearities, adaptive control of nonlinear systems via backstepping approaches has been intensively studied in the last decades (Bechlioulis & Rovithakis, 2008; Chen & Tao, 2016; Ge, Hong, & Lee, 2005; Kojic & Annaswamy, 2005; Krstic, Kanellakopoulos, & Kokotovic, 1995; Mao, Huang, & Xiang, 2017; Yu, Fei, & Li, 2010; Yu, Zhang, & Fei, 2013; Zhou, Wen, & Li, 2012). Since complex systems often involve switching phenomena, a special class of complex systems, namely switched nonlinear systems, has been used to model a wide range of complex systems, such as automobile (Xu & Antsaklis, 2004), power converters (Loxton, Teo, Rehbock, & Ling, 2009), flight control systems (Li, Wen, & Soh, 2001), communication networks (Zhang, Zhu, Ning, & Zheng, 2016; Zhang, Zhu, & Zheng, 2016) and many others (Huang & Xiang, 2016a, 2016b). Because of the interaction between continuous and discrete dynamics, adaptive control of switched nonlinear systems is more challenging than adaptive control of non-switched nonlinear systems.

To date, some research has been conducted on adaptive control of switched nonlinear systems, which can be grouped into two families: (1) the nonlinear functions of the subsystems are unknown; (2) the nonlinear functions are parametrised with unknown constants. For the first family, two approximating tools are widely used to approximate the uncertain nonlinear systems via adaptive laws, which are fuzzy membership functions (Li, Sui, & Tong, 2017; Long & Zhao, 2016; Niu, Karimi, Wang, & Liu, 2016; Zhao, Zheng, Niu, & Liu, 2015), and neural networks (Han, Ge, & Lee, 2009; Jiang, Shen, & Shi, 2015; Long & Zhao, 2015; Niu, Qin, & Fan, 2016; Zhao, Shi, Zheng, & Zhang, 2015). However, at least one of the following problems typically arises for control designs in this family: the performance cannot be prescribed a priori, being dependent on the actual parameters which are unknown (Han et al., 2009; Jiang et al., 2015; Li et al., 2017; Long & Zhao, 2015, 2016; Niu, Karimi, et al., 2016; Niu, Qin, & Fan, 2016; Zhao, Shi, et al., 2015; Zhao, Zheng, et al., 2015); stability cannot be guaranteed for arbitrarily fast switching (typically, average dwell-time switching constraint is necessary to guarantee stability) (Han et al., 2009; Long & Zhao, 2015, 2016; Niu, Karimi, et al., 2016). For the second family, the main design tools are: a reparametrisation lemma that overcomes the need for different estimators for different subsystems and can handle arbitrarily fast switching (Chiang & Fu, 2014); or a parameter separation technique that requires slow-switching signals (Long, Wang, & Zhao, 2015). While the reparametrisation lemma allows to achieve stability under arbitrarily fast switching, the state-of-the-art has only addressed adaptive regulation. In addition, the backstepping techniques in Chiang and Fu (2014) can only handle the restrictive case in which subsystems have the same sign of the input vector field. This restrictive condition implies that, for every subsystem of switched system, the control input will push the system in the same ‘direction’: this assumption is limiting in many settings, for example, the activation of the reverse gear of automobile or robotic applications. Therefore, a big open problem remains concerning how to design, under arbitrarily fast switching, an adaptive tracking controller with prescribed performance guarantees for uncertain switched nonlinear systems whose subsystems have possibly different signs of the input vector field. Solving this open problem is the objective of this work. This problem is more than a simple extension of Chiang and Fu (2014), Long et al. (2015), because the absence of a reference signal simplifies significantly the design of the virtual controllers in the regulation case. In fact, the presence of a reference signal introduces new terms in the reparametrisation that smooth virtual controllers based on the state-of-the-art backstepping designs cannot dominate. In view of this, how to design a family of smooth virtual controllers to cope with the aforementioned problem is challenging and requires a new backstepping design.

The main contribution of this work is threefold. First, we introduce a new reparametrisation lemma which is dependent on the reference model. By virtue of the reference-dependent reparametrisation lemma, we propose a new design of the virtual controllers and adaptive laws that solve the tracking problem of switched nonlinear systems in the parametric strict-feedback form. Second, we provide, under arbitrarily fast switching, an a priori bound for the steady-state performance of the tracking error, and a tunable bound for the transient performance. Finally, we enlarge the class of uncertain switched nonlinear systems for which the tracking problem can be solved in Chiang and Fu (2014). In particular, we relax the assumption that the input vector field of all subsystems have the same sign by introducing a new common Lyapunov function with a summation term concerning the input vectors.

The paper is organised as follows. The problem and some definitions are presented in Section 2. In Section 3, the proposed backstepping procedure is performed and an adaptive controller with a controller and a family of adaptive laws are introduced. In Section 4, stability results of the closed-loop nonlinear system are given. In Section 5, a numerical example is used to validate the proposed adaptive control schemes. The paper is concluded with Section 6.

Notations

The notations used in this paper are as follows. $\mathbb{R}$ and ${\mathbb{N}}^{+}$ represent the set of real numbers and positive natural numbers, respectively. The superscript T represents the transpose of a vector. The notation ‖·‖ represents the Euclidean norm. For a time signal, ‖·‖₂ represents the $L_2$ norm.

2. Problem formulation and preliminaries

This paper focuses on uncertain single-input-single-output switched nonlinear systems in the parametric strict-feedback form: (1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) where ${\bar{x}}_i={\left[x_1\dots x_i\right]}^T\in {\mathbb{R}}^i$, i = 1,… , n, $x={[x_1,\cdots ,x_n]}^T\in {\mathbb{R}}^n$ are the system states, $u\in \mathbb{R}$ is the input, $y\in \mathbb{R}$ is the output, ϕ _{ij, p} and ψ _p , j = 1,… , m, $p\in M$, are known and smooth functions with ψ _p > 0, ${\theta }_{j,p}\in {\mathbb{R}}^q$ and $b_p\in \mathbb{R}$, $p\in M$, are uncertain parameters, σ(·) denotes the piece-wise constant switching signal, d is a bounded external disturbance. The output y is desired to track a reference y _m.

The following assumptions are made:

Assumption 2.1:

The sign of b _p , $p\in M$, is known.

Assumption 2.2:

The disturbance d(·) satisfies |d(t)| ≤ ρ where ρ is an unknown positive constant.

Assumption 2.3:

The ith-order derivatives of y _m(·), i = 1, 2,… , n − 1, are measurable and bounded.

Remark 2.1:

There are several applications which can be modelled as in (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ), for example, continuous stirred tank reactors with two modes feed stream (Ma & Zhao, 2010), HVAC systems (Chiang & Fu, 2006) and multi-agent systems (Yang, Jiang, Cocquempot, & Zhang, 2011). Note that Assumptions 1–3 define a more general class of switched nonlinear systems than the class considered in Chiang and Fu (2014). In Chiang and Fu (2014), the switched system is restricted to a class where the functions ϕ _{ij, p} satisfy ϕ _{ij, p} (0) = 0, i = 1,… , n, j = 1,… , m, $p\in M$. In addition, in Chiang and Fu (2014), the parameters b _p must have the same sign, and a common lower bound is assumed to be known.

For the purpose of analysis, it is useful to define a family of positive constants ${\zeta }_p=\frac{1}{|b_p|}$, which are unknown. We denote the sequence of switching instants with: $\left\{t_1,\dots t_l,\dots |l\in {\mathbb{N}}^{+}\right\}$. In addition, the following definitions are provided:

Definition 2.1

[Global ultimate boundedness]: The uncertain switched nonlinear system (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ) under switching signal σ(·) is globally ultimately bounded if there exists a convex and compact set $C$ such that for every initial condition x(0) = x ₀, there exists a finite T(x ₀) such that $x\left(t\right)\in C$ for all t ≥ T(x ₀).

Definition 2.2

[Ultimate bound]: A signal w(·) is said to be globally ultimately bounded with ultimate bound b if there exists a positive constant b, and for any a ≥ 0, there exists T = T(a), where T is independent of t ₀, such that ‖w(t ₀)‖ ≤ a⇒‖w(t)‖ ≤ b,  ∀t ≥ t ₀ + T.

The problem to be solved in this work thus is formulated in the following:

Problem 2.1:

Design a control input u and a group of adaptive laws such that the output of the uncertain switched nonlinear system (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ) can track the reference signal y _m with performance guarantee under arbitrarily fast switching.

3. Methodologies

In order to proceed with the backstepping procedure, the following change of coordinate is made: (2) $$\begin{array}{ccc}\hfill z_1& =& x_1-y_{\mathrm{m}}\hfill \\ \hfill z_i& =& x_i-{\alpha }_{i-1}({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })-y_{\mathrm{m}}^{(i-1)},i=2,\cdots ,n\hfill \end{array}$$(2) where z ₁ is the tracking error, α _i−1 is the virtual controller, ${\bar{y}}_{\mathrm{m}}^{(i-1)}={[y_{\mathrm{m}}\cdots y_{\mathrm{m}}^{(i-1)}]}^T$ and $\widehat{\vartheta }$ is the estimate of ϑ which will be defined later.

Lemma 3.1:

(Reference-dependent reparametrisation lemma) For a family of smooth functions ${\varphi }_{ij,p}\left({\bar{x}}_i\right)$, i = 1,… , n, j = 1,… , m, $p\in M$, there exist a family of smooth positive functions φ _i , f _i and an unknown finite positive constant ϑ such that the following condition holds: (3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3)

Proof:

Considering that the parameter θ _{j, σ}, j = 1,… , m, belongs to a compact set, there exist a family of known smooth functions η _i (t) > 0 and uncertain constants κ _i > 0, i = 1,… , n, such that the following holds: $$\begin{array}{c}\hfill \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }\right|\le {\kappa }_i{\eta }_i\left({\bar{x}}_i\right)\end{array}$$ It suggests $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\kappa }_i{\eta }_i\left({\bar{x}}_i\right)+\left|\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}{\kappa }_k{\eta }_k\left({\bar{x}}_k\right)\right|\hfill \end{array}$$ Using similar reasoning as in Theorem 3.4 of Lin and Qian (2002), we can find a family of smooth positive functions φ _i , f _i and an unknown finite positive constant ϑ ≥ max  _{i = 1,… , n} (κ _i ) such that (3) holds. This completes the proof.

Remark 3.1:

Note that the reparametrisation (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ) is different with Chiang and Fu (2014), Lin and Qian (2002) where no reference signal y _m was considered. With y _m ≡ 0 and by assuming ϕ _{ij, p} (0) = 0, i = 1,… , n, j = 1,… , m, $p\in M$, the left side of (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ) can be linearly parametrised with respect to z _i , i.e. only terms of the form |z _i |φ _i , i = 1,… , n, are present. When using the backstepping approach, this gives rise to a quadratic term in z _i , i = 1,… , n, which simplifies the design of the control and adaptive laws. With y _m and ϕ _{ij, p} (0) possibly different than zero, a different design must be used.

Without a quadratic term in z _i , i = 1,… , n, a sign function of z _i is necessary for the design of the virtual controllers in the backstepping procedure, which leads to discontinuities (as underlined in Remark 3.4). As a consequence, the derivative of the virtual controllers in the inductive steps will diverge at the discontinuous points, which might result in instability of system (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ). In light of this, a series of smooth functions with a prescribed constant δ _i > 0 (i = 1,… , n) is used to approximate the sign function (Wen, Zhou, Liu, & Su, 2011; Zhou, Wen, & Zhang, 2004; Zhou et al., 2012) as follows: (4) $$\begin{array}{c}\hfill {\mathrm{sg}}_i\left(z_i\right)=\left\{\begin{array}{c}{\displaystyle \frac{z_i}{|z_i|},\left|z_i\right|\ge {\delta }_i}\hfill \\ {\displaystyle \frac{z_i}{{({\delta }_i^2-z_i^2)}^{n-i+2}+\left|z_i\right|},\left|z_i\right|<{\delta }_i}\hfill \end{array}\right.\end{array}$$(4) In addition, the following functions will be used to adjust the adaptation process: $$\begin{array}{c}\hfill {\chi }_i\left(z_i\right)=\left\{\begin{array}{c}1,|z_i|\ge {\delta }_i\hfill \\ 0,|z_i|<{\delta }_i\hfill \end{array}\right.\end{array}$$

Remark 3.2:

The functions sg _i ∈ [ − 1, 1] is (n − i + 2)th-order differentiable, and its maximum derivative is dependent on the pre-defined parameter δ _i . Note that the maximum derivative increases significantly as δ _i approaches zero. In Zhou et al. (2012), Wen et al. (2011), Zhou et al. (2004), the functions (4(4) $$\begin{array}{c}\hfill {\mathrm{sg}}_i\left(z_i\right)=\left\{\begin{array}{c}{\displaystyle \frac{z_i}{|z_i|},\left|z_i\right|\ge {\delta }_i}\hfill \\ {\displaystyle \frac{z_i}{{({\delta }_i^2-z_i^2)}^{n-i+2}+\left|z_i\right|},\left|z_i\right|<{\delta }_i}\hfill \end{array}\right.\end{array}$$(4) ) are used to avoid chattering in the last step of the backstepping procedure (controller design); on the other hand, in this work, (4(4) $$\begin{array}{c}\hfill {\mathrm{sg}}_i\left(z_i\right)=\left\{\begin{array}{c}{\displaystyle \frac{z_i}{|z_i|},\left|z_i\right|\ge {\delta }_i}\hfill \\ {\displaystyle \frac{z_i}{{({\delta }_i^2-z_i^2)}^{n-i+2}+\left|z_i\right|},\left|z_i\right|<{\delta }_i}\hfill \end{array}\right.\end{array}$$(4) ) is exploited to design a family of novel virtual controllers that, with the help of (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ), will guarantee stability of the switched nonlinear system (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ).

Remark 3.3:

Note that a widelyused approximation to the sign function sgn(z_i ), namely tanh (z _i ), accumulates the approximation error at each step while performing the backstepping method, which negatively impacts the performance of the tracking error. Another approximation, i.e. $z_i/\sqrt{z_i^2+{\xi }^2}$ or z _i /(|z _i | + ξ), with ξ being finite-energy and positive, has been adopted in Lai, Liu, Chen, and Zhang (2016), Li and Yang (2016) for the controller design in the last step of backstepping procedure. However, such approximation cannot be used in the virtual controllers because when ξ → 0 for t → ∞, the approximation tends to be discontinuous and thus not differentiable everywhere.

To keep the mathematical derivation concise, we will use φ _i , f _i , sg _i and χ _i to represent ${\varphi }_i({\bar{z}}_i,{\bar{y}}_{\mathrm{m}})$, $f_i({\bar{z}}_i,{\bar{y}}_{\mathrm{m}})$, sg _i (z _i ) and χ _i (z _i ), respectively. Define the estimation errors $\tilde{\vartheta }=\vartheta -\widehat{\vartheta }$, ${\tilde{\zeta }}_s={\zeta }_s-{\widehat{\zeta }}_s$ and $\tilde{\rho }=\rho -\widehat{\rho }$, where ${\widehat{\zeta }}_s$ and $\widehat{\rho }$ are the estimates of ζ _s and ρ, respectively. Now, we are ready to perform the backstepping procedure.

• Step 1: According to (2(2) $$\begin{array}{ccc}\hfill z_1& =& x_1-y_{\mathrm{m}}\hfill \\ \hfill z_i& =& x_i-{\alpha }_{i-1}({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })-y_{\mathrm{m}}^{(i-1)},i=2,\cdots ,n\hfill \end{array}$$(2) ), the derivative of z ₁ is (5) $$\begin{array}{c}\hfill {\dot{z}}_1=z_2+{\alpha }_1+\sum _{l=1}^m{\varphi }_{1l,\sigma }^T{\theta }_{\sigma }\end{array}$$(5) Consider the following Lyapunov function candidate: $$\begin{array}{c}\hfill V_1=\frac{1}{n+1}{\left(|z_1|-{\delta }_1\right)}^{n+1}{\chi }_1+\frac{1}{2{\gamma }_1}{\tilde{\vartheta }}^2\end{array}$$ with γ₁ > 0. Note that $d|z_1|/dt·{\chi }_1={\dot{z}}_1{\mathrm{sg}}_1{\chi }_1$. Differentiating V ₁ and using (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ) gives $$\begin{array}{ccc}\hfill {\dot{V}}_1& \le & {\left(|z_1|-{\delta }_1\right)}^n\left(z_2+{\alpha }_1\right){\chi }_1{\mathrm{sg}}_1\hfill \\ & & +{\left(|z_1|-{\delta }_1\right)}^n\left({\varphi }_1\vartheta +f_1\right){\chi }_1-\frac{1}{{\gamma }_1}\tilde{\vartheta }\dot{\widehat{\vartheta }}\hfill \end{array}$$ Using (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ), we design the common smooth virtual control law $$\begin{array}{ccc}\hfill {\alpha }_1& =& -\left(c_1+\frac{1}{4}\right){\left(|z_1|-{\delta }_1\right)}^n{\mathrm{sg}}_1-f_1{\mathrm{sg}}_1\hfill \\ & & -{\varphi }_1\widehat{\vartheta }{\mathrm{sg}}_1-\left({\delta }_2+1\right){\mathrm{sg}}_1\hfill \end{array}$$ which leads to $$\begin{array}{ccc}\hfill {\dot{V}}_1\left(t\right)& \le & -\left(c_1+\frac{1}{4}\right)\left(\right|z_1{|-{\delta }_1)}^{2n}{\chi }_1-\tilde{\vartheta }\left({\Xi }_1-\frac{1}{{\gamma }_1}\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\left(\right|z_1{|-{\delta }_1)}^n\left(|z_2|-{\delta }_2-1\right){\chi }_1\hfill \end{array}$$ with the tuning function Ξ₁ = (|z ₁| − δ₁) ⁿ φ₁χ₁.

• Step i (2 ≤ i ≤ n − 1): The derivative of z _i is (6) $$\begin{array}{ccc}\hfill {\dot{z}}_i& =& z_{i+1}+{\alpha }_i+\sum _{l=1}^m{\varphi }_{il}^T{\theta }_{\sigma }\hfill \\ & & -\sum _{j=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_j}\left(x_{j+1}+\sum _{l=1}^m{\varphi }_{jl,\sigma }^T{\theta }_{\sigma }\right)\hfill \\ & & -\frac{\partial {\alpha }_{i-1}}{\partial \widehat{\vartheta }}\dot{\widehat{\vartheta }}-\sum _{j=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}\hfill \end{array}$$(6) Consider the following Lyapunov function: (7) $$\begin{array}{c}\hfill V_i=V_{i-1}+\frac{1}{n-i+2}{\left(|z_i|-{\delta }_i\right)}^{n-i+2}{\chi }_i\end{array}$$(7) Design the virtual control law $$\begin{array}{ccc}\hfill {\alpha }_i& =& -\left(c_i+\frac{5}{4}\right){\left(|z_i|-{\delta }_i\right)}^{n-i+1}{\mathrm{sg}}_i-\left({\delta }_{i+1}+1\right){\mathrm{sg}}_i\hfill \\ & & -\left({\varphi }_i\widehat{\vartheta }+f_i\right){\mathrm{sg}}_i+\sum _{j=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_j}{x}_{j+1}\hfill \\ & & +{\gamma }_1\left(\sum _{k=2}^{i-1}{\left(|z_k|-{\delta }_k\right)}^{n-k+1}\frac{\partial {\alpha }_{k-1}}{\partial \widehat{\vartheta }}{\chi }_k{\mathrm{sg}}_k\right){\varphi }_i{\mathrm{sg}}_i\hfill \\ & & +{\gamma }_1\frac{\partial {\alpha }_{i-1}}{\partial \widehat{\vartheta }}{\Xi }_i+\sum _{j=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}\hfill \end{array}$$ with the tuning function Ξ _i  = (|z _i | − δ _i ) ^{n − i + 1}φ _i χ _i + Ξ _i−1. Considering (|z _i | − δ _i ) ^{n − i + 1}χ _i ≥ (|z _i | − δ _i − 1) and using Young's inequality, we have (8) $$\begin{array}{ccc}& & \frac{1}{4}{\left(|z_{i-1}|+{\delta }_{i-1}\right)}^{2(n-i+2)}{\chi }_{i-1}+{\left(|z_i|-{\delta }_i\right)}^{2(n-i+1)}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}{\left(|z_i|-{\delta }_i\right)}^{n-i+1}{\chi }_{i-1}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}\left(|z_i|-{\delta }_i-1\right){\chi }_{i-1}\hfill \end{array}$$(8) By substituting α _i in the derivative of V _i and using (8(8) $$\begin{array}{ccc}& & \frac{1}{4}{\left(|z_{i-1}|+{\delta }_{i-1}\right)}^{2(n-i+2)}{\chi }_{i-1}+{\left(|z_i|-{\delta }_i\right)}^{2(n-i+1)}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}{\left(|z_i|-{\delta }_i\right)}^{n-i+1}{\chi }_{i-1}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}\left(|z_i|-{\delta }_i-1\right){\chi }_{i-1}\hfill \end{array}$$(8) ), we find $$\begin{array}{ccc}\hfill {\dot{V}}_i& \le & -\sum _{j=1}^i{C}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-i+1)}+\tilde{\vartheta }\left({\Xi }_i-\frac{1}{{\gamma }_1}\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\left(\sum _{k=2}^i{\left(|z_k|-{\delta }_k\right)}^{n-k+1}\frac{\partial {\alpha }_{k-1}}{\partial \widehat{\vartheta }}{\chi }_k{\mathrm{sg}}_k\right)\left({\gamma }_1{\Xi }_i-\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\left(|z_{i+1}|-{\delta }_{i+1}-1\right){\chi }_i{\left(|z_i|-{\delta }_i\right)}^{n-i+1}\hfill \end{array}$$ where C _j  = c _j for j = 1,… , i − 1, and C _i  = c _i + 1/4.

• Step n: The derivative of z _n is $$\begin{array}{ccc}\hfill {\dot{z}}_n& =& b_{\sigma }{\psi }_{\sigma }u+\sum _{l=1}^m{\varphi }_{nl,\sigma }^T{\theta }_{\sigma }+d-\sum _{j=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}-y_{\mathrm{m}}^{\left(n\right)}\hfill \\ & & -\sum _{j=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial x_j}\left(x_{j+1}+\sum _{l=1}^m{\varphi }_{jl,\sigma }^T{\theta }_{\sigma }\right)-\frac{\partial {\alpha }_{n-1}}{\partial \widehat{\vartheta }}\dot{\widehat{\vartheta }}\hfill \end{array}$$ Consider the following Lyapunov function with γ_{2, s} > 0, $s\in M$, γ₃ > 0: (9) $$\begin{array}{c}\hfill V_n=V_{n-1}+\frac{1}{2}{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n+\sum _{s=1}^M\frac{|b_s|}{2{\gamma }_{2,s}}{\tilde{\zeta }}_s^2+\frac{1}{2{\gamma }_3}{\tilde{\rho }}^2\end{array}$$(9) Without loss of generality, we consider a switching interval [t _l , t _{l + 1}). Assume that subsystem p is active for t ∈ [t _l , t _{l + 1}). We let the estimates ${\widehat{\zeta }}_s$, with $s\in M/\left\{p\right\}$, be constant at the same value they had at the last switched-out instant of subsystem s before t _l . Then, for t ∈ [t _l , t _{l + 1}), the derivative of V _n is as follows: (10) $$\begin{array}{ccc}\hfill {\dot{V}}_n& \le & {\dot{V}}_{n-1}+\left(|z_n|-{\delta }_n\right)\left(b_p{\psi }_{p}u-y_{\mathrm{m}}^{\left(n\right)}\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & +\left(|z_n|-{\delta }_n\right)\left(\left|d\right|+{\varphi }_n\vartheta +f_n\right){\chi }_n\hfill \\ & & -\left(|z_n|-{\delta }_n\right)\sum _{j=1}^{n-1}\left(\frac{\partial {\alpha }_{n-1}}{\partial x_j}{x}_{j+1}+\frac{\partial {\alpha }_{n-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & -\left(|z_n|-{\delta }_n\right)\frac{\partial {\alpha }_{n-1}}{\partial \widehat{\vartheta }}\dot{\widehat{\vartheta }}{\chi }_n{\mathrm{sg}}_n-\frac{|b_p|}{{\gamma }_{2,p}}{\tilde{\zeta }}_p{\dot{\widehat{\zeta }}}_p-\frac{1}{{\gamma }_3}\tilde{\rho }\dot{\widehat{\rho }}\hfill \end{array}$$(10) where C _j  = c _j for j = 1,… , n − 2, C _{n −1} = c _n−1 + 1/4 and C _n  = c _n + 1. Define the following intermediate control law α _n : $$\begin{array}{ccc}\hfill {\alpha }_n& =& -\left(c_n+1\right)\left(|z_n|-{\delta }_n\right){\mathrm{sg}}_n+\left({\varphi }_n\widehat{\vartheta }+f_n\right){\mathrm{sg}}_n\hfill \\ & & -\sum _{j=1}^{n-1}\left(\frac{\partial {\alpha }_{n-1}}{\partial x_j}{x}_{j+1}-\frac{\partial {\alpha }_{n-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}\right)-y_{\mathrm{m}}^{\left(n\right)}\hfill \\ & & -{\gamma }_1\left(\sum _{k=2}^{n-1}{\left(|z_k|-{\delta }_k\right)}^{n-k+1}\frac{\partial {\alpha }_{k-1}}{\partial \widehat{\vartheta }}{\chi }_k{\mathrm{sg}}_k\right){\varphi }_n{\mathrm{sg}}_n\hfill \\ & & -{\gamma }_1\frac{\partial {\alpha }_{n-1}}{\partial \widehat{\vartheta }}{\Xi }_n+\widehat{\rho }{\mathrm{sg}}_n\hfill \end{array}$$ We add and substract (|z_n | − δ _n )α _n χ _n sg _n to (10(10) $$\begin{array}{ccc}\hfill {\dot{V}}_n& \le & {\dot{V}}_{n-1}+\left(|z_n|-{\delta }_n\right)\left(b_p{\psi }_{p}u-y_{\mathrm{m}}^{\left(n\right)}\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & +\left(|z_n|-{\delta }_n\right)\left(\left|d\right|+{\varphi }_n\vartheta +f_n\right){\chi }_n\hfill \\ & & -\left(|z_n|-{\delta }_n\right)\sum _{j=1}^{n-1}\left(\frac{\partial {\alpha }_{n-1}}{\partial x_j}{x}_{j+1}+\frac{\partial {\alpha }_{n-1}}{\partial y_{\mathrm{m}}^{(j-1)}}{y}_{\mathrm{m}}^{\left(j\right)}\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & -\left(|z_n|-{\delta }_n\right)\frac{\partial {\alpha }_{n-1}}{\partial \widehat{\vartheta }}\dot{\widehat{\vartheta }}{\chi }_n{\mathrm{sg}}_n-\frac{|b_p|}{{\gamma }_{2,p}}{\tilde{\zeta }}_p{\dot{\widehat{\zeta }}}_p-\frac{1}{{\gamma }_3}\tilde{\rho }\dot{\widehat{\rho }}\hfill \end{array}$$(10) ). Due to χ _n sg _n sg _n = χ _n , it follows: (11) $$\begin{array}{ccc}\hfill {\dot{V}}_n& \le & -\sum _{j=1}^n{C}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\hfill \\ & & +\left(\sum _{k=2}^n{\left(|z_k|-{\delta }_k\right)}^{n-k+1}\frac{\partial {\alpha }_{k-1}}{\partial \widehat{\vartheta }}{\chi }_k{\mathrm{sg}}_k\right)\left({\gamma }_1{\Xi }_n-\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\tilde{\vartheta }\left({\Xi }_n-\frac{1}{{\gamma }_1}\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\left(|z_n|-{\delta }_n\right)\left({\alpha }_n+b_p{\psi }_{p}u+\left|d\right|{\mathrm{sg}}_n\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & -\frac{|b_p|}{{\gamma }_{2,p}}{\tilde{\zeta }}_p{\dot{\widehat{\zeta }}}_p-\frac{1}{{\gamma }_3}\tilde{\rho }\dot{\widehat{\rho }}-\left(|z_n|-{\delta }_n\right)\widehat{\rho }{\chi }_n\hfill \\ & & -{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^2\left(|z_n|-{\delta }_n-1\right){\chi }_{n-1}\hfill \end{array}$$(11)

We finally introduce for t ≥ t ₀, the adaptive controller with the control input (12) $$\begin{array}{c}\hfill u=-\frac{1}{{\psi }_{\sigma \left(t\right)}}\mathrm{sgn}\left(b_{\sigma \left(t\right)}\right){\widehat{\zeta }}_{\sigma \left(t\right)}{\alpha }_n\end{array}$$(12) and the adaptive laws: (13a) $$\begin{array}{c}\hfill \dot{\widehat{\vartheta }}={\gamma }_1\sum _{i=1}^n{\left(|z_i|-{\delta }_i\right)}^{n-i+1}{\varphi }_i{\chi }_i,\widehat{\vartheta }\left(0\right)>0\end{array}$$(13a) (13b) $$\begin{array}{cc}\hfill {\dot{\widehat{\zeta }}}_{\sigma \left(t\right)}=& {\gamma }_{2,\sigma \left(t\right)}\left(|z_n|-{\delta }_n\right){\alpha }_n{\chi }_n{\mathrm{sg}}_n,{\widehat{\zeta }}_p\left(0\right)>0,\forall p\in M\end{array}$$(13b) (13c) $$\begin{array}{ccc}\hfill \dot{\widehat{\rho }}& =& {\gamma }_3\left(|z_n|-{\delta }_n\right){\chi }_n,\widehat{\rho }\left(0\right)>0\hfill \end{array}$$(13c)

Remark 3.4:

To show the advantage of using functions sg _i , i = 1,… , n, consider in Step 1 the Lyapunov function $V_1=\frac{1}{2}{z}_1^2+\frac{1}{2{\gamma }_1}{\tilde{\vartheta }}^2$. Then, ${\dot{V}}_1\le z_1(z_2+{\alpha }_1+\mathrm{sgn}\left(z_1\right)({\varphi }_1\vartheta +f_1))$. This would lead to the virtual controller α₁ = −c ₁ z ₁ − sgn(z ₁)(φ₁ϑ + f ₁), which is not admissible because of the discontinuous sign function.

Remark 3.5:

The adaptive law (13b(14) $$\begin{array}{ccc}\hfill \parallel z_1{\parallel }_2& \le & {\delta }_1+\frac{1}{c_1^{1/\left(2n\right)}}\left(\sum _{j=1}^n{\left(|z_j\left(0\right)|-{\delta }_j\right)}^{2(n-j+1)}\right.\hfill \\ & & +{\left.\frac{1}{{\gamma }_1}\tilde{\vartheta }{\left(0\right)}^2+\sum _{s=1}^m\frac{|b_s|}{{\gamma }_{2,s}}{\tilde{\zeta }}_s{\left(0\right)}^2+\frac{1}{{\gamma }_3}\tilde{\rho }{\left(0\right)}^2\right)}^{\frac{1}{2n}}\hfill \end{array}$$(14) ) is to be implemented as follows: at switch-in instant¹of subsystem p, $p\in M$, ${\widehat{\zeta }}_p\left(t_{p_l}\right)$ is taken from the estimates available at the previous switch-out instant of the same subsystem, i.e. ${\widehat{\zeta }}_p\left(t_{p_l}\right)={\widehat{\zeta }}_p\left(t_{p_{l-1}+1}\right)$.

4. Main results

In this section, stability results based on the proposed adaptive controller are stated.

Theorem 4.1:

All signals of the closed-loop formed by the switched system (1(1) $$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& x_{i+1}\left(t\right)+\sum _{j=1}^m{\varphi }_{ij,\sigma \left(t\right)}^T\left({\bar{x}}_i\right){\theta }_{j,\sigma \left(t\right)},i=1,\cdots ,n-1\hfill \\ \hfill {\dot{x}}_n\left(t\right)& =& b_{\sigma \left(t\right)}{\psi }_{\sigma \left(t\right)}\left({\bar{x}}_n\right)u\left(t\right)+\sum _{j=1}^m{\varphi }_{nj,\sigma \left(t\right)}^T\left({\bar{x}}_n\right){\theta }_{j,\sigma \left(t\right)}+d\left(t\right)\hfill \\ \hfill y\left(t\right)& =& x_1\left(t\right),\sigma \left(t\right)\in M:=\left\{1,\cdots ,M\right\}\hfill \end{array}$$(1) ), controller (12(12) $$\begin{array}{c}\hfill u=-\frac{1}{{\psi }_{\sigma \left(t\right)}}\mathrm{sgn}\left(b_{\sigma \left(t\right)}\right){\widehat{\zeta }}_{\sigma \left(t\right)}{\alpha }_n\end{array}$$(12) ) and adaptive laws (13), are bounded under arbitrarily fast switching. In addition, the tracking error z ₁ is globally ultimately bounded with the prescribed ultimate bound δ₁, and the $L_2$ norm of the tracking error is given as (14) $$\begin{array}{ccc}\hfill \parallel z_1{\parallel }_2& \le & {\delta }_1+\frac{1}{c_1^{1/\left(2n\right)}}\left(\sum _{j=1}^n{\left(|z_j\left(0\right)|-{\delta }_j\right)}^{2(n-j+1)}\right.\hfill \\ & & +{\left.\frac{1}{{\gamma }_1}\tilde{\vartheta }{\left(0\right)}^2+\sum _{s=1}^m\frac{|b_s|}{{\gamma }_{2,s}}{\tilde{\zeta }}_s{\left(0\right)}^2+\frac{1}{{\gamma }_3}\tilde{\rho }{\left(0\right)}^2\right)}^{\frac{1}{2n}}\hfill \end{array}$$(14)

Proof:

Substituting the adaptive laws (13) in (11(11) $$\begin{array}{ccc}\hfill {\dot{V}}_n& \le & -\sum _{j=1}^n{C}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\hfill \\ & & +\left(\sum _{k=2}^n{\left(|z_k|-{\delta }_k\right)}^{n-k+1}\frac{\partial {\alpha }_{k-1}}{\partial \widehat{\vartheta }}{\chi }_k{\mathrm{sg}}_k\right)\left({\gamma }_1{\Xi }_n-\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\tilde{\vartheta }\left({\Xi }_n-\frac{1}{{\gamma }_1}\dot{\widehat{\vartheta }}\right)\hfill \\ & & +\left(|z_n|-{\delta }_n\right)\left({\alpha }_n+b_p{\psi }_{p}u+\left|d\right|{\mathrm{sg}}_n\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & -\frac{|b_p|}{{\gamma }_{2,p}}{\tilde{\zeta }}_p{\dot{\widehat{\zeta }}}_p-\frac{1}{{\gamma }_3}\tilde{\rho }\dot{\widehat{\rho }}-\left(|z_n|-{\delta }_n\right)\widehat{\rho }{\chi }_n\hfill \\ & & -{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^2\left(|z_n|-{\delta }_n-1\right){\chi }_{n-1}\hfill \end{array}$$(11) ), we have for t ∈ [t _l , t _{l + 1}) $$\begin{array}{ccc}\hfill {\dot{V}}_n& \le & -\sum _{j=1}^n{c}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\hfill \\ & & +\left(|z_n|-{\delta }_n\right)\left({\alpha }_n+b_p{\psi }_{p}u+{\mathrm{sg}}_n\left|d\right|\right){\chi }_n{\mathrm{sg}}_n\hfill \\ & & -\frac{|b_p|}{{\gamma }_{2,p}}{\tilde{\zeta }}_p{\dot{\widehat{\zeta }}}_p-\frac{1}{{\gamma }_3}\tilde{\rho }\dot{\widehat{\rho }}-\left(|z_n|-{\delta }_n\right)\widehat{\rho }{\chi }_n\hfill \\ & & +{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^2\left(|z_n|-{\delta }_n-1\right){\chi }_{n-1}\hfill \\ & & -{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n-\frac{1}{4}{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^4{\chi }_{n-1}\hfill \end{array}$$ Using the same inequality indicated by (8(8) $$\begin{array}{ccc}& & \frac{1}{4}{\left(|z_{i-1}|+{\delta }_{i-1}\right)}^{2(n-i+2)}{\chi }_{i-1}+{\left(|z_i|-{\delta }_i\right)}^{2(n-i+1)}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}{\left(|z_i|-{\delta }_i\right)}^{n-i+1}{\chi }_{i-1}{\chi }_i\hfill \\ & & \ge {\left(|z_{i-1}|-{\delta }_{i-1}\right)}^{n-i+2}\left(|z_i|-{\delta }_i-1\right){\chi }_{i-1}\hfill \end{array}$$(8) ), we derive (15) $$\begin{array}{ccc}& & -{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n-\frac{1}{4}{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^4{\chi }_{n-1}\hfill \\ & & \le -{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^2\left(|z_n|-{\delta }_n-1\right){\chi }_{n-1}\hfill \end{array}$$(15) In addition, according to Assumptions 1–2, we have (16) $$\begin{array}{ccc}\hfill \left(|z_n|-{\delta }_n\right)\left({\alpha }_n-\mathrm{sgn}\left(b_p\right)b_p\widehat{\zeta }{\alpha }_n-\left|b_p\right|\tilde{\zeta }{\alpha }_n\right){\mathrm{sg}}_n{\chi }_n& =& 0\hfill \\ \hfill \left(|z_n|-{\delta }_n\right)\left(\left|d\right|-\widehat{\rho }-\tilde{\rho }\right){\chi }_{n}Y\le & 0\end{array}$$(16) According to (15(15) $$\begin{array}{ccc}& & -{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n-\frac{1}{4}{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^4{\chi }_{n-1}\hfill \\ & & \le -{\left(|z_{n-1}|-{\delta }_{n-1}\right)}^2\left(|z_n|-{\delta }_n-1\right){\chi }_{n-1}\hfill \end{array}$$(15) ) and (16(16) $$\begin{array}{ccc}\hfill \left(|z_n|-{\delta }_n\right)\left({\alpha }_n-\mathrm{sgn}\left(b_p\right)b_p\widehat{\zeta }{\alpha }_n-\left|b_p\right|\tilde{\zeta }{\alpha }_n\right){\mathrm{sg}}_n{\chi }_n& =& 0\hfill \\ \hfill \left(|z_n|-{\delta }_n\right)\left(\left|d\right|-\widehat{\rho }-\tilde{\rho }\right){\chi }_{n}Y\le & 0\end{array}$$(16) ), it holds for t ∈ [t _l , t _{l + 1}) (17) $$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{c}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\end{array}$$(17) Since the signals z _i (·) for i = 1,… , n, $\tilde{\vartheta }(·)$, ${\tilde{\zeta }}_p(·)$ for $p\in M$ and $\tilde{\rho }(·)$ are continuous at the switching instants, the Lyapunov function V _n (9(9) $$\begin{array}{c}\hfill V_n=V_{n-1}+\frac{1}{2}{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n+\sum _{s=1}^M\frac{|b_s|}{2{\gamma }_{2,s}}{\tilde{\zeta }}_s^2+\frac{1}{2{\gamma }_3}{\tilde{\rho }}^2\end{array}$$(9) ) is continuous for all t ≥ 0. The condition (17(17) $$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{c}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\end{array}$$(17) ) holds for all t ≥ 0, which implies that all signals of the closed-loop system are bounded. In addition, it immediately follows from (17(17) $$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{c}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\end{array}$$(17) ) that ${\dot{V}}_n<0$ when z _j > δ _j for all j = 1,… , n, which implies that z ₁ starting outside a compact set $B_{{\delta }_1}:=\left\{|z_1|\le {\delta }_1\right\}$ will enter $B_{{\delta }_1}$ within a finite time. In other words, an ultimate bound of the tracking error z ₁ is δ₁. Integrating (17(17) $$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{c}_j{\left(|z_j|-{\delta }_j\right)}^{2(n-j+1)}{\chi }_j\end{array}$$(17) ) from 0 to ∞, we have $$\begin{array}{c}\hfill \parallel z_1-{\delta }_1{\parallel }_2^{2n}\le \frac{1}{c_1}{\int }_0^{\infty }{\dot{V}}_n\left(t\right)dt\le \frac{1}{c_1}{V}_n\left(0\right)\end{array}$$ which results in (14(14) $$\begin{array}{ccc}\hfill \parallel z_1{\parallel }_2& \le & {\delta }_1+\frac{1}{c_1^{1/\left(2n\right)}}\left(\sum _{j=1}^n{\left(|z_j\left(0\right)|-{\delta }_j\right)}^{2(n-j+1)}\right.\hfill \\ & & +{\left.\frac{1}{{\gamma }_1}\tilde{\vartheta }{\left(0\right)}^2+\sum _{s=1}^m\frac{|b_s|}{{\gamma }_{2,s}}{\tilde{\zeta }}_s{\left(0\right)}^2+\frac{1}{{\gamma }_3}\tilde{\rho }{\left(0\right)}^2\right)}^{\frac{1}{2n}}\hfill \end{array}$$(14) ) using the definition of V _n in (9(9) $$\begin{array}{c}\hfill V_n=V_{n-1}+\frac{1}{2}{\left(|z_n|-{\delta }_n\right)}^2{\chi }_n+\sum _{s=1}^M\frac{|b_s|}{2{\gamma }_{2,s}}{\tilde{\zeta }}_s^2+\frac{1}{2{\gamma }_3}{\tilde{\rho }}^2\end{array}$$(9) ). This completes the proof.

Remark 4.1:

From a theoretical point of view, the ultimate bound of the tracking error (steady-state performance) can be made smaller by selecting a smaller δ₁. However, from a practical point of view, when δ _i , i = 1,… , n, tends to zero, the derivative of sg _i goes to infinity, which might lead to large control input and eventually numerical instability. It results that δ _i should be carefully chosen according to the maximum allowed control input and the numerical precision.

Remark 4.2:

According to (14(14) $$\begin{array}{ccc}\hfill \parallel z_1{\parallel }_2& \le & {\delta }_1+\frac{1}{c_1^{1/\left(2n\right)}}\left(\sum _{j=1}^n{\left(|z_j\left(0\right)|-{\delta }_j\right)}^{2(n-j+1)}\right.\hfill \\ & & +{\left.\frac{1}{{\gamma }_1}\tilde{\vartheta }{\left(0\right)}^2+\sum _{s=1}^m\frac{|b_s|}{{\gamma }_{2,s}}{\tilde{\zeta }}_s{\left(0\right)}^2+\frac{1}{{\gamma }_3}\tilde{\rho }{\left(0\right)}^2\right)}^{\frac{1}{2n}}\hfill \end{array}$$(14) ), the transient of the tracking error ($L_2$ norm) can be improved by increasing c _i , i = 1,… , n, γ₁, γ_{2, s} , $s\in M$ and γ₃.

5. Numerical example

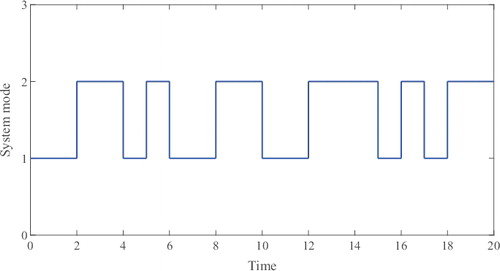
In this section, a simple but instructive example is used to show the effectiveness of the proposed control scheme. The following switched nonlinear second-order system with two subsystems is adopted: $$\begin{array}{ccc}& & \left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=x_2\left(t\right)+sin\left(x_1\right){\theta }_{\sigma \left(t\right)}\hfill \\ {\dot{x}}_2\left(t\right)=b_{\sigma \left(t\right)}u\left(t\right)+sin\left(x_1{x}_2\right)+d\left(t\right)\hfill \\ y\left(t\right)=x_1\left(t\right)\hfill \end{array}\right.\hfill \\ & & \left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=x_2\left(t\right)+cos\left(x_1^2\right){\theta }_{\sigma \left(t\right)}\hfill \\ {\dot{x}}_2\left(t\right)=b_{\sigma \left(t\right)}u\left(t\right)-cos\left(x_1{x}_2\right)+d\left(t\right)\hfill \\ y\left(t\right)=x_1\left(t\right)\hfill \end{array}\right.\hfill \end{array}$$ where θ₁ = 1, θ₂ = −1, d(t) = 0.1cos (2πt), b ₁ = −0.5, b ₂ = 2. The reference signal is taken as y _m(t) = 0.5cos (t) + 0.5. Consider the coefficients c ₁ = c ₂ = 1. Note that unknown terms θ₁, θ₂, d(t), b ₁ and b ₂ are used for simulation but not for control design. The following initial conditions are chosen: x ₁(0) = 3, x ₂(0) = 2, $\widehat{\vartheta }\left(0\right)=0.1$, ${\widehat{\zeta }}_1\left(0\right)={\widehat{\zeta }}_2\left(0\right)=0.1$ and $\widehat{\rho }\left(0\right)=0.1$. The adaptive gains are set as: γ₁ = 0.1, γ_{2, 1} = γ_{2, 2} = 0.1 and γ₃ = 0.1. The switching signal is designed as shown in Figure 1. 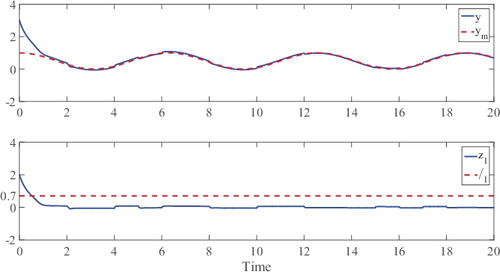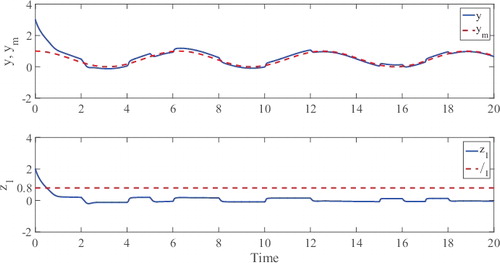To illustrate the performance of the tracking error z ₁ with different values of δ₁, without loss of generality, we choose the following two options: (a) δ₁ = δ₂ = 0.8; (b) δ₁ = 0.7, δ₂ = 0.8. Then, using the reparameterisation lemma, it follows: $$\begin{array}{c}\hfill {\varphi }_1=1,f_1=y_{\mathrm{m}}+1\end{array}$$ which leads to the first virtual control law $$\begin{array}{c}\hfill {\alpha }_1=-\frac{5}{4}{\left(|z_1|-{\delta }_1\right)}^2{\mathrm{sg}}_1-f_1{\mathrm{sg}}_1-\widehat{\vartheta }{\mathrm{sg}}_1-2{\mathrm{sg}}_1\end{array}$$ According to (3(3) $$\begin{array}{ccc}& & \left|\sum _{j=1}^m{\varphi }_{ij,\sigma }^T\left({\bar{x}}_i\right){\theta }_{j,\sigma }-\sum _{k=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial x_k}\sum _{j=1}^m{\varphi }_{kj,\sigma }^T\left({\bar{x}}_k\right){\theta }_{j,\sigma }\right|\hfill \\ & & \le {\varphi }_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\vartheta +f_i({\bar{x}}_i,{\bar{y}}_{\mathrm{m}}^{(i-1)},\widehat{\vartheta })\hfill \end{array}$$(3) ), it follows: $$\begin{array}{ccc}\hfill {\varphi }_2& =& \frac{5}{2}\left(\right|z_1|-{\delta }_1){\chi }_1+\frac{5}{4}\left(\right|z_1{|-{\delta }_1)}^2\frac{1}{{\delta }_1^6}{\bar{\chi }}_1\hfill \\ \hfill f_2& =& \frac{1}{{\delta }_1^6}{\bar{\chi }}_1\left(y_{\mathrm{m}}+1+\widehat{\vartheta }\right)+1\hfill \end{array}$$ where ${\bar{\chi }}_1$ is defined in a reverse manner of χ₁ as $$\begin{array}{c}\hfill {\bar{\chi }}_1\left(z_1\right)=\left\{\begin{array}{c}0,|z_1|\ge {\delta }_1\hfill \\ 1,|z_1|<{\delta }_1\hfill \end{array}\right.\end{array}$$ Hence, the intermediate controller α₂ is designed as follows: $$\begin{array}{ccc}\hfill {\alpha }_2& =& -2\left(|z_2|-{\delta }_2\right){\mathrm{sg}}_2+\left({\varphi }_2\widehat{\vartheta }+f_2\right){\mathrm{sg}}_2-\frac{\partial {\alpha }_1}{\partial x_1}{x}_2\hfill \\ & & -\frac{\partial {\alpha }_1}{\partial \widehat{\theta }}{\gamma }_1{\Xi }_2-\frac{\partial {\alpha }_1}{\partial y_{\mathrm{m}}}{\dot{y}}_{\mathrm{m}}+\widehat{\rho }{\mathrm{sg}}_2-y_{\mathrm{m}}^{\left(2\right)}\hfill \end{array}$$ and the controller u is as in (12(12) $$\begin{array}{c}\hfill u=-\frac{1}{{\psi }_{\sigma \left(t\right)}}\mathrm{sgn}\left(b_{\sigma \left(t\right)}\right){\widehat{\zeta }}_{\sigma \left(t\right)}{\alpha }_n\end{array}$$(12) ). The output of the switched system and the reference model, and the tracking error for options (a) and (b) are given in Figures 2 and 3, respectively, which show that the tracking error converges to the prescribed ultimate bounds 0.8 and 0.7, respectively, as predicted by the global ultimate boundedness results. In addition, it can be observed that a better steady-state performance is achieved with a smaller δ₁.

Figure 1. The switching signal.

Figure 2. Tracking performance with δ₁ = 0.8.

Figure 3. Tracking performance with δ₁ = 0.7.

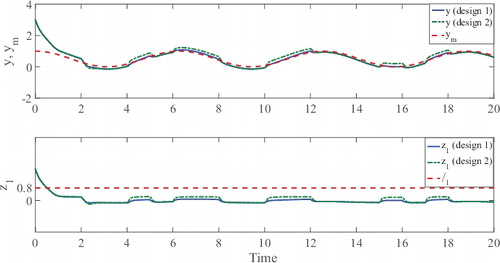
The transient performances of the tracking error under two different selections of pre-designed gains c ₁ and c ₂, γ₁, γ_{2, 1}, γ_{2, 2}, γ₃ are given in Figure 4, which shows that according to (14(14) $$\begin{array}{ccc}\hfill \parallel z_1{\parallel }_2& \le & {\delta }_1+\frac{1}{c_1^{1/\left(2n\right)}}\left(\sum _{j=1}^n{\left(|z_j\left(0\right)|-{\delta }_j\right)}^{2(n-j+1)}\right.\hfill \\ & & +{\left.\frac{1}{{\gamma }_1}\tilde{\vartheta }{\left(0\right)}^2+\sum _{s=1}^m\frac{|b_s|}{{\gamma }_{2,s}}{\tilde{\zeta }}_s{\left(0\right)}^2+\frac{1}{{\gamma }_3}\tilde{\rho }{\left(0\right)}^2\right)}^{\frac{1}{2n}}\hfill \end{array}$$(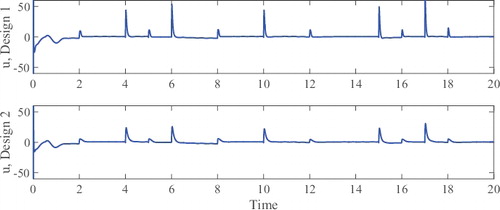14) ), a better transient performance is achieved by properly selecting the parameters. This is consistent with the results given in Theorem 4.1. Moreover, the evolution of the inputs u for the two different selections of gains are given in Figure 5, where the peaks are produced by the switching behaviours: we notice a trade-off between smaller tracking error and large control inputs.

Figure 4. Comparison of transient performance with different designs; Design 1: c ₁ = c ₂ = 1, γ₁ = 0.01, γ_{2, 1} = γ_{2, 2} = 1, γ₃ = 0.01; Design 2: c ₁ = c ₂ = 0.8, γ₁ = 0.005, γ_{2, 1} = γ_{2, 2} = 0.1, γ₃ = 0.005.

Figure 5. The evolution of the inputs u under Design 1 and Design 2, respectively.

6. Conclusions

Robust adaptive tracking of uncertain switched nonlinear systems has been investigated in this paper. Using a reference-dependent reparametrisation method, we have designed a set of novel differentiable virtual controllers, and an adaptive controller that overcomes the assumption of a common sign of the input vector fields. Global ultimate boundedness of the switched uncertain system can be guaranteed with the prescribed ultimate bound and adjustable $L_2$ norm of the tracking error. A numerical example has been used to show the effectiveness of the proposed method. Future work will focus on adaptive control design for switched nonlinear systems in the presence of time-varying delays.

Acknowledgments

This work was supported in part by the China Scholarship Council (CSC), File No. 20146160098, and the Young Scientist Fund of National Natural Science Foundation of China (NSFC), Grant No. 61703099.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

China Scholarship Council [grant number 20146160098]; Young Scientist Fund of National Natural Science Foundation of China (NSFC) [grant number 61703099].

Notes

1. The switch-in and switch-out instant pair of subsystem p, $p\in M$, is denoted by $(t_{p_l},t_{p_l+1})$ with $l\in {\mathbb{N}}^{+}$.