The role of authorial context in mathematicians’ evaluations of proof

ABSTRACT

We report on a series of task-based interviews in which nine mathematicians were asked to evaluate a series of six mathematical arguments, purportedly produced either by fellow mathematicians or undergraduate students. In this paper, we attend to the role of context in mathematicians’ responses, leading to four themes in expectations when evaluating the proofs that they read. First, mathematicians’ evaluations of identical arguments were sensitive to researchers’ manipulation of authorship, with most accepting arguments purportedly produced by a colleague while taking a more critical view of that same argument if produced by an undergraduate student. Our thematic analysis of interview responses led to three context-based factors influencing mathematicians’ responses when evaluating student-produced texts: course goals, instructors’ expectations, and assessment type. In the final section, we consider implications for researchers focused on understanding common practice amongst mathematicians as well as the pedagogic consequences of our findings for practice in the classroom.

KEYWORDS:

• Proof
• Grading
• Assessment
• Task-based interviews
• Contextual understanding

1. Introduction

Proof is central to undergraduate mathematics and is a known challenge for many students. In particular, students’ proof writing practices are a pivotal aspect of their mathematical apprenticeship. As instructors, we spend a lot of time evaluating students’ mathematical arguments in both written assessments and during informal in-class discussions. Yet, despite its importance, we know very little about the factors influencing mathematicians’ grading practices.

In recent decades, it has become increasingly popular to talk of mathematical practice, and mathematical proof in particular, as a socially constructed entity (Dawkins & Weber, 2017; Sfard, 2008). This is a far cry from the historically privileged position of mathematics as the pinnacle of certainty, above the empirical sciences in its search for a priori knowledge. While this increasing awareness of the social dimension of mathematical proof has permeated many aspects of research in undergraduate mathematics education, we feel that the social dimension of proof has gone under-examined with respect to mathematicians’ proof-reading practices and their grading of student-produced arguments.

We add to our understanding by focusing on mathematicians’ grading of six mathematical arguments one might expect to find in an undergraduate ‘Introduction to Proof’ (ITP) course, covering topics including elementary logic, set theory and mathematical argumentation. By choosing an instruction-based context for our research, we address the dual aims of understanding mathematicians’ epistemological beliefs about proof itself, and their pedagogic beliefs about grading students’ work .

Participating mathematicians were first shown three arguments and told they were produced by a fellow mathematician teaching an introduction to proof course. After being asked to evaluate the validity of the purported proof, mathematicians were then told that the same text was produced by an undergraduate student and asked if this changed their perspective. Following this task-based interview, mathematicians then participated in a more traditional semi-structured interview task in which they were asked more general questions about their approaches to evaluating the proofs that they read and what they expect students to gain from their exposure to (writing) proofs in undergraduate courses.

We begin this paper by discussing the social dimension of proof and its manifestations on mathematicians’ engagement with arguments produced by others. We discuss the role of context informing mathematicians’ evaluations of the proofs that they read, before turning to recent research on mathematicians’ grading of student-produced proofs. We then present our empirical research with mathematicians. We end this paper with commentary on the implications of our work for understanding of mathematicians’ grading practices and directions for future work.

2. The social nature of mathematics and mathematical proof

A proof becomes a proof after the social act of ‘accepting it as a proof’

– Manin (1977).

The social dimension of mathematics has seen much commentary in recent decades (Hanna, 1987; Hersh, 1997; Larvor, 2012). Many, including Manin (1977) and Sfard (2008), have discussed the acceptance of proofs by the community-at-large. Others have focused on the production of proofs as a social interaction between mathematical knowers, sometimes in research groups, and other times through more distant discursive practices (Martin & Pease, 2013). And others still, have focused on the process of learning mathematics as an apprenticeship into the mathematical community (Cobb & Yackel, 2016; Dawkins & Weber, 2017).

Dawkins and Weber (2017) enumerated a series of values and norms held by the mathematical community. The authors note that students’ famed difficulties with mathematical proof can be at least partially accounted for by a lack of appreciation for these values and norms. In this way, researchers have positioned learners of mathematics as apprentices into the mathematical community (Cobb & Yackel, 2016; Dawkins & Weber, 2017; Sfard, 2008). The learning process, hence, centers on coming to understand and appreciate the values and norms of the community.

We endorse this ‘apprenticeship model’ of learning mathematics and mathematical proof. Moreover, we note its importance in understanding how mathematicians read and evaluate students’ proofs. That is, when mathematicians evaluate student-produced proofs, they act to uphold the values and norms of the community. When a student unknowingly violates a norm in their writing, that student identifies themselves as an outsider to the community. It is the role of the mathematician, or instructor, to identify and correct the error to aid the student’s apprenticeship and hopefully guide that student’s future proof production. Lew and Mejía-Ramos (2019; 2020) capitalized on this norm-correcting behavior through the use of ‘breaching experiments’, in which mathematicians were presented with a series of potential violations in an attempt to draw out the values and norms most important to the mathematicians in their study. We return to the findings of Lew and Mejía-Ramos later, having discussed the consequences of the social dimension of mathematics on mathematicians’ reading practices more generally.

2.1. Mathematicians’ proof-reading practices

Mathematicians have been frequently observed not to agree on various tasks associated with proof (e.g., Inglis et al., 2013; Weber & Czocher, 2019). Weber and Mejía-Ramos (2011) identified three strategies used by mathematicians’ when evaluating the purported proofs of their peers: appealing to the authority of other mathematicians who read the proof, line-by-line reading, and modular reading. Weber (2018) focused, in particular, on the authorial context, arguing that mathematicians attend to myriad factors including the reputation of the author(s) and publication outlet, and the age and usage of the result at stake. This argument contradicts a common external conception of mathematics as an acontextual discipline in which ‘results are objective, infallible, and incorrigible’ (p. 239).

Weber’s theoretical assertions are supported in the literature, both on mathematicians’ research practice, and in their evaluation of student-produced texts. Inglis et al. (2013) found in a series of task-based interviews, that mathematicians disagreed on the validity of several purported proofs. These authors found that applied mathematicians were more likely to accept the validity of a given argument than their ‘pure’ colleagues. Similarly, Miller et al. (2018) found that mathematicians often awarded full marks for instructor-produced proofs but different scores for those same proofs when purportedly produced by students in multiple mathematical settings. These findings were predicted by Sfard (2008) who conjectured that mathematicians’ evaluations of the validity of given arguments ‘are probably the least uniform aspect[s] of mathematical discourses’ (p. 231).

On the other hand, Weber and Czocher (2019) found substantive agreement on a task similar to Inglis et al. (2013), noting that mathematicians appeared only to disagree on fringe examples like computer-aided or diagrammatic proofs. Davies et al. (2020) found similar results in a comparative judgement-based study, reporting a high degree of reliability between mathematicians’ endorsements of student-produced texts.

The extent and locus of the disagreement on mathematicians’ proof-reading practices remain open questions. In some cases, it seems that mathematicians demonstrate a high degree of agreement on what constitutes a good mathematical proof. In others, the participating mathematicians diverge. In the following section, we focus on the role of context in an attempt to unpack this question.

2.2. Mathematicians’ proof-reading practices: the role of context

Beyond authorship, several authors have noted other contextual factors motivating mathematicians’ judgement. Weber and Czocher (2019) considered two contextual factors guiding mathematicians’ responses: purpose and audience. Concerning purpose, Weber and Czocher found that mathematicians were ‘less tolerant of a gap if the goal of the proof was to rigorously establish’ a new result (p. 4) than if a proof were presented for ‘recreational purposes’ in an expository journal (ibid). The same authors referred to the knowledge base of the audience, and the perception of whether an intended reader was ‘capable of bridging the gap’ (ibid).

Returning to mathematicians’ reading of student-produced proofs, both Moore (2016) and Lew and Mejía-Ramos (2020) raised contextual factors influencing mathematicians’ behavior. Moore discussed mathematicians’ focus on more than just the ‘decontextualized mathematical text’, making frequent reference to students’ understanding and proof-production skills as entities both disconnected from the text-at-hand and relevant to the evaluation of that text. In a similar interview study of mathematicians’ reading, Lew and Mejía-Ramos (2020) noted the variety in (mathematicians’ perceptions of) linguistic conventions of proofs in textbooks, written by instructors on blackboards and student-produced proofs. Mathematicians held textbook proofs to higher standards of rigor than blackboard or student-produced proofs, and were more tolerant of poor grammar, mixed notations and missing verbal connectives from blackboard proofs than those produced by students.

3. Research questions

Having established that mathematicians’ readings of proofs are both highly variable and sensitive to at least some contextual features, it remains to understand the role of context in more detail. In light of the literature survey above, we pose three questions to guide the investigation that follows:

1. What can be learned about mathematicians’ epistemological beliefs about proof through the evaluation of (ostensibly) student-produced arguments?

2. How are mathematicians’ evaluations of proofs sensitive to information about the author of the proof?

3. How are mathematicians’ evaluations of proof influenced by the context in which the proof was produced?

4. Methods

The findings we present in the current paper are based on a reanalysis of the same dataset that formed the basis of Miller et al. (2018). Where Miller and colleagues focused primarily on the quantitative variance itself, in the present paper we focus on qualitative features associated with the role of context.

4.1. Participants

Nine research-active mathematicians were interviewed for this study. All participants were from the same university in the eastern United States, and all had taught at least one upper-level mathematics course on proof-based mathematics. Consistent with previous presentations of these data, we refer to the nine participants with labels M1 through M9 and refer to all with feminine pronouns.

4.2. Materials

We examined proofs of three propositions from number theory that might be proven in an ITP course. For each proposition, we generated two proofs. The Complete Proof (CP) was a proof that included detail sufficient for us to expect the proof to be judged as correct and valid without additional detail at the level of an ITP course. The Incomplete Proof (IP) was an abbreviated version of the Complete Proof that omitted some pieces of the proof, e.g., not defining newly introduced variables.

We present each proposition and its CP below, placing boxes around the text that we omitted from the Incomplete Proof.

Proposition 1:

If $n^2+1$ is a prime number greater than 5, then the digit in the 1’s place of n is 0, 4, or 6.

Proof 1:

Suppose that $n^2+1$ is a prime number greater than 5. Thus $n^2+1$ is odd and so $n$ is even. Then $n$ is of the form $10k+0$, $10k+2$, $10k+4$, $10k+6$, or $10k+8$. Then $n^2+1$ is of one of the following forms: $\begin{array}{rl}(10k+0{)}^2+1& =100k^2+1=10(10k^2)+1;\end{array}$ $\begin{array}{rl}(10k+2{)}^2+1& =100k^2+40k+4+1=10(10k^2+4k)+5;\end{array}$ $\begin{array}{rl}(10k+4{)}^2+1& =100k^2+80k+16+1=10(10k^2+8k+1)+7;\end{array}$ $\begin{array}{rl}(10k+6{)}^2+1& =100k^2+120k+36+1=10(10k^2+12k+3)+7;\end{array}$ $\begin{array}{rl}(10k+8{)}^2+1& =100k^2+160k+64+1=10(10k^2+16k+6)+5.\end{array}$ Of these, $n=10k+2$ and $n=10k+8$ yield expressions for $n^2+1$ that are clearly divisible by 5 and thus not prime (since $n^2+1>5$). The only choices for $n$, then, are those numbers with 1’s digits of 0, 4, or 6.

Proposition 2:

There exists a sequence of 100 consecutive integers, none of which is prime.

Proof 2:

We will show that the 100 consecutive integers 101! + 2, 101! + 3, 101! + 4, … , 101! +101 contains no primes. Since both terms of 101! + 2 contain a factor of 2, 2 is a common factor of 101! + 2 and thus 101! + 2 is not prime. Since both terms of 101! + 3 contain a factor of 3, 3 is a common factor of 101! + 3 and thus 101! + 3 is not prime. Similarly, for any $j\in \{2,3,4,\dots ,101\}$, $j$ is a factor of 101!$+j$ and thus 101!$+j$ is not prime. Thus, the sequence of 100 consecutive integers given above contains no primes.

Proposition 3:

Given two angles $x$ and $y$, we define that $x\sim y$ iff ${\sin }^{2}x+{\cos }^{2}y=1$. Show that $\sim$ is an equivalence relation on $\mathbb{R}$.

Proof 3:

(Reflexive): Let $x\in \mathbb{R}$. Since ${\sin }^{2}x+{\cos }^{2}x=1$ by Pythagorean Theorem, $x\sim x$.

(Symmetric): Let $x,y\in \mathbb{R}$ and $x\sim y$. So ${\sin }^{2}x+{\cos }^{2}y=1$. Using Pythagorean Theorem on both ${\sin }^{2}x$ and ${\cos }^{2}y$, we have $(1-{\cos }^{2}x)+(1-{\sin }^{2}y)=1$ which implies ${\sin }^{2}y+{\cos }^{2}x=1$ and hence $y\sim x$.

(Transitive): Let $x,y,$ and $z\in \mathbb{R}$, $x\sim y$ and $y\sim z$. So ${\sin }^{2}x+{\cos }^{2}y=1$ and ${\sin }^{2}y+{\cos }^{2}z=1$. Adding up these two equations we have $({\sin }^{2}x+{\cos }^{2}y)+({\sin }^{2}y+{\cos }^{2}z)=2.$ Rewriting we have ${\sin }^{2}x+({\cos }^{2}y+{\sin }^{2}y)+{\cos }^{2}z=2$. Thus ${\sin }^{2}x+1+{\cos }^{2}z=2$ or ${\sin }^{2}x+{\cos }^{2}z=1$ and hence $x\sim z$. Therefore $\sim$ is an equivalence relation.

The omissions in these proofs are not necessarily large jumps in logic. In fact, each mathematician was able to understand and judge the validity of the work with the omissions. However, as we will see, the context in which the proof was provided had a significant influence on how the mathematician viewed the work.

4.3. Procedure

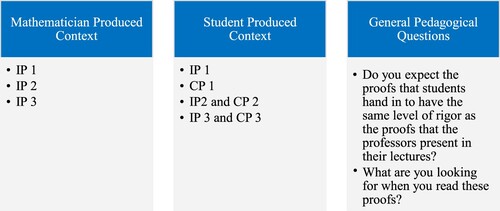
Each mathematician engaged in three phases of a task-based interview that was video recorded (see Figure 1 for a summary of these phases). First, the mathematicians were told that a colleague had presented IP 1 in lecture. They were asked if they thought the proof was correct and to comment on the pedagogical quality and appropriateness of the proof. This was repeated for IP 2 and IP 3.

Figure 1. Interview phases.

Second, each participant was presented with IP 1 again, but this time told that a student had produced the work instead of a colleague. They were asked to determine if the proof was correct and how many points they would assign on a ten-point scale. The mathematicians were then given CP 1 and asked the same questions. This process was repeated for Propositions 2 and 3 with the modification that the incomplete and complete proofs were presented together. The experience with Proposition 1 led them to immediately recognize that a second, potentially better proof would be coming; hence, they wanted to be able to compare them from the beginning.

For the third and final stage, the mathematicians were asked a series of general open-ended interview questions about the role of proof in their undergraduate courses.

4.4. Analysis

All interviews were transcribed for analysis. As the interview tasks had been designed with a mathematician-produced versus student-produced context, a deductive thematic approach was initially used (Braun & Clarke, 2006). We sought to identify how the author of the proof affected the mathematicians’ view of the proof. To this end, data were coded for instances of context that influenced the mathematicians’ views of the presented proof. During this process, some transcript excerpts were lightly edited for readability, but original meanings have been preserved in all cases.

As the mathematicians talked about how they would grade student work, it became evident that context was an important feature of how they would choose to assign points. The codes that were generated in relation to context gave rise to four broad categories of influence: authorial experience, course goals, expectations, and assessment type.

5. Results

The first of our four themes, authorial experience, explores the sensitivity of mathematicians’ evaluations to their understanding of the author. The latter three themes focus on evaluations of student-produced proofs only. The mathematicians who provided excerpts associated with each of the four themes are shown in Table 1.

Table 1. Categories of context for the grading of proofs.

Theme	Contextual Factors	Mathematicians
1	Authorial experience	M1, M2, M3, M4, M6, M7, M8, M9
2a	Course Goals	M2, M5, M7, M8, M9
2b	Technical Requirements	M1, M2, M3, M4, M5, M6, M7, M8, M9
2c	Assessment Type	M6, M7, M9

5.1. Theme 1: authorial experience

Participants were initially presented with the Incomplete Proofs and told that they were authored by a colleague (to be presented in an ITP course). In this context, mathematicians generally agreed that the proofs were good, sometimes without casting a particularly critical eye over the text. For example, when told the proof was produced by a colleague, M1 ‘read it with an assumption that what [they were] reading was going to be correct and good.’

Further, five mathematicians noted explicitly that the gaps were not overly problematic in this context. As M4 noted: ‘… it is the kind of thing that if I saw in a textbook, I would say good. Good that they did not put it in there, so the student has to think, why does this work?’ M7 commented,

But the way [the proof] is written, it is not necessarily a bad thing because I also like when people start asking these questions. When you just skip a step, but you don’t think that it is that big of deal, and [students] say, well, can you explain that.

Crucially, when evaluating validity, some mathematicians noted explicitly that the authorial context influenced their evaluation directly. M1, for example, admitted to being more skeptical of students’ work, before even reading the proof itself:

if you are telling me … this is something that a colleague presented … my default assumption is that [it] should be correct … It would be very, very surprising to me … I would wonder if maybe the student’s notes were incorrect or something like that … .

Others made more general points about proof production, and the increased scrutiny given when the text is purported produced by a student. When discussing both versions of the proof for Proposition 2, M8 stated,

… sometimes we assume people mean what we think they mean rather than what they actually, what they write. So sometimes [the student] gets away with [gaps in the proof] when you wouldn’t otherwise. In an [ITP] course you probably want to hold them a little more accountable. [CP 2] is much more clearly explained.

Moreover, even within the student population, this level of scrutiny was even sensitive to the level of the student. As M6 explained how she would grade Proposition 2, she stated that she would be okay with IP 2, if a real analysis level mathematics student handed it in. She would not be as convinced for an ITP student. Finally, M3 commented about giving students a little leeway on their written proofs because she does not expect the students to produce the same level of proofs she gives in lecture. M9 concurred with this by explaining ‘they are not going to get the proof even when you give them a fabulous explanation of it in class’ and thus she would not expect the level of student proof to rise to the level of her proofs.

5.2. Theme 2: Evaluating student-produced proofs

We now turn attention to our mathematicians’ responses to the purportedly student-produced proofs. All nine mathematicians raised the expectations laid out by the instructor as a factor influencing their grading of proofs. We identified three overlapping subthemes within these expectations: Expectations regarding course goals, technical requirements, and assessment types.

5.2.1. Theme 2a: Course goals

Five mathematicians commented on grading proofs based on the goals they held for the course for which the proof was produced. These comments most frequently referred to the level of rigor appropriate for the course, or to the appropriate use of notation and language.

Depending on the course, the details of a proof may be less important. Particularly in upper-division courses, details seemed to matter less. For example, M2 explained that a primary goal for her Discrete Mathematics course (junior level) is to have the right idea of a proof, noting when speaking about mathematical induction, ‘First, I just take a look, I usually do not pay attention to the details and the smaller algebra stuff. First, I take a quick glance to make sure they have the right idea.’ In talking about her Complex Variables course (senior level), M7 articulated, ‘I am … happy with proofs that have some serious gaps in them, but they show that they are going in the right direction, and they are using the right concept.’

For lower-level courses, such as Introduction to Proof, providing most, if not all, details was considered an important course goal. After commenting about the grading of both incomplete and complete proof, M7 was asked if she would go back and reassess IP 2 after assigning points to CP 2. She stated that she would not reassess, ‘unless this was part of the requirement for the course. I would say I need [to see] all the easiest of steps. I need [the gap in IP 2] explained, and if you don’t, you will lose points.’ Later, talking specifically about an ITP course, M7 noted, ‘I would like them to give me some crystal-clear arguments because this is the sole purpose of this [ITP] course.’

When M9 was grading Proposition 3, she remarked about the scope of variables not being present in IP 3. She noted that ‘it would depend on if that was what I focused on [in class].’ In other words, if it were a course goal that students should be thorough when writing proofs, then she would expect them to state the scope of variables. Hence, the level of detail that is expected is heavily dependent on the instructor’s goals for the class.

For some, course goals can change as the semester progresses. In the words of M7,

There are times when you give them examples in class that have a certain level of rigor, but as time goes on and as the students become more mature in their own abilities to reason and argue … .you can make statements and assumptions that they have an obligation to sit down and figure out what the details are or know what the implied statements are within that.

Learning to use mathematical notation was cited as a possible course goal. M5 commented about this when grading Proposition 2. She stated,

 … it depends on context. [the author of CP 2] knows how to handle notation better. Conceptually there is no difference between [the two proofs]. I would give both full-credit unless we were trying to learn how to use notation, then this [CP 2] would get full credit and [IP 2] wouldn’t.

In the discussion section to follow, we return to the goals of the course, and the importance of making these goals explicit to students.

5.2.2. Theme 2b: Expectations regarding technical requirements

All of our mathematicians identified technical requirements and the level of detail as playing an important role in their evaluation of the student-produced proofs. That said, approaches to technical requirements varied substantially between mathematicians. At one end of the spectrum, M1 laid out the expectations that she wanted a polished proof and would take away credit when a student’s proof did not meet these standards. She noted that she would ‘deduct heavily if it is just a series of equations’ in a student’s proof of a mathematical statement; however,

a correct proof, presented well, has [complete] sentences and the logic flows. If it is not as elegant as it could be or as streamlined as it could be, I may only take off – somewhere in the range of maybe like 10 percent. A small kind of … a small little thing, just to say, hey I think you can do better.

At the other end of the spectrum, M7 was happy to accept ‘proofs that have some serious gaps in them if they show that they are going in the right direction and that they are using the right concept’. Similarly, for M5, the technical details that are left out may not be problematic, as she noted when grading Proposition 1, ‘anyone who says what is on the paper here, wouldn’t say it without understanding it. So, jumping from the fact that n squared is even to n is even, that does not bother me at all.’

Others comments explicitly on contextual variation in their expectations regarding technical detail. In contrast, M2 used a graduated system in which expectations increased as the semester progressed. M2 stated

‘The first couple of weeks, I was kind of generous in grading. But once [we have reached] the middle or end of the semester, I told my students that they would have to write great mathematics … I would be more strict [with grading].

M4 described how she expected students to produce proofs that were more detailed than what she presented in the lecture. In her lectures, she is more often concerned about communicating the main idea of a proof rather than the details; she noted ‘Professors should be able to get away with more stuff, occasionally I have been known to say, I can do that, but you can’t.’ As a result, some students may be confused about the level of details to provide in their proofs. M4 acknowledges that it is then a challenge to make clear what the expectations are when writing proofs.

When grading proofs, professors are sometimes concerned with students showing technical details to establish the validity, but other times the technical detail is not needed when it is clear the proof shows student understanding.

5.2.3. Theme 2c: Expectations regarding assessment type

Three mathematicians indicated how their expectations changed based on the type of assessment that they were grading. All indicated that they would be less harsh in their grading in the context of an exam and stricter in the context of homework. The stress and time constraints of an exam situation allow for students to leave some gaps and not be penalized if the professor believes they can fill in those gaps.

M7 noted that she would be more critical in assessing a proof on homework or a take-home exam than for an in-class exam. She awarded IP 1 full marks and elaborated that she might be bothered if they turned it in for homework or a take-home exam, but ‘if it is an in-class exam or something that clearly the student thought about it and did it by himself or herself, it would be a little too harsh to take the points off.’

M6 commented that her expectations for proofs of proposition 2 would depend on whether they would have enough time to think about what needs to be proved and convey it in a proof. When the interviewer clarified that she would be more lenient on an exam but would want them to provide the details on homework, she responded in the affirmative. M9 would accept IP 2 on an exam since she is looking for whether the student understood the relevant ideas. ‘If I was saying I just want [the student] to prove this on a test … then what I am looking for is could [they] make a convincing argument that somebody could read and be convinced by … ’ She continued, ‘[as the student], I would make sure I understood step-by-step what I was doing. I think [showing detail] is important for homework, and they should be near perfect.’

6. Discussion

In this study, we interviewed nine mathematicians about their evaluation of six proofs: three complete proofs and three incomplete proofs. Our analysis focused on the contextual features that influenced mathematicians’ evaluation processes.

We reported two major findings. First, the status of the proof’s author had a substantial impact on the way mathematicians approached their reading and evaluation. The importance of authorship has been highlighted in the literature on mathematicians’ motivations for reading mathematical proofs for their own research (e.g., Weber et al., 2014), but little was known about the contrast in mathematicians’ proof-reading practices when authored by students or fellow mathematicians.

When speaking about a hypothetical lecturing context, several of our mathematicians asserted that they were not concerned about the technical accuracy of their colleagues’ proofs, noting that these proofs are most often shown to students to demonstrate the key ideas and may purposefully leave gaps for students to fill later, as they build a better understanding of the proof. Both of these sentiments were also reported in Weber’s (2012) similar study on mathematicians’ perspectives about pedagogical practice related to mathematical proof. In contrast, when evaluating ostensibly student-produced proofs, mathematicians were more concerned with technical detail and perceived gaps in the proof, citing the pedagogic necessity for students to articulate their understanding clearly throughout the proof.

Our second major finding is that context matters when assessing students’ proofs. That is, mathematicians’ reportedly evaluated student-produced proofs differently depending on the context in which they are grading. For example, three of our mathematicians reported assessing proofs differently in the context of homework, a quiz, or an examination. Five out of nine also commented on the role of the expectations that they have laid out in their classroom instruction. Several noted that if they had modeled using complete sentences, then they would expect the same from their students, especially in situations that were not time dependent. For time dependent situations, students are allowed more leeway in how they present their proofs.

These findings echo Lew and Mejía-Ramos (2019) who reported that mathematicians attended to the pedagogical context when deciding on appropriate standards of rigor and detail for student-produced proofs. Lew and Mejía-Ramos’ mathematicians noted that students are allowed to get away with things like purely symbolic mathematical phrases in an ITP course, but that they would not be allowable in their own professional communications (e.g., journal submissions).

6.1. Implications for research

Our mathematicians appeared to agree that the level of the course they are teaching affects what they expect students to be able to do and that the type of assessment determines what technical details are required. Yet, it is unclear how this interaction plays out, how these contextual factors govern students’ introduction to mathematical proof writing and the extent to which mathematicians agree on appropriate pedagogical practices with respect to proof writing.

In particular, there is disagreement on when students should be introduced to the linguistic conventions of proof writing. For some participants in our study, it seems that these can be left to later in the mathematical apprenticeship and that the courses they discuss should focus on more substantive mathematical content. While this notion of ‘cutting some slack’ for lower-level students has appeared in the literature on grading proof (e.g., Davies et al., 2020), it is more common to talk of linguistic conventions of proof-writing as belonging to an introductory course in proof writing (David & Zazkis, 2019; Lew & Mejía-Ramos, 2019). David and Zazkis (2019) characterized ‘Introduction to Proof’ courses as providing ‘opportunities for students to develop skills necessary to read and write proofs’ (p. 388). From their analysis of 176 publicly available syllabi, David and Zazkis concluded that while ITP courses vary substantively in mathematical content, most ‘emphasize proof-writing and formal mathematical argumentation as a major goal of the course’ (p. 399).

It is unclear from our data how strongly our participants hold their beliefs, or where they feel an emphasis on proof writing would be more appropriate, if anywhere. However, our data suggest there exists an important source of variation underlying the goal purported common to most ITP courses. That is, at what point do we expect students to make the transition to writing proofs consistent with the linguistic conventions of the mathematical community? While the extant literature suggests that the answer to this question lies simply in ITP courses, our analysis suggests that the issue may be more complicated, warranting more dedicated research, both on the beliefs of mathematicians/practitioners and on empirical best practices for students.

We, as practitioners and researchers ourselves, align ourselves with Lew and Mejía-Ramos (2019), who asserted that students should engage in writing about mathematics more often and much earlier in their schooling. However, we acknowledge that this belief is based on professional judgement rather than empirical research.

To generate the relevant empirical evidence in support of our beliefs, researchers will need assessment tools to evaluate students’ use and understanding of linguistic conventions. To this end, Lew and Mejía-Ramos (2019) proposed a mode of oral assessment, based on the reading aloud of mathematical texts. Through such a read aloud protocol, researchers may gain access to students’ contextualized thinking, and their moment-to-moment processing of the proof at hand. Further, in such real-time assessment, both assessors and students have the opportunity to ask clarification questions, minimizing the possibility that one elusive definition, theorem, or ancillary idea could result in an otherwise capable student scoring low on a task that they are mostly-equipped to answer. We need to be aware of how context may be influencing what we read or hear. We need to consider ways beyond written work to assess student interpretations of the mathematics.

6.2. Implications for practitioners

Having established the importance of contextual factors in grading, we advocate for a greater emphasis on communication between practitioners and students. In particular, our earlier analysis has highlighted the importance of instructors’ expectations in determining grading standards. It is important not only that practitioners be cognizant of their expectations, but that these expectations should be clearly communicated to students.

Prior research (Miller et al., 2018; Moore, 2016) has concentrated on assessing proofs based on a traditional grading scheme (score out of a total number of points for a particular proof), but mathematicians may want to consider alternate grading schemes like standards-based grading for proofs (Cooper, 2020; Stange, 2018). With these grading schemes, mathematicians can focus on values and norms that are important to the mathematical community (Dawkins & Weber, 2017) and make the intentions of the assessment of proof more explicit for students. Further, for these grading schemes, research has shown that students pay more attention to professors’ feedback in order to revise their proofs when points are not given (Butler, 1988; Pulfrey et al., 2011). We believe that this is crucial in helping students gain a better understanding of mathematical proofs.

Finally, we want to emphasize that a large part of what we want to accomplish in an Introduction to Proof course is helping students learn the mathematicians’ process along with the discourse of the discipline. Often, all students see from a mathematician is a final, polished product. As was pointed out by, for example, Tanswell and Rittberg (2020) and Weber et al. (2014), mathematicians’ proving practice is messy, fraught and full of uncertainty, and it is pedagogically valuable that students be exposed to this process early and often in their education. Hence, we call for structuring the course in such a way that promotes multiple drafts and revision before arriving at a final product (Jansen et al., 2017). Further, assessment practices should align with this path such that students have the opportunity to get feedback often in low-stakes situations to arrive at highly polished proofs and that high-stakes assessments focus on logical reasoning with less emphasis on a polished presentation.

7. Final remarks

It is clear that context plays an important role when mathematicians are assessing proofs. In this study, we have discussed the role of authorship in this process, as well as documenting some of the contextual factors influencing the evaluation process. We do not intend our analysis to be an exhaustive taxonomy of such factors. Rather, we intend to promote a more intentional discourse about the role of context, and to advance the claim that both researchers and practitioners are better placed to serve the student population when context is at the forefront of both practices.

Conflicts of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.