The role of generating questions in mathematical modeling

ABSTRACT

This study aims to clarify the role of generating questions in mathematical modeling and construct principles for teaching and learning mathematical modeling with an emphasis on generating questions. To achieve this purpose, the role of generating questions was determined by solving a sprinkler problem and considering the investigation process. Generating questions requires noticing the unknown and cognitive steps to elucidate the unknown and solve the problem. The process and outcome of generating questions were explored using an open-ended problem. This study demonstrates (1) the role in advancing mathematical modeling from various points of view, (2) the role of fostering mathematical modeling competencies, and (3) the role in facilitating the extension of the applicability of the mathematical model. Having established these roles, the principle of teaching and learning was constructed, which is expected to foster the ability to generate questions. This study demonstrates that, in mathematical modeling, generating questions is crucial for developing a clear sense of direction for modeling real-world problems. Furthermore, generating questions reflects on the structures of mathematical models, allowing the execution of the mathematical modeling process.

KEYWORDS:

• Mathematical modeling
• generating questions
• the roles of generating questions
• sprinkler problem

1. Introduction

One of the important goals of mathematics education is to develop the competency to solve problems in real-life situations mathematically. For this reason, many researchers have been working to isolate the competencies necessary to carry out mathematical modeling, i.e. to develop mathematical modeling competencies. However, various studies (Blum & Borromeo Ferri, 2009; Galbraith & Stillman, 2006; Ikeda & Stephens, 1998) have demonstrated that it is very difficult for students to carry out mathematical modeling. In particular, the process called ‘mathematization,’ which connects extra-mathematical domains with mathematical domains is the most difficult for students and has been clarified by many studies (Frejd & Ärlebäck, 2011; Galbraith & Stillman, 2006; Miwa, 1986a; Treilibs et al., 1980). Recent studies have pointed out the difficulties of students in the process of ‘pre-mathematization,’ which is the simplifying and structuring of real-world problems (Jankvisk & Niss, 2020; Maaβ, 2006), and the fact that even if they can solve a real-world problem, students cannot solve problems in other real-world events that have similar modeling directions (Niss & Blum, 2020; Stillman, 2000). These studies have demonstrated that students are unable to structure problems and modeling directions to make it easy for them to use mathematics on their own. These realities are similarly manifested among Japanese students (National Institute for Educational Policy Research, 2013).

To improve the above realities, this study focuses on ‘generating questions’ in mathematical modeling. I define this as follows: After noticing something unknown in a real-world event, experience and knowledge are applied, and under the assumption that the questions and confusions that arise should be solved, the directions for modeling are clarified and executed. The activity involves reflecting on the structure (components and relationships among them) and mathematical solutions of the obtained mathematical model and implementing the modeling process further. The importance of identifying questions in mathematical modeling has been pointed out in the past (Burkhardt et al., 1980; Treilibs et al., 1980). Additionally, the activity of generating questions helps to determine the directions for modeling by dividing the problem of real-world events into those that can be easily utilized by mathematics and leads to the awareness of the assumptions that support the obtained mathematical models, the creation of problems of other real-world events, and their solutions, which is expected to improve the situation pointed out above. Therefore, the activity of generating questions is an activity that should be emphasized. In recent years, there have been studies that have demonstrated the importance of activities related to question generation (Bonotto, 2010) and studies on task design that allow students to freely generate questions in mathematical modeling lessons (Stillman, 2015), suggesting that generating questions is still an important activity.

Here, as in the study by Stillman (2015), in mathematical modeling lessons, there is a need for tasks that provide students with the opportunity to generate questions freely from problems of real-world events. However, when teaching mathematics, tasks are often presented as embedded word problems (Kaiser, 1995), a situation that is an artificial dressing-up of some purely mathematical problem (Blum, 1993), and unrealistic tasks (non-authentic tasks) (Palm, 2008). In other words, the tasks are often only superficially related to the real world, and teachers set assumptions and questions that students can easily solve. In such a lesson, there is no opportunity for students to generate questions. Therefore, it is necessary to construct a principle of teaching and learning that emphasizes the activity of generating questions, but such a principle has not been constructed in past studies.

In this study, as basic research on the issues mentioned above, the specific activities of generating questions for a specific problem and the role of generating questions obtained from these activities were examined. This clarified role allows for the construction of a principle for teaching and learning mathematical modeling that recognizes the value and emphasizes the process of generating questions. Based on these considerations, the purpose of this study is to clarify the role of generating questions in mathematical modeling and construct the principle for teaching and learning mathematical modeling with an emphasis on generating questions.

2. Structure of this paper

The paper is set out as follows. In Section 3, the concepts of ‘mathematical modeling cycle’ and ‘mathematical modeling competencies’ are first specified, and then these concepts are briefly explained. Additionally, previous studies on generating questions are reviewed, similarities and differences between the concepts presented in previous studies and the concept of generating questions in this study are clarified, the originality of generating questions is determined, and the problems are identified. In Section 4, the background of the sprinkler problem, the character of the solver (the author), and the time required to solve the problem are explained. Then, the author’s process of solving the sprinkler problem is described. In Section 5, the core of this paper, the same solution process is reviewed, and the role of generating questions in mathematical modeling is demonstrated. Furthermore, based on the roles of generating questions in mathematical modeling, a principle of teaching and learning mathematical modeling that emphasizes generating questions is constructed. In Section 6, the applications and limitations of this study are discussed.

3. Theoretical framework relevant to this study and considerations regarding generating questions

3.1 Mathematical modeling cycle

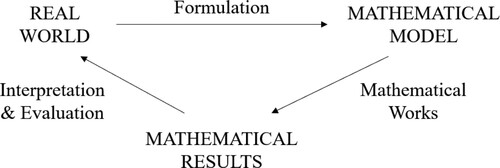
To describe the mathematical modeling process in more detail, various diagrams of the mathematical modeling cycle have been proposed (Blomhøj & Jensen, 2007; Blum & Leiβ, 2007; Pollak, 1979). Borromeo Ferri (2006) states that ‘These cycles are different, because they are dependent on various directions and approaches of how modelling is understood and in some cases, if complex or non complex tasks are used.’ (p.86). However, despite the differences, the mathematical modeling process commonly consists of the following steps (Figure 1): (1) formulation, (2) mathematical work, (3) interpretation and evaluation, and (4) improvement of the model; Step (4) usually involves repeating steps (1) and (3) several times (Miwa, 1986a).

Figure 1. The process of mathematical modeling (Miwa, 1986a, p. 402)

The process illustrated in Figure 2 (adapted from Maaβ, 2006) is specified as the mathematical modeling cycle in this study. This is because the transformation process from the extra-mathematical domain (the domain of the real world) to the domain of mathematics is described in more detail than in Figure 1, and both the process of the activity and the results obtained from it are distinguished. In the following sections, the specified process is described.

Figure 2. Mathematical modeling cycle in this study (Maaβ, 2006, p. 115)

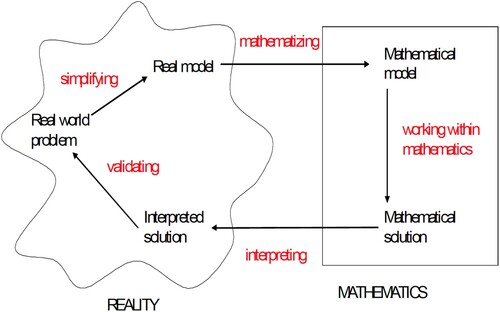
The amoeba on the left side of Figure 2 represents reality, and the mathematical modeling process begins with the real-world problem. Then, by simplifying and structuring the problem (pre-mathematization), the real model is obtained. By mathematizing the obtained real model, it is transferred to the mathematical domain (indicated by the rectangle), and the mathematical model is derived. By working within mathematics on a mathematical model, a mathematical solution can be found. Finally, the mathematical solutions are interpreted, and the interpreted solutions are evaluated against real-world problems. If the interpreted solution is not proven appropriate, the mathematical modeling cycle is carried out again (Maaβ, 2006). Note that the mathematical modeling does not proceed linearly in the order illustrated here but skips or returns to certain steps (Borromeo Ferri, 2007).

A characteristic feature of the mathematical modeling cycle illustrated in Figure 2 is that it describes the process of structuring a real-world problem to obtain a model of reality. If the process of structuring is interpreted to include the division of real-world problems into situations that can be easily used by mathematics, then Figure 2 describes the key process simply, as this process includes the main activities of generating questions.

3.2. Mathematical modeling competencies

Mathematical modeling competencies are the competencies needed to carry out modeling. For this reason, many studies describe them as a competency (called a sub-competencies) required for each step of the mathematical modeling cycle. For example, Galbraith and Clatworthy (1990) specify four competencies for the modeling process: ‘C1. Ability to specify problem clearly; C2. Ability to formulate an appropriate model; C3. Ability to solve the mathematical problem including mathematical solution, interpretation, validation, and evaluation/refinement; C4. Ability to communicate results in a written and oral form’ (p.140), which aligns with the modeling process. In addition to these, Hall (1984) includes ‘Ability to work effectively in a group’ (p. 145), which includes the ability to discuss in a group, and OECD (2009) includes ‘monitoring and controlling the modeling process’ (p. 106), which includes metacognitive competencies related to modelling. Furthermore, Kaiser (2007) states that ‘Modelling competencies include, … not only the ability but also the willingness to work out problems, with mathematical aspects taken from reality, through mathematical modelling.’ (p. 110), and includes awareness and attitude toward mathematical modeling.

It is clear from these previous studies that there are various provisions for mathematical modeling competencies. Among them, Maaβ (2006) takes a comprehensive view of the mentioned sub-competencies and specifies them as follows:

Modelling competencies include abilities and skills to conduct modelling processes adequately and in a goal-oriented way; as well as the willingness to put these abilities and skills into practice.

In detail modelling competencies contain

1. Sub-competencies to carry out the single steps of the modelling process

   • Competencies to understand the real problem and to set up a model based on reality.

   • Competencies to set up a mathematical model from the real model.

   • Competencies to solve mathematical questions within this mathematical model.

   • Competencies to interpret mathematical results in a real situation.

   • Competencies to validate the solution.

2. Metacognitive modelling competencies.

3. Competencies to structure real-world problems and to work with a sense of direction for a solution.

4. Competencies to argue in relation to the modelling process and to write down this argumentation.

5. Competencies to see the possibilities mathematics offers for the solution of real-world problems and to regard these possibilities as positive. (2006, p. 139)

In this list, A includes the competencies required for each step of the modeling process, and B includes the competencies to think about, reflect on, and control the thinking process through the mathematical modeling cycle. D is the competency to discuss with others, and E includes the competencies related to awareness and attitude, which can be seen to encompass the modeling competencies of the above studies. The mathematical modeling competencies of Maaβ (2006) will be used in this study. This is because Maaβ’s mathematical modeling competencies are unique in that it emphasizes the competencies to work with a sense of direction for a solution (C). The C competencies have been inherent in the modeling process. However, for the students, in addition to the ones illustrated in section 1, they have difficulties such as distorting the true nature of events by over-simplifying (Maaβ, 2006) or failing to create models by randomly generating components (Treilibs et al., 1980). Thus, Maaβ emphasizes the need for the C competencies because of the emerging difficulties with thinking about creating a mathematical model for a purpose and then carrying out the modeling process. With the competencies to structure problems and work with a sense of direction for solving them (C), students can be expected to capture the structure and recognize the similarities with the real-world problems they have solved, not only when solving the initial real-world problem but also when finding other real-world problems. Based on the above, the competencies to work with a sense of direction for the solution (C) is essential. Furthermore, as explained in section 1, generating questions is closely related to Maaβ’s C competencies as generating questions helps determine the sense of direction for modeling.

3.3. Review of previous studies related to generating questions

3.3.1. The importance of specifying questions in mathematical modeling

Treilibs et al. (1980) focused on the following five component skills in the formulation (in Figure 2, simplifying and mathematizing) of the mathematical modeling process, one of which is ‘Specifying questions.’

GV – Generating variables – the ability to generate the variables or factors which might be pertinent to the problem situation.

SV – Selecting variables – the ability to distinguish the relative importance of variables in the building of a good model.

Q – Specifying questions – the ability to identify the specific questions crucial to the typically ill-defined realistic problem.

GR – Generating relationship – the ability to identify relationships between the variables inherent in the problem situation.

SR – Selecting relationship – the ability to distinguish the applicability of possible relationships to the problem situation. (1980, p. 29)

They illustrated the following problem to measure the skill of specifying questions (Q):

Q1 THE PROBLEM

A factory uses tin in the production of its goods. A manager has the responsibility of ensuring that stocks of tin are always available.

YOUR TASK

State concisely what information the manager must give to the clerk who orders the tin. (Treilibs et al., 1980, p. 32)

Treilibs et al. also provide the list of possible correct answers for the task in Q1 as follows:

How much tin to order

When to order the tin

What type or quality of tin to order

From whom to order, including considerations of price and reliability of supply

(p. 32)

These answers are generated by extracting elements from the real world, and they are questions that need to be answered before the problem can be considered solved (Treilibs et al., 1980, p. 32). They created similar problems for other abilities and examined the correlations between the scores, and found a close relationship between GR and Q and SR and Q (Treilibs et al., 1980, p. 40). This result supports the fact that questions are closely related to the sense of direction for modeling, as mentioned in section 1.

However, the study by Treilibs et al. does not provide a specific description of the students’ specifying questions, i.e. what questions they specified. Will students be able to specify and generate questions? Therefore, in the next section, the literature of English et al. (2005), which emphasizes problem posing in mathematical modeling lessons, will be analyzed.

3.3.2. Mathematical modeling lessons with an emphasis on problem posing

According to English et al., ‘problem posing’ is an integral part of the modeling cycle (English et al., 2005). They conducted research on the difficulty of the problem-posing aspect of mathematical modeling with elementary school children and argued that problem-solving as well as problem posing should be incorporated into modeling activities in order that the students be able to function effectively in a world that is demanding more flexible, creative, and future-oriented mathematical thinkers and problem solvers. Additionally, the following illustrates how English et al. construct the framing of questions and problems:

As in real-life situations, modelling activities often comprise information that might be incomplete, ambiguous, or undefined, with too much or too little data, and they might involve visual representations that require interpretation. Numerous questions and problems arise as children try to make sense of this information, elicit and work with the embedded mathematical ideas, and modify and refine their models. (2005, p. 156)

To demonstrate the above, they conducted lessons based on the ‘cyclone problem.’ The ‘cyclone problem’ is a problem in which a project official on the Club Trop Resorts development committee is considering how to determine two locations to avoid when building the next resort in Queensland (see English et al., 2005). After a large amount of data was presented at the beginning of the lesson, the children generated various questions, such as ‘are all the factors equally important?’ (English et al., 2005, p. 158). Additionally, when the children created mathematical models, the question ‘how to best represent their findings?’ was generated (English et al., 2005, pp. 160–161). Furthermore, after solving the ‘cyclone problem’ in Queensland, Australia, the ‘cyclone problem’ in Western Australia was tackled, and the results of the solution were presented on a poster. By doing this, the teacher was asking them to think about ‘what will happen in other states?’ This is because English et al. emphasize that reminding children that the model should apply to other similar situations is an essential feature of mathematical modeling (English et al., 2005, p. 157).

As evident from mathematical modeling lessons that emphasize problem posing, students generate various questions in solving modeling problems. They also mention that by sharing questions to solve modeling problems in the lesson, students generate important mathematical ideas and use various mathematical models to represent what they discover from them (English et al., 2005, p. 162). Furthermore, what is noteworthy about English et al.’s lesson is that they present problem situations that are like the problems they have solved. In this way, students can repeat the mathematical modeling cycle and solve problems in other real events with a similar sense of direction for modeling, which is suggestive in the lesson’s structure.

Nevertheless, English et al.’s study does not describe the process of how they designed the ‘cyclone problem,’ i.e. the modeling problem. What task design processes do teachers need to carry out to allow students to freely generate questions in lessons? In the next section, Stillman’s research (2015), including an investigation activity with a task design of modeling with an emphasis on problem posing, will be further analyzed.

3.3.3. Task design activity for modeling that the development of problem finding and posing abilities

Stillman (2015) argues that problem finding, the process of finding a problem that can be solved, is an even more important cognitive step than problem processing. Stillman presents investigation activities, including task examples and task design, to provide ideas on how teachers can initiate problem finding and problem-posing activities in classrooms that focus on mathematical modeling.

As an example of a task design process, first, Stillman illustrates pictures of water bottles taken at the NEWater¹ exhibition (Figure 3). These pictures function as a stimulus for finding problems (Stillman, 2015, p. 49).

Figure 3. Water bottle display (Stillman, 2015, p. 50)

From the illustrations, Stillman finds the following problems: ‘How high is the display? How many bottles did it take to make it? How much water would those bottles hold?’ (p. 49). However, she points out that these are not important questions that we need to know. As the bottle is disposed of once, Stillman posed the problem ‘What is the impact on our environment of single-use water bottles?’ (Stillman, 2015, p. 50). Next, to investigate this mathematically, data were collected. In doing so, she generated the question, ‘What sort of information might we need to investigate this mathematically in a way that involves mathematical modeling?’ (p. 50). The findings demonstrated the carbon footprint from the production to the disposal of plastic drink bottles.² Further, the recycling rate and amount of waste in Singapore and the percentage of waste incinerated at the waste energy plant and the Semakau Landfill were also detailed. To answer a broader problem, Stillman asked: ‘Will Singapore be able to reach its Zero waste Targets? Will the lifespan of Semakau landfill be able to be extended another 50 years?’ (pp. 50-51). Stillman collected data that were important for the problem, but they were not investigated further. Summarizing this investigative activity, Stillman stated: ‘this process of drilling down from superficial surface questions to more in-depth questions develop modelers’ insightfulness in problem posing’ (p. 51). Stillman also argues that in mathematical modeling, it is essential for the modeler to be given the freedom to determine their own problems because, by crafting problems, they are better able to find problems in real-world situations that require mathematizing. Additionally, she offers the idea of having students find problems and then consider whether they can be mathematized in a mathematical modeling lesson, considering that students may worry about whether the problems they posed on their own can be mathematized or whether they are suitable for modeling.

Stillman’s investigation activities, including task design, suggest that it is important for teachers to find a problem by looking at a real-world situation, such as a photograph, and to carry out the process of generating and examining questions, such as whether the problem requires modeling, and then posing the problem. In a mathematical modeling lesson, having students pose problems and then examining whether they can be mathematized is an important activity in recognizing the importance of formulating a sense of direction for modeling.

3.3.4. Originality of generating questions in this study and identifying issues

Previous studies related to generating questions in mathematical modeling have demonstrated the importance of identifying the question (Treilibs et al., 1980). Subsequent studies have implemented modeling lessons that emphasize problem-setting (English et al., 2005), and based on the task design process, have provided ideas on how to begin problem finding and problem posing in modeling lessons (Stillman, 2015). Additionally, in the activities of ‘specifying questions,’ ‘problem finding,’ and ‘problem posing’ for modeling, the question is generated in the formulation step (especially simplifying in Figure 2), the direction of modeling is determined, the modeling process is repeated, and questions are generated continuously. These activities have something in common with generating questions.

However, there is a decisive difference between the concepts of the above previous studies and the concept of generating questions. This is because previous studies do not provide detailed descriptions of ‘noticing’ and ‘doubt.’ Generating questions involves both noticing and doubt, and these cognitive steps are necessary to generate questions. Recent modeling studies have focused on the study of noticing (Galbraith, 2015; Galbraith et al., 2017). In particular, ‘productive Modelling-Oriented Noticing’ involves the process of (a) sifting through information to notice what is relevant and what is irrelevant, (b) comparing and relating relevant information with prior experiences and knowledge, and (c) combining the relevant information to generate productive alternatives for decision making when responding to events as they carry out a modelling activity. This process has been demonstrated to provide a way to study problem finding and problem posing and is useful in task design study (Stillman, 2019).

Additionally, noticing is an important cognitive step in constructing the principle of teaching and learning mathematical modeling with an emphasis on generating questions because how to generate the first noticing is key to carrying out the activity of generating questions. However, there have been no studies that have focused on the noticing of generating questions. Therefore, focusing on generating questions adds to the existing literature as it includes the cognitive steps necessary to generate questions. In addition to the issues mentioned above, there has been insufficient research on how to embody the processes of generating questions, solving questions, reflecting on the solution process in lessons, and developing the competencies to execute solutions. However, in previous studies on setting up learning environments to develop mathematical modeling competencies, suggestions on interventions and instructions for students to carry out modeling have been described (e.g. Aydin-Güç & Baki, 2019; Blomhøj & Jensen, 2007; Blum & Borromeo Ferri, 2009). These suggestions can be taken into account when constructing principles for teaching mathematical modeling with an emphasis on generating questions (see section 5.2 below).

To solve the above issues, first, this study will detail the activity process of generating questions. Furthermore, to describe the activity process in detail, relying on Stillman’s (2015) investigation activity including task design, a real-world problem was posed, and an investigation activity was carried out that continuously generated questions. Based on these investigation activities, ideas and findings were explored, and this led to the determination of the role of generating questions in mathematical modeling.

4. Mathematical modeling problem and investigation process

4.1. Sprinkler problem and background of the solver

In posing the real-world problem to be investigated in this study, the ‘linear irrigation problem,’ a commonly researched problem, is used as a problem that has been solved (Barrett, 2000; Swetz & Hartzler, 1991). Linear irrigation systems consist of a long pipe of sprinklers with wheels that move slowly through a rectangular field. The problem is as follows:

Suppose your uncle is designing an irrigation system for his farm in eastern North Carolina. His land is very flat, and the fields, which are rectangular in shape, are roughly 2200 feet long and 1000 feet wide. Your uncle is considering a linear irrigation system, which is essentially one long pipe to water each field. A linear irrigation system is generally set on wheels that keep it above the level of the plants. Nozzles are placed periodically along the pipe, and each nozzle sprays water in a circular region. The entire system moves slowly down the field, watering the plants beneath it as it moves.

There are 20 sprinkler nozzles available to your uncle. He has enough pumps to maintain water pressure so that each nozzle delivers a uniform spray to a circular region 50 feet in radius with a flow rate of 10 gallons per minute. How far apart should the nozzles be placed to produce the most uniform distribution of water on a field 1000 feet wide? (Barrett, 2000, p. 267)

Multiple models can be used to solve this problem, such as circular equations and functions (Swetz & Hartzler, 1991). However, linear irrigation is carried out in large-scale agriculture in the United States and is uncommon in Japan in terms of culture and hence, is not likely to appeal to Japanese students. Additionally, Miwa (1986b) considered whether teaching materials need to be culturally suited to the cultures of the teachers.

To eliminate the problems mentioned above, pollution can be used as a link to the sprinkler problem. This is because pollution, such as air and noise pollution, is a familiar problem for students, and there is sufficient meaning to solve the problem. Among them is the problem of sand dust in schoolyards from a Japanese article:

Dust and sand from the ground.School and neighbors are confused.

Suddenly, a strong wind blows and dust rolls up … On a dry day at a school ground, sand and other debris are blown up when a strong wind blows. Some of the neighbors and school staff have complained about the damage, saying, ‘Even if I open the window a little, it comes into the room,’ and ‘A number of children have gotten conjunctivitis in their eyes.’ The boards of education of each municipality have taken measures such as sand nets and water sprinkling, but they have not been able to adequately respond to the situation because they are dealing with nature. (Sekido, 2014)

Thus, the problem is set as follows: Neighboring residents are embarrassed because sand dust from the schoolyard can cause sand dust to enter the school rooms, and it can cause conjunctivitis because of sand dust entering the student’s eyes. Subsequently, teachers in X Junior High School³ will review the use of sprinklers to reduce the sand dust. Sprinklers have been installed in X Junior High School, but there are failure points, and as they have been installed, their functioning has reduced. Under these conditions, the following problem with sprinklers was solved. Eight sprinklers were installed in the schoolyard of X Junior High School (Figure 4). However, two sprinklers near the center (Point Q, Point R) have failed. Should these two sprinklers be repaired?

As the solver of the above problem, a graduate student studying mathematical modeling in school mathematics, I have more mathematical knowledge and more experience in solving modeling tasks than the public. However, although I have solved linear irrigation problems, I have little knowledge of sprinklers and was unfamiliar with the context of the sand dust problem. Therefore, although there may be some influences such as few (or no) questions in the domain of mathematics (working within mathematics in Figure 2), by carrying out investigation activities (considering task design) on problems of real-world problems with which the author is not familiar, it is possible to clarify the process and role of generating questions including noticing, in mathematical modeling. Additionally, it is assumed that the questions in the domain of mathematics are generated depending on the prior knowledge of the target grade.

4.2. Solution process

4.2.1. Information about sprinklers and identifying their components

To solve the above problem, the factors to focus on are the shape of the schoolyard, the performance of the sprinklers, and the water bill. The amount of watering, the watering range, and the water bill, which correspond to the performance, were unknown. Additionally, the shape of the schoolyard was regarded as rectangular, according to Figure 4. Among the sprinklers in the schoolyard of Figure 4, six sitting type sprinklers (hereinafter referred to as the sitting type) were at the side of the schoolyard, and two embedded type sprinklers (hereinafter referred to as the embedded type) were installed near the center of the schoolyard. The sprinklers were both standardized models (Figure 5).

Figure 4. Sprinklers in the schoolyard of X Junior High School (Google, n.d. Map A)

Figure 5. Types of sprinklers (left side: sitting type, right side: embedded type)

4.2.2. Derivation of watering radius

One of the main aspects of reviewing the use of sprinklers is to understand the extent to which the schoolyard can be watered when the sprinklers are in operation. First, it is noticed that the sprinkler coverage is the most important component to be considered among the components identified above. The reason is that without deriving this value, it is not possible to capture the watering required in the schoolyard. However, it is unknown how much water is sprayed by the sprinklers in X Junior High School, and doubt arises as to whether it can be obtained. If the range of the sprinklers can be determined, the watering required can also be determined. Thus, the generated question was:

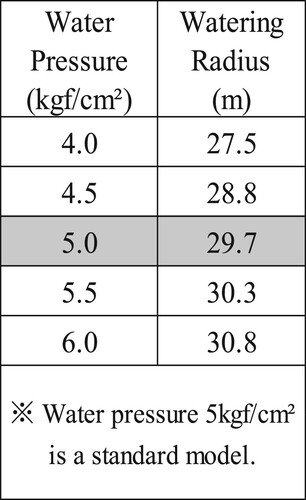
What is the sprinkler watering radius at X Junior High School? (i)

To solve the question (i), the sprinkler radius for the standard model sprinkler was investigated. Therefore, data from Company H’s³ catalog was collected (Figure 6):

Figure 6. Catalog data of Company H (right: water pressure, left: watering radius)

The X Junior High School sprinklers were the standard model, so the watering radius is 29.7 m. However, the sprinklers in the target school may be outdated as they have been in use for eight years. Therefore, to solve question (i), it is necessary to operate the sprinklers in the target school and investigate the watering radius. Then, it was decided to evaluate the aging of the sprinklers at X Junior High School by comparing the data with the catalog data (Figure 6). However, the method to determine the watering range is unknown. Thus, the generated question was:

How do we determine the actual watering radius for spraying? (ii)

To answer the question (ii), the author found the following solutions: (I) actual measurement; (II) measurement by the trajectory of water droplets released from the sprinkler; and (III) measurement by similarity. To apply each solution, one of the sitting-type sprinklers that had not broken down was put into operation (Figure 7), and solution (I) was attempted. However, the farther away from the sprinkler, the more difficult it was to determine whether the schoolyard was wet or not, so the watering radius could not be measured.

Figure 7. Sprinklers in action

Therefore, it was decided to use solution (II) or (III) to determine the watering radius. In this study, the watering radius was determined with solution (III), measurement by similarity. This is because solution (II) uses advanced mathematical knowledge, such as the equation of motion considering air resistance and the projected area of the sphere, and it was difficult to create a mathematical model by trajectory.⁴ On the other hand, a mathematical model based on similarity can be obtained by calculating a proportional equation, and this is because it can be relatively simple to create a model. Thus, question (ii) could be solved.

To create a mathematical model by similarity, it was decided to check the sprinklers from a distance by taking pictures from the top of the school building, taking into account that the measurements could not be taken from close to the sprinklers. When viewing the schoolyard from the third floor of the school building, the watering area could be seen (Figure 8).

Figure 8. Watering range, seen from above

From Figure 8, water was sprayed on the schoolyard within the range of the watering radius. Also, in Figure 8, the tennis court is a soft tennis court (soft rubber balls instead of hard yellow balls are used), and the sprinkled water has reached the white line at the back of the central court. Therefore, the watering radius can be determined by finding the distance from the sprinkler to the white line behind the central court. This can be determined by using an aerial photo (Figure 9). The process from mathematizing to validation of the mathematical solution is illustrated below.

Figure 9. Rectangular Model (Google, n.d. Map B)

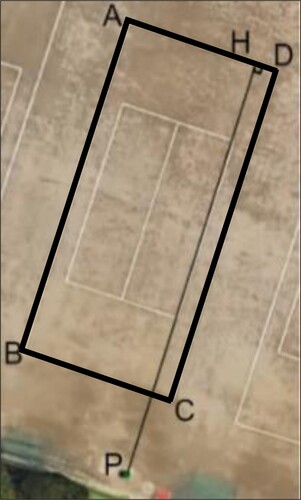
The sprinkler is point P, and the tennis court is the rectangular ABCD (Figure 9). Let a perpendicular line be drawn from point P to segment BC, and let H be the point of intersection with segment AD. The distance PH $(x)$ then needs to be determined. In the illustration, the segment PH is 14.2 cm, and the segment BC is 5.3 cm. According to the standard length of a soft tennis court, the length of BC is 10.97 m (Japan Soft Tennis Association, 2004). The calculation was as follows: $14.2:x=5.3:10.97\Rightarrow x\stackrel{\stackrel{.}{=\phantom{{}_x}}}{\cdot }29.4$ This means that the watering radius was approximately 29.4 m. In the catalog data collected in Figure 6, the watering radius was listed as 29.7 m. Therefore, it can be said that there is no significant difference when compared with the mathematical solution. Accordingly, it can be concluded that the sitting type sprinkler in X Junior High School is not very obsolete.

4.2.3. Description of the watering situation in the schoolyard

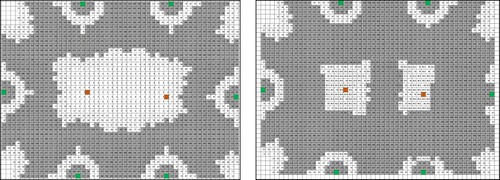
As above, the watering radius was found to be approximately 29.4 m. Based on this, how to water the schoolyard could be determined. As additional information, the sitting type sprinkler rotates 180° and water is sprayed out of the sprinkler. Consequently, when the circular model of the watering radius was calculated and applied according to the drawing of the schoolyard, the watering range of the schoolyard could be calculated as follows (Figure 10 left). Here, the watering range after the repair is illustrated if the embedded type is normal (Figure 10 Right). This is why it is necessary to compare this with the situation after repair because this determines whether it needs to be repaired. It is assumed that the sprinkler will be as good as new after repair, and based on catalog data, the embedded type is assumed to rotate 360° and have a watering radius of 29.7m.

Figure 10. Watering range of the circular model (left: current, right: after repair [Google, n.d. Map A])

As mentioned above, it is clear from Figure 10 that the schoolyard was within the watering radius. Thus, in the current situation, the side of the schoolyard was watered, but the center of the schoolyard was not. After the repair, the entire schoolyard was being watered. However, in both cases, the circular models overlapped, and it was noticed that after the repair, there were areas where the circles were double, triple, or quadruple. Additionally, the doubt arose that Figure 10 does not clarify the amount of water sprayed within the sprinkler radius and the overlapping areas. Thus, the generated question was:

How much water reaches different locations within the watering radius, and how do we know how much? (iii)

As a solution to determine the amount of water sprayed at a particular location in the schoolyard, it was recalled that creating a distribution figure would be effective. This is because a distribution figure is a map that illustrates the distribution of an event (in this study, the amount of water sprayed) and allows us to understand the differences between events and the circumstances of that event. In this study, it was not possible to find a solution to question (iii) other than making a distribution figure.

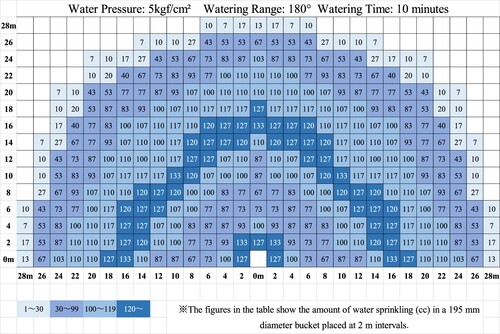
To collect the data to solve this problem, it is common to arrange buckets at equal intervals and investigate the amount of water sprinkling into the buckets over a certain time (Okamura, 1968). Based on this method, it is assumed that a square is used to represent an evenly spaced arrangement. Also, we can assume that the range includes the amount of water sprayed by the bucket. In this study, the data collected by Company H was used to create the following water distribution model (Figure 11). The mathematical model in Figure 11 illustrates that the buckets (diameter 19.5 cm) were placed at 2 m intervals, and the amount of water spray (cc) when operating for 10 min as inputted into each square. Additionally, Figure 11 illustrates the sprinkler distribution model for the sitting type, but the embedded type has the same performance except that it is placed on the ground and rotates 360°, and accordingly, the amount of water sprayed is half that of each square in Figure 12. The square representing 0 m is assumed to be a sprinkler.

Figure 11. Water distribution model of the sitting type based on the data of Company H

Figure 12. The water distribution model I (Current situation; right: An enlarged part of the left side)

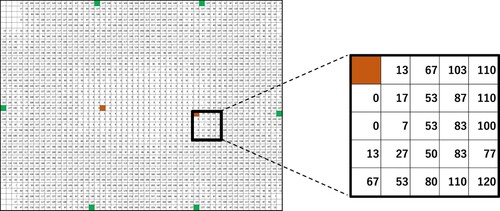
It was possible to create a mathematical model that can capture the watering situation within a watering radius by representing the evenly spaced arrangement as a square and incorporating the numerical values. This solved the problem (iii).

As the schoolyard was regarded as a rectangle, the rectangle was divided into squares with a scale of 2 m, and the numerical values were input in Excel according to the model in Figure 11 to create a mathematical model to grasp the watering situation in the schoolyard of X Junior High School (Figure 12). The sitting type is represented by green squares and the embedded type by brown squares.

From the watering distribution model created, the amount of watering at each location in the schoolyard and the difference between them can be calculated, and the watering situation can be captured more precisely than the circular model applied in Figure 11. For example, in the current situation, the maximum amount of water spray was 243 cc (maximum value), and the minimum amount of water spray was 0 cc (minimum value). After the repair, the maximum value was 247 cc, and the minimum value was 7 cc, and it was possible to investigate the amount of water spray within the water distribution radius.

However, this model included six or eight sprinklers operating for ten minutes. It is unknown if it was necessary to spray water for ten minutes. It might be better to increase the time used to reduce the dust, but the water bill will also increase as a result, and the water bill must be considered. Additionally, just because the water is sprayed, whether the watering level is enough to prevent sand dust from rising was unknown. The watering distribution model needs to be further improved. Thus, the generated question was:

How to determine the operating time for efficient sand dust removal considering the water bill? (iv)

4.2.4. Proportion of meeting the water spray volume for sand dust removal and standard water spray time

To solve this question (iv), it is necessary to know the amount of water spray necessary to eliminate the dust. According to Company H, if water of approximately 90 cc or more is sprayed, sand dust will not occur. In this study, it is assumed that the value of 90 cc is the criteria for the amount of water sprayed for the occurrence of sand dust. The setting of this criteria generates the following question:

How do we determine how well the criteria (90cc or more) are met among the squares that divide the schoolyard? (v)

First, in each sprinkling distribution model I, the squares that received 90 cc or more water were colored (gray) to identify the locations that received 90 cc or more of water (Figure 13). The reason for this is that by coloring the squares, it is possible to grasp the status of the watering distribution that meets the criteria.

Figure 13. The water distribution model II (left: current, right: after repair)

Comparing the two models, there does not seem to be much difference, only that the area around the center is colored more. However, as this is an ambiguous visual judgment, it is necessary to understand the degree of watering that meets the criteria more precisely. One way to do this is to quantify the degree of watering. Another possible method is to change the color of the water spray according to the amount of water sprayed, as illustrated in Figure 11, but this method is more ambiguous because the view of the water spray may change depending on how the color is determined. However, quantification allows for a concise expression of watering conditions and straightforward numerical comparison. In this study, it will be quantified using a proportion. From the rectangle in Figure 13, the long side is 51, and the short side is 38, so the number of squares in the schoolyard that can be sprayed is 51 × 38 = 1938. However, the total number of squares $\text{(}{N}_{\text{total}})$ is 1930 because it was necessary to deduct the number of squares that are sprinklers. If the number of squares that received 90 cc or more of water $\text{(}{N}_{\ge 90\text{cc}})$ are counted, the proportion of the schoolyard that receives 90 cc or more of water $(P_{\text{\%}})$ can be calculated. That is, the proportion can be obtained by the following equation. ${\text{P}}_{\text{\%}}=\frac{{\text{N}}_{\ge 90\text{cc}}}{{\text{N}}_{\text{total}}}\times 100$ In the current situation, the number of squares receiving 90 cc or more of water $\text{(}{N}_{\ge 90\text{cc}})$ was 1201, and the proportion was approximately 62% (1201/1930$\stackrel{\stackrel{.}{=\phantom{{}_x}}}{\cdot }$62). Similarly, this was about 76% after repair, and so the difference is approximately 14%. This is the calculated proportion for ten minutes of watering. To find the efficient water spray time, it is necessary to find the proportions for other times. Thus, the generated question was:

How much does the proportion that meets the criteria change when watering is applied for varying periods? (vi)

Tables 1 and 2 illustrate the proportion of each minute that meets the criteria (receiving 90 cc or more of water) in the current situation and after repair. To find the proportion per minute, it is assumed first that the amount of water sprayed on each square increases proportionally. Hence, the amount of water sprayed in 1 min for each square is 1/10 of the amount of water sprayed in 10 min. Based on the values and the above equation $\text{(}{\text{P}}_{\text{\%}}={\text{N}}_{\ge 90\text{cc}}\times 100/{\text{N}}_{\text{total}})$, the proportion that met the criteria in one minute was calculated. The amount of water sprayed in two minutes is obtained by multiplying the amount of water sprayed on each square in one minute by two, and then the proportion in two minutes is derived in the same way. These proportions are then plotted in coordinates, and the graphed mathematical model (Figure 14) is called the proportional model.

Table 1. Proportion that receives 90 cc or more of water to x minute (current situation)

x(min)	1	2	3	4	5	6	7	8	9	10
%	0	0	0	1	5	9	15	37	59	62
x(min)	11	12	13	14	15	16	17	18	19	20
%	70	73	75	79	79	79	81	82	82	82

Table 2. Proportion that receives 90 cc or more of water to x minute (after repair)

x(min)	1	2	3	4	5	6	7	8	9	10
%	0	0	0	2	12	32	43	58	72	76
x(min)	11	12	13	14	15	16	17	18	19	20
%	82	83	87	89	90	90	92	93	93	95

Figure 14. Proportional model (x: minutes, y: %; left: current situation, right: after repair)

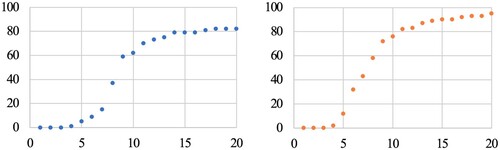
From the current situation in Table 1, to make the proportion of squares receiving 90 cc or more of water 50% or more, it is necessary to water for at least nine minutes. Additionally, there are no squares that meet the criteria (i.e. 0%) for less than three minutes. Furthermore, looking at the left of Figure 14, the proportion receiving more than 90 cc of water illustrates a significant increase in the change from 5% in five minutes to 70% in eleven minutes, but the change in the proportion after 70% in eleven minutes becomes less and less, approaching 82% over time. Here, ‘efficient’ in question (iv) is assumed to be the boundary point at which the change in the proportion satisfying the criteria becomes less (less efficient). Based on this assumption, it is assumed that the boundary point in Table 1 is eleven minutes, and eleven minutes is the efficient operating time in the current situation. However, looking at the right of Figure 14, the proportion receiving 90 cc or more of water illustrates a significant increase in change from 12% at five minutes to 72% at nine minutes, but the change in proportion after 72% at nine minutes becomes less and less, gradually approaching 93% over time. Therefore, based on the previous assumption, nine minutes can be considered as an efficient operating time after the repair. When the operating time is set to eleven minutes and nine minutes, the proportion that satisfies the criteria is about 70% in both cases, so the operating time is useful for comparing the current situation with that after repair.

4.2.5. Numbers of times the area is sprinkled

From the above investigation, questions (iv) to (vi) could be solved. However, the time determined above is only the efficient time for watering at one time. Therefore, it is necessary to find the time until the next watering. This is because the teachers think it would be better to spray water once at a specific time, but when this happens, the ground will soon dry up, sand dust may occur, and there may be complaints from neighboring residents. Nevertheless, it was necessary to think about the sprinkling cycle because the water bill will be affected if the watering is repeated, as mentioned above. Thus, the generated question was:

How do we determine how long it will take for 90cc of water to dry and make dust? (vii)

To solve this question, it is assumed that the next time to spray water is when the sand reaches a state where it may appear as dust. There is no other way to understand this than to collect data on actual sand conditions through experiments.

In conducting the experiment, the method necessary to spray uniformly in a certain range involved measuring the time it takes for an instrument to spray 90 cc using a spray bottle. Next, 90 cc of water was sprayed in a circle of the same size as the bucket used by Company H, and sand was put on the surface into a plastic cup every ten minutes. After that, the sand was poured from the cup to see if sand dust was produced. The experiment took place on an open space on a university campus. The experiment was set up as follows (Figure 15).

Figure 15. A series of experimental processes

The supposition of the experiment is that the sand to be sprayed is well dried and that dust is produced when it is blown by the wind. Moreover, to collect the data, the experiment was conducted by preparing 30, 60, and 90 cc circles. On the day of the experiment (June 30, 2018), the air temperature was approximately 31 °C, the humidity was 64%, and the wind velocity was approximately 6 m/s (the wind velocity for the sand dust). The experimental results are as follows (Table 3).

Table 3. The presence or absence of sand dust when pouring the sand sprayed with water collected in a cup.

According to Table 3, after ten minutes, when pouring the sand sprayed with 30 cc of water, sand dust occurs. Also, after twenty minutes, for sand sprayed with 60 cc sand dust occurs. Even if the sand was sprayed with 90 cc, sand dust occurs after thirty minutes. If the proportional relationship is maintained, it can be predicted that sand dust may occur even after 270 cc of water after 90 min.

Based on the above results, the water distribution model I of nine minutes in the after repair and eleven minutes of the current situation, which was obtained previously, was created to determine after how many minutes the area watered will be dry. The maximum amount of watering after the repair was 222.3 and 267.3 cc for the current situation. Assuming that watering is done again when even the square with the maximum watering rate dries up, watering is needed once every ninety minutes in the current state and once every eighty minutes after repair.

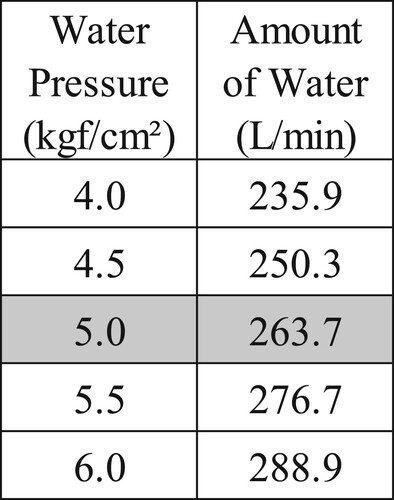
4.2.6. Deciding to repair the system

From the solution to each of the questions generated above, it could be considered whether X Junior High School should repair the embedded type sprinklers. As a first assumption, the watering period is set for the four-month period from June to September, when the temperature is high, the sand in the schoolyard is dry, and a lot of dust is produced. It was assumed that this would continue for the next five years. In these periods, if the watering is performed once every 90 min within working hours (eight hours) on weekdays, the water will need to be sprinkled five times a day. Whether or not to repair the system depends on how X Junior High School sets the standard of the proportion that receives 90 cc or more. Therefore, the relationship between the proportion of squares 90 cc or more and the water bill for five years will be calculated and compared for the case with and without repair. To do so, it is necessary to know the cost of repairs. According to Company H, it costs 50,000 yen to repair the system. The water bill was calculated based on the number of times the schoolyard is sprinkled per day and the fact that the sprinklers at X Junior High School are not obsolete (see question [i]), and based on the data that the watering volume of the standard model is 263.7 L/min (Figure 16). Subsequently, the water sprayed for two months was calculated and converted into cubic meters (m³). Next, the price of water (yen/m³) was examined from the two-month water rate table of the city where X Junior High School is located. Then, the five-year bill (yen) was calculated based on the amount of water sprayed (m³) and the checked rate (yen/m³). Taking these factors into account, the mathematical model is as follows (Figure 17).

Figure 16. Amount of water used per minute (L/min)

Figure 17. Judgment model for repairs (x: %, y: ten million yen; dotted line: no repair, solid line: with repair)

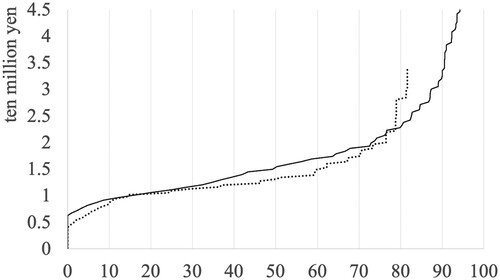
From this model, the water bill is almost unchanged between 10% and 30%, and the intersection of the graph is about 80%. Based on the above results, if the sprinkling needs to be 80% or more, the system should be repaired, and if it is less than that, it is not necessary to repair the system. Now, the standard of the sprinkling time of the current situation is 11 min, and the proportion at that time is 70%. Therefore, if the sprinklers are used for this amount of watering time, X Junior High School should decide not to repair the embedded type sprinklers.

4.2.7. Developmental problems

When solving the sprinkler problem, in the current situation illustrated in Figure 14, it was noted that 90 cc or more of water was not sprayed in the center of the schoolyard. The situation where one embedded type is installed at the center of the schoolyard needs to be considered. In other words, two sprinklers may not be necessary when watering around the center; thus, as a further consideration, the following question was generated:

If water needs to be sprinkled near the center, is one or two embedded type sprinklers preferable? (viii)

To solve this question, it is possible to use the models created thus far: the water distribution model II in Figure 13 and the proportion model in Figure 14. The water distribution model and the proportion model are as follows (Figure 18). The water distribution model in Figure 18 illustrates eleven minutes of each situation. Additionally, eleven minutes is a standard watering time from the proportion model in the upper right. Comparing these, although there are more colored parts in one sprinkler than in the failure, none are 90 cc near the center of the schoolyard. However, in the case of two sprinklers, water is sprayed so that the center receives 90 cc or more for 11 min. Consequently, to eliminate the lack of watering near the center, water can be sprayed to prevent sand dust if two sprinklers are installed rather than one.

Figure 18. Water distribution model of each situation (upper left: one sprinkler, lower left: two sprinklers, lower right: failure) and the proportion model of one embedded type sprinkler (x: minutes, y: %)

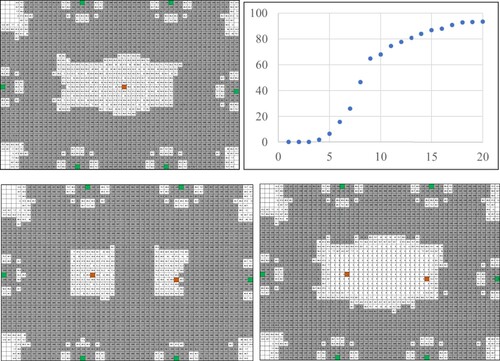
However, another developmental consideration could be in the direction of looking back at the structure of mathematical models and considering whether the mathematical models that have been created could be used for other real-world events. For the sprinkler problem, the water distribution model for the schoolyard (Figure 12 and Figure 13) was particularly important in solving the problem. Thus, the generated question was:

What other real-world events has the water distribution model been applied to? (ix)

To solve question (ix), first, the structure of the water distribution model was reviewed in detail. The water distribution model was a mathematical model that could capture the watering situation within a watering radius by representing the equally spaced arrangement of buckets as squares and incorporating numerical values into the squares. In abstraction, the model represented the distribution of an event (the amount of water sprayed in this study) and allowed us to understand the differences between the events.

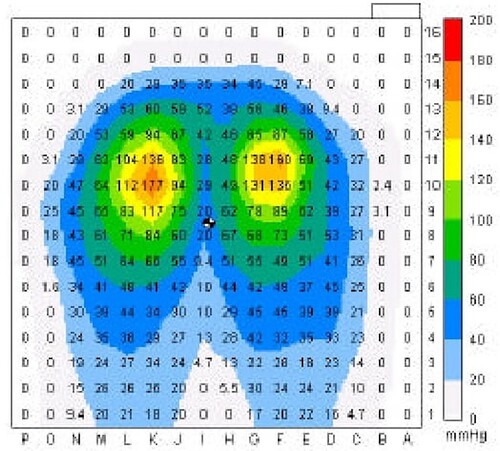
Other real-world events that could provide useful information by representing the distribution of an event were recalled, such as ‘body pressure.’ Sitting comfort can be evaluated by examining the distribution of body pressure, and conditions in which the pressure is evenly distributed are comfortable (Fujimaki, 2005). To examine the distribution of body pressure, the seat surface of a chair is considered to be a square, and the seat surface is further divided into squares, and a pressure value (in mmHg) is incorporated in each square. Additionally, the color is changed according to the section of the pressure value (for example, the closer to red, the higher the pressure value; the closer to light blue, the lower the pressure value) to make it easier to understand the difference in pressure values (Figure 19). The pressure distribution model in Figure 19 has the same structure as the water distribution model. This confirms that the water distribution model can be applied to other real-world events.

Figure 19. Body pressure distribution model (Fujimaki, 2005, p. 11)

5. Discussion

5.1. The role of generating questions in mathematical modeling

5.1.1. Role 1. The role in advancing mathematical modeling from various points of view

In this section, the sprinkler problem investigation process is first reviewed based on the ‘productive Modelling-Oriented Noticing’ process (Stillman, 2019) to analyze how noticing leads to the generating questions.

To solve the problem of whether to repair the sprinklers near the center of the schoolyard at X Junior High School, the components related to the repair were identified: the shape of the schoolyard, the performance of the sprinklers, and the water rates. Additionally, it was noticed that the watering range was unknown among the performance factors, and without clarifying this, the aspect of sprinkling could not be captured. This noticing corresponds to ‘(a) sifting through information to notice what is relevant and what is irrelevant.’ To find the watering range, the company’s catalog data was referred to, but it was noticed that the sprinklers were obsolete, and it was unknown (confusion and doubt) whether the sprinklers would sprinkle as the data indicated. This is a noticing that corresponds to ‘(b) comparing and relating relevant information with prior experiences and knowledge,’ as the catalog data was compared with prior experiences regarding obsolescence; that is, ‘performance declines as time passes.’ From these notices and doubts, questions (i) and (ii) were generated, and it was also noticed that to find the watering radius, the similarity was used from photographs of watering situations. This noticing corresponds to ‘(c) combining the relevant information to generate productive alternatives for decision making,’ as the watering radius was determined by combining the photograph and similarities.

The circular model was then applied, but from observation of the watering situation, it was noticed that there was overlap in the circles, and the lack of details (confusion) generated question (iii), and a watering distribution model was created to understand the situation. The noticing of the overlap corresponds to the noticing in (c), as the decision was made to combine the data about the schoolyard with the circular model to get a more detailed understanding of the watering situation.

After solving question (iii), it was noticed that the water distribution model I assumed that the sprinkler was operating for ten minutes in retrospect, and questions were generated by comparing it to prior experience with sprinkler operation time and the need to clarify the water sprinkling time generated question (iv). This noticing is in (b) because it relates the assumptions that underpin the water distribution model I compared to prior experience with operating time. Similarly, creating a proportional model from the water distribution model II also corresponds to the realization in (b), as it was noticed that the assumption of the water distribution model II was ‘operating for ten minutes.’

After obtaining the operating times from the proportional model created in solving question (v) and question (vi), it was noticed that the operating times and water bill are closely related, and question (vii) was generated. Finally, after solving question (vii), it was noticed that the number of sprinkling times, the water bill, and the proportion that meets the criteria (90 cc) could be combined, and a repair decision model was created to decide on whether or not to repair the sprinkler. This noticing is (c).

As described above, it is evident that in the solving of the sprinkler problem, mathematical modeling has been advanced from various points of view for a real-world event. Thus, a rich set of mathematical models was created, including a circular model of geometry to illustrate the watering range, a water distribution model to illustrate the watering situation, a proportion model to illustrate the degree of watering that meets the criteria, and a repair decision model to make decisions on whether to repair or not. These models were able to be created due to the questions generated from the ‘Productive Modelling Oriented Noticing’ and their solutions.

5.1.2. Role 2. The role of fostering mathematical modeling competencies

These problem-solving processes can be reviewed from the viewpoint of these mathematical modeling competencies. First, the sprinkler problem itself is a ‘real-world problem’ (see Figure 2). Then, the problem was ‘simplified and structured’ by identifying the relevant components (shape of the schoolyard, performance of the sprinkler, and water bills) and solving the problem based on the identified components. This corresponds to ‘Competencies to understand the real problem and to set up a model based on reality,’ which is a sub-competency of Maaβ’s A in (2006). In solving question (i) regarding the performance of the sprinkler, the sprinkler was considered a point, and the tennis court was ‘mathematized’ as a rectangle. This corresponds to ‘Competencies to set up a mathematical model from the real model,’ which is a sub-competency of A. Also, a mathematical solution was found using the similarity. This is the ‘Competencies to solve mathematical questions within this mathematical model.’ In addition to interpreting the mathematical solutions obtained, the sprinklers were validated with respect to obsolescence by comparing them with catalog data. The former is the ‘Competencies to interpret mathematical results in a real situation,’ and the latter is the ‘Competencies to validate the solution’ in sub-competency A. The mathematical modeling cycle in Figure 2 is now apparent.

Furthermore, after solving questions (i) and (ii), and creating a circular model applying the watering radius to validate the watering situation in the schoolyard, a new question (iii) regarding the amount of watering within the radius was generated, and a watering distribution model was created to solve it. Thus, questions are generated, and to solve them, the obtained models and solutions are validated, and new questions are generated from them. As the modeling cycle is repeated, it can be expected to develop ‘Sub-competencies to carry out the single steps of the modeling process.’ Additionally, the water distribution model I in Figure 13 was also taken as a reflection of the fact that it was a mathematical model that assumed that it was operating for ten minutes. This corresponds to ‘B. Metacognitive modeling competencies’ because the students thought about and reflected on their own ideas through the ‘mathematizing’ of the mathematical modeling cycle. Therefore, it is expected to develop ‘B. Metacognitive modeling competencies’ by generating questions about the structure of mathematical models. Moreover, by generating questions from various points of view, it is possible to determine the sense of direction for modeling, which is expected to foster the ‘C. Competencies to structure real-world problems and work with a sense of direction for a solution.’

5.1.3. Role 3. The role in facilitating the extension of the applicability of the mathematical model

In solving the sprinkler problem, question (viii) was generated by changing the location and the number of sprinklers set up, i.e. installing one sprinkler in the middle of the schoolyard, because the center of the schoolyard was not sprinkled in the current situation of the water distribution model II in Figure 13. In other words, from the reflection of the set situation, questions were generated by parametrizing them, which allowed the developmental problem to be solved. By generating and solving such questions, the water distribution model can be applied not only to the sprinklers installed in X Junior High School but also to various other cases because the sprinkler locations can be changed to any location in the schoolyard, and the number of sprinklers can be increased or decreased. This is an opportunity to expand the applicability of the mathematical model (generalize the mathematical model).

Moreover, question (ix) was generated by reflecting on the structure of the mathematical model and whether the mathematical model that had been created could be used for other real-world events. By generating and solving question (ix), it was found that the water distribution model is a mathematical model for understanding one real-world situation, i.e. the sprinkler watering situation, and can be used to understand the distribution of body pressure, which provides an opportunity to expand the applicability of the mathematical model to other real-world events (a generalization of the mathematical model). In solving question (ix), reflecting on the structure of the water distribution model and abstracting the uses of the model allowed other real-world events to be recalled. Moreover, mathematical models for recalled real-world events were investigated by comparing them with mathematical models created. Through these activities, it is expected that an understanding of the mathematical model created (in this case, the sprinkler distribution model) will be achieved and a new understanding of real-world events.

5.2. Construction of a principle of teaching and learning mathematical modeling with an emphasis on generating questions

Based on the role of generating questions in mathematical modeling found in the previous section, the findings of previous studies on generating questions, and the suggestions in previous studies for setting up learning instruction and learning environments aimed at developing mathematical modeling competencies, the principles for structuring mathematical modeling lessons with an emphasis on generating questions were developed (Table 4).

Table 4. Construction of teaching and learning principle of mathematical modeling with an emphasis on generating questions

In the first part of the lesson, the teacher presents an open real-world problem (the first problem statement in a sprinkler problem), and the students begin to grasp the problem (presenting problem). This is designed so that students can feel the need to investigate and work naturally and problem solve the problems.

Next, to solve an open problem, generating questions (such as question (i) in sprinkler problem) to be solved in the problem and deciding the sense of direction for the modeling are carried out (generating questions: stage 1). To generate such questions and facilitate the identification of the various components at a later stage, the teacher prepares materials (such as newspapers, videos, and data on the event) on the real-world problem. The materials are designed to incorporate elements relevant to problem-solving and those that are discarded. The preparation of such materials is a way to approach the fact that students may have prior experience with the real-world events of the presented problem, but may not have much knowledge about them. Aydin-Güç and Baki (2019) pointed out that the preparation of materials and their use motivate students and enhance the learning environment according to the activities, which is also emphasized in designing a learning environment that supports the development of mathematical modeling competencies. As a specific activity in this stage, students first compare and relate the information in the open problem with their prior experiences and knowledge (including the content of the materials) (‘(b) comparing and relating relevant information with prior experiences and knowledge’ in ‘productive Modelling-Oriented Noticing’).

Furthermore, from the comparisons and associations, students notice the unknowns, and through discussions with each other and with the teacher, they consider whether they can be mathematized (Stillman, 2015), and based on this consideration, they generate questions to be solved and decide on the sense of direction for modeling. Note that this sequence of activities is based on the directed autonomy teaching approach, in which students decide, through discussions with each other and with the teacher, which choices are in line with their educational focus (in this case, the performance of mathematical modeling) and personal interests. (Blomhøj & Jensen, 2007, p. 50).

As the next activity of generating questions: stage 1, insofar as real-world problems are intertwined with various elements, extraneous elements will be discarded, and the real-world problem will be simplified and idealized. Then, activities are conducted to identify components of the real-world problems (component identification stage). In conducting this activity, the teacher asks, ‘What do we need to focus on to solve the question?’ and encourages students to generate as many components as possible from their prior knowledge and materials. Then the teacher asks, ‘What components are necessary?’ and also ‘What components are not necessary?’ to clarify the components to be discarded. This kind of asking is an approach that encourages students to ‘(a) sifting through information to notice what is relevant and what is irrelevant’ and is also a ‘strategic intervention’ (Blum & Borromeo Ferri, 2009, p. 52) that has been suggested to be appropriate to support teachers in solving modeling tasks.

Thus, in teaching and learning that emphasizes generating questions, the teacher’s role is to enrich the activities related to the ‘direction to solve the problem’ and encourage generating questions. It is also the teacher’s role to make the students realize that the activity of identifying the components is essential for solving real-world problems.

Once the components have been identified, this is followed by an activity to examine the data and predict the relationships between the components to facilitate the investigation of the problem to be solved. Also, for clarification, a question about the relationship among the components is generated (generating questions: stage 2). This is a teacher’s approach to set the modeling direction and improve the anticipation of creating a mathematical model. Through these activities, students create mathematical models (equations and graphs) of the relationships between components and move to the stage of finding a mathematical solution based on mathematical models.

Subsequently, students are asked to present how they solved the problem to arrive at the mathematical solution. Then they need to discuss the model (Aydin-Güç & Baki, 2019), validate the mathematical model for the generating question in generating questions: stage 2, and proceed to the stage of solving the question. When moving to the interpretation and validation stages in a lesson, a gap may have arisen between mathematical conclusions surrounding a certain question and the real world. The mathematical models created are deemed insufficient to solve the problem. Additionally, students may notice new events that have not been fully captured by the model or consider components that have not been addressed in the investigation (interpreting and validation stage). In this regard, it is the teacher’s role to acknowledge the alternatives that the modeling direction has created and encourage the students to generate new questions. Specifically, the teacher asks, ‘What are the components necessary to create a new mathematical model?’ and ‘Can we create other mathematical models by combining information to better capture the phenomenon?’ These strategic interventions encourage the generation and selection of components to be considered; develops the setting of new assumptions and review of assumptions, enriches the noticing of ‘(c) combining the relevant information to generate productive alternatives for decision making,’ and generates new questions (generating questions: stage 3). Generating new questions (e.g. question (iii) in the sprinkler problem) in generating questions: stage 3 will lead to modeling from various viewpoints. This leads to the repeating of the modeling cycle. Therefore, activities corresponding to the role in advancing mathematical modeling from various points of view (Role 1) can be expected.

After solving the questions generated from various points of view, deriving the conclusions of the problem, and completing the ‘interpreting and validation stage,’ the derivation of the conclusions and the questions developed by the students themselves are generated (better modeling stage). Better modeling can involve, for example, creating a generalized model from a model of a special situation by parametrizing constant numbers or incorporating new components, or generalizing a model by reflecting on the structure of a mathematical model and considering its applicability to other real-world events. This activity corresponds to the role in facilitating the extension of the applicability of the mathematical model (Role 3). Note that if the students do not find new real-world events after reflecting on the mathematical model, the teacher’s role is to follow English et al. (2005) and present other real-world problems with similar modeling directions.

In this principle of teaching and learning, it is expected that students will carry out the activity of determining the direction to solve a problem or the sense of direction for modeling from a certain point of view (Maaβ’s C competencies [2006]), and the process of generating questions by noticing (including productive modelling-oriented noticing). In addition to solving the question, the entire mathematical modeling process (competencies A) should be carried out, which includes activities to reflect on the modeling process (competencies B) and developmental activities. Furthermore, in identifying components, generating questions, and validating models, students are expected to discuss with each other and the teacher (D competencies). Through these activities, students are expected to recognize that mathematics can be used to solve real-world problems and thus gain a sense of the usefulness of mathematics (competencies E). Therefore, the teaching and learning of mathematical modeling with an emphasis on generating questions can be expected to foster all mathematical modeling competencies (A, B, C, D, E) (Role 2) according to Maaβ (2006). In summary, the roles of generating questions in mathematical modeling and the implications for teaching and learning presented in previous studies have been taken into account, and the process of generating, solving, and reflecting on questions has been embodied in the principles of teaching and learning.

6. Concluding remarks

This study aimed to clarify the role of generating questions in mathematical modeling and construct the principles for teaching and learning mathematical modeling with an emphasis on generating questions. Consequently, the roles of (1) advancing mathematical modeling from various points of view, (2) fostering mathematical modeling competencies, and (3) facilitating the extension of the applicability of the mathematical model were determined. In particular, the roles of generating questions can be expected to enhance the development of mathematical modeling competencies and mathematical activities such as extension activities, which have been emphasized in pure mathematics. Also, clarifying the roles of generating questions and presenting the specific activities of generating questions through an investigation process of real-world problems (considering the task design process) is an important outcome in this study. Furthermore, based on the roles of generating questions, a principle for teaching and learning mathematical modeling that emphasizes the generating of questions was constructed. In particular, the most notable difference from the learning environments described in previous studies was the inclusion of activities to generate questions that consider the promotion of noticing and the inclusion of activities to generalize mathematical models to expand the applicability of the model. One way to teach based on this principle is to practice it in a typical Japanese mathematics lesson (see Becker et al., 1990; Stigler & Hiebert, 1999). Such lessons are expected to emphasize the variety of students’ thinking and to realize creative learning activities even in mathematical modeling lessons.

In this study, the role of generating questions in mathematical modeling was clarified using the introspective method. Further studies are needed to strengthen their roles. Although the principle of learning and teaching has been developed based on the roles found, empirical evidence of the effectiveness of this principle has not been achieved. Future research should put this lesson into practice according to the constructed principle and examine its results.

Acknowledgments

I would like to thank Editage (www.editage.jp) for English language editing.

The author is also grateful to the anonymous reviewers for their thorough and pertinent comments and suggestions, which have very much helped the revision of the manuscript and improved it considerably.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 High-quality reclaimed water produced by further purifying treated wastewater with advanced membrane technology.

2 In the process of the procurement of raw materials from production, transportation, and disposal after consumption, the amount of greenhouse gases emitted by the product accumulates through the consumption of electricity and fuel that is converted to CO₂.

3 The X Junior High School in this study is a public junior high school in Saitama Prefecture in Japan. The sprinklers from Company H are used in that school, and the data were provided by Company H.

4 Assuming that the water droplet is a sphere, the coordinates of the droplet after t seconds are obtained as follows: $\left(\frac{v_0\cos \theta }{k}(1-e^{-kt})\text{, }-\frac{g}{k}t+\frac{1}{k}\left(v_0\sin \theta +\frac{g}{k}\right)(1-e^{-kt})\right)$where ($v_0$: Initial velocity of water droplet, $\theta$: Angle of nozzle, $k$: Resistance coefficient of sphere, $g$: Gravitational acceleration)