Evaluating the effect of a blended collaborative/game-based learning strategy for skill reinforcement on undergraduate engineering

Abstract

This study evaluates the implementation of a collaborative/game-based learning strategy on final year B.Sc. students focused on reinforcing the Taylor theorem (a mathematical concept previously learned, usually forgotten over time and widely used in chemical engineering) and analyses its effect on their academic performance. To this end, the design of educational card games based on basic rules was proposed to students in their fifth semester (as soon as the mathematical concept is covered in their courses) and applying these games to students in the eighth semester as a reinforcement tool (who needed to apply the concept again). A mixed quasi-experimental design was carried out in which the performance and perception of the students were evaluated. The instruments used were a validated Likert-type perception test with an alpha of 0.91 and a knowledge test applied before and after the intervention. It was found that the retention rate of this mathematical concept went from 22.6% to 50%, showing an improvement in learning Taylor's series. Compared to the traditional class, the game significantly improved performance, promoting the development of skills such as creativity, innovation, participation, leadership, goal management and motivation and was recognised by the students as an innovative way of learning. In conclusion, implementing unconventional collaborative learning strategies improves academic performance and promotes skill development in engineering students.

KEYWORDS:

• Taylor theorem
• educational games
• learning strategies
• collaborative learning
• knowledge reinforcement

1. Introduction

The first chemical engineering programme began at the Massachusetts Institute of Technology (MIT) in 1888, and since then, different programmes have been created around the world that, through their curricular structures and lesson plans, have adapted to changes in science and responded to the needs of industry and society, strengthening the discipline and projecting it into the future (Mazzarri et al., 2012). These adjustments have occurred in tandem with transformations in the educational systems of the world to improve learning processes and ensure the quality of education. The characteristics of today’s students (millennials of the technology age with easy access to information and content at their fingertips) show that they have grown by overcoming challenges thanks to the continuous development of digital skill and collective learning, which have been strengthened since childhood. This is supported by Escobar et al. (Escobar Blanco et al., 2016) who concluded that skills learning is a life-life process, which poses a challenge within educational institutions.

Therefore, the implementation of strategies aimed at providing continuity for skills development can positively influence the training process. This is how some educational entities, to improve their results, have implemented complementary strategies to traditional ones, such as challenge-based learning (Fidalgo-Blanco et al., 2017), experiential learning (López Granados & García Zuluaga, 2016), learning in the environment (Ruiz-Robledillo et al., 2018), problem-based learning, case-based learning (Fernandez Serrano, 2018), and game-based learning (Montes González et al., 2018; Vélez et al., 2019) . A very useful approach complementing those mentioned above is collaborative learning, a strategy that promotes the development of transferable skills through team activities to achieve defined goals (Azizan et al., 2018; Bezard et al., 2020) and properly implemented in the classroom, it facilitates learning between classmates (Hammad et al., 2022).

Game-based learning (GBL) has been applied in different environments and formats, including digital games and board games. In the last decade, a significant number of these have been developed in virtual platforms, with favourable outcomes in the acquisition or development of skills (Rodríguez & Fernández-Batanero, 2017; Tucker & Moyer-Packenham, 2021). Valencia et al. (2016) demonstrated that by simulating scenarios in serious gaming, skills are strengthened for global software development, facilitating knowledge appropriation and gaining experience to solve problems in that context. On the other hand, Ebrahimzadeh and Sepideh (2017) found that grammatical, spelling and vocabulary skills were improved through video games in the process of learning a language.

Although digital games have been widely used in education, board games continue to have great influence when they are developed to promote learning. Vera-Monroy et al. (2020) developed a board game that increased the learning of a chemistry topic, improving academic performance by 22% compared to the control group. Along the same lines, Taspinar et al. (2016) demonstrated that teaching can be enjoyable and successful if gamification elements are included within the educational practices in a board game, for which they designed a prototype that was used in different learning environments and offered various themes.

In engineering, GBL has been implemented to cement learning. Paredes Rodriguez et al. (2016) implemented a board game that helped teach the subject Inventory Control for an Industrial Engineering programme, generating a discussion space in which knowledge was built collaboratively. The game developed by Sosa Espinosa et al. (2018)facilitated learning in the subject of Spatial Planning and Urbanism for a civil engineering programme, with students successfully appropriating knowledge and applying it to real contexts. For a Systems Engineering programme, it was demonstrated including a game within the training process fostered teamwork and greater commitment in the students (Gómez-Álvarez et al., 2017). In Chemical Engineering, implementing a board game for the Thermodynamics course was well-received and led to a large improvement in students’ performance. In this game, the participants moved along a board with contextualised and applied questions (recognised as cognitive obstacles) that had to be overcome to complete a mission (Blanco-Marigorta et al., 2019).

This demonstrates that the development of the skills that graduates must have to perform in society and respond to the challenges of the twenty-first century is facilitated by the implementation of unconventional strategies that promote learning, the appropriation of topic knowledge, teamwork and communication, ensuring comprehensiveness, mainly in those topics recognised by students as complex, difficult to understand and boring (Monnot et al., 2020; Sanders et al., 2020). Such is the case for understanding and applying the Taylor theorem as a tool to solve some of the problems arising in the context of Chemical Engineering. This theorem is introduced in the Differential Calculus courses, taken again in the courses on Numerical Analysis/Numerical Methods and applied in later courses in the degree. The coursework related to the Taylor theorem is characterised by being developed from the basic sciences, addressed very generally and without applicability, which makes it complex to learn and difficult to appropriate and apply. For this reason, it is necessary to carry out a study from the engineering side on the teaching of this subject and its direct disciplinary application through innovative strategies that facilitate its learning.

This article shows how the implementation of a blended collaborative/game-based learning (through innovative card games inspired by existing ones in the market) can help in reinforcing skills on final year students in engineering, who need to apply the Taylor theorem previously learned and sometimes forgotten over time. The first part presents the mathematical foundations and the applications that the Taylor theorem has in various fields of engineering. Second, the study methodology and the outcomes are presented. Finally, a detailed analysis of the outcomes is performed, and the findings are concluded.

2. Theory

2.1. Taylor’s theorem

The Taylor theorem is used to provide numerical solutions to problems in the engineering framework since it allows approximating any differentiable function as a sum of different polynomials. Its definition is based on the work done by Taylor (published in 1715) being defined in one or more dimensions (Hazewinkel, 2002).

Let $\mathit{U}$ be an open set of $\mathbb{R}$ and consider a function $f:\mathit{U}\to \mathbb{R}$. If $f$ is infinitely differentiable in$a$, the Taylor theorem is the power series given by Equation (1) (Hazewinkel, 2002; Königsberger, 2002). The partial sum shown in Equation (2) corresponds to the Taylor polynomials of degree $k$. Therefore, if $f$ is $n$ times differentiable in $a$, the different Taylor polynomials would be expressed according to the order (or number of terms that compose them). In this way, there are zero-degree polynomials (Equation 3), first-order (Equation 4), or in general, polynomial of degree $n$ (shown in Equation 5) (Königsberger, 2002; Lax & Terrell, 2014). (1) $\begin{array}{rl}& \sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(a)}{n!}(x-a{)}^n\end{array}$(1) (2) $\begin{array}{rl}& P_k(x):=\sum _{n=0}^k\frac{f^{(n)}(a)}{n!}(x-a{)}^n\end{array}$(2) (3) $\begin{array}{rl}& P_0(x)=f(a)\end{array}$(3) (4) $\begin{array}{rl}& P_1(x)=f(a)+f^{{}^{\mathrm{\prime }}(a)}(x-a)\end{array}$(4) (5) $\begin{array}{rl}& P_n(x)=f(a)+f^{\mathrm{\prime }}(a)(x-a)+f^{\mathrm{\prime \prime }}(a)\frac{{(x-a)}^2}{2!}+\dots +f^n(a)\frac{{(x-a)}^n}{n!}+\dots \end{array}$(5)

It is also necessary to define the oscillation of $f^{(n)}$ on the interval $[a,b]$, which is denoted by $C_n$ and is defined according to Equation (6): (6) $C_n=M_n-m_n$(6) where $M_n$ is the maximum and $m_n$ is the minimum of $f^{(n)}$ on $[a,b]$. With the above elements, it is possible to define the Taylor Theorem. Let $f$ be an infinitely differentiable function in an interval $[a,b]$, $C_n$ the oscillation of$f^{(n)}$, and suppose that Equation (7) is satisfied. (7) $\underset{n\to \mathrm{\infty }}{lim}\frac{C_n}{n!}(b-a{)}^n=0$(7) Therefore, $f$ can be represented at each point of $[a,b]$ by the Taylor theorem (Equation 8) (Lax & Terrell, 2014), and therefore, Taylor polynomials uniformly converge to $f$ on $[a,b]$ (8) $f(x)=\underset{n\to \mathrm{\infty }}{lim}{P}_n(x)=\sum _{k=0}^{\propto }\frac{f^{(k)}(a)}{k!}(x-a{)}^k$(8) In various engineering applications, Equation (8) is usually expressed in terms of the remainder, obtaining Equation (9). The remainder is defined in Equation (10) and expresses the $n+1$ remaining terms of the series. It also usually defines the Taylor theorem in terms of the difference $(x-a)$, referring to it as $h$, whose definition is presented in Equation (11) (Holmes, 2009). (9) $\begin{array}{rl}f(x)& =f(a)+f^{\mathrm{\prime }}(a)(x-a)+\frac{1}{2}{f}^{\mathrm{\prime \prime }}(a)(x-a{)}^2+\dots +\frac{1}{n!}(x-a{)}^n{f}^{(n)}(a)+R_{n+1}\end{array}$(9) (10) $\begin{array}{rl}{R}_{n+1}& =\frac{1}{(n+1)!}(x-a{)}^{n+1}{f}^{(n+1)}(\eta )\end{array}$(10) (11) $\begin{array}{rl}f(x+h)& =f(x)+h{f}^{\mathrm{\prime }}(x)+\frac{1}{2}{h}^2{f}^{\mathrm{\prime \prime }}(x)+\dots +\frac{1}{n!}{h}^n{f}^{(n)}(x)+R_{n+1}\end{array}$(11) Equations (9) and (11) are the most used since they allow approximations of complex functions to first- and second-order polynomials. The remaining terms of the infinite series are grouped in the remainder ($R_{n+1}$), which is known as the truncation error (Chapra & Canale, 2006). The Taylor theorem can be extended to functions with two or more variables, for which Equation (11) can be rewritten in vector notation (Equation 12), where $\mathit{x}=(x_1,x_2,\dots ,x_n)$, $\mathit{h}=(h_1,h_2,\dots ,h_n)$ and $D=h\cdot \mathrm{\nabla }$. This last term is expanded in Equation (13). (12) $\begin{array}{rl}f(\mathit{x}+\mathit{h})& =f(\mathit{x})+\mathrm{Df}(\mathit{x})+\frac{1}{2}{D}^{2}f(\mathit{x})+\dots +\frac{1}{n!}{D}^{n}f(\mathit{x})+R_{n+1}\end{array}$(12) (13) $\begin{array}{rl}D& =h_1\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_1}+h_2\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_2}+\dots +h_k\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_k}\end{array}$(13) The Taylor theorem would then be expressed using the Hessian matrix H (Equations 14 and 15). (14) $\begin{array}{rl}f(\mathit{x}+\mathit{h})& =f(\mathit{x})+\mathit{h}\cdot \mathrm{\nabla f}(\mathit{x})+\frac{1}{2}{\mathit{h}}^{\mathit{T}}\mathit{H}\mathit{h}+\dots \end{array}$(14) (15) $\begin{array}{rl}\mathit{H}& =\left(\begin{array}{cccc}{\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1^2}}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2\mathrm{\partial }{x}_1}& \cdots & {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_k\mathrm{\partial }{x}_1}}\\ {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1\mathrm{\partial }{x}_2}}& {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2^2}}& \cdots & {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_k\mathrm{\partial }{x}_2}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1\mathrm{\partial }{x}_k}}& {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2\mathrm{\partial }{x}_k}}& \cdots & {\displaystyle \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_k^2}}\end{array}\right)\end{array}$(15) The concept can be extrapolated to a vector of functions with multiple variables, in which case the Taylor theorem is expressed according to Equation (16). (16) $\mathit{f}(\mathit{x}+\mathit{h})=\mathit{f}(\mathit{x})+(\mathrm{\nabla }\mathit{f}(\mathit{x})\cdot \mathit{h})+\dots$(16) where $\mathit{f}(\mathit{x})=(f_1(\mathit{x}),f_2(\mathit{x}),\dots ,f_m(\mathit{x}))$ and, $\mathit{x}=(x_1,x_2,\dots ,x_n)$ and the term $\mathrm{\nabla }\mathit{f}(\mathit{x})$ is defined in Equation (17). (17) $\mathrm{\nabla }\mathit{f}(\mathit{x})=\left(\begin{array}{cccc}{\displaystyle \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_1^{}}}& {\displaystyle \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_2}}& \cdots & {\displaystyle \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_k}}\\ {\displaystyle \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_1}}& {\displaystyle \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_2}}& \cdots & {\displaystyle \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_k}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\mathrm{\partial }{f}_m}{\mathrm{\partial }{x}_1}}& {\displaystyle \frac{\mathrm{\partial }{f}_m}{\mathrm{\partial }{x}_2}}& \cdots & {\displaystyle \frac{\mathrm{\partial }{f}_m}{\mathrm{\partial }{x}_k}}\end{array}\right)$(17)

2.2. Applications in engineering

The Taylor theorem is the basis for constructing the Newton–Raphson method, used to identify roots of nonlinear equations, and it is because any function can be approximated to a first-order polynomial (keeping the first two terms of the series and truncating the others), as shown by Equation (4) (Chapra & Canale, 2006). From there, the best-known one-dimensional form of the numerical method is obtained, as shown in Equation (18). (18) $x_{j+1}=x_j-\frac{f(x_j)}{f^{\mathrm{\prime }}(x_j)}$(18) where j indicates the corresponding iteration.

Equation (18) can be extrapolated to a more general model aimed at solving a system of nonlinear equations. Starting from Equation (16) and making a first-order approximation, one arrives at Equations (19) and (20). The Newton–Raphson method is simplified by solving Equation (19) with respect to$\mathit{h}$ and upon adjusting the new value of$\mathit{x}$ using Equation (20) in each iteration$j$ (Linge & Langtangen, 2016). (19) $\begin{array}{rl}(\mathrm{\nabla }\mathit{f}({\mathit{x}}_{\mathit{j}})\cdot \mathit{h})& =-\mathit{f}({\mathit{x}}_{\mathit{j}})\end{array}$(19) (20) $\begin{array}{rl}{\mathit{x}}_{\mathit{j}+1}& ={\mathit{x}}_{\mathit{j}}+\mathit{h}\end{array}$(20) Equation (16) is also used in the analysis of process dynamics for implementing control systems. The mathematical models analysed in the Control courses are based on having linear systems (although this is not always the case). This is where the linearisation of functions is of interest for analysing dynamic systems, since, although there is a truncation error associated with linearisation, it is possible to approximately know the dynamic behaviour of many systems. From this linearisation of functions, the stability of the system can be determined, finding the transfer functions that represent it or analysing its stability through the state-space matrix (Seborg et al., 2016; Smith & Corripio, 2005). In addition, several simulators and computational tools base their calculation algorithms on this theorem to mathematically simplify a complex problem.

The Taylor theorem is so relevant that several authors have worked on the development of strategies that facilitate its learning, such as Román and Barreno (2016), who developed a didactic module in MATLAB, demonstrating that the implementation of this tool helped in the teaching-learning process of the study of series, poles, and residues of the complex plane. Costa and Rossignoli (2017), described useful methodological and didactic aspects to facilitate learning basic concepts in linear algebra that are necessary in engineering programmes and that are not easily related to the application in their careers, including the Taylor theorem.

2.3. Collaborative and game-based learning (GBL) in engineering

As seen before, the Taylor Series can be built from elementary building blocks to form an approximation to a particular function, and this fact can be used as the backbone of a collaborative learning strategy, given the fact that a team can build different function definitions by iteratively adding terms to an infinite sum. In this sense, Collaborative Learning (CL) is used as an educational constructivist strategy aimed to transform the classroom into a social learning environment with a participatory and collective construction approach in which the appropriation of knowledge and the development of competencies are promoted among all the participants (Nasir et al., 2021). Authors like (Aşıksoy et al., 2021) consider that peer learning can be achieved by means of gamification processes that include interactive activities and challenges mediated by competencies and involving some type of recognition, resulting in favoured participation and the development of diverse skills in students. This fact has been reinforced by Yu (2021), whose results showed better results in knowledge tests for those groups in which strategies involving competition among students were used.

The usefulness and applicability of collaborative learning coupled with gamification have been evaluated in different learning environments. On the one hand, relevant works have been reported to illustrate the benefits of peer learning in playful scenarios across different areas of knowledge, such as Purnamawati et al. (2021), who designed an active learning tool for digital electronics which generated not only satisfactory results in terms of skills development but was very well evaluated by students for being very practical and fun. The most important aspect highlighted by the authors is the ease with which students acquired and appropriated knowledge in environments other than traditional ones, where participants recognised that learning in the company of others helped to overcome conceptual gaps. On the other hand, the complexity of engineering education relies on a strong mathematical component, therefore, institutions and professors seek to develop strategies that facilitate the appropriation of knowledge and promote meaningful learning. For this reason, some authors showed that the use of gamification in basic mathematics courses for engineers helped to improve learning, promoted relevance, confidence, and satisfaction in students, in addition to reducing academic dropout (Zabala-Vargas et al., 2021). In higher courses, gamification has also shown excellent results, as shown by Chans and Portuguez Castro (2021), who demonstrated that sixth and seventh-semester students showed the same motivation as basic students when playful proposals were included in the classroom, generating motivation and commitment, as well as improving attitude and generating greater attendance to the classroom activities designed in the course.

3. Method

This study aimed to evaluate the effect of the gaming tool ‘Playing cards to apply Taylor’s theorem’ on the academic performance of chemical engineering students, who learned this topic from the mathematical viewpoint and later (in their final year) were required to remember and apply it in a particular context of chemical engineering. To this end, the study was carried out in two phases: The first one corresponded to the design of a gaming tool based on some previously declared rules. This design was performed by 5th semester students, who recently learned the Taylor theorem and had still fresh the concept in their minds. The second phase covered the application of these designed tools on 8th semester student, who required to apply the concept. This study was based on a mixed approach, incorporating both qualitative and quantitative information gathering student perceptions and assessing student performance on a knowledge test.

3.1. Design

As mentioned above, the concepts related to the Taylor theorem are introduced in differential calculus, reinforced in numerical analysis, and applied in last semester/year undergraduate courses such as process control. In those courses the students develop Problem Solving skills as a learning outcome, in addition to Teamwork and Innovation. In this study, fifth-semester chemical engineering students, who were studying topics related to numerical analysis in their study plan, were invited to develop the following activity: In the session corresponding to Taylor’s theorem, the subject was presented theoretically, and as an evaluation strategy, a collaborative learning methodology was implemented, where they were asked freely and autonomously to organise working groups in order to propose gaming tools that would allow applying the previously explained concept. The following rules were developed within the framework of this activity:

• It must be a multiplayer board game, or at least, a gaming tool that had a group collaboration when playing it.

• The start of the game should be the function to approximate, the order of the approximation and the point around which the approximation was to be made. For the Equation (9), one must select $f(x),a$ and the number of terms to add in the series.

• Each group had the freedom to assign its own name and establish the rules of the game.

Taking inspiration from current board games was valid. The game should not be completely new or unknown to whoever used it, with the understanding that the learning objective was not learning the mechanics of a new game but rather applying previous knowledge and experiences to improve the learning of the Taylor theorem.

At the end of the design phase, the research team evaluated the gaming tools and selected those which accomplished all specified rules. These gaming tools were used later (in the next phase) on 8th-semester students as a strategy to reinforce this mathematical concept to solve problems in the chemical engineering context. The selected course to validate the games was ‘Process Dynamics and Control’, given the need to linearise nonlinear equations and thus, to find the transfer function of a dynamic system.

For the development of the study, the 8th semester students were divided into two groups: the first group received the normal teaching/reinforcement session of the Taylor theorem, and the second group used the previously designed collaborative activity. All the students were evaluated against perceived and academic performance in the specific use of the theorem.

3.2. Instruments

The study was developed as pretest/posttest quasi-experimental research, performing an evaluation prior to implementing the learning strategy and another after implementing it (Rojas Cairampoma, 2015). The mixed approach consisted of a qualitative analysis related to the student’s perception and a quantitative analysis regarding their performance with the strategy used.

To collect information on student perception, a survey with a Likert scale ranging from 1 to 5 was developed, consisting of 36 items, divided into 7 groups: development of specific, general, systematic, interpersonal skills, impact of the strategy and finally, recognition of weaknesses and strengths. Based on these items, the following analysis characteristics were established: 1. Smaller gap between theory and practice, 2. Participation, 3. Innovation, 4. Decision-making, 5. Written communication, 6. Creativity, 7 Goal management, 8. Intellectual stimulation, 9. Motivation, 10. Interpersonal communication, 11. Conflict management, 12. Negotiation, 13. Leadership, 14. Innovative learning, 15. Appropriate time and 16. Good learning strategy.

The effect of the gaming tool on academic performance was carried out by administering an open-ended test that directed the student to solve an exercise applying the Taylor theorem before and after implementing the two learning strategies. The test was evaluated according to three performance categories: Score 1–0%. The student does not remember how the problem is solved or did not provide any results; Score 3–50%. The student slightly remembers how to implement the series and provides incorrect results and Score 5–100%. The student clearly remembers how to apply the series to the proposed problem and answers correctly.

3.3. Participants

In the first phase of the study (corresponding to the construction of the gaming tools), 20 students in their 5th semester were organised into 5 groups of 4 students. They were studying the course ‘Optimization in Chemical Engineering’ worth 2 academic credits at a Colombian university. This course covers topics of numerical analysis for chemical engineers. The second phase of the study (corresponding to the application of the constructed tool) included 163 students of the 8th semester who were studying the subject ‘Process Dynamics and Control’ worth 4 academic credits. These measurements were taken between years 2021 and 2023. In this phase, the reference group (TRAD-01) was made up of 71 students, and the experimental group (GAME-01) was made up of 92 students. The students of the TRAD-01 group were reinforced in the Taylor theorem through the traditional class, where the application of this mathematical concept was presented in a masterful way, while the students of the GAME-01 group remembered the theorem through the gaming tools, consisting of five decks that met the requested rules. At this point, the concept of ‘traditional classroom’ is defined as a teaching-centered approach, in which the teacher is the main actor who exposes the topics and mobilises information in a unidirectional way, while the students assume passive roles as receivers of knowledge.

3.4. Procedure

The gaming tools designed by the 5th semester students were applied to the participants who formed the group GAME-01, with the following methodology: first, the students solved a knowledge test to identify their prior knowledge; second, the students in their work teams read the instructions from the decks, assumed roles and played (Figure 1); finally, in the next class session, the test was applied again. The same sequence was implemented with the TRAD-01 group, but in the second step, they attended the traditional class without participating in the game.

Figure 1. Implementation of the gaming tool in chemical engineering students (Source: prepared by author)

3.5. Data processing

The perception assessments applied to the 8th semester students (who participated in the study) were analysed, determining the mean and the deviation. The outcomes of the quantitative pretest/posttest were classified into 4 groups: PRE-GAME-01, POST-GAME-01, PRE-TRAD-01 and POST-TRAD-01. The data were analysed in pairs, and descriptive statistical analysis was performed. To evaluate the statistical significance of the outcomes, a one-way ANOVA test was performed with 95% confidence, the factor being the learning strategy applied.

4. Results and discussion

4.1. Game designed by 5th semester students

Table 1 shows the characteristics of the games designed by the students of the course ‘Optimization in Chemical Engineering’. It is noteworthy that some of the proposals were inspired by traditional card games. The images of the games are shown in Figure 2.

Table 1. Description of the games developed by the 5th semester students.

ID	NAME	OBJECTIVE	Players	INSPIRED BY
BARAJA_1	Taylorfun	Placing all the player’s chips on the predetermined functions on the table, before their competitors	2–3 or 4 players	Solitaire®
			Play in pairs
BARAJA_2	Taylor series	Not having any cards left after completing the approximation of the functions previously placed on the table	2–5 players	Uno®/Solitaire®
BARAJA_3	Taylor-Q	Manage to run out of chips, completing the different series.	2–5 players	Rummi-Q®
BARAJA_4	Idiot	Complete the Taylor series by flipping one card, showing it to the other participants	4 players	Idiot
BARAJA_5	Optimizing One	Running out of cards when completing the approximation of the functions previously placed on the table	2–5 players	Uno ®

Figure 2. Games designed by the students: (a) BARAJA_1 (Taylorfun) (b) BARAJA_2 (Taylor series) (c) BARAJA 3 (Taylor-Q) (d) BARAJA_4 (idiot) (e) BARAJA_5 (Optimizing One).

Table 2. ANOVA between PRE-TRAD-01 and PRE-GAME-01 groups.

	Degrees of Freedom	Sum of Squares	Average Squares	F value	P value
Strategy	1	0.09	0.027	0.021	0.880
Residuals	78	47.83	1.283

Source: Prepared by the authors.Source: Prepared by the authors.

Table 3. ANOVA for POST-TRAD-01 and POST-GAME-01 groups.

	Degrees of Freedom	Sum of Squares	Average Squares	F value	P value
Strategy	1	47.42	47.42	25.59	2.78E-6
Residuals	77	142.65	1.85

Source: Prepared by the authors.

4.2. Perception of students

The student perception instrument was validated with a Cronbach's alpha of 0.91, showing excellent internal consistency. The comparison of the average scores given by the students for the analysis characteristics between the TRAD-01 and GAME-01 groups are presented in Figure 3.

Figure 3. Assessment of the analysis characteristics of the TRAD-01 and GAME-01 groups. 1. Smaller gap between theory and practice, 2. Participation, 3. Innovation, 4. Decision-making, 5. Written communication, 6. Creativity, 7. Goal management, 8. Intellectual stimulation, 9. Motivation, 10. Interpersonal communication, 11. Conflict management, 12. Negotiation, 13. Leadership, 14. Innovative learning, 15. Appropriate time and 16. Good learning strategy (Source: Prepared by the authors).

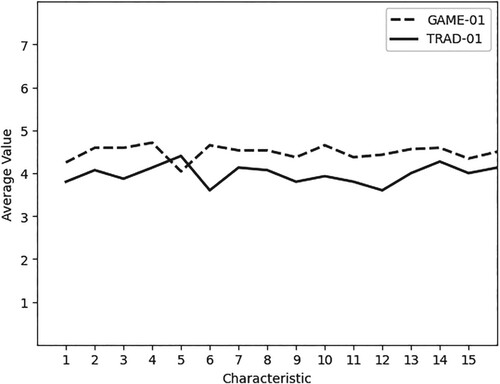
Figure 3 shows that the use of the Game impacted students, strongly promoting skills such as creativity and innovation, which should be noted if these two characteristics are part of the group of transferable skills required for engineers that will be working in the 5th Industrial revolution, as argued by Raj et al. (2020)

On the other hand, leadership, participation, goal management and motivation had higher scores by more than 0.5 points compared to the traditional strategy, corroborating the results of Gómez-Álvarez et al. (2017), who demonstrated that alternative and innovative collaborative learning strategies motivate students and promote skills that facilitate training processes. The perception of the students also showed that the strategy managed to reduce the gap between theory and practice by stimulating the intellect and promoting decision-making, characteristics expected when innovative learning scenarios are provided that respond to the skills of the new generation of students (Vera-Monroy et al., 2022).

Written communication was the characteristic that allowed verifying the honesty with which the students responded to the perception instrument, considering that, due to the nature of the game strategy, it should not be rated highly. This was evidenced in the outcomes, as it is the only characteristic in which the gaming strategy had less value than the traditional one. It is important to note that the students perceived that the game was a good learning strategy that was academically beneficial when developed at the same time as the traditional strategy. Similar outcomes were demonstrated by other authors (Paredes Rodriguez et al., 2016; Sosa Espinosa et al., 2018).

4.3. Effectiveness of the game strategy

The outcomes of the tests applied to the students before and after intervening with the learning strategies are shown in Figures 4–6. The first analysis was to compare whether the initial groups were similar; Figure 4 shows the performance (expressed in percentage) obtained for the PRE-GAME-01 and PRE-TRAD-01 groups.

Figure 4. Comparison between PRE-TRAD-01 and PRE-GAME-01 groups: 1- The student does not remember how to solve the problem; 3 The student slightly remembers how to implement the series with wrong results. 5- The student clearly remembers how to apply the series to the proposed problem and answers correctly (Source: Prepared by the authors).

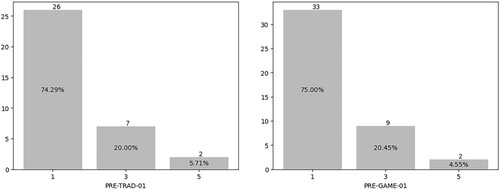
Figure 4 showed that the average performance of the two groups is similar, confirmed with a p-value greater than 0.05, demonstrating that there is not enough statistical evidence to assume that the two groups have different knowledge. This is very valuable because it allows us to infer that any changes in the final outcomes are attributed to the effect of the learning strategies implemented (Table 2).

After confirming that the samples were statistically similar, the outcomes of the POST-GAME-01 and POST-TRAD-01 groups were compared (Figures 5 and 6).

Figure 5. Traditional strategy: comparison of the PRE-TRAD-01 and POST-TRAD-01 groups. 1- The student does not remember how to solve the problem; 3 The student slightly remembers how to implement the series with wrong results. 5- The student clearly remembers how to apply the series to the proposed problem and answers correctly (Source: Prepared by the authors).

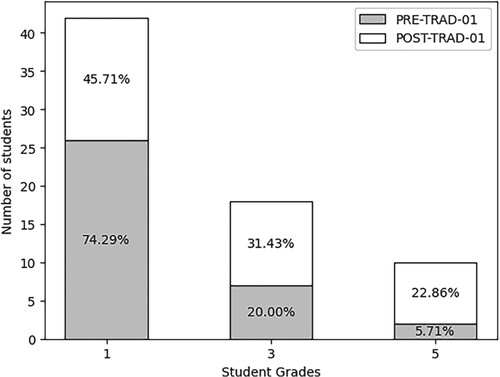
Figure 6. Game strategy, comparison of the PRE-GAME-01 and POST-GAME-01 groups. 1- The student does not remember how to solve the problem; 3 The student slightly remembers how to implement the series with wrong results. 5- The student clearly remembers how to apply the series to the proposed problem and answers correctly (Source: Prepared by the authors).

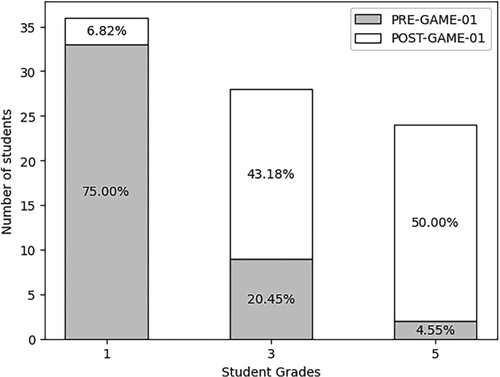
Figures 5 and 6 show that the two learning strategies implemented to develop the Taylor theorem topic had a positive effect on the training process of the students, which could be evidenced by the increase in average performance obtained. The previous outcomes showed that the game had a greater positive effect on student performance than the traditional class. This was corroborated with the ANOVA test (Table 3), in which a p-value less than 0.05 was obtained at a confidence level of 95%. This showed that the teaching strategy significantly affected the outcomes, proving that the academic performance of the students in the Taylor theorem topic does depend on the implemented strategy.

The results of the study showed the benefits of implementing the gaming strategy to reinforce learning and application of Taylor’s theorem, since in addition to considerably and significantly improving the academic performance of students, it also favoured the development of important skills for the engineering profile, which reinforces the conclusions drawn by other researchers (Taspinar et al., 2016; van Putten et al., 2022; Vera-Monroy et al., 2020)

5. Conclusions and perspectives

Implementing innovative strategies framed in collaborative learning such as ‘playing cards to apply Taylor’s theorem’ facilitates reinforcement, learning and application of the topic in the students of the course ‘Optimization in Chemical Engineering’, since they managed to propose a playful alternative that would allow them to formulate this theorem for its use in subsequent semesters. On the other hand, the students of the ‘Dynamics of Processes and Control’ course who applied the game improved their academic performance, as supported by the outcomes. The experience of having games designed by 5th semester students motivates the participation of young people in their 8th semester, who consider it an innovative way to learn.

The gaming tool significantly enhances creativity and innovation, two important skills for professionals that will be developed within engineering 4.0. This study demonstrates that the implementation of educational games within the classroom generates unconventional academic spaces that promote the development of skills such as participation, leadership, goal management and motivation, being recognised by students as an excellent learning strategy that brings theory to practice. It is important to recognise that the designed tool reinforces the appropriation of the topics related to Taylor series, however, it does not promote new learning, since it is necessary that the students previously know the theory that underlies the topic and, in addition, they must have a solid foundation in mathematics. In addition, the games designed by the students were based on models of routinely used board games, so that all participants knew the general rules, which suggests that the strategy is reproducible if known game dynamics are used, which does not require an additional investment of time and resources to learn new games.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by Universidad de La Sabana.