Students’ self-regulated learning of university mathematics in different learning environments

Abstract

Self-regulated learning is important, due to the large share of self-study time for learning mathematics at university, but it is still underresearched.Theoretically and practically, it is of particular interest to understand patterns that lead to different self-regulated learning processes, in order to identify approaches to support students learning. In this study, we analyse students’ appraisals of different elements of three different learning environments in Germany (on-campus, online) and Finland (on-campus) for their congruence with students’ goals. According to Boekaerts’ dual processing model of self-regulated learning, such appraisals define students’ purposes of self-regulation. We analyse interview data of two students per learning environment, in each environment one with a focus on learning goals and one on just ‘surviving the course’. Our results provide a detailed description of the variety of the six students’ self-regulated learning processes as well as a synthesis of students’ appraisals of different elements of the learning environments, indicating the importance of students’ appraisals of the relevance of mathematical contents, implications of exercise assessments, and coping potential, especially in terms of peer learning. These results have practical implications for ‘supporting students’ self-regulated learning processes which are discussed.

KEYWORDS:

• Goals
• appraisals
• self-regulated learning
• teachers’ and students’ practices at university level
• assessment practices in university mathematics education
• individual support

1. Introduction

Self-regulated learning is the process through which learners attempt to monitor, regulate, and control their learning processes according to their goals and the contextual features of the learning environment (Pintrich, 2000). Self-regulated learning is of particular importance in learning environments in which learners have the freedom and the responsibility to set their own goals for learning and find their own ways of structuring their learning processes to pursue these goals. Mathematics learning at universities is to a large extent organised in exactly such learning environments: For example, at German and Finnish universities, it is common practice that about two-thirds of the time scheduled for mathematics modules is assigned to self-study, in which students need to organise and regulate their learning by themselves (Göller, 2020; Lahdenperä et al., 2022).

Despite this importance, students’ self-regulated learning processes are still under-researched in university mathematics education. In particular, there is almost no research on the interactions of students’ learning processes, their goals, and (their appraisals of) different elements of the learning environment (such as the type of given support structures, lectures, exercises, assessments, peers, etc.). This perspective has the potential to contribute to our understanding of students’ well-documented difficulties in university mathematics education (Artigue, 2021; Gueudet, 2008, 2023; Moore, 1994; Thomas & Klymchuk, 2012; Winsløw & Rasmussen, 2020) and their impact on students’ motivation, emotions, self-concepts, or attitudes towards mathematics (Di Martino et al., 2023; Gildehaus & Liebendörfer, 2021; Göller & Rück, 2022), with practical implications for the development of support measures for reducing these difficulties (Biehler et al., 2021; Lawson et al., 2020; Rämö et al., 2021).

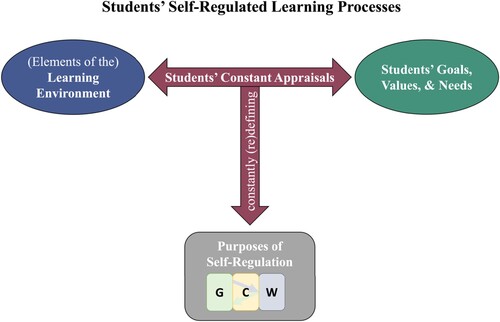
Therefore, the present paper aims to qualitatively analyse university mathematics students’ self-regulated learning processes with a special focus on their goals, their appraisals of different elements of their learning environments, as well as the interactions of students’ goals, appraisals, and purposes of self-regulation (cf. Figure 1). Our theoretical basis will be Boekaerts’ (2011) dual processing model which has been shown to be fruitful for analysing mathematics students’ self-regulated learning processes (Göller, 2020; Göller & Rück, 2022), and which will be introduced in section 2.1. While other models of self-regulated learning mostly have a strong focus on students’ learning and performance goals, Boekaerts’ (2011) model prominently includes students’ values and needs for well-being which are of great importance in challenging, exhausting, or frustrating learning environments such as university mathematics education (Göller, 2020; Göller & Gildehaus, 2021; Hailikari et al., 2016; Liebendörfer & Hochmuth, 2015; Martínez-Sierra & García-González, 2016; Sierpinska et al., 2008). As goals and appraisals play a key role in Boekaerts’ model, we will have a deeper look into goal and appraisal theories (section 2.1) for a better understanding of these processes. This theoretical groundwork allows us to discuss existing studies on self-regulated learning in different learning environments of university mathematics education (section 2.2) and to formulate our research questions in more detail (section 2.3), which guide our methodological approach (section 3) and the presentation of the findings of our study (section 4). Finally, we discuss theoretical and practical implications of these findings (section 5).

Figure 1. Schematic representation of the theoretical framework informed by Boekaerts’ (2011) dual processing model of self-regulated learning. G: Growth; W: Well-being, C: Commitment.

2. Theory

Self-regulated learning is defined as ‘an active, constructive process whereby learners set goals for their learning and then attempt to monitor, regulate, and control their cognition, motivation, and behaviour, guided and constrained by their goals and the contextual features in the environment’ (Pintrich, 2000, p. 453). This definition entails the assumptions (1) that learners have an active and constructive role in their learning processes, by constructing their own meanings, goals, and strategies, (2) that learners have the potential to control these processes, (3) that learners have specific goals (or standards, or values, or needs) which guide these processes and against which (the outcome of) these learning processes can be evaluated, and (4) that these learning processes are mediators between learners personal characteristics and the characteristics of the learning environment (Pintrich, 2000). This indicates that a student who is regulating their learning has set learning goals, and then constantly monitors and reflects on their progress. Furthermore, the student, if needed, adjusts their study processes accordingly, and overall, the student’s goals and the learning environment have a guiding and constraining role in these processes.

There are multiple theoretical models of self-regulation (Panadero, 2017). As discussed earlier, we utilise Boekaerts (2011) dual processing model of self-regulated learning for this study.

2.1. Boekaerts’ dual processing model of self-regulated learning

Boekaerts’ (2011) dual processing model of self-regulated learning theorises that learners constantly appraise contextual features of the learning environment and tasks for their congruence with their personal goals, values, and needs. Depending on these appraisals, the focus of students’ self-regulated learning processes dynamically shifts toward one of the following three identified purposes of self-regulation: (G) expanding knowledge and skills (Growth), (W) preventing threat to the self (Well-being), or (C) protecting one’s commitment to the task (Commitment). From the perspective of learning, expanding knowledge and skills (G) i.e. having the focus on the learning task is the most desirable purpose of self-regulation. According to Boekaerts (2011), this takes place if a student appraises the learning situation as being congruent with their personal goals, values, and needs. In contrast, if a student appraises the learning situation as not being congruent with their personal goals, values, and needs, the focus will shift to preventing threats to the self (W). This takes place for example if a task is appraised as being irrelevant or too difficult. Here, the learning situation poses a (potential) threat to the student’s well-being, and consequently, the task is appraised as an obstacle rather than a catalyst for achieving the set goals resulting for example in disengagement. The third purpose of self-regulation, namely protecting one’s commitment (C), refers to the shifts between the two other purposes. For example, a student may at first be committed to a learning task and later experience obstacles that threaten their well-being. In this case, the student’s constant appraisals of the learning situation will shift their focus from the learning task (G) towards the self (W), but they can then make efforts to reroute their focus towards the learning task (G) and in this way, protect their commitment to the task (C).

To utilise Boekaerts’ (2011) dual processing model in analysing students’ learning experiences, there is a need to operationalise the model’s two focal concepts, namely the goals and the appraisals. In the following, we present the goals in light of Pintrich (2000), and the appraisals as seen in Scherer’s (2001, 2009) component process model.

Learners’ goals can be defined as behaviours or outcomes that they are consciously attempting to perform or attain (Zimmerman et al., 2015). Pintrich (2000) distinguishes learners’ goals into learning goals which focus on increasing competence (e.g. understanding a mathematical theorem or proof), and performance goals which focus on the attainment of positive judgments from others (e.g. good grades). Especially learning goals, but also, to a slightly smaller extent, performance goals are positively correlated with academic achievement and favourable learning strategies (for meta-analyses see Credé & Phillips, 2011; Schneider & Preckel, 2017). In addition to such learning and performance goals, which refer directly to learning or assessment, students’ values and needs are represented in goals such as protecting one’s well-being which are also relevant for self-regulated learning processes (Boekaerts, 2011), especially if the learning environment is as challenging, exhausting, or frustrating as often in university mathematics education (Göller & Gildehaus, 2021; Hailikari et al., 2016; Liebendörfer, 2018; Liebendörfer & Hochmuth, 2015; Martínez-Sierra & García-González, 2016; Sierpinska et al., 2008).

Appraisal theories assume that persons’ thoughts and emotions are largely inseparable and arise from their perceptions – their appraisals – of the environment (Ellsworth, 2013; Moors et al., 2013). Therefore, it is not so much the learning environment itself, but the learners’ appraisal of the features of the environment that influences their self-regulated learning. According to Scherer’s (2001, 2009) component process model, there are four major appraisal objectives which influence the appraisal of an event or a situation (i.e. the set of momentary circumstances, Tekoppele et al., 2023): relevance, implications, coping potential, and normative significance. First, persons will appraise how relevant an event is for them and if it directly affects them or their social reference group (Scherer, 2001, 2009). Second, persons will assess what implications or consequences the situation might have and how these implications affect their well-being and their immediate or long-term goals (Scherer, 2001, 2009). Third, persons will appraise how well they can cope with or adjust to the situation and its consequences (coping potential), and finally, the person will appraise the significance of the situation for their self-concept (internal standards) and for social norms and values (external standards; Scherer, 2001, 2009).

Both these perspectives can be combined for university mathematics education as we illustrate in the following example: When a lecturer hands out a mathematical exercise for self-study (element of the learning environment), students will appraise if working on this exercise is relevant to their goals: e.g. for learning a specific mathematical content (learning goal), for passing a future examination (performance goal), or for their well-being, if working on the exercise might be frustrating or exhausting. Students may expect that it will be possible for them to attain a solution, but that they will need great effort and the help of a friend (coping potential). They will need to negotiate if they will make the effort considering the consequences (whatever they might be in that situation) of not working on the task or not attaining a solution (implications). Students also might consider copying the solution of a friend regarding its significance for their self-image (internal standards) and possible rules or norms regarding copying of their social group (external standards).

2.2. Mathematics students’ self-regulated learning in different learning environments

There are hints regarding the potential of the composition of different elements of the learning environment (such as lectures, exercises, assessment, peers, etc.) for students’ self-regulated learning processes (Gueudet & Pepin, 2018; Kock & Pepin, 2018; Lahdenperä et al., 2022). For example, in institutional settings in which solving weekly exercises in self-study is part of the assessment, students’ self-regulated learning tends to be dominated by working on these exercises (Göller, 2020). In the example given at the end of section 2.1, it can be expected that students’ appraisal of the exercise will depend on whether the exercise is part of the assessment or not (especially regarding its implications). Generally, students’ self-regulated learning is often strongly oriented towards exam-related goals (Anastasakis et al., 2017), which e.g. highlights the importance of assessment practices for students’ self-regulated learning (Göller, 2017). Such findings also highlight the potential of exercises, assessment practices, or other elements of the learning environment to support, guide, or constrain students in organising and focusing their learning processes.

As a result of the COVID-19 pandemic, universities at least temporarily had to introduce online teaching, which introduced for many students a fully digital learning environment that was new in many ways. One of the challenges was that in such online learning environments during the pandemic many students missed the routines and the structure given by going to university and having a daily routine (Radmer & Goodchild, 2021). For some students, it is documented that, while online live lectures and tutorials helped them to structure their learning, asynchronous teaching by providing videos where students had to decide for themselves when to watch them, was a big challenge (Liebendörfer et al., 2023). Such results point out the (maybe even bigger) importance of students’ abilities to self-regulate their learning in such online environments.

Research indicates that overall, the level of students’ self-regulation of learning in first-year mathematics courses can be considered low (Lahdenperä et al., 2022). However, there is evidence that student-centred learning environments can support students to shift from unregulated learning towards more regulated learning (Lahdenperä et al., 2022). Lahdenperä (2022) identified four central characteristics of university mathematics learning environments that contributed to students’ (un)regulated learning practices: the weekly tasks, teaching, peer support, and scaffolding. This finding is in line with Pintrich’s (2000) and Boekaerts' (2011) conceptualisation that self-regulated learning and especially students’ appraisals mediate between learners’ goals and the (elements of the) learning environment. In this study, we focus on mathematical contents, mathematical exercises, assessment of exercises, peer learning, as well as tutors and scaffolding as possibly influential elements of the learning environments for self-regulated learning of university mathematics.

2.3. Research questions and aims of the study

Concluding, this paper aims to better understand students’ self-regulated learning processes in university mathematics education, especially in terms of their goals and appraisals of different elements of their learning environments. Therefore, we contrast different institutional settings (cf. section 3.1) and focus on students’ self-regulated learning when working on mathematical exercises which have been shown to be one of the most prominent learning situations for mathematics students at the university (Göller, 2020; Lahdenperä et al., 2021). First, we aim to understand mathematics students’ self-regulated learning on an individual level. We, therefore, aim at a case-based description of individuals’ self-regulated learning in terms of their goals and appraisals of the elements of their learning environment:

• RQ 1: How do mathematics students self-regulate their learning of university mathematics in terms of their goals and appraisals of the elements of different learning environments when working on mathematics exercises?

Second, we aim at understanding at a more abstract, conceptual level students’ appraisals (relevance, implications, coping potential, significance) of the different elements of the learning environment for congruence and incongruence with their goals (horizontal arrow in Figure 1), which according to Boekaerts (2011) defines students’ purposes of self-regulation (vertical arrow in Figure 1):

• RQ 2: When and how are different elements of the learning environments appraised as (in)congruent with students’ goals?

By answering these research questions, we additionally aim to discuss what support measures and learning environments are conducive to enabling as many students as possible to participate in university mathematics in a way that is congruent with their personal goals, values, and needs.

3. Methods

To answer our research questions, we analysed interview data of six different students from three different universities (one in Finland, two in Germany) which varied widely in the institutional context they provided (cf. section 3.1). The interview data stem from three different research projects (Gildehaus & Liebendörfer, 2021; Göller, 2020; Lahdenperä, 2022) with different research foci. However, the interviews also shared a lot of commonalities: We analysed one interview per student at a similar stage in their studies. At the time of the analysed interviews, all six students attended a course on theorem-proof-based Linear Algebra and had already participated in at least one mathematics examination at university. All the interviews contained questions about what students did in the last weeks when they studied for their mathematics courses, especially for their course in Linear Algebra, what goals they had set for their courses and their learning, and how they appraised their learning and their learning environments. Each interview was conducted by one of the three authors, had a length of approximately one hour, and was transcribed verbatim and completely. The interviewed students gave their active consent that the interview data could be analysed scientifically and that the results of this analysis including anonymized quotations could be published for scientific reasons.

3.1. Sample and features of the different learning environments

The sample was theoretically chosen by contrasting different learning environments and students with different goals: Out of three different institutional settings (Germany on campus, Germany online, Finland on campus) we chose two students respectively (cf. Table 1). For each of the three institutional contexts, we chose two students with contrasting goals: One student with strong learning goals and one student who reported (almost) no learning goals and only the performance goal to ‘survive the course’ i.e. somehow pass the examinations of the course. This pre-coding of students’ main goals was already done for other studies (see Göller et al., 2023 for further explanations on this).

Table 1. Overview of the theoretically chosen sample.

Student	Institutional setting	Study Programme	Main Goal
Toni	Germany on campus	Mathematics major	Focus on learning goals
Kim	Germany on campus	Teacher student	Survive the course
Liv	Germany online	Teacher student	Focus on learning goals
Luca	Germany online	Teacher student	Survive the course
Lumi	Finland on campus	Mathematics major	Focus on learning goals
Tuisku	Finland on campus	Statistics major	Survive the course

In the following, we will give some more details on the six students and the institutional settings they studied in.

In the German institutional on-campus setting, Toni (all names changed; we use gender-neutral names, as gender is not the focus here) was a mathematics major, and Kim was a higher secondary (Gymnasium, grades 5–13, student’s age 10–19) preservice teacher with mathematics as one of two (compulsory) subjects. At the time of the interviews (in their second semester at university), they both attended a nine-credit proof-based Linear Algebra course with mathematical content such as general vector spaces, subspaces, linear mappings, and scalar products. These courses consisted of lectures (twice a week) where mathematical theory (i.e. definitions, examples, theorems and their proofs) was presented mainly on a chalkboard and exercises that were handed out every week. Students had to work on these exercises in self-study (homework) and submit their solutions which then were corrected, graded, and discussed in a separate lesson. To pass such a course, 50% of all points for the exercises must have been achieved (to be admitted to the exam) and a written examination (which determined the grade for the course) had to be passed. In their first semester, Toni and Kim passed all their mathematics courses with grades between 7 and 9 out of 15 (best possible) in the exams (which is comparatively good, as about half of the students fail these courses). Toni got minimally better grades in the exams while Kim got more points for the exercises (Kim was among the best 10% of those who reached points for the exercises).

In the German online setting, similar to Kim, Luca and Liv were both higher-secondary teacher students in mathematics. At the time of the interview, they were studying at a medium-sized German university in their second semester. Due to the COVID-19 pandemic, they both attended an online Linear Algebra course that contained similar content as described for Toni and Kim. The lecture was held online weekly (in a face-to-face setting, it usually took place twice a week) and was not recorded. Students were asked to work through additional course materials themselves and to prepare questions for the lecture. The lecturer also recommended further resources (e.g. self-made videos or other videos on the web). To be admitted to the exam, students had to hand in solutions to weekly exercises (homework), earning at least 50% of the possible points. Students were offered a weekly full-class tutorial where solutions to the previous week’s homework were presented online. Additionally, smaller tutorials (about 20 students each) took place online as well, where further tasks to prepare for the homework were discussed. Neither tutorial was recorded. Students could drop into an online mathematics learning support centre, where they could ask tutors additional questions, e. g. about the homework. In their first semester, Liv was easily admitted to the first exam. Luca struggled with the weekly homework more but was also admitted. Both of them passed the course at the end of the semester.

In the Finnish institutional setting (on-campus), Lumi was a mathematics major, and Tuisku was a statistics major studying a compulsory minor subject in mathematics. They were both first-year students who attended a five-credit proof-based Linear Algebra and Matrices course with mathematical content such as general vector spaces, subspaces, linear mappings, and scalar products (for more details see Lahdenperä et al., 2022). The course was implemented with Extreme Apprenticeship combining inquiry-based mathematics education with a flipped learning approach (see Rämö et al., 2021). The students started to study a new topic by solving introductory exercises. After submitting them, they attended lectures that were based on student discussions and focused on the main contents and their connections. After the lectures, the students solved more challenging problems and a new set of introductory exercises. To support students in solving the weekly exercises, they were offered guidance in an open learning space for several hours a day. Students received bonus points for completing the exercises. In Finland, exams are low stakes and students can retake them as many times as they want. Both Lumi and Tuisku received the maximum amount of bonus points (≥ 90% of tasks completed). Lumi got a grade of 5 and Tuisku a grade of 3 (out of 5, ‘good’) from the course exam.

3.2. Data analysis

To analyse the data we used qualitative content analysis (Kuckartz, 2019) with the goals and appraisals given in Table 2 and introduced in section 2 as concept-driven (deductive) categories. We further refined our categories data-driven (inductively), for example with regard to which element of the learning environment the deductive categories referred, how different goals were further specified (or what other important goals were reported e.g. becoming a teacher, cf. Table 2), or which coping potentials were discussed. For RQ 1, we present the ‘case-oriented analysis’ (for details see Kuckartz, 2019) which means that we describe the self-regulated learning processes of each of the six students in terms of the categories given in Table 2. For RQ 2, we present the ‘category-based analysis’ (for details see Kuckartz, 2019) which means that we describe our comparison of all codings for elements of the learning environment (mathematical contents of the course, mathematical exercises, assessment of exercises, peer learning, tutors) with students’ goals and appraisals. The given quotations were translated from Finnish or German by the authors.

Table 2. Definitions and examples of the codes applied.

Category	Definition	Example
Goals	Behaviours or outcomes that students are attempting to perform or attain	I want to be a teacher.
Learning goal	Learning goals focus on increasing competence	I want to learn something new and not have to repeat something.
Performance goal	Performance goals focus on the attainment of positive judgments from others	I deal with it as much as I can, and try to pass the examination somehow, but I honestly don’t care how quickly I forget it
Protect well-being	Students’ values and needs are represented in students’ goals such as protecting one’s well-being	every week you have this stress of having the exercises […] this constant thought that I have to hand in a mathematics homework next week and I don’t know when I should plan it into my schedule […] that just puts me under pressure and that just completely takes away the joy.
Appraisals
Relevance:relevantpleasantness	Does the situation have consequences for my goals, values, or needs (relevant)? Is it intrinsically pleasant or unpleasant? (pleasantness)	In elementary geometry I notice now at least that there is some content that I can actually use for school. And there I want to get ahead somehow. Because then I realise that I will really need it at some point. (relevant)
		That just completely takes away the joy. (unpleasant)
Implications:conduciveobstacle	Is the situation conducive (supportive, beneficial) or obstructive (an obstacle, not conducive) to reaching my goals?	The tutor gave me a small hint that I was missing but I got to do it myself so that the joy of discovery was not wasted, […] that made me feel very mathematical, that was the supporting power. (conducive)
Coping potential	How can the situation or its consequences be controlled, influenced, or coped with?	You learned somehow that you can rely on each other. […] if you’re not doing so well, the others are there, too, and together you manage somehow.
Normative significance: internal standardsexternal standards	Overall assessment of the situation with respect to compatibility with self-concept, values (internal), social norms and moral rules (external)	Of course, I can sit down with them, but there’s also a lot of copying. And I’m more of a person who thinks you should try to do what you can, and then sit down together, talk about the things you can’t do, and just talk about it at all. That’s what I miss. (internal)

4. Results

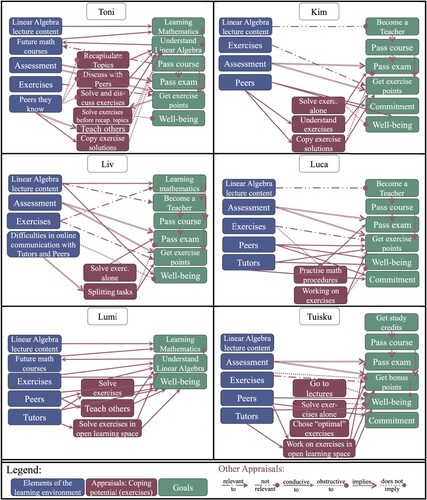
In the following, we qualitatively describe the six students’ self-regulated learning of university mathematics in terms of their goals and appraisals of the elements of different learning environments when working on mathematics exercises (RQ 1) on a case-based level. Figure 2 gives a visualisation and summary of these case-based descriptions. After that (section 4.2), we present on a more abstract level when and how different elements of the learning environments are appraised as congruent or incongruent with students’ goals (RQ 2).

Figure 2. Visualisation of the six students’ appraisal processes.

4.1. Results for RQ 1: case-based descriptions of Toni’s, Kim’s, Luca’s, Liv’s, Lumi’s, and Tuisku’s self-regulated learning

In the German on-campus setting, Toni’s self-regulated learning was mainly guided by their strong learning goals (mastering the mathematical contents). Toni also reported performance goals (passing exams, getting good grades), but these performance goals were rather seen as feedback regarding their learning goals in the sense that a good examination grade was appraised as a basis for learning in future mathematics courses (implication: conducive). Beyond the actual examination grade (external standard), Toni’s main goal was to be satisfied with their performance by their own (internal) standards. The following excerpt gives an insight into these complex interrelationships and the ordering of these different goals:

I’ve set myself the goal of passing all the modules. […] I want to attend other modules; I want to learn something new and not have to repeat something […] And above all, I want to be satisfied with my performance at the end. […] If I pass by such a narrow margin, then there is obviously a lot I haven’t understood. […] Then it’s difficult to go on to the next semester, where maybe some module builds on that. Then you cannot keep up, then you get problems. […] I want to have a good grade without any sloppy mistakes or anything like that, baby mistakes. And then I can go into the next semester with a clear conscience because I know: OK, I’ve understood something, I’ve taken something with me. And I can now look forward to the next modules because we’re learning even more and above all many interesting things because the basics are over. Now come the interesting things.

In line with their learning goal, Toni tried to deeply understand each topic (learning goal). However, they had chosen so many courses that they ‘have a time problem’ (coping potential, obstacle). This meant that often the pace of the lecture and the submission of the exercises did not match their personal learning pace. Therefore, Toni often recapitulated the topics ‘retrospectively’ and had to do the exercises without having understood the topic well enough (internal standard) due to the submission deadline (limited coping potential). This way, Toni appraised the assessment of the exercises as a time-consuming obstacle as it implied task solving without proper (internal standard) understanding (not goal-conducive).

I’m sort of learning things retrospectively. […] You cannot do it the other way around. Because there are so many things to do. […] Sometimes I even manage to learn the topic before handing in the exercise. And I notice that it really makes a difference. If you have learned the topic beforehand and really grasped it, then the exercises don’t take ten hours. Then they might take two or so. It just takes forever, if you don’t have a clue, then you have to read it again ten times. Hmm, can you write it like that or not? Does what’s written here make any sense at all? […] Then in the exercise [lesson] you understand how you can solve the task and why you can solve it that way. But that still has nothing to do with really learning and understanding the topic. It only has something to do with the fact that you have understood and learned how to solve this one task. But nothing general.

Generally, Toni appraised working on the exercises as only partly conducive to their learning goals, as understanding a topic was appraised to be more than having solved a task. Toni was even annoyed (relevance: pleasantness) by some tasks that did not match their image of mathematics (‘You don’t need a six-by-six matrix with numbers like that. So yes, that did upset me. I just think it doesn’t have much to do with mathematics anymore. That’s calculating.’). There were always tasks to which they ‘have no idea’ and which they could not solve (obstacles). Accordingly, Toni appraised the institutional requirement of getting 50% of the points for the exercises correctly as a bigger obstacle (‘the most difficult thing about studying is getting the admission’) than the exams (‘the exams are definitely much easier than the exercises that we have’).

At the time of the interview, Toni worked on the exercises mostly on their own (coping potential). In their first semester, they had a peer group in which they regularly explained their solutions to others, but ‘when I have a question, they don’t even have the idea that you can ask such a question’. In their second semester, Toni had not found peers that matched their level and internal standards:

There really aren’t that many left who have attended everything and passed everything and aren’t physicists or teachers. […] And with the other group it’s like this, they always meet just before the submission, so to speak, one day or so, in the library and then do it [working on the exercises]. Of course, I can sit down with them, but there’s also a lot of copying. And I’m more of a person who thinks you should try to do what you can, and then sit down together, talk about the things you can’t do, and just talk about it at all. That’s what I miss. Then I just don’t like to be there. And then there are others who are so good that they always do it alone anyway. And they do it alone, do the whole exercise sheet and everything is great. Well, they already have it. Of course, you can ask them something if there’s something wrong, but that’s not really a learning group.

In summary: Toni’s main goal was to learn mathematics. However, the restrictive institutional setting for assessing exercises rather inhibited Toni’s self-regulated learning to unfold according to their values and needs towards growth. An additional hurdle was the lack of peers that Toni appraised to have similar goals, values, and needs.

Kim’s main goal was to become a teacher. Therefore, they wanted to ‘get through’ the exams (performance goal). Most of the mathematical content and exercises, especially Linear Algebra and mathematical proofs, Kim appraised as not being relevant nor conducive to their goal of becoming a teacher.

In elementary geometry, I notice now at least that there is some content that I can actually use for school. And there I want to get ahead somehow. Because then I realize that I will really need it at some point. With Linear Algebra it’s more like, I deal with it as much as I can, and try to pass the exam somehow, but I honestly don’t care how quickly I forget it, as long as I don’t need it again for the later modules. Because I’m just interested in my profession and not really in proofs that I’ll never need again.

However, Kim appraised working on the exercises as being conducive to their goal to pass the examination (performance goal). From their experience of the first semester exams, they concluded that ‘if you don’t work on the exercises during the semester and just copy them each time, […] then it gets tough before the exam’ and that the most important thing was to try to understand the solutions of the exercises, but also that they ‘don’t think it’s really necessary to have the knowledge to solve all the exercises yourself’ (implication: conducive). Working on the exercises alone (coping potential) was constraint by Kim’s appraisals of anticipated effort (obstacle), but also by motivational obstacles ‘I don’t really have the drive to do maths all by myself’:

And in my opinion, it is simply too much time that is demanded. Especially those [exercises for the] two courses in parallel, if I wanted to do them BOTH every week on my own, then I would have to spend 30 hours with the exercises, something like that. At least 20. And no normal person can do that in addition to university.

Besides the given anticipated amount of time necessary to work on the exercises alone, this quotation also showed Kim’s appraisal of this amount regarding internal (‘in my opinion, it is simply too much time’) and external standards (‘no normal person can do that’).

Consequently, Kim worked on the exercises almost only together with their ‘math crew’ of four students (coping potential). Together they could solve less than half of the exercises (obstacle). There were always tasks where they ‘haven’t found any approach at all on [their] own’, or ‘don’t know how to write it down’. When writing proofs, Kim was ‘never really sure if they’re correct’, and ‘with some tasks [they] don’t even understand the task’ (obstacle). So, before the submission deadline, they asked other students and exchanged solutions with them and eventually copied these solutions (coping potential).

In the German online setting, Liv described their goal as ‘learning more in mathematics’ (learning goal), ‘being good’ (performance goal) and also becoming a good teacher. They described that those goals were closely connected to each other: ‘You have to be good at what you do [mathematics] to be able to teach it’ (internal standard).

In contrast to many of their peers, e.g. Kim and Luca, Liv also described insecurities about the relevance of the Linear Algebra contents for their future goal of becoming a teacher, but was less rigorous on this:

I’m also looking forward to learning more in terms of my studies, but at least so far, I don’t have the perspective that this will help me much at school. […] But maybe it’s also because my studies haven’t quite finished yet, […] because at some point in mathematics, everything somehow belongs together and it all fits and maybe then it also comes that you can really bring this university math now at the end even stronger together with the school math.

Liv thus appraised their overall studies as mainly conducive and relevant to their goals. They described ‘enjoying their studies, even though it is hard from time to time’ (pleasantness, obstacles). However, they experienced several obstacles within the online context. Specifically, the online tutorials and the absence of personal interactions were described as obstacles to both their learning and performance goals:

You couldn’t even just ask a question, there are a lot of inhibitions […] You didn’t have that kind of relationship with your tutor, because it’s just difficult over such a distance.

Furthermore, situations like asking their peers something about the lecture during lunch were described as missing (obstacle).

Even though Liv stated that they preferred working on the exercises at least partly together with their peers, they perceived that as too challenging to organise during the online setting and decided to split the tasks (coping potential). Each member of their learning group thus focused on one of the tasks, that were then brought together and copied from each other. Liv described that in this way, they relatively easily managed to get enough points to be admitted to the examination (conducive to their performance goal of getting exercise points). When learning for the exams though, Liv struggled with some of the exercises they had not worked on their own and realised: ‘You have to do it on your own, if you want to pass the exam’ (not conducive to their performance goal of passing the exam). Thus, they experienced goal conflicts as their internal standard would see continuous learning and effort as conducive to successfully participating in exams in mathematics, while they just tried to learn the missed-out exercises right before the examination (coping potential). This again, was seen to be happening based on the online context though (obstacle). Thus, Liv appraised most of their obstacles and challenges as circumstances based on the online context.

Luca’s goal was ‘to survive’ and become a teacher. They just wanted to pass their exams to finish their studies (performance goal). Thus, they appraised the mathematical content at university as conducive only to their performance goal, but not to their future goal of becoming a teacher: ‘I have to be able to do it now until the exam. After the exam, I can safely forget it again’.

They appraised mostly mathematical procedures as conducive to passing the examination and thus described one of their learning goals as practising applying them:

write some instructions, how do I proceed when this and that problem arises? […] [Some] are more complicated, where you might also like to have a few more exercises [to practice].

However, the weekly exercises, that were necessary to be admitted to the exams, Luca appraised rather an obstacle to this goal, because they were so challenging, time-consuming, and necessary to be done that there was no time to practice these procedures (limited coping potential):

You can look for them [exercises to practice] on the internet, but there’s just no time because you have to get points.

‘Getting points’ on the weekly exercises was appraised as the most challenging situation for them in their studies (obstacle), which constantly put them under pressure and prevented them from reaching the learning goals:

every week you have this stress of having the exercises […] this constant thought that I have to hand in a math homework next week and I don’t know when I should plan it into my schedule […] that just puts me under pressure and that just completely takes away the joy.

Here, Luca also clearly stated their absence of control and power over their situation, feeling controlled by the exercises that structure their daily life (coping potential) and take away their joy (pleasantness).

They reported receiving at least some help in the online learning support centre, where they regularly attended office hours together with their ‘math crew’ (coping potential). This crew and their learning together were described as most helpful (conducive), specifically when facing motivational obstacles:

You learned somehow that you can rely on each other. […] If you’re not doing so well, the others are there, too, and together you manage somehow. It’s [referring to their studies, mainly the exercises] still very difficult now and then. Sometimes, we all lack motivation [to work on the exercises], but someone is always there to say, ‘Come on, guys, we have to keep going’.

Given the online situation, they did not appraise specific obstacles in this context. Luca stated that they felt less connected to their studies and identified less as a student, basically studying from home. However, they also stated that they never really identified with the idea of mathematics anyway:

I want to be a teacher; I don’t want to be a mathematician. […] So, on the whole, I don’t see myself as a mathematician. For me, it’s just the means to an end. So, I study math to become a teacher later.

They appraised conducive that the learning centre and their meetings with their crew could take place online. While that online setting did challenge their mathematical communication (‘Our WhatsApp group with thousands of pictures, to show what you thought’) this was not appraised as a big obstacle, but something they could cope with (coping potential).

In the Finnish institutional setting (on-campus), Lumi set learning goals for the course. They stated that ‘[the goal] was like deeper learning, like to truly understand the matters’. They also set goals for their entire mathematics studies as they understood mathematics as cumulative (internal standard). Lumi stated:

[My goal was also] to do the groundwork thoroughly because this course is part of the basic studies, and when you do the groundwork thoroughly, it’s then easier to build on top of it.

Lumi regarded solving the mathematics exercises as very important (conducive) to their learning. They had a weekly schedule to work on the tasks and came to the open learning space on specific days to solve the problems (coping potential). Lumi appraised the gradually increasing difficulty of the tasks very positively; this helped them to create a solid foundation for their further learning (conducive) and it was appraised as a pleasant learning outcome (pleasantness). Furthermore, the exercises supported Lumi’s understanding of the learning objectives of the course, as well as created positive feelings about themselves as a mathematics student (pleasantness). They stated:

I like this model in which you start with introductory tasks and then progress to more challenging ones. […] I’ve realised that you learn by doing, and in [this course] we created the grounds. […] [T]here was a variety of the weekly tasks […] starting from the basics and then progressing towards the challenging ones. I enjoyed that because it was so clear to understand what we are expected to know. […] It was a very joyous course, […] I had this feeling that I could solve the tasks and understand the different types of tasks. […] I felt more confident like I would master things.

Thus, being able to solve the tasks supported Lumi according to their internal standards of growing into mathematics; they stated that ‘the tasks made my enthusiasm towards mathematics grow’ (pleasantness). Also, Lumi went through the model solutions for the weekly exercises to meet their internal standards for learning mathematics (coping potential, conducive).

Lumi came to the open learning space on a regular basis (coping potential). Lumi solved some of the exercises by themselves in self-study and some in collaboration with other students. In the open learning space, ‘[…] we had this regular group with whom we sat together’. Lumi appraised this peer collaboration as supporting (conducive) their own perception of themselves as a mathematician (internal standards) as they were able to take a leading role in the group collaboration. Also, they perceived peer collaboration as supporting their learning goals (conducive), as teaching others helped them understand mathematics even further (coping potential). They stated:

Because I had understood and mastered the topics, I was on firm grounds, so I was in a more advisory role in [our group of students]. […] [Y]ou learn the best when you teach it yourself, so I learned even more when explaining things to others.

In the open learning space, Lumi’s learning goals were supported by the guidance offered by the tutors (conducive, pleasantness, internal standards). They stated:

I was supported by the experiences of success, […] the tutor gave me a small hint that I was missing but I got to do it myself so that the joy of discovery was not wasted, […] that made me feel very mathematical, that was the supporting power.

Furthermore, the guidance supported Lumi’s regulation of emotions throughout the problem-solving process. They stated:

I worked on the tasks [in the open learning space]. I have seen it very beneficial, the guidance and working there. […] [B]eneficial because, well, you don’t need to get frustrated if some [task] doesn’t start to unfold.

Finally, Lumi referred to the whole course. They appraised it as a fun course for being so relevant to their learning goals (relevance, pleasantness, conducive). They stated:

This [course] has been fun, I have had many fun experiences […] related to situations like when I sit on top of a gym ball in [the open learning space] and write on the table with a marker pen and […] the tutor next to me has given some piece of advice and then you realise that oh, like this, and then you write in a big hurry because you just got it. Like those are the best.

Tuisku’s goals for the course were dominantly performance goals, as ‘the aim was of course to pass the course and get the study credits’. Furthermore, they acknowledged that there is a possibility for setting also learning goals, as they stated that ‘[this course] is compulsory for statistics students and it’s obviously compulsory for a reason’. Despite realising that there are various goal options, they eventually chose the performance goal as the main goal for the course:

I did realise that [the course] might be useful. And I wanted to be about successful. But when I realised that [the course] is quite a bit harder, I of course thought that it is just enough that I pass and so.

In general, Tuisku appraised solving the exercises very positively as well as relevant to their mathematics study (pleasantness): ‘I don’t like to sit in the lectures, […] working on the tasks was much nicer and more rewarding’.

Furthermore, they often opted out of the lectures and moved to the open learning space to solve the tasks together with their peers to align the situation with their goals (coping potential). Coping potential was also increased for Tuisku by various tasks: ‘In [this course], we had a whole bunch of exercises, so you had multiple options, so it felt like yes, some of these will unfold’.

Concerning assessment, Tuisku appraised solving the tasks positively as ‘collecting the [bonus] points [from solving the tasks] was very motivating’ (conducive, pleasantness). For this, they had set a goal for the percentage of completed tasks and tried to cope with these set performance goals. However, they appraised the tasks as obstacles as they were not always successful in meeting the set goals:

I aspired to solve the majority of the tasks, preferably all, but as long as I remember I didn’t accomplish that very well.

One of the obstacles in meeting the performance goal was caused by challenges in time management. Tuisku tried to cope with this obstacle by optimising their limited time to meet the submission deadlines (coping potential). For example, they stated:

The one point you get from a task is of different value in different tasks in terms of time. Like right away when you see that this is an easier but laborious task […], it gives you this feeling that timewise, this doesn’t pay off.

For Tuisku, it was important to come to the open learning space to solve the tasks (conducive). They stated that they solved the tasks mostly in the open learning ‘with my friends and asked for help a lot from the tutors’ (coping potential). The tasks were challenging, but Tuisku appraised these obstacles such that they also had resources to influence the situation (coping potential):

[The tasks] started to feel already very difficult […] so it was very useful to be there the whole time raising a hand to get help. […] [T]he [tasks on this course] were such that when you got a small hint from a tutor, then by reflecting together [with peers] the tasks started to unfold.

These instances for solving the tasks in the open learning space were appraised also as being ‘pleasant as the tutors were nice, […] and the atmosphere [in the open learning space] very supportive’. Furthermore, the social component in the open learning space was very important for Tuisku (pleasantness). They stated:

For me, it was very motivating that I could spend the day together with others working on the tasks, chatting, having lunch and breaks in between. Like the day was very nice already because there was some […] social interaction.

In this vein, the support provided by the peers and the tutors was central for Tuisku to meet their performance goals. This is further emphasized by the fact that Tuisku could have missed skills to work on the tasks individually, as ‘if you didn’t finish [the tasks in the open learning space], you didn’t get back to them so easily at home’. However, the support provided by the tutors was not always enough (obstacles), as ‘the feedback didn’t always result in understanding’.

4.2. Results for RQ 2: appraisals of different elements of the learning environments

The presentation of the results of RQ 2 will be organised by the elements of the learning environments and students’ appraisals of them. In Figure 2, this is visualised by the arrows leaving the respective elements of the learning environment.

The mathematical contents of the course were mainly appraised in terms of relevance. These appraisals were strongly connected to students’ learning goals. Additionally, the case of Tuisku indicates how such learning goals might be discarded when the anticipated effort to learn these contents is appraised as too high. Overall, the appraisals of relevance and anticipated effort (obstacles) to learn the contents seem to be crucial for the contents of the course being appraised as congruent or incongruent with students’ goals.

Mathematical exercises and tasks had many different functions in the regarded learning environments (e.g. feedback, introduction of topics, assessment, examination preparation) and were thus mainly appraised regarding their implications (see assessment) or coping potential. Appraisals of incongruence mostly appeared when tasks were appraised as too challenging or time-consuming (obstacle), as limiting (or with limited) coping potential or as conflicting with internal standards (e.g. Toni, Luca) regarding the learning of mathematics or long-term goals (e.g. Kim).

The assessment of the exercises (e.g. 50% hurdle) was strongly related to students’ appraisals regarding their implications. Rigorous forms of assessment might on the one hand strengthen the conduciveness of working on exercises for performance goals and on the other hand limit coping potential for students’ learning goals (e.g. Toni, Luca). In the Finnish context, Lumi and Tuisku shared the (internal and external) standards of solving the exercises being conducive to both learning and performance goals which was highly congruent with the Finnish learning environment.

Peer learning and collaborations were appraised as conducive to different goals of the students (learning, performance, well-being). Peer collaborations increased coping potential and supported students’ self-regulated learning on many levels (cognitive, affective, motivational), especially if it enabled space for discussions (cf. Toni) and if the learning environment offered low-level support if all group members got stuck (cf. German vs. Finnish context). Missing peer collaborations were appraised as a main obstacle in the online learning environment (Liv). Overall, peer collaborations were thus almost without exception appraised as being highly congruent with students’ goals.

When available (German online and Finnish contexts), students appraised tutoring and guidance as congruent with their goals. In both contexts, the help received from the tutors was appraised as increasing coping potential as well as being conducive to learning and performance goals. For Liv, this showed in appraising the absence of in-person meetings with the tutors as an obstacle to their learning goals. For Luca, in contrast, it was mainly the necessary help they received for their weekly exercises (performance goal). For Lumi and Tuisku, the guidance was appraised as conducive to their goals and offering coping potential as it resolved most of the incongruence created by the challenging exercises (obstacles).

5. Discussion

In this paper, we aimed to qualitatively analyse university mathematics students’ self-regulated learning in terms of their goals and appraisals with a focus on the learning situation of working on mathematical exercises in three different learning environments in Germany and Finland (RQ 1). Thereby, we aimed to identify when and how different elements of the learning environments are appraised as congruent or incongruent with students’ goals (RQ 2), as these appraisals define different purposes of self-regulation (Boekaerts, 2011). To do so, we analysed interview data of two students per learning environment, one with a focus rather on the learning goal of mastering the mathematical contents and one with a focus rather on the performance goal of just passing (‘surviving’) the course in each learning environment.

One major result of this study is the great variety and the substantial differences in the six interviewed students’ appraisals depending on their respective goals and the different elements of the learning environments (RQ 1, Figure 2). Additionally, the results illustrate and highlight how many different (potentially conflicting) goals are incorporated in individuals which must be reconciled in the appraisal process. This means that the question of whether a learning situation is congruent or incongruent with students’ goals that is central for the purpose of self-regulation in Boekaerts’ (2011) dual processing model of self-regulated learning is highly complex. To better understand these appraisal processes an analysis of relevance, implications, coping potential, and significance (Scherer, 2001, 2009) helped to identify patterns when and how different elements of the learning environments are appraised as congruent or incongruent with students’ goals (RQ 2). These patterns have theoretical and practical implications which will be discussed in the following section along these four major appraisal objectives (Scherer, 2001, 2009).

5.1. Theoretical and practical implications

Appraisals of relevance mostly referred to the mathematical contents of the Linear Algebra course as a whole. There were substantial differences (provoked by the chosen sample) between students with a focus on the learning goal of mastering the mathematical contents and those with the performance goal of just passing the course without further learning goals. The case of Tuisku who first considered learning goals but only stuck to their performance goals when they realised that the course might be ‘quite a bit harder’ (obstacle) indicates that students’ goals should not be seen as a constant given. This is in line with Boekaerts’ (2011) model which theorises that the purposes of self-regulated learning vary according to students’ constant appraisals. In fact, the pattern that students start with more pronounced learning goals but give up on them, when reaching those learning goals is appraised to be accompanied by too many obstacles, too much effort, and too limited coping potential is found in other studies too (Göller & Rück, 2022). In this case, an appraisal of the low relevance of the mathematical contents could indicate that students experience too many obstacles and unsatisfactory coping potential for reaching their learning goals and therefore give up on them. This perspective gives rise to practical interventions that focus on strategies to overcome these obstacles and provide more coping potential (like the Finnish learning environment; see Rämö et al., 2021 for more details).

Another perspective could be, to focus directly on students’ relevance appraisals. It is well documented that the relevance of the mathematics contents at university for (future) teachers is a much-discussed issue (Even, 2011; Gildehaus & Liebendörfer, 2021; Wasserman et al., 2018; Zazkis & Leikin, 2010). Accordingly, there are attempts to increase relevance appraisals e.g. by introducing special tasks for preservice teachers to explicate the relevance of the mathematical contents for teachers (Eichler & Isaev, 2022; Hoffmann, 2021; Wasserman et al., 2023; Weber et al., 2023). However, it is currently not yet evident whether such approaches can indeed contribute to higher relevance appraisals (Rach, 2022; Rach & Schukajlow, 2023). From our theoretical perspective, it could be argued that appraisal of pleasantness is a part of the relevance appraisals and should therefore be considered in this discussion. There are studies underlining the connection between missing pleasantness and coping potential with alienation from university mathematics (Solomon & Croft, 2016). Our results rather support this direction (e.g. the cases of Tuisku and Luca).

Interestingly, in this sample, the three students with pronounced learning goals reported distinct internal standards (significance) of what mathematics and mathematics learning are about: For Toni, this means that understanding mathematics was more than knowing how to solve a certain task, for Liv that ‘at some point in mathematics everything somehow belongs together’, and Lumi highlighted the ‘cumulative’ character of mathematics. While for Toni and Lumi, the relevance of the mathematical contents was a given anyway, Liv used their standard as an argument for a possible relevance of the contents for them as a teacher. There are some studies that indicate the positive effects of such ‘dynamic beliefs’ on students’ mathematics interest (Liebendörfer & Schukajlow, 2020), study satisfaction, and drop-out intention (Geisler, 2023). In our study, Toni’s, Liv’s and Lumi’s self-regulated learning was oriented towards growth while Kim, Luca, and Tuisku rather picked specific tasks which were conducive to their performance goals. This raises questions about the connections of such beliefs with self-regulated learning and how such beliefs may (or need to) change for a positive appraisal of university mathematics (Göller, 2023), which should be investigated in future studies.

Coping potential mostly referred to (working on) the exercises. This traces back to internal standards as for all analysed students except Toni, learning mathematics seemed to mean solving mathematics exercises. Coping potential was limited by assessment practises and when students did not know how to proceed. In such cases, peer learning or tutors played a crucial role with positive effects also for students’ well-being and commitment. Despite the technical limitations, this was even apparent in the online context of this study as well as in other studies in online contexts (Kempen & Liebendörfer, 2021; Liebendörfer et al., 2023). Theoretically, this means that the availability of peers and tutors increases coping potential and thus allows students more freedom to shape their self-regulated learning according to their goals, values, and needs. In the two German contexts, coping potential reached its limits when all peers did not know how to proceed (obstacle) while the Finnish learning environment provided enough support measures to overcome such obstacles. Accordingly, this availability of peers and tutors should be considered when designing learning environments for university mathematics courses.

Regarding implications, we first want to point out the significance of assessment practises. It is well known that students’ self-regulated learning is oriented towards exam-related goals (Anastasakis et al., 2017), which was also apparent in the present study. One major theoretical implication of this study is the complex appraisal process reconciling implications for different goals of the learning environment and of different possible strategies (coping potential). This means it is not only the element of the learning environment that is appraised for its implications (Scherer, 2001, 2009). The appraisal for implications for different goals includes also (and in this data set even foremost) different strategies (cf. Figure 2). This means that from all possible strategies, students try to choose the one which is appraised to be most conducive to their (most important) goals and which does not conflict with other important goals (cf. Figure 2). This can also explain how, for example in both German contexts, tasks that are too difficult or time-consuming (conflicting with well-being) but need to be done (performance goals, assessment of exercises) can lead to copying of solutions, unpleasantness (e.g. Luca: ‘that just puts me under pressure and that just completely takes away the joy’), and giving up learning goals (Göller & Gildehaus, 2021; Göller & Rück, 2022; Hailikari et al., 2016; Liebendörfer & Hochmuth, 2015; Martínez-Sierra & García-González, 2016). This leads back to the discussion of relevance (see above).

Overall, the present study showed the great complexity of students’ appraisal processes when learning mathematics at university. This means that to understand students’ appraisals of congruence or incongruence of the learning environment with their goals that define the purpose of their self-regulation (Boekaerts, 2011), it was very helpful to integrate Scherer’s (2001, 2009) categories of relevance, implications, coping potential, and normative significance. While it is evident from the data that the appraisal process is not as linear as theoretically described, the detailed analysis of these categories allows for a deeper discussion and understanding of known difficulties in learning mathematics at the university (e.g. Gueudet, 2023).

5.2. Limitations and outlook

When interpreting the results, the small qualitative sample has to be considered. Of course, the chosen two students per institutional context cannot represent the respective learning environments and students as a whole. Also, it has to be considered that the interview data are retrospective self-reports which only represent the time of the interview. Based on these data, it is e.g. not possible to determine how these goals and appraisals of the interviewed students emerge, how these appraisals determine students’ behaviour or if these appraisals are rather students’ explanation or justification for their behaviour in the respective learning environments.

Nevertheless, in total, the results show the potential of qualitative comparisons of different institutional learning environments to reveal similarities and differences in students’ goals and appraisals, as well as their significance for their self-regulated learning, which allows insights regarding the potential impacts of support structures and pedagogical interventions.

Authors’ contributions

Conceptualisation: RG, LG, JL; Methodology: RG, LG, JL; Data Curation: RG, LG, JL; Data analysis: RG, LG, JL; Validation: RG, LG, JL; Writing – Original Draft: RG, LG, JL; Writing – Review &Editing: RG, LG, JL; Project administration: RG; Visualisation: RG.

Disclosure statement

No potential conflict of interest was reported by the authors.