Teaching evolution using a card game: negative frequency-dependent selection

Abstract

Teaching biological evolution can be difficult on a number of levels, be it student confusion arising from prior conceptions and the controversy surrounding evolution, or simply because the material is complex. Games and simulations can help to convey complex topics and also to increase variety in teaching methods. Here I describe a card game that can be used to teach the advanced topic of protected polymorphism in higher education settings. Protected polymorphism is allelic variation resulting from negative frequency-dependent selection; when the fitness of an allele increases when it becomes rare, the allele will be ‘protected’ from extinction. Negative frequency-dependent selection is proposed to maintain genetic variation in nature, which is required for evolution by natural selection. Protected polymorphisms primarily play a role in biological interactions, such as immune systems, plant-pathogen interactions, sexual selection and predator-prey interactions. The card game described here uses plant pollination alleles as an example. The game is played using eleven stocks of traditional playing cards per group of about six students. Specific topics addressed include negative frequency-dependent selection, polyploidy, dominance, selfing and inbreeding depression.

Keywords:

• Active learning
• card game
• biological evolution
• negative frequency-dependent selection
• self-incompatibility
• outcrossing

Introduction

Biological evolution is a difficult subject to teach but it has been identified as the most fundamental field in biology and it is thus critical that it is taught well. It is difficult because prior student conceptions may lead to misunderstanding of the evolutionary concepts being taught, because student awareness of the controversy surrounding evolution may lead to confusion, and also because it simply is complex material (Alters 2005; Alters and Nelson 2002; Sinatra et al. 2003). Teaching evolution will be more effective if more hands-on labs are available that promote active learning (Alters and Nelson 2002; Gibson, Drown, and Lively 2015). Games, simulations and other active learning approaches are highly effective for teaching complex ideas (Barnett 2009), strongly increase performance in the STEM (science, technology, engineering and mathematics) educational fields (Freeman et al. 2014) and decrease the performance gap between traditional and non-traditional students (Haak et al. 2011). This is at odds with the fact that traditional lecturing is still the main go-to method in higher education (e.g. in a 2010–2011 survey over 60% of STEM professors in the USA reported using extensive lecturing as their primary teaching method [Hurtado et al. 2012]).

Here I describe a card game that can be used to teach evolutionary principles at postsecondary levels in an active way. My motivation to design this game came from personal experience as a university lecturer. As outlined above, exclusively lecturing on conceptual topics may not render the results aimed for and this has been also my experience. A combination of teacher-centred and student-centred instructional methods can improve science learning (Treagust 2006). Students engage (behave, feel and think) differently with different types of teaching and, hence, combining lectures with activities has the potential to result in overall higher student engagement (Fredricks, Blumenfeld, and Paris 2004). Interest, a key factor in engagement and learning, can develop but not in isolation; more interactive kinds of engagements with the topic can develop an initially started interest (e.g. in lectures) into deeper levels of interest (Hidi and Renninger 2006). Furthermore, when students interact in a group, more of their emotions can be observed (Pekrun 2006), which can help the teacher to better understand their comprehension of the material as well as their expectations, goals and interests (Wigfield and Eccles 2000). Finally, activities involving biological material are not very portable because they are restricted to region and season. For these reasons, I wanted to include an activity with the following conditions: group work, possible in any season and anywhere, with low-cost and easily obtained materials, yet complex enough to engage post-secondary level students. A card game on an advanced topic in evolution satisfies these conditions.

Arguably one of the central issues of biological evolution is the origin and maintenance of variation, because without heritable variation there can be no evolution by natural selection (as background information on the basics of this topic I recommend the online resource ‘Natural and artificial selection’ [HHMI 2017] for college-level students, and for graduate students the two first chapters from the text book ‘Elements of evolutionary genetics’ [Charlesworth and Charlesworth 2010]). Where does all this variation – diversity at the level of species, populations, individuals – come from and how is it maintained? The rationale that variants with the highest fitness will increase in frequency leads to the paradoxical prediction that variation should disappear, leaving no variation for selection to act on (see e.g. Kingsolver and Diamond 2011; as a simple hands-on exercise that demonstrates this to students I suggest to use the software ‘Allele A1’ [Herron and Freeman 2014]).

Negative frequency-dependent selection is an evolutionary force that explains how genetic variation can be maintained at the intraspecific level (i.e. alleles, which are different genetic variants at the same locus) in spite of ongoing natural selection. If more than one allele exists for a locus in a species, that locus is called polymorphic. Polymorphisms are very common; when two human genomes are compared, a single nucleotide polymorphism is encountered every 1000–2000 bases (Sachidanandam et al. 2001). An allele’s fitness may depend on its frequency in the population. In situations in which the fitness of an allele increases as it becomes less common, alleles are protected from extinction. The allelic frequency ‘bounces off’ the extinction line (see Figure 1). The resulting polymorphism is called a ‘protected polymorphism’. The term ‘negative’ refers to the inverse relation between fitness and frequency: as frequency goes down, fitness goes up. Negative frequency-dependent selection typically plays a role in biological interactions, such as immune systems, plant-pathogen interactions, sexual selection and predator-prey interactions (see e.g. Aguilar et al. 2004; Van der Hoorn, De Wit, and Joosten 2002). As in-depth reading material on negative frequency-dependent selection I suggest the review by Richman (2000). The card game described here uses plant pollination alleles as an example (suggested reading material on this topic is Silva and Goring [2001]) (Figure 2).

Figure 1. Illustration of negative frequency-dependent selection leading to protected polymorphism.

Notes: Grey line indicates allele fitness (which is defined as the average over the fitnesses of individuals carrying that allele in a population), black line allele frequency. When an allele’s frequency becomes low, its fitness goes up which protects it from going extinct.

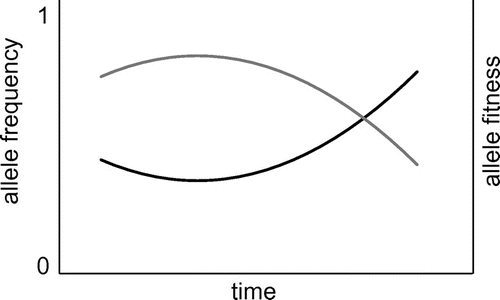
Figure 2. Schematic view of Sporophytic Self Incompatibility (SSI) in plants.

Notes: A monoecious diploid plant with genotype S₁S₂ produces pollen grains which carry either the S₁ or the S₂ allele. Phenotypically, however, each pollen grain carries both the S₁ and S₂ recognition proteins on its outer wall (this is different in Gametophytic SI, where the pollen grain carries only the recognition protein produced by its own genotype). If a pollen grain lands on the stigma of its parental plant (or one with a similar genotype) it may germinate but growth of the pollen tube down the style is stopped, because the S-proteins of the stigma and the pollen grain fit like a lock-and-key. A pollen grain from a plant with a different genotype, in contrast, such as S₃S₄, will germinate and its pollen tube will grow down to the style to the ovary, allowing fertilisation between the male and female gametes. If the phenotype of pollen grain and stigma have at least one expressed parental allele in common, which can be the case both in case of selfing and with certain outcrossed combinations, fertilisation is prevented

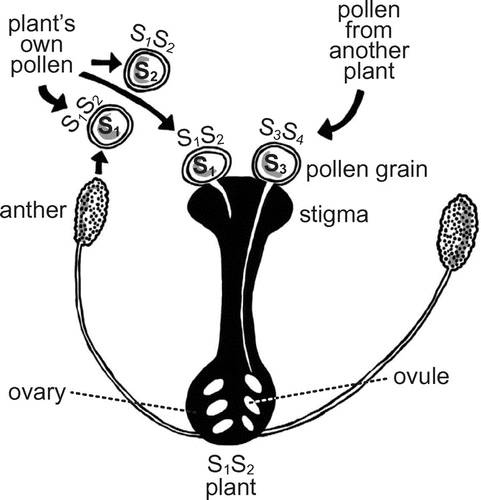
Plants that are monoecious (hermaphrodite) often have mechanisms in place to avoid self-fertilisation, some of which are molecular (Barrett and Harder 1996). For example, recognition proteins may be expressed on the pollen grains and on the stigmas and act as a lock-and-key system (Castric and Vekemans 2004). If the key (pollen) fits the lock (stigma), the pollen is recognised as probably self and rejected for fertilisation. Fertilisation happens only when none of the pollen keys fit the lock. This is an example of frequency-dependent selection: if an allele becomes common in a population, its pollinations will fail more and more often (Igic, Bohs, and Kohn 2006). The latter is because, when a plant carries common alleles, it shares those alleles with many other plants and therefore its pollen is often wrongly recognised by other plants as self-pollination and rejected. Thus, its fitness decreases.

In order to demonstrate advanced evolutionary principles, higher education courses on evolutionary biology would benefit from incorporating active components. Ideally these active components are not very costly or time consuming and can be done anywhere and in any season. For the purpose of teaching the complex matter of protected polymorphisms I designed a card game that simulates negative frequency-dependent selection in action.

Methods

To play the five part card game described here, eleven stocks of traditional playing cards are needed per group of about six students. It is recommended that the teacher prepares the sorted stocks prior to playing the game, because it takes quite some time. All kings, queens, jacks and jokers are removed from the stocks as they are not used during the game. All parts consist of one student playing ‘male function’ as well as dealer and four or five students playing ‘female function’. Each part begins with the group discussing a starting question and formulating a hypothesis and/or prediction. The players need the ‘Fertilization Score Card’ to collect data during part 2 of the game. It generally takes about two hours to play all five rounds.

The starting questions and learning goals of the parts are summarised in Table 1. Supplementary material A explains in detail how to play the five parts, and it should be given to the dealer. Supplementary material B contains instructions to be handed out to the players. Supplementary material C is the Fertilisation Score Card belonging to part 2.

Table 1. Learning goals and starting questions of game with regard to negative frequency-dependent selection.

	Learning goals	Starting questions
Part 1		how many homozygotes and heterozygotes do you expect
		in a natural population with SSI?
	outcrossing promotes heterozygosity
	1a) in SSI, offspring are only produced when sexual partners share no alleles
	1b) homozygotes should not be found in the population
Part 2		what is the consequence for alleles if their fitness
		depends on how common they are?
	negative frequency-dependent selection maintains allelic diversity
	2a) fitness of an allele depends on its frequency in the population
	2b) expected equilibrium frequencies in the population are equal
Part 3		what would happen if we increased
		the number of alleles carried by each individual?
	ploidy level influences the phenotype
	3a) polyploidy is detrimental to pollination success in SSI
Part 4		will allele frequencies be different if some alleles are dominant over others?
	dominance affects fitness
	4a) with dominance among alleles, there will be more successful pollinations
	4b) the more recessive an allele, the higher its equilibrium frequency
Part 5		how will allelic diversity change if we add a mutant that can self-fertilize?
	reproduction via selfing carries substantial costs and benefits
	5a) selfing can be very advantageous
	5b) inbreeding depression is a disadvantage of selfing

Note: SSI = sporophytic self-incompatibility (sporophytic means that both alleles are expressed on the pollen grain).

The dealer studies each part before starting so that he/she knows what the expected outcomes are. The dealer will lead the game as well as the discussion among the players, with input from the teacher when necessary, until all players understand the learning goals for that part. The players discuss the starting question and formulate a hypothesis/prediction. Next, the players try to figure out how to obtain highest scores, and in doing so grasp the learning goals. After each part, the dealer summarises the learning goals and the players evaluate their hypothesis/prediction.

Part 1 introduces the students to the game and how it is played. They try out a number of male/female card combinations to see when fertilisation fails and when it is successful. The dealer guides them to predict what genotypes are formed in the offspring until they understand that homozygotes are never produced, and that, hence, outcrossing promotes heterozygosity. Part 2 lets the students discover that allele fitness depends on allele frequency in such a way that negative frequency-dependent selection maintains allelic diversity. Part 3 explores the same idea with the extension of higher ploidy levels. This will give students the opportunity to repeat the newly gained insights in a different setting. Part 4 is the much more complex extension of dominance among alleles. Students debate among each other whether equilibrium frequency of alleles will depend on dominance, and if so, in which direction. Part 5 explores how mating systems may evolve and change the dynamics of selection. One student evolves a ‘selfing’ strategy and changes the rules of the game, winning easily until the penalty of inbreeding depression is added.

Debriefing by the teacher recaps all learning goals after all parts of the game are played out.

Conclusions/discussion

Since designing this game in 2005 I have played it with various groups of university students at the BSc and MSc levels. In my experience, having more than two or three groups playing at the same time requires the help from an additional teacher. The latter can be a motivated student from the class, who needs to be instructed beforehand. Depending on prior student knowledge, the game takes about two hours to play. In addition, debriefing at a later moment will take up to half an hour. Students are generally very active during the game. Behaviour will differ between groups and can range from noisy fun or competitive battle to collegial effort or concentrated silence.

As a teacher you can steer the learning process in a number of ways, depending on the group process as it develops and whether you know (some of) the students from other classes. For example, it may be helpful to let students switch roles during the course of the game. Furthermore, the male function is best played by a student who is quick to grasp the learning goals. Debriefing is best done during a later contact moment such as the next day. Debriefing can also be very insightful for the teacher and will demonstrate how many students understood how many things.

The game may be less effective for some sets of students than others. For example, it has been shown that active learning is more effective for non-traditional than for traditional students (Haak et al. 2011). Also, students who are very quick or very slow to grasp the concepts taught may disengage from the game. In that case games such as these will even inhibit learning and to some extent teacher intervention can help solve this (e.g. make a quick learner the dealer or form differentiated groups).

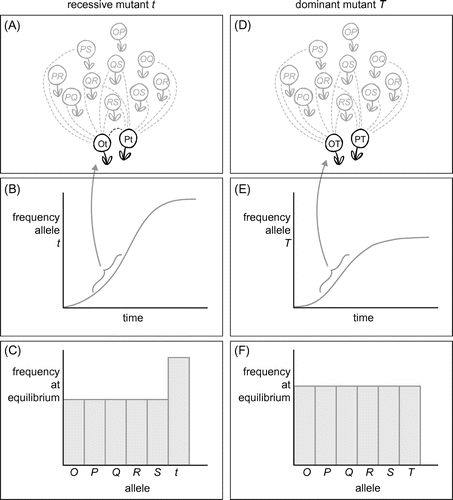
The most complex and difficult to grasp part is learning goal 4b (Table 1). Getting all students to understand the prediction that, at equilibrium, recessive alleles should have higher frequencies than dominant alleles (Stevens and Kay 1989), takes considerably longer than any of the other topics. Debriefing the next day is particularly useful for repeating this part. To recap the basics of what dominance means for the effect of selection without frequency dependence, I suggest to use the software ‘Allele A1’ (Herron and Freeman 2014). Furthermore, it is helpful to talk with students about following a population containing only dominant alleles (O, P, Q, R) through time. Let a recessive allele (say, t) newly arise (e.g. by mutation) and compare it with a newly arisen dominant allele (say, T). The reasoning is illustrated in Figure 3. At first, t and T will sit in a heterozygote together with a dominant allele (say, O). The phenotype of the Ot individual will be O and it will not produce offspring with any other individuals carrying allele O. The same holds for the OT individual: their phenotype will be OT, but since there are no other individuals carrying T yet, they will only fail to produce offspring with plants carrying allele O. This leads to an initial exponential increase of t as well as T, as can be seen in the earliest time section in Figure 3(B) and (E). The difference starts in the middle time section (accolades in Figure 3(B) and (E)) and is illustrated in panels A and D of Figure 3. The frequency of the new allele has increased so that is can now be found in heterozygotes Ot and Pt (Figure 3(A)) or OT and PT (Figure 3(D)). It can now be seen that the recessive mutant t has an advantage compared to the dominant mutant T: heterozygotes Ot and Pt can produce viable offspring, because the mutant allele is not expressed. Heterozygotes OT and PT, however, cannot produce offspring, because the expressed T allele is preventing it. In other words, individuals carrying a new recessive allele suffer no non-self reproduction failures, which puts them at an advantage compared to individuals carrying only dominant alleles. For a given frequency, the fitness of a recessive allele is therefore higher than that of a dominant allele. At some point, of course homozygotes tt will be formed, and they will not be able to produce offspring with other tt plants, but the recessive allele will continue to be mostly ‘hidden behind’ dominant alleles. Equilibrium is reached when fitness of all alleles is equal. In a situation with only dominant alleles this means that also the frequencies of all alleles will be equal (Figure 3(F)). It should now be clear that recessive alleles will reach higher equilibrium frequencies than dominant alleles (Figure 3(C)).

Figure 3. Explanation of why recessive alleles reach a higher frequency at equilibrium than dominant alleles in SSI plants. Panels A–C show the dynamics of a newly evolved recessive allele, panels D–F that of a new dominant one. Top panels (A, D: focal plants black, rest of population grey) depict the critical time phase when a new allele has increased and is found in several heterozygotes. Dashed lines indicate potential fertilisation partners. Panel D shows that heterozygotes carrying a new dominant allele already begin to miss out on non-self crosses, while this is not yet the case for the recessive mutant (black dotted line in panel A). Middle panels (B, E) show the frequency increase of the mutant alleles through time. The exponential increase ends sooner for the dominant (E) than for the recessive allele (B). Bottom panels give equilibrium frequency distributions: dominant alleles will have lower frequencies at equilibrium than recessive alleles.

The game was designed for advanced students at the BSc and MSc level. Potentially, only the first three parts of the game could be played with non-biology students or less advanced students as a bare-bones version. The topic learnt would then still be negative frequency-dependence, while omitting the very complex extension of dominance. Particularly in combination with letting the students analyse the data they collect in part 2 and by letting them use the software ‘Allele A1’ (Herron and Freeman 2014) earlier in the course, the game parts 1–3 could make a useful biology module for high school students. In addition, the game or its shorter version may also be used in other settings than classrooms, e.g. as active workshops in science museums, at science fairs, or during open days and recruitment events.

Creative teachers may want to develop similar games for related topics. This would be feasible for other biological settings of negative frequency-dependence, such as rock-paper-scissors dynamics or predator-prey relationships (Clarke 1969; Sinervo and Lively 1996). To cover topics that do not involve frequency-dependence would however require a very different type of game, perhaps not using playing cards.

In conclusion, this card game can be used as an active learning tool to teach an advanced topic of biological evolution to small groups of postsecondary students. Playing the game stimulates peer-level discussions among students. This game may promote a deeper understanding than the same material taught using traditional lecturing, although this has not been tested. Games such as this one can be used to design courses or curricula with a diversity of learning experiences, and to extend one’s teaching method repertoire as a teacher.

Disclosure statement

No potential conflict of interest was reported by the author.

Supplemental data

Supplemental data for this article can be accessed https://doi.org/10.1080/00219266.2017.1420677

Acknowledgements

I thank all undergraduate students who played this game with me at the University of Amsterdam, Groningen University (both in the Netherlands) and the Royal Netherlands Institute for Sea Research from 2005 through 2017, and Dörte Poszig for providing helpful suggestions for an earlier draft of the manuscript.