Generation of nuclear data using Gaussian process regression

ABSTRACT

A new approach for generating nuclear data from experimental cross-section data is presented based on Gaussian process regression. This paper focuses on the generation of nuclear data for proton-induced nuclide production cross-sections with a nickel target. Our results provide reasonable regression curves and corresponding uncertainties and demonstrate that this approach is effective for generating nuclear data. Additionally, our results indicate that this approach can be applied in experimental design to reduce the uncertainty of generated nuclear data.

KEYWORDS:

• Gaussian process regression
• nuclear data
• nuclide production cross-section
• uncertainty

1. Introduction

Nuclear data play a vital role in the field of nuclear science and technology (i.e. nuclear energy, medical and industrial applications of radiation sources, radiation protection, and radioactive waste management). These data are most often evaluated via theoretical nuclear models based on nuclear data evaluation codes, such as CCONE [1], EMPIRE [2], and TALYS [3], which fit experimental cross-section data and integrated experiments. Moreover, for energies above the applicable range of these codes (up to several hundred MeV), Monte Carlo spallation reaction simulations based on intranuclear cascade (INC) plus de-excitation models are applied to evaluate nuclear data (e.g. JENDL high-energy file [4] and HEIR [5]). Although it is generally accepted that these models describe spallation reactions fairly well, considerable discrepancies between the experiments and these nuclear models have been reported in the literature [6–9]. While it is desirable to resolve these discrepancies by improving the nuclear models or tuning the model parameters, this approach requires substantial amount of time and effort.

As an alternative to nuclear models, regression based on the least-squares method (e.g. GMA [10] and SOK [11]) is often applied to evaluate nuclear data. Regression based on Gaussian processes [12], hereafter referred to as Gaussian process regression (GPR), has attracted widespread interest in fields such as pattern recognition, machine learning, and nuclear applications [13–17]. Because GPR models give predictive distributions for regression problems, this technique may be a powerful tool not only for evaluating nuclear data but also for determining the corresponding uncertainty.

In this paper, we apply GPR to generate nuclear data, focusing on the proton-induced nuclide production cross-sections at energies ranging from 100 MeV to 3 GeV. As an example, this study treats four individual spallation products for a nickel (${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni) target: ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^7$Be, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{22}$Na, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{48}$Cr, and ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co. The natural abundances of the nickel isotopes are assumed as 68.08% (${ }^{58}$Ni), 26.22% (${ }^{60}$Ni), 1.14% (${ }^{61}$Ni), 3.63% (${ }^{62}$Ni), and 0.93% (${ }^{64}$Ni). Experimental cross-section data were taken from the EXchange FORmat (EXFOR) experimental nuclear reaction database [18] (i.e. Titarenko et al. [19], Budzanowski et al. [20], Neumann [21], Michel et al. [22], Schiekel et al. [23], and Rayudu [24]). Furthermore, to investigate the impact of experimental data and their uncertainties on GPR results, experimental data recently measured at the Japan Proton Accelerator Research Complex (J-PARC) (Takeshita et al. [25]) were employed. In this experiment, the cross-sections for 0.4-, 1.3-, 2.2-, and 3.0-GeV proton-induced reactions were measured using the activation method. Although the experimental uncertainty is currently being estimated by Takeshita et al., the uncertainty in the number of incident protons, which is the dominant source of the total uncertainty, is expected to be smaller than that of other experiments due to the precise intensity of the J-PARC proton beams and well-calibrated proton intensity monitors [26]. Therefore, in this study, we assume that the total uncertainties are uniform at 6% (1$\sigma$), which is smaller than the typical experimental uncertainties of approximately 10% measured in similar experiments (e.g. Titarenko et al. [19], Michel et al. [22]).

This paper is organized as follows. Section 2 describes our methodology for generating nuclear data using the GPR technique. In Section 3, we present GPR results for proton-induced nuclide production cross-sections, in addition to nuclear model calculations performed using the Liège INC model version 4.6 [27] coupled to the generalized evaporation model [28] (INCL4.6/GEM) and evaluated nuclear data from the JENDL high-energy file (JENDL-HE/2007). We also demonstrate the applicability of GPR to nuclear data generation. Finally, our conclusions are presented in Section 4.

2. Methodology

2.1. Generation procedure

Suppose that we have $N$ measured data points (measurement energy points ${\mathit{x}}_N$ and corresponding cross-sections with uncertainties [one standard deviation, 1$\sigma$] ${\mathit{t}}_N\pm \mathit{\delta }{\mathit{t}}_N$) for a certain nuclear reaction and that we aim to generate a set of cross-sections for certain $M$ energy points ${\mathit{x}}_M$ (the generated cross-section set is written as ${\mathit{t}}_M$).

To avoid negative (non-physical) values for the generated cross-section set, we estimate ${\mathit{t}}_M$ as follows:

1. Take the logarithm of (${\mathit{t}}_N$, $\delta {\mathit{t}}_N$) to obtain (${\hat{\mathit{t}}}_N$, $\delta {\hat{\mathit{t}}}_N$), where ${\hat{\mathit{t}}}_N=ln{\mathit{t}}_N$ and $\delta {\hat{\mathit{t}}}_N=ln({\mathit{t}}_N+\delta {\mathit{t}}_N)-$ ${\hat{\mathit{t}}}_N$.

2. Calculate target variables ${\hat{\mathit{t}}}_M$ by GPR using (${\hat{\mathit{t}}}_N$, $\delta {\hat{\mathit{t}}}_N$) as training data. As addressed in the next subsection, ${\hat{\mathit{t}}}_M$ follows an $M\times M$ multivariate Gaussian distribution with a mean ${\hat{\mathit{\mu }}}_M$ and covariance ${\widehat{\text{SigmA}}}_{M,M}$: ${\hat{\mathit{t}}}_M\sim \mathcal{N}({\hat{\mathit{\mu }}}_M,{\widehat{\text{SigmA}}}_{M,M})$

3. Take the exponential of (${\hat{\mathit{\mu }}}_M$, ${\hat{\mathit{\sigma }}}_M$) to obtain the set ${\mathit{t}}_M=\{{\mathit{\mu }}_M,{\mathit{\sigma }}_M^{\mathrm{U}},{\mathit{\sigma }}_M^{\mathrm{L}}\}$ as

   (1) ${\mu }_M=\exp ({\widehat{\mu }}_M),$(1)
   (2) ${\mathit{\sigma }}_M^{\mathrm{U}}=exp\left({\hat{\mathit{\mu }}}_M+{\hat{\mathit{\sigma }}}_M\right)-exp({\hat{\mathit{\mu }}}_M),$(2)
   (3) ${\mathit{\sigma }}_M^{\mathrm{L}}=exp({\hat{\mathit{\mu }}}_M)-exp\left({\hat{\mathit{\mu }}}_M-{\hat{\mathit{\sigma }}}_M\right),$(3)

where ${\hat{\mathit{\sigma }}}_M$ represents the standard deviation of ${\widehat{\text{SigmA}}}_{M,M}$, and ${\mathit{\sigma }}_M^{\mathrm{U}}$ and ${\mathit{\sigma }}_M^{\mathrm{L}}$ indicate the upper and lower standard deviations, respectively.

Additionally, because the energy axis is often scaled logarithmically in graphic representation, the energy points ${\mathit{x}}_N$ were converted to ${\hat{\mathit{x}}}_N=\mathrm{l}\mathrm{o}{\mathrm{g}}_{10}{\mathit{x}}_N$, and ${\hat{\mathit{x}}}_N$ values were used as input data points in GPR.

2.2. Gaussian process regression

Following the above assumptions and treatment, a zero-mean Gaussian process defines the joint probability distribution of ${\hat{\mathit{t}}}_N$ and ${\hat{\mathit{t}}}_M$ as a multivariate Gaussian distribution with mean ${\mathbf{0}}_{N+M}$ and covariance ${\mathbf{C}}_{N+M}$, which is given by

(4) $\begin{array}{l}p({\widehat{t}}_{N+M})=\mathcal{N}({\widehat{t}}_{N+M}|0_{N+M},C_{N+M,N+M})\\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}=\mathcal{N}\left(\left(\begin{array}{c}{\widehat{t}}_N\\ {\widehat{t}}_M\end{array}\right)|\left(\begin{array}{c}{0}_N\\ 0_M\end{array}\right),\left(\begin{array}{cc}{C}_{N,N}& C_{N,M}\\ C_{M,N}& C_{M,M}\end{array}\right)\right),\end{array}$(4)

where the ($i,j$)-th element of ${\mathbf{C}}_{N,N}$ is expressed as

(5) $C({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j)=k({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j)+{\mathrm{\Sigma }}_{ij}.$(5)

The first term $k({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j)$ represents the kernel function, and the second term ${\mathrm{\Sigma }}_{ij}$ is Gaussian noise, written as

(6) ${\mathrm{\Sigma }}_{ij}={\left(\delta \hat{t}\right)}_i{\delta }_{ij}{\left(\delta \hat{t}\right)}_j,$(6)

where ${\delta }_{ij}$ is the Kronecker delta. Note that the choice of the kernel function and that of the Gaussian noise affect the generation of ${\hat{\mathit{t}}}_M$. The elements of the $N\times M$ matrix ${\mathbf{C}}_{N,M}$, $M\times N$ matrix ${\mathbf{C}}_{M,N}(={\mathbf{C}}_{N,M}^{\mathrm{T}})$, and $M\times M$ matrix ${\mathbf{C}}_{M,M}$ are of the form:

(7) $C({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j)=k({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j).$(7)

By applying the theorem for conditional Gaussian distributions (see Appendix A) to Equation (4)(4) $\begin{array}{l}p({\widehat{t}}_{N+M})=\mathcal{N}({\widehat{t}}_{N+M}|0_{N+M},C_{N+M,N+M})\\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}=\mathcal{N}\left(\left(\begin{array}{c}{\widehat{t}}_N\\ {\widehat{t}}_M\end{array}\right)|\left(\begin{array}{c}{0}_N\\ 0_M\end{array}\right),\left(\begin{array}{cc}{C}_{N,N}& C_{N,M}\\ C_{M,N}& C_{M,M}\end{array}\right)\right),\end{array}$(4) , we obtain the conditional probability distribution $p({\hat{\mathit{t}}}_M|{\hat{\mathit{t}}}_N)$, expressed as

(8) $p({\widehat{t}}_M|{\widehat{t}}_N)=\mathcal{N}({\widehat{t}}_M|{\widehat{\mu }}_M,{\widehat{\Sigma }}_{M,M}),$(8)

where the mean ${\hat{\mathit{\mu }}}_M$ and covariance ${\widehat{\text{SigmA}}}_{M,M}$ are expressed as follows:

(9) ${\hat{\mathit{\mu }}}_M={\mathbf{C}}_{N,M}^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N,$(9)

(10) ${\widehat{\text{SigmA}}}_{M,M}={\mathbf{C}}_{M,M}-{\mathbf{C}}_{N,M}^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\mathbf{C}}_{N,M}.$(10)

2.3. Kernel function and hyperparameters

For the kernel function, this study uses the following radial basis function:

(11) $k({\hat{\mathit{x}}}_i,{\hat{\mathit{x}}}_j)={\theta }_{1}exp\left(-\frac{{\theta }_2}{2}\parallel {\hat{\mathit{x}}}_i-{\hat{\mathit{x}}}_j{\parallel }^2\right),$(11)

where $\mathit{\theta }=({\theta }_1,{\theta }_2)$ is a set of hyperparameters, which is optimized by finding the solution that maximizes the log-likelihood function $lnp({\hat{\mathit{t}}}_N|\mathit{\theta })$, written as

(12) $lnp({\hat{\mathit{t}}}_N|\mathit{\theta })=-\frac{1}{2}ln|{\mathbf{C}}_{N,N}|-\frac{1}{2}{\hat{\mathit{t}}}_N^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N-\frac{N}{2}ln(2\pi )$(12)

In this study, we use the gradient method, in which we obtain an optimal set of $\theta$ by updating the parameter set using the following equation:

(13) ${\theta }_{k+1}={\theta }_k-\eta \frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_k}lnp({\hat{\mathit{t}}}_N|\mathit{\theta }),$(13)

where $k$ is the iteration number and $\eta$ is the learning rate. Applying Equation B.1(B.1) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}ln|\mathbf{C}|=\mathrm{T}\mathrm{r}\left({\mathbf{C}}^{-1}\frac{\mathrm{\partial }\mathbf{C}}{\mathrm{\partial }x}\right).$(B.1) in Appendix B and Equation B.2(B.2) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left({\mathbf{C}}^{-1}\right)=-{\mathbf{C}}^{-1}\frac{\mathrm{\partial }\mathbf{C}}{\mathrm{\partial }x}{\mathbf{C}}^{-1}.$(B.2) in Appendix B to Equation (12)(12) $lnp({\hat{\mathit{t}}}_N|\mathit{\theta })=-\frac{1}{2}ln|{\mathbf{C}}_{N,N}|-\frac{1}{2}{\hat{\mathit{t}}}_N^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N-\frac{N}{2}ln(2\pi )$(12) , we obtain the derivative of $lnp({\hat{\mathit{t}}}_N|\mathit{\theta })$ as:

(14) $\begin{array}{cc}\frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_k}lnp({\hat{\mathit{t}}}_N|\mathit{\theta })=& -\frac{1}{2}\mathrm{T}\mathrm{r}\left({\mathbf{C}}_{N,N}^{-1}\frac{\mathrm{\partial }{\mathbf{C}}_{N,N}}{\mathrm{\partial }{\theta }_k}\right)\\ \hspace{0.17em}& +\frac{1}{2}{\hat{\mathit{t}}}_N^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}\frac{\mathrm{\partial }{\mathbf{C}}_{N,N}}{\mathrm{\partial }{\theta }_k}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N.\end{array}$(14)

3. Results and discussion

Figure 1 shows nuclide production cross-sections for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^7$Be, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{22}$Na, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{48}$Cr, and ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reactions. In these figures, we plot two regression lines with their uncertainty bands, i.e. prior and posterior, in comparison with the JENDL-HE/2007 evaluations and the INCL4.6/GEM calculations. The prior and posterior lines present the GPR results given by using the experimental dataset without and with the inclusion of the experimental data of Takeshita et al., respectively, and the line and band represent the mean and $\pm$2$\sigma$ about the mean, respectively. The optimal $\mathit{\theta }$ values for the GPR results are summarized in Table 1; here, for the initial set of $\mathit{\theta }$ and the learning rate for solving the optimization problem, we use $\mathit{\theta }=(1,2.5)$ and $\eta =0.00001$, respectively. We see that both sets of GPR results show reasonable agreement with each experimental dataset for all cases, and the curves are updated by the new experimental data. Although INCL4.6/GEM and JENDL-HE/2007 can account for the trends of nuclide production to some degree, these results do not agree with the experimental data. Furthermore, for JENDL-HE/2007, large gaps are observed at 250 MeV, which is attributed to a difference in the nuclear models employed in nuclear data evaluation below and above 250 MeV (see Watanabe et al. [4]).

Figure 1. Nuclide production cross-sections for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^7$Be, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{22}$Na, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{48}$Cr, and ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reactions. The dashed blue line and the light blue band present the mean of the generated predictive distribution and $\pm$2$\sigma$ about the mean, respectively, generated from the experimental dataset without experimental data from Takeshita et al. The green line and the light green band present the mean of the generated predictive distribution and $\pm$2$\sigma$ about the mean, respectively, generated from the experimental dataset including the experimental data from Takeshita et al.

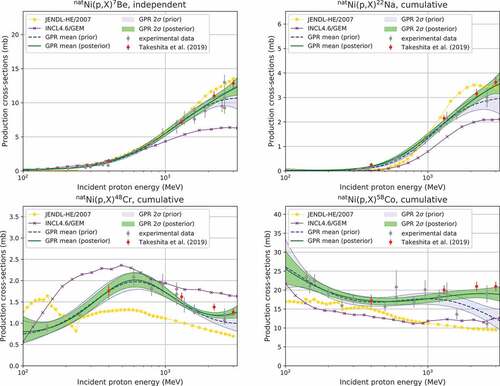
Table 1. Optimal hyperparameters.

Product	New exp.	${\theta }_1$	${\theta }_2$
${ }^7$Be (i)	Prior	$1.56$	$2.31$
${ }^7$Be (i)	Posterior	$1.71$	$2.39$
${ }^{22}$Na (c)	Prior	$2.34$	$3.16$
${ }^{22}$Na (c)	Posterior	$2.50$	$3.01$
${ }^{48}$Cr (c)	Prior	$0.96$	$2.67$
${ }^{48}$Cr (c)	Posterior	$1.09$	$3.08$
${ }^{58}$Co (c)	Prior	$2.09$	$2.01$
${ }^{58}$Co (c)	Posterior	$2.87$	$0.82$

(i): independent yield.

(c): cumulative yield.

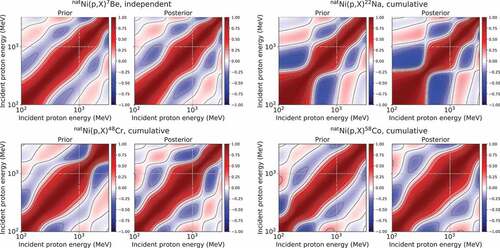
Figure 2 presents the relative standard deviations ${\sigma }_M^{\mathrm{U}}$ and ${\sigma }_M^{\mathrm{L}}$ (1σ) for the four reactions, and Figure 3 depicts the correlation matrices of for the same reactions. Note that the information for these variables is explicitly derived from GPR as afunction of the incident proton energy, in contrast to traditional models such as the linear regression model. Acomparison between the prior and posterior results in Figures 2 and 3 shows that the uncertainties are reduced by inclusion of new experimental data near measurement energies of 400 MeV and 1.3, 2.2, and 3 GeV. Accordingly, these data alter the correlation matrices, indicating that the experiment conducted by Takeshita etal. advances the generation of nuclide production cross-sections for a Ni target, particularly in the GeV range.

Figure 2. Relative uncertainties (1$\sigma$) in the generated cross-sections $t_M$ for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^7$Be, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{22}$Na, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{48}$Cr, and ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reactions. The solid and dashed blue lines present the upper and lower bounds of 1$\sigma$, respectively, generated from the experimental dataset without the experimental data of Takeshita et al. The solid and dashed blue lines present the upper and lower bounds of 1$\sigma$, respectively, generated from the experimental dataset with the experimental data from Takeshita et al.

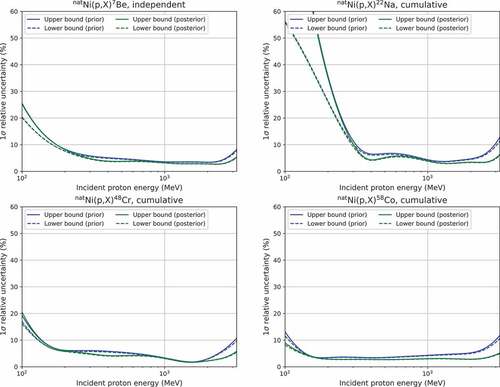
Figure 3. Correlation matrices among the target variables ${\hat{t}}_M$ for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^7$Be, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{22}$Na, ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{48}$Cr, and ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reactions.

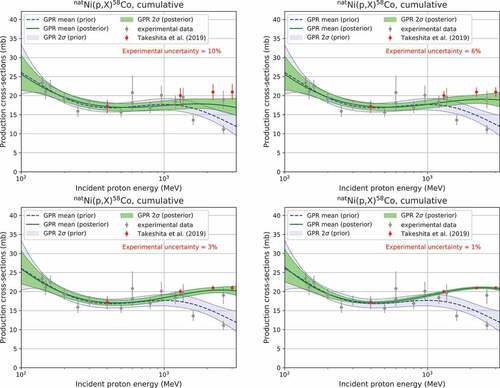
Figure 4 displays GPR results for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reaction under different experimental uncertainties. Here the uncertainties for the experiments of Takeshita et al. were assumed to be 10%, 6%, 3%, and 1% (1$\sigma$), whereas those of the other experiments were not changed. As intuitively anticipated, the mean GPR curves shift toward the experiment values as the experimental uncertainties decrease. Thus, the uncertainty of experimental values directly affects the regression curves, suggesting that the generation of nuclear data requires a careful estimation of the experimental uncertainty.

Figure 4. Comparison of GPR results for the ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni($p,X$)${ }^{58}$Co reaction under different experimental uncertainties.

4. Conclusion

We have applied the GPR technique to generate nuclear data, focusing on proton-induced nuclide production cross-sections for a ${ }^{\mathrm{n}\mathrm{a}\mathrm{t}}$Ni target. Reasonable curves with corresponding uncertainties were obtained, and the results indicate that this approach is effective for generating nuclear data. Moreover, our results suggest that this approach can be applied in experimental design to reduce the uncertainty of generated nuclear data. However, some limitations are worth noting. This study focused on proton-induced nuclide production cross-sections with relatively simple shapes. We did not examine nuclear data with complicated shapes, such as fission cross-sections for actinide nuclei. Furthermore, this study treated a relatively small experimental dataset. The dataset was sufficient; however, we did not apply large or small experimental nuclear datasets. Therefore, future work will explore the applicability of this approach for such types of nuclear data.

Acknowledgments

The author would like to thank Dr. K. Nishihara of the Japan Atomic Energy Agency for his review of the manuscript and his comments.

Disclosure statement

No potential conflict of interest was reported by the author.

Appendix A.

Theorem for conditional Gaussian distributions

The following theorem was used to derive Equations (8)(8) $p({\widehat{t}}_M|{\widehat{t}}_N)=\mathcal{N}({\widehat{t}}_M|{\widehat{\mu }}_M,{\widehat{\Sigma }}_{M,M}),$(8) –(10(10) ${\widehat{\text{SigmA}}}_{M,M}={\mathbf{C}}_{M,M}-{\mathbf{C}}_{N,M}^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\mathbf{C}}_{N,M}.$(10) ) from Equation (4)(4) $\begin{array}{l}p({\widehat{t}}_{N+M})=\mathcal{N}({\widehat{t}}_{N+M}|0_{N+M},C_{N+M,N+M})\\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}=\mathcal{N}\left(\left(\begin{array}{c}{\widehat{t}}_N\\ {\widehat{t}}_M\end{array}\right)|\left(\begin{array}{c}{0}_N\\ 0_M\end{array}\right),\left(\begin{array}{cc}{C}_{N,N}& C_{N,M}\\ C_{M,N}& C_{M,M}\end{array}\right)\right),\end{array}$(4) . The proof can be found in the text by Bishop [13].

If a joint probability distribution for two sets of variables ${\mathit{\zeta }}_a$ and ${\mathit{\zeta }}_b$ is Gaussian $\mathcal{N}(\mathit{\zeta }|\mathit{\mu },\text{SigmA})$, where

(A.1) $\zeta =\left(\begin{array}{c}{\zeta }_a\\ {\zeta }_b\end{array}\right),$(A.1)

(A.2) $\mathit{\mu }=\left(\begin{array}{c}{\mathit{\mu }}_a\\ {\mathit{\mu }}_b\end{array}\right),$(A.2)

and

(A.3) $\text{SigmA}=\left(\begin{array}{cc}{\text{SigmA}}_{aa}& {\text{SigmA}}_{ab}\\ {\text{SigmA}}_{ba}& {\text{SigmA}}_{bb}\end{array}\right),$(A.3)

then, the conditional distribution of ${\zeta }_a|{\zeta }_b$ is also Gaussian $\mathcal{N}({\mathit{\mu }}_{a|b},{\text{SigmA}}_{a|b})$, where

(A.4) ${\mu }_{a|b}={\mu }_a+{\Sigma }_{ab}{\Sigma }_{bb}^{-1}({\zeta }_b-{\mu }_b),$(A.4)

(A.5) ${\text{SigmA}}_{a|b}={\text{SigmA}}_{aa}-{\text{SigmA}}_{ab}{\text{SigmA}}_{bb}^{-1}{\text{SigmA}}_{ba}.$(A.5)

Appendix B.

Formulas for derivatives of the log-determinant and inverse of a matrix

The following mathematical formulas were used to derive Equation (14)(14) $\begin{array}{cc}\frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_k}lnp({\hat{\mathit{t}}}_N|\mathit{\theta })=& -\frac{1}{2}\mathrm{T}\mathrm{r}\left({\mathbf{C}}_{N,N}^{-1}\frac{\mathrm{\partial }{\mathbf{C}}_{N,N}}{\mathrm{\partial }{\theta }_k}\right)\\ \hspace{0.17em}& +\frac{1}{2}{\hat{\mathit{t}}}_N^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}\frac{\mathrm{\partial }{\mathbf{C}}_{N,N}}{\mathrm{\partial }{\theta }_k}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N.\end{array}$(14) from Equation (12)(12) $lnp({\hat{\mathit{t}}}_N|\mathit{\theta })=-\frac{1}{2}ln|{\mathbf{C}}_{N,N}|-\frac{1}{2}{\hat{\mathit{t}}}_N^{\mathrm{T}}{\mathbf{C}}_{N,N}^{-1}{\hat{\mathit{t}}}_N-\frac{N}{2}ln(2\pi )$(12) .

• The derivative of the log-determinant of a square matrix $\mathbf{C}$ with respect to a scalar $x$ is given by

(B.1) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}ln|\mathbf{C}|=\mathrm{T}\mathrm{r}\left({\mathbf{C}}^{-1}\frac{\mathrm{\partial }\mathbf{C}}{\mathrm{\partial }x}\right).$(B.1)

• The derivative of the inverse of a square matrix $\mathbf{C}$ with respect to a scalar $x$ is given by

(B.2) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left({\mathbf{C}}^{-1}\right)=-{\mathbf{C}}^{-1}\frac{\mathrm{\partial }\mathbf{C}}{\mathrm{\partial }x}{\mathbf{C}}^{-1}.$(B.2)