Nonuniform particle distribution and interference between removal mechanisms during unsteady aerosol deposition from a rising spherical bubble

ABSTRACT

Most of the practical computer models available today on aerosol pool scrubbing are built on the basis of fundamental assumptions introduced by Fuchs for his model published in 1955 (in Russian). The primary assumptions are that particle concentration in the bubble can be regarded as uniform and that particle removal mechanisms can be regarded as mutually independent. The present paper shows that these assumptions can cause considerable under- or overprediction of removal rates when applied to particles with radii in the submicrometer range. This size range, known to be where removal mechanisms are generally inefficient, is of particular interest in pool scrubbing study. The present paper, while not being the first to point out the problems with Fuchs’s assumptions, provides a comprehensive description on how the assumptions fail in the submictometer range based on comparisons of Fuchs model predictions against Lagrangian tracking simulations. The simulations, performed for particles of 0.1 to 1.0 $\mu$m in radius, advected by circulating gas flow in a spherical bubble rising in a water pool, show interference between inertial migration and Brownian diffusion of particles through the development of nonuniform particle concentration profile.

Graphical Abstract

KEYWORDS:

• Pool scrubbing
• Lagrangian particle tracking
• deposition
• thermal hydraulics
• diffusion

1. Introduction

The radioactive source term to the environment under nuclear reactor severe accident conditions needs to be limited by all available means. Pool scrubbing is among those counted on for retention of radionuclides vapor and aerosols in, e.g. BWR pressure suppression pool and PWR steam generator secondary side [1,2]. Although the pool scrubbing process will show different appearances depending on the injection geometry and gas velocity [3,4], its last stage, spanning the majority of the total height, will always take the form of small bubbles rising buoyantly in water. Since this stage takes over residues from the preceding processes and stages, the bubbles therein will consist primarily of noncondensable gases laden with aerosol particles with a narrowed size distribution around the so-called Greenfield gap [5], a size range between a few tens of nanometer and ~1 $\mu$m in aerodynamic radius, where the basic deposition mechanisms (sedimentation, inertial impaction and Brownian diffusion) are all inefficient. Quantification, experimental and analytical, of pool scrubbing performance for such particle sizes has therefore gathered considerable research interest [6–8]. Works published recently on this issue include those focusing on the influence of bubble and pool parameters [9–13].

Existing models for pool scrubbing analysis, including those used in computer codes including VANESA [14], SPARC [15], BUSCA [16], SUPRA [17], SRT [13], POSCAR [11] and I-COSTA [12], are mostly based on the pioneering work of Fuchs in 1964 [18]. Fuchs’s model takes a single-control-volume lumped parameter approach to modeling particle removal from the bubble. This implies that the particles in the bubble are assumed to have an approximately uniform concentration profile. The model further assumes that the particle deposition mechanisms are mutually independent such that the deposition velocity is given by the sum of velocities due to the individual mechanisms. The deposition velocity due to the Brownian diffusion is calculated by applying Higbie’s penetration theory [19] to the particle transfer inside the bubble. This choice has been criticized repeatedly for being fundamentally inadequate [20,21] since the theory is applicable only to transfer at the surface of a large well-mixed bulk. It is noted that this choice fits (unnecessarily) well in the frame of simplification assumptions on uniformity and independence.

The assumption of independent mechanisms may represent a fair approximation when the particle deposition is dictated by a single dominant mechanism. This, however, will not be the case for particle sizes close to the deposition velocity minimum where the inertial and Brownian contributions are both small and comparable to each other. Under such conditions, possible interference between the two mechanisms may affect the particle deposition flux.

The adequacy of the Fuchs model’s assumptions, of concentration uniformity and mechanisms independence, has been addressed by analyzing particle transport and deposition by using an Eulerian (continuum based) model with one-dimensional approximation [22] and three-dimensional Lagrangian particle tracking [23]. While these studies show non-uniform concentration profile evolving with time and deviations from Fuchs model predictions in particle deposition rate, the underlying mechanisms, including the possible interference between the deposition mechanisms, are not discussed in depth.

The present work is based on three-dimensional Lagrangian simulations of particles with sizes between 0.1 and 1.0 $\mu$m in radius where the dominant mechanisms for particle retention are inertial impaction and Brownian diffusion. The simulations show that the inertial transport causes faster-than-average particle depletion around the center of recirculating flow inside the bubble, producing a surface-peaked concentration profile like in cyclone separators, with surface-to-average concentration ratio increasing with elapsed time. As such, the inertial deposition rate becomes increasingly greater than the Fuchs model prediction. The influence of diffusion is observable for the smallest particle radius simulated (0.1 $\mu$m) but in a much different way from the Fuchs model’s presumption: a quick growth of bubble-surface diffusion layer causes a transition of dominant removal mechanisms from unsteady Brownian diffusion to inertial migration. Fuchs’s model, based on the penetration theory, predicts a time-invariant deposition velocity corresponding to a very thin diffusion layer, and hence largely overpredicts the removal rates for small particles.

Fuchs-based computer models are used widely for predicting pool scrubbing performance even in the latest journal papers obviously without adequate recognition of the above problems. The present paper intends to contribute to closing such knowledge gap.

2. Mathematical models

2.1. Fluid phase

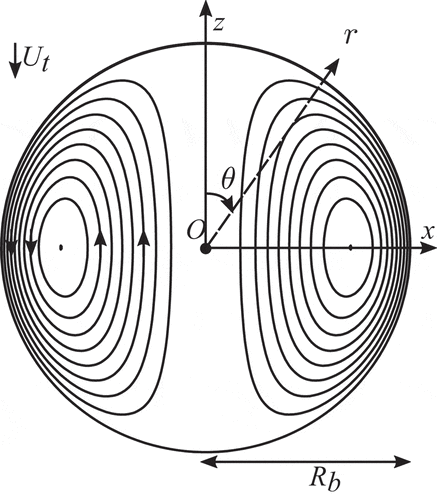
We consider a single bubble with a radius $R_b$ rising steadily in stationary water at a terminal velocity $U_t$. At room temperature, bubbles with a radius of less than about 0.5 mm will be spherical [24]. The bubble internal flow is assumed to be steady in the frame moving with the rising bubble, and modeled by Hill’s spherical vortex [25] as has been done in many studies in literature including those cited in Introduction. The contribution of steam condensation (i.e. steam movement to the bubble interface) is ignored since the bubbles to be modeled will consist primarily of noncondensable gases. Figure 1 shows schematically the Hill’s spherical vortex streamlines.

Figure 1. Schematic of Hill’s spherical vortex.

The Stokes stream function $\psi$ for Hill’s spherical vortex, satisfying velocity continuity with an external flow, approximated by a potential flow, can be written for spherical coordinate system r $\hspace{0.17em}=\left(r,\theta ,\phi \right)$ as:

(1) $\begin{array}{c}\psi \left(r,\theta \right)=-\frac{3U_t}{4R_b^2}\left(R_b^2-r^2\right)r^2{sin}^2\theta ,r\le R_b.\end{array}$(1)

The bubble rise velocity $U_t$ is obtained using Peebles and Garber correlation [26,27]

(2) $\begin{array}{c}{U}_t=0.33g^{0.76}{{\nu }_l}^{-0.52}{R}_b^{1.28}\text{break}\mathrm{f}\mathrm{o}\mathrm{r}\text{break}2<\mathrm{R}{\mathrm{e}}_b<4.02{\mathrm{M}}^{-0.214},\end{array}$(2)

where $\mathrm{M}=g{\mu }_l^4/{\rho }_l{\sigma }^3$ is the Morton number with ${\nu }_l$, ${\rho }_l$, $g$, $\sigma$, and ${\mu }_l$ being the kinematic viscosity of the continuous phase (water), the density of water, the gravitational acceleration, surface tension, and the dynamic viscosity of water, respectively. This correlation has been used in pool scrubbing studies, e.g. [22,23,28], and covers small bubble radii including the value assumed in the present study (0.5 mm).

The bubble internal velocity U$\hspace{0.17em}=\left(U_r,U_{\theta },0\right)$ is given as follows:

(3) $\begin{array}{c}\mathit{U}=\mathrm{r}\mathrm{o}\mathrm{t}\left(\frac{\psi }{rsin\theta }{\mathit{e}}_{\phi }\right),\end{array}$(3)

where ${\mathit{e}}_{\phi }=\left(0,0,1\right)$ is the unit vector in the $\phi$ direction.

2.2. Particle motion

We consider monodispersed solid spherical particles of radius $R_p$ and density ${\rho }_p$ small enough for the Stokes law to hold. The particles are assumed to move independently of each other and do not affect the flow field. The assumption is valid for dilute aerosols: Brownian coagulation can be ignored for particle number concentrations less than ${10}^{14}/{\mathrm{m}}^3$ [29] and the fluid-particle interactions can be taken to be one-way when the particle volume fraction is less than ${10}^{-4}$ [30]. The particle number concentrations and volume fractions considered in the present study are less than ${10}^{13}/{\mathrm{m}}^3$ and less than $4\times {10}^{-5}$, respectively. To simulate the motion of a particle of mass $m_p=4/3\pi {\rho }_p{R}_p^3$, centered instantaneously at ${\mathit{x}}_{\mathit{p}}\left(t\right)$ and moving with velocity ${\mathit{v}}_{\mathit{p}}\left(t\right)$ in a steady flow $\mathit{U}$ of gas with density ${\rho }_g=1.172\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$ and dynamic viscosity ${\mu }_g=1.863\times {10}^{-5}\mathrm{P}\mathrm{a}\cdot \mathrm{s}$, we use the equation of motion in the form proposed by Maxey and Riley [31] with a Brownian force term:

(4a) $\frac{d{\mathit{x}}_p}{dt}={\mathit{v}}_p,$(4a)

(4b) $m_p\frac{d{\mathit{v}}_{\mathit{p}}}{dt}={\mathit{F}}_{\mathit{d}}+{\mathit{F}}_{\mathit{B}}+{\mathit{F}}_{\mathit{a}}+{\mathit{F}}_{\mathit{s}}+{\mathit{F}}_{\mathit{g}},$(4b)

where ${\mathit{F}}_{\mathit{d}}$, ${\mathit{F}}_{\mathit{B}}$, ${\mathit{F}}_{\mathit{a}}$, ${\mathit{F}}_{\mathit{s}}$, and ${\mathit{F}}_{\mathit{g}}$ are Stokes drag, Brownian, added mass, fluid stress gradient, and gravitational forces, respectively. The history and lift forces are ignored since they are known to be small in gas-solid flows [32]. The drag force is given by the Stokes law

(5) $\begin{array}{c}{\mathit{F}}_{\mathit{d}}=f\left(\mathit{U}-{\mathit{v}}_{\mathit{p}}\right),\end{array}$(5)

where $f$ is the drag coefficient

(6a) $\begin{array}{c}f=\frac{6\pi {\mu }_g{R}_p}{C_c},\end{array}$(6a)

(6b) $\begin{array}{c}{C}_c=1+\frac{\lambda }{R_p}\left(1.257+0.4\mathrm{e}\mathrm{x}\mathrm{p}\left(-1.1\frac{R_p}{\lambda }\right)\right),\end{array}$(6b)

where $C_c$ is the Cunningham correction factor that deviates from unity when the particle radius is not much larger than the mean free path $\lambda$ of gas molecules. The values of coefficients in Equation (6b)(6b) $\begin{array}{c}{C}_c=1+\frac{\lambda }{R_p}\left(1.257+0.4\mathrm{e}\mathrm{x}\mathrm{p}\left(-1.1\frac{R_p}{\lambda }\right)\right),\end{array}$(6b) are those obtained by Davies [33] for air. Brownian force is modeled as a Gaussian white noise random process [34]:

(7) $\begin{array}{c}{\mathit{F}}_{\mathit{B}}=\mathit{\zeta }\sqrt{\frac{2k_b^2{T}^2}{D_B\mathrm{\Delta }t}},\end{array}$(7)

where ζ, $k_b$, $D_B$, $T$, and $\mathrm{\Delta }t$ are Gaussian random numbers with zero means and unit variances, Boltzmann constant, Brownian diffusion constant, gas temperature, and time step, respectively. The Brownian constant $D_B$ is obtained using the Stokes-Einstein relation:

(8) $\begin{array}{c}{D}_B=\frac{k_{b}T}{f},\end{array}$(8)

The added mass, fluid stress gradient, and gravitational forces are

(9a) $\begin{array}{c}{\mathit{F}}_{\mathit{a}}=\frac{2}{3}\pi {\rho }_g{R}_p^3\left(\frac{D\mathit{U}}{Dt}-\frac{D{\mathit{v}}_{\mathit{p}}}{Dt}\right),\end{array}$(9a)

(9b) $\begin{array}{c}{\mathit{F}}_{\mathit{s}}=\frac{4}{3}\pi {\rho }_g{R}_p^3\frac{D\mathit{U}}{Dt},\end{array}$(9b)

and

(9c) $\begin{array}{c}{\mathit{F}}_{\mathit{g}}=\frac{4}{3}\pi R_p^3\left({\rho }_p-{\rho }_g\right)\mathit{g},\end{array}$(9c)

where $\mathit{g}=\left(0,0,-g\right)$ is the gravitational acceleration vector. By using these relations, Equation (4) can be rewritten as follows:

(10a) $\begin{array}{c}\frac{d{\mathit{x}}_{\mathit{p}}}{dt}={\mathit{v}}_{\mathit{p}},\\ \hspace{0.17em}\end{array}$(10a)

(10b) $\left(m_p+m_a\right)\frac{d{\mathit{v}}_{\mathit{p}}}{dt}=f\left(\mathit{U}-{\mathit{v}}_{\mathit{p}}\right)+\mathit{\zeta }\sqrt{\frac{2k_b^2{T}^2}{D_B\mathrm{\Delta }t}}+2\pi {\rho }_g{R}_p^3\mathit{U}\cdot \mathrm{\nabla }\mathit{U}+\frac{4}{3}\pi R_p^3\left({\rho }_p-{\rho }_g\right)\mathit{g},$(10b)

where $m_a=2/3\pi {\rho }_g{R}_p^3$ is the added mass.

2.3. Fuchs model

The extent of aerosol removal is commonly expressed using the decontamination factor $DF$ or the depletion efficiency $\epsilon$. The $DF$ and $\epsilon$, defined based on the total number of particles $N_p$ in the system of interest, are

(11a) $\begin{array}{c}DF\left(t\right)=\frac{N_p\left(0\right)}{N_p\left(t\right)}\ge 1,\end{array}$(11a)

(11b) $\begin{array}{c}\epsilon \left(t\right)=1-\frac{1}{DF\left(t\right)}.\end{array}$(11b)

Fuchs’s model [18] assumes that the decay of $N_p$ with time is given by

(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12)

where ${\alpha }_j$ is the removal coefficient for mechanism $j$. The coefficients for inertia ${\alpha }_i$ and gravity ${\alpha }_g$ are:

(13a) $\begin{array}{c}{\alpha }_i=\frac{9{\tau }_p{U}_t^2}{2R_b^2},\end{array}$(13a)

(13b) $\begin{array}{c}{\alpha }_g=\frac{3g{\tau }_p}{4R_b},\end{array}$(13b)

where ${\tau }_p=\left(m_p+m_a\right)/f$ is the particle relaxation time. Equations (12)(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12) and (13a(13a) $\begin{array}{c}{\alpha }_i=\frac{9{\tau }_p{U}_t^2}{2R_b^2},\end{array}$(13a) ) calculate the inertial removal rate as the particle concentration taken as $n_p=N_p/V_b$, where $V_b$ is the volume of the bubble, times the inertial (centrifugal) terminal velocity of the particle approximated by $\left[||\mathit{U}\left(R_b,\theta \right)|{|}^2/R_b\right]{\tau }_p$, integrated over the bubble surface. Similarly, Equations (12)(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12) and (13b(13b) $\begin{array}{c}{\alpha }_g=\frac{3g{\tau }_p}{4R_b},\end{array}$(13b) ) calculate the gravitational removal rate based on the terminal velocity for gravity $\mathit{g}{\tau }_p$.

The removal coefficient for Brownian diffusion ${\alpha }_B$ is derived based on the penetration theory [19] and is given by:

(13c) $\begin{array}{c}{\alpha }_B=1.8\sqrt{\frac{U_t{D}_B}{R_b^3}},\end{array}$(13c)

Equation (12)(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12) means that $N_p$ decays exponentially at a rate proportional to the sum of coefficients. Each coefficient should then be inversely proportional to the characteristic time of respective particle removal mechanisms, even when the linear superposition approach taken by Equation (12)(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12) could be justified. In Equations (13a)(13a) $\begin{array}{c}{\alpha }_i=\frac{9{\tau }_p{U}_t^2}{2R_b^2},\end{array}$(13a) and (13b(13b) $\begin{array}{c}{\alpha }_g=\frac{3g{\tau }_p}{4R_b},\end{array}$(13b) ), the inertial and gravitational characteristic times are reasonably taken to be the bubble characteristic length $R_b$ divided by the respective particle terminal velocity. In Equation (13c)(13c) $\begin{array}{c}{\alpha }_B=1.8\sqrt{\frac{U_t{D}_B}{R_b^3}},\end{array}$(13c) , on the other hand, the diffusional characteristic time is taken, disputably, to be the square root of the product of diffusive and advective characteristic times.

The assumption in Equations (12)(12) $\begin{array}{c}\frac{d{N}_p}{dt}=-N_p\sum _j{\alpha }_j,\end{array}$(12) and (13) that the particle removal rate is proportional to $n_p=N_p/V_b$ means that a lumped parameter (ideally mixed bubble) approach is taken. The temporal variation of concentration distribution is not taken into account. Then, the relative magnitudes of coefficients, time independent, can be expressed using the nondimensional numbers for transport phenomena.

(14a) $\begin{array}{c}\frac{{\alpha }_i}{{\alpha }_g}=\frac{6U_t^2}{g{R}_b}=6\mathrm{F}{\mathrm{r}}^2,\end{array}$(14a)

(14b) $\begin{array}{c}\frac{{\alpha }_i}{{\alpha }_B}=2.5\mathrm{P}{\mathrm{e}}^{0.5}St,\end{array}$(14b)

where $\mathrm{F}\mathrm{r}=U_t/\sqrt{g{R}_b}$, $\mathrm{P}\mathrm{e}=U_t{R}_b/D_B$, and $\mathrm{S}\mathrm{t}={\tau }_p{U}_t/R_b$ are Froude, Péclet, and Stokes numbers, respectively. Equation (14a)(14a) $\begin{array}{c}\frac{{\alpha }_i}{{\alpha }_g}=\frac{6U_t^2}{g{R}_b}=6\mathrm{F}{\mathrm{r}}^2,\end{array}$(14a) shows that the importance of gravity relative to inertia depends only on bubble velocity and radius. It is found that the gravity effect on particle removal is much smaller than the inertia effect regardless of the bubble radii.

3. Numerical conditions and validation

The particles are initially distributed randomly in the bubble. Each particle has a velocity equal to the local fluid velocity, ${\mathit{v}}_{\mathit{p}}\left(t=0\right)$ = $\mathit{U}$, but starts being accelerated at $t=0$, following the equation of motion, Equation (4). Each particle is tracked until the following removal condition is satisfied.

(15) $\begin{array}{c}||{\mathit{x}}_{\mathit{p}}||>R_b-R_p,\end{array}$(15)

Parameters and their values for simulations are listed in Table 1, where $N_{p0}$ and $P$ are the initial number of particles and pressure, respectively. Three particle radii are chosen from the range where all the removal mechanisms are known to be inefficient [8]. The Cunningham correction factor used in the Stokes law (Equation (6a)(6a) $\begin{array}{c}f=\frac{6\pi {\mu }_g{R}_p}{C_c},\end{array}$(6a) ) is obtained using the equation of Davies (Equation (6b)(6b) $\begin{array}{c}{C}_c=1+\frac{\lambda }{R_p}\left(1.257+0.4\mathrm{e}\mathrm{x}\mathrm{p}\left(-1.1\frac{R_p}{\lambda }\right)\right),\end{array}$(6b) ) as $C_c=1.865,$ $1.163,$ and $1.082$ for $R_p=0.1\mu \mathrm{m},0.5\mu \mathrm{m},$ and $1.0\mu \mathrm{m}$, respectively, showing that the flow around the particle starts deviating from the continuum regime for the smallest radius.

Table 1. Parameters of numerical simulation

$N_{p0}$	$R_b$$\left(\mathrm{m}\mathrm{m}\right)$	${\rho }_p$$\left(\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\right)$	$R_p$ $\left(\mu \mathrm{m}\right)$	$T$$\left(\mathrm{K}\right)$	$P$$\left(\mathrm{P}\mathrm{a}\right)$	$\mathrm{\Delta }t$$\left(\mathrm{s}\right)$	$U_t$$\left(\mathrm{m}/\mathrm{s}\right)$
5000	0.5	2000	0.1, 0.5, and 1.0	300	$1.0\times {10}^5$	$0.5{\tau }_p$	0.159

The simulation program was tested against a benchmark problem where 1000 particles were initially placed on a single point in a stationary fluid and then allowed to follow the equation of motion, Equation (4), with the gravity term nullified. Figure 2(a) compares the root mean square (RMS) displacement of particles obtained from simulations (dots) with the theoretical values $\mathrm{R}\mathrm{M}\mathrm{S}\left[{\mathit{x}}_{\mathit{p}}\right]=\sqrt{6D_{B}t}$ for Brownian motion (solid lines). The agreement is satisfactory for all the conditions tested.

Figure 2. (a) Root-mean-square displacement for Brownian particles with $R_p=0.1\mu \mathrm{m}$, $R_p=0.5\mu \mathrm{m}$, and $R_p=1.0\mu \mathrm{m}$ as a function of time. The lines are theoretical predictions and the dots are the results of the numerical simulation. (b) Fraction of remaining particles $\left(1-\epsilon \right)$ as a function of time calculated with the fourth-order Runge-Kutta (RK) and the first-order Euler schemes. Time steps are $\mathbf{\Delta }t=0.1{\tau }_p$, $\mathbf{\Delta }t=0.5{\tau }_p$, and $\mathbf{\Delta }t=2.0{\tau }_p$. The particle radius $R_p=0.5\mu \mathrm{m}$.

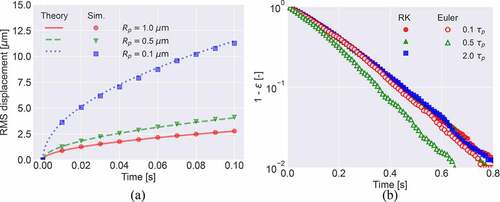
For particle tracking simulations, it is commonly recommended to keep the time step $\mathrm{\Delta }t$ small enough as compared to the relaxation time ${\tau }_p$ [35]. Since this requirement becomes demanding when sub-micron particles with small ${\tau }_p$ are to be simulated, we performed test calculations to find how much the requirement could be relaxed in our particular cases. The results are shown in Figure 2(b) for the fraction of remaining particles $\left(1-\epsilon \right)$ vs. time calculated for $R_p=0.5\mu \mathrm{m}$ with different values of $\mathrm{\Delta }t$ and different integration schemes. The fourth-order Runge-Kutta, used as the standard scheme in our simulations, shows no systematic deviation with an increase in $\mathbf{\Delta }t$, even when $\mathbf{\Delta }t$ is increased to $2.0{\tau }_p$. This suggests that a higher order integration scheme can accommodate larger time steps than ${\tau }_p$ at least for certain cases. In contrast, the first-order Euler scheme requires much smaller time step than ${\tau }_p$ as shown in the same figure.

4. Results and discussion

Simulation results are presented and compared with Fuchs model predictions for three cases where the particle removal mechanisms were considered fully or partially as summarized in Table 2. The mechanisms considered in each case are represented by the forces activated in simulations, and by the removal coefficients deployed in Fuchs model calculations, respectively. In Table 2, those in the parentheses are known to have relatively small influences on the results. Namely, the major contributors here are inertia and diffusion.

Table 2. The forces considered in the numerical simulation and the removal coefficients used in the Fuchs model calculations

	Simulation	Fuchs
Case 1	${\mathit{F}}_{\mathit{d}}+{\mathit{F}}_{\mathit{B}}+\left({\mathit{F}}_{\mathit{a}}+{\mathit{F}}_{\mathit{s}}+{\mathit{F}}_{\mathit{g}}\right)$	${\alpha }_i+{\alpha }_B+\left({\alpha }_g\right)$
Case 2	${\mathit{F}}_{\mathit{d}}$	${\alpha }_i$
Case 3	[20]	${\alpha }_B$

Table 2 can be read that Case 1 considers both inertia and diffusion (and others), Case 2 inertia alone, and Case 3 diffusion alone. Case 3 calculation was conducted only with the Fuchs model. To perform simulation for Case 3, i.e. particle motion due to Brownian diffusion (advection-diffusion) without inertial displacement, some artificial treatment would become necessary. Instead of doing that, we use a numerical solution for that case, in an approximation form shown in Mills and Hoseyni [20], for comparison with other cases. Note that inertial displacement of a particle is calculated in simulations as the consequence of the lack of enough fluid forces for retaining the particle on a curved streamline, while it is calculated by Fuchs’s model as caused by an inertial (centrifugal) force.

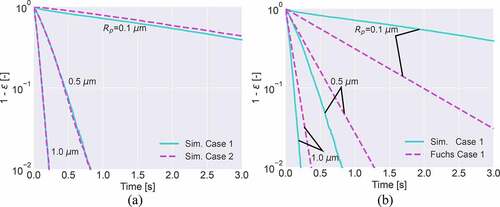
Figure 3(a) compares simulation results for Cases 1 and 2. First of all, it is clear that the particle removal rate decreases quickly as the particle size decreases. For larger sizes, $R_p=0.5$ and $1.0\mu \mathrm{m}$, no meaningful differences are seen between the two cases, showing that the inertial removal prevails for both sizes, i.e. the inertial effect is much greater than the gravitational and diffusional effects (that are considered in Case 1 but not in Case 2). For a smaller particle size $R_p=0.1\mu \mathrm{m}$, however, slightly faster removal is seen for Case 1 than for Case 2. The difference between the two cases occurs immediately after the initiations of removal, and remains almost constant after about 1 s.

Figure 3. Fraction of remaining particles $\left(1-\epsilon \right)$ as a function of time for (a) the Case 1 and Case 2 simulations and (b) the Case 1 simulation and the Fuchs model predictions for Case 1, for particle radii $R_p=0.1\mu \mathrm{m},0.5\mu \mathrm{m},$ and $1.0\mu \mathrm{m}$.

The $R_p$ dependence of the difference between Cases 1 and 2 should be related to the $R_p$ dependence of forces considered or unconsidered in the two cases. We can express the $R_p$ dependence of the individual forces as ${\mathit{F}}_{\mathit{d}}\propto R_p$, ${\mathit{F}}_{\mathit{a}}+{\mathit{F}}_{\mathit{s}}\propto R_p^3$, ${\mathit{F}}_{\mathit{g}}\propto R_p^3$, and ${\mathit{F}}_{\mathit{B}}\propto \sqrt{R_p}$, if we ignore the weak dependence of the Cunningham correction factor $C_c$ on $R_p$. This scaling consideration shows that the importance of Brownian diffusion increases with the decrease in particle size, and suggests that the difference between Cases 1 and 2 results for $R_p=0.1\mu \mathrm{m}$ stems from the diffusion effects in the early phase of the transient. This problem will be further discussed later in this paper.

Figure 3(b) shows comparisons between the present simulation and Fuchs model prediction for Case 1 with the three particle radii. Overall, the Fuchs model predictions show considerably smaller dependence on $R_p$ than the simulations. For larger particle sizes $R_p=0.5$ and $1.0\mu \mathrm{m}$, subject to inertia-dominated removal as found in Figure 3(a), Fuchs model initially shows a fairly good agreement with the simulations, as long as $\left(1-\epsilon \right)>0.7$, but then starts predicting slower removal than the simulations. In contrast to this, for a smaller particle size $R_p=0.1\mu \mathrm{m}$, the Fuchs model predicts much faster removal than the simulation.

Figure 4 shows further comparisons for $R_p=0.1\mu \mathrm{m}$, seeking for the cause of the large difference seen in Figure 3(b) between the Fuchs model and simulations, with the aid of Case 2 calculations. The Case 2 results, with consideration of the inertia effect alone, show no significant difference between the Fuchs and simulation results. The difference becomes significant only when the Brownian diffusion is considered as in Case 1, while this would not immediately mean that the diffusion effect alone is responsible for the difference.

Figure 4. Fraction of remaining particles $\left(1-\epsilon \right)$ as a function of time in the range of $0.0<t<1.0$ for the Case 1 and 2 simulations, Fuchs model predictions for Cases 1 and 2, and Mills and Hoseyni [20] proposed curve for Case 3, all for particle radius $R_p=0.1\mu \mathrm{m}$.

Inertial displacement occurs necessarily when solid particles are advected by gas flow along curved streamlines, as in the present problem. Therefore, evaluation of Brownian diffusion effect separately from the inertial displacement could be done only through thought experiments. Shown in Figure 4 for comparison with simulations and Fuchs model prediction is a curve proposed by Mill and Hoseyni [20] based on an approximate expression for analytical solution obtained by Calderbank and Korchinski [36] for the unsteady advection-diffusion problem formulated by Kronig and Brink [37] for Hill’s vortex flow. The Kronig and Brink problem concerns the advection-diffusion of scalar quantity (heat or dissolved mass) for the limiting case of $\mathrm{R}\mathrm{e}\to 0,\mathrm{P}\mathrm{e}\to \mathrm{\infty }$. Mills and Hoseyni proposed application of this solution to Brownian particle diffusion in the same flow. As depicted in Figure 4, the Mills and Hoseyni curve shows a faster particle removal than the inertia-alone (Case 2) solutions until 0.5 s, but a slower removal thereafter, suggesting, again, that diffusion effect could be important at the beginning of the transient.

The temporal change of the particle concentration profile was derived from the simulation results by counting the particles remaining in each of ten equal-volume, concentric toroidal regions defined to be bounded by stream surfaces (i.e. the isosurface of $\psi$). Figure 5 shows normalized particle number density $n_p\left(t\right)/n_p\left(0\right)$: $n_p\left(0\right)=N_{p0}/V_b$ plotted against normalized stream function $\xi =\psi /\mathrm{m}\mathrm{a}\mathrm{x}\left(\psi \right)$, where $\xi =0$ corresponds to the bubble surface and $\xi =1$ to the vortex center. The results are obtained from simulations conducted with an enhanced initial particle number $N_{p0}=10,000$ and repeated five times to reduce the random error.

Figure 5. The distribution of particle concentration $n_p\left(t\right)$ normalized by the initial value $n_p\left(0\right)$ and 95% confidence intervals for (a) $R_p=1.0\mu \mathrm{m}$ and (b) $R_p=0.1\mu \mathrm{m}$.

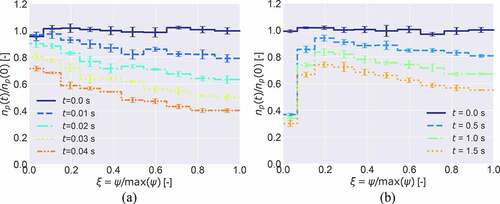
For $R_p=1.0\mu \mathrm{m}$ (Figure 5(a)), nonuniformity in particle concentration starts forming over the entire bubble cross-section upon the initiation of transient, and develops with time, with a maximum concentration near the bubble surface and a minimum at the vortex center. This nonuniformity, resulting from inertial migration of particles, apparently has an effect to raise the particle flow rate across the bubble surface, i.e. the particle removal rate. The Fuchs model does not consider such nonuniformity but simply assumes that the near-surface concentration to be the same as the volume average. This explains why the Fuchs model starts predicting slower particle removal than the simulation soon after the initiation of transient (Figure 3(b)).

For $R_p=0.1\mu \mathrm{m}$ (Figure 5(b)), the particle concentration starts indicating a steep drop toward the bubble surface (to be discussed in detail later in the paragraph below the Equation (17). Except for this near-surface change, nonuniformity in concentration forms over the entire bubble cross-section in a similar fashion to that for $R_p=1.0\mu \mathrm{m}$. The nonuniformity however develops more slowly because of a slower particle migration. The concentration distribution shown in Figure 5(b) looks similar to the results of an Eulerian one-dimensional calculation by Ghiaasiaan and Yao [22].

For discussing the particle removal rate, $d{N}_p/dt$, or $d\left(1-\epsilon \right)/dt$, quantitatively in relation to removal mechanisms, it is convenient to use the Sherwood number, or nondimensionalized mass transfer coefficient, $\mathrm{S}\mathrm{h}=2R_{b}k/D_B$, where $k$ is the mass transfer coefficient. Figure 6 shows $\mathrm{S}\mathrm{h}$ for $R_p=0.1\mu \mathrm{m}$ as a function of the non-dimensional time, or Fourier number, $t_D=t{D}_B/R_b^2.$ The Sherwood number was calculated from the simulation results by using the relation [24]

(16) $\begin{array}{c}\mathrm{S}\mathrm{h}=\frac{2}{3\left(1-\epsilon \right)}\frac{d\epsilon }{d{t}_D}.\end{array}$(16)

Figure 6. Sherwood number ($\mathrm{S}\mathrm{h}$) as a function of non-dimensional time $t_D=t{D}_B/R_b^2$ for the Case 1 and Case 2 simulations, Fuchs model predictions for Case 2 and Case 3, and Mills and Hoseyni [20] curve, for particle radius $R_p=0.1\mu \mathrm{m}$.

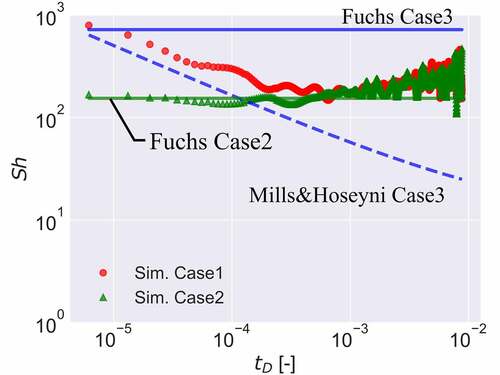
Since $\epsilon$ obtained from simulations indicate large fluctuations with time, the time differentiation was applied to $\epsilon$ fitted by a smooth function. Figure 6 also shows the Fuchs models translated into Sherwood numbers:

(17a) $\begin{array}{c}\mathrm{S}\mathrm{h}=\frac{2}{3}\frac{R_b^2}{D_B}{\alpha }_i=3\mathrm{P}\mathrm{e}\mathrm{S}\mathrm{t}\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a}\right),\end{array}$(17a)

(17b) $\begin{array}{c}\mathrm{S}\mathrm{h}=\frac{2}{3}\frac{R_b^2}{D_B}{\alpha }_B=1.2\mathrm{P}{\mathrm{e}}^{0.5}\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{B}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\right).\end{array}$(17b)

At the beginning of the transient in Figure 6, two curves reflecting Brownian diffusion, i.e. Case 1 simulation and Mills and Hoseyni [20] curve, show as high $\mathrm{S}\mathrm{h}$ as ${10}^3$, followed by steep decreases with time. This is characteristic to unsteady advection-diffusion (Colombet et al. [38] and Juncu [39]). The initial removal rate is predicted to be high since the transient starts with a uniform particle concentration in the bubble where the bubble surface concentration is forced to be zero at $t=0$. (Despite high Péclet number $\mathrm{P}\mathrm{e}=U_t{R}_b/D_B\sim {10}^5$, the Sherwood numbers obtained from Case 1 simulation are only about twice as large as the analytical solution for pure diffusion ($\mathrm{R}\mathrm{e}=0$ and $\mathrm{P}\mathrm{e}=0$) [38]). The removal rate decreases quickly as the near-surface concentration drops, as has been seen in Figure 5(b), to form a diffusion layer (a vacancy layer with low particle concentration) whose thickness increases with time. While the diffusion-alone model (Mills and Hoseyni) predicts a continuous, exponential decay of $\mathrm{S}\mathrm{h}$, Case 1 simulation starts deviating from that at $t_D\sim {10}^{-4}$ and finally converges with Case 2 (inertia-alone) simulation result. Both simulations then indicate a gradual increase in $\mathrm{S}\mathrm{h}$, reflecting the near-surface peaking of concentration shown in Figure 5(a). Fuchs’s inertial model fails to capture this increase in $\mathrm{S}\mathrm{h}$, since the model does not consider nonuniformity in concentration.

Fuchs’s diffusion model predicts time-independent $\mathrm{S}\mathrm{h}$ since it does not take into account of the development of the diffusion layer with time. The model is based on the penetration theory [19] which considers a steady diffusion into (or from) a surface flow on a large fluid volume (bulk) unaffected by the surface diffusion. In other words, the theory assumes the surface diffusion layer to be much thinner than the fluid bulk dimension. This basic assumption provides a time independent $\mathrm{S}\mathrm{h}$. It is, therefore, inadequate to apply this theory to the bubble internal flow, a recalculating flow in a small fluid volume (without a bulk), where the near-surface concentration gradient can vary significantly with time, directly affecting the surface transfer coefficient. The inadequacy of Fuchs’s diffusion model has an actual influence as an overprediction of the overall particle removal rate for smaller particle sizes, as shown in Figure 3(b) for $R_p=0.1\mu \mathrm{m}$, for which Fuchs’s model (mis)calculates the Sherwood number for diffusion to be about five times larger than that for inertial migration as shown in Figure 6. The ratio of the two Sherwood numbers, given by the inverse of Equation (14b)(14b) $\begin{array}{c}\frac{{\alpha }_i}{{\alpha }_B}=2.5\mathrm{P}{\mathrm{e}}^{0.5}St,\end{array}$(14b) , decreases with $R_p$ and hence the influence of the diffusion model disappears for larger particle sizes for which $2.5\mathrm{P}{\mathrm{e}}^{0.5}\mathrm{S}\mathrm{t}$ is of the order of unity or more.

We have observed for $R_p=0.1\mu \mathrm{m}$ a transition from diffusion- to inertia-driven particle removal. Although the two mechanisms coexist through the end of transient, their relative importance changes with time. During the initial transient before $t_D\sim {10}^{-4}$ for $R_p=0.1\mu \mathrm{m}$, the particles near the bubble surface are removed by advection-diffusion (i.e. Brownian motions of particles advected by fluid flow) so quickly that the inertial migration is unable to make up the loss in the near-surface region. The resultant self-decay of diffusional removal leads to transition from this diffusion-driven phase, hereafter called Phase I, to the next phase, Phase II, where the removal rate is determined by inertia alone. The advection-diffusion plays only a passive, secondary role. Although the duration of Phase I is very short for $R_p=0.1\mu \mathrm{m}$, it will increase with decreasing $R_p$. The diffusion layer is clearly visible in the concentration map for $R_p=0.1\mu \mathrm{m}$ (Figure 5(b)) but indiscernible for $R_p=1.0\mu \mathrm{m}$ (Figure 5(a)). This can be explained by one-dimensional consideration of particle transport that predicts the layer thickness to be $\sim D_B/v_t$ where $v_t$ is the inertial terminal velocity perpendicular to the stream surfaces that varies approximately as $R_p^2$. Although the diffusion layer continues to exist, it does not add any resistance or driving force for particle removal. Meanwhile, as the near-surface-peaked concentration profile develops with time, as shown in Figure 5(a) for $R_p=1.0\mu \mathrm{m}$, the concentration gradient in the bubble internal region increases. Therefore, there is a possibility that an inward back diffusion takes place to such an extent that it starts limiting the outward, inertial migration, as suggested by Laker and Ghiaasiaan [23]. This possible situation, Phase III, has not been observed in our simulations.

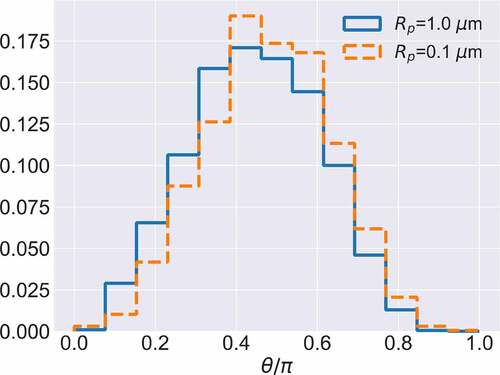
Figure 7 shows a normalized histogram of angular location $\theta /\pi$ at which particles reach the bubble surface. Regardless of particle size, particles tend to be removed near the bubble equator $\theta /\pi =0.5$, where inertial removal is prompted by a high surface velocity and Brownian removal is also accelerated by the increase in concentration gradient caused by dense streamlines. For $R_p=0.1\mu \mathrm{m}$, the histogram is approximately symmetrical with respect to the bubble equator, reflecting the sinusoidal variation of surface velocity $\mathit{U}$ with $\theta$ given by Equations (1)(1) $\begin{array}{c}\psi \left(r,\theta \right)=-\frac{3U_t}{4R_b^2}\left(R_b^2-r^2\right)r^2{sin}^2\theta ,r\le R_b.\end{array}$(1) and (3(3) $\begin{array}{c}\mathit{U}=\mathrm{r}\mathrm{o}\mathrm{t}\left(\frac{\psi }{rsin\theta }{\mathit{e}}_{\phi }\right),\end{array}$(3) ). The histogram for $R_p=1.0\mu \mathrm{m}$, on the other hand, is skewed to show that more particles are removed in the northern hemisphere of the bubble than in the southern hemisphere, suggesting the influence of streamwise ($\theta$-wise) decay of near-surface particle concentration. Kronig and Brink [37] proposed, for advection-diffusion extraction of a substance from a falling droplet, that the concentration of dissolved substance could be taken to be uniform on a given streamline if the characteristic time of diffusion is much larger than the time of circulation along the streamline. This criterion, written as $\mathrm{P}\mathrm{e}\gg 1$, is well satisfied in the present calculations where $\mathrm{P}\mathrm{e}=U_t{R}_b/D_B\gg {10}^5.$ A more restrictive criterion appropriate for the conditions of present calculations will be that the characteristic time of inertial removal $R_b^2/\left({\tau }_p{U}_t^2\right)$ must be much larger than the characteristic time of circulation. This is written as $\mathrm{S}\mathrm{t}={\tau }_p{U}_t/R_b\ll 1$. Since the Stokes number measures the tendency of a particle to inertially deviate from a curved streamline of viscous fluid, in the present problem it measures the progression tendency of inertia-driven particle migration and removal. In fact, the particle removal velocity normal to the bubble inner surface is approximately given by $\mathrm{S}\mathrm{t}\left(\mathit{U}\cdot \mathit{U}\right)/U_t$, as assumed by Fuchs in deriving his inertial removal coefficient ${\alpha }_i$ (Equation (13a)(13a) $\begin{array}{c}{\alpha }_i=\frac{9{\tau }_p{U}_t^2}{2R_b^2},\end{array}$(13a) ). The comparison in Figure 7 between two cases, correspond to $\mathrm{S}\mathrm{t}=8.2\times {10}^{-3}$ for $R_p=1.0\mu \mathrm{m}$ and $\mathrm{S}\mathrm{t}=1.4\times {10}^{-4}$ for $R_p=0.1\mu \mathrm{m}$, suggests that, as the particle removal velocity increases with $\mathrm{S}\mathrm{t}$, the streamwise decline of near-surface concentration becomes significant enough to cause an appreciable shift in particle flux distribution.

Figure 7. Normalized histograms of angular location $\theta /\pi$ at which particles reach the bubble surface, for particle radii $R_p=1.0$ and $0.1\mu \mathrm{m}$.

5. Conclusion

Brownian and inertial removals of aerosol particles from a bubble rising in water have been studied by performing Lagrangian particle tracking simulations. The results have been presented and discussed with a focus on the development of particle concentration profile and its influence on removal rates in conjunction with the interference between the removal mechanisms. Comparison has been made with predictions by Fuchs’s model (1964) used widely although it is based on simplifications including lumped parameter approach for concentration and linear superposition assumption for the influence of different removal mechanisms.

The results from simulations conducted for particles with radii ranging between 0.1 and 1.0 $\mu \mathrm{m}$, moving in a 0.5 mm radius bubble rising steadily at 0.159 m/s can be summarized as follows. Brownian diffusion plays a definitive role only at the very beginning of transient. The rest of the transient is dominated by inertial migration. Fuchs’s model for diffusional removal is unphysical in that it assumes the process to be quasi-steady and unaffected by inertial migration while the real process is highly transient and is quickly integrated into inertial removal. Such fundamental difference results in a significant overprediction of the total removal rate for small $R_p$. The inertial migration produces a near-surface-peaked concentration profile in the bubble that results in faster particle removal than predicted by Fuchs’s model based on a lumped parameter (ideally mixed bubble) approach. It appears that the particle concentration tends to be nonuniform also in the streamwise direction with an increase in particle Stokes number, affecting the distribution of the removal rate on the bubble surface. In summary, the present Lagrangian particle tracking simulations have provided useful information for improved modeling of macroscopic phenomena controlling the particle removal from a rising bubble. The main conclusions summarized above are qualitative and concern the inadequacy of fundamental assumptions in the Fuchs model. Naturally, they are not sensitive to parameter values, but are based on a steady-flow assumption that may provide a reasonable approximation to reality for bubble radii smaller than a few millimeters. The dependence of quantitative results ($1-\epsilon$ vs. time) on particle and bubble parameters represents mixed influence of different mechanisms. We plan to address this problem through dimensional analyses.

Disclosure statement

No potential conflict of interest was reported by the author(s).