Memorization versus conceptual practice with number combinations: their effects on second graders with different types of mathematical learning difficulties

ABSTRACT

The study set out to explore different mathematical difficulties among 877 second-grade children and to test the effect of memorization versus conceptual practices with number combinations. It used a latent profile analysis of baseline measurements of digit writing speed, number combination fluency, multidigit calculation, and number sense skills to identify six latent classes: three mathematical learning difficulty classes, two typical classes, and one high-achieving class. The memorization practice produced superior improvement for all classes of students except the high-achievers class. These results suggest that memorization practice with basic number combinations should not be considered poor teaching practice. It is important for teachers to incorporate practices with number combinations that focus on speed and memorization, even for children who struggle with mathematics.

KEYWORDS:

• Mathematical learning difficulties
• number combinations
• memorization practice
• conceptual practice
• latent profile analysis

This study takes as a starting point the notion that fluency with number combinations is an important mathematics skill (Loewenberg Ball et al., 2005; NMAP, 2008; Schoenfeld, 2004). However, such fluency (arithmetic facts) is a well-known challenge for children with mathematical learning difficulties (Reigosa-Crespo et al., 2012). Although researchers may have reached a consensus on the importance of building fluency with number combinations, they continue to debate which type of practice is best suited to obtain this fluency. One side argues that children should focus on concepts first; then when they have mastered number concepts, they can move on to drills and practice exercises that are meaningful and not just rote memorization (Baroody et al., 2009; Boaler, 2015; Henry & Brown, 2008; NCTM, 2014). The other position argues that both conceptual and procedural learning play important roles in building fluency with number combination (NMAP, 2008). Several studies support the use of timed exercises (e.g., Baroody et al., 2014; Fuchs et al., 2021). Rote memorization is, however, viewed as an unproductive approach in mathematical teaching (NCTM, 2014). This debate merits empirical investigation. Few studies have explicitly evaluated memorization versus conceptual practices, that is, untimed exercises that only focus on understanding (e.g., Fuchs et al., 2013), and no study has investigated this issue in relation to learners with different levels of achievement (mathematical learning difficulties, low achievement, typical achievement, and high achievement).

The purpose of the study was twofold: first, to test the effects of memorization and conceptual practices on the development of number combinations (NC) skills among second graders, and second, to compare the results of the two interventions in different achievement groups.

Mathematical learning difficulties

Children are considered to have a mathematical learning difficulty (MD) if they are underachieving in mathematics, often defined by standardized or non-standardized test scores. To be able to develop effective instruction for children with MD, it is important to understand the variety of reasons why a child may have MD: the main ones being school absences, poor teaching, and cognitive deficits (Lewis & Fisher, 2016). If a child’s MD is linked to a cognitive deficit, it may be that the child has a specific learning disorder. When screening children for MD, the focus should be on number sense skills and calculation skills as these skills are primary indicators of MD regardless of underlying factors (Gersten et al., 2011; Rousselle & Noël, 2007; Träff et al., 2017). Thus, children with MD are usually identified by using test score cut-offs on either a single measure or multiple measures of number sense skills and or arithmetic ability (Lewis & Fisher, 2016; Rousselle & Noël, 2007; Träff et al., 2017). Previous research has classified two groups of children with MD: children with mathematical learning disabilities (MLD) and low-achieving (LA) children (Murphy et al., 2007). Murphy et al.’s study identified different profiles between the MLD and LA groups in terms of mathematical achievement. However, the overlap between the MLD and LA groups is large, and it is possible that the two groups are part of an achievement continuum (Geary et al., 2012). In intervention studies, MLD and LA are often considered within the same difficulty group, defined as achievement scores below the 25th percentile (Dennis et al., 2016). Children with MLD have difficulties with fluent retrieval of NC and number processing, and these kinds of problems result in great difficulties in arithmetic skills (Geary et al., 2012). NC dysfluency is a type of MD that is three times more common than MLD, with a prevalence estimate of 9.35% compare to 3.4% (Reigosa-Crespo et al., 2012). Several prevalence studies indicate that around six percent of students have MLD (Devine et al., 2013, 2018). Furthermore, Morsanyi et al. (2018) showed that between grades four and seven this prevalence decreases from 7.4% to 3.8%.

Achievement heterogeneity

An alternative to the cut-off approach is to use the whole sample distribution and apply latent variable analysis to identify different achievement groups. Several longitudinal studies focusing on kindergarteners have employed latent variable analysis (Geary et al., 2009; Hong & You, 2012; Wong et al., 2014; Zhang et al., 2020). These studies found that the best models had 4–5 achievement classes, including a MLD class and a LA class. In these four studies, the MLD class accounted for 6–10% of the sample, while the LA class accounted for 17–50% of the sample.

Swanson et al. (2018) looked at cross-sectional data from 447 third graders at risk of MLD, also considering reading ability and intelligence together with calculation and problem-solving, to determine whether a unique latent class existed. They found that a three-class solution had the best model fit, with one class identified as average achievers, a second class identified as at risk for MLD, and a third class identified as poor problem solvers. The number of students in the MLD risk class constituted around 10–15% of the sample.

In summary, the above research demonstrates that latent variable analysis is an effective approach for identifying different achievement groups. This study, similar to prior research, used a number combination test, a multidigit mental calculation test, and a number sense skills test, along with digit-writing speed test. This test was included for two reasons: first, the number combination test required the children to write their answers, and so to control for writing speed, the writing digit test was incorporated. Second, research has indicated that both fine motor skills and number writing skills can be an important predictor of arithmetic skills (Clayton et al., 2020; Raghubar et al., 2015), and the digit-writing speed test has the potential to measure both number-writing skills per se and fine motor skills.

Practice with number combinations

Several studies have investigated the effect of different type of practices in children with mathematical learning difficulties. Burns et al. (2015) used a single-case methodology to investigate procedural versus conceptual teaching in relation to students with difficulties learning basic arithmetic in the first through third grades. Their results show that the efficacy of the intervention (conceptual or procedural) depended on whether the student exhibited conceptual or procedural difficulties. Although the study was a single-case study, it suggests that children can have either conceptual or procedural difficulties with number combinations. For children with conceptual difficulties, interventions should focus on conceptual issues, and on procedural issues for children with procedural difficulties.

Tournaki (2003) tested strategy-focused instruction versus A drill-and-practice procedure in second graders and compared these to a control condition. The researcher examined the effect of eight sessions on children with MLD and children without MLD. Strategy instruction involved teaching the minimum addend strategy (starting with the larger number and adding the smaller number by counting). Drill and practice used two forms of tasks that should be solved during a lesson. The lesson time for both conditions was 15 min. The results showed that children with MLD obtained better results following strategy-focused instruction than they with drill and practice (Cohens d = 1.52). In the drill-and-practice condition, children with MLD performed worse than children without MLD (Cohens d = 0.73). This was not the case in strategy-focused instruction. Both drill and practice and strategy-focused instruction were better than the control condition, regardless of whether the child had MLD or not (Cohen’s d = 1.53 for strategy and 1.35 for drill and practice). The results seem to favor strategy-focused instruction over drill and practice, although both conditions did emphasize speed during practice. In another study, Fuchs et al. (2009) compared two tutoring programs, one focused on drills and fluency practice and another that included conceptual instruction (Pirate Math) but also entailed some fluency training. The results showed that pure fluency training (Cohen’s d = 0.55 compared to a control group) was as good as fluency and conceptual tutoring (Cohen’s d = 0.62 compared to control group) for NC skills. Fuchs et al. however, used memorization-focused fluency training (e.g., timed drills) in both condition groups, and the fluency practice included some conceptual aspects. Thus, it is not possible to fully evaluate the different effects of conceptual instruction versus and memorization practice on children’s fluency with NC.

Baroody et al. (2014) investigated the differences between the effects of unguided practice, guided practice with a use-a-ten strategy, and guided subtraction practice on first graders’ fluency with basic subtraction and addition combinations. The training was carried out using a computer program that followed five steps, the first two of which were identical and prepared the children for the next three steps. In the unguided practice, the children solved and practiced number combinations without any guidance. In the use-a-ten strategy guided practice teachers guided and instructed the children to associate “add with eight and nine combinations” with combinations that involved sums of ten. In guided subtraction version, the teachers guided and instructed the children to use addition to solve subtraction combinations. The study found that the guided subtraction practice was superior in improving fluency with untrained number combinations (Hedges’ g = 0.50 vs. use-a-ten, and 0.45 vs. unguided). However, the guided subtraction and unguided practice groups outperformed the use-a-ten strategy group for fluency with trained number combinations (Hedges’ g = 1.46 and 0.95, respectively). The study found no difference between the guided and unguided groups. The authors concluded that using addition to solve a subtraction combination can be one way of achieving meaningful memorization. However, all three study conditions included timed training, and therefore no explicit conclusions can be made about the significant of timed versus untimed practice when practicing NC.

Greene et al. (2018) investigated the effect of fluency training in third- and fourth-grader students tutored by fifth-grade peers using NC on flash cards. The training was carried out three times a week, 30 min each session, for eight weeks. The intervention focused primarily on memorization, using timed drills, and encouraging the children to respond as accurately and quickly as possible. The control group received conventional lessons. The study detected a major positive effect from fluency with number combinations intervention (Cohen’s d = 1.77). The sample was small, however, with only 15 children in the intervention group and 14 in the control group. Nevertheless, the study showed that adding procedural fluency training enhances fluency.

Fuchs et al. (2013) tested a tutoring program for at-risk first graders. Tutoring took place outside the regular classroom, in the form of 30-minute one-on-one sessions, three times a week. The lessons had the same conceptual number knowledge focus but differed in terms of the individual procedural aspect, which took up five minutes out of each session. The study randomized 300 low-risk children and 206 at-risk children to the control condition, 195 at-risk children to the timed practice, and 190 at-risk children to untimed practice. The results showed that both tutoring conditions were favorable compared to the no-tutoring condition, but the timed condition (memorization-focused) training was superior to the untimed training condition (Cohen’s d = 0.43). In 2019, Fuchs et al. reanalyzed the results to test whether students’ pre-intervention skills in math could determine whether they responded to the intervention. They found no support for a relationship between pre-intervention skills and strength of response to the intervention.

Overall, prior research suggests that using some memorization training enhances children’s fluency with number combinations. However, only one study has compared timed versus untimed practice, and its results indicate that timed exercises are an important aspect of training fluency with number combinations (Fuchs et al., 2013).

Although these studies suggest that both memorization and conceptual training are recommended, some researchers have argued that timed drills and a focus on memorization could be harmful to children’s development of fluency with number combinations. It is imperative to investigate this notion empirically, as the argument against memorization training of number combinations seems to be primarily inferred from theory rather than empirical research (e.g., NCTM, 2014).

The present study

This study addressed three research questions. The first question was to investigate and compare the effects of memorization versus conceptual practice on the development of NC skills in second-grade students. The second question asked what kinds of MD might be detected from baseline measurements using latent profile analysis. Specifically, the study aimed to empirically evaluate the distinction between an MLD group and an LA group. The third question asked whether the effect of memorization versus conceptual practice on the development of NC fluency differed depending on children’s mathematical achievement level, as defined in the latent profile analysis.

Method

Participants

Written consent was obtained from the legal guardians of 877 Swedish children (408 girls) from 20 schools, with a mean age of 8.22 years (SD = 0.53). The researchers used an index provided by the municipality to assess socioeconomic status (SES). The index measured the number of children with parents who only had only a junior high school education (grades 1–9) compared to the whole municipality. The participating schools had indices ranging from 0 to 3.5: zero indicates that the number of children with parents who only attended junior high school did not differ from the mean number in the municipality. An index of 3.5 means that 3.5 times as many students had parents with only a junior high school education compared to the whole municipality. The participants in the memorization condition came from slightly higher index schools (F (2, 873) = 6.94, p = .001, partial η²= 0.02), but we detected no differences between the control group and the other two conditions. This means that the children in the memorization condition were, on average, slightly more disadvantaged in terms of SES compared to the children in the conceptual condition.

Project organization

The project was a collaboration between the municipality and university researchers. The main project group consisted of three researchers and three teachers involved with developing mathematics teaching at the central level. Each project group member was assigned several schools, which they had weekly contact with. The project group met each week to discuss implementation issues to ensure that the fidelity of the program was high.

Procedure

Initially, 33 school principals indicated that they wanted to participate in the study. The final sample consisted of 5 control schools, 7 memorization schools, and 8 conceptual schools (see supplemental materials, Figure S1). The schools that dropped out before the project started did so mainly due to organizational problems, such as understaffing or involvement with other projects. Some dropouts during the intervention phase related to the above-mentioned issues, which did not become evident at that school until the project had started. Some dropout schools also have more specific reasons for dropping out, such as the testing being complicated, the different tasks in the booklet not being of sufficient quality, feeling that the children were not developing their skills, and concern that the project was too time consuming. When we reviewed the data, we found that none of the more specific reasons was connected to the children’s actual performance. Children at the schools that dropped out developed at a reasonable rate, and we suspect that the above-mentioned reasons were primarily an effect of the teachers’ feelings about the project. Some of the dropouts were due to unrelated reasons (e.g., one school was damage by fire). The project started with a preparation week, during which teachers explained the various parts of the project and testing, and training took place. The children were also able to do the digit speed test during this week to train for the test procedure. The children were encouraged to do their best throughout the project.

Research design and experimental conditions

The schools’ representatives reported that it was impossible to rearrange classes, and it would have been impossible for each school to administer all three conditions (control, conceptual, and memorization) in parallel. Due to these practical reasons, we used a cluster-randomized design with schools being the level of randomization.

Each of the experimental conditions was offered three times a week at the end of the ordinary math lesson, for 15 min each session. The study included fourteen 15-minute lessons. The regular teachers implemented the experimental conditions following a pre-written lesson plan and using exercise booklets during practice (see supplemental material). The key features of the intervention were explicit instructions from the teacher (5 min) and individual exercises using the exercise booklet (10 min). The booklets and lesson plan were developed with the help of math teachers who were recognized by the municipality as being highly competent. The teachers ensured that the conceptual practice condition and memorization practice condition were up-to-date in terms of how the practice was to be performed. In total, 210 min of teaching was offered over five weeks; and of these 210, 140 min were allocated to working with the booklet that the experimental groups used. At the time of the intervention, the schools reported that they focused on arithmetic with addition and subtraction, with and without carrying over tens, in the range up to 1,000. The present intervention focused on number combinations up to 10 and therefore represented an area of knowledge that all the children were already somewhat familiar with.

Conceptual practice

The students worked through the exercise booklet without any time limit. Teachers instructed and encouraged them to use manipulatives and the visual aids in the booklet. Students were given the message that they should try to understand each problem. Different types of tasks were used (see supplemental material – for example, Figure S2). The children used pictures to do the calculation task, as shown in Figure S2. No symbolic digit was visible in some of the tasks, while other tasks used both pictures and symbolic digits. The children could use either symbols or pictures to solve some of the tasks. An important feature of the conceptual training was access to concrete manipulatives and pictures that supported an analog representation of a numerical expression.

Memorization practice

The children worked through each exercise booklet in two blocks. The exercises were timed by the teacher, allowing two minutes for each block. Teachers encouraged the students to do as many tasks as they could during the two minutes, and they gave the students the message that they should try to memorize the answers as quickly as possible. The tasks used only symbolic digits (see supplemental material Figure S3 for an example of the tasks), and the children were given the correct answers after each block.

Control group

The control group received conventional teaching that involved both procedural and conceptual training with respect due arithmetic’s content relevant to the age group. Thus, they worked with similar content as the experimental conditions. Teachers in the control group did not receive instruction from the research group regarding instruction method and content of the lessons.

Fidelity

The researchers ensured intervention fidelity by using preplanned lesson plans for the teachers and booklets for the children. All teachers also had written information about the project and knew what the project team expected from them as participants. The researchers contacted the schools each week via email correspondence and phone calls or personal visits and meetings with participating teachers to check fidelity. Many of the schools that had problems adhering to the plan did drop out before randomization or during the intervention phase (see Figure S1). The schools that continued in the program had effective communication with their project group contact person.

Measures

The authors developed four paper-and-pencil measures for administration in the participating classrooms: digit writing speed, number combinations (NC), multidigit mental calculation (MMC), and number-sense skills (NSS). The teachers and children prepared and trained for these test procedures in the week prior to testing. Films showed what the students should do, and a nine-year-old child modeled the procedure. The researchers provided written instructions to teachers during the preparation phase, as well as verbal reinforcement, if necessary, to ensure the fidelity of the testing procedure. Digit writing speed and NC fluency tests were administrated five times, with the order of items varying between measurement timepoints.

Digit writing speed test

The students were presented with a left-hand column of digits and instructed to write the same digits in the right-hand column: e.g., 3 = ___. The dependent measure was the number of digits written correctly during a 60-second interval. Following the guidelines of Koo and Li (2016) the ICC estimates and their confidence interval were calculated using SPSS version 28 based on a mean-rating (k = 5), absolute-agreement, 2-way mixed-effects model. For digit writing speed the ICC was .85, 95% CI = .81–.88 indicating good reliability.

Number combinations

The students were asked to solve basic addition (e.g., 3 + 1) and subtraction (e.g., 3–1) problems with a time limit of one minute, working through the problems as quickly as possible. The dependent measure was the total number of correct answers, and the maximum score was 36. Following the guidelines of Koo and Li (2016) the ICC estimates and their confidence interval were calculated using SPSS version 28 based on a mean-rating (k = 5), absolute-agreement, 2-way mixed-effects model. For number combinations the ICC was .94, 95% CI = .92–.96 indicating excellent reliability.

Multidigit mental calculation

This test consisted of 26 multidigit addition and subtraction problems (e.g., 73 + 12, 15–9) presented in ascending order of difficulty. The first problems were single-digit. No time limit was set, but teachers encouraged the children to do their best and work through the problems without spending too much time on problems if they got stuck. The maximum score was 26. The Cronbach’s alpha, based on scores from 203 children, was .91.

Number-sense skills

The number-sense skills test included number patterns problems, questions on the ten-base system, counting skills, comparison of the magnitude of digits (e.g., “which number is numerically larger?”), and number line estimations. No time limit was set, teachers encouraged the children to work through the problems and not spent too much time on one problem. The maximum score was 22. The Cronbach’s alpha, based on scores from 203 children, was .85.

Analytic approach and statistical analysis

We ran an a priori power calculation via ANCOVA using the G*Power software (version 3.1) to establish the number of participants needed to detect an effect size of 0.15 (η²) for the main intervention. With alpha set to .05 and power set to .80, the number of participants needed was 432. The primary analytical models were fitted using the Mplus software (version 8.4). We used three different sets of analytical models to answer the research questions. First, we tested whether there was an overall effect from the training over time using latent growth curve modeling. The practice conditions were contrast coded so we could compare intervention vs. control (contrast 1), and memorization practice vs. conceptual practice (contrast 2). We then fitted a linear growth model, in which the slope was regressed on the two contrast variables and the intercept in order to control for students’ initial ability level (similar to ANCOVA). Effect sizes, in the form of standardized mean differences (d), were derived from model-implied means (Feingold, 2009). We used non-normality robust maximum likelihood (MLR option in Mplus) to deal with missing data following the missing-at-random assumption, and we used the same procedure to obtain accurate standard errors under deviations from normality.

We then constructed a series of latent profile analyses (LPA) models to investigate potential subgroups of mathematical abilities at baseline. The LPA process reduces students’ heterogeneous baseline abilities to a discrete set of homogeneous, unobserved (latent) subgroups based on covariation among the observed scores for the various measures (digit writing speed, number combination skills, number sense skills, and multidigit mental calculation). We compared models with a different numbers of classes empirically using three statistical methods for measuring goodness-of-fit: Bayesian Information Criterion (BIC; Schwartz, 1978), sample size adjusted BIC (SSABIC) and Akaike’s Information Criterion (AIC; Akaike, 1987) With each of these methods, a lower score indicates a better fit. We used the Lo-Mendell-Rubin adjusted loglikelihood ratio test (Lo et al., 2001) to compare successive models; with this test, a significant loglikelihood ratio indicates that the model with more classes provides a better fit for the data. We also calculated entropy values for each LPA model, where high values indicate a reduced risk of misclassifying individuals (i.e., better classification quality).

Finally, once the number of classes at baseline was empirically determined using LPA, we proceeded to test the effect of the training conditions as a function of these classes (i.e., moderation). We used latent growth curve modeling to model change in NC fluency. We also included the classes and conditions, and their multiple interactions, as fixed-effect predictors of intercept (initial level) and linear slope to estimate whether the effect of training on changes in fluency varied as a function of class.

Due to the nesting of the data – that is, children nested in classrooms – we calculated intra–classroom correlations (ICCs) in this field experiment to provide an estimate of the design effect. The ICCs for the post-intervention NC fluency measurement point was .12. Given that clustering can affect standard errors, we re-estimated the growth model, controlling for the nesting of students within classrooms (using type Complex in Mplus) and compared it with a model without such a correction. The results were almost identical, with estimates differing only at the third decimal place. We therefore concluded that the nesting effect could be ignored, and we therefore present the models without corrections.

Results

Overall effect of the intervention conditions on number combination skills

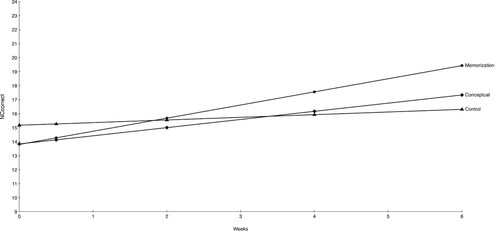
For the number combinations measure, a linear growth model displayed a statistically significant effect with contrast 1, unstandardized beta = 0.60, SE  = 0.07, p < .001, d = 0.57 (95% CI 0.44–0.71). Contrast 2 on the linear slope also revealed a statistically significant effect, unstandardized beta = 0.36, SE = 0.06, p < .001, d = 0.34 (95% CI 0.23–0.45). These results indicates that the two practice conditions outperformed the control condition, with the memorization condition outperforming the conceptual condition, irrespective of the students’ baseline mathematical abilities. Figure 1 depicts the overall effect of the interventions over time.

Figure 1. The effects of memorization and conceptual practice and control condition on NC.

Note. NC = number combinations.

Fit statistics and the selection of latent class solution

Table 1 presents descriptive statistics for the baseline latent class indicators, and material Table S1 in the supplemental material summarizes the fit statistics for the LPA models that were fitted, ranging from one to seven models. The six-class solution yielded the best overall fit, with a high entropy (.83, which reflects good classification quality) and fit significantly better than solutions with fewer classes.

Table 1. Descriptive sample statistics for the data used in the latent profile analysis.

Measure	Mean (n)	SD	Min-Max	Skewness	Kurtosis
Digit writing speed	31.96 (819)	6.30	2–36	–1.69	2.31
Number combination fluency	13.94 (820)	6.33	1–36	1.06	1.91
Number sense skills	12.86 (767)	5.16	0–25	–0.32	–0.72
Multidigit mental calculation	15.56 (734)	6.13	0–26	–0.42	–0.59

Interpretation of the latent classes

Table 2 lists the means and standard deviations for the baseline assessment indicators (timepoint 1) for each class, based on the six-class LPA model. Figure S4 presents the model-implied means for each indicator as a function of class. This final model yielded two latent classes of MD students and one small class of MLD students (3.8% of the sample) whose performance level was low on all measurements compared to the other classes. The first of the two MD classes was relatively large (23.6%) and consisted of students whose performance profile showed they were fast at writing digits (on par with typical achievers, TA) but performed poorly on the number sense and multidigit mental calculation tests. They also performed better at number combinations than the class with MLD. This class was labeled fast low achievers (FLA) due to their stronger digit-writing speed and weaker achievement in the math skills tests. The second class of MD students was labeled low achievers (LA) because their test scores were not as low as the MLD class but were lower overall compared to typical achiever class.

Table 2. Descriptive statistics for the six-class solution.

Class	N (% of the sample)	Mean (SD)
		Speed (1.54)	NC (4.06)	NSS (4.25)	MMC (4.92)
1 MLD	30 (3.8)	12.59	7.12	9.13	9.51
2 FLA	205 (23.6)	35.41	11.12	9.03	10.94
3 LA	87 (10.4)	21.09	9.79	10.80	12.60
4 TA	353 (38.9)	35.62	16.09	15.72	18.77
5 HA	43 (5.5)	35.95	30.59	16.40	21.18
6 STA	147 (17.7)	28.57	11.65	12.16	14.69

Note: MLD = mathematical learning disability, FLA = fast low achievers, LA = low achievers, TA = typical achievers, HA = high achievers, STA = slow typical achievers, NC = number combinations, NSS = number sense skills, MMC = multidigit mental calculation.

In the final six-class solution, we also identified two classes without MD or MLD: typical achievers (TA, 38.9% of the total sample) and slow typical achievers (STA, 17.7% of the total sample). The overall performance of the latter group was lower than that of the TA class but higher than the MLD, FLA, and LA classes. Students in the STA class could be misidentified as having math learning difficulties based on their performance profile. Finally, the model also included one class of high achievers (HA, 5.5%), with an overall performance profile that was higher than that of all other classes. The three difficulty classes accounted for 37.8% of the sample, while the typical classes made up 56.6% of the sample (see the supplemental material Figure S4 to see a more detailed breakdown by class.)

Do the effects of memorization and conceptual practices differ for children with mathematical learning difficulties at baseline?

To answer the third research question, the researchers developed a second growth model that used two contrast variables – C1, practice conditions vs control, and C2, memorization vs conceptual practice – five dummy-coded class variables (with the TA class as the reference), and contrast * dummy-coded class interaction as predictors of the model’s intercept and linear slope. Table 3 presents the results of the model.

Table 3. Results of a linear growth model examining the conditional effect of training.

Paths	Unstandardized beta (SE)	p-value	Cohens d	95% CI for d
				LL	UL
Intercept on control vs EXP	−0.75 (0.33)	.024	−0.12	−0.22	−0.02
Intercept on conceptual vs memorization	−0.28 (0.30)	.354	−0.04	−0.14	0.05
Intercept on TA vs MLD	−9.36 (0.74)	<.001	−1.48	−1.68	−1.28
Intercept on TA vs FLA	−5.84 (0.35)	<.001	−0.92	−1.03	0.82
Intercept on TA vs LA	−6.52 (0.47)	<.001	−1.03	−1.17	−0.89
Intercept on TA vs HA	13.60 (0.64)	<.001	2.15	1.95	2.36
Intercept on TA vs STA	−4.99 (0.38)	<.001	−0.79	−0.91	−0.67
Slope on intercept	0.09(0.01)	<.001	0.08	0.06	0.10
Slope on control vs EXP	0.80 (0.11)	<.001	0.76	0.55	0.97
Slope on conceptual vs memorization	0.40 (0.10)	<.001	0.38	0.19	0.57
Slope on TA vs MLD	0.58 (0.18)	.001	0.55	0.22	0.89
Slope on TA vs FLA	0.46 (0.10)	<.001	0.43	0.24	0.63
Slope on TA vs LA	0.29 (0.10)	.017	0.27	0.08	0.46
Slope on TA vs HA	−1.56 (0.27)	<.001	−1.48	−1.96	−0.98
Slope on TA vs STA	0.24 (0.09)	<.001	0.23	0.06	0.40
Slope on control vs EXP * TA vs MLD	−0.21 (0.33)	.416	−0.20	−0.67	0.28
Slope on control vs EXP * TA vs FLA	-.41 (0.18)	.021	−0.40	−0.73	−0.06
Slope on control vs EXP * TA vs LA	−0.51 (0.18)	.005	−0.48	−0.81	−0.15
Slope on control vs EXP * TA vs HA	−0.70 (0.41)	.090	−0.66	−1.42	0.10
Slope on control vs EXP * TA vs STA	−0.11 (0.19)	.461	−0.11	−0.39	0.18
Slope on conceptual vs memorization * TA vs MLD	−0.20 (0.33)	.591	−0.19	−0.87	0.50
Slope on conceptual vs memorization * TA vs FLA	0.08 (0.15)	.603	0.08	−0.21	0.36
Slope on conceptual vs memorization * TA vs LA	−0.12 (0.20)	.472	−0.11	−0.41	0.19
Slope on conceptual vs memorization * TA vs HA	−0.27 (0.32)	.538	−0.26	−1.09	0.57
Slope on conceptual vs memorization * TA vs STA	−0.08 (0.17)	.652	−0.07	−0.38	0.24

Note: CI = confidence interval, LL = lower limit, UL = upper limit, TA = typical achievers, MLD = mathematical learning disability, FLA = fast low achievers, LA = low achievers, HA = high achievers, STA = slow typical achievers.

To test whether these latent classes helped account for variability in outcomes beyond the overall effects of the interventions, the researchers used a constrained model in which the main effect of the class variables and their interactions with the experimental conditions were set to zero and then compared to a model in which these effects were freely estimated. A Satorra-Bentler scaled chi-square difference test for model comparison was 852.01, which is statistically significant (df = 20, p < .001) and indicates that the latent class variables did, in fact, account for a significant amount of variation in outcome beyond the overall effect of intervention training. Thus, individual differences in initial math ability accounted for a significant amount of the variation in number combination development.

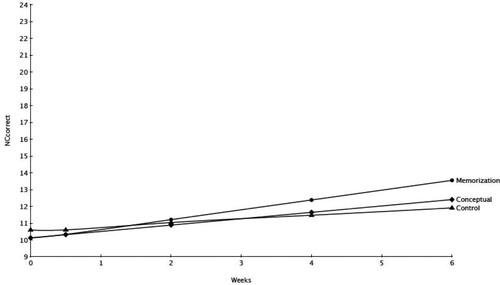
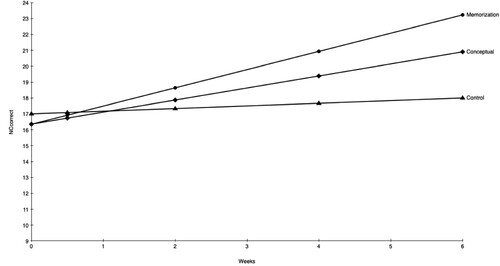
The main effects of class were also evident: the MD and MDL classes, as well as the STA class, improved at a greater rate over the course of the study compared with the typical class, irrespective of the training condition. The HA class, in contrast, improved at a slower rate than the TA class. In addition, there was some evidence that the effect of training depended on class. Two-way interaction effects between the first contrast (training vs. control) and class were statistically significant for the FLA and LA classes. This indicates that the experimental effect of training (relative to the control group) was stronger in the typical group than in the other classes. However, this effect primarily reflected the lower effectiveness of the conceptual training condition. A post hoc analysis revealed that the memorization condition had a steeper slope of improvement than the control group for both the LA class (p = .009, d = 0.42) and the FLA class (p < .001, d = 0.71), but no such difference was detected for the conceptual training condition for either the FLA class (p = .263, d = 0.18) or the LA class (p = .156, d = 0.20). Figures 2 and 3 depict the mean trajectory as a function of both condition and class for the LA and TA classes (see supplemental material Figure S5 for FLA class). There were no statistically significant two-way interaction effects that included contrast 2 (i.e., conceptual vs. memorization training).

Figure 2. The effects of memorization and conceptual practice and control condition on NC in the LA class.

Note. NC = number combinations, LA = low achievers.

Figure 3. The effects of memorization and conceptual practice and control condition on NC in the TA class.

Note. NC = number combinations, TA = typical achievers.

Discussion

This study investigated and compared the effects of memorization versus conceptual practice on the development of NC skills in second-grade students. Secondly, what kinds of MD achievement classes could be detected from baseline measurements using latent profile analysis. Thirdly the study tested if the effect of memorization versus conceptual practice on the development of NC fluency differed depending on children’s mathematical achievement level, as defined in the latent profile analysis. The overall effect of the different practice conditions suggests that the memorization condition was the superior way to practice number combinations. This implies that memorization should not be viewed as a poor form of practice (Baroody et al., 2009; Boaler, 2015; Henry & Brown, 2008; NCTM, 2014), and in fact should be viewed as a good form of practice. This aligns with findings in previous studies that included memorization practice in their interventions (Baroody et al., 2014; Burns et al., 2015; Fuchs et al., 2009; Tournaki, 2003). It is important to note that these previous studies did not contrast memorization and conceptual practices and instead incorporated memorization into all their conditions.

One purpose of the study was to explore what kinds of MD we could identify in the sample group and evaluate the effects of two different types of NC practice on different classes. We expected to find at least two classes of MD: one corresponding to MLD and one corresponding to low achievement, a model in line with Murphy et al.’s (2007) seminal paper. Instead, we found three classes of students with difficulties (MLD, FLA, and LA) and one class of students that could be mistaken for having math difficulties (STA). This finding supports the critique of using cut-off scores to determine whether children have difficulties (Lewis & Fisher, 2016). We would not have been able to identify three classes of students with difficulties and two types of typical achieving students using cut-off scores. The MLD class appears to be similar to Reigosa-Crespo et al.’s (2012) developmental dyscalculia group, suggesting that the prevalence of MLD among second graders is lower than the six percent that researchers often suggest (Morsanyi et al., 2018). Instead of one group of LA, our findings suggest two groups: one that is fast at writing digits despite otherwise low achievement (FLA) and one group of overall low achievers. The two LA classes together make up 34% of the sample. This is a higher percentage than previous research using cut-off scores suggests (Cowan & Powell, 2013; De Smedt & Gilmore, 2011; Geary et al., 2008; Murphy et al., 2007). It is possible that studies designed using cut-off scores underestimate the number of children in the LA group. One previous study using latent class analysis found a considerable higher prevalence of LA, e.g., 50% (Geary et al., 2009). Hong and You (2012) also estimated the low achieving class as accounting for 52% of their sample. Other studies that have used some type of latent class/profile analysis have estimated the low achieving class at around 25% (Swanson et al., 2018; Zhang et al., 2020). However, this is the first study to separate the LA class into two subgroups: FLA and LA This is probably due to the inclusion of the digit writing test. Digit writing is a test that can capture both fine motor skills and number writing skills, which are predictors of arithmetic skills (Clayton et al., 2020; Raghubar et al., 2015); it is therefore important to include this measure in such analyses. The present study is also the first to separate the typical achiever class into two distinct sub-classes: STA and TA. Our identification of an HA class is in keeping with the findings of previous studies.

Do memorization and conceptual practices have different effects depending on whether children have mathematical difficulties and what type they have? The present study finds clear evidence that memorization practice is an effective practice for all children, including those with mathematical difficulties. This finding adds to the work of Fuchs et al. (2013) and Greene et al. (2018), who have previously shown that memorization is an effective practice for children with mathematical difficulties. It is important to further investigate whether any of the subgroups of children or types of difficulties do not benefit from memorization training. All the evidence supports the use of memorization practice for students of all mathematical learning classes except for the HA class. No previous study has contrasted different practice and different achievement classes, and therefore our demonstration of a positive effect from memorization is a novel finding in the literature on this topic.

The present study has several limitations that the reader should be aware of. First off, attrition was high, with a dropout level that was unfortunately so high that the study should be considered a quasi-experimental study rather than being a randomized controlled trial. The drop out was evenly distributed between conditions so it should not have impacted the result. The large number of missing data points is also a limitation in the present study. A third limitation is the lack of power for examining the impact of the interventions on the MLD class. However, considering that the memorization practice had clearly superior effects on the other difficulty classes, it is probably fair to assume that the MLD class may have the same outcome pattern as the FLA and LA classes. It is important to note that our identification of different classes of MD is exploratory in nature, and it will be important that future research seek to validate the six achievement classes found here. Future research could also investigate in more depth whether memorization and conceptual practice have different effects among the different difficulty classes, and especially for students with MLD, class, due to the low power in the present study. Future research could also include measures on cognitive abilities to further investigate why memorization practice is superior compared to conceptual practice with number combinations.

These results emphasize the importance of practicing NC with speed, and its findings contribute a degree of nuance to the debate over rote memorization as a training practice. Our study is the first to contrast conceptual practice without a speed element and memorization practice, and our results suggest that practices focusing on rote memorization of NC is the best practice for most children, except for high achievers who have already attained a high level of automation. Teachers should incorporate timed memorization when planning their NC training practices.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Swedish Research Council by a grant, 2016-05287, awarded to the first author. We have no conflict of interest to disclose.