Bayesian Design of Experiments Using Approximate Coordinate Exchange

ABSTRACT

The construction of decision-theoretical Bayesian designs for realistically complex nonlinear models is computationally challenging, as it requires the optimization of analytically intractable expected utility functions over high-dimensional design spaces. We provide the most general solution to date for this problem through a novel approximate coordinate exchange algorithm. This methodology uses a Gaussian process emulator to approximate the expected utility as a function of a single design coordinate in a series of conditional optimization steps. It has flexibility to address problems for any choice of utility function and for a wide range of statistical models with different numbers of variables, numbers of runs and randomization restrictions. In contrast to existing approaches to Bayesian design, the method can find multi-variable designs in large numbers of runs without resorting to asymptotic approximations to the posterior distribution or expected utility. The methodology is demonstrated on a variety of challenging examples of practical importance, including design for pharmacokinetic models and design for mixed models with discrete data. For many of these models, Bayesian designs are not currently available. Comparisons are made to results from the literature, and to designs obtained from asymptotic approximations. Supplementary materials for this article are available online.

Keywords:

• Computer experiments
• Gaussian process emulator
• High-dimensional design
• Smoothing

1. Introduction

Bayesian design of experiments is a natural paradigm for many problems arising in the physical sciences and engineering, particularly those concerning the estimation of nonlinear models where design performance, as measured by classical optimality criteria, is dependent on the a priori unknown values of the model parameters. A decision-theoretic approach, reviewed by Chaloner and Verdinelli (1995), determines an optimal allocation of experimental resources via maximization of the expected utility (1) $$U\left(\mathit{}\mathbf{\delta }\right)=\int {\int }_{\Psi ,\mathcal{Y}}u(\mathit{}\mathbf{\delta },\mathit{}\mathbf{\psi },\mathbf{y})\pi (\mathbf{y},\mathit{}\mathbf{\psi }|\mathit{}\mathbf{\delta })d\mathbf{y}d\mathit{}\mathbf{\psi }.$$(1) Here, the utility u(δ, ψ, y) quantifies the experimenter's gain from using design $\mathit{}\mathbf{\delta }\in \mathcal{D}$ to obtain data $\mathbf{y}\in \mathcal{Y}$ assuming model parameter values ψ ∈ Ψ, with the statistical model defined through the joint density function π(y, ψ | δ) = π(y | ψ, δ)π(ψ). As an example, assume the ith response is modeled as y_i = g(x_i; θ) + ϵ_i with the x_i defining values taken by a controllable variable, θ being a vector of unknown parameters defining the mean response, and observation error ϵ_i ∼ N(0, σ²) (i = 1, …, n). Then ψ^T = (θ^T, σ²), δ = (x₁, …, x_n)^T, and likelihood π(y | ψ, δ) is a multivariate normal density function. The utility function u(δ, ψ, y) will typically be a function of some posterior quantities of ψ (see Section 3.1).

Selection of a fully Bayesian optimal design ${\mathit{}\mathbf{\delta }}^{★}=\text{arg}{\text{max}}_{\mathit{}\mathbf{\delta }\in \mathcal{D}}U\left(\mathit{}\mathbf{\delta }\right)$ has traditionally been challenging for all but the most straightforward utility functions and models due to the high-dimensional and, typically, analytically intractable integrals in (1(1) $$U\left(\mathit{}\mathbf{\delta }\right)=\int {\int }_{\Psi ,\mathcal{Y}}u(\mathit{}\mathbf{\delta },\mathit{}\mathbf{\psi },\mathbf{y})\pi (\mathbf{y},\mathit{}\mathbf{\psi }|\mathit{}\mathbf{\delta })d\mathbf{y}d\mathit{}\mathbf{\psi }.$$(1) ). Some recent progress has been made using simulation-based methodologies for low-dimensional problems, that is, small numbers of controllable variables and/or small numbers of design points, see Ryan et al. (2016) and references therein. There are, however, no methods available for decision-theoretic Bayesian optimal, or near-optimal, multi-variable design for nonlinear models. The methodology in this article fills this important gap, and is demonstrated on generic problems of practical importance including pharmacokinetic studies and experiments that produce discrete data. Previous attempts to obtain fully Bayesian optimal designs for these types of experiment have been extremely limited.

In a landmark article for low-dimensional design problems, Müller and Parmigiani (1996) proposed selection of a design by maximizing a surrogate function found by approximating U(δ) for a small number, m, of designs using simulation, and then smoothing the resulting values, $\tilde{U}\left({\mathit{}\mathbf{\delta }}_1\right),\dots ,\tilde{U}({\mathit{}\mathbf{\delta }}_m$). See also Jones et al. (2016) and Weaver et al. (2016). In essence, these approaches perform a computer experiment to construct a statistical emulator for the approximation $\tilde{U}\left(\mathit{}\mathbf{\delta }\right)$, a research area where there has been huge activity in recent years (see, e.g., Dean et al. 2015, sec. V). For an experiment with n runs and v variables, δ has nv elements. Therefore, application of this approach to design for multi-variable models suffers from a curse of dimensionality, requiring (i) the construction of emulators in very high dimensions; (ii) large, for example, space-filling, designs composed of selections of points from an nv-dimensional space, leading to (iii) a prohibitive number of evaluations of $\tilde{U}\left(\mathit{}\mathbf{\delta }\right)$, particularly if $\tilde{U}\left(\mathit{}\mathbf{\delta }\right)$ is computationally expensive.

Our approach overcomes these problems by building a series of one-dimensional emulators for the approximated expected utility. We emulate $\tilde{U}\left(\mathit{}\mathbf{\delta }\right)=\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$ as a function of only the ith “coordinate” (or element) δ_i conditional on δ_(i) = (δ₁, …, δ_{i − 1}, δ_{i + 1}, δ_nv)^T, the values of all coordinates excluding the ith (i = 1, …, nv). When these emulators are combined with a continuous version of the coordinate exchange algorithm (Meyer and Nachtsheim 1995), an effective and computationally efficient design selection methodology results. Conditional, coordinate-wise, optimization is key to overcoming the curse of dimensionality described above.

Until relatively recently, the usual approach to Bayesian design was to use a normal distribution as an asymptotic approximation to the posterior distribution of ψ (e.g., Chaloner and Larntz 1989). For standard utility functions (see Section 3.1.2), use of such a pseudo-Bayesian approach leads to the integrand in (1(1) $$U\left(\mathit{}\mathbf{\delta }\right)=\int {\int }_{\Psi ,\mathcal{Y}}u(\mathit{}\mathbf{\delta },\mathit{}\mathbf{\psi },\mathbf{y})\pi (\mathbf{y},\mathit{}\mathbf{\psi }|\mathit{}\mathbf{\delta })d\mathbf{y}d\mathit{}\mathbf{\psi }.$$(1) ) no longer depending on the data y. The resulting integral, with respect to ψ, typically has much lower dimension and can be approximated using efficient deterministic quadrature rules (Gotwalt, Jones, and Steinberg 2009). However, the appropriateness of such approximations for small experiments is open to question.

For high-dimensional design, an alternative to the use of a normal approximation was suggested by Ryan et al. (2014). These authors combined the simulation-based approach of Müller (1999) (see also Müller, Sanso, and De Iorio 2004; Amzal et al. 2006) with a dimension-reduction scheme to find designs for single-variable nonlinear models (v = 1) variables and a large number of runs. Designs were restricted to those formed from a sampling scheme defined via two parameters, for example, the initial design point and a spacing parameter. An optimal design in this subclass then consists of the best choices of these two parameters, a substantially easier optimization problem to solve.

In contrast to either applying an asymptotic approximation or restricting attention to a subset of the design space, both of which may result in the selection of inefficient designs with respect to the exact expected utility, we attempt to find optimal or efficient designs for the original problem across the whole design space via an approximate optimization scheme. These three different approaches are compared in Section 3.

The remainder of the article is organized as follows. In Section 2, we describe approximate coordinate exchange for finding decision-theoretic Bayesian designs, including the use of Monte Carlo integration and Gaussian process emulators to approximate the expected utility. The methods are applied to a range of challenging and practically relevant examples in Section 3 including models for which Bayesian design has previously been computationally infeasible. We summarize the advantages of our approach in Section 4 and highlight some ongoing work.

2. Approximate Coordinate Exchange (ACE)

We first establish some notation. Suppose that a design consists of n runs or points, each of which determines the settings of v controllable variables and results in a single observation of the response variable. Let D denote the n × v design matrix with kth row d_k specifying the settings of the v factors in the kth run (k = 1, …, n). Let q = nv, then the design may be represented as a q-vector $\mathit{}\mathbf{\delta }=\mathrm{vec}\left(\mathbf{D}\right)\in \mathcal{D}\subset {\mathbb{R}}^q$, where vec( · ) denotes vectorization via stacking the columns of a matrix and $\mathcal{D}$ is the q-dimensional design space.

The proposed algorithm for decision-theoretic Bayesian design has two phases. Phase I applies a novel coordinate exchange algorithm where, for each coordinate, maximization of U(δ) is replaced by maximization of a surrogate function $\widehat{U}\left(\mathit{}\mathbf{\delta }\right)$. Phase I tends to produce clusters of design points that are very similar in the values of the controllable variables. Such clustering is common in heuristic design search (see also Gotwalt, Jones, and Steinberg 2009). Hence, in Phase II, we check if the points in each cluster can be consolidated into a replicated design point using a point exchange algorithm (Atkinson, Donev, and Tobias 2007, chap. 12). Replication of points is common in optimal design for parametric models and a key principle of design of experiments (Wu and Hamada 2009, chap. 1). In Phase II, the candidate set is the design found from Phase I. The two phases form an approximate coordinate and point exchange algorithm which, for brevity, we call the ACE algorithm.

In Section 2.1, we define the ACE algorithm. For Steps 2a–2c of the algorithm, we assume the availability of (i) a Monte Carlo approximation of the expected utility, (2) $$\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})=\tilde{U}\left(\mathit{}\mathbf{\delta }\right)=\sum _{l=1}^{B}u(\mathit{}\mathbf{\delta },{\mathbf{y}}_l,{\mathit{}\mathbf{\psi }}_l)/B,$$(2) with {y_l, ψ_l}^B_{l = 1} a random sample from the joint distribution with density π(y, ψ | δ); (ii) coordinate-designs ${\xi }_i=\{{\delta }_i^1,\dots ,{\delta }_i^m\}\in {\mathcal{D}}_i$ at which we evaluate $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$, where ${\mathcal{D}}_i\subset \mathbb{R}$ is the domain for the ith coordinate; and (iii) a suitable one-dimensional emulator, $\widehat{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$, for $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$. Further details are given in Section 2.2, with examples in Section 2.4.

ACE is designed to solve a stochastic optimization problem, as only approximations to the expected utility are available formed as linear combinations of realizations of the random variable u(δ, y, ψ). As such, proposed changes to the design in Steps 2d and 4e of the algorithm are accepted with probability derived from a Bayesian test of the difference in the means of Monte Carlo approximations to the expected utility for the current and proposed designs. Further details are given in Section 2.3.

The R package acebayes (Overstall et al. 2017) provides an implementation of ACE and is available on CRAN.

2.1 The ACE Algorithm

1.	Choose an initial design δ0 and set the current design δC = δ0. $$\begin{array}{c}\hfill PhaseI:Coordinateexchange.\end{array}$$Phase I finds designs through a sequence of one-dimensional computer experiments. For each coordinate of the design, a computer experiment is performed where (i) all other design coordinates are taken as fixed; (ii) the numerical approximation (2(2) $$\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})=\tilde{U}\left(\mathit{}\mathbf{\delta }\right)=\sum _{l=1}^{B}u(\mathit{}\mathbf{\delta },{\mathbf{y}}_l,{\mathit{}\mathbf{\psi }}_l)/B,$$(2) ) is evaluated for a small number of values of the single coordinate (Steps 2a and 2b below), and (iii) a Gaussian process surrogate is constructed and maximized to suggest a new value of the coordinate (Steps 2c and 2d). As discussed above, this suggested coordinate is accepted with probability obtained from a Bayesian test of equality of the Monte Carlo approximations of the expected utility for the original design and the design with the new coordinate, reflecting the stochastic nature of the Monte Carlo approximation. An optimal design is then found via repetition of this sequence of computer experiments (Step 3). A simple example of the application of Phase 1 is given in Section 2.4.
2.	For i = 1, …, q, (a) Select an m point coordinate-design ${\xi }_i=\{{\delta }_i^1,\dots ,{\delta }_i^m\}\in {\mathcal{D}}_i$. (b) Evaluate $\tilde{U}\left({\delta }_i^1\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C),\dots ,\tilde{U}\left({\delta }_i^m\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C)$. (c) Construct $\widehat{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C)$ by fitting a statistical model to ${\{{\delta }_i^j,\tilde{U}\left({\delta }_i^j\right)\}}_{j=1}^m$. (d) With probability p†I, set ${\delta }_i^C={\delta }_i^{†}=\arg {\max }_{{\delta }_{\mathrm{i}}\in {\mathcal{D}}_{\mathrm{i}}}\widehat{\mathrm{U}}\left({\delta }_{\mathrm{i}}\right|{\mathit{}\mathbf{\delta }}_{\left(\mathrm{i}\right)}^{\mathrm{C}})$, where (3) $$p_{\mathit{I}}^{†}=1-T_{2B-2}\left(-\frac{B\tilde{U}\left({\mathit{}\mathbf{\delta }}^{C†}\right)-B\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)}{\sqrt{2B{\widehat{\nu }}_{\mathit{I}}}}\right),$$(3) T2B − 2 is the probability distribution function for a t distribution with 2B − 2 degrees of freedom, δC† = (δC1, …, δCi − 1, δ†i, δCi + 1, …, δCq)T, and $$\begin{array}{c}\hfill {\widehat{\nu }}_{\mathit{I}}=\frac{{\sum }_{l=1}^B{\left[u\left({\mathit{}\mathbf{\delta }}^{C†},{\mathbf{y}}_l^{†},{\mathit{}\mathbf{\psi }}_l^{†}\right)-\tilde{U}\left({\mathit{}\mathbf{\delta }}^{C†}\right)\right]}^2+{\sum }_{l=1}^B{\left[u\left({\mathit{}\mathbf{\delta }}^C,{\mathbf{y}}_l^C,{\mathit{}\mathbf{\psi }}_l^C\right)-\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)\right]}^2}{2B-2},\end{array}$$for {y†l, ψ†l}Bl = 1 and {yCl, ψCl}Bl = 1 independent random samples from π(y, ψ | δC†) and π(y, ψ | δC), respectively.
3.	Repeat Step 2 NI times. $$Phase\mathit{\text{II:}}Pointexchange.$$Phase II consolidates clusters of similar points in a design arising from Phase I. A point exchange algorithm is employed with a candidate list formed from the points in the Phase I design. First, the design point is found whose replication maximizes the approximation to the expected utility. A replicate of this point is then added to the design (Steps 4a and 4b). Second, from this new (n + 1)-point design, the point is found whose deletion leads to the n-point design with highest approximated expected utility (Steps 4c and 4d). Finally, the new design with these two points swapped is accepted with probability once again arising from a Bayesian test for equality of the Monte Carlo approximations (Step 4e). These steps are replicated to find an optimal design (Step 5).
4.	(a) For k = 1, …, n, let δ(1)k = vec(D(1)k), where $$\begin{array}{c}\hfill {\mathbf{D}}_k^{\left(1\right)}={\left[{\left({\mathbf{D}}^C\right)}^{\mathrm{T}}{\left({\mathbf{d}}_k^C\right)}^{\mathrm{T}}\right]}^{\mathrm{T}},\end{array}$$and dCk is the kth row of DC, the design matrix for δC. (b) Let $k^{†}=\arg {\max }_{\mathrm{k}}\tilde{\mathrm{U}}\left({\mathit{}\mathbf{\delta }}_{\mathrm{k}}^{\left(1\right)}\right)$ and set ${\mathbf{D}}^{\left(2\right)}={\mathbf{D}}_{k^{†}}^{\left(1\right)}$. (c) For h = 1, …, n + 1, let δ(3)s = vec(D(3)h), where $$\begin{array}{c}\hfill {\mathbf{D}}_h^{\left(3\right)}={\left[{\left({\mathbf{d}}_1^{\left(2\right)}\right)}^{\mathrm{T}}\dots {\left({\mathbf{d}}_{h-1}^{\left(2\right)}\right)}^{\mathrm{T}}{\left({\mathbf{d}}_{h+1}^{\left(2\right)}\right)}^{\mathrm{T}}\dots {\left({\mathbf{d}}_{n+1}^{\left(2\right)}\right)}^{\mathrm{T}}\right]}^{\mathrm{T}},\end{array}$$and d(2)h is the hth row of D(2). (d) Let $h^{†}=\arg {\max }_{\mathrm{h}}\tilde{\mathrm{U}}\left({\mathit{}\mathbf{\delta }}_{\mathrm{h}}^{\left(3\right)}\right)$ (e) With probability p†II, set ${\mathit{}\mathbf{\delta }}^C={\mathit{}\mathbf{\delta }}_{h^{†}}^{\left(3\right)}$, where (4) $$p_{\mathrm{II}}^{†}=1-T_{2B-2}\left(-\frac{B\tilde{U}\left({\mathit{}\mathbf{\delta }}_{h^{†}}^{\left(3\right)}\right)-B\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)}{\sqrt{2B{\widehat{\nu }}_{\mathrm{II}}}}\right)$$(4) and $$\begin{array}{c}\hfill {\widehat{\nu }}_{\mathrm{II}}=\frac{{\sum }_{l=1}^B{\left[u\left({\mathit{}\mathbf{\delta }}_{h^{†}}^{\left(3\right)},{\mathbf{y}}_l^{\left(3\right)},{\mathit{}\mathbf{\psi }}_l^{\left(3\right)}\right)-\tilde{U}\left({\mathit{}\mathbf{\delta }}_{h^{†}}^{\left(3\right)}\right)\right]}^2+{\sum }_{l=1}^B{\left[u\left({\mathit{}\mathbf{\delta }}^C,{\mathbf{y}}_l^C,{\mathit{}\mathbf{\psi }}_l^C\right)-\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)\right]}^2}{2B-2},\end{array}$$with {y(3)l, ψ(3)l}Bl = 1 a random sample from $\pi (\mathbf{y},\mathit{}\mathbf{\psi }|{\mathit{}\mathbf{\delta }}_{h^{★}}^{\left(3\right)})$.
5.	Repeat Step 4 NII times.
6.	Return δ⋆ = δC.

The decision on when to terminate a run of the algorithm, that is, choice of N_I and N_II, is complicated by the stochastic nature of the approximation to the expected utility. For the examples in Section 3, N_I = 20 and N_II = 100 are sufficient to achieve approximate convergence. Here, convergence is assessed graphically from trace plots of $\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)$ against iteration number; see Section 3.2 for examples of such plots.

To avoid local optima, the algorithm is run M times (in embarrassingly parallel fashion) with each run starting from a different, randomly chosen, initial design δ₀ (a random Latin hypercube design, unless otherwise stated). The selected design, δ^⋆, is the design having the highest average approximate expected utility, averaged across C sets of Monte Carlo simulations. In this article, M = C = 20 was used, unless otherwise stated.

2.2 Emulation via Computer Experiments (Steps 2a–2c)

In Phase I of the algorithm, a sequence of one-dimensional emulators is constructed for $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$, i = 1, …, q (Step 2c). A variety of smoothing or interpolation techniques could be applied to construct each emulator. Müller and Parmigiani (1996) used local polynomial regression to emulate low-dimensional design utilities. We adopt a Gaussian Process (GP) regression model (see, e.g., Rasmussen and Williams 2006), which is widely used for computer experiments, and use the posterior predictive mean as an emulator. Let $$\begin{array}{ccc}\hfill {\widehat{\mu }}_i& =& \sum _{j=1}^m\tilde{U}\left({\delta }_i^j|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C\right)/m,\hfill \\ \hfill {\widehat{\sigma }}_i^2& =& \sum _{j=1}^m{\left(\tilde{U}\left({\delta }_i^j|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C\right)-{\widehat{\mu }}_i\right)}^2/(m-1),\hfill \end{array}$$and $z\left({\delta }_i\right)=\left(U\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C)-{\widehat{\mu }}_i\right)/{\widehat{\sigma }}_i$ for any ${\delta }_i\in {\mathcal{D}}_i$. The GP model assumes that any vector $\mathbf{z}\left(\zeta \right)={[z\left({\delta }^1\right),\dots ,z\left({\delta }^{m_0}\right)]}^{\mathrm{T}}$, for $\zeta =\{{\delta }^1,\dots ,{\delta }^{m_0}\}\in {\mathcal{D}}_i^{m_0}$ and integer m₀, has joint distribution $\mathrm{N}\left({\mathbf{0}}_{m_0},\mathbf{A}\left(\zeta \right)\right)$, with ${\mathbf{0}}_{m_0}$ the m₀ zero-vector and A(ζ) an m₀ × m₀ covariance matrix. Hence, the posterior predictive mean of $\tilde{U}\left(\delta \right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$ at an arbitrary $\delta \in {\mathcal{D}}_i$ can be derived using standard results on the conditional distribution of normal random variables and used as an emulator: $$\begin{array}{ccc}\hfill \widehat{U}\left(\delta |{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C\right)& =& {\widehat{\mu }}_i+{\widehat{\sigma }}_i\mathrm{E}\left[z\left(\delta \right)|\mathbf{z}\left({\xi }_i\right)\right]\hfill \\ & =& {\widehat{\mu }}_i+{\widehat{\sigma }}_i\mathbf{a}{(\delta ,{\xi }_i)}^{\mathrm{T}}\mathbf{A}{\left({\xi }_i\right)}^{-1}\mathbf{z}\left({\xi }_i\right).\hfill \end{array}$$Under the common assumption of a squared exponential correlation function, A(ξ_i) and a(δ, ξ_i) have entries $$\begin{array}{ccc}\hfill \mathbf{A}{\left({\xi }_i\right)}_{st}& =& exp\left\{-\rho {\left({\delta }_i^s-{\delta }_i^t\right)}^2\right\}+\eta I(r=s),\hfill \\ \hfill \mathbf{a}{(\delta ,{\xi }_i)}_s& =& exp\left\{-\rho {\left({\delta }_i^s-\delta \right)}^2\right\},\hfill \end{array}$$for s, t = 1, …, m, where I(E) is the indicator function for the event E, and ρ, η > 0 are unknown parameters. The inclusion of nugget η ensures the emulator will smooth, rather than interpolate, the Monte Carlo approximations of the expected utility. To limit computational complexity, at each iteration we find maximum likelihood estimates of ρ and η via Fisher scoring (see, e.g., Pawitan 2001, pp. 174–177). In contrast, a fully Bayesian approach would require application of a Markov chain Monte Carlo algorithm to construct each emulator, substantially increasing the computational cost of the algorithm.

At each iteration of Step 2a, a coordinate-design ξ_i = (δ¹_i, …, δ^m_i) must be chosen at which to evaluate $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$. We use a space-filling design, specifically a randomly selected one-dimensional Latin hypercube design (see, e.g., Santner, Williams, and Notz 2003, chap. 5), constructed by dividing ${\mathcal{D}}_i$ into m equally sized sub-intervals, and then generating a point at random from each interval. We set m = 20, unless otherwise stated. This choice of m is conservative relative to the rule of thumb (Loeppky, Sacks, and Welch 2009) of setting m equal to 10 times the number of input dimensions (suggesting m = 10 in our case). We have, however, found it works well in practice for a variety of different types of examples, giving accurate emulators and not being overly computationally demanding.

2.3 Adjusting a Design Coordinate (Step 2d) or Point (Step 4e)

To make a change to the ith coordinate in Step 2d, we first find δ†_i, the value of the coordinate that maximizes the emulator. We find the maximum by evaluating $\widehat{U}\left(\delta |{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C\right)$ for 10,000 uniformly generated points in ${\mathcal{D}}_i$. This discretization of the problem has proved both more reliable than continuous optimization and sufficiently computationally efficient.

Choice of δ†_i is subject to both Monte Carlo error, from the evaluation of $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$, and emulator error from the estimation of $\widehat{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)})$ resulting, for example, from an inappropriate choice of correlation function or errors in estimating ρ and η. It is clearly impossible to use usual residual diagnostics (Bastos and O’Hagan 2009) to check emulator adequacy at each iteration of the algorithm. Instead, emulator error is eliminated from the decision to adjust a design coordinate by performing additional Monte Carlo integration to calculate the probability p†_I in (3(3) $$p_{\mathit{I}}^{†}=1-T_{2B-2}\left(-\frac{B\tilde{U}\left({\mathit{}\mathbf{\delta }}^{C†}\right)-B\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)}{\sqrt{2B{\widehat{\nu }}_{\mathit{I}}}}\right),$$(3) ). This quantity is the posterior probability that $\mathrm{E}\left[u(\mathit{}\mathbf{\psi },\mathbf{y},{\mathit{}\mathbf{\delta }}^{C†})\right]>\mathrm{E}\left[u(\mathit{}\mathbf{\psi },\mathbf{y},{\mathit{}\mathbf{\delta }}^C)\right]$ under noninformative prior distributions and using Monte Carlo samples {ψ^C_l, y_l^C}^B_{l = 1} and {ψ†_l, y†_l}^B_{l = 1}, assuming both u(ψ†, y†, δ^C†) and u(ψ^C, y^C, δ^C) are normally distributed with equal variances. See also Wang and Zhang (2006) for use of a classical hypothesis test in a simulated annealing algorithm. If this normality assumption were severely violated, a more sophisticated test procedure could be adopted at greater computational cost.

A similar test is performed at Step 4e in Phase 2 of the algorithm to calculate p†_II in (4(4) $$p_{\mathrm{II}}^{†}=1-T_{2B-2}\left(-\frac{B\tilde{U}\left({\mathit{}\mathbf{\delta }}_{h^{†}}^{\left(3\right)}\right)-B\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)}{\sqrt{2B{\widehat{\nu }}_{\mathrm{II}}}}\right)$$(4) ). We demonstrate the effect of Step 2d in the next section.

2.4 Illustrative Example

In this section, we illustrate the ACE methodology, in particular the combination of Steps 2c and 2d in selecting and accepting a proposed change to the design. To enable assessment of the algorithm, we consider the analytically tractable problem of finding a one-point optimal design for the single-variable Poisson model y|β ∼ Poisson(e^βx). There is a single design coordinate, δ = x ∈ [ − 1, 1], and hence our notation is simplified by replacing δ by x in this example. A priori, we assume β ∼ N(0.5, 1) and adopt the utility function that leads to pseudo-Bayesian D-optimality (Section 3.1.2), given by $$\begin{array}{ccc}\hfill u(\beta ,y,x)& =& log\mathcal{I}(\beta ;x)\hfill \\ & =& 2log\left|x\right|+\beta x,\hfill \end{array}$$where $\mathcal{I}(\beta ;x)$ denotes the Fisher information. The expected utility is U(x) = 2log |x| + 0.5x and the optimal design is x^⋆ = 1.

To simulate one iteration of Phase I of the ACE algorithm, we generate a coordinate-design ξ¹ = {x¹, …, x^m} as a Latin hypercube and, for each x^j, evaluate $$\begin{array}{c}\hfill \tilde{U}\left(x^j\right)=2log\left|x^j\right|+\frac{x^j}{B}\sum _{i=1}^B{\beta }_l,\end{array}$$where {β_l}^B_{l = 1} for B = 2 is a sample from an N(0.5, 1) distribution. Figure 1(a) shows U(x) plotted against x with the points ${\{x^j,\tilde{U}\left(x^j\right)\}}_{j=1}^m$ and the GP emulator $\widehat{U}\left(x\right)$ superimposed (Steps 2a, 2b, and 2c). Clearly $\widehat{U}\left(x\right)$ is maximized at x† = 1, and hence this candidate point should be compared to the current point x^C (Step 2d). Figure 1(b) shows the median posterior probability, p†_I, of accepting this candidate point against x^C, calculated from repeated calculation of (3(3) $$p_{\mathit{I}}^{†}=1-T_{2B-2}\left(-\frac{B\tilde{U}\left({\mathit{}\mathbf{\delta }}^{C†}\right)-B\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)}{\sqrt{2B{\widehat{\nu }}_{\mathit{I}}}}\right),$$(3) ) for multiple Monte Carlo samples. This probability is very close to one for nearly all values of x^C except for x^C ≈ x†, where the probability reduces to 1/2.

Figure 1. Poisson example in Section 2.4. (a), (c) expected utility U(x) against x, with Monte Carlo evaluations $\tilde{U}\left(x\right)$ at the coordinate-design points and GP emulator $\widehat{U}\left(x\right)$; (b), (d) median probability p†_I of accepting the candidate point against the current point, x^C. [Coordinate-designs are: ξ¹ for (a), (b); ξ² for (c), (d)].

For a second coordinate-design, ξ² (a different Latin hypercube), the results in Figure 1(c) and 1(d) are obtained. Here, the GP emulator could be viewed as inadequate with the estimate of η being too small, resulting in near interpolation of the $\tilde{U}\left(x^j\right)$. From Figure 1(c), $\widehat{U}\left(x\right)$ is maximized at x† = −1 and hence this becomes the candidate point. The median posterior acceptance probability, Figure 1(d), is now only close to one if $\tilde{U}\left(x^C\right)$ is low, that is, |x^C| < 0.5. Crucially, x† will be rejected with high probability if x^C is close to the optimal design; at x^C = 1, the probability drops to zero.

3. Substantive Examples

The ACE algorithm is now used to find decision-theoretic Bayesian designs for three important cases: a compartmental model, (hierarchical) logistic regression, and dose–response under model-averaging. The designs are found for commonly used utility functions and, where possible, compared to existing results.

The supplementary material for this article provides a detailed vignette that demonstrates the use of the acebayes package to find designs for the following examples, and R code to allow their straightforward reproduction.

3.1 Utility Functions

In this section, we assess and compare designs found using variants on two utility functions, Shannon information gain (SIG) and negative squared error loss (NSEL). In practice, the form of the chosen utility function should be driven by the aims of the experiment and may often incorporate a cost function. We assume throughout that the model parameters can be expressed as ψ^T = (θ^T, γ^T), with θ a p-vector of parameters of interest and γ a (P − p)-vector of nuisance parameters.

The SIG utility for θ is given by (5) $$\begin{array}{ccc}\hfill u^S(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })& =& log\pi \left(\mathit{}\mathbf{\theta }\right|\mathbf{y},\mathit{}\mathbf{\delta })-log\pi (\mathit{}\mathbf{\theta })\hfill \\ & =& log\pi \left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })-log\pi (\mathbf{y}\left|\mathit{}\mathbf{\delta }\right),\hfill \end{array}$$(5) where (5(5) $$\begin{array}{ccc}\hfill u^S(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })& =& log\pi \left(\mathit{}\mathbf{\theta }\right|\mathbf{y},\mathit{}\mathbf{\delta })-log\pi (\mathit{}\mathbf{\theta })\hfill \\ & =& log\pi \left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })-log\pi (\mathbf{y}\left|\mathit{}\mathbf{\delta }\right),\hfill \end{array}$$(5) ) follows from an application of Bayes’ theorem and is often more useful for computation. A SIG-optimal design maximizes U^S(δ) = E_{ψ, y}[u^S(θ, y, δ)]. This is equivalent to maximizing the expected Kullback–Liebler distance between the marginal posterior and prior distributions of θ, and is also equivalent to minimizing the expected entropy of the posterior distribution for θ.

The NSEL utility for θ is given by (6) $$u^V(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })=-\sum _{w=1}^p{\left[{\theta }_w-\mathrm{E}\left({\theta }_w\right|\mathbf{y},\mathit{}\mathbf{\delta })\right]}^2.$$(6) An NSEL-optimal design maximizes the expected utility U^V(δ), which is equivalent to minimizing the expectation of the trace of the posterior covariance matrix of θ with respect to the marginal distribution of y.

3.1.1 Evaluating the Expected Utility via Numerical Approximation

For many statistical models, including most nonlinear models, evaluation of u^S(θ, y, δ) and u^V(θ, y, δ) requires numerical approximation. For given values of y and θ, the components of (5(5) $$\begin{array}{ccc}\hfill u^S(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })& =& log\pi \left(\mathit{}\mathbf{\theta }\right|\mathbf{y},\mathit{}\mathbf{\delta })-log\pi (\mathit{}\mathbf{\theta })\hfill \\ & =& log\pi \left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })-log\pi (\mathbf{y}\left|\mathit{}\mathbf{\delta }\right),\hfill \end{array}$$(5) ) can be approximated as $$\begin{array}{ccc}\hfill \tilde{\pi }\left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })& =& \frac{1}{\tilde{B}}\sum _{b=1}^{\tilde{B}}\pi \left(\mathbf{y}\right|\mathit{}\mathbf{\theta },{\widetilde{\mathit{}\mathbf{\gamma }}}_b,\mathit{}\mathbf{\delta }),\hfill \\ \hfill \tilde{\pi }\left(\mathbf{y}\right|\mathit{}\mathbf{\delta })& =& \frac{1}{\tilde{B}}\sum _{b=1}^{\tilde{B}}\pi \left(\mathbf{y}\right|{\widetilde{\mathit{}\mathbf{\theta }}}_b,{\widetilde{\mathit{}\mathbf{\gamma }}}_b,\mathit{}\mathbf{\delta }),\hfill \end{array}$$where ${\{{\widetilde{\mathit{}\mathbf{\theta }}}_b,{\widetilde{\mathit{}\mathbf{\gamma }}}_b\}}_{b=1}^{\tilde{B}}$ is a size $\tilde{B}$ random sample from the prior distribution of ψ = (θ, γ). These quantities can be incorporated into a nested, or double-loop, Monte Carlo approximation of U^S(δ): $$\begin{array}{c}\hfill {\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)=\frac{1}{B}\sum _{l=1}^B[log\tilde{\pi }\left({\mathbf{y}}_l\right|{\mathit{}\mathbf{\theta }}_l,\mathit{}\mathbf{\delta })-log\tilde{\pi }\left({\mathbf{y}}_l\right|\mathit{}\mathbf{\delta })],\end{array}$$ with {y_l, θ_l}^B_{l = 1} a sample from the joint distribution of the response and parameters. Intuitively, the “inner sample” of size $\tilde{B}$ is used to approximate the two marginal likelihoods in (5(5) $$\begin{array}{ccc}\hfill u^S(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })& =& log\pi \left(\mathit{}\mathbf{\theta }\right|\mathbf{y},\mathit{}\mathbf{\delta })-log\pi (\mathit{}\mathbf{\theta })\hfill \\ & =& log\pi \left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })-log\pi (\mathbf{y}\left|\mathit{}\mathbf{\delta }\right),\hfill \end{array}$$(5) ), the first marginal to γ and the second to both γ and θ, and the “outer sample” of size B is then used to approximate the expected utility with respect to the joint distribution of y and θ. This approximation is biased for U^S(δ) due to the bias in $log\tilde{\pi }\left(\mathbf{y}\right|\mathit{}\mathbf{\theta },\mathit{}\mathbf{\delta })$ and $log\tilde{\pi }\left(\mathbf{y}\right|\mathit{}\mathbf{\delta })$. However, under regularity conditions satisfied by most models of practical importance (Severini 2000, pp. 80–81), this bias is of order ${\tilde{B}}^{-1}$ (Ryan 2003) and hence asymptotically negligible.

For NSEL, E(θ_w | y, δ) in (6(6) $$u^V(\mathit{}\mathbf{\theta },\mathbf{y},\mathit{}\mathbf{\delta })=-\sum _{w=1}^p{\left[{\theta }_w-\mathrm{E}\left({\theta }_w\right|\mathbf{y},\mathit{}\mathbf{\delta })\right]}^2.$$(6) ) can be approximated via importance sampling: $$\begin{array}{c}\hfill \tilde{\mathrm{E}}\left({\theta }_w\right|\mathbf{y},\mathit{}\mathbf{\delta })=\frac{{\sum }_{b=1}^{\tilde{B}}{\tilde{\theta }}_{lw}\pi \left(\mathbf{y}\right|{\widetilde{\mathit{}\mathbf{\theta }}}_b,{\widetilde{\mathit{}\mathbf{\gamma }}}_b,\mathit{}\mathbf{\delta })}{{\sum }_{b=1}^{\tilde{B}}\pi \left(\mathbf{y}\right|{\widetilde{\mathit{}\mathbf{\theta }}}_b,{\widetilde{\mathit{}\mathbf{\gamma }}}_b,\mathit{}\mathbf{\delta })},\end{array}$$where ${\{{\widetilde{\mathit{}\mathbf{\theta }}}_b,{\widetilde{\mathit{}\mathbf{\gamma }}}_b\}}_{b=1}^{\tilde{B}}$ is a random sample from the prior distribution of ψ, and ${\tilde{\theta }}_{bw}$ is the wth element of ${\widetilde{\mathit{}\mathbf{\theta }}}_b$. Hence, the following nested Monte Carlo approximation of the expected utility is obtained: $$\begin{array}{c}\hfill {\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)=-\frac{1}{B}\sum _{l=1}^B\sum _{w=1}^p{[{\theta }_{lw}-\tilde{\mathrm{E}}\left({\theta }_w\right|{\mathbf{y}}_l,\mathit{}\mathbf{\delta })]}^2,\end{array}$$where θ_lw is the wth element of θ_l. Here, the inner sample is used to approximate the posterior expectation, and the outer sample used to approximate the expected utility. Importance sampling has commonly been used to estimate posterior quantities for Bayesian design (see Ryan et al. 2016 and references therein), although the approximation of the expected utility will again be biased due to bias in $\tilde{\mathrm{E}}{\left({\theta }_w\right|\mathbf{y},\mathit{}\mathbf{\delta })}^2$.

In the examples, we set $\tilde{B}=B=1000$ for the evaluation of $\tilde{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C)$ in Step 2b of the ACE algorithm (chosen from practical experience). For the comparisons in Steps 2d and 4e, we set $B=\tilde{B}=20,000$.

3.1.2 Evaluating the Expected Utility via Normal Approximation

The following approximations to U^S(δ) and U^V(δ) are commonly used (Atkinson, Donev, and Tobias 2007, chaps. 10, 18), justified via a normal approximation to the posterior distribution of ψ: $$\begin{array}{ccc}\hfill {\varphi }^S\left(\mathit{}\mathbf{\delta }\right)& =& -{\mathrm{E}}_{\mathit{}\mathbf{\psi }}(log|{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\left|\right)\hfill \\ & =& -{\int }_{\Psi }log\left|{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\right|\pi \left(\mathit{}\mathbf{\psi }\right)d\mathit{}\mathbf{\psi },\hfill \\ \hfill {\varphi }^V\left(\mathit{}\mathbf{\delta }\right)& =& -{\mathrm{E}}_{\mathit{}\mathbf{\psi }}\left[\mathrm{tr}\left\{{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\right\}\right]\hfill \\ & =& -{\int }_{\Psi }\mathrm{tr}\left\{{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\right\}\pi \left(\mathit{}\mathbf{\psi }\right)d\mathit{}\mathbf{\psi },\hfill \end{array}$$with $\mathcal{I}(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })$ the Fisher information matrix for ψ, or an approximation thereof, and A = [I_p, 0_{p × (P − p)}]^T with I_p the p × p identity matrix and 0_{a × b} the a × b zero matrix. Designs that maximize φ^S and φ^V are sometimes referred to as pseudo-Bayesian D- and A-optimal designs, respectively. Note that these expressions also result from taking expectations of the utility functions $$\begin{array}{ccc}\hfill u^D(\mathit{}\mathbf{\psi },\mathbf{y},\mathit{}\mathbf{\delta })& =& -log|{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}|,\hfill \\ \hfill u^A(\mathit{}\mathbf{\psi },\mathbf{y},\mathit{}\mathbf{\delta })& =& -\mathrm{tr}{\left\{{\mathbf{A}}^{\mathrm{T}}\mathcal{I}(\mathit{}\mathbf{\psi };\mathit{}\mathbf{\delta })\mathbf{A}\right\}}^{-1},\hfill \end{array}$$which do not depend on y. Unbiased Monte Carlo approximations to φ^S(δ) and φ^V(δ) can be obtained via sampling from the prior distribution for ψ: $$\begin{array}{ccc}\hfill {\widehat{\varphi }}^S\left(\mathit{}\mathbf{\delta }\right)& =& -\frac{1}{B}\sum _{l=1}^{B}log\left|{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{({\mathit{}\mathbf{\psi }}_l;\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\right|,\hfill \\ \hfill {\widehat{\varphi }}^V\left(\mathit{}\mathbf{\delta }\right)& =& -\frac{1}{B}\sum _{l=1}^B\mathrm{tr}\left\{{\mathbf{A}}^{\mathrm{T}}\mathcal{I}{({\mathit{}\mathbf{\psi }}_l;\mathit{}\mathbf{\delta })}^{-1}\mathbf{A}\right\}.\hfill \end{array}$$For comparison of designs, the D-efficiency of design δ₁ relative to design δ₂ is defined as (7) $${\text{Eff}}_D({\mathit{}\mathbf{\delta }}_1,{\mathit{}\mathbf{\delta }}_2)=100\times exp\left\{\left[{\widehat{\varphi }}^S\left({\mathit{}\mathbf{\delta }}_1\right)-{\widehat{\varphi }}^S\left({\mathit{}\mathbf{\delta }}_2\right)\right]/p\right\}.$$(7)

3.2 Compartmental Model

Compartmental models are applied in pharmacokinetics to study how materials flow through an organism, and have been used extensively to demonstrate optimal design methodology (Atkinson et al. 1993; Gotwalt, Jones, and Steinberg 2009). The archetypal design problem is to choose n sampling times δ = (t₁, …, t_n)^T, in hours, at which to measure the concentration in a subject of a previously administered drug. Here, concentration is modeled as y_i ∼ N(a(θ)μ(θ; t_i), σ²b(θ; t_i)) , where θ = (θ₁, θ₂, θ₃)^T are the parameters of interest, σ² > 0 is a nuisance parameter, a( · ) and b( · ; ·) are application-dependent functions, and μ(θ; t_i) = exp ( − θ₁t_i) − exp ( − θ₂t_i).

For this problem, Ryan et al. (2014) assumed that $$\begin{array}{ccc}\hfill a\left(\mathit{}\mathbf{\theta }\right)& =& \frac{400{\theta }_2}{{\theta }_3({\theta }_2-{\theta }_1)},b(\mathit{}\mathbf{\theta };t_i)=\left(1+\frac{a{\left(\mathit{}\mathbf{\theta }\right)}^2\mu {(\mathit{}\mathbf{\theta };t_i)}^2}{10}\right),\hfill \\ \hfill {\sigma }^2& =& 0.1,\hfill \end{array}$$and found designs using the SIG utility function. Independent log-normal prior distributions were assumed for the elements of θ with, on the log scale, each having common variance 0.05 and expectations log (0.1), log (1), and log (20) for θ₁, θ₂, and θ₃, respectively. These authors also incorporated the constraint max _{s, t = 1, …, n}|t_s − t_t| ⩾ 0.25, that is, that sampling times must be at least 15 min apart. It is straightforward to incorporate this constraint into design search using the ACE algorithm. In Step 2d, $\widehat{U}\left({\delta }_i\right|{\mathit{}\mathbf{\delta }}_{\left(i\right)}^C)$ is maximized over a set ${\mathcal{D}}_i$ that satisfies the constraint. Phase II of the ACE algorithm is then omitted as replicated sampling times are not permitted.

Ryan et al. (2014) restricted their search for an SIG-optimal design to the class of designs defined via a dimension reduction scheme (DRS) that set the n sampling times to scaled percentiles of a Beta(α₁, α₂) distribution. Hence, the design problem was reduced to selecting two parameters, α₁ and α₂. The Müller (1999) simulation algorithm was used to sample from an artificial posterior distribution for α₁, α₂, with unnormalized density equal to the integrand in (1(1) $$U\left(\mathit{}\mathbf{\delta }\right)=\int {\int }_{\Psi ,\mathcal{Y}}u(\mathit{}\mathbf{\delta },\mathit{}\mathbf{\psi },\mathbf{y})\pi (\mathbf{y},\mathit{}\mathbf{\psi }|\mathit{}\mathbf{\delta })d\mathbf{y}d\mathit{}\mathbf{\psi }.$$(1) ). The chosen design was then the scaled quantiles from the Beta distribution obtained from using the posterior modal values of α₁ and α₂.

We compare this design with three designs found from ACE: (i) an SIG-optimal design; (ii) a pseudo-Bayesian D-optimal design; and (iii) an optimal choice of α₁, α₂ for the Beta DRS. For this latter design, the sampling times are given by $t_j=24\times Q(\frac{j}{n+1};{\alpha }_1,{\alpha }_2)$, with Q(r; α₁, α₂) the rth quantile of the Beta(α₁, α₂) distribution. In Step 2d of the ACE algorithm, the sets ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ are given by $$\begin{array}{ccc}\hfill {\mathcal{D}}_1& =& \{x\in {\mathbb{R}}^{+}:\underset{j=1,\cdots ,n-1}{min}|Q\left(\frac{j}{n+1},x,{\alpha }_2\right)\hfill \\ & & -Q\left(\frac{j+1}{n+1},x,{\alpha }_2\right)|>\frac{0.25}{24}\},\hfill \\ \hfill {\mathcal{D}}_2& =& \{x\in {\mathbb{R}}^{+}:\underset{j=1,\cdots ,n-1}{min}|Q\left(\frac{j}{n+1},{\alpha }_1,x\right)\hfill \\ & & -Q\left(\frac{j+1}{n+1},{\alpha }_1,x\right)|>\frac{0.25}{24}\}.\hfill \end{array}$$

For the SIG- and D-optimal designs, Figure 2(a) and 2(b) shows trace plots of the approximate expected utility at each iteration of the algorithm. Approximate convergence is demonstrated, for both utility functions, through each run of the algorithm resulting in a similar value of $\tilde{U}\left(\mathit{}\mathbf{\delta }\right)$ after a relatively small number of iterations. Convergence is, however, achieved more quickly for pseudo-Bayesian D-optimality, which does not require approximation of posterior quantities. This criterion also displays greater consistency in the final approximated expected utility between runs of the algorithm.

Figure 2. (a), (b) Trace plots of $\tilde{U}\left({\mathit{}\mathbf{\delta }}^C\right)$ for each iteration of the ACE algorithm for SIG and pseudo-Bayesian D-optimality utilities, respectively; in each plot, the black line shows the trace of the expected utility for the best design; (c) designs found from the ACE algorithm: unrestricted SIG-optimal, pseudo-Bayesian D-optimal, Beta DRS SIG-optimal, together with the Ryan et al. (2014) Beta DRS SIG-optimal designs; (d) boxplots for 20 evaluations of ${\tilde{U}}^S\left({\mathit{}\mathbf{\delta }}^{★}\right)$ for designs from these four methodologies; (e) approximate expected utility surface for SIG as a function of the Beta DRS parameters; parameter values corresponding to the Ryan et al. (2014) and the ACE DRS designs are marked.

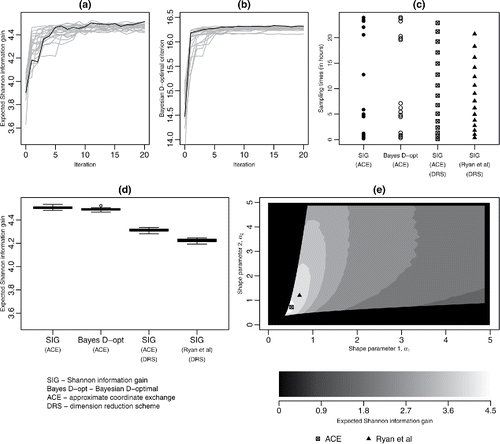
The sampling times for the four designs, shown in Figure 2(c), indicate that the designs using dimension-reduction do not display the clustering of points evident in the SIG and pseudo-Bayesian D-optimal designs. The boxplots in Figure 2(d), from 20 evaluations of ${\tilde{U}}^S\left({\mathit{}\mathbf{\delta }}^{★}\right)$ (B = 20,000) for each design, confirm that larger approximate expected utilities are obtained, up to a 5% improvement, when DRS is not used. Here, the pseudo-Bayesian D-optimal design provides a good approximation to the SIG-optimal design.

The DRS design found from ACE outperforms the Ryan et al. (2014) design. To explore this result further, the expected utility surface was investigated as a function of α₁ and α₂ by sampling 40,000 (α₁, α₂) pairs from [0, 5]² and evaluating ${\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)$ for each pair. The resulting expected utility surface is shown in Figure 2(e), where ${\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)=0$ for parameter pairs that do not satisfy the 15 min constraint. Both methods identify the relatively small region of high expected utility; the sampling-based algorithm (Müller 1999; Ryan et al. 2014) fails to identify the optimum point within this region.

3.3 Logistic Regression in Four Factors

Fully-Bayesian design for multi-variable logistic regression has not appeared in the literature, although Hamada et al. (2001) found an SIG-optimal design for a single-variable model and Woods et al. (2006) were the first to find multi-variable pseudo-Bayesian D-optimal designs. Here, we find designs for a first-order logistic regression model in four variables where the response is measured for G groups of n_g runs, that is, n = Gn_g. Let y_st ∼ Bernoulli(ρ_st) be the tth response from the sth group (s = 1, …, G; t = 1, …, n_g), with $$\begin{array}{ccc}\hfill log\left(\frac{{\rho }_{st}}{1-{\rho }_{st}}\right)& =& {\beta }_0+{\omega }_{s0}+({\beta }_1+{\omega }_{s1})x_{1st}+({\beta }_2+{\omega }_{s2})x_{2st}\hfill \\ & & +({\beta }_3+{\omega }_{s3})x_{3st}+({\beta }_4+{\omega }_{s4})x_{4st}\hfill \\ & =& {\mathbf{x}}_{st}^{\mathrm{T}}\left(\mathit{}\mathbf{\beta }+{\mathit{}\mathbf{\omega }}_s\right),\hfill \end{array}$$where $\mathit{}\mathbf{\beta }\in {\mathbb{R}}^5$ are the parameters of interest, and ${\mathit{}\mathbf{\omega }}_s\in {\mathbb{R}}^5$ (i = s, …, G) are the group-specific nuisance parameters (or “random effects”). Let X = (X^T₁ ⋅⋅⋅ X_G^T)^T be the n × 5 model matrix where X_s is the n_g × 5 matrix with tth row given by x^T_st. The design matrix D is formed as the last four columns of X, δ = vec(D) has length q = 4n, and ${\mathcal{D}}_i=[-1,1]$ for i = 1, …, q.

The following independent prior distributions for each element of β are assumed: (8) $$\begin{array}{ccccc}{\beta }_0\sim \mathrm{U}[-3,3],& & {\beta }_1\sim \mathrm{U}[4,10],& & {\beta }_2\sim \mathrm{U}[5,11],\\ {\beta }_3\sim \mathrm{U}[-6,0],& & {\beta }_4\sim \mathrm{U}[-2.5,3.5].\end{array}$$(8) We find designs for two different prior distributions for each ω_s (s = 1, …, G): (i) a prior point mass at ω_s = 0 for all s, resulting in standard logistic regression with homogenous groups; (ii) a hierarchical prior distribution in which the elements of ω_s are independent and identically distributed as ω_sr ∼ U[ − λ_r, λ_r], for r = 0, …, 4, with λ_r > 0 unknown and having triangular prior density $\pi \left({\lambda }_r\right)=\frac{2(L_r-{\lambda }_r)}{L_r^2}$ with (L₀, …, L₄) = (3, 3, 3, 1, 1).

3.3.1 Logistic Regression With Homogenous Groups

We use ACE to find designs that maximize the SIG and NSEL expected utilities for homogenous logistic regression with ω_s = 0 and n = 6, …, 48. For comparison, we also find pseudo-Bayesian D- and A-optimal designs. We also compare to maximin Latin hypercube (LH) designs (Morris and Mitchell 1995). For this example, the starting designs for the algorithm were a locally D-optimal design (for SIG and Bayesian D) and a locally A-optimal design (for NSEL and Bayesian A), found from ACE via maximization of ψ^S(δ) or ψ^V(δ), respectively, using a point prior distribution for each parameter with support at the mean of each prior distribution in (8(8) $$\begin{array}{ccccc}{\beta }_0\sim \mathrm{U}[-3,3],& & {\beta }_1\sim \mathrm{U}[4,10],& & {\beta }_2\sim \mathrm{U}[5,11],\\ {\beta }_3\sim \mathrm{U}[-6,0],& & {\beta }_4\sim \mathrm{U}[-2.5,3.5].\end{array}$$(8) ). 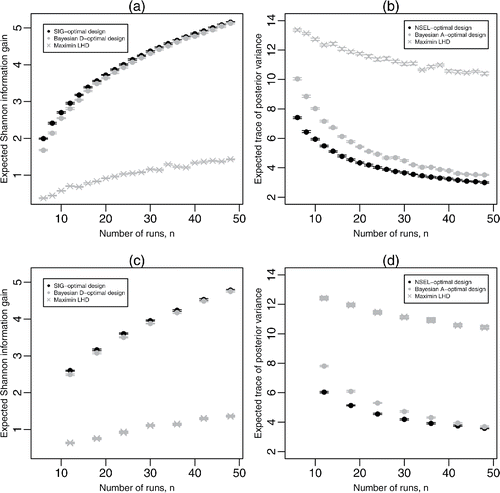Figure 3 presents results (minimum, mean, maximum) of 20 evaluations of (a) ${\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)$ for the SIG-optimal, Bayesian D-optimal, and maximin LH designs, and (b) $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ for the NSEL-optimal, Bayesian A-optimal, and maximin LH designs, using B = 20,000 Monte Carlo samples. For small n, on average there are substantial differences in expected utility between the fully Bayesian and pseudo-Bayesian designs, with the SIG-optimal design having expected Shannon information gain up to 20% larger than the Bayesian D-optimal design and the NSEL-optimal design having expected trace of the posterior covariance matrix up to 27% smaller than the Bayesian A-optimal design. For both SIG and NSEL, as n increases, the difference in expected utility between these designs and the pseudo-Bayesian designs decreases. For SIG, these findings agree with asymptotic results on the convergence, under certain regularity conditions, of the posterior distribution to a normal distribution (see, e.g., Gelman et al. 2014, pp. 585–588). The maximin LH designs, which are model-free space-filling designs, perform poorly under both SIG and NSEL utilities and are not competitive with the model-based designs.

Figure 3. Results from 20 evaluations of (a) ${\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)$ for SIG-optimal, pseudo-Bayesian D-optimal, and maximin Latin hypercube designs, and (b) $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ for NSEL-optimal, pseudo-Bayesian A-optimal, and maxmin Latin hypercube designs, for homogenous logistic regression; (c) and (d) show the same evaluations for hierarchical logistic regression. For the latter two plots, for each value of n, 20 different random assignments are made of the points of the Latin hypercube design to the G groups, and each resulting design is evaluated 20 times. For each design, the central plotting symbol denotes the mean expected Shannon information gain or expected average posterior variance, with the two horizontal lines denoting the minimum and maximum of these quantities.

As there are no comparable results on fully-Bayesian design for multi-variable logistic regression in the literature, we compare the pseudo-Bayesian D-optimal designs for n = 16 and n = 48 found from ACE with designs from the approach of Gotwalt, Jones, and Steinberg (2009). We independently implemented the methodology of these authors to obtain designs for n = 16 and n = 48; we also compare to the n = 16 run design published by Gotwalt, Jones, and Steinberg (2009). For each of these three designs, we calculated the average of D-efficiency (7(7) $${\text{Eff}}_D({\mathit{}\mathbf{\delta }}_1,{\mathit{}\mathbf{\delta }}_2)=100\times exp\left\{\left[{\widehat{\varphi }}^S\left({\mathit{}\mathbf{\delta }}_1\right)-{\widehat{\varphi }}^S\left({\mathit{}\mathbf{\delta }}_2\right)\right]/p\right\}.$$(7) ) over 20 Monte Carlo approximations (each with B = 20,000) relative to the appropriately sized design from ACE. The published 16-run design has average efficiency of 82%; the designs from our implementation perform similarly to the ACE designs, with average efficiencies of 99.9% and 101.3% for n = 16 and n = 48, respectively.

3.3.2 Hierarchical Logistic Regression

For hierarchical logistic regression, we again find SIG-optimal and NSEL-optimal designs, along with pseudo-Bayesian D- and A-optimal designs using an approximation to the Fisher information (Pawitan 2001, p. 467). We set n_g = 6 and G = 2, …, 8, leading to n = 12, 14, …, 48. To reduce the computational burden, B = 1000 was used in Step 4e to find SIG-optimal designs. Previous research has found pseudo-Bayesian D-optimal designs for smaller numbers of variables and group sizes (Waite and Woods 2015).

Figure 3(c) and 3(d) shows results from 20 evaluations of ${\tilde{U}}^S\left(\mathit{}\mathbf{\delta }\right)$ and $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ for the SIG-optimal and pseudo-Bayesian D-optimal designs, and the NSEL-optimal and pseudo-Bayesian A-optimal designs, respectively. Again, the performances of maximin LH designs are included for reference (see figure caption for details). A comparison with Figure 3(a) and 3(b), respectively, shows lower expected gains in Shannon information and higher expected posterior variance for the hierarchical logistic regression model due to additional uncertainty introduced by the group-specific parameters. As with designs for homogenous logistic regression, the difference in expected utility between the pseudo-Bayesian designs and the fully-Bayesian designs decreases as n increases, and the LH designs perform poorly.

3.4 Binomial Regression Under Model Uncertainty

Uncertainty over the choice of statistical model π(y, ψ | δ) is common in practice, and has been addressed in pseudo-Bayesian design for generalized linear models by Woods et al. (2006). To demonstrate Bayesian optimal design under model uncertainty, we find follow-up designs for the beetle mortality study of Bliss (1935), a common example used to illustrate binomial regression. In the original dataset, 481 beetles were each administered one of eight different doses (in mg/L) of carbon disulfate. We broadly follow the case study analysis of O’Hagan and Forster (2004, pp. 423–433), who reproduced the data, and assume interest lies in providing a model-averaged posterior distribution of the lethal dose 50 (LD50), the dose required to achieve 50% mortality.

We assume that the binary indicator of death for each beetle is an independent Bernoulli random variable. The number, y_k, of deaths from dose x_k is modeled as y_k ∼ Binomial(n_k, ρ_k), where ρ_k is the probability of death for the kth dose, which was administered to n_k beetles, ∑ⁿ_{k = 1}n_k = 481. We denote the link function by g(ρ_k) = η_k, with η_k the linear predictor and consider six models formed by the Cartesian product of three link functions and two linear predictors: the logit, g(ρ_k) = log {ρ_k/(1 − ρ_k)}, the c-log-log, g(ρ_k) = log { − log (1 − ρ_k)}, and the probit, g(ρ_k) = Φ^{− 1}{ρ_k}, with Φ{ · } the standard normal distribution function; and first-order (η_i = β₀ + β₁x_i) and second-order (η_i = β₀ + β₁x_i + β₂x²_i) linear predictors.

Let $u\in \mathcal{U}=\{1,\cdots ,6\}$ denote the model indicator (see Table 1) and let β_u denote the vector of regression parameters under model u. LD50 is then given by $$\begin{array}{ccc}& & \text{LD}\left({\mathit{}\mathbf{\beta }}_u\right)\hfill \\ & & =\left\{\begin{array}{cc}\frac{w-{\beta }_0}{{\beta }_1}\hfill & \text{for}u=1,3,5\hfill \\ & \left(\text{first-order}\text{linear}\text{predictor}\right)\hfill \\ \frac{-{\beta }_1+\sqrt{{\beta }_1^2-4{\beta }_2({\beta }_0-w)}}{2{\beta }_2}\hfill & \text{otherwise},\hfill \end{array}\right.\hfill \end{array}$$where w = log { − log (0.5)} for the c-log-log link function, and 0 otherwise. We use unit information prior distributions (Ntzoufras, Dellaportas, and Forster 2003) for β_u | u under each model and set π(u) = 1/6 for u = 1, …, 6. The posterior model probabilities for each model are approximated using importance sampling to evaluate the marginal likelihood of each model, and given in Table 1. Samples from the posterior distribution of the model parameters are generated for each of the six models using the Metropolis–Hastings algorithm, and then weighted by π(u | y) to produce a sample from the joint posterior distribution β_u, u | y of regression parameters and model indicator. A sample from the model-averaged posterior distribution of LD50 can be obtained by evaluating $\text{LD}\left({\mathit{}\mathbf{\beta }}_u\right)$ for each sampled parameter vector.

Table 1. Approximate posterior model probabilities, π(u | y), for the beetle mortality data.

u	Link function	Linear predictor	π(u | y)
1	Logit	1st order	0.0216
2	Logit	2nd order	0.0686
3	C-log-log	1st order	0.7580
4	C-log-log	2nd order	0.0612
5	Probit	1st order	0.0304
6	Probit	2nd order	0.0602

We consider the design of a follow-up experiment using a further n₀ (potentially new) doses. Each dose is to be administered to $n_{0k_0}$ beetles (k₀ = 1, …, n₀) and, in each group, the number, $y_{0k_0}$, of beetles that die is recorded. Let y₀ be the n₀ × 1 vector of the numbers of beetles that die in the follow-up experiment. We assume that $n_{0k_0}$ is unknown and adopt a Poisson(λ) prior distribution. Hence $y_{0k_0}\sim \mathrm{Poisson}\left(\lambda {\rho }_{k_0}\right)$. We choose λ = 60, consistent with the values of n_k in the original dataset, and find designs for n₀ = 1, …, 10 to estimate the value of LD50 under the NSEL utility function by maximizing $$\begin{array}{ccc}& & U^V\left(\mathit{}\mathbf{\delta }\right)\hfill \\ & & =-\sum _{u=1}^6\pi \left(u\right|\mathbf{y}){\int }_{\mathcal{Y}}{\int }_{{\mathcal{B}}_u}\left[\text{LD}\left({\mathit{}\mathbf{\beta }}_u\right)\right.{\left.-\mathrm{E}\left(\text{LD}\left({\mathit{}\mathbf{\beta }}_u\right)|{\mathbf{y}}_0,\mathbf{y},\mathit{}\mathbf{\delta }\right)\right]}^2\hfill \\ & & \times \pi ({\beta }_u,{\mathbf{y}}_0|u,\mathbf{y})d{\mathit{}\mathbf{\beta }}_{u}d{\mathbf{y}}_0,\hfill \end{array}$$where design δ is the n₀ × 1 vector of doses and ${\mathcal{B}}_u$ is the parameter space for model u. For the purposes of design and modeling, we assume that ${\delta }_i\in {\mathcal{D}}_i=[-1,1]$ for all i = 1, …, n₀ but transform the doses to the original scale [1.6907, 1.8839] for the presentation of results.

We can approximate U^V(δ) by $$\begin{array}{c}\hfill {\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)=-\frac{1}{B}\sum _{l=1}^B{[\text{LD}\left({\mathit{}\mathbf{\beta }}_{ul}\right)-\widehat{\mathrm{E}}\left(\text{LD}\left({\mathit{}\mathbf{\beta }}_u\right)\right|{\mathbf{y}}_{0l},\mathbf{y},\mathit{}\mathbf{\delta })]}^2,\end{array}$$where {β_ul, u_l, y_0l}^B_{l = 1} is a random sample from the joint distribution with density π(β_u, u, y₀ | y), and $$\begin{array}{c}\hfill \widehat{\mathrm{E}}\left(\text{LD}\left({\mathit{}\mathbf{\beta }}_m\right)|{\mathbf{y}}_0,\mathbf{y},\mathit{}\mathbf{\delta }\right)=\frac{{\sum }_{b=1}^{\tilde{B}}\text{LD}\left({\widetilde{\mathit{}\mathbf{\beta }}}_{\tilde{u}b}\right)\pi \left({\mathbf{y}}_0\right|{\widetilde{\mathit{}\mathbf{\beta }}}_{\tilde{u}b},{\tilde{m}}_b)}{{\sum }_{b=1}^{\tilde{B}}\pi \left({\mathbf{y}}_0\right|{\widetilde{\mathit{}\mathbf{\beta }}}_{\tilde{u}b},{\tilde{m}}_b)},\end{array}$$where ${\{{\widetilde{\mathit{}\mathbf{\beta }}}_{\tilde{u}b},{\tilde{m}}_b\}}_{b=1}^{\tilde{B}}$ is a random sample generated from the joint distribution with density π(β_u, u | y).

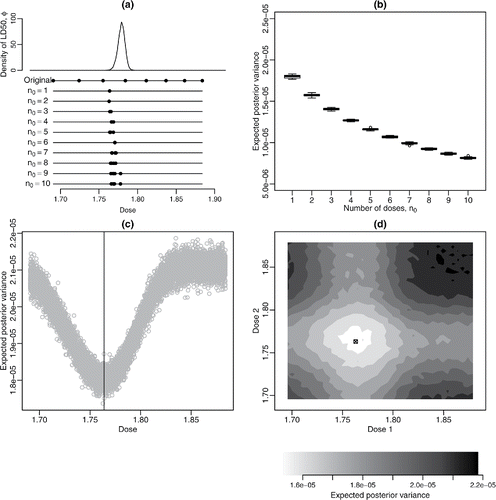
Figure 4 summarizes the results from the ACE algorithm. The doses in the NSEL-optimal design lie in the lower tail of the (original) posterior distribution of LD50 for all values of n₀, see Figure 4(a). For n₀ > 1, the doses are concentrated near a single point (1.77), for example, four replicate points occur for n₀ = 10. The approximate expected posterior variance of LD50, $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$, rapidly decreases as n₀ is initially increased from 1, see Figure 4(b); the rate of decrease slows as n₀ becomes larger.

Figure 4. (a) Posterior density for LD50, the original experimental doses and optimal doses (in mg/L) for each value of n₀; (b) boxplots of 20 evaluations of $-{\tilde{U}}^V\left({\mathit{}\mathbf{\delta }}^{★}\right)$ for each n₀ for the NSEL-optimal designs; (c) negative approximate expected utility $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ against dose for n₀ = 1; the vertical line indicates δ^⋆. (d) negative approximate expected utility $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ against dose for n₀ = 2; ⊠ indicates δ^⋆.

To further investigate the selected designs, the expected utility surface and the performance of the ACE algorithm, we randomly generated 10,000 designs for n₀ = 1 and n₀ = 2 uniformly from ${\mathcal{D}}_1$ and ${\mathcal{D}}_1^2$, respectively. For each design, we evaluate $-{\tilde{U}}^V\left(\mathit{}\mathbf{\delta }\right)$ and plot against dose; see Figure 4(c) for n₀ = 1 and Figure 4(d) for n₀ = 2. The NSEL design identified by ACE is marked in each plot and, for both values of n₀, the minimum negative expected utility is achieved. The variance of the original model-averaged posterior distribution for LD50 is 2.10 × 10^{− 5}. Hence for both n₀ = 1 and n₀ = 2, it is clear that choosing a design composed of only very high or low doses would have resulted in a negligible expected reduction in variance.

4. Discussion and Future Work

The ACE methodology proposed in this article provides a step-change in the nature and complexity of statistical models and experiments for which Bayesian designs can be obtained. It may be used to find decision-theoretic designs whenever it is possible to simulate values from the prior distribution of the model parameters and responses from the statistical model. The combination of emulating an approximation to the expected utility and the coordinate exchange algorithm has allowed much larger problems to be tackled than was previously possible, both greater numbers of runs and more controllable variables. The algorithm also matches or exceeds the performance of existing approaches for smaller problems, and offers a clear advantage for design selection over the application of a dimension reduction scheme. The new designs made possible by this methodology also allow previously impossible benchmarking of designs from asymptotic approximations.

As presented, ACE can be applied to numerous important practical problems using the available R package. We have applied, or are in the process of applying, ACE to problems from chemical development and biological science. There are also a variety of extensions that could be made to ACE to increase its computational efficiency and applicability. We now highlight a few of these areas.

In ongoing work, we are extending and applying the methodology to find designs for statistical models where the likelihood function is only available numerically as the output from an expensive computer code (see also Huan and Marzouk 2013). Such models include those described by the solution to a system of nonlinear differential equations, which are increasingly studied in the field of uncertainty quantification (e.g., Chkrebtii et al. 2015).

Convergence of the algorithm may be improved through a reparameterization of the design to remove dependencies between coordinates (e.g., Fletcher 1987, p. 19) that can be evident in efficient designs for some models. Such dependencies could be identified through pilot runs of the algorithm or by studying properties of pseudo-Bayesian designs. Additionally, the computational burden of the algorithm could be further reduced by employing alternative approaches to perform each one-dimensional optimization step in the algorithm. For example, a sequential strategy could use an expected improvement criterion modified for stochastic responses (e.g., Pichney et al. 2013).

Alternative strategies could also be adopted for the approximation of the expected utility. Zero-variance Monte Carlo (Ripley 1987, pp. 129–132, Mira, Solgi, and Imparato 2013) could be used to reduce the variance of the Monte Carlo estimator through the introduction of negative correlations via antithetic variables. Combining deterministic approximations, such as expectation propagation, with Monte Carlo methods would remove the need for nested simulation and may work well for nonlinear regression models with normal prior distributions.

Supplementary Materials

The supplementary material includes the designs discussed in the article, and documentation and code to reproduce all the examples. The R package acebayes that implements the ACE algorithm is available on CRAN (https://cran.r-project.org/package=acebayes).

Acknowledgments

This work was supported by the U.K. Engineering and Physical Sciences Research Council through Fellowship EP/J018317/1 for D.C. Woods. The authors thank the editor, an associate editor, and two reviewers for comments that improved the article, and the participants at the “Bayesian Optimal Design of Experiments” workshop (Brisbane, Australia, December 2015; http://www.bode2015.wordpress.com) for useful discussions on extensions and future work. The authors acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work.