Measurement errors and misestimation: their effects on drinking outcomes

KEYWORDS:

• alcohol use disorder
• treatment outcomes
• drink size
• standard drink
• statistical power
• data simulation

This article is referred to by:

Consumption outcomes in clinical trials of alcohol use disorder treatment: Consideration of standard drink misestimation

Definitions and measures form the foundation for epidemiological, clinical trials, or any other quantitative research. Thus, the operational definitions and measurements of substance use we select determine what we actually study. The differences in the operational definition of use can also reflect philosophical views (e.g., abstinence-based versus harm reduction approaches), produce substantial differences in prevalence estimates, and affect statistical power.

In this issue of The American Journal of Drug and Alcohol Abuse, Kirouac and her colleagues (1) compared two outcome measures of alcohol intake in the COMBINE medication trial (2) to investigate drink size misestimation. Both indices were based on the number of heavy drinking days. One was the percent of heavy drinking days over a defined follow-up period and the other was whether or not there were any heavy drinking days. The first measure is a continuous value and the second one is a binary value. This paper investigated how the two indices would react to various levels of drink size misestimation and influence a clinical trial‘s effect size. If we were dealing with textbook data (i.e., normally distributed) and simple error (i.e., unbiased data), the results could have been predicted from basic statistical theory. However, the real world seldom offers us such pristine data. From an applied statistics perspective, Kirouac and colleague contributions are very interesting because of the use of simulations that incorporate real-life situations such as heavy drinking day counts into statistical considerations. These situations are often studied in statistics in a more abstract and idealized way.

Suppose, in addition to the usual standardized self-report measures of how many drinks a subject had each day (the measured observed values), we also had an independent and accurate knowledge of exactly how many drinks the subject consumed (the true values). The self-report measure is subject to vagaries such as an imperfect memory (error). Classical measurement theory formalizes this type of situation by positing that the observed value equals the true value plus some error. The reliability coefficient (3) reflects the percentage of a score that represents variability in the true values, which can be used to understand phenomena; the rest is noise. The error makes it harder to learn from these phenomena.

The reliability of a measured score directly affects the expected effect size in a trial. For example, if a new treatment medication reduced the number of heavy drinking days, it would affect the true number of drinks consumed and not affect the subjects‘ imperfect memory (the error). Thus, if there is a genuine treatment effect acting on the true values, it changes the true values and not the error. In the extreme situation when there is no error, the reliability is perfect (i.e., it takes the value 1.0) and the effect size for the true outcome values equals the effect size of the observed phenomenon. However, there is always some error and as the amount of random error is increased, the effect size of the true values is diluted proportional to the square root of the reliability, such that it will be lower than 1.0 in the presence of error (4–6). Simulating a real issue in the addiction field, Kirouac and her colleagues used increasing drink size misestimation rather than increasing a random error (with mean zero), so the effect of increasing noise appears somewhat different than would be predicted from measurement theory based on normally-distributed and unbiased data. Increasing the misestimation decreased the effect size, which in turn lowered the statistical power.

The other issue Kirouac and her colleagues investigated was the loss of power switching from a continuous measure to a dichotomy. Here, the choice was the percent of heavy drinking days contrasted with no versus any heavy drinking days. There can be a heavy cost to pay for dichotomizing a continuous variable. Based on statistical theory, assuming a linear model and normal distribution of the outcome variable, a dichotomy will – at best – reduce the effect size to approximately 80% (7,8). A medium sized Cohen‘s d for the continuous measure, say 0.5, would be reduced to about 0.4 (0.5 * 0.80). This assumes that the cut point for the dichotomy is at the mean of the continuous variable dichotomized. As the cut point moves away from the middle of the distribution, the reduction becomes more dramatic. The numbers derived by Cohen (7) and earlier rely firmly on these mathematical assumptions. Thus, the use of simulations and real data by Kirouac and colleagues was vital to find out how dichotomizing percent heavy drinking days affects the effect sizes.

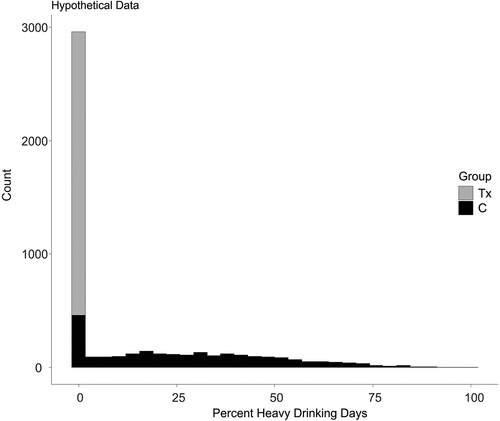
As Cohen (7) notes, however, there are cases where dichotomizing the data might increase the effect size and power. He goes on to suggest that these counterexamples might be unusual. To demonstrate this concept visually, I generated a somewhat unrealistic hypothetical study where all of the patients in the treatment group were successful and had zero heavy drinking days at follow-up. In contrast, the patients in the control group had a population mean of 25.2% heavy drinking days and a standard deviation of 20.7%. Only some control subjects had zero heavy drinking days. These data appear in Figure 1 for 5,000 hypothetical cases. Cohen‘s h based on the binary (no heavy drinking days versus any heavy drinking days) was 2.27. Cohen‘s d comparing the mean percent drinking days was 1.72. In this case, given that h and d are comparable, the power for the dichotomy is larger than for the continuous measure. So, while generally we might expect a reduced effect size from dichotomizing the data resulting in a loss of power, that outcome is not guaranteed. The paper by Kirouac and her colleagues revisited this important question and asked how much of a reduction might occur with real data and drink misestimation. They found that dichotomizing the scores reduced the effect sizes. Additionally, they noted that increasing the drink misestimation weakened the effect size.

Figure 1. Real GDP per capita in Kazakhstan.

An earlier study by Falk and his colleagues also used clinical trial data to look at the dichotomous versus continuous indices of heavy drinking days (9). Unlike the Kirouac et al. study, Falk and his group did not see a decrease in the effect size using the dichotomous outcome. Generally, the dichotomy showed roughly as good or larger effect sizes. The earlier study, however, did not consider the error associated with drink size misestimation.

In one sense, the results of these investigations are clear. Adding random error or misestimation weakens effect sizes. Studies need to invest the effort to standardize their outcome measures. The standardization needs to minimize both random error and misestimation. Misestimation could easily produce biased results. For example, if people who drank more also tended to show more drink misestimation and then drank less, which affected their drink misestimation, the effect size might be erroneously increased since there was more bias in the baseline than in the follow-up assessment. In another sense, the jury is still out whether to use a continuous versus a dichotomous outcome. Using real data, one study found that the binary variable worked well (9), another study found that it did not work in the presence of drink misestimation (1). As Cohen noted, other situations could make a dichotomy perform better than the continuous measure (7). One major contribution of the Kirouac et al. study is that it reminds us to continue worrying about measurement.