The advantage of mixing examples in inductive learning: a comparison of three hypotheses

Abstract

Mixing examples of different categories (interleaving) has been shown to promote inductive learning as compared with presenting examples of the same category together (massing). In three studies, we tested whether the advantage of interleaving is exclusively due to the mixing of examples from different categories or to the temporal gap introduced between presentations. In addition, we also tested the role of working memory capacity (WMC). Results showed that the mixing of examples might be the key component that determines improved induction. WMC might also be involved in the interleaving effect: participants with high spans seemed to profit more than participants with low spans from interleaved presentations. Our findings have relevant implications for education. Practice schedules should be individually customised so society as a whole can profit from differences between learners.

Keywords:

• Interleaving
• inductive learning
• individual differences
• working memory

The publication of ‘Learning Concepts and Categories …’ by Kornell and Bjork (2008) caused a small stir in the field of applied cognitive psychology. The commotion is understandable as the study revealed findings that run counter to the expectations of the majority of the participants and the authors themselves. In a task of inductive learning of painting styles, Kornell and Bjork hypothesised that seeing examples of a category together should help find commonalities between those examples and thus abstract the common features that conform the category. In contrast, they found that inductive learning of a concept or category could be promoted by presenting exemplars of that category intermixed with exemplars of other categories (spacing), rather than presenting all exemplars from one category together (massing). More specifically, they presented their participants with paintings by 12 different relatively unknown painters and tested afterwards their knowledge of the styles by asking them to classify paintings not seen during the training. In several experiments in which they manipulated presentation style as within or between subjects, the same results were found and replicated: mixing paintings by different authors resulted in better accuracy in the classification test than presenting all the paintings from the same author together. In addition, when participants were asked about their performance after doing the test, they consistently rated massing as the superior strategy, although their results revealed the opposite.

As an explanation of their finding, Kornell and Bjork (2008) proposed that the interleaving of examples from different categories helped participants see the differences between the categories and determined thus the advantage of the spaced condition. They argued that in fact it might have been interleaving alone, regardless of temporal spacing, that gave the advantage to the spaced conditions. This assertion prompted Kang and Pashler (2012) to try to separate the effects of interleaving from those of temporal spacing. In their study, they compared massed and interleaved conditions with a temporal-spaced condition (in fact a massed condition where a time interval was introduced between presentations). In addition, they had in their design simultaneous conditions in which examples were presented together from the same category (Experiment 1) and from different categories (Experiment 2). According to their expectations, interleaving paintings produced the best performance, only matched by the simultaneous presentation of examples from different categories.

The results of Kang and Pashler (2012) have since been replicated by Zulkiply and Burt (2013) who also found no effect of temporal gap in an inductive learning task. However, Birnbaum, Kornell, Bjork, and Bjork (2013) found that introducing a time interval between examples in a massed condition improved performance (see Vlach, Sandhofer, and Kornell (2008) for a similar result with children). They concluded that temporal space helps induction as long as it is not combined with the interleaving of the exemplars. This should not come as a surprise because after all spacing effects are very robust. One characteristic feature of spacing effects is that they increase after a delay (Cepeda et al., 2009). Considering that in all the previously mentioned studies, testing occurred immediately after the learning phase (except in Kang and Pashler where there was a 20-min delay), the question arises as to whether the effect of temporal spacing could show up more strongly, even in combination with interleaving, when a meaningful delay is introduced. Thus, one of the aims of the present study was to test the effect of temporal spacing after a one-day delay.

A second aim was to test three competing accounts explaining the advantage of mixing vs. massing presentations. A first account has been termed the discrimination hypothesis and is focused exclusively in the interleaving component of the manipulation. According to the hypothesis, interleaving gives the learner the opportunity to compare examples of different categories and search for differences, which helps to better discriminate among the categories being learned (Wahlheim, Dunlosky, & Jacoby, 2011). This strategy should be optimal when there is a high degree of similarity between the categories because if the differences are very salient, there is no need to compare examples to find those differences. The hypothesis thus predicts that interleaving examples promotes induction when categories are difficult to discriminate; however, if categories are easy to discriminate, then the massing of examples should favour induction. The discrimination hypothesis was first proposed by Kurtz and Hovland (1956) who found that massing examples of simple artificial categories (easy to discriminate) promoted performance in an inductive test, as compared to intermixing examples of different categories. Kang and Pashler (2012) used paintings (difficult to discriminate categories) and compared four different conditions: simultaneous presentation of same category examples, simultaneous presentation of different category examples, massed and interleaved. Their results showed no difference between the simultaneous-different and interleaved conditions, with participants in both conditions outperforming those in the simultaneous-same and massed conditions. This result was replicated and extended recently by Zulkiply and Burt (2013) who also used artificially created categories and manipulated the degree of discriminability. The results of their study showed an advantage of massing in highly discriminable categories but an advantage of interleaving when categories were low in discriminability, giving strong support to the discrimination hypothesis. Carvalho and Goldstone (2014) also reported a similar interaction between category structure and type of presentation where interleaving helped learning of categories with high degree of similarity, whereas blocking (massing) helped learning of categories with low degree of similarity.

An alternative and not necessarily exclusive explanation of the advantage of mixing examples is based on distributed retrieval from long-term memory. According to Dunlosky, Rawson, Marsh, Nathan, and Willingham (2013), massing exposures to a concept implies that when the second example is presented, the representation of the first example might still be in working memory so its retrieval is not necessary. However, in spaced training, the presentation of the second example might trigger the automatic retrieval of the representation of a previous example or simply demand the explicit retrieval of category-related information. This act of retrieval would serve to strengthen the path and contribute to the strong performance on a later test. Rohrer and Taylor (2007) illustrate the idea of distributed retrieval with a task of learning to solve mathematical problems. When students practice solving mathematical problems under a massed schedule, they simply apply the same procedure repeatedly. However, under an interleaved schedule, the students practice with different types of problems, therefore they have to classify every problem into a category in order to retrieve the appropriate procedure to solve it. The process of continuous retrieval of category-related information and classification of new exemplars might be the key to the advantage of interleaving (Rohrer, 2012). This study-phase retrieval account also received support from the previously described study by Birnbaum et al. (2013). Birnbaum and colleagues found that when degree of juxtaposition between categories was controlled (thus controlling discrimination processes), larger temporal spacing benefitted inductive learning.

The study-phase retrieval hypothesis and the discrimination hypothesis hold different predictions regarding the role of working memory capacity (WMC) in interleaving effects. According to the study-phase retrieval hypothesis, the advantage of interleaving is related with increased practice in the act of retrieval from long-term memory, rather than with the capacity to hold simultaneously different representations (as proposed by the discrimination hypothesis). If the advantage of interleaving is due to extra practice in the retrieval of the concepts from long-term memory, then differences in WMC should not influence the interleaving effect. However, if the advantage of interleaving is a result of the opportunity to compare examples from different categories, then differences in WMC might have an influence: those individuals who can hold more features of the immediately preceding example should be able to do a more thorough comparison with the current example and thus better discriminate between the categories represented. Thus, a second aim of the present study was to test the effect of WMC in the interleaving effect.

A third explanation of the advantage of mixing examples is the voluntary attention hypothesis, according to which participants simply find less interesting the repetitions under massed than spaced conditions and consequently choose to pay less attention (Dempster, 1989). The hypothesis fits nicely with the results of metacognitive analyses (Kornell & Bjork, 2008; Kornell, Castel, Eich, & Bjork, 2010; Logan, Castel, Haber, & Viehman, 2012) that show how participants might get misled by the sense of fluency promoted by massed repetitions. Although the hypothesis was proposed first by Hintzman, Summers, Eki, and Moore (1975), it has made a comeback recently under the name of attention–attenuation hypothesis (Wahlheim et al., 2011). Wahlheim and colleagues predicted that if individuals pay less attention to successive examples of the same category when they are presented under massed conditions, then their accuracy on a recognition test should also decrease as a function of order of presentation. In order to test this hypothesis, they had their participants study pictures of bird families under massed or spaced conditions and asked them afterwards to recognise the same exemplars seen during training. According to their expectations, accuracy in the recognition test decreased after the first presentation in the massed condition but remained relatively constant in the spaced condition.

The attention–attenuation hypothesis was also indirectly tested by Kornell et al. (2010) through the comparison of induction and repetition conditions. The task was inductive learning of painting styles (as in Kornell & Bjork, 2008) and presentation style (massed or spaced) was manipulated within-subjects. In addition, in the induction condition, participants saw six examples of each painter and were asked later to classify new examples, whereas in the repetition condition, they saw only one example of each painter and were asked later to classify the same example. Although the study was not designed as a test of the attention–attenuation hypothesis, the authors reasoned that if a decrease in interest and attention to repetitions in the massed condition is the key to the spacing effect, then this decrease should be even greater when the example used is exactly the same on every repetition; therefore, the spacing effect should be bigger in the repetition than in the induction condition. Their results however failed to show this interaction in marked contrast to those of Wahlheim et al. (2011). One obvious difference between the two studies is that Kornell et al. did not include in their design a test of studied items; so, in the present study, we addressed that point by adding a test of the items presented during training to the design of Kornell and colleagues.

The present study

The present study was designed to address the discrepancy in results between Wahlheim et al. (2011) and Kornell et al. (2010). In addition, we tried to further research the contribution of temporal spacing to the interleaving effect in the paradigm introduced by Kornell and Bjork (2008). Last and as a test of the discrimination hypothesis, we wanted to investigate whether WMC is involved in the advantage of interleaved presentations. We conceptualise working memory (WM) following Engle and colleagues (Conway et al., 2005) as a multicomponent system responsible for keeping information active under the interference of ongoing processing activities. In this view, WMC is related with domain-general, rather than domain-specific, executive attention. Therefore, in Experiment 1, we replicated the design of Kornell and Bjork with the addition of a test of studied items in order to test the attention–attenuation hypothesis and a WM span task designed to obtain a measure of WMC. In Experiment 2, we repeated the same design manipulating the temporal gap between participants. Experiment 3 also included a manipulation of the temporal gap and, in addition, participants had to come one day later to be tested again.

Experiment 1

The first experiment broadly replicated the basic design of Kornell and Bjork (2008), where presentation style is manipulated within-subjects and induction is tested in an immediate test. In addition, we also added a test of studied items to try to replicate the results of Wahlheim et al. (2011). We expected an advantage of spacing in general, as well as higher accuracy and/or lower reaction time with the first item presented under massed conditions in the test of studied items.

Method

Participants

The participants were 23 undergraduate students of the University of Groningen who took part in the study voluntarily. Their average age was 23.09 (SD = 2.22), and 57% were female.

Materials

The experiment was run on personal desktop computers with 51-cm colour monitors and standard keyboards. The computers were located in individual cabins and participants sat at approximately 60 cm from the computer screen. Stimuli were presented and responses were registered with a programme written in E-prime (Schneider, Eschman, & Zuccolotto, 2002)

The materials used during the inductive learning task were taken from the Kornell and Bjork (2008) study and consisted of 10 paintings showing skyscapes or landscapes by each of 12 relatively unknown artists: Georges Braque, Henri-Edmond Cross, Judy Hawkins, Philip Juras, Ryan Lewis, Marilyn Mylrea, Bruno Pessani, Ron Schlorff, Georges Seurat, Ciprian Stratulat, George Wexler and YieMei. Six paintings by each artist were used during the study phase and one of the four remaining un-seen paintings was used during the test phase.

Working memory capacity was assessed through an automated symmetry span task (Kane et al., 2004). Performance in complex span tasks, such as the reading span, operation span or symmetry span, is supposed to reflect the ability to keep information active while retrieving extra information from long-term memory. The storage component (amount of information retrieved) is similar among the tasks. However, the processing component (information manipulated) changes, being verbal in the reading span, numerical in the operation span and spatial in the symmetry span. For this reason, we chose the automated symmetry span as our measure of WMC. In the automated symmetry span task, participants have to remember sets of coloured squares on a 4 × 4 grid while performing a concurrent task (verify the symmetry of black-and-white matrix patterns). The sets range from 2 to 5 elements and every set is presented three times, randomly ordered per participant. A trial of the automated symmetry span task starts with the presentation of the figure for the symmetry judgement task. Once the participant has responded, the 4 × 4 grid is presented for 650 ms with one of the squares shaded in red. After a full set of red squares has been presented, the participant is prompted to recall their locations in serial order by clicking with the mouse on an empty grid.

Procedure

Participants read and signed first a consent form and after this, they performed the automated symmetry span task and the inductive learning task. The instructions for both tasks were given through the computer screen and participants were informed that they could ask the researcher at any moment if something was not clear.

The inductive learning task consisted of a study phase and a testing phase. During the study phase, 72 paintings, 6 by each of the 12 artists, were randomly selected per participant and shown on the computer screen for 3 s with the name of the artist displayed above the painting. The artists were assigned randomly per participant to the massed (M) or spaced (S) conditions. In the massed condition, the paintings of one artist constituted one block, whereas in the spaced condition, a block was formed by one painting by each of the six artists. The order of presentation of the six spaced artists was randomised and thus different for each participant but kept constant throughout the blocks of the study phase. The study phase consisted thus of 12 blocks with 6 paintings each and the order of the blocks was MSSMMSSMMSSM. Immediately after the study phase, the test phase followed. The test phase involved a test of new items, paintings not-seen during the study phase, followed by a test of studied items, the 72 paintings used during study. One painting from each artist was selected randomly per participant to be used during the test of new items. Each painting was presented on the left side of the screen while a numbered list with the names of the 12 artists was shown on the right (see Figure 1). The participant was instructed to type the number of the author of the painting at the bottom of the screen. No time limit was given for the response and no feedback was provided. The interface during the test of studied items was identical to that of the test of new items, and the 72 paintings were presented in 6 blocks of 12 paintings (one by each artist). The order of the paintings within a block was randomised per participant.

Figure 1. Screenshot of the computer on a given trial during the testing phase.

Following the testing phase, the meaning of the terms massed and spaced was explained to the participants and they were asked the following question: ‘Which do you think helped you learn more, massed or spaced?’ The response options were: ‘massed’, ‘spaced’ and ‘about the same.’

Results and discussion

Classification of new items

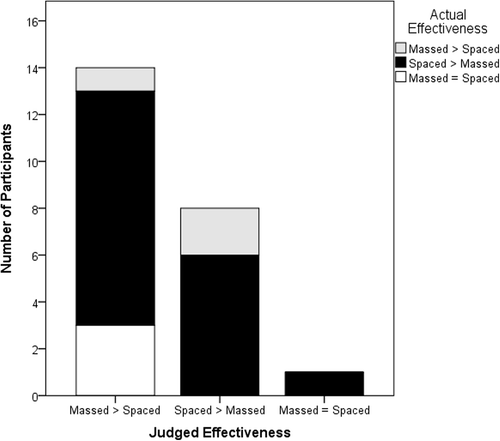
As predicted, the proportion of correctly identified artists during the test of the new items was greater under spaced (M = .62) than massed (M = .39) conditions (t [23] = 4.1, p < .001). This result, replicating the findings of Kornell and colleagues, was in marked contrast with the perception of the participants. As Figure 2 shows, 61% of participants thought they learned better when paintings were presented in a massed fashion, but 74% actually did better when paintings were presented under spaced conditions.

Figure 2. Judged effectiveness of presentation style in Experiment 1, as a function of actual effectiveness (the number of participants within each judged category is divided according to their actual performance).

Classification of studied items

The data from the test of studied items were analysed in terms of accuracy. The expectation, according to the attention–attenuation hypothesis (Wahlheim et al., 2011), was that the item presented first under massed conditions would be recalled more accurately than the following items, whereas order of presentation would not make a difference under spaced conditions. A two-way within-subjects ANOVA was carried out on the proportion of correct answers with presentation style (spaced or massed) and order of presentation (first to sixth) as within-subjects factors. The results revealed only a main effect of presentation style. As in the test of new items, participants were more accurate with painters presented under spaced than massed conditions (means .63 and .44, respectively, (F [1, 22] = 18.75, p < .001, ηp²= .46)¹. However, and as Figure 3 shows, there was no effect of order of presentation (F [5, 110] = 1.39, p = .23, ηp²= .06) or interaction between presentation style and order of presentation (F [5, 110] = .64, p = .66, ηp²= .03).

Figure 3. Average accuracy during the test of studied items in Experiment 1, as a function of presentation style (spaced or massed) and order of presentation (one to sixth). Error bars depict the standard error of the mean.

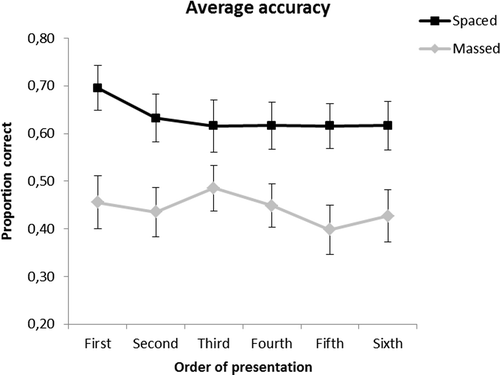
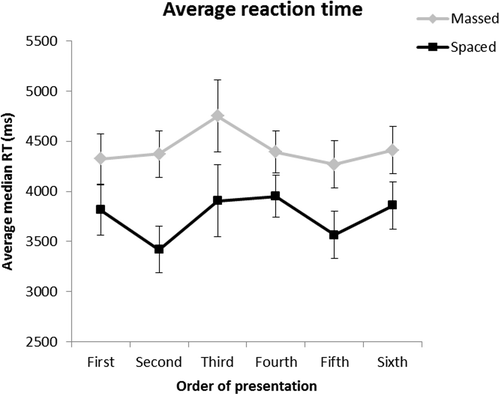
To rule out the possibility that the extra attention paid to the first item under massed conditions could manifest itself in faster recognition time rather than greater accuracy (i.e. reaction time/accuracy trade-off), we also analysed the data from the test of studied items in terms of reaction time. Therefore, we carried out a two-way within-subjects ANOVA on median RT, with presentation style (spaced or massed) and order of presentation (first to sixth) as within-subjects factors. The analysis of the RT (Figure 4) replicated the results of the analysis of accuracy. There was a main effect of presentation style with spaced painters being identified faster than massed ones (median RTs of 3.6 and 4.2 s, respectively, (F [1, 22] = 13.56, p < .001, ηp²= .38), but no effect of order of presentation (F [5, 110] = .62, p = 0.68, ηp²= .03) or interaction (F [5, 110] = .47, p = .80, ηp²= .02). Figures 3 and 4 show that there was no trade-off in the effect of presentation style; painters presented under spaced conditions were identified faster and more accurately than those under massed conditions.

Figure 4. Average reaction time (mean of medians) during the test of studied items in Experiment 1, as a function of presentation style (spaced or massed) and order of presentation (one to sixth). Error bars depict the standard error of the mean.

Relation of working memory capacity

Finally, and in order to explore the possible involvement of working memory capacity in inductive learning, we calculated the correlation between accuracy in the tests (studied and new items) and WMC scores. The scores in the WMC task were calculated as the sum of all perfectly recalled sets (Conway et al., 2005). Two participants were excluded for failing to reach the criterion of 85% accuracy in the concurrent symmetry judgement task. The correlations between WMC scores and accuracy in massed items were very small and non-significant (r [21] = .035, p = .882 and r [21] = −.004, p = .986, in the test of studied and new items, respectively). The correlations between WMC and accuracy in spaced items, although stronger than under massed conditions, were also non-significant (r [21] = .241, p = .294 and r [21] = −.128, p = .581, in the test of studied and new items, respectively). A clear caveat of the present study is the size of the sample; therefore, in the next study, we set to replicate the same basic design with a larger number of participants.

Experiment 2

The second experiment replicated the first one with the addition of a manipulation of the temporal gap between-subjects. The expectation is that if spacing adds to interleaving, then we should see an interaction effect showing the best performance in the case of the spaced, long gap condition. As in Experiment 1, we were also interested in testing the attention–attenuation hypothesis through a test of studied items and investigating the role of WMC.

Method

Participants

The participants were 88 first-year students (78% female) at the University of Groningen who took part in the study in exchange for course credit. Their average age was 21.2 (SD = 3.25). Four participants who failed to perform at a minimum of 85% accuracy during the symmetry task were excluded from the analyses.

Materials

The materials were identical to those used in Experiment 1.

Procedure

The procedure was the same as in Experiment 1 with the difference that participants were assigned to one of two gap conditions. In the short gap condition, paintings were presented during the study phase for 5 s, whereas in the long gap condition, the presentation time was extended to 10 s per painting. In addition and to keep the length of the gap constant within conditions, the order of the study blocks was modified to be the following: MSMSMSMSMSMS. As in Experiment 1, the order of presentation of the spaced artists was kept constant in all the blocks of the study phase (after being randomised per participant). This implies that the time interval between study trials, i.e. length of the gap, of any given spaced artist, was 55 s in the short gap condition (30 s from a massed block plus 25 s from the other 5 spaced paintings) and 110 s in the long gap condition. Our design consisted of presentation style (massed or spaced) as a within-subjects variable and gap condition (short or long) as a between-subjects variable. In addition, scores in the working memory capacity task were divided through a median-split and participants were thus assigned to low or high WMC groups. The dependent variables were accuracy scores in the tests of new and studied items.

Results

Classification of new items

Accuracy in the test of new items was analysed with a mixed ANOVA with gap condition (short or long) and WMC (low or high) as between-subjects factors and presentation style (massed or spaced) as a within-subjects factor. Table 1 shows the means for all the conditions of the design. Results revealed a significant effect of presentation style (F [1, 80] = 47.61, p < .001, ηp²= .373) which shows that authors studied under spaced conditions were identified more accurately (M = .68) than those studied under massed conditions (M = .47). The effect of gap condition was marginally significant (F [1, 80] = 3.93, p = .051, ηp²= .047), showing an advantage for the long vs. the short gap condition (M = .62 and M = .53, respectively). Finally, the high WMC group was also more accurate than the low WMC group (M = .63 and M = .53, respectively; (F [1, 80] = 4.41, p = .039, ηp²= .052). None of the interactions approached significance.

Table 1. Mean proportion accuracy (SE between parentheses) in the test of new items in Experiment 2 as a function of presentation style, gap condition and WMC.

		Massed	Spaced
Short gap	Low WMC	.37 (.06)	.56 (.06)
	High WMC	.49 (.05)	.71 (.05)
Long gap	Low WMC	.48 (.05)	.70 (.05)
	High WMC	.56 (.06)	.76 (.06)

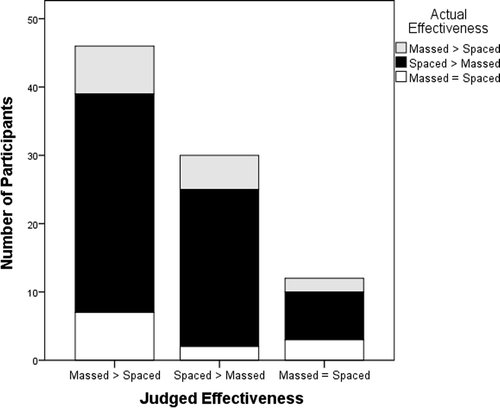
The comparison of judged with actual effectiveness also replicated the findings of Experiment 1. As Figure 5 shows, 52% of participants judged massing to be the most effective presentation style when in reality, spacing was more effective for 70% of them.

Figure 5. Judged effectiveness of presentation style in Experiment 2, as a function of actual effectiveness (the number of participants within each judged category is divided according to their actual performance).

Classification of studied items

The data from the test of studied items was analysed regarding accuracy and reaction time. Accuracy scores (proportion mean correct) were submitted to a mixed ANOVA with presentation style (massed or spaced) and order of presentation (first to sixth) as within-subjects factors and gap condition (short or long) and WMC (low or high) as between-subjects factors (see Table 2 for the means).

Table 2. Mean proportion accuracy and mean RT (SE between parentheses) in the test of studied items in Experiment 2 as a function of presentation style, gap condition and WMC.

		Massed		Spaced
		Accuracy	RT (ms)	Accuracy	RT (ms)
Short gap	Low WMC	.45 (.06)	4029 (262)	.59 (.05)	3311 (252)
	High WMC	.48 (.05)	3930 (222)	.72 (.04)	3857 (213)
Long gap	Low WMC	.56 (.05)	4246 (227)	.72 (.04)	3920 (218)
	High WMC	.54 (.06)	4331 (270)	.76 (.05)	3756 (259)

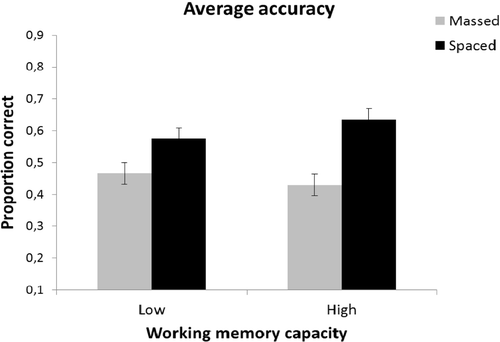
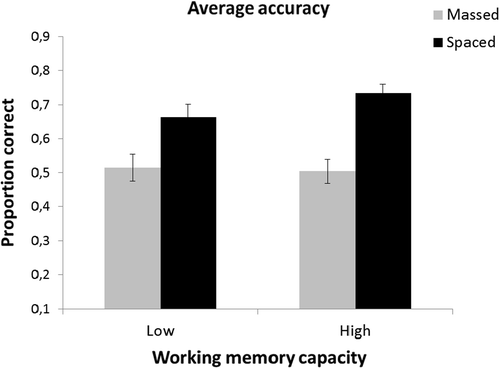
The results showed a significant effect of presentation style (F [1, 80] = 60.12, p < .001, ηp²= .429) with paintings under spaced conditions (M = .69) being identified more accurately than paintings under massed conditions (M = .51). There was also a marginally significant effect of gap condition (F [1, 80] = 3.68, p = .059, ηp²= .044), showing that participants in the long gap condition were more accurate (M = .64) than those in the short gap condition (M = .56). Finally, there was also a marginally significant interaction between presentation style and WMC (F [1, 80] = 2.87, p = .094, ηp²= .035). As Figure 6 shows, the advantage of spaced presentations was more pronounced in individuals with high WMC. The main effects of order of presentation (F [5, 400] = 1.68, p = .138, ηp²= .021) and WMC (F [1, 80] = 1.00, p = .319, ηp²= .012) were not significant nor were any of the remaining interactions.

Figure 6. Average proportion accuracy during the test of studied items in Experiment 2, as a function of presentation style (spaced or massed) and WMC (low or high). Error bars depict the standard error of the mean.

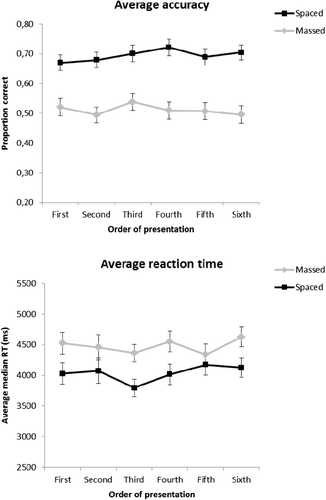
Median reaction times during the test of studied items were also analysed with a mixed ANOVA with presentation style (massed or spaced) and order of presentation (first to sixth) as within-subjects factors and gap condition (short or long) and WMC (low or high) as between-subjects factors. Painters presented under spaced conditions were identified faster than those under massed conditions (M = 3970.40 and M = 4429.97, respectively, (F [1, 80] = 15.55, p < .001, ηp²= .163). There were no effects of position (F [5, 400] = .52, p = .756, ηp²= .007), WMC (F [1, 86] = .11, p = .739, ηp²= .001) or gap condition (F [1, 80] = 1.04, p = .309, ηp²= .013), and none of the interactions approached significance. Figure 7 shows that the first item presented under massed conditions was not recognised better or faster than the following items. Our results thus failed to support the attention–attenuation hypothesis.

Figure 7. The upper panel shows average proportion accuracy and the lower panel average reaction time (mean of medians) during the test of studied items in Experiment 2, as a function of presentation style (spaced or massed) and order of presentation (one to sixth). Error bars depict the standard error of the mean.

Discussion

Experiment 2 replicated the main results of Experiment 1; those are: advantage of spaced presentations and mismatch between perceived and actual performance. As in Experiment 1, we failed to support the attention–attenuation hypothesis. The lengthening of the temporal gap had a positive effect on inductive learning; however, this effect did not interact with presentation style. In addition, we found some support for a possible link of WMC with the spacing effect: all participants seemed to profit from spaced as compared to massed presentations; however, those with high WMC seemed to profit more. Although the result should be considered cautiously because the difference was not statistically significant, Figure 6 shows that low and high WMC individuals did not differ in their performance on massed items (means .51 and .50, respectively), but high WMC seemed to be related with an advantage in classifying spaced items (means .66 and .73 for low and high WMC).

Experiment 3

A key feature of Experiment 2 is that the manipulation of the temporal gap involved an extension of the presentation time, from 5 s in the short gap condition to 10 s in the long gap condition. This manipulation obviously brings extra study time as an additional difference between the conditions. In the third experiment, the temporal gap between examples was filled with a mathematical task in which participants were asked to solve simple arithmetical problems. In addition, a delayed test was added to check the possibility that the effect of gap would show more strongly after a meaningful delay between study and test phases (Cepeda et al., 2009).

Method

Participants

Participants were 118 first-year students (77% female) of Psychology at the University of Groningen who took part in the study in exchange for course credit. Three participants failed to come to the delayed test. After random allocation, 55 participants followed the training under the long gap condition and 60 did under the short gap condition.

Materials

As in Experiments 1 and 2, we used 10 paintings by the 12 authors introduced by Kornell and Bjork (2008). Six paintings per author were randomly selected per participant and were used during the training phase. From the four paintings left per author, two more were selected to use on each of the two inductive tests; therefore, both the immediate and delayed inductive tests consisted of 12 new paintings per author that were presented in a different randomised order per participant. In addition, we constructed a set of 72 simple arithmetic problems that involved the addition of two numbers of two or three digits generated by the computer. These 72 problems were presented in a different random order per participant.

Procedure

The experiment took place in a multi-station lab where up to eight participants could be tested simultaneously. During the first session, participants first signed a consent form and did the WMC task and the inductive learning task. The inductive learning task was identical to that of Experiment 2 with the difference that paintings were presented for 5 s in both the short and the long gap conditions. Each painting was followed in the long gap condition by a screen showing an arithmetical problem and a rectangle where the participant was instructed to write the response. The participant had a maximum time of 13 s to give the response after which feedback was given. The feedback informed the participant of whether the response had been correct or incorrect (in which case the correct response was given) and asked to prepare for the next painting. The display time of the feedback was adjusted according to the response time so both events together lasted 15 s.

We also changed the order of the blocks during the study phase task to SMSMSMSMSMSM to avoid any recency effects that could favour the spaced condition. After the study phase, participants performed a small distraction task which consisted of counting backward by 3 s from 547 during 15 s. The immediate test started after the distraction task. The following day, participants came back for the delayed test. Both immediate and delayed tests were identical in format to the test of new items used in Experiments 1 and 2. Participants were also asked to give their opinion after the immediate test as to which of the two strategies they found most useful. WMC scores were divided through a median split in low and high and the resultant variable was used as a between-subjects factor. Our design thus consisted of WMC and temporal gap as independent between-subjects variables and presentation style as a within-subjects factor. Accuracy scores in both inductive tests were used as dependent variables.

Results

Comparison of performance in immediate and delayed tests

Accuracy scores in the immediate and delayed test were analysed with a mixed ANOVA with temporal gap (long or short) as between- and test (immediate or delayed) and presentation style (massed or spaced) as within-subjects factors (see Table 3 for the means).

Table 3. Mean proportion accuracy (SE between parentheses) in the immediate and delayed tests in Experiment 3 as a function of presentation style and gap condition.

		Immediate test	Delayed test
Short gap	Massed	.41 (.03)	.31 (.03)
	Spaced	.58 (.03)	.51 (.03)
Long gap	Massed	.44 (.03)	.36 (.03)
	Spaced	.58 (.03)	.53 (.03)

The results showed main effects of test (F [1, 113] = 23.31, p < .001, ηp²= .171) and presentation style (F [1, 113] = 71.51, p < .001, ηp²= .388). The effect of temporal gap was not significant (F [1, 113] = .34, p = .562, ηp²= .003) and there were no interaction effects. The effect of test shows a greater accuracy in the immediate test (.51) than in the delayed (.43). The effect of presentation style shows an advantage in accuracy for spaced (.56) vs. massed (.38) presentations. The results show that the marginal effect of temporal gap reported in Experiment 2 might have been the result of extra study time rather than increasing the gap.

Working memory capacity and accuracy in the immediate test

As in the previous experiments, WMC scores were divided through a median split into high or low after excluding participants (N = 15) with accuracy below 85% in the symmetry task. A mixed ANOVA was carried on the accuracy scores from the immediate test with presentation style (massed or spaced) as within- and temporal gap (short or long) and WMC (high or low) as between-subjects factors (see Table 4).

Table 4. Mean proportion accuracy (SE between parentheses) in the immediate and delayed tests in Experiment 3 as a function of presentation style, gap condition and WMC.

		Immediate test		Delayed test
		Massed	Spaced	Massed	Spaced
Short gap	Low WMC	.42 (.05)	.59 (.05)	.32 (.05)	.53 (.05)
	High WMC	.42 (.05)	.60 (.05)	.29 (.05)	.51 (.05)
Long gap	Low WMC	.51 (.05)	.56 (.05)	.40 (.05)	.58 (.05)
	High WMC	.67 (.05)	.56 (.05)	.40 (.05)	.57 (.06)

The analysis showed only a main effect of presentation style (F [1, 98] = 32.38, p < .001, ηp²= .248) and a marginal interaction between presentation style and WMC (F [1, 98] = 3.06, p = .083, ηp²= .030). There were no main effects of temporal gap (F [1, 98] = .98, p = .323, ηp²= .010) or WMC (F [1, 98] = .09, p = .758, ηp²= .001), nor were there any other interactions. The main effect of presentation style shows an advantage for spaced as compared to massed presentations (mean accuracies .60 and .45, respectively). The marginal interaction shows a relatively bigger spacing effect in the case of high WMC individuals (see Figure 8).

Figure 8. Average proportion accuracy during the immediate test of Experiment 3, as a function of presentation style (spaced or massed) and WMC (low or high). Error bars depict the standard error of the mean.

Working memory capacity and accuracy in the delayed test

Scores in the delayed test were also analysed through a mixed ANOVA with presentation style (massed or spaced) as within- and temporal gap (short or long) and WMC (high or low) as between-subjects factors. The results of this analysis showed again the main effect of presentation style (F [1, 95] = 40.25, p < .001, ηp²= .298) and a marginal effect of temporal gap (F [1, 95] = 3.72, p = .056, ηp²= .038). The effect of WMC was not significant (F [1, 95] = .16, p = .684, ηp²= .002) nor were any of the interactions (see Table 4). The main effect of presentation style showed a greater accuracy in the spaced (M = .54) than in the massed (M = .35) condition. The main effect of temporal gap shows an advantage of the long as compared to the short gap condition (.48 and .41 mean accuracies, respectively).

The last analysis involved comparing actual with perceived performance and the results replicated the findings of the previous experiments: whereas 63% of participants thought that massing was better or equal to spacing, 60% of them did better when paintings were presented under spaced conditions.

Combined correlational analysis of Experiments 1, 2 and 3

The two most directly comparable tests in the three reported experiments are the test of new items (in Experiments 1 and 2) and the immediate test (in Experiment 3). In both types of tests, the inductive knowledge of the participants is tested with a set of new examples immediately after the training session. In order to inspect the involvement of WMC in induction with a bigger sample, we combined the data from the tests in the three experiments (N = 208) and carried out a correlational analysis. The results showed no relation between WMC scores and accuracy in massed items (r [208] = .107, p = .123). However, WMC scores were positively correlated with performance in spaced items (r [208] = .141, p = .042).

Discussion

Our results showed that the temporal gap is probably not involved in the advantage conferred by mixing presentations. This result adds to the growing body of evidence pointing to interleaving rather than spacing as the cause of the advantage of mixing presentations in the paradigm introduced by Kornell and Bjork (2008). Temporal gap only had a marginal effect in the delayed test. This effect reflected the greater accuracy of long vs. short conditions. Although the advantage of long gap was present in both levels of presentation styles, the difference between long and short was significant under massed (t [97] = −2.07, p = .041) but not under spaced (t [97] = −1.09, p = .278) presentations. Last, the marginal interaction between WMC and presentation style shows the same direction than the marginal interaction reported in Experiment 2. These last results and the results of the combined correlational analysis of the three experiments indicate a possible relation between WMC and the interleaving effect.

General discussion

Kornell and Bjork (2008) argued that spacing helps induction (it is not the enemy). Our results are in line with previous studies (Birnbaum et al., 2013; Kang & Pashler, 2012; Zulkiply & Burt, 2013) indicating that interleaving rather than temporal spacing seems to be the manipulation that promotes inductive learning. The participants in our study also showed a strong discrepancy between their perceived and their actual performance: consistently, a majority of participants favoured massing as the most useful method when, in fact, spacing gave the most advantage. In addition, we failed to find support for the attention–attenuation hypothesis applying a test of studied items (following Wahlheim et al., 2011). Finally, we found some preliminary evidence of a relationship between WMC and the interleaving effect, which has clear and relevant educational implications.

Considering the robustness of the spacing effect, it is surprising that separating the study occasions did not improve accuracy in the induction test. In Experiment 2, we found that extending the temporal gap seemed to improve performance across massed and spaced conditions. However, when we controlled for study time in Experiment 3, this pure effect of temporal gap disappeared. Increasing the time between presentations only improved performance in the delayed test of Experiment 3. Although the increase in accuracy was present in both types of presentation styles, the difference was significant only under massed conditions. This finding is in line with results of Birnbaum et al. (2013): spacing seems to have value when it does not interfere with discriminative processing (i.e. not in combination with interleaving). In addition, it fits the literature in the spacing effect (Cepeda et al., 2009) which shows that extending the time interval between learning opportunities often promotes performance more strongly when tested after a delay.

Our first two experiments contained a test of studied items with the purpose of replicating the results of Wahlheim et al. (2011). We did not find in this test a difference in accuracy or RT as a function of order of presentation in the massed condition. Our results thus failed to replicate their findings and support the attention–attenuation hypothesis. This result should obviously not be interpreted as a cue to disregard the role of attention. Attention-based theories are still among the most supported accounts of the advantage of spaced presentations and study (Delaney, Verkoeijen, & Spirgel, 2010; Dempster, 1989; Dunlosky et al., 2013). The key to the discrepancy between our results and those of Wahlheim and colleagues might be related to subtle differences in the experimental design. Wahlheim et al. used judgements of learning (JOLs) as a tool to measure metacognition in their participants. These JOLs were collected after each item presented during the learning phase and they required participants to estimate their likelihood of correctly assigning the current picture to their correct category during the later testing phase. Although the methodology can give valuable insight into the perceived processing advantage of the different presentation styles, it also introduced an extra temporal gap between presentations during the learning phase. This extra gap which converted their massed condition into a ‘massed temporally spaced condition’ following the terminology used by Zulkiply and Burt (2013) might explain why Wahlheim et al. failed to find a spacing effect in their singles condition (which constituted an exact replication of Kornell & Bjork, 2008) and the discrepancy between their results and ours.

Our most promising results are those related to the role of WMC in the interleaving effect. In Experiment 2, participants with high spans profited more than those with low spans from spaced presentations in a test of studied items. This result was replicated in the immediate test of Experiment 3. Both effects were only marginally significant; however, a combined correlational analysis with the data from the tests immediately following training in the three experiments showed a significant correlation between WMC scores and accuracy with spaced items, while failing to show a similar relation with massed items. In addition, we should consider that the classification into participants with low spans and participants with high spans was made through a median split which means that the scores might not have been as extreme as it could have been desired, minimising the possible influence of WMC. So, when we consider all the described findings, we think that there are good reasons to continue researching the relation between WMC and the interleaving effect.

The question of the involvement of WMC in the interleaving effect is interesting from theoretical and practical points of view. Originally, we hypothesised that if differences in WMC made an influence in the spacing effect, then the discrimination account would receive strong support. The finding, the reasoning continued, would show that the advantage of interleaving is due to the contrast and comparison between information of different and adjacent categories, and when individuals can hold extra information while doing this comparison, then performance increases. This argument assumed a stronger involvement of WMC in storage and attention control than in retrieval. Recent research however shows that differences in WMC do make an influence in retrieval from long-term memory (Shipstead, Lindsey, Marshall, & Engle, 2014; Unsworth, Brewer, & Spillers, 2013). Therefore, our findings must be interpreted as support for both hypotheses, the discrimination account and the study-phase retrieval hypothesis.

From a practical point of view, the results show that applying current research to educational practice is an even more urgent matter than it was previously thought (Bjork, 1994; Dempster, 1988; Rohrer, 2012), as the loss might be greatest with the brightest learners. Future research should address the question with a bigger, and maybe a more varied sample that allows capturing the extreme differences in WMC that can be found in real-world populations.

Acknowledgement

The author wishes to thank Professor Addie Johnson for suggestions on a previous version of this manuscript.

Disclosure statement

No potential conflict of interest was reported by the author.

Notes

1. We used partial eta squared (ηp²) as measure of effect size instead of eta squared (η²) as this last measure cannot easily be compared between studies. Although Cohen (1988) provided benchmarks for comparing effect sizes of eta squared (small = .01, medium = .06, large = .14) he also advised to use this as a last resort and to preferably compare the obtained effects to those in the literature.