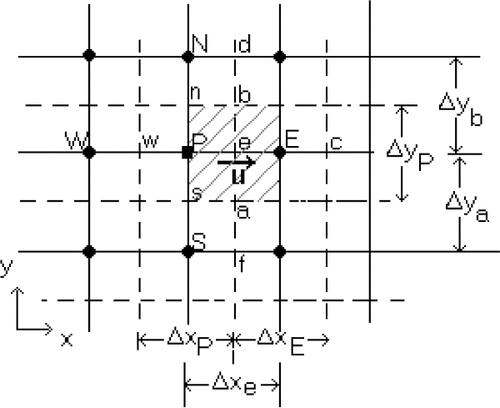The Effect of a Magnetic Field on the Melting of Gallium in a Rectangular Cavity

ABSTRACT

The role of magnetic field and natural convection on the solid–liquid interface motion, flow, and heat transfer during melting of gallium on a vertical wall is reported in this paper. The classical geometry consisting of a rectangular cavity with uniform but different temperatures imposed at two opposite side walls, insulated top, and bottom walls is considered. The magnetic field is imposed in the horizontal direction. A numerical code is developed to solve for natural convection coupled to solid–liquid phase transition and magnetic effects. The corresponding streamlines and isotherms predicted by the numerical model serve to visualize the complicated flow and temperature field. The interplay between the conduction and convection modes of heat transfer stimulated by the combination of the buoyancy-driven flow and the Lorentz force on the fluid due to the magnetic field are studied. The results show that the increase of Rayleigh number promotes heat transfer by convection, while the increase of Hartmann number dampens the strength of circulating convective currents and the heat transfer is then mainly due to heat conduction. These results are applicable in general to electrically conducting fluids and we show that magnetic field is a vital external control parameter in solid–liquid interface motion.

Introduction

Heat transfer in thermally driven flows accompanied by moving solid–liquid phase boundary is common in several research fields, to name a few, metallurgy, crystal growth, electronics cooling, and thermal storage [1]–[3]. The natural convection in the liquid during melting can affect the rate of melting and the solid–liquid interface [4]–[10]. In case of electrically conducting fluids, the melting process in addition, is influenced by the interaction of magnetic field with the liquid, creating a Lorentz force that interacts with the buoyancy force in determining the flow and temperature fields in the melt. Therefore, magnetic field can be a control parameter in the solid–liquid phase change process in electrically conducting fluids [11[, [12].

The role of natural convection on the solid–liquid interface motion during melting of gallium, a pure metal with a low Prandtl number, in a rectangular cavity subjected to differential heating and cooling has been studied experimentally by Gau and Viskanta [13]. In spite of the high thermal conductivity of gallium, the authors showed the significant role of natural convection during melting from a vertical sidewall on the phase-change boundary, the melting rate, and the heat transfer rate. This classical work is followed by several significant contributions in understanding the role of natural convection in the melting process for various configurations and boundary conditions [14], [15].

The interaction of magnetic field in an electrically conducting liquid and the effect on the flow and the heat transfer characteristics is explored more recently. Zehtabiyan-Rezaie, Mirzaei, and Saffar-Avval [16] investigated the effect of magnetic field in a KOH-water solution in a developing and fully developed flow, showing a positive impact of magneto-hydrodynamics (MHD), to augment heat transfer. Numerical analysis of hydromagnetic mixed convective transport in a differentially heated, vertical lid-driven square enclosure is performed by Chatterjee and Halder [17]. They showed that the application of the magnetic field counteracts the buoyancy-driven convection.

There is limited literature on the influence of magnetic field on the solid–liquid phase change boundary and the heat transfer phenomenon in a metal cavity. In a recent paper, Bondareva and Sheremet [18] studied the effect of inclined magnetic field on the natural convection melting in a square cavity with a local heater located at the bottom wall. They showed that the melting process is significantly influenced by the presence of a magnetic field.

In spite of the classical problem presented by Gau and Viskanta [13] on the influence of natural convection in the melting process in a vertical cavity, with differential boundary conditions, the influence of the magnetic field with this configuration and boundary conditions is not reported, to the best of authors' knowledge. This case is a practical situation in many applications, in systems with phase change thermal storage, in purification of metals in metallurgy, a constant temperature is applied on a vertical side (wall) and the opposite side (wall) is in contact with a constant temperature reservoir. The primary objective of this paper is to gain an understanding of the interplay between natural convection and heat conduction in the melt region of the rectangular cavity subjected to an external horizontal magnetic field. The two vertical side walls are held at constant but different temperatures, while the horizontal top and bottom walls are considered adiabatic. The phase change material used in the study is gallium with a Prandtl number, Pr ≈ 0.028, similar to the work of Gau and Viskanta [13]. The enthalpy–porosity method is used to track the motion of the solid–liquid interface. The mass, momentum, and energy equations are numerically solved using the control volume-based finite element method. The corresponding streamlines predicted by the numerical model serve to visualize the complicated structure of the flow field. The effect of horizontal magnetic field on the natural convection and the solid–liquid interface motion are investigated.

Mathematical formulation

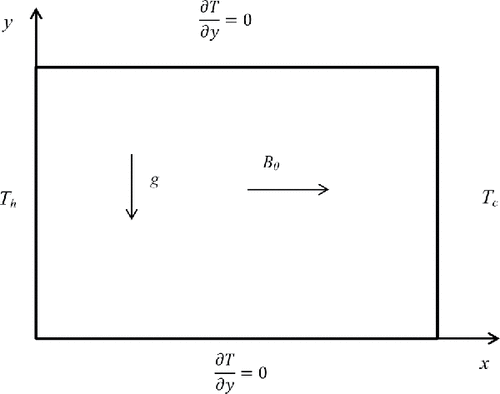
Figure 1 shows the schematic diagram of the physical system consisting of a rectangular cavity with an aspect ratio of 0.714 and is filled with pure solid gallium, initially at a temperature T_c, lower than the melting point temperature T_l. The left and right vertical sides are held at isothermal hot T_h and cold T_c end wall temperatures, respectively, with T_h > T_l > T_c. The top and bottom faces of the cavity are insulated. As gallium begins to melt from the left wall, the solid–liquid phase boundary develops in the cavity. In the melt, both heat conduction and heat convection play a role, where as in the solid phase the heat transfer is only due to heat conduction. The flow is assumed to be two-dimensional, laminar, and in-compressible. The thermophysical properties of the material are constant and the viscous dissipation and pressure work are neglected.

Figure 1. Physical model of the storage cavity and the boundary conditions.

The governing equations describing natural convection and conduction within the phase change material are given below [19]:

• Continuity: (1) $$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$(1)

• x momentum: (2) $$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{{\rho }_f}\left(-\frac{\partial p}{\partial x}+\mu {\nabla }^{2}u+bu\right)$$(2)

• y momentum: (3) $$\begin{array}{ccc}\hfill \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}& =& \frac{1}{{\rho }_f}(-\frac{\partial p}{\partial y}+\mu {\nabla }^{2}v+bv\hfill \\ & & +\rho \beta g(T-T_{ref})-\sigma {B_0}^{2}v)\hfill \end{array}$$(3)

Where T_ref is the melting temperature T_l. The Boussinesq approximation for the buoyancy effect represented by the second last term on the right hand side of the equation is used to simulate the effect of gravity body force. The last term on the right hand side represents the Lorentz force induced by the external magnetic field on the liquid.

• Energy (liquid phase): (4) $$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_f{\nabla }^{2}T-\frac{h_{la}}{c_f}\left(\frac{\partial f}{\partial t}\right)$$(4)

The last term represents the energy absorption during the melting process.

• Energy (solid phase): (5) $$\frac{\partial T}{\partial t}={\alpha }_s{\nabla }^{2}T$$(5)

The enthalpy–porosity formulation, as proposed by Brent, Voller, and Reid [19] is used to mathematically define the solid–liquid phase change process. In this approach, a parameter b is defined in the momentum equations (Eqs. 2(2) $$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{{\rho }_f}\left(-\frac{\partial p}{\partial x}+\mu {\nabla }^{2}u+bu\right)$$(2) and 3(3) $$\begin{array}{ccc}\hfill \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}& =& \frac{1}{{\rho }_f}(-\frac{\partial p}{\partial y}+\mu {\nabla }^{2}v+bv\hfill \\ & & +\rho \beta g(T-T_{ref})-\sigma {B_0}^{2}v)\hfill \end{array}$$(3) ) to gradually reduce the velocities from a finite value in the liquid to zero in the solid, over the computational cell that undergoes the phase change. This can be achieved by assuming that such cells behave like a porous media with porosity is equal to liquid fraction. Based on the Carman–Kozeny relation, the coefficient b is defined as follows (6) $$b=-\frac{C_1{(1-f)}^3}{f^2+C_2}$$(6)

In this equation, f = 1 and f = 0 are the liquid and solid regions, respectively. f can take values between 0 and 1 in the mushy zone (liquid and solid). The constant C₁ has a large value (10⁷–10¹⁵) to suppress the velocity as the cell becomes solid and C₂ is a small constant to avoid a division by zero when a cell is fully located in the solid region, namely f = 0. The choice of the constants is arbitrary. However, the constants should ensure enough suppression of the velocity in the solid region and should not influence the numerical results significantly [20]. In this work, C₁ = 1 × 10⁷ kg.m⁻³.s⁻¹ and C₂ = 0.001 are used.

The governing equations are reduced to the non-dimensional form by using the following variables: X = x/H, Y = y/H, U = uH/α_f, V = vH/α_f, θ = (T − T_l)/(T_h − T_l), P = pH²/ρα_f²,and dimensionless parameters Fo = α_ft/H² is the Fourier number, B = bH²/ρ_fα_f is the dimensionless form of b , Ra = gβ(T_h − T_l)H³/ν_fα_f is the Rayleigh number, Ste = c_f(T_h − T_l)/h_la is the Stefan number, $Pr={\upsilon }_f/{\alpha }_f$ is the Prandtl number, and $Ha=H{B}_0\sqrt{\sigma /\mu }$ is the Hartmann number.

The dimensionless continuity, x momentum, y momentum, and the energy equations are, respectively (7) $$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0\left[3pt\right]$$(7) (8) $$\frac{\partial U}{\partial Fo}+U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+Pr{\nabla }^{2}U+BU\left[3pt\right]$$(8) (9) $$\frac{\partial V}{\partial t}+U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+Pr{\nabla }^{2}V+RaPr\theta +BV-H{a}^{2}PrV$$(9) (10) $$\frac{\partial \theta }{\partial Fo}+U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}={\nabla }^2\theta -\frac{1}{Ste}\left(\frac{\partial f}{\partial Fo}\right)$$(10)

The initial and boundary conditions are

• At initial time, Fo = 0, U = V = 0 and θ = −0.18

• For the left wall, U = V = 0 and θ = 1

• For the right wall, U = V = 0 and θ = −0.18

• For the horizontal walls, U = V = 0 and $\frac{\partial \theta }{\partial Y}=0$

• For melting front, U = V = θ = 0

The absorption of latent heat during melting is included as a source term in the last term on the right side of Eq. (10(10) $$\frac{\partial \theta }{\partial Fo}+U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}={\nabla }^2\theta -\frac{1}{Ste}\left(\frac{\partial f}{\partial Fo}\right)$$(10) ). The latent heat content of each control volume is evaluated after each energy equation iteration cycle. Based on the latent heat content, a liquid fraction for each control volume is determined. For control volumes containing a liquid phase of the substance, f is set to 1, and for control volumes containing solid phase, f is set to 0. The control volumes with values of f between 0 and 1 are treated as a mushy zone. The phase change is assumed to be non-isothermal, so the idea of the mushy zone is introduced to gradually switch off the velocities from liquid to solid at the solid–liquid interface [20]. In this study, the thickness of the mushy zone is equal to the control volume.

Numerical method of solution

The dimensionless governing equations (Eqs. 7–10) along with the boundary conditions are discretized by employing the finite-volume technique. This method is found to be suitable for numerical solution of the model equations describing phase change processes [21]. The power law scheme, which is a combination of the central difference and the upwind schemes, is used to discretize the convection terms. The calculation domain is discretized into a two-dimensional staggered grid, as shown in Figure 2. The velocity components are stored midway between the control volume surfaces. The SIMPLE algorithm proposed by Patankar [22] is used to solve the discretized and coupled continuity, momentum and energy equations. A line by line solver based on the tri-diagonal matrix algorithm is used to solve iteratively the algebraic discretized equations [22].

Figure 2. Control volume for U-velocity in a staggered grid.

The enthalpy is expressed as a function of temperature using the method proposed by Voller [23]: (11) $$h=\left\{\begin{array}{ccc}\hfill c_{s}T& \hfill T<T_s& \hfill Solid\\ \hfill c_{f}T+\frac{h_{la}(T-T_s)}{(T_f-T_s)}& \hfill T_s\le T\le T_l& \hfill Mushy\\ \hfill c_{f}T+h_{la}+c_f(T_l-T_s)& \hfill T>T_l& \hfill Liquid\end{array}\right.$$(11)

Furthermore, assuming a linear profile, the enthalpy of the control volume is equal to the sum of the solid and liquid phase enthalpies. (12) $$h_{cv}=h_{la}f+c_f(T_E-T_l)f-c_s(T_l-T_{{}_W})(1-f)$$(12) where T_E and T_W are the left and right temperatures of the control volume, respectively. Rearranging Eq. (12(12) $$h_{cv}=h_{la}f+c_f(T_E-T_l)f-c_s(T_l-T_{{}_W})(1-f)$$(12) ), the liquid fraction in the control volume is equal to (13) $$f=\frac{h_{cv}+c_s{T}_l-{\mathrm{c}}_{\mathrm{s}}{T}_W}{h_{la}+c_f{T}_E-c_f{T}_l+c_s{T}_l-c_s{T}_{{}_W}}$$(13)

The solid–liquid interface is determined by the liquid fraction contour f = 0.5. This formulation of the enthalpy method removes numerical oscillations in both temperature and moving boundary position, and produces a marked improvement in the accuracy of the results, particularly for cases with a large ratio of the latent heat to sensible heat. The following steps are employed to simulate the phase change process in this study:

1.	Guess the initial velocity, pressure, and temperature field.
2.	Solve the momentum (Eqs. 8(8) $$\frac{\partial U}{\partial Fo}+U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+Pr{\nabla }^{2}U+BU\left[3pt\right]$$(8) and 9(9) $$\frac{\partial V}{\partial t}+U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+Pr{\nabla }^{2}V+RaPr\theta +BV-H{a}^{2}PrV$$(9) ) and obtain velocity field.
3.	Solve the energy (Eq. 10(10) $$\frac{\partial \theta }{\partial Fo}+U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}={\nabla }^2\theta -\frac{1}{Ste}\left(\frac{\partial f}{\partial Fo}\right)$$(10) ) to obtain the temperature in the liquid and the solid zone.
4.	Solve the enthalpy equation to obtain the enthalpy field according to Eq. 11(11) $$h=\left\{\begin{array}{ccc}\hfill c_{s}T& \hfill T<T_s& \hfill Solid\\ \hfill c_{f}T+\frac{h_{la}(T-T_s)}{(T_f-T_s)}& \hfill T_s\le T\le T_l& \hfill Mushy\\ \hfill c_{f}T+h_{la}+c_f(T_l-T_s)& \hfill T>T_l& \hfill Liquid\end{array}\right.$$(11) .
5.	Obtain liquid fraction from Eqs. (12(12) $$h_{cv}=h_{la}f+c_f(T_E-T_l)f-c_s(T_l-T_{{}_W})(1-f)$$(12) and 13(13) $$f=\frac{h_{cv}+c_s{T}_l-{\mathrm{c}}_{\mathrm{s}}{T}_W}{h_{la}+c_f{T}_E-c_f{T}_l+c_s{T}_l-c_s{T}_{{}_W}}$$(13) ).
6.	Solve the above steps until convergence in each time step.
7.	Continue by repeating above steps until melting ends.

To carry out the above-mentioned approach, a FORTRAN code is developed.

Results and discussion

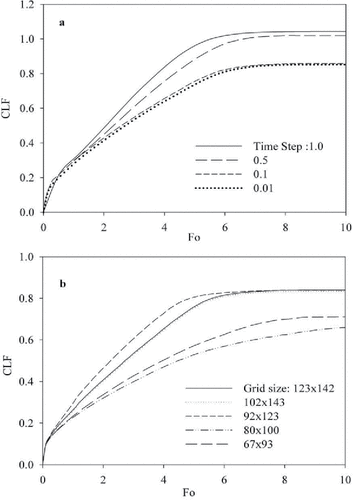
A grid independency study is performed for various grid sizes with a time step size in the range of 0.1–0.01. The cavity liquid fraction (CLF), the ratio of the volume of the molten substance to the volume of the cavity is chosen as the monitoring variable. A grid size of 123 × 92 grids with a time step of 0.1 yielded sufficient accuracy, as shown in Figure 3.

Figure 3. Cavity liquid fraction (CLF) as a function of dimensionless time (Fo) for various time steps (a) and grid sizes (b).

Most of the numerical studies reported in the literature compared their results with the experimental analysis performed by Gau and Viskanta [13]. Brent, Voller, and Reid [19] used enthalpy–porosity approach to investigate numerically the melting of pure gallium in a rectangular cavity without magnetic field effect. They also validated their numerical study with experimental findings of Gau and Viskanta [13]. The same test case is used to validate the present model. Therefore, the boundary conditions of T_h = 38°C, T_c = 28.3°C, with an initial temperature of 28.3°C on the domain size of 88.9 × 63.6 mm (R = 0.714) is used. Figure 4 shows the simulation results of the melting front inside the cavity at different times and also includes the results of Brent, Voller, and Reid [19] and Gau and Viskanta [13]. A maximum error of 5% is observed between the data from the present model and the results of Brent, Voller, and Reid [19]. However, a deviation larger than 5% is observed when compared with experimental data of Gau and Viskanta [13], which could be attributed to the three-dimensional nature of the experiments. Similar conclusions are drawn by several researchers [6], [15], [18], [19] who benchmarked their numerical model with the data of Gau and Viskanta [13]. The same geometry and initial temperature condition are used in the calculations hereafter.

Figure 4. Numerical code validation of the present study with the numerical results of Brent, Voller, and Reid [19], and the experimental study of Gau and Viskanta [13].

A systematic study is performed to evaluate the effect of parameters on the melting of gallium inside the cavity. The physical properties of gallium and the governing non-dimensional parameters are tabulated in Table 1. The results are presented in two parts: First the effect of temperature difference between the heated wall and the melting point on the flow and heat transfer process is studied by varying the Rayleigh number. Second, the effect of the external magnetic field superimposed on the buoyancy effect is studied by varying the Hartmann number In both these parts, the streamlines in the liquid melt, the liquid–solid boundary, the isotherms in the melt, the liquid fraction in the cavity, and the average Nusselt number at the warm wall are computed as a function of time.

Table 1. Thermophysical properties of gallium and other non-dimensional parameters used in this study.

Parameter	Value
Density, ρf	6093 kg.m^− 3
Volumetric thermal expansion coefficient of liquid, β	1.2 × 10^− 4°C^− 1
Thermal conductivity, k	32.0 W.m^− 1.°C ^− 1
Melting point, Tl	29.78°C
Latent heat fusion, hla	80160 J.kg^− 1
Thermal diffusivity, ′af	1.38 × 10^− 5 m^2.s^− 1
Acceleration due to gravity, g	9.81 m.s^− 2
Aspect ratio, R	0.714
Prandtl number, Pr	0.0216
Ratio of heat capacity of solid and liquid, cs/cf	1.0
Ratio of thermal conductivity of solid and liquid, ks/kf	1.0

The effect of Rayleigh number

Rayleigh number represents the strength of buoyancy force in a fluid. Four values of Rayleigh numbers, namely, 10³, 10⁴, 6.5 × 10⁵, and 10⁶ are chosen for this study to cover the broad range of the temperature differences between the wall and the melting point. The Rayleigh number, Ra = 6.5 × 10⁵ is chosen to compare our results with experimental data of Gau and Viskanta [13]. Figure 5 shows the streamlines for various Rayleigh numbers at three different dimensionless times (Fourier number) of melting process, Fo = 2.5, 5.0, and the steady state. The vorticity in the liquid phase is due to the natural convection induced by the left warm wall and the cold solid boundary. The molten liquid rises up along the hot wall and then descends near the solid–liquid interface in a clockwise direction. As a result, the top section of the cavity encounters warm molten flow in comparison to the bottom, leading to a convex shape of the melting front.

Figure 5. Streamlines at three different dimensionless times (Fo) for various Rayleigh numbers (Ra) and Ha = 0.

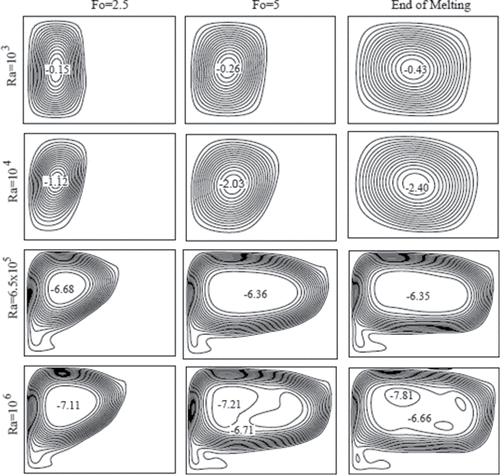
At the start of melting process, the primary mode of heat transfer in the melt is due to heat conduction. As time elapses, buoyancy-driven clockwise currents develop and intensify in the melt, as shown in Figure 5. The warm melt first encounters the solid at the top and is subsequently cooled by exchanging heat to the solid. Therefore, the solid–liquid melting front begins to recede quickly at the top compared to the bottom. The number labeled in the center of the streamlines in Figure 5 is the maximum strength of the circulating flow, and the minus sign indicates the flow is in clockwise direction. As can be seen in Figure 5, for larger Rayleigh numbers, the strength of the circulating flow increases and the streamlines are denser.

Figure 6 shows the isotherms for various Rayleigh numbers during three time lapses of the melting process. The numbers labeled on the isotherm lines indicate dimensionless temperature. It is observed that for low Rayleigh numbers the isotherms are smooth and almost parallel between the top and bottom walls, confirming our earlier hypothesis that the heat transfer mode in this case is primarily due to heat conduction. At higher Rayleigh numbers, the isotherms are curved, indicating departure from primarily heat conduction to also include heat convection driven by buoyancy flow.

Figure 6. Isotherms at three different dimensionless times (Fo) for various Rayleigh numbers (Ra) and Ha = 0.

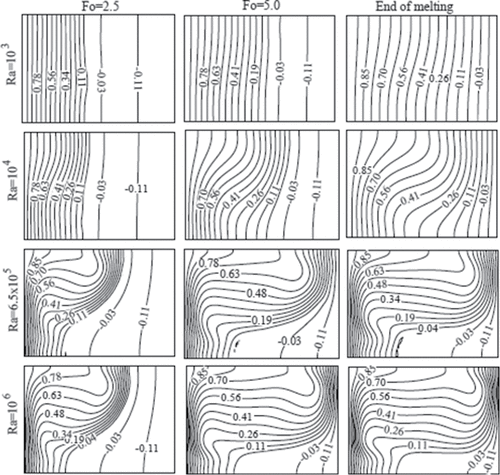
Figure 7 shows the shape and position of melting front at the previously considered times and Rayleigh numbers. The numbers labeled in the plot indicate the liquid fraction in the cavity. The liquid fraction is the volume of molten substance to the volume of the cavity. As predicted from the isotherms in Figure 6, the solid–liquid phase boundary in Figure 7 is nearly vertical for lower Rayleigh number. As time elapses and for larger Rayleigh numbers, the shape of the melting front becomes curved. At the end of melting phase, when a steady state condition is approached, a small quantity of solid remained in all the cases, because the right wall of the cavity is maintained at a temperature lower than the melting point of gallium. The shape of the remnant solid in the steady state is a signature of the role of the convection and conduction in the heat transfer during the melting process.

Figure 7. The solid–liquid phase interface at three different dimensionless times (Fo) for various Rayleigh numbers (Ra) and Ha = 0.

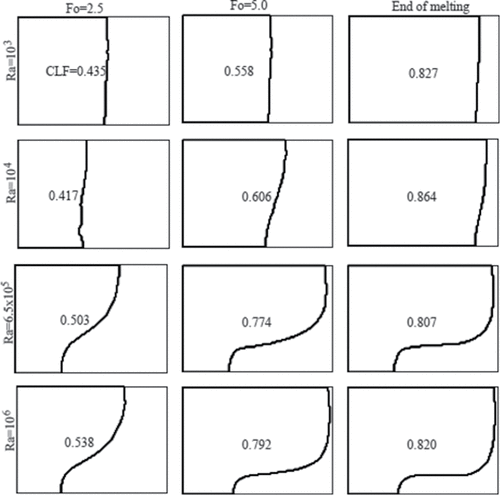
The liquid volume fraction in the cavity as a function of dimensionless time (Fourier number) for the considered Rayleigh numbers is shown in Figure 8. The liquid fraction is about the same for all Rayleigh numbers during the early time process (Fo < 1) because the primary mode of heat transfer is due to heat conduction. As the convective mode of heat transfer becomes significant at a later time, the liquid fraction begins to vary with Rayleigh number. As suggested by Raithby and Hollands [24], the heat transfer rate increases with Rayleigh numbers for natural convection in a cavity heated from a side. Therefore, it is expected that for a larger Rayleigh number, the melting rate increases due to natural convection, and consequently the steady state condition would be reached in a shorter time. The numerical results shown in Figure 7 confirm this hypotheses, where for Ra = 6.5 × 10⁵ and 10⁶, the liquid fraction approaches steady state much earlier than for Ra = 10³ and 10⁴. Table 2 shows the dimensionless time when steady state condition is approached for various Rayleigh numbers. It should be noted that for Ra = 10⁴, the final liquid fraction in the steady state condition is more than that for other Rayleigh numbers. The most probable reason is that at lower Rayleigh numbers (Ra = 10³ and 10⁴), heat conduction is the predominant heat transfer mode and gallium has a high thermal conductivity. However, at Ra = 10⁴ the strength of convection is larger than that at Ra = 10³, as shown in Figure 5. The final liquid fraction in the cavity for the considered Rayleigh numbers is given in Table 2. The local Nusselt number at the hot wall is a good indicator of heat transfer rate and is calculated as $NuY=-?e\acute{/}?X$. The average Nusselt number can be obtained by integrating the local Nusselt number along the hot wall. Figure 9 shows the average Nusselt number (Nu_avg) on the hot wall as a function of the dimensionless time (Fo). The Nusselt number is expected to increase with Rayleigh number, because the local flow velocity and subsequently the heat transfer rate increase.

Figure 8. Evolution of the CLF in dimensionless time (Fo) for various Rayleigh numbers (Ra) and Ha = 0.

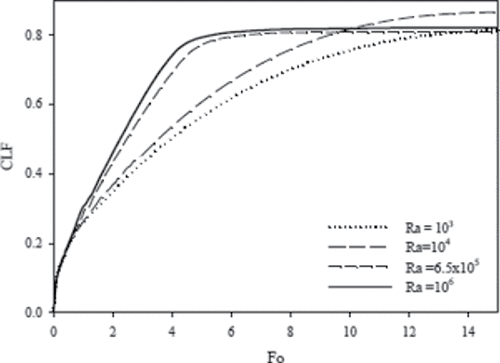
Table 2. The dimensionless time (Fo) for approaching steady state, and the corresponding cavity liquid fraction for various Rayleigh numbers (Ra).

Ra	Fo	Cavity liquid fraction
10^3	17.6	0.826
10^4	15.4	0.864
6.5 × 10^5	7.3	0.807
10^6	7.5	0.820

Figure 9. Average Nusselt number at the hot wall as a function of dimensionless time (Fo) for different Rayleigh numbers (Ra) and Ha = 0.

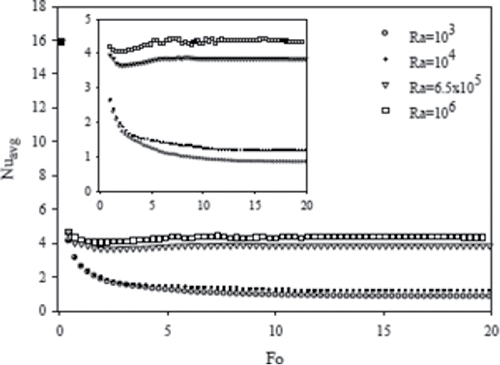
At early time, the melt layer is relatively thin, leading to a large Nusselt number. As the melt layer thickness increases, the thermal resistance increases and the Nusselt number decreases and reaches a constant value in the steady state.

The effect of Hartmann number

In addition to the melting phenomenon presented above, the superposition of horizontal magnetic field on the flow and heat transfer process was studied. Four values of Hartmann number (Ha = 0, 25, 50, 100) were chosen because the magnetic fields associated with these numbers could be realized with permanent magnets [25]. All the results are presented for a fixed Rayleigh number equal to Ra = 6.5 × 10⁵. Figures 10 and 11 show streamlines and isotherms, respectively, for various Hartmann numbers. In the absence of magnetic field (Ha = 0), a strong circulating cell covers most of the melting region (see Figure 10). The shape of the streamlines, as well as the density of the cells, indicate the strength of the natural convection heat transfer. As noted by Sheikholeslami and Ganji [26], magnetic field can dampen the natural convective currents of electrically conducting liquid. The melt consisting of liquid gallium can be therefore influenced by the external magnetic field. The increase in magnetic field strength decreases the intensity and the strength of the streamlines, as can be seen in Figure 10. The area covered by the liquid in a certain time also decreases with increasing magnetic field.

Figure 10. Streamlines at three different dimensionless times (Fo) for various Hartmann numbers (Ha) and Ra = 6.5 × 10⁵.

Figure 11. Isotherms at three different dimensionless times (Fo) for various Hartmann numbers (Ha) at Ra = 6.5 × 10⁵.

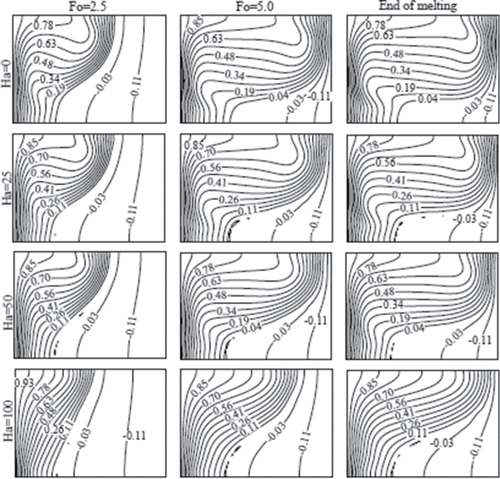
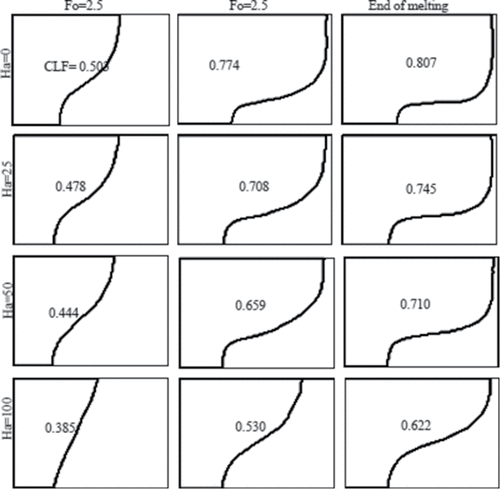
Figure 11 shows the isotherms in the cavity for several Hartmann numbers and the previously considered times. As the Hartmann number increases, the isotherms become more vertical, indicating increasing role of heat conduction. This behavior is also reflected in the shape of the solid–liquid interface, as shown in Figure 12. At a fixed time, the amount of liquid fraction also decreases with increasing magnetic field (see Figure 11), because convective heat transfer decreases.

Figure 12. Solid–liquid interface at three different dimensionless times (Fo) for various Hartmann numbers (Ha) and Ra = 6.5 × 10⁵.

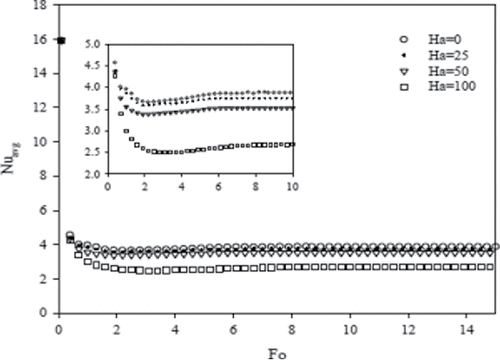
The CLF as a function of time is shown in Figure 13. At initial time (Fo < 1), it is observed that increasing the Hartmann number has no considerable effect on the melting rate, because only heat conduction plays a major role in the heat transfer process. However, as the melting continues, the melting rate decreases with increasing Hartmann number. This observation clearly shows that heat convection is dampened at increasing magnetic field. Table 3 shows the dimensionless time when steady state condition is approached for various Rayleigh numbers and the corresponding steady state liquid fraction. The steady state liquid fraction decreases with increasing Hartmann number. The final liquid fraction of gallium in the cavity is given in Table 3 for different Hartmann numbers. It is observed that the liquid fraction decreases for higher values of Hartmann numbers because of the decrease in heat convection. The average Nusselt number at the hot wall of the cavity decreases as the magnetic field strength is increased, as can be seen in Figure 14. The reason is due to the decrease of circulation, and subsequently the convective heat transfer. At the early time of melting, the magnetic field has limited effect on Nusselt number because the main mode of heat transfer is conduction.

Figure 13. Evolution of the CLF in dimensionless time (Fo) for different Hartmann numbers (Ha) and Ra = 6.5 × 10⁵.

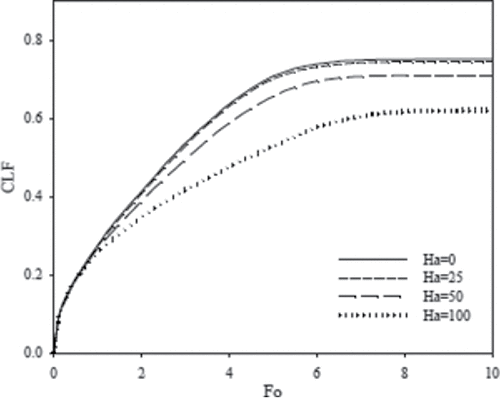
Table 3. The dimensionless time (Fo) for approaching steady state, and the corresponding cavity liquid fraction for various Hartmann numbers (Ha). The Rayleigh number in all these cases is Ra = 6.5 × 10⁵.

Ha	Fo	Cavity liquid fraction
0	7.3	0.807
25	7.7	0.745
50	8.2	0.710
100	9.6	0.621

Figure 14. Average Nusselt number at the hot wall versus dimensionless times (Fo) for different Hartmann numbers (Ha) and Ra = 6.5 × 10⁵.

The effect of magnetic field on solid–liquid phase boundary, the flow and heat transfer process of gallium melting from a vertical wall is studied. Strong coupling of buoyancy-driven convective flow and Lorentz force due to magnetic field are observed at the middle and late times in the melting process, when sufficient melt is present in the cavity. The flow and temperature fields reveal the interplay between conduction and convection modes of heat transfer. Similar physical phenomenon is expected for other electrically conducting fluids. Magnetic field is therefore a useful external parameter to control the solid–liquid phase change process in these fluids.

Conclusions

The numerical solutions for the flow and the temperature fields of a melting solid in a rectangular cavity subjected to differential temperature boundary conditions have been obtained. The calculated flow, and temperature field, and the solid–liquid interface are used to study the effect of buoyancy-driven flow and magnetic field on the interplay between the heat conduction and convection in the liquid melt. Without an external magnetic field, during the early time, the solid–liquid phase boundary is almost vertical and the isotherms in the melt are also vertical, revealing that the major heat transport process is due to heat conduction in the melt. At later time, the buoyancy flow develops and intensifies in the liquid melt, leading to bending of isotherms in the melt and enhanced heat transfer from the boundary. With the application of magnetic field in the horizontal direction, the resulting Lorentz force on the electrically conducting melt counteracts the buoyancy force and retards the circulating flow, reducing convective heat transport. The CLF in the steady state and the average Nusselt number at the warm boundary decrease with increasing Hartmann number. The study shows that magnetic field is an effective parameter to control the melting of electrically conducting materials.

Nomenclature
b	=	enthalpy–porosity coefficient, kg.m− 3.s− 1
B	=	dimensionless enthalpy-porosity coefficient
B0	=	magnetic field, T (teslas)
c	=	specific heat, J.kg− 1.°C − 1
CLF	=	cavity liquid fraction
f	=	liquid fraction
Fo	=	Fourier number
g	=	gravity, 9.81 m.s− 2
Ha	=	Hartmann number
h	=	enthalpy, J.kg− 1
hla	=	latent heat of fusion, J.kg− 1
H	=	cavity dimension in y direction, m
k	=	thermal conductivity, W.m− 1.°C − 1
L	=	cavity dimension in x direction, m
Nuavg	=	average Nusselt number
NuY	=	local Nusselt number
p	=	pressure, N.m− 2
P	=	dimensionless pressure
Pr	=	Prandtl number
R	=	aspect ratio (H.L− 1)
Ra	=	Rayleigh number
Ste	=	Stefan Number
T	=	temperature, °C
t	=	time, s
u,v	=	velocity in the x, y direction, m.s− 1
U,V	=	dimensionless velocity
x,y	=	Cartesian coordinate, m
X,Y	=	dimensionless Cartesian coordinate

Greek symbols
α	=	thermal diffusivity, m2.s− 1
β	=	expansion coefficient, °C − 1
μ	=	dynamic viscosity, N.s.m− 2
ν	=	kinematic viscosity, m2s− 1
θ	=	dimensionless temperature
ρ	=	density, kg.m− 3
σ	=	electrical conduction, S.m− 1

Subscripts
c	=	cold
cv	=	control volume
E	=	east, the left boundary of the control volume
f	=	fluid
h	=	hot
l	=	melting point
la	=	latent
ref	=	reference
s	=	solid
W	=	west, the right boundary of the control volume

Acknowledgment

Yadollahi Farsani acknowledges the support of Shahrekord University for providing travel grant to perform part of the work described in this paper at University of Twente.

Additional information

Notes on contributors

Rouhollah Yadollahi Farsani

Rouhollah Yadollahi Farsani is a Ph.D. student in the energy conversion group in the Department of Mechanical Engineering at Shahrekord University, Shahrekord, Iran. His topic of research is the numerical simulation of melting and solidification phenomena in nanoparticle-enhanced phase change materials under the effect of magnetic field.

Afrasiab Raisi

Afrasiab Raisi is an associate professor at the Department of Mechanical Engineering, Shahrekord University, Shahrekord, Iran. He received his B. Eng. Degree in mechanical engineering from the Ferdowsi University of Mashhad, Iran, in 1992, and M.Sc. and Ph.D. in mechanical engineering from the Isfahan University of Technology, Iran, in 1995 and 2001, respectively. In 2001, he joined the Department of Mechanical Engineering at Shahrekord University as an assistant professor, and became an associate professor in 2015. His current research interests include forced and natural convection heat transfer, convective heat transfer in nanofluids and non-Newtonian fluids, melting and solidification, and conduction microscale heat transfer.

Afshin Ahamadi Nadooshan

Afshin Ahmadi Nadooshan received his B.E. degree in mechanical engineering from Isfahan University of Technology, Iran, in 1995, master's degree from Sharif University of Technology, Iran, in 1997, and Ph.D. in mechanical engineering from Isfahan University of Technology in 2006. In 2011, he joined the Department of Mechanical Engineering, Shahrekord University, as an assistant professor. His current research interests include energy efficiency optimization, turbulence, two-phase flow and air conditioning.

Srinivas Vanapalli

Srinivas Vanapalli graduated (honors) in mechanical engineering from the Indian Institute of Technology, Madras. He has worked in Germany and later obtained a degree in electrical engineering (cum laude) at the University of Twente. His Ph.D. research was funded by Dutch Technology Foundation, during which he was also a guest researcher at National Institute of Standards and Technology, Boulder, USA. After his Ph.D. in 2008, he moved to Energy Research Center of the Netherlands in Petten and in 2011 returned to the University of Twente. He currently holds a tenure track position at University of Twente. His research interests are concentrated in the areas of micro-(nano)scale thermal/fluidic phenomena in meso-scale systems spanning a wide temperature range (from cryogenic to room temperature), cryocoolers, and multifunctional thermal insulation, and compact thermal devices.