Uncertainty in contact angle estimates from a Wilhelmy tensiometer

Abstract

The uncertainty in contact angles from the Wilhelmy tensiometer was analyzed using standard error propagation techniques involving partial derivatives across the full range of wettability, from completely wetting to non-wetting surfaces. Uncertainties in force, sample perimeter, and liquid surface tension of 1% were shown to yield uncertainty in contact angles of a few degrees over the middle range of wettability, but exceeded 10° at the extremes.

Keywords:

• Wilhelmy
• tensiometer
• contact angles
• uncertainty
• error propagation

Introduction

Contact angle measurements are used widely to assess wettability and cleanliness of surfaces as well as the potential for creating a high-quality adhesive bond.[1–4] The two most widely used techniques employ either sessile drops or a Wilhelmy tensiometer.

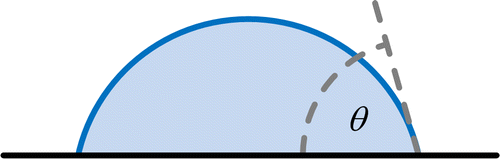
In sessile drop measurements, a small volume of liquid is usually deposited onto a horizontal solid surface and allowed to spread. Liquid may be added to or withdrawn from the drop to advance or retract its contact line, then a contact angle (θ), depicted in Figure 1, is measured between the solid surface and a tangent line originating from the triple point between the liquid, solid, and surrounding gas.

Figure 1. A sessile liquid drop and its contact angle (θ).

In traditional Wilhelmy tensiometer measurements, a solid is immersed or withdrawn from a liquid while measuring force.[5] Alternatively, the Wilhelmy tensiometer can be used to measure wettability inside capillary tubes. Here, the liquid reservoir is raised until the bottom of the tube just touches the liquid; after liquid has risen to its ultimate height in the tube, the maximum force measured by the tensiometer is used to estimate a contact angle.[6] Proper analysis of the interplay between capillary forces and any buoyancy allows for indirect estimation of contact angles.[7–9] The working equation for immersion or withdrawal of a buoyancy neutral substrate or liquid rise inside a tube is [5](1)

where f is the capillary force measured by the tensiometer, p is the perimeter of the specimen, and γ is the surface tension of the liquid.

To compare data from different samples, different operators or different techniques, it is imperative to know the uncertainty in measurements. The uncertainty in contact angle measurements is generally reported to be ±1°–2°.[10] However, these values can vary significantly, often increasing at the extremes of wettability. For example, the uncertainty in direct measurement with sessile drops is higher for very small (<10°) or very large (>160°) angles due to difficulties in locating the point of contact, positioning of the baseline, and constructing a tangent to the drop profile.[10–18] Uncertainty in indirect estimates from the dimensions and/or volumes of sessile drops also is higher at the limits of wettability.[16] Relative uncertainty of the height-diameter [19–21] and the volume-diameter methods [22] increases as θ approaches 0°, whereas uncertainty in the height-diameter method grows as θ tends toward 180°.[16]

Uncertainty from the Wilhelmy tensiometer has received less attention. Miller and Young [23] were among the first to discuss the lack of precision of the Wilhelmy tensiometer at small θ values due to the nature of the cosine function. Martin and Vogler [8] developed computerized methods and algorithms for processing data from Wilhelmy tensiometers. In their work, they demonstrated that propagation of measurement error through the cosine function caused uncertainty in θ to diverge for small values of θ. Tretinnokov and Ikada [24] developed a tensiometer technique that employs a ‘picture frame’ specimen (a rectangular flat sheet with a rectangular hole) to eliminate the influence of buoyancy and thereby the need to extrapolate to zero immersion depth. Comprehensive analysis of their technique showed that uncertainty grows asymptotically as θ → 0°.

In this work, the uncertainty in the estimates of contact angles from Wilhelmy tensiometer measurements was analyzed across the full range of wettability, from completely wetting surfaces with θ → 0° to non-wetting surfaces with θ → 180°.

Analysis

We begin an analysis of the uncertainty of the Wilhelmy tensiometer by defining several parameters. The absolute uncertainties in the measurement of f, p, and γ are δf, δp, and δγ. Their corresponding relative uncertainties are as follows:(2) (3)

and(4)

If it is supposed that the uncertainties of f, p, and γ are independent of each other and random, then uncertainty in contact angle (δθ) can be estimated using standard error propagation techniques involving partial derivatives,[25](5)

where ∂θ/∂f, ∂θ/∂p, and ∂θ/∂γ are partial derivatives of Equation (1). Inserting these partial derivatives into Equation (5) and rearranging terms yields Equation (6),(6)

Equation (6) can be rewritten in terms of relative uncertainties by combining with Equations (2)–(4),(7)

Finally, replacing the f/pγ terms of Equation (7) with cosθ in accordance with Equation (1) and simplifying with the aid of several trigonometric relations yields a simple equation for estimating δθ in terms of θ and the relative uncertainty in f, p, and γ,(8)

Results and discussion

Figure 2 shows the absolute uncertainty of the contact angle (|δθ |) for the Wilhelmy tensiometer as a function of the contact angle (θ) and the relative uncertainties in the measured force (Δ_f), sample perimeter (Δ_p), and liquid surface tension (Δ_γ), per Equation (8(8) ). Uncertainties from the computation of θ from f, p, and γ are relatively low in the middle of the range of measurable values. For example, if Δ = Δ_f = Δ_p = Δ_γ = 0.01, then the absolute uncertainty in θ between 25° and 155° is ≤ 2°. However, at the extremes, uncertainty in θ increases asymptotically – between 15° and 25° (or 155° and 165°), δθ = ±2–4°; between 5° and 15° (or 165° and 175°), δθ = ±4–11°.

Figure 2. Absolute uncertainty of the contact angle (|δθ |) estimated from Equation (8) for the Wilhelmy tensiometer as a function of the contact angle (θ) and the relative uncertainties in the measured force (Δf), sample perimeter (Δp) and liquid surface tension (Δ_γ).

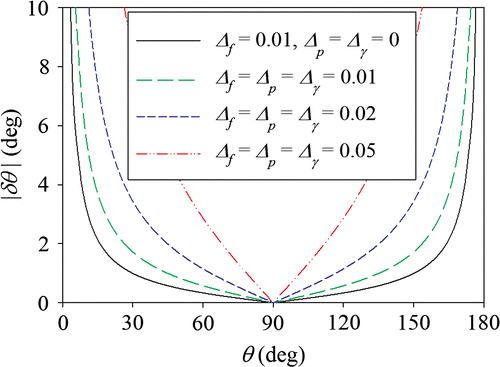
As the uncertainty in f, p or γ increases, so does the uncertainty in θ. For θ = 25° or 155°, if Δ = Δ_f = Δ_p = Δ_γ = 0.01, then δθ = ±2°. If Δ = 0.02, then δθ = ±4°. If Δ = 0.05, then δθ = ± 11°.

Equation (8) and Figure 2 indicate that if a surface exhibits a contact angle of θ = 90°, then δθ = ±0°. The general nature of Equation (8) arises from assuming that the relative uncertainty in the force, perimeter, and liquid surface tension is constant over the full range of contact angles. While this is a reasonable assumption for perimeter and liquid surface tension, it is an over simplification for force. As θ → 90°, f → 0, and Δ_f becomes large.

A more correct, but less general version of Equation (8) could include the absolute uncertainty in the force,(9)

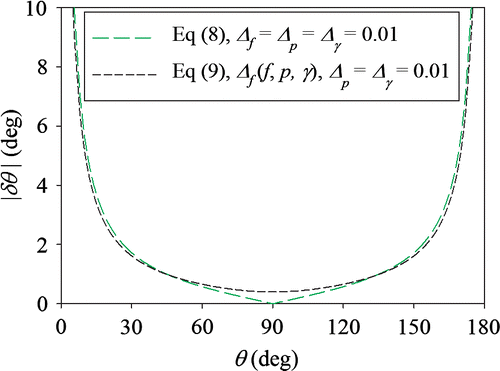
In this form, the relative uncertainty from the perimeter and surface tension does not propagate at θ = 90°, but the uncertainty in force does. Figure 3 shows a comparison of the absolute uncertainty of the contact angle (|δθ |) estimated from Equations (8) and (9); for Equation (8), it is assumed that Δ_f = Δ_p = Δ_γ = 0.01; for Equation (9), p = 2 mm, γ = 72 mN/m, δf = 1 μN and Δ_p = Δ_γ = 0.01. The curves have similar shapes, except near θ = 90°. For Equation (9), |δθ | does not go to zero, but bottoms at ±0.4°.

Figure 3. A comparison of the absolute uncertainty of the contact angle (|δθ |) estimated from Equations (8) and (9) for the Wilhelmy tensiometer as a function of the contact angle (θ). For Equation (8), Δf = Δp = Δ_γ= 0.01. For Equation (9), p = 2 mm, γ = 72 mN/m, δf = 1 μN and Δp = Δ_γ= 0.01.

Buoyancy has been ignored for several reasons. It is not relevant if a tensiometer is used for capillary rise measurements where the tube just touches the surface of the liquid (no immersion) or if the solid substrate being immersed or withdrawn has the same density as the wetting liquid. To be fair, these two cases are less common; tensiometers are more frequently employed with liquid–solid combinations that differ in density. Nevertheless, neglecting buoyancy simplifies the mathematics and yields a general expression for uncertainty, Equation (8). If buoyancy were included, the uncertainty in the contact angles could be even greater.

Conclusions

Uncertainty in contact angles from the Wilhelmy tensiometer was estimated to be small in the middle of the range, but increased asymptotically at the extremes of wettability.

Acknowledgements

The author thanks to M. Acevedo, L. Castillo, D. Downs, J. Doyon, and D. Meyer for their support.

Disclosure statement

No financial interest or benefit has arisen from the direct application of their research.