A three-dimensional transient computational study of 532-nm laser thermal ablation in a geometrical model representing prostate tissue

Abstract

Objective: Laser with 532-nm wavelength (GreenLight^TM) is clinically approved to treat benign prostatic hyperplasia (BPH). However, low rate of tissue ablation and excessive thermal coagulation are shortcomings of this therapy. The goal of this study was to use a mathematical model to identify clinically viable laser settings that have the potential to improve treatment time and outcomes.

Methods: A three-dimensional transient computational model was developed, validated against analytical and experimental results, and utilized to investigate the response of tissues subjected to continuous-wave and pulsed lasers emitting 532-nm light (GreenLight^TM laser). The impact of laser power (10–125 W), pulse duration (100 ns and 100 µs) and pulse frequency (10 and 100 Hz) on tissue ablation and coagulation rates and sizes was explored.

Results: Good agreement between the computational model and analytical and experimental results was found. Continuous-wave laser results in 13% less coagulation zone thickness and 10% higher ablation rate than the low frequency pulsed laser. With increasing laser power; ablation rate is expected to increase linearly, while coagulation zone thickness is expected to increase asymptotically. Pulse frequency influence on tissue ablation and coagulation is relevant at high power, but pulse duration is found to have minimal effect at all powers.

Conclusions: Laser thermal tissue ablation employing continuous wave mode lasers outperforms that employing pulsed mode lasers. Laser power settings should be carefully selected to maximize the rate of tissue ablation and minimize tissue coagulation.

Keywords:

• Thermal ablation
• coagulation
• pulse duration
• pulse frequency
• prostatectomy
• laser power

Introduction

Treating benign prostatic hyperplasia (BPH) using high power lasers has been an active area of clinical use over the last few decades [1]. The US Food and Drug administration approved the use of GreenLight^TM laser, emitting at 532 nm wavelength to treat BPH. This laser treatment is associated with minimal bleeding; short hospitalization time; and low recurrence rates [2–4]. However, the small ablation rate (i.e. physical tissue removal/vaporization rate) represents a continuous challenge, especially in larger prostate glands [5]. In addition, the relatively thick coagulation zone (i.e. irreversible thermal damage of tissue that remains in place) of 2 mm, may slow down the healing and thus increase the postoperative irritation symptoms [6]. In order to address these limitations, a better understanding of GreenLight^TM laser tissue thermal ablation is needed.

The influence of the surgical procedure’s parameters; specifically, laser scanning speed and laser working distance, on tissue ablation outcome has been investigated theoretically and experimentally [7–9], and optimum values of scanning speed and working distance were reported and predicted. However, limited studies have evaluated the importance of tissues’ and lasers’ parameters in GreenLight^TM laser tissue thermal ablation [10,11]. In the present study, we are particularly interested in the effect of laser’s parameters: average power, pulse duration and pulse frequency. Set-ups for experimental adjustment and investigation of GreenLight^TM laser’s parameters are complicated; hence, a predictive theoretical model could be utilized.

Two heuristic laser ablation models are widely used: blow-off and steady-state models [12]. The blow-off model is applicable for short laser pulses with very low pulse frequency such that no ablation occurs during the pulse, and no thermal accumulation occurs between pulses. The steady-state model is applicable for long laser pulses that allow ablation process to reach a steady state. It can be assumed that the actual laser ablation process is somewhere between these two processes; where tissue ablation can take place during laser pulses, and the importance of laser temporal profiles is likely encompassed in the transient (unsteady state) part of the ablation process. Hence more advanced models are needed.

Several researchers have studied laser tissue ablation theoretically with varying success [13–17]. Several laser tissue ablation modeling advancements were accomplished by McKenzie, through a three-zone 1D steady-state model [18]; Partovi et al. through a 3D steady-state model [19]; and Venugopalan et al. [20] through a dimensionless 1D steady state model. In these models, laser tissue ablation was assumed a water vaporization process; while optical scattering was not directly incorporated. These models did not consider transient response; thus, they couldn’t be used to explicitly study the importance of laser temporal profiles. Further, the predictions made by these models for the influence of laser powers on coagulation sizes were different. Majaron et al. [21] developed a 1D transient thermo-mechanical model that incorporated mechanical and thermodynamic properties of tissues, while assuming laser tissue ablation a water phase change process under changing pressure and volume. However, their model was sub-ablative; that is, simulation had been halted just before ablation commenced. Also, optical scattering was not accounted for in the model. The limitations of the above mentioned models are summarized in Table 1.

Table 1. Limitations of previous laser ablation models.

Model	Limitations
McKenzie [18]	One-dimensional, steady state, and no scattering
Partovi et al. [19]	Steady state, no precise scattering
Venugopalan et al. [20]	One-dimensional, steady state, and no scattering
Majaron et al. [21]	One-dimensional, sub-ablative, and no scattering

Herein, we present a new computational model to simulate Greenlight^TM laser thermal tissue ablation in a 3D geometry. The model is transient and explicitly incorporating optical scattering. The model is utilized to assess the dependency of tissue ablation and coagulation on pulse duration, pulse frequency, and power of Greenlight^TM laser delivered in continuous-wave (CW) or pulsed modes. This model could be used to guide future preclinical and clinical studies

Methods

Model set-up

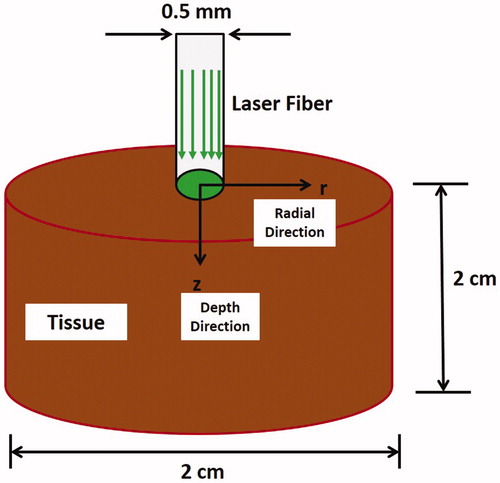
The relationship between laser’s parameters and tissue ablation outcome was investigated using a transient 3D axisymmetric model. A cylinder with diameter and length of 2 cm was used as a geometrical model of the tissue (Figure 1). The investigated laser’s parameters were: pulse frequency, pulse duration, and power. A collimated Greenlight^TM laser emitting light at 532 nm wavelength, which has a uniformly distributed profile over a spot size of 0.5 mm in radius, was employed. The laser beam was maintained centered at the tissue surface (i.e. r = 0) during the entire simulation time of 3 s.

Figure 1. Schematic diagram showing the set-up for simulating Greenlight^TM laser tissue ablation process.

Laser tissue ablation was assumed a water vaporization process as in [20]. Due to the complexity of involved phase changes, the enthalpy method that is based on an energy balance argument, was adopted; and the governing equation can now be defined as [22]: (1) $$\frac{\partial h}{\partial t}=\nabla ·(\mathrm{k}\nabla T)+\stackrel{·}{Q}$$(1) where h is the enthalpy per unit volume (J m ⁻³), k is the thermal conductivity (W m ⁻¹ K ⁻¹), T is the temperature (°C), and $\dot{Q}$ is the rate of laser heat generation (W m ⁻³). The variable-photon Monte Carlo (MC) method, described in details in [23], was utilized to determine light intensity (J cm ⁻²) distribution and then the laser heat generation term, i.e. Q(r, z). Photon positions were first tracked in 3-D Cartesian coordinates, and then they were transformed into cylindrical coordinates. The domain was divided into control volumes, as shown in Figure 2, and for each control volume the discretized energy balance equation is written as: (2) $$\begin{array}{c}{h}_{r,z}^{{}_{t+\Delta t}}-h_{r,z}^t=2\pi \Delta \mathrm{z}\hspace{0.17em} \Delta \mathrm{t} \left[\left(r-\frac{\Delta \mathrm{r}}{2}\right)\hspace{0.17em} \hspace{0.17em} q_{r-\frac{ \Delta \mathrm{r}}{2}}-\left(r+\frac{\Delta \mathrm{r}}{2}\right) q_{r+\frac{\Delta \mathrm{r}}{2}}\right]\\ +2\pi r\Delta \mathrm{r} \Delta \mathrm{t}\left(q_{z-\frac{\Delta \mathrm{z}}{2}}-q_{z+\frac{\Delta \mathrm{z}}{2}}\right)+Q(r,z)\end{array}$$(2) where Δt is the time step (second); Δr is the grid size in the radial direction (m); Δz is the grid size in the axial direction (m); and q is the heat flux (W m ^{− 2}), according to Fourier’s law. A linear temperature profile between the nodes was utilized [24]. For water vaporization process, the temperature T and the enthalpy per unit volume h can be related as: (3) $$T=\{\begin{array}{l}\frac{h}{\rho {\mathrm{C}}_{\mathrm{p}}},\hspace{1em}h<\rho {\mathrm{C}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{v}}\\ {\mathrm{T}}_{\mathrm{v}},\hspace{1em}\rho {\mathrm{C}}_{\mathrm{p}}{\mathrm{T}}_v<h<\rho {(\mathrm{C}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{v}}+{\mathrm{L}}_{\mathrm{v}})\end{array}\}$$(3) where ρ, C_p, T_v and L_v are the tissue density (kg m⁻³), specific heat capacity (J kg⁻¹ K⁻¹), water vaporization temperature (°C), and latent heat of vaporization (J kg⁻¹). The thermo-physical and optical properties used in the current study are summarized in Table 2.

Figure 2. The axisymmetric computational control volume that is used in the model and showing heat fluxes and heat generation.

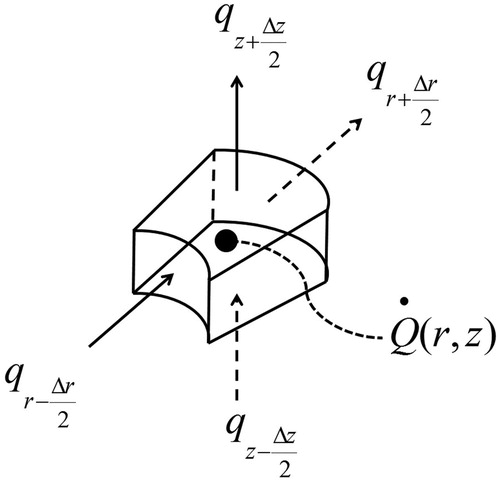
Table 2. Values of the parameters that were used in the computational model [25–28].

Property/parameter	Value
Average density	ρ = 1000 kg m^−3
Thermal conductivity	k = 0.6 W m^−1 K^−1
Specific heat capacity	cp = 4187 J kg^−1 K^−1
Latent heat of vaporization	Lv = 2.27*10^6 J kg^−1
Vaporization temperature	Tv = 100 °C
Energy of ablation	habl = 2.7 *10^6 J m^−3
Absorption coefficient	µa = 1 cm^−1
Scattering coefficient	µs = 100 cm^−1
Anisotropy factor	g = 0.9

The process was assumed adiabatic, and the normal human body temperature of 37 °C was used as an initial condition. Equations 1–3 were solved simultaneously and explicitly, and enthalpies and temperatures were calculated, updated, and stored after each time step. Updated enthalpies were compared with an ablation enthalpy threshold, defined as: (4) $${\mathrm{h}}_{\text{abl}}=\rho {(\mathrm{C}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{v}}+{\mathrm{L}}_{\mathrm{v}})$$(4)

Whenever a control volume’s enthalpy exceeded h_abl, the control volume was instantly removed from the computational domain (i.e. ablated without interfering with light or heat distributions), and the boundary conditions were updated by imposing them on the newly emerged boundary control volumes. Although tissue coagulation is a kinetic process, the temperature threshold for tissue coagulation can be set at 65 °C, as this temperature threshold has been used [20,29–31]. Thus, when a control volume’s temperature reached 65 °C, it was marked as coagulated until the end of the simulation. The ablation process (i.e. removal of the control volumes from the simulation’s domain) was the exclusive mechanism for dynamic change of the simulation’s tissue domain in contrast to the coagulation process which didn’t induce any dynamic change to the simulation. Time steps (Δt) ranging from 100 ns to 0.5 ms, depending on pulse durations and frequencies and on the stability condition of the explicit scheme, were used. The grid size in both radial and axial directions was set to 50 µm.

The ranges of the investigated parameters were chosen according to the commercially available GreenLight^TM lasers used for treating BPH [1]. The range of tested parameters are summarised in Table 3. Simulated laser tissue treatment was mainly evaluated in terms of: coagulation zone thickness, following Kang et al. [7]; coagulation depth, which is the tissue coagulation thickness along the laser beam axis (i.e. r = 0); and ablation rate, calculated as: ablated tissue volume/time.

Table 3. The values of laser parameters employed in the computational model.

Results	Pulse duration	Pulse frequency (Hz)	Power (W)
Figure 5	CW	CW	50
Figure 6	100 ns, 100 µs, and CW	10, 100, and CW	10
Figure 7	100 ns, 100 µs, and CW	10, 100, and CW	100
Figure 8	CW	CW	10, 20, 30, 40, 50, 60, 70, 80, 90, 100, and 125

Validation of the computational model against analytical model

The one-dimensional steady-state analytical model developed by Venugopalan et al. (see Table 1) was chosen [20]. The tissue was assumed a one-dimensional pure absorbing medium with a length of 10 mm and an absorption coefficient (µ_a) of 1 mm⁻¹. The thermo-physical tissue properties summarized in Table 2 were used. Thermal ablation simulation was induced by continuous wave laser with laser irradiance of 100 W/mm². Spatial grid size (Δx) was refined until discretization error became negligible. Temporal grid size (Δt) was refined in compliance with the stability condition of the employed explicit numerical scheme. Another condition imposed while refining Δt was that the accumulated energy within a control volume during the time step should not exceed the heat of ablation threshold. Adiabatic boundary conditions were imposed. The simulation was stopped when ∼70% of the tissue was ablated. The comparison with the analytical solution was carried out in terms of steady-state temperature profile and tissue front position, whose rate of change is the ablation velocity.

Validation of the computational model against experimental results

In the experimental set-up, a Q-switched KTP laser (Green-Light PV laser, American Medical Systems, Minnetonka, MN) with a power setting of 80 W was used. Rat hind limb muscle was used as the tissue model. Tissue scattering was considered significant and the assumed optical properties were [25]: 0.15 mm⁻¹ absorption coefficient, 9.1 mm⁻¹ scattering coefficient, and 0.9 anisotropy index. The laser beam was delivered to the tissue via an end-firing fibre with a beam divergence of 9 degrees [9]. The fibre was fixed to a computerized stage that allowed controlled movement of the fibre in all directions. The fibre’s tip was maintained at a distance of 2 mm from the tissue surface and was scanned at various speeds (treatment speeds) to induce 2 cm long wounds. A tissue slice in the middle of the induced wound was dissected, and the cross-section area of the ablated tissue was measured.

Results

As shown in Figure 3(A, B), an excellent agreement between the computational and analytical models was found after refining the spatial grid size to a value of 0.01 mm. The temperature profile was captured at the time point when ∼20% of the tissue was ablated. The temperature remained constant at 100 °C in the vapor–liquid mixture region. Outside this region, the temperature decayed exponentially to 37 °C (the initial temperature). Tissue front position remained at zero value until ablation had commenced, then it increased linearly with time indicating a constant ablation velocity.

Figure 3. Validation of the computational model against analytical and experimental results. (A) temperature profile of analytical and computational models, (B) tissue front position of analytical and computational models, and (C) Ablation area obtained experimentally and from the computational model [9].

Figure 4. Light energy density (J cm ^{− 2}) distribution in a tissue after irradiating by laser pulse of 1 J cm ^{− 2} fluence and 0.5 mm spot radius. (A) Distribution prior to ablation crater had formed. (B) Distribution after ablation crater had formed.

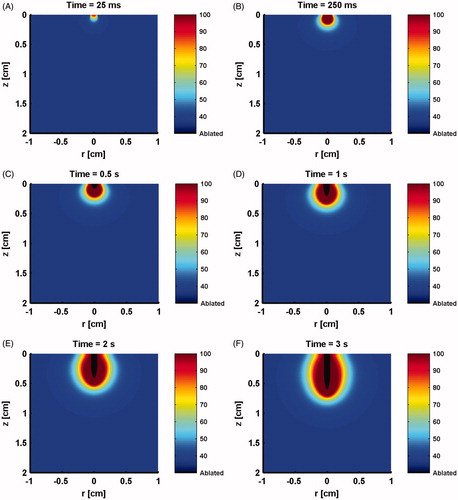
Figure 5. Longitudinal sections showing model predicted evolving temperature profile and ablation crater resulting from irradiation by a 50 W CW laser at times of: (A) 25 ms, (B) 250 ms, (C) 0.5 s, (D) 1 s, (E) 2 s, (F) 3 s.

Figure 3(C) shows ablation area obtained by the computational model at several selected treatment speeds in comparison with those obtained experimentally. The general trend of the exponential decaying in ablation area with increasing treatment speed that was obtained experimentally was reasonably captured by the computational model. Moreover, and despite the deviation between the model and the experiment at 0.5 and 4 mm/s treatment speeds, the model and experimental results were in a good agreement.

Figure 4(A) shows the distribution of laser energy (J cm⁻²) prior to ablation, which is similar to what is reported in [23]. However, once ablation commences, the evolving ablation front (ablation crater) is shown to distort the distribution of the laser energy (Figure 4(B)). This attenuation of energy distribution will have a subsequent effect on ablation and coagulation processes. Therefore, it was very important to keep track of the ablated tissue front throughout the simulation. Figure 5 shows the model prediction of evolving ablation crater and temperature profile at several time points during the ablation process for a CW laser with 50 W.

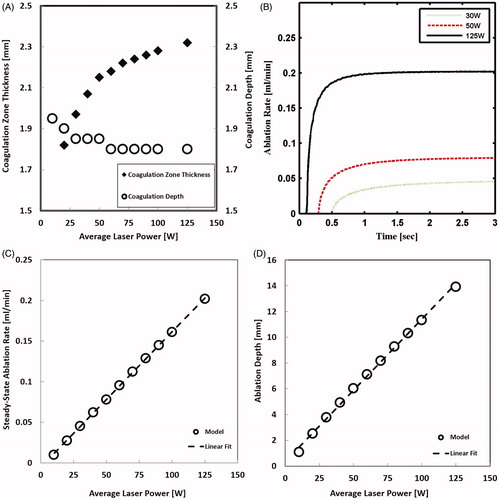
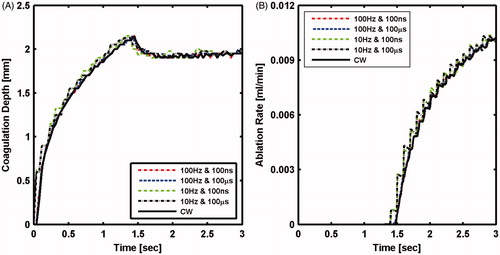
The influence of laser pulse duration and frequency on ablation outcome was first investigated at low power of 10 W. As shown in Figure 6(A), coagulation depth increased monotonically to a value of 2.15 mm at the time point of 1.5 s. Subsequently, coagulation depth decreased asymptotically to 1.9 mm, forming a peak that coincided with the onset of ablation (Figure 6(B)). The decrease in coagulation depth is due to the movement of the tissue ablation front that is compressing the temperature profile. At this low power, there was insignificant effect of pulse duration and frequency on either ablation rate or coagulation depth, which implies insignificant importance of laser temporal profile at such low powers.

Figure 6. Tissue laser ablation outcomes evaluated in terms of (A) coagulation depth and (B) ablation rate after irradiating with 10 W CW mode and pulsed mode lasers at selected pulse durations and pulse frequencies.

At higher power of 100 W, the calculated coagulation depth at lower frequency of 10 Hz was noticeably different from the one computed for CW. At a higher frequency (100 Hz), the coagulation depth was similar to the one computed for the CW laser (Figure 7(A)). The 10 and 100 Hz pulses resulted in 15 and 2% larger coagulation zone thickness, respectively, than the CW laser, as shown in Figure 7(B). It is predicted that tissue treated at low frequency will sustain more thermal damage than that treated with high frequency or CW lasers. Initial oscillations in ablation rate occurred due to pulsing nature; however, ablation rate, on average, increased exponentially with time until it saturated within 0.6 s after ablation had commenced. Steady-state ablation rate at the low and high frequencies were 10 and 1.5%, respectively, smaller than ablation rate with CW laser (Figure 7(C)). The pulse duration did not have influence on either coagulation or ablation sizes.

Figure 7. Tissue laser ablation outcomes evaluated in terms of (A) coagulation depth; (B) coagulation zone thickness; and (C) ablation rate after irradiating with 100 W CW mode and pulsed mode lasers at selected pulse durations and pulse frequencies.

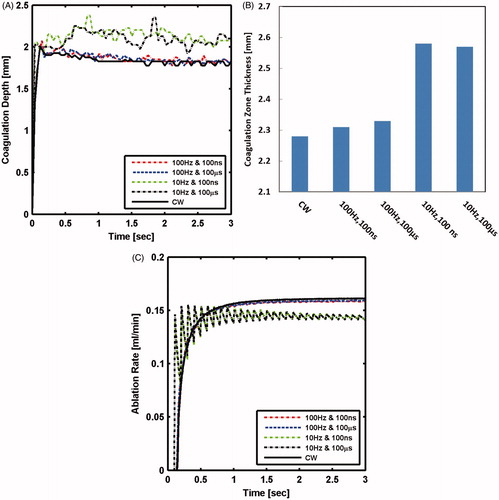
Figure 8(A) shows that coagulation zone thickness for CW laser increased monotonically with power and converged to an asymptotic value of 2.3 mm. The coagulation zone thickness increased by more than 40%; whereas, coagulation depth decreased by 10%, when power increased from 10 to 125 W.

Ablation rate increased exponentially with time, and the increase was steeper at higher power (Figure 8(B)). Shortly after the onset of ablation, ablation rate tended to saturate to a steady-state value. The steady-state ablation rate was linearly correlated to the power, as shown in Figure 8(C). Ablation depth that was calculated at the end of simulation also changed linearly with power (Figure 8(D)). The predicted increase in ablation rate and depth with power agrees with general experimental findings [7,32,33]. Specifically, the linear dependency of ablation rate and depth are in line with experimental results but for a different type of laser [34]. It is now expected that more ablation size and rate will be attained by continuously increasing laser power.

Figure 8. Tissue laser ablation outcome evaluated in terms of (A) coagulation zone thickness and coagulation depth, (B) ablation rate (C) steady-state ablation rate, and (D) ablation depth after irradiating with CW mode laser using different power settings.

Discussion

The accuracy of the numerical scheme adopted in the current computational model is tested through model validation against an analytical solution. The convergence of the computational solution to the analytical solution suggests acceptable accuracy of the numerical scheme and concludes that the computational model behaves as expected compared with analytical models.

The correctness of the dynamic behavior of the applicator was assessed by validating the computational model against experimental results obtained at various treatment speeds. The capability of the computational model in capturing the general trend of treatment speed effect on ablation area, and the good matching of the experimental results at 1, 1.5, 2, and 3 mm/s treatments speeds support the accuracy of the model. On the other hand, the deviation between the model and the experimental results at the very low and very high treatment speeds of 0.5 and 4 mm/s, respectively, competes against model accuracy. This deviation is likely due to not incorporating some effects into the current model such as optical shielding, tissue carbonization, back scattering at the edge of ablation crater, residual mechanical stresses in the tissue, and/or dynamic tissue properties. Attention and addressing of such deviation is warranted in future works.

The minimal impact of pulse duration may seem inconsistent with the thermal confinement concept and with other commonly reported experimental results. However, thermal confinement concept is based on comparing diffusive heat propagation length during a laser pulse with the optical penetration depth, but it does not account for the effect of moving tissue ablation front [12,35]. This renders thermal confinement concept inapplicable to study GreenLight^TM laser thermal ablation of BPH.

Similarly, reported experimental studies were either sub-ablative (i.e. no physical removal of tissue) as in [36], or ablative processes employing few pulses as in [37,38]. Thus, these studies can’t explain the importance of pulse duration in high power laser tissue ablation applications as in the case of laser prostatectomy; where a large volume of tissue removal in minimal time is required (i.e. large ablation rate) [19,20]. Another source of possible discrepancy between experimental studies could be changes of laser’s parameters while investigating other parameters as in [39,40], for example, where laser power/irradiance was being changed while changing pulse durations. Such issues were discussed before in [20,21]. In addition, using multiple laser pulses at very low pulse frequency of 1 Hz, for instance, could be confusing since such low frequency will allow complete heat relaxation between pulses. This in turn will imitate a single pulse ablation process that has a very low ablation rate.

It is expected that more efficient treatment of higher ablation rate and lesser thermal damage can be achieved by adopting CW mode; hence, the performance of CW laser with wider range of powers was evaluated with our mathematical model. The predicted increase of lateral thermal damage that is represented by coagulation zone thickness with increasing power is in a good agreement with experimental findings [7,8], and the predicted decrease in axial thermal damage that is presented by coagulation depth with increasing power agrees with predictions of 1D analytical ablation models [18,20]. Consequently, optimal laser power in terms of minimizing thermal damage will specifically depend upon surgical applications and modalities. For instance, for procedures requiring removal of whole tissue’s surface, axial thermal damage is more important; thus, lower power will be preferred. However, for applications where tissue cutting/drilling is sought; lateral thermal damage is more important; hence, higher power would be favored.

Since laser power is directly proportional with coagulation zone thickness and ablation rate and indirectly proportional with coagulation depth, maximizing ablation and minimizing coagulation can’t be achieved simultaneously by varying the power. This suggests that there is no absolute optimum laser power; in fact, some compromise should be made depending on the surgical procedure and its specific desired outcomes. This requires further computational work to better understand and select the best value for the power. These investigations can be fulfilled by considering a whole tissue (a whole prostate for instance) and then conducting a complete laser ablation simulation until all unwanted tissues are removed/ablated. Optimum power, tailored to different tissue sizes and geometries and to a whole surgical procedure time, can then be anticipated.

Experimental work complementing the current study is warranted in the future. Also, future enhancements of the current model may be beneficial. For instance, in the current model, laser tissue ablation was assumed a water vaporization process that is taking place at a constant pressure. But, in reality, laser ablation is an explosive process that causes elevations in tissue pressures and temperatures beyond atmospheric pressure and water boiling temperature, respectively. The explosive nature of the process would require lower ablation threshold as predicted by Elkhalil et al. [9]. The lower the ablation threshold is, the more ablated tissue is, the less tissue residual energy is, and thus the less thermal damage is. Therefore, the current model is expected to under predict ablation volume and over predict coagulation volume. Such speculated model’s sensitivity issue should be investigated in the future through uncertainty quantification of the different model’s parameters. Perhaps, a hybrid model which blends isobaric and isochoric conditions through pressure-temperature relationships accounting for mechanical properties of tissues could better reflect the explosive nature of the process. Also, incorporating dynamic optical and thermo-physical properties of tissues in future models could be possible.

Conclusions

In this study, a computational 3D transient Greenlight^TM laser tissue ablation model was developed utilizing the enthalpy method. The model was compared with analytical solutions and experimental results; and acceptable agreement was found. The model represents an important extension of previous laser tissue ablation models by considering the transient behavior in multipulse ablative laser tissue treatment while explicitly accounting for optical scattering.

No significant effect of pulse duration on tissue ablation and coagulation is predicted. Tissue ablation and coagulation dependency on pulse frequency is noticeable at high laser power; where the model predicts that lasers operated in CW mode will outperform those operated in pulsed mode. Also, a complex effect of the power on ablation is predicted; where laser power could be chosen to minimize coagulation size or maximize ablation rate but not both. This suggests the need for further studies where a whole tissue ablation is taken into consideration.

Acknowledgements

We would like to thank the American Medical Systems, LLC, USA for providing the laser system and the Faculty of Computer and Information Technology at the Jordan University of Science and Technology, Jordan for providing access to its computing facilities to execute all the computations and simulations in this work..

Disclosure statement

No potential conflict of interest was reported by the authors.