The Single-Fiber Collision Rate and Filtration Efficiency for Nanoparticles I: The First-Passage Time Calculation Approach

Abstract

We describe an approach to filtration-efficiency calculations as an alternative to the traditional depth filtration theory. The new approach involves linking the single-fiber efficiency to the collision rate coefficient/kernel between nanoparticles and fibers, and correspondingly inferring the collision kernel via dimensionless mean first-passage time (MFPT) calculations. This method has the advantage of easily incorporating the influences of particle diffusion, inertia, and particle size; therefore, all filtration mechanisms can be considered simultaneously. Through non-dimensionalization of the equation of motion for a particle in MFPT calculations (the Langevin equation), it is shown that both the single-fiber efficiency E_f and dimensionless particle-fiber collision kernel, H, are functions of the ratio of particle radius to filter-fiber radius, R, the solid volume fraction in the filter, V_f, the ratio of particle persistence distance to the particle-filter collision distance, Kn_D (the diffusive Knudsen number), and the ratio of the particle translational kinetic energy to the thermal energy χ_f. Using a Kuwabara flow-cell model to define the geometry and flow field, MFPT calculations are used to determine H and E_f for nanoparticles in atmospheric pressure systems, i.e., when particle inertia is negligible but when diffusion and interception act in tandem to collect particles. From MFPT results, regression equations for both H and E_f are developed. A comparison is made between MFPT results and commonly invoked depth-filtration single-fiber efficiency relationships, experimentally measured values, and H equations derived from Sherwood number correlations based upon measurements of heat transfer from a fluid flowing perpendicular to an array of cylinders. Good agreement is found with both measurements and previously developed equations over a wide range of parameter space.

Copyright 2014 American Association for Aerosol Research

INTRODUCTION

The removal of nanoparticles from flowing aerosols via fibrous filtration is of considerable industrial utility, and there exist long-established experimental and theoretical approaches to examine nanoparticle deposition on filter fibers (Davies 1952; Stechkina and Fuchs 1966; Yeh and Liu 1974a, b; Emi et al. 1982; Lee and Liu 1982a, b; Vanosdell et al. 1990; Shapiro et al. 1991; Wang et al. 2007; Wang and Otani 2012). Most often, in depth-filtration theory, filter performance is described via the penetration of nanoparticles through a filter, P (the ratio of the number concentration of particles exiting the filter to the number concentration incident on it), which is linked to the single-fiber efficiency, E_f, through the relationship (Lee and Liu 1982b): [1] where w is the filter thickness, V_f is the solid volume fraction of fibers within the filter medium, and a_f is the fiber radius [assumed monodisperse in Equation 1[1] , with corrections to this approach needed to account for filter-fiber polydispersity (Dhaniyala and Liu 1999; 2001b; Podgorski et al. 2011)]. Calculation of E_f routinely involves the use of a cell model, i.e., an idealized depiction of a filter's geometry and the flow field through a filter, which facilitates calculations of particle trajectories through a filter medium (Stechkina and Fuchs 1966; Yeh and Liu 1974a; Lee and Liu 1982b). The models used most frequently are those of Kuwabara (1959) and Happel (1959) and simplifications of them [e.g., Lamb's flow model (1932)], all of which define the cell as a two-dimensional circular region of radius b = V_f ^−1/2a_f, containing an inner solid circle of radius a_f. Through calculation of the mass flow rate of particles exiting the cell model relative to the flow-rate incident, single-fiber efficiencies are determined (Stechkina and Fuchs 1966; Yeh and Liu 1974a). Although particle motion within a filter is influenced by both thermal motion and inertia, and particles are finite-sized relative to fiber radii, prior evaluations of single-fiber efficiencies have generally invoked the assumption of particle deposition onto fibers by a particular filtration mechanism (i.e., deposition via solely diffusion, inertia, or interception). For instance, E_D, the single-fiber efficiency due to diffusion alone, is evaluated through use of continuum mass-transfer equations with particle inertia and the particle radius (relative to the fiber radius) assumed to be negligible. For E_I, the single-fiber efficiency for impaction, particle thermal motion is neglected (as is the particle size), and Lagrangian trajectory calculations enable single-fiber efficiency determination. Finally, for E_R, the efficiency due to interception, particles are assumed to follow fluid streamlines precisely, yet collide with a filter fiber when their centers are a distance a_p + a_f (the sum of the particle and fiber radii) from the fiber center. The total single-fiber efficiency is then calculated using additivity rules as E_f  =  E_D + E_I + E_R, or independence rules as E_f  =  1−(1−E_D)(1−E_I)(1−E_R).

In the filtration of nanoparticles, deposition via inertia is typically negligible, and a number of prior studies have, therefore, examined the single-fiber efficiency for diffusion (Kirsch and Fuchs 1968; Stechkina and Fuchs 1966; Lee and Liu 1982b) and interception (Friedlander 1957; Brown and Wake 1991). Most of these studies find diffusion to be the dominant mechanism of nanoparticle deposition and give similar results for the scaling between E_D and the dimensionless ratio Pe = 2U₀a_f/D (the Peclet number, where U₀ is the incident (free-stream) flow velocity onto the filter and D is the particle diffusion coefficient). Nonetheless, there remain several reasons for continued theoretical examination of the deposition of nanoparticles on fibrous filters, as well as for the determination of the single-fiber efficiency through alternative methods. First, Stechkina and Fuchs (1966) as well as Kirsch et al. (1974) note that additivity rules do not necessarily lead to correct single-fiber collection efficiencies and that an additional correction factor, E_DR, must be incorporated for improved single-fiber efficiency calculation. Lee and Liu (1982b) similarly note that, although algebraic, the single-fiber efficiency terms E_D, E_R, and E_DR are cumbersome to work with, and improved relationships could be developed. Moreover, use of the additivity or independence rules when particle thermal motion and size have an influence is conceptually misleading. An individual particle cannot be stated to have deposited solely due to interception or diffusion alone; no particle has zero diffusive motion and all particles are finite sized. In lieu of invoking additivity or independence rules, a single, simple equation to appropriately predict single-fiber collection efficiency accurately is, therefore, desirable.

Furthermore, several of the more commonly invoked depth-filtration relationships for E_D derive from cell models with restricted boundary conditions. Stechkina and Fuchs (1966) utilized Lamb's flow cell model to examine diffusional deposition, invoking the boundary condition that the number concentration of particles is equal to N₀, the baseline concentration, at a distance r = ∞ from the center of the cell. However, the distance r = ∞ cannot be defined in a cell model; once a particle reaches beyond a distance b from the center of the cell, it now resides within a new cell (at a random location), i.e., no particle can ever be larger than a distance b from a cell center, and the boundary condition at r = ∞ can only be defined when V_f → 0. This condition additionally implies that the filter fiber is collecting a negligible number of particles (the upstream and downstream concentrations are identical); therefore, it is only valid for E_D → 0. Yeh and Liu (1974a) also invoked this boundary condition at r = ∞, placing the same restrictions on their results. Lee and Liu (1982b) used the modified boundary conditions dn/dr = 0 (the particle radial concentration gradient) and n = N₀ at r = b, which again leads to results that are only valid when E_D → 0. The predictions of these cell models, which are some of the most frequently invoked in filtration studies, need to be compared with results derived from models free of restricted boundary conditions.

We note finally that there are pedagogical reasons for further examination of filtration. Fibrous filtration is a quintessential aerosol collision phenomenon, in which particles, driven by thermal motion and fluid flow, collide with other entities (fibers). The link between collision rates (number of collisions between entities in the gas phase per unit volume per unit time) for other such aerosol collision phenomena, namely, coagulation (Fuchs 1964), condensation (Fuchs and Sutugin 1970), and diffusion charging (Fuchs 1963) is well-known, and these phenomena are often introduced in textbooks (Hinds 1999; Friedlander 2000) and lectures in a connected fashion. Fibrous filtration, however, is often introduced as a control technology distinct from these processes, without consideration of the connection between the equations for single-fiber efficiency and the collision rates between particles and fibers.

With these issues in mind, the purpose of this work is to theoretically determine the single-fiber efficiency for the filtration of nanoparticles by connecting it to the collision rate for particles with filter fibers. The collision rate is determined through a combination of dimensional analysis and mean first-passage time (MFPT) calculations in a Kuwabara flow cell model. This approach applies the Langevin equation of motion (Ermak and Buckholz 1980; Gupta and Peters 1985) to monitor particle trajectories, enabling consideration of all filtration mechanisms simultaneously; therefore, it gives rise to equations free of additivity assumptions. Langevin equation-based calculations have been used previously to examine fibrous filtration (Ramarao et al. 1994), with notable recent work by Balazy and Podgorski (Balazy and Podgorski 2007; 2008; Podgorski and Balazy 2008). Although the physics of the model invoked here is, indeed, similar to these prior works, the determination of the collision rate is unique, as are the resulting dimensionless equations. Recently, our group has used the dimensional analysis-MFPT calculation approach to find simple dimensionless collision-rate expressions for condensation, coagulation, aggregation, and the diffusion charging of particles (Gopalakrishnan and Hogan 2011). The equations have been extended to non-spherical particle shapes (Gopalakrishnan et al. 2011, 2013; Thajudeen et al. 2012) and singular contact potential interactions have also been considered (Ouyang et al. 2012). Here, we describe in detail how this approach is extended to spherical nanoparticle deposition onto fibers. In a subsequent report (Thajudeen et al. 2014), we demonstrate that the resulting equations are applicable to particles of arbitrary shape.

THEORETICAL METHODS

Fluid Flow in the Cell Model

As noted in the introduction, we invoke the two-dimensional Kuwabara (1959) cell model to describe the fluid flow around a cylindrical fiber within a staggered array of fibers. A unit cylindrical cell surrounding each fiber, for which the vorticity is zero on the cell boundary, is defined with dimensionless outer radius b* = b/(a_p + a_f) = V_f ^−1/2/(1 + R), where R = a_p/a_f. Correspondingly, the dimensionless stream function for the two-dimensional flow through the cell (Yeh and Liu 1974a) is given as [2] where , B = −(1 − V_f), C = 2, , , r is the dimensionless radial coordinate (normalized by a_p + a_f), and θ = 0 denotes the upstream direction in the cell. This enables determination of the dimensionless radius and angular velocities through the relations and , respectively.

Due to deposition on fiber surfaces, the average particle concentration in a parcel of aerosol moving through a filter, n_p, decreases over time at rate dn_p/dt: [3] where β is the two-dimensional collision kernel/collision rate coefficient (m² s⁻¹), n_f is the fiber number concentration, and t is the parcel's residence time within the filter. Similar to studies of particle–particle collisions (Gopalakrishnan and Hogan 2011), we non-dimensionalize the collision kernel as [4a] where m_p is the mass of particles, and f is the particle friction coefficient (Davies 1945). The change in particle number concentration is then expressed as [4b]

Collision Rate in the Absence of Flow

Prior to examining particle migration through the noted fluid flow field, we remark that, in the absence of fluid flow, the collision of a particle with a fiber is analogous to the problem of two-dimensional coagulation of a smaller entity with larger, stationary entity (or of condensation of a heavy vapor molecule onto an extremely long fiber). In instances where the smaller entity's persistence distance ([kTm_p]^1/2/f, where kT is the thermal energy) is substantially less than the collision length scale (a_p + a_f), the collision kernel collapses to its mass transfer continuum limit form, which can be determined from Fick's second law: [5a] where the subscript c denotes the continuum limit. The dimensionless two-dimensional collision kernel under these conditions is expressed as [5b] where Kn_D is the diffusive Knudsen number, as defined in prior studies of collision processes (Dahneke 1983; Gopalakrishnan and Hogan 2011; Thajudeen et al. 2012): [5c]

In the opposite free molecular/ballistic limit, the collision kernel can be determined in a manner analogous to the collision rate of ions/electrons with cylindrical Langmuir probes excluding the influence of potential interactions (Mott-Smith and Langmuir 1926; Allen 1992): [6a] where the subscript F denotes the free molecular limit and the corresponding dimensionless equation is [6b]

Equations (5a–c) and (6a–b) have not been utilized in prior examinations of fibrous filtration; however, in the limit of low flow or particles of high diffusivity, these equations will describe the rate of deposition of particles onto fibers in the continuum and free molecular regimes, respectively. The former is particularly relevant for nanoparticles at atmospheric pressure and room temperature, and any solution for the nanoparticle–fiber collision rate coefficient should collapse to Equation (5a)[5a] as the flow velocity approaches zero. Meanwhile, Equation (6a)[6a] would only find relevance for submicrometer fibers (Podgorski et al. 2006; Yun et al. 2007) at reduced pressure. To our knowledge, fibrous filtration under these circumstances, outside the mass transfer continuum regime, has not been previously examined, but is of interest in particle removal by nanofibers (Ahn et al. 2006). We therefore intend to examine this regime in the future; in the present report, Equations (6a) and (6b) are only used in the verification of invoked simulation approach.

FIG. 1. Schematic describing the MFPT approach to determine dimensionless collision kernels. Relevant dimensionless length scales for calculation are labeled, and a depiction of particle motion is provided.

Collision Rate from Mean First-Passage Times

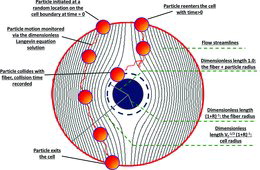
A schematic describing MFPT calculations (Narsimhan and Ruckenstein 1985; Gopalakrishnan and Hogan 2011) is provided in Figure 1. To determine the dimensionless collision kernel in the presence of fluid flow, calculations are conducted as follows: particles are introduced one at a time at a random location on the surface of the cell model with a prescribed V_f. A particle's dimensionless velocity vector and dimensionless position vector are updated via a dimensionless solution to the Langevin equation (Ermak and Buckholz 1980): [7a] [7b] [7c] [7d]

is the dimensionless gas velocity vector at location , with components in polar coordinates of [U*_r, U_θ*]. Moreover, in Equations (7a–d), and are Gaussian distributed random vectors with mean values of zero and the noted variances (in two dimensions). χ_f is the particle translational energy to thermal energy ratio (Lindquist et al. 2014): [8] where U₀ is the upstream velocity of the fluid flow. Therefore, χ_f is an input into calculations along with Kn_D, V_f, and R; it is these four dimensionless parameters on which H depends. As a particle moves about the cell, it eventually either (1) leaves the cell or (2) collides with the fiber (which occurs when its scalar distance from the center of the cell is less than unity). In case (1), the particle in question is reintroduced at a random location on the cell surface, as it is considered to have entered a new cell, and the dimensionless time continues to accrue. The new position on the cell surface is only accepted if the particle's next step of motion takes it further into the cell; if it leaves again immediately, the timestep is not added to the total time for collision, and a new position is selected. For this reason, the random introduction scheme we employ circumvents the need to prescribe an initial concentration distribution on the cell surface, which is necessary with alternative approaches. Conversely, when (2) occurs, the total time required for the collision, τ_col, is recorded, a new particle (with identical χ_f, Kn_D, V_f, and R) is introduced on the cell surface, and the procedure is repeated. After n_col particle-fiber collisions have been monitored, the average time for collision (MFPT, τ_mean) is calculated as: [9a]

The dimensionless collision rate is subsequently calculated from the equation: [9b]

For a set of input values, simulations are carried out until the standard deviation of H is less than 1% of its average value over the prior 100 collisions and after at least 500 collisions have occurred. With these criteria, values of H are calculated 10 times and the subsequently reported values are the average of ten independent calculations (i.e., they derive from more than 5000 collisions). In addition, simulations require the use of sufficiently small timesteps to correctly monitor motion when the particle and fiber are in close proximity to one another. We find that timesteps selected with the restriction Δτ ⩽ 0.005Kn^{− 2}_D*min(1, χ_f^{− 1/2}) are acceptable for mitigating finite timestep influence.

We note that, because of the flow model employed, non-continuum flow influences, dependent upon the ratio of the gas molecule mean free path to the fiber radius (the Knudsen number, Kn), are presently neglected, but could be considered in calculations through use of Kn-dependent cell models (Pich 1966; Yeh and Liu 1974a). Similar to non-continuum mass-transfer effects, such non-continuum flow effects would become important for low-pressure conditions as well as for nanofiber filters. The influence of viscous interaction between a fiber and particle on particle motion is additionally neglected. Moreover, we note that the traditional Peclet number can be expressed as [10a] and the traditional Stokes number (St) as [10b]

The link between the dimensionless parameters used here and the traditional Peclet and Stokes numbers clearly shows that the dimensionless collision rate can be expressed as a function of V_f, R_, St, and Pe (as is common convention for the single-fiber efficiency). We alternatively opt to express results in terms of H(V_f, R, χ_f, Kn_D), noting that, in the absence of fluid flow or under conditions where it negligibly influences particle motion, Pe→0 and St→0; however, as evidenced by Equations (5b) and (6b), under these circumstances, the dimensionless collision rate is not clearly defined from V_f and R only.

The Single-Fiber Efficiency

Equation (1)[1] arises from integration of the equation: [11a] where z is the distance a parcel of aerosol has traversed through a filter. For a parcel of aerosol entering the filter at a specific time, the differential in distance dz is linked to the differential in time, dt, through the relationship dz = U₀dt/(1 − V_f). Combining Equations (4b) and (11a) leads to [11b]

The single-fiber efficiency is, thus, linearly proportional to the ratio of the dimensionless collision kernel to Stokes number under all conditions. Such proportionality can be found not only for fibrous filtration, but also for any system in which particle migration and deposition is facilitated by fluid flow [e.g., a system of spherical collectors (Gupta and Peters 1985)].

RESULTS AND DISCUSSION

The Zero-Flow Collision Kernel

We first validate the MFPT calculation approach by examining cases with χ_f = 0. With R = 0, V_f = 6.83 × 10⁻⁴, and V_f  =  3.42 × 10⁻³, dimensionless collision kernel calculation results are displayed in Figure 2 for 0.05 < Kn_D < 50. In the Kn_D → 0 and Kn_D → ∞ limits, H is expected to collapse to Equations (5b) and (6b), respectively. Convergence to these equations is evident in MFPT results; with Kn_D below approximately 0.2, results are within 10% of Equation (5b)[5b] . For both volume fractions, and for Kn_D above approximately 10, results are similarly within 10% of Equation (6b). Further evident in Figure 2 are the slightly volume-fraction-dependent values of H at low Kn_D as well as the convergence of both volume fraction results to similar values at high Kn_D, again in line with analytical predictions. We, therefore, find that MFPT calculations can approximately match known analytical results for dimensionless collision kernels, and conclude that the MFPT approach is an accurate method for dimensionless kernel determination under a wide range of conditions.

FIG. 2. The dimensionless collision kernel as function of the diffusive Knudsen number for a cylindrical cell model in the absence of fluid flow (χ_f = 0), as determined by MFPT calculations. Circles (red): V_f = 6.83 × 10⁻⁴; squares (blue): V_f = 3.42 × 10⁻³; long dashed line (red): Equation (5b)[5b] calculated values with V_f = 6.83 × 10⁻⁴; short dashed line (blue): Equation (5b)[5b] calculated values with V_f = 3.42x 10⁻³; solid line (black): Equation (6b) calculated values.

Collision Kernel for the Low Kn_D, Low χ_f limit

Ideally, a large number of MFPT calculations would enable inference of a single function H(V_f, R, χ_f, Kn_D) which is valid for the entire range of interest for all independent parameters. However, the development of such a function is of narrow value without additional Kn effects on the fluid flow considered, which are also present at high Kn_D. The development of a five-parameter-dependent dimensionless collision kernel expression is beyond the scope of the present study due to the computational expense involved and the difficulties in collapsing such results to a single expression. We thus limit MFPT calculations to the inertialess, continuum limit, for which Kn_D → 0 and χ_f^1/2Kn_D → 0 (low Stokes number) and which is applicable for the filtration of nanoparticles by supermicrometer fibers at modest free-stream velocities. Because Equation (5b[5b] ) describes the dimensionless collision kernel as χ_f → 0, and because single fiber efficiency relationships in these circumstances are usually expressed in terms of Pe, we opt to fit MFPT calculation results to the functional form: [12a]

Correspondingly, the single-fiber efficiency equation becomes: [12b]

FIG. 3. Values of the parameter (H/H_C – 1) with H determined from MFPT calculations and H_C calculated with Equation (5b)[5b] for (a) V_f = 0.01 and (b) V_f = 0.07. Circles (red): R = 0; squares (blue): R = 0.03; triangles (yellow): R = 0.10. Plots such as those displayed are used to determine the coefficients C₁ and C₂ as functions of V_f and R.

This functional form was chosen based on examination of initial calculation results, and is convenient because simulations directly enable determination of the coefficients C₁ and C₂. To do so, we evaluated more than 2700 MFPT results (and, therefore, performed more than 10⁷ collision calculations) with Kn_D < 0.1, χ_f^1/2/Kn_D < 10⁴, χ_f^1/2Kn_D < 0.1, V_f ≤ 0.1, and R ≤ 0.2. Although random Kn_D and χ_f values satisfying the noted criteria are selected, calculations are performed for specific (V_f, R) pairs, with V_f = 5 × 10⁻³, 7 × 10⁻³, 0.01, 0.03, 0.07, and 0.10, and R = 0, 0.01, 0.03, 0.07, 0.10, and 0.20 (a 6 × 6 matrix). C₁ and C₂ values are then determined via power law regression of the value (H/H_C) – 1 as a function of χ_f^1/2/Kn_D. Such plots for select conditions are shown in Figures 3a and b and results are summarized in Table 1. Most regression-inferred coefficients are found to be within 5% of the equations:

TABLE 1. Values of the coefficients (a) C₁ and (b) C₂ determined from regressions, as functions of R and V_f

	Vf
(a) C1 values	0.005	0.007	0.01	0.03	0.05	0.07	0.1
R  0.00	0.605	0.626	0.596	0.526	0.504	0.491	0.508
0.01	0.580	0.610	0.569	0.520	0.502	0.490	0.492
0.03	0.548	0.550	0.549	0.492	0.441	0.442	0.443
0.07	0.494	0.472	0.466	0.411	0.383	0.371	0.354
0.10	0.459	0.378	0.408	0.383	0.351	0.338	0.335
0.20	0.311	0.333	0.346	0.282	0.241	0.239	0.277
(b) C2 values
	0.005	0.007	0.010	0.030	0.050	0.070	0.100
R  0.00	0.394	0.382	0.383	0.388	0.386	0.387	0.380
0.01	0.406	0.406	0.400	0.396	0.397	0.396	0.393
0.03	0.430	0.422	0.442	0.421	0.434	0.432	0.431
0.07	0.471	0.477	0.475	0.485	0.495	0.497	0.509
0.10	0.501	0.540	0.518	0.519	0.532	0.542	0.548
0.20	0.628	0.615	0.602	0.641	0.671	0.677	0.660

[13a] [13b]

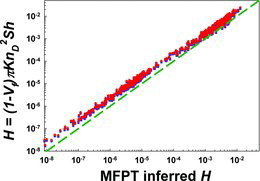
A comparison of MFPT-inferred dimensionless collision kernels to Equation (12a)[11b] values, using both Equations (13a) and (13b) as well as the tabulated values of C₁ and C₂, is shown in Figure 4. In addition, shown in this plot are lines corresponding to 1:1, 1:1.25, and 1:0.75 results. Evident is that across approximately 7 orders of magnitude in dimensionless collision kernel, the developed regression equations agree reasonably well with MFPT results whereas by construction they are valid as χ_f  →  0 and as Kn_D → 0. Further, although not clear in Figure 4, we find that the majority of inferred H values are within 10% of the regression equation-calculated values (using either equation calculated or tabulated values of C₁ and C₂); therefore, we propose that Equation (12a)[11b] can be used to determine the filter fiber particle collision kernel accounting for diffusion and interception simultaneously, and correspondingly that Equation (12b)[12a] can be used to estimate the single-fiber efficiency for nanoparticle filtration. We note, however, that while Equations (13a) and (13b) are reliable in the range examined with calculations, extrapolation outside this range will likely lead to incorrect dimensionless collision kernel calculation.

FIG. 4. A comparison of the dimensionless collision kernels inferred from MFPT calculations to those calculated from Equation (12a)[11b] (Modeled H). Circles (red): C₁ and C₂ determined Equations (13a) and (13b). Squares (blue): tabulated C₁ and C₂ values used for calculations. The central dashed line (black) denotes 1:1 values, whereas the outer dashed lines (gray) denote 1:1.25 and 1:0.75 values.

Comparison to Depth-Filtration Theory

As described in the introduction section, some of the assumptions made in the development of single-fiber equation relationships in classical depth-filtration theory require further scrutiny. Comparison of MFPT results and the regression relationship developed to depth-filtration theory predictions is, thus, warranted. The single-fiber efficiency for diffusion provided by Lee and Liu (1982b), which is in line with the predictions of earlier authors (Stechkina and Fuchs 1966), is given as: [14a] where Ku is the Kuwabara number: [14b]

The single-fiber efficiency for interception, also from the analysis of Lee and Liu (1982b), is expressed as: [14c]

Finally, the diffusion–interception correction factor, provided by Kirsch et al (1974), is expressed as: [14d]

Figure 5 displays the values of E_D, E_D + E_R, and E_D + E_R + E_DR compared with the single-fiber efficiencies determined from MFPT calculations (using Equation 11b[11a] ). The plotted results are grouped into those with R ≤ 0.03 (Figure 5a), and those with R ≥ 0.07 (Figure 5b). Considering calculations with R ≤ 0.03, good agreement is found between MFPT-inferred single-fiber efficiencies and E_D + E_R at small E_f (below ∼0.1), and with E_D + E_R + E_DR for 0.1 < E_f < 0.5. Above this value however, classical filtration results are systematically lower than MFPT calculation values. Similarly, MFPT calculation results agree well with E_D + E_R (while in vast disagreement with E_D alone) with R ≥ 0.07 and at low total E_f (below ∼0.2), agree with E_D + E_R + E_DR at intermediate E_f values, and at high E_f depth-filtration predictions are systematically below MFPT calculation results. The agreement between depth-filtration theory predictions and the calculations without the need for the diffusion–interception correction factor at low E_f is somewhat expected; an overall low E_f is an implicit assumption in the theoretical development of expression for E_D in classical depth filtration (Lee and Liu 1982b; Stechkina and Fuchs 1966; Yeh and Liu 1974a). The agreement between MFPT calculations and E_D + E_R + E_DR for intermediate values of E_f additionally validates the rationality of the additivity approach for single-fiber efficiency calculations (with an interaction parameter for higher efficiency filters). However, the disagreement between MFPT calculations and depth-filtration theory predictions at the highest E_f values is most likely an issue with depth-filtration theory equations; high E_f results from low χ_f^1/2/Kn_D (low Pe) values, where the single-fiber efficiency begins to converge to the zero flow limit equation (Equation (11b)[11a] with H = H_C). Balazy and Podgorski (2007) similarly report disagreement between Brownian dynamics calculations and depth-filtration theory predictions when diffusion and interception (but not inertia) influence particle deposition. Moreover, because MFPT calculations find better agreement with either E_D + E_R or E_D + E_R + E_DR, we propose it is simpler to use Equation (12b)[12a] for single-fiber efficiency estimation to simultaneously account for collection by diffusion and interception than to use additivity rules and interaction parameters.

FIG. 5. Depth filtration predicted single-fiber efficiencies as compared to those inferred from MFPT calculations. (a) Calculated with R ≤ 0.03; (b) calculations with R ≥ 0.07. Circles (red): diffusion collection only (Equation (14a)); squares (blue): combined diffusion and interception collection (Equation (14a) + Equation (14c)[14b] ); triangles (yellow): combined diffusion and interception collection with the correction term (Equation (14d)[14c] ) included.

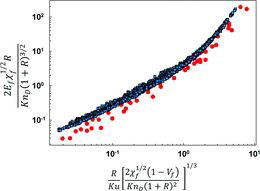
We additionally compare MFPT calculations to experimental data reported by Lee and Liu (1982b) in Figure 6. For this comparison, results are plotted with the parameter 2E_fχ_f^1/2R/(Kn_D[1 + R]^3/2) as a function of (R/Ku)(2[1 − V_f]χ_f^1/2/[Kn_D(1 + R)²])^1/3, a functional dependency suggested from traditional depth-filtration theory. MFPT results, indeed, collapse to a single curve for all χ_f, Kn_D, R, and V_f, similar to the displayed experimental results. However, as was also found in Lee and Liu's comparison to depth-filtration theory, experimental measurements are systemically lower on this plot than calculations. Disagreement between calculations and experiments with real filters is attributable to polydispersities in filter fiber volume fraction and fiber radii (Dhaniyala and Liu 2001a, b). There have been several theoretical efforts devoted to developing models to account for such polydispersities (Podgorski 2009; Podgorski et al. 2011). We suggest that the combination of these models with the single-fiber efficiency equations developed here would lead to better agreement with experimental results, as such models lead to a reduction in overall filtration efficiency.

FIG. 6. Comparison of MFPT results to the experimental measurements provided by Lee and Liu (1982a,b). The parameters noted on the abscissa and ordinate are equivalent to those used by Lee and Liu (1982b). Circles (red): experimental results from Lee and Liu (1982); squares (blue): MFPT calculations.

Comparison to Heat Transfer Correlations

The heat transfer analog to fibrous filtration is the heat transfer from a fluid flowing perpendicular to a bank of cylinders held at fixed temperature. This situation was examined experimentally by Zukauskas (1972), and we can compare MFPT calculation results directly to his experimentally derived correlations under conditions where R = 0 (interception is not applicable in heat transfer). For low Reynolds’ numbers and evenly spaced cylinders, Zukauskas's results can be approximately described by the equation: [15a] for staggered arrays of cylinders and the equation: [15b] for aligned arrays of cylinders. Sh in Equations (15a) and (15b) is the Sherwood number (note, in Zukauskas's work, correlations are provided in terms of the Nusselt number), which is linked to H through the equation: [15c]

For all R = 0 simulations performed, Equation (15c) predictions are compared to MFPT calculation results in Figure 7, for both staggered and aligned arrays. Unlike the experimental comparison to filtration results, MFPT-inferred dimensionless collision rates are slightly lower compared to the collision rates derived from heat-transfer measurements. Nonetheless, over seven orders of magnitude in H results remain close to one another. When taken in combination with the comparison to filtration measurements (where interception was considered), we find that overall MFPT calculations follow closely experimental results in two distinct, but related, systems.

FIG. 7. A comparison of H calculated from equation (15c) for staggered (circles, red) and aligned (squares, blue) cylinders to results of MFPT calculations under all conditions where R = 0. Dashed curve (green): a 1:1 guideline.

CONCLUSIONS

We have employed MFPT calculations to determine the dimensionless collision rate between particles and filter fibers using a Kuwabara (1959) flow cell model, and subsequently linked the dimensionless collision rate to the single-fiber efficiency. Both the dimensionless collision rate and single-fiber efficiency are evaluated as functions of the interception parameter R, the fiber solid volume fraction V_f, the particle's translational kinetic energy to thermal energy ratio χ_f, and the diffusive Knudsen number Kn_D. These parameters can be directly transformed to the traditional Peclet and Stokes numbers for comparison to conventional theories. MFPT calculation results are found to correctly collapse to known analytical expressions in the absence of fluid flow, and a regression equation from over 10⁷ calculations is developed to predict single-fiber efficiencies accounting for particle diffusive motion and interception. Use of the MFPT calculation approach does not require many of the assumptions made in the development of depth-filtration theory; therefore, the calculations performed here serve as a test of the validity of traditional single-fiber efficiency equations. In contrast to the traditional methods, the MPFT approach can be easily extended to filtration of arbitrarily shaped particles and allows for the consideration of additional simultaneous particle deposition mechanisms (inertia, electrostatic). Finally, the results and method reported in this work provide a direct link between the equations of particle collisions with filter fibers and particle–particle collisions (e.g., coagulation); both can be developed through MFPT calculations with cell models.

ACKNOWLEDGEMENTS

The authors thank the University of Minnesota Supercomputing Institute (MSI) for providing the high performance computing resources used in MFPT calculations.

FUNDING

This work was supported by the University of Minnesota Center for Filtration Research (CFR).

NOMENCLATURE

af	=	fiber radius
ap	=	particle radius
b	=	cell radius
C1, C2	=	fit coefficients
D	=	diffusion coefficient
Ef	=	single-fiber efficiency
ED	=	single-fiber efficiency due to particle diffusion
EDR	=	interception–diffusion correction factor
EI	=	single-fiber efficiency due to particle impaction
ER	=	single-fiber efficiency due to particle interception
f	=	particle friction coefficient
H	=	dimensionless collision kernel
Hc	=	dimensionless collision kernel, mass transfer continuum limit
HF	=	dimensionless collision kernel, mass transfer free molecular limit
Kn	=	Knudsen number, Kn = 2λ/ap
KnD	=	diffusive Knudsen number,
kT	=	thermal energy
Ku	=	Kuwabara number,
mp	=	particle mass
np	=	particle number concentration
nf	=	fiber number concentration
ncol	=	number of particle-fiber collisions
P	=	penetration
Pe	=	Peclet number,
R	=	interception parameter, R = ap/af
r	=	radial position
St	=	Stokes number,
Uo	=	free stream fluid velocity
Ur	=	radial flow velocity
Uθ	=	angular flow velocity
	=	dimensionless gas velocity vector
Vf	=	solid volume fraction
	=	dimensionless velocity vector
w	=	filter thickness
	=	dimensionless position vector

Symbols and Greek Letters

*	=	Dimensionless quantity
β	=	two-dimensional collision kernel
βc	=	collision kernel, mass transfer continuum limit
βF	=	collision kernel, mass transfer free molecular limit
χf	=	Particle translational energy to thermal enery ratio, χf = mpU20kT− 1
Δτ	=	dimensionless timestep
λ	=	gas mean free path
ψ	=	cell model streamfunction
τmean	=	mean first-passage time