The Single-Fiber Collision Rate and Filtration Efficiency for Nanoparticles II: Extension to Arbitrary-Shaped Particles

Abstract

We extend the equations for the dimensionless collision kernel and filtration efficiency, attained previously via mean first-passage time (MFPT) calculations, to particles of arbitrary shape. Specifically, we show that the regression equations for the dimensionless collision rate found considering particle-fiber collisions driven by simultaneous diffusion and interception remain valid for non-spherical particles, provided that an appropriate collision length scale for the non-spherical particle (L) is defined and incorporated into the definitions of the dimensionless collision rate (H) and the diffusive Knudsen number (Kn_D). Regression equations are provided to calculate this length scale for quasifractal aggregates of varying fractal dimension, as well as cylinders. MFPT calculations reveal that, over ∼5 orders of magnitude in H, these regression equations for the collision length are valid. Furthermore, using the previously attained proportionality between the predicted dimensionless collision rate and the single-fiber efficiency, comparison is made between the equations presented here and measurements of the penetration of both multiwalled carbon nanotubes and quasifractal aggregates through fibrous filters. Reasonable agreement is found between measured and predicted single-fiber efficiencies in both circumstances, supporting the use of the single-fiber efficiency calculation approach we developed.

Copyright 2014 American Association for Aerosol Research

INTRODUCTION

As discussed in detail in a companion study (Hunt et al. 2014), the single-fiber efficiency, which is commonly determined as a means to predict the penetration of particles through fibrous filter media, is linearly proportional to the particle-fiber collision rate. Determination of the particle penetration through a filter can, therefore, be reframed as a collision rate-determination problem, which, as shown in the companion study and elsewhere, can be solved under a variety of circumstances via mean first-passage time (MFPT) calculations (Narsimhan and Ruckenstein 1985; Gopalakrishnan and Hogan 2011; Gopalakrishnan et al. 2013b). Specifically for particle-fiber collisions, MFPT calculations show that the dimensionless collision kernel (H) within a Kuwabara (1959) flow cell model, neglecting particle inertia, is described by the following equation: [1a] [1b] [1c]

where Kn_D is the diffusive Knudsen number (Dahneke 1983; Gopalakrishnan and Hogan 2011), R is the particle size to fiber size ratio, and V_f is the filter solid-volume fraction. For spherical particles and cylindrical fibers, H, Kn_D, R, and χ_f are defined by the following respective equations: [2a] [2b] [2c] [2d]

where β is the two-dimensional collision rate coefficient/kernel, f is the particle friction factor (Dahneke 1973; Zhang et al. 2012), m_p is the particle mass, k is the Boltzmann's constant, T is the temperature,U₀ is the fluid flow velocity upstream of the filter, and a_p and a_f are the particle and fiber radii, respectively. Correspondingly, the penetration (P) of spherical particles through a filter of thickness w can be calculated as: [3]

In an earlier report (Hunt et al. 2014), Equation (3) was shown to agree reasonably well with the predictions of traditional depth-filtration theory considering particle deposition by diffusion and interception (Stechkina and Fuchs 1966; Kirsch et al. 1974; Lee and Liu 1982) as well as correlations derived from experimental measurements of the heat transfer from banks of cylinders (Žukauskas 1972); therefore, Equation (3) can be used as an alternative to prior methods to estimate nanoparticle penetration through fibrous filter media under conditions where χ_f^1/2/Kn_D < 10⁴, χ_f^1/2Kn_D < 0.1, V_f ≤ 0.1, and R ≤ 0.2. However, like in the classical depth filtration theory, Equations (1–3) have been developed considering only spherical particles. High-temperature synthesis in the gas phase routinely leads to the formation of non-spherical nanoparticles composed of a number of point-contacting primary spheres (aggregates/agglomerates; ref. Schmidt-Ott et al. 1990; Sorensen 2011), which are collected via filtration for later use. Further, non-spherical aggregates are frequently a byproduct of incomplete combustion reactions (Chakrabarty et al. 2009; Sorensen et al. 2003; Latin et al. 2013), and fibrous filtration is a commonly used method to control such particulate combustion emissions. Therefore, calculations of particle penetration applicable to non-spherical particles are of considerable interest.

The purpose of this report is, thus, to extend the MFPT calculation approach to determine the dimensionless particle-fiber collision rate considering non-spherical particles, while continuing to account for particle deposition due to diffusion and interception. This issue has been the focus of both experimental and numerical studies previously. Specifically, Kim et al. (2009) examined experimentally the penetration of quasifractal aggregates of varying morphology through fibrous filters. By measuring particle penetration as a function of “mobility equivalent diameter” (with a differential mobility analyzer [DMA]) they were able to compare the penetrations for particles of differing morphology yet having similar diffusion coefficients. At small mobility diameters (higher diffusion coefficients), particle morphology was observed to minimally influence penetration, while at higher mobility diameters (lower diffusion coefficients) it was observed that aggregates were captured more efficiently. Similar findings have been reported by Seto et al. (2010) and, later, by Wang et al. (Wang et al. 2011a,b), and both found that, at larger mobility diameters, carbon nanotubes and nanotube bundles were collected more efficiently than their spherical counterparts. Balazy and Podgorski (2007) used calculations of Brownian Dynamics (with a similar framework to the MFPT approach) to examine aggregate deposition onto fibers, but without explicitly accounting for the aggregate morphology and, instead, assuming particular relationships for aggregate effective radii/collision length scales. In doing so, they also predicted enhanced deposition for aggregates. Collectively, these studies demonstrate that non-spherical particles deposit onto filter fibers more efficiently; however, they also indicate that further investigation into the filtration of non-spherical particles is warranted, with more detailed modeling of particle morphology.

In the subsequent sections, the modifications to the results of the MFPT calculation required to determine the dimensionless collision kernel for non-spherical particles with cylindrical fibers are described. Analysis is performed for quasifractal aggregates composed of point-contacting, monodisperse, primary spheres as well as for cylindrical particles. It is shown that, for these non-spherical particles, Equations (1a–c) remain valid, and it is only the definitions provided in Equations (2a–c) that need to be modified slightly.

THEORETICAL METHODS

Collision Length Scale Calculations for Non-Spherical Particles

As noted by Hunt et al. (2014), as with coagulation and diffusion charging, particle deposition onto filter fibers can be analyzed as a transported limited-collision processes. In examining collisions between a point mass and a non-spherical particle (Gopalakrishnan et al. 2011, 2013b), as well as two non-spherical particles (Thajudeen et al. 2012), it has been found that the dimensionless collision kernel valid for sphere–sphere collisions also applies to collisions involving non-spherical entities, provided the modified collision length scales are incorporated into the dimensionless parameters H and Kn_D. Here, we similarly define collision length scales for non-spherical particles with circular fibers to recast H, Kn_D, and R, which enables us to test the hypothesis that Equations (1a–c) remain valid with appropriately modified definitions of these parameters. We note that the analysis differs slightly from prior studies of particle–particle collisions; particle–particle collisions occur in a three-dimensional environment, for which a collision radius (the Smoluchowski radius) can be defined for diffusive collisions (the continuum regime), and a collision-projected area (two-dimensional) can be defined for ballistic collisions (the free molecular regime; ref. Thajudeen et al. 2012). Conversely, particle–filter fiber collisions may be treated as two-dimensional when filter fibers are modeled as infinitely long, which leads to the requirement that only a ballistic collision length scale be defined (i.e., diffusive collision rates are not a function of collision length scale in two-dimensional environments).

The ballistic collision length for a particle of arbitrary shape with an infinitely long fiber is defined as the orientationally averaged maximum distance of closest approach at which the particle and fiber are in contact. An outline of the calculation procedure for this collision length scale is provided in Figure 1, which is the two-dimensional analog to the orientationally averaged collision area calculation approach described by Zurita-Gotor and Rosner (2002) and Thajudeen et al. (2012). We consider a non-spherical particle approaching a cylindrical fiber at a specific orientation and random location. Irrespective of the particle's trajectory, at closest approach, the particle's center of mass will be at a distance a_f + x from the center of the fiber, and, therefore, it is at a distance x from the edge of the fiber. For the orientation in question, at the distance of closest approach, the particle may or may not be in contact with the fiber, which is readily determined by checking if any portion of the particle crosses the x-axis origin (when the axes are aligned, as is depicted in Figure 1). By selecting random particle orientations (in three dimensions) and examining values of x selected from a uniform distribution between zero and a value x_max, the collision length between particle and fiber can be defined as a_f + L, where L is calculated as: [4]

FIG. 1. Depiction of the procedure used to calculate the collision length scale L for an arbitrary-shaped particle with a cylindrical filter fiber of radius a_f. x denotes the distance of a particle's center of mass to the fiber surface when at closest approach. In determining L, random particle orientations and values of x are selected to see if the particle and fiber overlap.

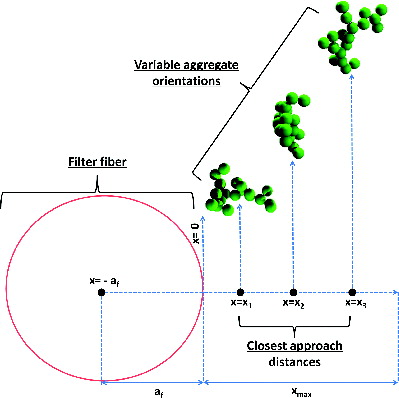
In Equation (4), N_col is the number of trials resulting in contact, and N_tot is the total number of trials. Provided that (1) x_max is sufficiently large, such that the particle does not collide with the fiber in any orientation when its distance of closest approach is x_max, and (2) a sufficient number of trials are performed (i.e., more than 5000), such that N_col/N_tot < 1, then L is independent of both N_tot and x_max. When these criteria are satisfied, a_f + L is the orientationally averaged collision length scale and, with this collision length defined, we propose that Equations (1a–c) remain valid, with Equations (2a–c) modified as: [5a] [5b] [5c]

We note that, because the definition of χ_f does not involve a description of particle size and shape, the definition of χ_f in Equation (2d) remains valid for all particles. From Equation (4), it is evident that L = a_p for spherical particles; therefore, Equations (5a–c) are more general versions of Equations (2a–c). Although L can be calculated for any particle with the noted procedure, here we calculate L for quasifractal aggregates composed of point contacting, equal-radius spheres, which approximately obey the relationship: [6]

where N_mon is the number of monomer spheres per aggregate, k_f is the pre-exponential factor, R_g is the aggregate's radius of gyration, a_mon is monomer radius, and D_f is the fractal dimension. In doing so, aggregates are produced which satisfy Equation (6) (to within 0.1% error) using a cluster–cluster algorithm described by Fillipov et al. (2000) in the range N_mon = 20–1000, k_f = 1.3 and 1.7, and D_f = 1.5–2.4. This algorithm is selected because it is found to produce aggregates with structural characteristics (Huang et al. 1998) similar to those of similar k_f and D_f generated by diffusion-limited aggregation algorithms. However, to generate aggregates with D_f = 1.3 and 2.7, we opt to use the sequential algorithm (Filippov et al. 2000; Thajudeen and Hogan 2012); with the cluster–cluster algorithm, it is difficult to generate such nearly linear (D_f = 1.3) and highly compact (D_f = 2.7) aggregates. Both the cluster–cluster and sequential algorithms are capable of producing random structures, and for each N_mon, k_f, and D_f examined, 10 aggregates are produced (which are described by the coordinates of their monomers). We similarly calculate L for cylinders of varying radii, a_cyl, and aspect ratios (R_cyl, the cylinder's radius to length ratio). For both aggregates and cylinders, regression equations (for L/a_mon for aggregates and for L/a_cyl for cylinders, respectively) are developed, enabling direct calculation of L from the structural descriptors of the particle in question.

Non-Spherical Particle MFPT Calculations

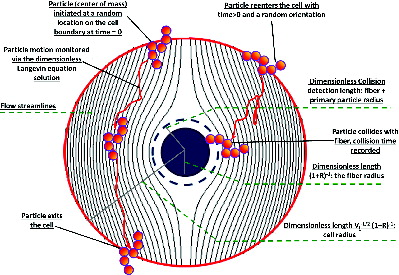
The validity of Equations (5a–c) is examined via the determination of H from MFPT calculations for quasifractal aggregates. The calculation procedure is represented in Figure 2. As in the investigation of spherical particle filtration (Hunt et al. 2014), MFPT calculations are performed by monitoring a particle's motion in a Kuwabara flow cell using a dimensionless solution to the Langevin equations. For a non-spherical particle, we define the dimensionless velocity vector as and its dimensionless position as , leaving the solution to the equations of motion as Equations (7a–d) of Hunt et al. (2014). Simulations are, therefore, performed similarly to the manner described by Hunt et al., to determine H as a function of input Kn_D, R (which scales the dimensionless radii of primary particles), χ_f, and V_f. We, again, restrict simulations to situations to the conditions χ_f^1/2/Kn_D < 10⁴, χ_f^1/2Kn_D < 0.1, V_f ≤ 0.1, and R ≤ 0.2. Inertial effects are included in particle motion, although such effects are small for the range of dimensionless input variables examined. The rotational motion of aggregates during their migration through the Kuwabara cell is neglected; based upon the calculations of Zurita-Gotor and Rosner (2002), rotations are not expected to substantially alter the particle–fiber collision rate for values of R in the noted range. The only differences between the MFPT calculation approach for non-spherical particles and spherical particles arise when (1) checking if the particle collided with the central fiber, and (2) re-introducing the particle into the Kuwabara cell in instances where it leaves the cell prior to collision. In (1), with spherical particles, collision was assured when the particle center was a dimensionless distance ≤1 from the center of the cell. Conversely, in the case of aggregates, each portion of the aggregate must to examined to determine whether it is in contact with the central fiber. For example, for aggregates with a dimensionless primary particle radius , if any primary sphere center is at a distance or less from the center of the Kuwabara cell, collision has occurred. In (2), each time an aggregate is introduced into the Kuwabara cell, either to commence a calculation or because it left the cell without collision, it is oriented randomly (about its center of mass, and in three dimensions) via the selection of three Euler angles. MFPT calculations are performed for the eight noted aggregates in Table 1. We note that, while L is used in the non-dimensionalization of the equations of motion for aggregates, this choice is arbitrary; any length scale can be used to normalize dimensions. However, if another length scale is selected, computational results must be rescaled to infer the input Kn_D and R, and the output H (Gopalakrishnan et al. 2011).

Table 1. A summary of the quasifractal aggregates used in mean first-passage time calculations

Aggregate #	Image	Df	Nmon	L/amon
1		1.8	10	3.73
2		1.8	100	13.22
3		2.3	10	3.11
4		2.3	100	8.79
5		1.78	50	9.07
6		2.4	100	8.27
7		1.78	200	19.17
8		2.0	200	15.38

FIG. 2. Depiction of the mean first-passage time calculation approach for aggregates, which may be contrasted with the method of Hunt et al. (2014) for spherical particles.

RESULTS AND DISCUSSION

Non-Spherical Particle Collision Length Scale and Comparison to MFPT Calculations

Plots of L/a_mon as a function of R_g/a_mon for aggregates (averaged over 10 aggregates) and L/a_cyl as a function of 1/R_cyl are shown in Figures 3a and 3b, respectively. Interestingly, for aggregates, results collapse to curves independent of k_f; L/a_mon versus R_g/a_mon is nearly linear (R² > 0.999), with slope dependent on D_f in all instances. The linear slope (1/α) linking L/a_mon to R_g/a_mon, as determined from calculations, is summarized in Table 2. Moreover, combining all results leads to the regression equations: [7a] [7b]

Table 2. A summary of the slopes (1/α) linking L/a_mon to R_g/a_mon for quasifractal aggregates

Df	1/α
1.3	0.89
1.5	1.03
1.8	1.19
2.0	1.27
2.2	1.33
2.4	1.37
2.7	1.37

FIG. 3. Plots of the collision length scale to radius ratio as a function of R_g/a_mon (a) for aggregates and (b) 1/R_cyl for cylinders.

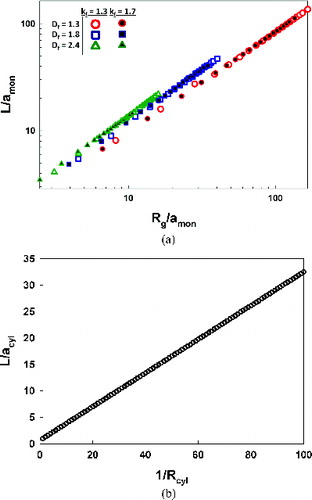
Results for cylinders lead to the regression equation: [7c]

We note that the regression equations for L of aggregates and cylinders gives distinctly different results from the approach of Balazy and Podgorski (2007), who assumed that L = [(2+D_f)/D_f]^1/2R_g, i.e., that L is equal to the approximate outer radius of an aggregate. The outer radius and the values of L calculated here only agree well with one another as D_f → 3, and differ by a factor of up to 2 at lower fractal dimensions. Substantial disagreement between L and the outer radius is also found for cylinders, as the outer radius would be defined as half the cylinder length. Therefore, when examining both chain-like aggregates and cylinders, the calculations here are in clear disagreement with the calculations of Balazy and Podgorski (2007).

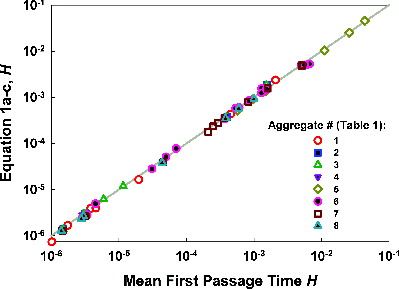
The predictions of Equations (1a–c), using the definitions in Equation (5a–c) and results of MFPT calculation for quasifractal aggregates, are plotted against one another in Figure 4. For guidance, a 1:1 line is additionally displayed. Across ∼5 orders of magnitude in H, independent of aggregate shape, equation predictions and MFPT calculation results typically agree to within 10% of one another. This is similar to the agreement found between Equation (1a–c) predictions and MFPT calculations with spheres. Therefore, we propose that Equation (1a–c) can be used with confidence to predict the dimensionless collision rate and, subsequently, the single-fiber efficiency, for non-spherical particles.

FIG. 4. A comparison of H inferred from mean first passage time calculations to the values of H calculated with Equations (1a–c) for quasifractal aggregates, with properties specified in Table 1. A 1:1 line is shown for guidance.

Comparison to Experimental Measurements

We now use both Equation (1a–c) predictions and MFPT simulations to compare them to the experimental measurements of the penetration of multiwalled carbon nanotubes through fibrous filters reported by Seto et al. (2010). These penetration experiments were performed using multiwalled nanotubes with three different radii and aspect ratios, characterized by electron microscopy. A summary of the comparison is provided in Table 3, wherein calculations of the parameters χ_f, Kn_D, V_f, R, and H are based on the reported particle penetrations, face velocities, the filter volume fraction (0.049), and average filter-fiber radius (1.4 μm). To define Kn_D, it is necessary to calculate the mass (although in the absence of inertia, the mass does not influence results) as well as the friction factor of the particles under examination. Modeling nanotubes as straight cylinders, the mass can be calculated from knowledge of the nanotube material density, radius, and aspect ratio. Particle friction factors can be inferred through use of a DMA; however, while Seto et al. (2010) used a DMA upstream of their filtration system to classify particles based on their electrical mobilities (charge to friction factor ratios), many particles transmitted through the DMA may have been multiply charged (Gopalakrishnan et al. 2013a) and, for nanotubes with supermicrometer lengths, particles may have aligned during migration in an electrostatic field (Kasper and Shaw 1982). With the assumption that the nanotube does not align preferentially in any direction as it migrates through the filter medium, its friction factor (and similarly the friction factor of any particle) can be calculated considering non-continuum drag effects as (Dahneke 1973; Zhang et al. 2012): [8a]

Table 3. A summary of the comparison of equation predictions to the measurements of Seto et al. (2010). The noted length and a_cyl values correspond to the lengths and radii of the nanotubes studied; R, Kn_D, and χ_f are the calculated values based upon the reported nanotube and filter fiber dimensions, and U₀ is the reported filter-face velocity. E_f (exp.) refers to experimentally measured values, while E_f (pred.) refers to Equation (9) predictions made either with Equations (1a–c) or with MFPT calculation results. The percentage difference (% Diff.) between experiments and calculations is normalized by experimental single-fiber efficiencies

								Equation (1a–c)		MFPT Calculations
Length (nm)	acyl (nm)	R	KnD × 10^3	U0 (m/s)	χf	H × 10^4	Ef (exp.)	Ef (pred.)	% Diff.	Ef (pred.)	% Diff.
1100	27.0	0.26	2.49	0.05	2.66	6.25	0.109	0.088	19.3%	0.099	9.2%
1100	27.0	0.26	2.49	0.10	10.65	9.64	0.090	0.068	24.5%	0.081	9.2%
1100	27.0	0.26	2.49	0.15	23.96	12.47	0.078	0.058	25.0%	0.070	9.9%
1100	27.0	0.26	2.49	0.30	95.84	19.43	0.062	0.045	26.8%	0.065	−5.4%
1100	27.0	0.26	2.49	0.50	266.22	27.00	0.059	0.038	36.0%	0.063	−5.6%
1300	28.5	0.31	2.30	0.05	3.51	7.19	0.092	0.099	−6.9%	0.119	−28.6%
1300	28.5	0.31	2.30	0.10	14.02	11.41	0.078	0.078	−0.5%	0.100	−28.7%
1300	28.5	0.31	2.30	0.15	31.55	14.98	0.073	0.068	6.7%	0.095	−29.1%
1300	28.5	0.31	2.30	0.30	126.20	23.95	0.061	0.055	10.5%	0.084	−37.1%
1300	28.5	0.31	2.30	0.50	350.56	33.90	0.054	0.046	13.4%	0.085	−57.4%
2100	28.5	0.49	1.70	0.05	5.66	10.15	0.143	0.169	−18.0%	0.217	−51.9%
2100	28.5	0.49	1.70	0.10	22.65	17.53	0.125	0.146	−17.1%	0.204	−63.5%
2100	28.5	0.49	1.70	0.15	50.97	24.18	0.118	0.134	−13.7%	0.203	−72.3%
2100	28.5	0.49	1.70	0.30	203.86	41.96	0.100	0.116	−16.1%	0.192	−91.9%
2100	28.5	0.49	1.70	0.50	566.29	63.03	0.087	0.105	−20.2%	0.195	−124.1%

where μ is background gas dynamic viscosity, λ is the gas molecule hard sphere mean free path, PA is the particle's orientationally averaged projected area, and R_S is the particle's Smoluchowski radius (Gopalakrishnan et al. 2011), equated with its hydrodynamic radius via the Hubbard–Douglas approximation (Douglas et al. 1994). Shown previously (Hansen 2004), for cylinders R_S and PA are given by the following equations: [8b] [8c]

Therefore, for all cylinders under investigation, L, R_s, and PA, and, therefore, Kn_D, R, and χ_f (length scale independent) are calculable, as is H by either the regression equations or from MFPT simulations directly. Following the prior report (Hunt et al. 2014), the single-fiber efficiency, E_f, is related to H via the equation: [9]

Values of E_f inferred from (1) the measurements of Seto et al. (2010), (2) extrapolations of the regression Equations (1a–c), and (3) directly from MFPT simulations using the input Kn_D, χ_f, V_f, and R corresponding to the mean values for each carbon nanotube sample reported by Seto et al. are displayed in Table 3. In addition, for each of the three mobility-classified nanotubes examined, these values are plotted as a function of χ_f^1/2/Kn_D in Figure 5, with predictions of Equation (9) shown for R = 0.26, 0.31, and 0.49 (the inferred values for the provided nanotube and filter-fiber dimensions), respectively. Results are plotted in this manner because single-fiber efficiencies are solely a function of χ_f^1/2/Kn_D, which is proportional to the Peclet number (Hunt et al. 2014), once R and V_f are specified.

FIG. 5. A comparison of predicted (dashed lines for regression predictions and closed symbols for MFPT results) and measured (open symbols) single-fiber efficiencies as a function of χ_f^1/2/Kn_D for multiwalled carbon nanotube deposition on a fibrous filter. Measurement results are taken from Seto et al. (2010).

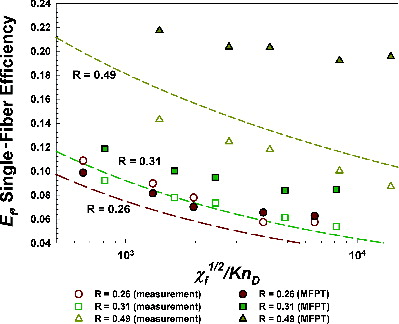
Furthermore, although disparities between measurements, regression-based calculations, and MFPT results are certainly evident for all three nanotube types, qualitatively, calculations agree well with measurements, and agree well with measurements quantitatively in a number of circumstances (e.g., for R = 0.26 measurements and MFPT calculations are within 10% of one another). Given that none of the parameters input into calculations were “fit” to force agreement with measurements, and simultaneously that a number of features of experiments were not considered in calculations, we believe this comparison supports the applicability of the presented equations for non-spherical particle filtration modeling. Specifically, not included in calculations are the polydispersities in nanotube diameters and lengths, which are non-negligible even downstream of a DMA, the possible preferential orientations of nanotubes as they migrate through the filter, filter-fiber radius, and volume fraction polydispersities, as well as possible electrostatic influences on nanotube motion. Unfortunately, each of these influences is rather involved to consider in detail; we are aware of no study (theoretical or experimental) of non-spherical particle filtration that has considered all such effects in modeling filtration.

For additional comparison of calculations to measurements, we also utilize the results of Kim et al. (2009), who studied the penetration of soot aggregates through fibrous filters. Aggregates were characterized through tandem DMA-aerosol particle mass analyzer (APM; Tajima et al. 2011), yielding the effective mass-mobility exponent (D_mm) for examined particles (Scheckman et al. 2009). However, while the mass-mobility exponent provides some description of particle morphology, it is not equivalent to the fractal dimension of particles (Sorensen 2011), and for particles with mobility equivalent diameters in the 10–500 nm size range at room temperature and atmospheric pressure, a link between the mass-mobility exponent and fractal dimension has not yet been clearly established. Therefore, as with the comparison to nanotube penetration data, there is considerable ambiguity into the true morphology of the particles under examination. With this issue in mind, we make comparison to soot aggregate measurements as follows: DMA and APM measurements yielded the aggregate friction factor (quantified by the mobility equivalent diameter, d_m, which was selected to be 30, 50, 100, 150, 200, 250, and 300 nm) and mass, respectively, and, through electron microscopy, Kim et al. found the average filter-fiber radius (a_f) was 950 nm, the average primary particle radius (a_mon) was 9.25 nm, and the filter volume fraction (V_f) was 0.050. As they are not known for the measured aggregates, we assume values of D_f = 1.5, 1.75, & 2.5 with k_f = 1.3, and for each assumed D_f value, N_mon is calculated using Equation (8a) with the expressions provided by Thajudeen et al. (2012) for R_s and PA for quasifractal aggregates: [10a]

[10b]

[10c]

[10d] [10e] [10f]

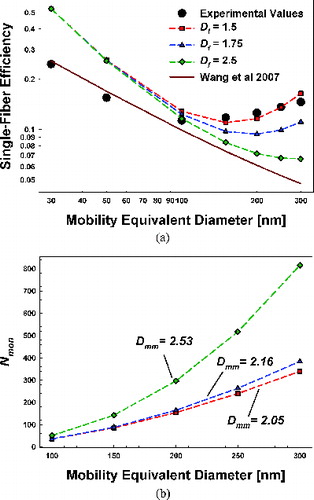
Equations (10a–f) are regression equations based upon direct calculation of both R_s and PA for computationally generated aggregates with k_f = 1.3 and D_f = 1.3–2.6. Subsequently, we calculate L via Equations (7a–b). Figure 6a is a plot of the single-fiber efficiency as a function of mobility-equivalent diameter for the unsintered aggregates (the room temperature sample) of the study by Kim et al. (2009). Experimental results are plotted along with calculations for three different fractal dimensions. In addition, results are provided directly in Table 4, which additionally lists the calculated χ_f, N_mon, Kn_D, and R values for each assumed fractal dimension. Finally, in Figure 6a, the regression curve E_f = 0.84Pe^−0.43 (where Pe = 2χ_f^1/2/[(1+R)Kn_D]) is plotted, which was reported by Wang et al. (2007) to agree well with experimental single-fiber efficiency measurements for the same filters used by Kim et al. (2009) when challenged with spherical particles. This regression curve leads to prediction distinct from the traditional equations of depth-filtration theory as well as the equations derived from MFPT calculation. Evident in Figure 6a, its predictions agree well with measurements at d_m = 30 and 50 nm, but do not agree with measurements of larger aggregates. Single-fiber efficiency curves predicted using MFPT-derived equations for all aggregates, conversely, are in much better agreement with measurements than the filter-specific regression equation (as well as the calculations of Kim et al. [2009]). In particular, the single-fiber efficiency calculations with D_f = 1.50 are within 15% of all measurements in the d_m = 100–300 range. Figure 6b displays a calculated N_mon as a function of the mobility equivalent diameter in the d_m = 100–300 range. N_mon versus d_m plots yield the mass-mobility exponent, and for D_f = 1.5, the inferred value of D_mm = 2.05 is in remarkably good agreement with the value of D_mm = 2.06 determined experimentally. As the single-fiber efficiency measurements and mass-mobility exponent measurements are independent of one another, we find excellent agreement with calculations for D_f = 1.5, k_f = 1.3 (with no other fit parameters) again supports the use of the presented dimensionless collision rate and single-fiber efficiency equations for non-spherical particles.

Table 4. A summary of the comparison between model predictions and the measurements of Kim et al. (2009) for the single-fiber efficiency for a fibrous filter collecting soot aggregates. The comparison is for unsintered particles only. d_m denotes the mobility equivalent diameter of the particles examined. All other dimensionless parameters are based upon the filter properties and penetration data provided by Kim et al. (2009). The number of monomers per aggregate (N_mon), R, Kn_D, E_f (pred.), and % Diff are calculated for different assumed fractal dimensions of 1.5, 1.75, and 2.0

	From Experiment
	dm (nm)	χf	Ef (exp.)
	30	0.06	0.246
	50	0.19	0.155
	100	0.73	0.113
	150	1.74	0.118
	200	0.33	0.126
	250	4.99	0.136
	300	7.05	0.146
Df = 1.5
Nmon	R	KnD	Ef (pred.)	% Diff.
2.3	0.015	0.0317	0.527	113.9%
7.6	0.033	0.0202	0.260	67.6%
35.8	0.093	0.0109	0.129	13.6%
85.4	0.166	0.0080	0.110	−6.9%
154.3	0.247	0.0021	0.116	−7.6%
239.9	0.331	0.0055	0.136	−0.6%
339.5	0.417	0.0047	0.165	12.6%
Df = 1.75
Nmon	R	KnD	Ef (pred.)	% Diff.
2.3	0.016	0.0317	0.527	114.0%
7.4	0.031	0.0202	0.259	67.2%
36.0	0.077	0.0110	0.123	8.9%
88.4	0.129	0.0083	0.097	−17.5%
164.7	0.184	0.0022	0.094	−25.5%
263.5	0.241	0.0059	0.100	−27.1%
383.7	0.298	0.0051	0.111	−24.0%
Df = 2.5
Nmon	R	KnD	Ef (pred.)	% Diff.
2.4	0.016	0.0317	0.527	114.0%
8.7	0.027	0.0203	0.258	66.2%
50.8	0.055	0.0112	0.116	2.6%
142.9	0.084	0.0086	0.084	−29.1%
295.9	0.112	0.0074	0.072	−42.9%
517.4	0.140	0.0064	0.068	−50.5%
815.7	0.168	0.0057	0.067	−54.2%

FIG. 6. (a) A plot of the single-fiber efficiency for soot aggregates from the experiments of Kim et al. (2009) as well as predicted single-fiber efficiencies for fractal dimensions of 1.5, 1.75, and 2.5. Moreover, the empirical fit of Wang et al. (2007) for the same filters with spherical particles is shown here, with which the single-fiber efficiency is calculated via the equation: E_f = 0.84Pe^−0.43. (b) A plot of the number of monomers per aggregate determined from Equation (8a) as a function of mobility diameter. The resulting mass-mobility exponents (D_mm) are labeled.

CONCLUSIONS

Following a procedure analogous to that of Thajudeen et al (2012), we have shown how to apply the MFPT-inferred particle-fiber dimensionless collision kernel expression to particles of arbitrary shape, and provide algebraic equations specifically for calculations with quasifractal aggregates and cylinders. The resulting collision rate calculations are directly linked to the single-fiber efficiency. Unique from prior approaches wherein non-spherical particle filtration was examined (Balazy and Podgorski 2007), in the presented approach, particle geometries were taken into account explicitly, and the effective collision length scales for particles were calculated directly (not assumed). This leads to different single-fiber efficiency equations than have been developed elsewhere. Predicted single-fiber efficiencies are in reasonable agreement with those measured for well-characterized carbon nanotubes and good agreement with those measured for soot aggregates with a fit fractal dimension. The equations developed here should aid in analyzing measurements of non-spherical particle penetration through fibrous filters. Future applications of the MFPT approach should additionally enable determination of the collision rate between particles and non-spherical filter fibers, or with non-fibrous media (e.g., sintered metal spheres).

ACKNOWLEDGMENTS

The authors thank the University of Minnesota Supercomputing Institute (MSI) for providing the high performance computing resources used in MFPT calculations.

Additional information

Funding

This work was supported by the University of Minnesota Center for Filtration Research (CFR).