Generalized TEMOM Scheme for Solving the Population Balance Equation

Abstract

This article proposes a novel generalized Taylor expansion method of moments (TEMOM) scheme for solving the population balance equation. The proposed scheme can completely overcome the shortcoming of the existing TEMOM and substantially improve the accuracy for both integer and fractional moments. In the generalized TEMOM, the optimal number of equations is 2+1, where is an integer greater than zero. The existing TEMOM is a special case of the generalized TEMOM when is 1. The generalized TEMOM was tested for aerosols undergoing Brownian coagulation in the continuum regime, and it was verified to achieve nearly the same accuracy as the quadrature method of moments (QMOM) with a fractional moment sequence, and higher accuracy than the QMOM with an integer moment sequence. Regarding accuracy and efficiency, the generalized TEMOM scheme was verified to be a competitive method for solving the population balance equation.

Copyright 2015 American Association for Aerosol Research

1. INTRODUCTION

In particle process engineering and the environment, aerosols demonstrate unstable properties because of Brownian coagulation; thus, the aerosol size distribution always varies with time (Thornton 2004). This process can be characterized mathematically by solving the governing equation of aerosol dynamical processes (i.e., the Population Balance Equation, PBE) (Friedlander 2000; Ramkrishna and Singh 2014). Smoluchowski first proposed the PBE in 1917, and Müller subsequently modified it in 1928 (Smoluchowski 1917; Müller 1928). However, even if only Brownian coagulation is involved, the PBE cannot be solved analytically. Various methods for solving the PBE have been proposed in nearly the past century, including the method of moments (Hulburt and Katz 1964; Lee et al. 1984; Williams 1986; McGraw 1997; Frenklach 2002; Marchisio et al. 2003c; Yu et al. 2008), the sectional method (Gelbard and Seinfeld 1980; Landgrebe and Pratsinis 1990; Talukdar and Swihart 2004; Kostoglou 2007), and the Monte Carlo method (Kraft 2005; Morgan et al. 2006; Zhao et al. 2010; Zhao and Zheng 2013). These methods have their advantages and disadvantages in efficiency and accuracy (Yu et al. 2008; Vogel et al. 2014).

Among all the methods for solving the PBE, the method of moments is considered the most suitable method to couple with Computational Fluid Dynamics (CFD) for resolving realistic aerosol problems. Furthermore, because of its computational cost requirement, which is the lowest, and its relative simplicity of implementation, the method of moments is the most commonly used numerical approach in the aerosol field (Hulburt and Katz 1964; Lee et al. 1984; Williams 1986; Pratsinis 1988; Barrett and Jheeta 1996; McGraw 1997; Frenklach 2002; Yu et al. 2008; Yu and Lin 2009). Hulburt and Katz first introduced this method in 1964 for studying agglomerate formation and subsequent growth; however, their work has not found wide applicability because of the difficulty of expressing transport equations for the moments of the particle size distribution (Marchisio et al. 2003b). The method of moments has become a highly practical method since 1984 when Lee et al. applied a log-normal size distribution assumption to their model on the basis of previous researchers' work (Cohen and Vaughan 1971; Lee et al. 1984). Under the assumption of a log-normal size distribution, the PBE can be replaced with a system comprising three ordinary differential equations in which crucial indexes for characterizing aerosol properties, including particle number intensity, mass intensity, geometric mean size, and geometric standard deviation of number distribution, can be easily obtained. Because of its practical application, Lee's log-normal method of moments (log MM) quickly became a predominant method for studying aerosol dynamics until a substantially superior method of moments was proposed in 1997 (i.e., the quadrature method of moments, QMOM). The QMOM successfully overcomes the shortcoming of the log MM of which the aerosol size distribution must follow a log-normal distribution; thus, the QMOM is substantially more reliable in both mathematics and physics compared with the log MM, and it was verified to be suitable for a wider scope of application (McGraw 1997). The QMOM was further markedly improved by subsequent researchers, and many of its variants were presented (Marchisio et al. 2003a; Upadhyay and Ezekoye 2003, 2006; Marchisio and Fox 2005; Yuan et al. 2012). However, the QMOM and its variants have a lower efficiency compared with the log MM. This is because the number of equations in the QMOM and its variants is twice the quadrature points and the procedure used for determining weights and abscissas from moments must be executed using a product-difference algorithm or other similar algorithms, which usually requires substantial computational time. Similar to the QMOM, the Taylor expansion method of moments (TEMOM) is another method that does not require an assumption for aerosol size distribution (Yu et al. 2008). The number of equations in the TEMOM is identical to the number of objective variables, and no additional calculation for determining weights and abscissas is required. The TEMOM has been verified as a competitive method in terms of both efficiency and accuracy compared with its competitors, including the QMOM and log MM, and it has also shown rapid development in nearly the past eight years (Yu and Lin 2009a,b; Xie et al. 2012; Xie and He 2013; Chen et al. 2014; Xie 2015; Yu et al. 2015a,b). Other methods similar to the QMOM and TEMOM are also available for solving the PBE. In the Laguerre quadrature approximation method, Barrett and Jheeta expressed as a p-th order polynomial in k, where is the k-th moment (Barrett and Jheeta 1996). The method of moments with interpolative closure (MOMIC) is another mathematically rigorous method for solving the PBE (Frenklach 2002). Yu et al. (2008) conducted an accuracy comparison among the QMOM, TEMOM, log MM, and Barrett's model for Brownian coagulation in both the continuum regime and free molecular regime.

Various methods of moments share a common difficulty in the achievement of closure for the moment ordinary differential equations that are converted from the PBE through an integral transformation (Hulburt and Katz 1964; Lee and Chen 1984; Williams 1986; McGraw 1997; Frenklach 2002; Upadhyay and Ezekoye 2006). The log MM is typically used to accomplish this by presuming a special functional form of particle size distribution (Lee and Chen 1984), whereas the QMOM, MOMIC, and TEMOM all do not involve any physical assumption and are used to accomplish this through introducing diverse rigorous mathematical techniques (McGraw 1997; Frenklach 2002; Yu et al. 2008). For methods of moments, the particle size distribution cannot always be accurately represented with a very large, even an infinite number of moments (McGraw et al. 1998). Fortunately, one is usually more interested in integrals over the particle size distribution, including moments, than in the detailed shape of the particle size distribution itself. Therefore, it is feasible to replace the infinite number of differential equations by a small number of equations, usually for lower order moments, without losing the most crucial index for characterizing aerosol properties. This approach has been verified for all the well-known methods of moments, including log MM, QMOM, MOMIC, and TEMOM; they are all successful methods relying on this approach. However, the choice of the number of ordinary differential equations and the type of moment sequence of lower orders might substantially affect the accuracy of the method for solving the PBE (Upadhyay and Ezekoye 2006). To our knowledge, Upadhyay and Ezekoye are the first to systematically study the impact of the choice of the number of equations as well as the type of moment sequence on the accuracy of the QMOM and direct quadrature method of moments (DQMOM). They determined that a higher accuracy can be achieved with a higher number of lower orders and a fractional moment sequence, although this might be affected by the particular stage of time evolution and specific dynamical process. Although the TEMOM was proposed nearly eight years ago, the mechanisms of this solution associated with the selection of various types of moment sequence and different numbers of ordinary differential moment equations have not been investigated.

The TEMOM has been verified as a successful method for resolving multiple aerosol dynamical processes, including both external and internal processes such as coagulation, nucleation, condensation, and transport (Yu and Lin 2010; Xie et al. 2012). However, a recent study (Yu et al. 2015b) reported that this method has shortcomings in both the scope of application and the accuracy for the fractional moment at the initial stage. The geometric standard deviations in the free molecular regime and continuum regime were reported to be limited to 1.601 and 1.699, respectively (Yu et al. 2015a), which substantially weaken the competitiveness of the TEMOM. In addition, the TEMOM exhibits low accuracy for fractal moments such as and in the initial stage, which is discussed in Section 3 in this article. The existing TEMOM entails using only the integer moment sequence and third-order Taylor expansion solution for achieving the closure of moment equations. According to the study by Upadhyay and Ezekoye (2006), the shortcoming of the existing TEMOM may be resolved by using a fractional moment sequence and a higher order of the Taylor series expansion. However, this has not been investigated in previous studies. Recently, we used the direct Taylor expansion technique to achieve a closure of ordinary differential moment equations by using a fractional moment sequence and observed that a higher accuracy can be achieved compared to the existing TEMOM (Chen et al. 2014). However, in this method, the process of numerically obtaining a derivation with various orders is associated with a high computational cost; its realistic application is thus limited. Therefore, it is imperative to propose a new TEMOM with a higher accuracy than the existing TEMOM but with the same efficiency.

This study proposed a highly reliable but generalized approach for solving the PBE (i.e., the generalized TEMOM). The proposed generalized TEMOM is designed to overcome the shortcoming of the existing TEMOM; this is achieved by introducing a different type of the fractional moment sequence and using a higher reserved order of the Taylor series expansion. We verified the proposed generalized TEMOM by conducting a test involving Brownian coagulation in the continuum regime. Furthermore, the generalized TEMOM can be easily extended to other dynamics such as condensation and breakage. The derivation of the generalized TEMOM in the free molecular regime and in the continuum-slip regime for agglomerates is shown in the online supplementary information (SI). This article is organized as follows: A brief description of the new method is presented in the Theory section, including the theory relevant to the new method and its detailed derivation. The computational parameters used in the calculation are presented in the Computation section. In the Results and Discussion section, we verify the generalized TEMOM through comparison with the benchmarked sectional method (SM) and other well-known methods of moments, including the QMOM and log MM.

2. THEORY

Numerous previous studies have presented the theory relevant to the PBE as well as various numerical and analytical solutions (Friedlander 2000; Marchisio et al. 2003a; Marchisio and Fox 2005; Upadhyay and Ezekoye 2006; Kostoglou 2007). Thus, only a brief description of the generalized TEMOM is presented here. Since the pioneering work of Smoluchowski (1917), the Smoluchowski Equation (SE), i.e., a simplified form of the PBE only involving Brownian coagulation, has become a basic equation for investigating aerosol Brownian coagulation problems. In this work, we limited our study to this equation rather than a general PBE involving multiple dynamics. Müller (1928) later developed the integro-differential form of SE, which is expressed as follows:[1] where is the number of particles whose volume is between and at time t, and is the collision kernel for two colliding particles of volumes and ′. The coagulation kernel has diverse forms in the free molecular regime, continuum regime, and continuum-slip regime (Pratsinis 1988; Lee et al. 1997), and the mathematical forms of these kernels are particularly complicated. Therefore, the solution usually requires different treatment in each regime. For brevity, only the derivation and verification in the continuum regime are presented in this article, whereas the derivation in the free molecular regime and continuum-slip regime is provided in the SI.

In a general method of moments for solving the SE (Hulburt and Katz 1964; Pratsinis 1988; Upadhyay and Ezekoye 2003), the disposition is to convert Equation (1) into an ordinary differential equation (ODE) with respect to k-th moments, . To achieve this, must be multiplied on both sides of Equation (1), and this equation must then be integrated over the entire size range; finally, the moment equation converted according to the size distribution can be obtained (Upadhyay and Ezekoye 2003):[2] where . Equation (2) is a fundamental equation for all the methods of moments, including the QMOM and its variants, TEMOM, and log MM, although they all must be further mathematically closed using a different closure model for moments. In the QMOM and its variants (McGraw 1997; Marchisio et al. 2003a; Marchisio and Fox 2005), the double integral operator is replaced with a summation by using an effective Gaussian integral technique. In the TEMOM and log MM (Lee et al. 1984; Yu et al. 2008), however, the following definition for the k-th moment, , must be introduced:[3]

When Equation (3) is substituted into Equation (2) followed by the application of a specific coagulation kernel, the double integral operator on the right-hand side of Equation (2) can be removed; consequently, the integral-differential equation is converted into an ODE, which is easier to solve using common mathematical techniques such as the fourth-order Runge-Kutta method.

In the continuum regime, the coagulation kernel takes the following expression (Pratsinis 1988):[4] where , denotes the Boltzmann constant, T denotes the air temperature, and denotes the gas viscosity. When Equations (3) and (4) are introduced, Equation (2) can be further expressed as follows:[5] where The polynomial on the right-hand side of Equation (5) is composed of both integer and fractal moments. Some of the fractal moments prevent the closure of moment Equation (5); thus, these fractal moments must be further addressed using a suitable closure model. In a study on the log MM (Lee et al. 1984), the authors introduced a closure model for arbitrary moments based on a log-normal assumption for particle size distribution, whereas in our previous work (Yu et al. 2008), we proposed an alternative closure model involving a Taylor expansion technique; we used the proposed model to achieve a closure of Equation (5). However, in the existing TEMOM, we observed it has two shortcomings. First, the accuracy of the existing TEMOM cannot be further improved using this closure model because only a third-order Taylor expansion is executed; second, the scope of application of the existing TEMOM is limited. Yu et al. (2015a,b) verified that the geometric standard deviation of the existing TEMOM is limited to 1.000–1.699 in the continuum regime and 1.000–1.601 in the free molecular regime. In this study, we propose an alternative closure model by constructing a fractal moment consequence, which can overcome the two mentioned shortcomings of the existing TEMOM. This approach has been successfully executed by Upadhyay and Ezekoye (2006) for improving the QMOM and DQMOM.

To develop a new closure model to overcome the shortcomings of the existing TEMOM, we must first define a new variable, q, which has a relation to the particle volume , as follows:[6] where φ is an integer greater than zero. Next, we construct another power function, , where is an arbitrary value. Now, we expand the power function by using the Taylor expansion technique around a fixed value, . The expansion point will be defined subsequently. The truncation orders of the Taylor series expansion for must satisfy a criterion (i.e., the number of truncation orders in the expansion of must be equal to 2φ +1). For example, if φ is 1, the number of truncation orders is 3. Table 1 shows the expansion expressions of for φ = 1, 2, 3, and 4 according to this criterion.

TABLE 1 Expressions for , , and in the closure model

1
2
3
4

=1

; ;

=2

= 3

= 4

Once the truncated Taylor series is obtained for , it is multiplied by , and then integrated from 0 to as follows:[7]

On the basis of the definition for as shown in Equation (3), the following expression can be obtained from Equation (7):[8]

Equation (8) is the closure model for arbitrary moments, which can be used to achieve a closure of Equation (5). Clearly, is a function depending on φ; Table 1 shows its expressions with respect to φ. As an example, if φ is 1, Equation (8) should be[9]

This is the closure model in the existing TEMOM model (Yu et al. 2008; Yu and Lin 2009). When φ is increased, the number of terms in the polynomial for increases. The accuracy of the closure model is also increased because the higher order of the Taylor series expansion is reserved. Similarly, we can easily set the φ value of the closure model to 5 or greater.

In the implementation of the Taylor expansion procedure, in addition to the number of truncation orders, the expansion point must be specified. In this article, is defined as follows:[10]

Although the geometric mean volume based on the log-normal size distribution theory, , seems highly reasonable as an expansion point, it does not reach the expected level in the current Taylor expansion methods of moments, as mentioned in our previous work (Yu et al. 2008) and in Xie and He (2013). If is 1, represents the averaged volume, which is the same as the expansion point in the existing TEMOM model.

The aforementioned derived closure models are general and can be used for any coagulation kernel such as kernels in the continuum-slip regime, free molecular regime, and continuum regime (Lee et al. 1997; Otto et al. 1999). We also investigated whether can be defined as , and observed that the results obtained using and were always the same. Thus, we concluded that the definitions of using and are equivalent.

For implementing the proposed generalized TEMOM, the number of explicit variables in Equation (5) are not arbitrary; it is . For any , the explicit variables that must be solved are , k = 0,1,2,. As an example, when is 1, Equation (5) becomes[11]

Once all the fractional moments in Equation (11), including , , , and , are replaced with the closure model shown in Equation (8) (), Equation (11) becomes[12] where . Equation (12) is a closed system of ODEs and is identical to Equation (18) in the existing TEMOM (Yu et al. 2008), which is easy to solve using common mathematical techniques such as the fourth-order Runge-Kutta method. Similarly, the detailed expressions for ODEs for moments can be easily obtained when is specified as 2, 3, 4, or higher. However, as increases, the complexity of the structure of ODEs increases substantially.

We present a brief description of the operating procedure of the proposed generalized TEMOM, which involves but is not limited to Brownian coagulation. For implementing the generalized TEMOM, the kernel (or kernels) with respect to a specific dynamics (or joint dynamics) must be given in advance—with it the PBE can be established (or Smoluchowski mean-field theory can be used); for example, Equation (1) must be first established if Brownian coagulation is expected to be studied. The number of internal coordinate of the PBE might be more than 1 depending on the specific problem. Once the PBE is established, it needs to be converted to a system of ODEs with respect to moment. Moment conversion involves multiplying the PBE by and then integrating it from 0 to ; for example, Equation (1) is converted to Equation (2) following the same procedure. The terms on the right hand side of Equation (2) could not be directly integrated out at this stage. Next, the definition for k-th moment, i.e., Equation (3), must be introduced. With Equation (3), integral terms on the right-hand side of Equation (2) can be replaced with polynomials composed by k-th moments. Usually, the converted moment ODEs through implementing the above integral operation is composed by not only explicit variables but also implicit variables, such as Equation (5). These implicit variables prevent the closure of the system of ODEs, which must be further replaced with a suitable approximated model, or called by closure model. In this work, we proposed to use a new closure model shown in Equation (8) to achieve the final closure of the system of ODEs with respect to moment . Once the system of ODEs, e.g., Equation (5), is obtained, all implicit variables will be replaced with a general closure model shown in Equation (8). Consequently, the system of ODEs with respect to automatically becomes a closed system, which can be further solved with common mathematical techniques such as the fourth-order Runge-Kutta method. Here, it needs to point out that must be specified before applying Equation (8) to the unclosed moment ODEs. This is because the value of determines what kind of moment sequence should be used, and also determines the number of equations in the system.

The implementation of the generalized TEMOM is easy. The users only need to establish their own PBE according to their specific problems, and then convert this PBE to an unclosed system of ODEs, e.g., Equation (5). Once all the implicit variables in the unclosed system of ODEs with respect to k-th moment are replaced with the universal closure model shown in Equation (8), the closure of this system is achieved. In conclusion, we summarize the procedure of the generalized TEMOM step by step for the convenience of application.

1. Establish the specific governing equation for the evolution of aerosol size distribution according to aerosol dynamics (i.e., the PBE); e.g., Equation (1).

2. Convert the PBE to an ODEs with respect to , e.g., Equation (5). The number of equations in the ODE system for moments is For any , the explicit variables that must be solved are , k = 0,1,2,. For example, when is specified to be 1, the number of equations in the ODE system is 3, and the explicit variables are , , and , as shown in Equations (11) and (12).

3. Specify φ and correspondingly specify the closure model , as shown in Table 1; if a higher accuracy is required, φ = 3 is recommended, otherwise φ = 1.

4. Specify the Taylor expansion point, , depending on φ specified in Step c.

5. Calculate the ODEs for moments together with the closure model shown in Table 1 with an appropriate initial condition.

3. COMPUTATION

In this study, we determined the dimensionless solution and initial specification for k-th moments according to procedures highlighted in previous studies (Pratsinis 1988; Upadhyay and Ezekoye 2003). If the moment is scaled using the expression[13] and the time is scaled using , all initial dimensionless moments can be expressed as follows:[14] where = and is the initial geometric standard deviation of aerosols. Here,

A moving SM was used as a benchmark method to verify the accuracy of the proposed generalized TEMOM; this SM can also be used to compare the accuracy among different methods of moments. In studies on the PBE, the SM is typically considered a reference model to verify other models, particularly for methods of moments (Otto et al. 1999). To ensure the reliability of the referenced SM, a low section factor value of 1.025 and high section number of 500 were used in the calculation. A refinement study on the SM has been conducted, which ensures the SM is accurate enough as a benchmarked method. In addition, the reliability of the SM is also verified in Section 4.1 by comparing it to exact values.

4. RESULTS AND DISCUSSIONS

In this study, four critical moment quantities for aerosols, namely , served as the objects for the examination. These four quantities were used because they directly or indirectly related to the actual physical properties of aerosols, and they also usually are used as objects for evaluating the effectiveness of a method (McGraw 1997; Friedlander 2000; Upadhyay and Ezekoye 2006). We examined the relative errors of the generalized TEMOM scheme to the benchmark as well as the effect of on the accuracy of the generalized TEMOM. In addition, we used two other methods of moments commonly used for solving the SE, namely the log MM (Lee et al. 1997) and the QMOM (McGraw 1997), for comparison. In evaluating the performance of the QMOM, we distinguished the integer moment sequence from the fractional moment sequence by adopting procedures described by Upadhyay and Ezekoye (2006). For the integer moment sequence, quadrature points, namely 3, 4, 5, and 6, were assessed, whereas for fractional moment sequences, two types of sequence, namely and , were assessed. For each type, the quadrature point was set to 6 and 3, respectively. The fractional moment sequence was calculated according to the procedures described by Upadhyay and Ezekoye (2006) for the QMOM method, in which the fractional moment sequence was first converted into an integer moment sequence and then resolved using the Gaussian Quadrature method.

4.1. Verification of Closure Models for Moments by Using a Specific Log-Normal Distribution

Our objective was to evaluate the accuracy of the truncated closure model in terms of , as shown in Table 1. A simple but highly suitable approach is to specify a log-normal size distribution of which arbitrary moments can be analytically obtained through an integral operation (Pratsinis 1988):[15]

Once the particle number concentration , geometric standard deviation of the number distribution , and geometric mean volume are specified, any k-th moments can be exactly specified. Thus, it is feasible to use Equation (15) as a benchmark solution to verify other models, and this has been conducted in numerous studies (Upadhyay and Ezekoye 2006; Yu et al. 2008). In the current study, we applied the methods of moments, including the generalized TEMOM, QMOM, and log MM, to reproduce the four critical moment quantities for aerosols, namely , and then to verify and compare the accuracy of these methods. Note here the study in this section is not an evolution problem, and the study on the evolution of an aerosol undergoing Brownian coagulation will be given in Section 4.2.

We used a log-normal distribution with a geometric standard deviation of 1.200 as an initial condition. We provided the specific dimensionless solution for moments in our previous work (Yu et al. 2008). The solution of the log MM was identical to the exact solution. Table 2 shows the aforementioned four moments reproduced using these three methods of moments and the SM. The integer moments and were both the same for all methods of moments, except QMOM(3,3). For fractional moments, including , when is increased, the solutions from the generalized TEMOM scheme increasingly approached the exact solutions. When is 3, 4, and 5, the generalized TEMOM scheme returned the same solutions as the exact solutions for both fractional moments, indicating that is sufficiently accurate for generating fractal moments. When the nodes were increased from 3 to 6, the QMOM involving an integer moment sequence also increasingly approached the exact solutions. However, even for the QMOM involving Node 6, the solutions for both fractional moments were different from the exact solutions. This again verifies the observation reported by Upadhyay and Ezekoye (2006) that increasing the Gaussian quadrature points cannot always increase the accuracy of the model. Regarding fractional moment sequences, QMOM(3,3) produced more accurate solutions for both than QMOM(6,2) did, indicating that using a lower-order moment sequence with less quadrature points might be a more effective solution for producing a lower-order moment. We compared the integer moment sequence with the fractional moment sequence and determined that the fractional moment sequence demonstrated a higher accuracy. The same results were observed by Upadhyay and Ezekoye (2006) for aerosol deposition. From the aforementioned comparison, we conclude that the generalized TEMOM executed for equal to or greater than 3 has superior accuracy to the QMOM involving the integer moment sequence. Although using a higher number of quadrature points might lead to a higher accuracy for the QMOM involving a lower fractal moment sequence (Upadhyay andEzekoye 2006), this process is not discussed in this article because it is not within the scope of our study. In addition, it is observed from Table 1 that the SM return the same results as exact values, indicating it is feasible to be used as benchmark in this study.

TABLE 2 Moments obtained from different closure models as the initial geometric standard deviation is 1.200

				QMOM (NQ,F)						Generalized TEMOM Scheme
Moments	Exact Value	Log MM	SM	(3,1)	(4,1)	(5,1)	(6,1)	(3,3)	(6,2)	1	2	3	4	5
m0	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.00000	1.00000	1.000000	1.000000	1.000000	1.000000	1.000000
m1/3	1.016759	1.016759	1.016759	1.019634	1.018368	1.017842	1.017579	1.016760	1.016761	1.010396	1.016651	1.016759	1.016759	1.016759
m2/3	1.068742	1.068742	1.068742	1.070715	1.069774	1.069407	1.069232	1.068743	1.068742	1.062053	1.068817	1.068742	1.068742	1.068742
m2	1.819098	1.819098	1.819098	1.819098	1.819098	1.819098	1.819098	1.818736	1.819098	1.819098	1.819098	1.819098	1.819098	1.819098

4.2. Verification of the Generalized TEMOM in Evolution

In Section 4.1, the proposed generalized TEMOM as well as two other commonly used methods of moments were verified by comparing them with an analytical solution for a specific size distribution. In this section, we further verify the methods of moments by characterizing their relative errors to the referenced SM in the process of time evolution for aerosols undergoing Brownian coagulation in the continuum regime. Similar to that in Section 4.1, the four moments, namely , were used as the study objects.

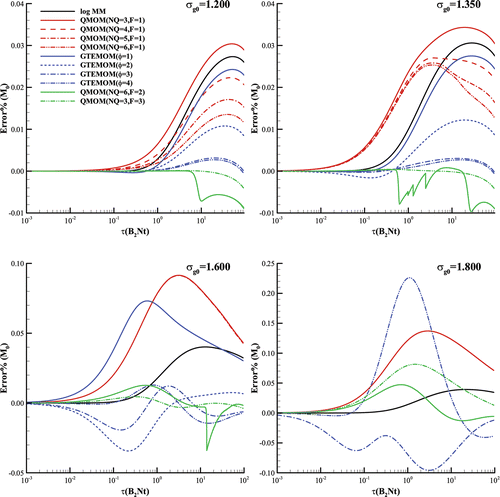
4.2.1. Integer Moments m₀ and m₂

The zeroth moment, , represents the total particle number concentration; thus, it is one of the most crucial quantities for characterizing aerosol properties (Pratsinis 1988). In the present study, we first verified the proposed generalized TEMOM scheme for this quantity by comparing it with the benchmarked SM. The relative errors are defined as follows:[16] where is an arbitrary variable calculated using the methods of moments, and is the referenced SM. We investigated aerosols with dissimilar initial geometric standard deviations (Figure 1). The initial geometric standard deviation was set to 1.200, 1.350, 1.600, and 1.800 (Figure 1), which covers the most common geometric standard deviations of natural aerosols. If the geometric standard deviation is higher, the aerosol size distribution can be considered a combination of several unimodal aerosols (Whitby and McMurry 1997; Jeong and Choi 2004). Thus, the model proposed in this work can still be applied to cases involving higher geometric standard deviations. In the continuum regime, the geometric standard deviation is theoretically 1.32 if a self-preserving size distribution is achieved (Lee and Chen 1984).

FIG. 1. Relative errors of methods of moments to the benchmarked SM for ₀.

As depicted in Figure 1, when the initial geometric standard deviation was set to 1.200, 1.350, and 1.600, the Error% for the proposed generalized TEMOM scheme decreased with an increase in , indicating that the accuracy of the generalized TEMOM scheme increases with the increase of . Specifically, when was set to 3 and 4, the Error% for these three cases were nearly the same, suggesting that the accuracy of the generalized TEMOM scheme is not evidently increased when is greater. Compared with the QMOM involving an integer moment sequence and the log MM, the generalized TEMOM with exhibited superior accuracy. Compared with the QMOM with fractional moment sequences, the generalized TEMOM with also demonstrated advantages with a geometric standard deviation of 1.200 and 1.350. When the geometric standard deviation was set to 1.600, the generalized TEMOM with has showed nearly the same accuracy as QMOM(3,3) and QMOM(6,2). For the QMOM involving an integer moment sequence, the solutions were always the same, and the curves for these solutions could not be distinguished from each other when the geometric standard deviation was set to 1.600 and 1.800. This indicates that the accuracy of the QMOM with an integer moment sequence cannot be increased by increasing the number of quadrature points for aerosols having higher geometric standard deviations.

For a relatively high initial geometric standard deviation of 1.800, the generalized TEMOM scheme was executed only for = 3 and 4. The same treatment is shown in Figures 2–4. In a recent study, the initial TEMOM was confirmed to be invalid with an initial geometric standard deviation more than 1.699 (Yu et al. 2015a). The generalized TEMOM with 1 and 2 exhibited the same shortcoming as the existing TEMOM; thus, they cannot be executed for an initial geometric standard deviation of 1.800. Among all the investigated methods, the QMOM(3,3) and log MM achieved the highest accuracy in the evolution process. The generalized TEMOM with registered nearly the same accuracy as that of the QMOM involving an integer moment sequence. In contrast to the cases involving initial geometric standard deviations of 1.200, 1.350, and 1.600, the generalized TEMOM with = 4 did not exhibit a superior accuracy to that with except in the initial time range.

FIG. 2. Relative errors of methods of moments to the referenced SM for .

Figure 1 indicates that as the initial geometric standard deviation increases, the accuracy of all investigated moment models decreases. This further verifies that the initial geometric standard deviation is a critical factor affecting the accuracy of methods of moments (Otto et al. 1999; Yu et al. 2015b). In addition, for initial geometric standard deviations of 1.200 and 1.350, the Error% for the QMOM involving an integer moment sequence decreased as the number of quadrature points increased, which is consistent with that observed for the generalized TEMOM scheme; however, for initial geometric standard deviations of 1.600 and 1.800, all QMOMs with an integer moment sequence yielded the same results, suggesting that the number of quadrature nodes has no effect on the accuracy for the zeroth moment when the initial geometric standard deviation is relatively high. We compared the QMOM with an integer moment sequence with that with a fractional moment sequence. We observed that the QMOM with a fractional moment sequence demonstrated a higher accuracy, which is the same as that observed in the study by Upadhyay and Ezekoye (2006). In addition, because the generalized TEMOM with 3 and 4 registered a similar accuracy as the QMOM for large initial geometric standard deviations, we conclude that the generalized TEMOM scheme is a reliable model that overcomes the shortcoming of the initial TEMOM whose initial geometric standard deviation must be less than 1.699 (Yu et al. 2015a). We verified that as increases, the geometric standard deviation can be set to a value greater than 1.800. In this case, the generalized TEMOM achieves nearly the same accuracy as that of the QMOM with an integer moment sequence. Here, a notable observation is that the log MM achieves high accuracy for when the initial geometric standard deviation is 1.800, although a log-normal size distribution must be implicitly employed.

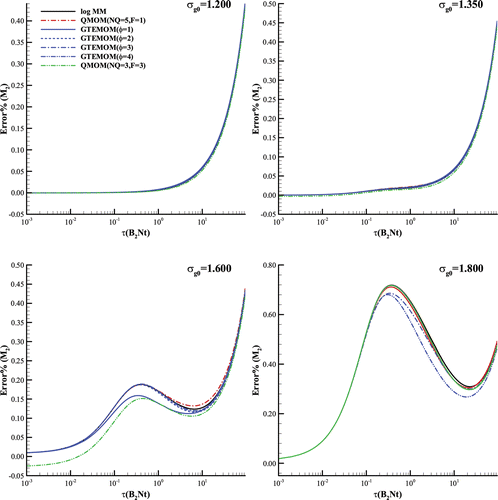
Same as , the second moment, , is another commonly used quantity for evaluating the reliability of a method of moments (Pratsinis 1988; Upadhyay and Ezekoye 2003; Yu et al. 2008). It is a polydispersity index for characterizing an aerosol (Settumba and Garrick 2003). Here, similar to the study on , we used the same four geometric standard deviations as initial conditions for study. Figure 2 depicts the comparison of various methods of moments for errors relative to the referenced SM for . No clear differences were observed among the investigated methods of moments, particularly when the initial geometric standard deviation was set to a relatively low value such as 1.200, 1.350, or 1.600. When the initial geometric standard deviation was set to 1.800, the generalized TEMOM with exhibited superior accuracy to all the other methods; however, when the geometric standard deviation was increased, the Error% increased for all the methods of moments. This also indicates that the condition of the initial size distribution influences the accuracy of all the methods of moments (Yu et al. 2015b).

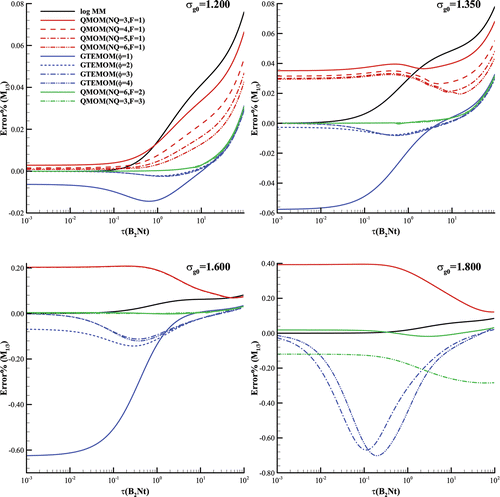
4.2.2. Fractal Moments m_1/3 and m_2/3

Except for the generalized TEMOM scheme with , the fractal moments, including and , must be generated by further executing the closure models for moments, as described in Section 4.1. Although the two fractal moments are directly related to the aerosol physical properties (i.e., the mean diameter and mean surface area; Seinfeld and Pandis 2012), studies on them are substantially few compared with those on other aerosol quantities such as the total concentration, geometric mean volume, and second moment (Otto et al. 1999; Marchisio and Fox 2005; Yu et al. 2008). In this section, we mainly evaluate the accuracy of the proposed generalized TEMOM for producing these two quantities. Similar to the study on the zeroth moment presented in Section 4.2.1, Figure 3 illustrates the relative errors of various methods of moments to the referenced SM for the quantity ; in this evaluation, four initial geometric standard deviations of the number distribution , were studied.

FIG. 3. Relative errors of methods of moments to the referenced SM for .

When the initial geometric standard deviation was not high (i.e., equal to or less than 1.6), the accuracy of the generalized TEMOM increased with the value of (Figure 3). Similar to the case of studied in Section 4.2.1, the generalized TEMOM with and 4 registered nearly the same accuracy for , indicating that is sufficient for producing this quantity with reliable accuracy. A crucial observation was that the generalized TEMOM executed for and 4 successfully captured the evolution of in the initial evolution process, which is nearly the same as two fractional QMOMs (i.e., [NQ = 6, F = 2] and [NQ = 3, F = 3]); however, for QMOMs with an integer moment sequence and the generalized TEMOM with , it is observed they could not capture the evolution of . The generalized TEMOM with is actually the existing TEMOM model presented in the study by Yu et al. (2008). When the geometric standard deviation was set to a relatively high value (i.e., 1.800), the generalized TEMOMs with and 4 also reached nearly the same accuracy levels, and were close to that of the QMOM with an integer moment sequence. Similar to the case involving in Section 4.2.1, the log MM also demonstrated a notably high accuracy for this quantity.

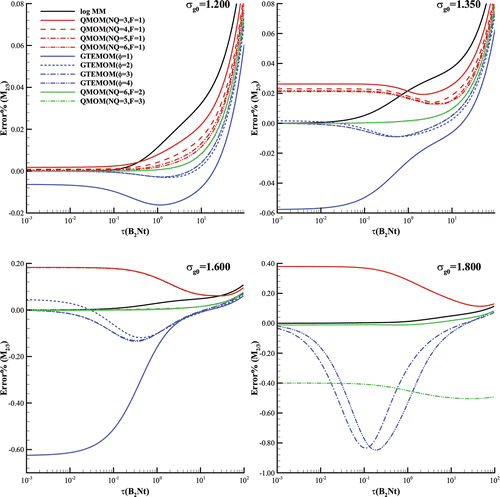
Figure 4 shows the relative errors of the methods of moments to the benchmarked SM for ; the same four initial geometric standard deviations were studied. Similar to , the generalized TEMOMs with and 4 for were superior to all QMOMs with an integer moment sequence for ; furthermore, they exhibited superior performance to the log MM for . Similar to , the QMOMs with an integer moment sequence and the generalized TEMOM with could not reliably produce in the initial evolution process. However, this was overcome by increasing for the generalized TEMOM and using a fractional moment sequence for QMOM.

FIG. 4. Relative errors of methods of moments to the referenced SM for .

In conclusion, for the fractional moments, such as and shown and investigated in Figures 3 and 4, we confirmed that some classical methods including the QMOM with an integer moment sequence and the existing TEMOM (i.e., the generalized TEMOM with ) could not produce reliable solutions in an initial evolution stage. This shortcoming was resolved by increasing the value for the generalized TEMOM and replacing the integer moment sequence with a fractional moment sequence for QMOM. When the initial geometric standard deviation was low (i.e., equal to or less than 1.600), the generalized TEMOMs with and 4 achieved nearly the same accuracy as the QMOMs with a fractional moment sequence, but higher accuracy than the QMOMs with integer moment sequences. When the initial geometric standard deviation was set to a relatively high value, the generalized TEMOMs with and 4 registered lower accuracy levels than those of the QMOMs with a fractional moment sequence, but still nearly the same accuracy levels as those of the QMOMs with an integer moment sequence. When the initial geometric standard deviation was set to 1.800, the log MM exhibited high accuracy for the two investigated fractional moments, and its accuracy was nearly the same as those of QMOMs with a fractional moment sequence.

4.3. Efficiency

To evaluate the advantage and disadvantage of a model for solving the PBE, both accuracy and efficiency must be equally considered. This is because with the advancement in computing power, the coupling between the PBE and the CFD has been used as a primary tool for investigating aerosol dynamical processes such as coagulation and nucleation (Buesser and Pratsinis 2012; Buffo and Marchisio 2014; Vogel et al. 2014). To successfully simulate aerosol dynamical processes under a practical engineering condition, considerable computational costs are required for iteratively solving Navier-Stokes equations for the CFD. Thus, the computational cost for the PBE must be as low as possible. Here, we present the computational times required by the investigated methods under the same numerical condition (Table 3). The SM was associated with the highest computational cost because a high sectional number (i.e., 500) was used to ensure high accuracy. The computational costs for the QMOM and generalized TEMOM were dependent on the selected number of quadrature points and the value, respectively. For example, if only the first three moments are required, NQ and should be set to 3 and 1, respectively, consequently indicating that the number of equations is six for the QMOM and three for the generalized TEMOM. Thus, the generalized TEMOM considerably reduces the computational cost. For QMOM, another drawback is that the weights and abscissas must be determined using the product-difference algorithm from the lower-order moments, which also substantially consumes time (McGraw 1997). Table 3 shows that the generalized TEMOM with costs 5 s, whereas the QMOM with NQ = 3 costs 19 s for QMOM(3, 1) and 18 s for QMOM(3, 3). We assumed that the computational cost is mainly dependent on the number of equations for the generalized TEMOM, whereas for the QMOM, in addition to the number of equations, the time consumed for determining weights and abscissas must also be considered. In conclusion, the generalized TEMOM is a more efficient method for solving the PBE compared with the QMOM.

TABLE 3 Computational time through executing the fourth-order Runge-Kutta method with a fixed time step, 0.001, and a total scaled time, 100, for all methods

		QMOM (NQ,F)						Generalized TEMOM Scheme ()
SM	Log MM	(3,1)	(4,1)	(5,1)	(6,1)	(3,3)	(6,2)	1	2	3	4
∼72 h	∼6 s	∼19 s	∼36 s	∼52 s	∼567 s	∼18 s	∼550 s	∼5 s	∼17 s	∼36 s	∼160 s

The initial geometric standard deviation is 1.350.

5. CONCLUSION

We propose a novel generalized TEMOM scheme for solving the PBE. In this scheme, a new Taylor expansion method was executed to obtain a moment closure model with arbitrary accuracy by adjusting the truncation orders of the Taylor series expansion. The new generalized TEMOM successfully overcomes the shortcomings of the existing TEMOM (Yu et al. 2008), whose geometric standard deviation must be less than a certain value and whose fractional moments at an initial stage cannot be accurately captured. We confirm that the accuracy of the generalized TEMOM can be arbitrarily increased by increasing the truncation orders of the Taylor series expansion.

The new generalized TEMOM was tested using aerosols undergoing Brownian coagulation in the continuum regime. Four critical aerosol quantities, namely , were used as objects for study. The accuracy of the generalized TEMOM was evaluated by comparing its results with analytical solutions and SM solutions. Other two recently prominent methods of moments, namely the log MM and QMOM, were also executed for comparison. The existing TEMOM is a special case of the new generalized TEMOM scheme when where is an integer determining the terms of the moment closure model, 2. The accuracy of the proposed generalized TEMOM increases when the value of increases. We confirm in this study that when the initial geometric standard deviation is less than 1.600, is sufficiently accurate for producing moments of which the accuracy is nearly the same as that of the QMOM with a fractional moment sequence and higher than that of the QMOM with an integer moment sequence. When the initial geometric standard deviation of number distribution is increased, the new generalized TEMOM has nearly the same accuracy as the QMOM with an integer moment sequence. Compared with the QMOM, the proposed generalized TEMOM exhibits less computational cost when the same objective moments are required for capture, indicating its superior efficiency. The new generalized TEMOM is a general scheme for solving the PBE, and is not just limited to Brownian coagulation in the continuum regime. It can be easily extended to study agglomerate dynamics and multiple dynamics over the entire size regime. With the generalized TEMOM, any k-th moments, including integer and fractional moments, can be predicted with high accuracy.

NOMENCLATURE

Table

NQ	quadrature point of QMOM
	fractional number used in QMOM
N	particle number concentration density, m^−3
B2	collision coefficient for the continuum-slip regime
kB	Boltzmann constant, J·K^−1
mk	k-th moment of particle size distribution
Mk	dimensionless k-th moment of size distribution
T	time, s
T	temperature, K
q0	Taylor expansion point,
	particle volume, m^3
q	q =
φ	integer greater than 0
	geometric mean particle volume, m^3
N	initial total particle number concentration, m^−3
Df	mass fractal dimension (1–3)

Greek letters

Table

μ	gas viscosity
β	particle collision kernel
Λ	mean free path of the gas, m
	geometric mean deviation of size distribution

Abbreviations

Table

CFD	computational fluid dynamics
DQMOM	direct quadrature method of moments
Log MM MOMIC	log-normal method of moments method of moments with interpolative closure
ODE	ordinary differential equation
PBE	population balance equation
QMOM	quadrature method of moments
SE	smoluchowski equation
SM	sectional method
TEMOM	taylor expansion method of moments

SUPPLEMENTAL MATERIAL

Supplemental data for this article can be accessed on the publisher's website.

FUNDING

This research was supported by Zhejiang Provincial Natural Science Foundation of China under Grant No. LQ15A020002, the Sino-German Research Project under Grant No. GZ971, and the National Natural Science Foundation of China under Grant No. 11372299 and No. 11132008.