Simulating aerosol chamber experiments with the particle-resolved aerosol model PartMC

ABSTRACT

This article presents a verification and validation study of the stochastic particle-resolved aerosol model PartMC. Model verification was performed against self-preserving analytical solutions, while for validation three experiments were performed where the size distribution evolution of coagulating ammonium sulfate particles was measured in a cylindrical stainless steel chamber. To compare with the chamber measurements, PartMC was extended to include the representation of fractal particle structure and wall loss. This introduced five unknown parameters to the governing equation, which were determined by a combination of scanning electron microscopy (SEM) analysis and an objective optimization procedure. Excellent agreement between modeled and measured size distributions was achieved using the same set of parameters for all three experiments. Assuming spherical particles led to model results that were inconsistent with the measurements. The best agreement between model and measurement was obtained for the fractal dimension of 2.3, indicating that the non-spherical structure of the particle agglomerates in the chamber needed to be taken into account.

© 2017 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction

Stochastic particle methods are widely used across different communities in science and engineering. Gillespie (1975) set a milestone in applying this technique to the evolution of physical particle populations by developing the exact stochastic simulation algorithm (SSA) to simulate the collision of cloud droplets. Since then many studies have developed this method further (Eibeck and Wagner 2001; Gillespie et al. 2009; Roh et al. 2011). Variants of this method have been used to investigate the evolution of specific particle systems, for example, for aerosol applications in industry (Wells et al. 2006; Shekar et al. 2012), astrophysics (Ormel and Spaans 2008; Okuzumi et al. 2009), oceanography (Jokulsdottir and Archer 2016), and atmospheric sciences (Shima et al. 2009; Riemer et al. 2009).

This article applies the stochastic particle-resolved “Particle Monte Carlo” model PartMC (Riemer et al. 2009) to the simulation of aerosol particles in an aerosol chamber. PartMC was developed to simulate the evolution of aerosol particles in the atmosphere. Atmospheric aerosol particles typically consist of a complex mixture of different chemical species, with sizes ranging from a few nanometers to tens of micrometers (Pöschl 2005; Seinfeld and Pandis 2006; Kolb and Worsnop 2012). The particle-resolved approach is suitable for modeling such a system, as it explicitly resolves the full composition space without any a priori assumptions about particle composition. Since the per-particle composition governs the aerosols’ optical properties and their ability to form cloud droplets, these details are important for determining the aerosol impact on climate (Zaveri et al. 2010).

The PartMC model was coupled with the state-of-the-art aerosol chemistry model MOSAIC (Zaveri et al. 2008) to treat gas chemistry, particle phase thermodynamics, and dynamic gas-particle mass transfer. PartMC-MOSAIC has been used to simulate aerosol processes in the atmosphere for a wide range of topics. For example, Riemer et al. (2010) and Fierce et al. (2015) applied the model to quantify black carbon aging time scales. Ching et al. (2012) and Ching et al. (2016) investigated the impact of aerosol mixing state on cloud droplet formation. Other model applications included the heterogenous oxidation of soot surfaces (Kaiser et al. 2011), and the characterization of the aerosol evolution in ship plumes (Tian et al. 2014).

The contributions of this study are the verification and validation of PartMC to simulate aerosol processes in a chamber environment. We use the term “verification” here to refer to “the process of determining that a computational model accurately represents the underlying mathematical model and its solution,” and “validation” to refer to “the process of determining the degree to which a model is an accurate representation of the real world from the perspective of the intended uses of the model” (ASME 2006). This study not only necessitated implementing chamber-specific loss processes such as wall loss and sedimentation, but also required representing fractal-like agglomerates and developing an objective optimization procedure to estimate required model parameters. As such, this article lays the foundation for using PartMC as a tool to interpret and design aerosol chamber experiments in the future.

The manuscript is organized as follows. Section 2 states the governing equation for the evolution of the population in the chamber environment and describes the treatments of wall loss and fractal particle dynamics in our PartMC model. Section 3 presents the verification of the coagulation code using self-preserving size distributions. Section 4 describes the chamber experiments and presents the code validation procedure, and Section 5 summarizes our findings.

2. Model description

2.1. Governing equation for the chamber environment

Our aim was to simulate the evolution of an aerosol particle population after it is introduced into an aerosol chamber. To isolate the impact of coagulation and wall loss on the size distribution evolution, additional particle emissions are not introduced after the start of the simulation. Further, we consider only the evolution of a single, non-volatile aerosol species in the chamber, excluding gas-to-particle conversion and aerosol chemistry in our current model framework. The relevant processes are therefore coagulation, dilution, and wall losses due to diffusion and sedimentation. We assume that the aerosol population in the chamber is well-mixed, which justifies a box model approach. The differential equation governing the time evolution of the aerosol size distribution n(μ,t) in the chamber environment is[1] In Equation (1[1] ), K(μ,ν) (m³s⁻¹) is the coagulation coefficient between particles with constituent masses μ and ν, n(μ, t) (m⁻³ kg⁻¹) is the aerosol number distribution at time t, λ_dil(t) (s⁻¹) is the dilution rate, and α^D(t) (s⁻¹) and α^S(t) (s⁻¹) are the wall loss rate coefficients due to diffusion and sedimentation, respectively.

2.2. The PartMC simulation algorithm

PartMC is a 0-D or box model that solves Equation (1[1] ). It explicitly resolves the composition of many individual aerosol particles within a well-mixed computational volume, making this a “particle-resolved” simulation. A detailed description of the numerical methods used in PartMC is given in Riemer et al. (2009) and DeVille et al. (2011). The code is open-source under the GNU General Public License (GPL) version 2 and can be downloaded at http://lagrange.mechse.illinois.edu/partmc/.

In brief, the particle population in the volume of interest is resolved by a large number of discrete computational particles, in our applications typically on the order of 10⁴ to 10⁶. The relative positions of particles within the computational volume are not tracked. Over the course of the simulation, the mass of each constituent species within each particle is tracked. The relevant processes for this study, namely, Brownian coagulation, dilution, and wall losses due to diffusion and sedimentation, are simulated with a stochastic Monte Carlo approach by generating a realization of a Poisson process. Using the “weighted flow algorithm” by DeVille et al. (2011) improves the model efficiency and reduces ensemble variance.

We used 10⁵ computational particles to initialize the simulations shown in this article. If the number of computational particles drops below half of the initial number because of the various loss processes, the number of particles is doubled by duplicating each particle, which corresponds to a doubling of the computational volume. This is a common Monte Carlo particle modeling approach to maintain accuracy (Liffman 1992). To quantify the stochastic error of the PartMC simulations, we repeated each simulation with different random seeds and calculated means and standard deviations. The number of repeats, N_run, was set to 10 in our case. The standard deviation of the size distribution obtained from the ensemble runs is the uncertainty from PartMC, denoted by σ_partmc, which is divided by to obtain the uncertainty in the mean (the SEM or standard error of the mean).

For the code development in this study, we branched from PartMC version 2.2.0 to implement the chamber wall loss treatment (Section 2.3), and extended the treatment of Brownian coagulation to include fractal particles (Section 2.4). The additions are available in version 2.4.0.

2.3. Chamber wall loss treatment

A challenge for chamber studies arises from quantifying wall losses due to particle diffusion and sedimentation to the chamber wall. Misestimation of these wall losses can result in inaccurate interpretation of the experimental results, as shown, for example, for secondary aerosol yield measurements by Matsunaga and Ziemann (2010). Modeling wall loss is difficult because the process can depend on aerosol particle size, the material of the chamber, the electric charge distribution, and the turbulence in the chamber. Past studies have proposed detailed formulations to quantify the wall loss rate (Crump and Seinfeld 1981; McMurry and Rader 1985; Park et al. 2001; Verheggen and Mozurkewich 2006). They often introduce parameters that are difficult to constrain and that might vary between different experiments. Therefore, inverse approaches that use size distribution measurements to constrain these unknown parameters are often conducted to obtain the functional forms of wall loss rate (Pierce et al. 2008).

In this study, we followed the method to parameterize wall losses by Naumann (2003), which is based on Fuchs (1964) and van de Vate and ten Brink (1980). The wall loss rates due to diffusion and sedimentation are size-dependent and given by[2] [3]

In Equations (2[2] ) and (3[3] ), (m²s^{− 1}) is the diffusion coefficient for particle μ, R_me,μ (m) is the particle mobility equivalent radius of particle μ, A_D (m²) is the diffusional deposition area, δ_D (m) is diffusional boundary layer thickness, and V (m³) is the volume of the chamber. The thickness δ_D has the following formulation based on Fuchs (1964) and Okuyama et al. (1986),[4] where k_D (m) is a chamber-specific parameter that can vary between different experimental set-ups. The constant a is a coefficient that was theoretically determined by Fuchs (1964) to be 0.25, and D₀ = 1 m² s⁻¹ is the unit diffusion coefficient, which is formally needed to obtain dimensional consistency. In Equation (3[3] ), R_m,μ(m) is particle mass-equivalent radius of particle μ, and A_S (m²) is the sedimentation area. As shown in Section 4.2, the unknown parameters in the wall loss equations, k_D and a, are determined through an optimization procedure based on particle size distribution measurements.

2.4. Fractal particle treatment

Irregular, fractal-like particles, including soot (Lapuerta et al. 2006; Moldanová et al. 2009) and soot-inorganic mixtures (Wentzel et al. 2003), are ubiquitous in both natural environments and technical applications. In addition, fractal-like agglomerates can also be formed from packing of spherical primary particles (Eggersdorfer and Pratsinis 2014). These particles exhibit significantly different dynamics and optical properties from those of spherical particles (Chen et al. 1990; Wu and Friedlander 1993; Sorensen 2001; Pranami et al. 2010), such as enhanced coagulational growth due to the increased collision cross-section. In this study, we implemented the formalism of fractal particles described in Naumann (2003). As we will show in Section 4.3, this is essential to successfully model the evolution of the observed size distributions. Details of the model implementation can be found in Section 1 of the online supplemental information (SI). In general, the number of monomers, N, in a fractal-like agglomerate can be related to the particle geometric radius R_geo by[5] where f is the volume filling factor quantifying how much of the available volume will be occupied by spherical monomers, R₀ (m) is the radius of the monomers, and d_f is the fractal (or Hausdorff) dimension that determines the growth rate of fractal agglomerates due to collision processes (Wu and Friedlander 1993). Similar to the wall loss parameters k_D and a, the fractal dimension d_f is an unknown parameter in our simulation, which will also be determined by the optimization procedure detailed in Section 4.2.

An important, implicit assumption of the Naumann (2003) formalism is that the number of monomers N is sufficiently large, i.e., larger than 100, as shown by the analysis in Sorensen (2011). Since in our case N is smaller than 100, care has to be taken with interpreting the results, and we will discuss this issue in detail in Section 4.3. We further assume the primary particles constructing the fractal agglomerates are non-overlapping, equal-size spheres (constant R₀) with homogenous density, which is a common assumption in theoretical analyses (Ulrich and Subramanian 1977; Koch and Friedlander 1990). We also assume that d_f and f will not change during the evolution of particles, although studies have argued that the fractal dimension may change as the size distribution of fractal agglomerates evolves (Kostoglou and Konstandopoulos 2001; Artelt et al. 2003). We will justify these assumptions in Section 4.2.1.

3. Model verification of fractal treatment

When Brownian coagulation is the dominant mechanism for particle growth, particle size distributions assume an asymptotic shape after a sufficiently long time, independent of the initial size distribution (Friedlander and Wang 1966; Friedlander 2000). These so-called self-preserving size distributions are represented by graphing the dimensionless particle number density function ψ(η) as a function of the dimensionless particle volume η (Equation (S-12)). The detailed formalism is provided in Section 2 in the SI.

In this study, the implementation of the fractal particle treatment in PartMC was verified by comparing the simulated self-preserving size distributions to those from theoretical results reported in Vemury and Pratsinis (1995) in both free molecular and continuum regimes. We followed the scenario set-up and model initialization of Vemury and Pratsinis (1995) as well as Naumann (2003).

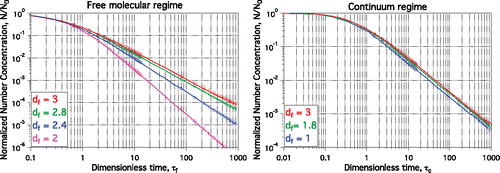
Figures 1 and 2 show the verification of the size distributions and the total number concentrations, respectively, for different fractal dimensions. Perfect agreement is observed, confirming the successful implementation of the fractal particle treatment in PartMC. The error bars in Figure 1 show the 95% confidence intervals from 10 ensemble PartMC runs. They were too small to be visible in Figure 2. The decay of normalized number concentrations in Figure 2 is graphed vs. dimensionless times τ_f (free molecular regime) and τ_c (continuum regime). The dimensionless times τ_f and τ_c are defined in Equations (S-13) and (S-14), respectively.

Figure 1. Self-preserving size distributions in the free molecular regime (left panel) and continuum regime (right panel) obtained from PartMC simulations (symbols) and the Vemury and Pratsinis (1995) code (lines) at different fractal dimensions (d_f). The error bars represent 95% confidence intervals from 10 ensemble runs. The self-preserving size distribution is defined in Equation (S-12).

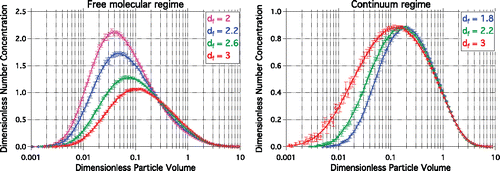
Figure 2. Normalized number concentration decay as a function of dimensionless time obtained from PartMC simulations (symbols) and the Vemury and Pratsinis (1995) code (lines) for various d_f values in free-molecular regime (left panel) and continuum regime (right panel). The dimensionless time is defined in Equation (S-13) for the free molecular regime and Equation (S-14) for the continuum regime.

4. Comparison with measurements for validation

4.1. Chamber measurements

Experiments were conducted in a 209 L, cylindrical, stainless steel chamber (Figure S-1) that was electrically grounded. The chamber was filled during the first 6 or 10 min (see below for details) of each experiment with dried, poly-disperse, charge-neutralized ammonium sulfate aerosol that was generated by atomizing an aqueous 0.0001 g cm⁻³ ammonium sulfate solution with a constant output atomizer (Model 3076, TSI Inc., Shoreview, MN, USA; Figure S-1a). The aerosol generated was dried with a custom silica gel diffusion dryer and charge neutralized with a custom neutralizer (BMI Inc., Hayward, CA, USA) containing four 500 μC Polonium 210 sources (Staticmaster 2U500, Amstat Corp., Mundelein, IL, USA). The aerosol was then diluted with 26.5 L min⁻¹ of dry, particle-free air (generated by passing through a high efficiency particle air [HEPA] filter), and particles with an aerodynamic diameter greater than 500 nm were removed with a greased two-stage Berner-type impactor (Berner et al. 1979) before entering the chamber. The pressure during filling was equilibrated by leaving the sampling port open into the laboratory fume hood.

After filling the chamber with atomized aerosol, the atomizer setup was disconnected from the chamber and the evolution of the size distribution was measured every 7 min with a modified scanning mobility particle sizer instrument (SMPS, TSI Instruments, 3934, Figure S-1b). This instrument consisted of a Polonium 210 neutralizer (Amstat Corp., Staticmaster 2U500), a differential mobility analyzer (DMA, TSI3071A), and a condensation particle counter (CPC, TSI 3022A) operating in low flow mode (0.3 L min⁻¹). A modification of the original instrument’s configuration was the use of a HEPA-filtered recirculating sheath airflow that was set to 2.4 L  min⁻¹. Air flow rates were checked and adjusted by comparing them to a primary standard airflow calibrator (Gilian Gilibrator, Sensidyne Corp., St. Petersburg, FL, USA) for each experiment. The voltage up-scan time was set to 300 s and the down-scan time was set to 60 s. These settings allowed a sizing range of particle diameters between 15.4 and 1000 nm. The delay time and sizing accuracy of the SMPS system was evaluated by performing up- and down-scans for 200 ± 5 nm and 350 ± 6 nm mono-disperse polystyrene latex (PSL) spheres (3200A/3350A, Thermo Scientific Corp., Waltham, MA, USA). The aerosol instrument manager software (TSI AIM Version 9.0, TSI Inc.) was used to collect and process the data from the SMPS system. The embedded multiple particle charge correction inversion algorithm from the TSI aerosol instrument manager software accounted for multiply charged particles. The pressure during sampling was equilibrated by having a bleed port at the chamber inlet. The measurements have estimated uncertainties of 1.5% for the flow rate (σ_flow), and of 5% for determining the particles size (σ_size). In addition, Poisson statistics were applied to approximate the raw count uncertainty (σ_count).

Three experiments were performed with Experiments 1 and 2 having a chamber filling time of 6 min and Experiment 3 having a filling time of 10 min. The initial size distributions for the simulations were taken to be the measured distributions after filling was completed. The code directly read in the particle number counts in the SMPS size bins. As a summary, the initial number concentrations, mean diameters, and standard deviations are listed in Table 1.

Table 1. Initial conditions for ammonium sulfate experiments from UIUC chamber measurements.

Exp. ID r	Initial conc. (cm^−3)	Initial mean diam. (nm)	Initial standard dev. (nm)
1	4.275 · 10^5	114	53.9
2	3.548 · 10^5	93.2	53.8
3	1.196 · 10^6	71.5	48.9

The evolution of the particle size distribution was tracked in each experiment for a minimum of 5 h. The relative humidity and temperature monitored near the inlet and at the outlet of the chamber ranged from 3.2 to 9.1% and from 19.5 to 22.2°C, respectively, for all experiments. Temperature and relative humidity were measured with a Sensirion SHT-75 sensor (Sensirion Corp., Stäfa, Switzerland).

Filter samples were collected at the end of each experiment by drawing the barrel’s remaining contents through 47 mm PTFE Membrane Filters (FGLP04700, Merck Millipore, Billerica, MA, USA). These samples were then used in scanning electron microscopy (SEM) imaging to obtain information about the microstructure of particles. The instrument was an FEI Company (Hillsboro, OR, USA) XL30 ESEM-FEG environmental scanning electron microscope, operated in HiVac mode. The imaging parameters were 5 kV and spot size 3 (2.1 nm) at a 10-mm working distance. The samples were received dry, mounted on aluminum stubs with double-stick carbon tabs (SPI Supplies, West Chester, PA, USA), sputter coated (Desk-2 turbo sputter coater, Denton Vacuum, Moorestown, NJ, USA) with ca. 6 nm of gold-palladium, and grounded using Flash-Dry (SPI Supplies) silver paint before imaging.

4.2. Determination of model parameters

Including wall loss and fractal dynamics introduces five unknown parameters in the governing equation, namely, two parameters in Equation (4[4] ) for the wall loss treatment (prefactor k_D and exponent a), and three in Equation (5)[5] (fractal dimension d_f, radius of primary particles R₀, and volume filling factor f). As we will show in Section 4.2.1, we used SEM images to estimate the parameters f and R₀. We determined the remaining three parameters by a global optimization procedure as described in Section 4.2.2.

4.2.1. Determination of parameters f and R₀

Figure 3 shows the SEM images of the filters at the end of Experiment 1, after about 6 h of evolution. The particles show as bright agglomerates, some of which are highlighted with red circles in Figure 3. Note that the fibrous and smoother agglomerated material is the Teflon filter. The images reveal that over the course of the experiment, the dry ammonium sulfate particles formed agglomerates consisting of spherical primary particles.

Figure 3. Scanning electron microscope (SEM) images of the particle filter from Experiment 1 at different resolutions. The fibrous and smoother agglomerated material is the Teflon filter.

SEM images were analyzed using image analysis software (ImageJ version 10.2, NIH) to estimate the values of the radius of primary particles R₀ and the volume filling factor f. The primary particles are not mono-disperse, but show a size distribution with a number-based median diameter of about 90 nm. Figure S-2 shows the histogram of the size distribution of 130 particles identified from the SEM images. Since in the current model implementation, the primary particle size is set to a constant value during the entire simulation time, we tested the sensitivity of the predicted size distribution to different R₀ values.

Figure S-3 shows the comparison of the number distribution at t = 280 min from Experiment 1 using three R₀ values: 15 nm (the smallest), 45 nm (medium), and 80 nm (maximum). All other parameters are kept constant for the three simulations. The resulting size distributions have a maximum percentage difference (between the simulations with R₀ = 15 nm, and 80 nm) of 24% at a particle diameter of 100 nm, and 5% at 200 nm. Based on the uncertainty quantification as described below in Section 4.2.2, we can estimate the overall measurement uncertainty as 40% and 15% at 100 nm and 200 nm, respectively (see the light gray [orange band] in Figure 4). We therefore conclude that even extreme variations in R₀ values cause variations of the results that remain within the measurement uncertainties. This justifies setting R₀ to a fixed value, and we chose 45 nm, which is the median radius from the sample.

Figure 4. Simulated (“PartMC”) and measured (“Barrel”) particle size distributions from Experiment 1 at 7 min, 70 min, and 210 min (top to bottom). Shaded areas represent ± 3σ as described in Equation (7[7] ). The highest line (blue curve) in the bottom panel represents the simulated distribution assuming d_f = 3.

The volume filling factor f accounts for the fact that the spherical primary particles can occupy only as much as 74% of the available volume. Given the closely packed structure as shown in Figure 3, we assumed that 70% of the available volume would be occupied by the monomers (close to the extreme case), corresponding to an f value of 1.43. Similarly to the sensitivity test regarding R₀, we tested the sensitivity to the choice of parameter f. Figure S-4 shows the number distribution comparison from simulation results using f = 1.35, 1.43, and 2.0, corresponding to the monomers occupying 74%, 70%, and 50% of the available volume, respectively. The maximum percentage difference (between f = 1.35 and 2.0) is again small, being equal to 25% at a particle diameter of 100 nm and 14% at 200 nm. Therefore, a fixed f value of 1.43 was chosen for the model simulation.

4.2.2. Optimization procedure

With the determination of R₀ and f values in the previous section, the governing equation described in Section 2 now has three unknown parameters remaining: k_D and a in Equation (4[4] ) for the wall loss calculation, and d_f in Equation (5[5] ) for the fractal formalism. To find the appropriate values for these unknown parameters, inverse approaches using non-linear least-square fitting optimization on size distribution measurements have often been conducted (Pierce et al. 2008). We applied a similar approach in this study. To determine the combination of free parameters that gives the best agreement between simulation and measurements, we produced an ensemble of simulations for which we varied the parameters systematically between simulations. The best fit was determined when a chosen error metric was minimized across all simulations.

We jointly optimized k_D, a, and d_f by exhaustively searching over a pre-defined parameter domain. We considered all combinations of (k_D, a, d_f) with k_D varying from 0.025 m to 0.095 m with increments of 0.005 m, a varying from 0.22 to 0.27 with increments of 0.01, and d_f varying from 1.5 to 3.0 with increments of 0.1. These values are within the ranges reported in previous studies (Bunz and Dlugi 1991; Naumann 2003) and included the minimum in the interior of the domain. This amounts to a total of 14,400 simulations, generated by 15 × 6 × 16 cases, with each case repeated 10 times with different random seeds.

We define E_r,j to be the weighted ℓ²-norm of the difference in the discretized number size distributions of simulation and measurement at time j for experiment number r:[6] where n_sim,r,i,j and n_mea,r,i,j are the simulated and measured number concentration densities in size bin i at time j for experiment r, respectively, and N_bin is the number of size bins. The weighting factor σ_r,i,j is the uncertainty that arises from both the measurement and the simulation. Similar to the approach in Moore et al. (2010), the total uncertainty at time j for the ith size bin and experiment r is[7]

The total error metric, ε_r, for experiment r is defined as the root mean square of the relative errors over the entire simulation period:[8] where N is the total number of time steps. The three experiments are combined by taking the root mean square error to give the total error ε by[9]

The best-fit values for k_D, a, d_f are found by determining the minimum value of ε:[10]

Care has to be taken regarding the physical interpretation of the d_f value obtained, since our aggregates only contain a small number of monomers. The implications of this fact are discussed in the next section.

4.3. Results

With datasets from three experiments available, we performed the optimization procedure on the data from all experiments combined. We obtained k_D = 6.0 cm, a = 0.26, and d_f = 2.3 as best fit estimates with the errors ε₁ = 8.09, ε₂ = 9.62, and ε₃ = 14.91 for Experiments 1, 2, and 3, respectively.

The coefficient k_D is proportional to the laminar boundary layer and can vary between different experimental setups (Bunz and Dlugi 1991). Our best estimate for k_D (6.0 cm) is very similar to the results by van de Vate and ten Brink (1980) who determined k_D = 4.8 cm as their best fit. Bunz and Dlugi (1991), in contrast, found best agreement by reducing k_D to 0.5 cm. For the parameter a, Bunz and Dlugi (1991) reported a value of 0.25 from previous theoretical derivations by Fuchs (1964) and 0.274 from their experiments. Our optimal values for a is 0.26, close to these previously reported values. Our optimal fractal dimension of 2.3 is clearly below the value of 3 for spherical particles, but it is significantly higher than the value of 1.78 ± 0.1 predicted by diffusion-limited cluster-cluster aggregation (DLCA) theory (Sorensen 2011).

In our case, the reason that d_f is higher than the theoretically expected value can be explained by the fact that the aggregates only contain a small number of monomers (N < 100). As described in Sorensen (2011), in this case the scaling of the mobility diameter R_me can be written as[11] where is the true fractal dimension. As detailed in the SI, Equation (S-3), we are using the Naumann (2003) relationship[12]

Importantly, h_KR does not depend on N, and so we see that in the small-N case the parameter d_f in the Naumann (2003) model that we use is in fact the mass-mobility scaling exponent D_m described by Sorensen (2011), which is defined by the relationship .

Equating Equations (11[11] ) and (12[12] ) gives a relationship between the fitted parameter d_f and the true fractal dimension :[13]

From our optimization procedure, we obtain the value d_f = 2.3, so equating the exponents of N in (13[13] ) allows us to compute that the true fractal dimension implied by our model is . This matches the theoretically expected value of 1.78 ± 0.1 for DLCA processes (Sorensen 2011).

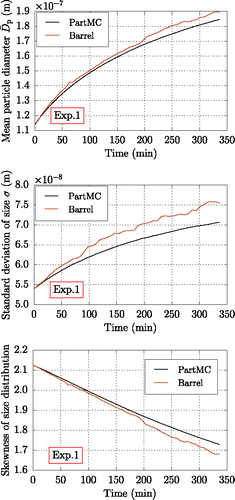
Figure 4 shows the evolution of measured and simulated number size distributions at 7 min, 70 min, and 210 min for Experiment 1 using the best-estimate parameters for this experiment. The number size distributions in Figure 4 and similar figures are shown as a function of mobility diameter. The shaded areas indicate the estimated uncertainty based on Equation (7[7] ) with the width of 3σ, i.e., we expect 99% of the values to be within the bounds of the shaded range. Note that the maximum values on the vertical axes change between the three panels to ensure readability. For the entire simulation time of about 3.5 h, the simulated distributions match the experimental results within the uncertainties. This is further shown by displaying the time evolution of several key parameters of measured and simulated size distributions, including mean diameter, standard deviation, and skewness, as shown in Figure 5. For comparison, we also simulated the size distribution when spherical particles are assumed throughout the entire simulation (blue trace in the right-most panel of Figure 4). This simulation result does not capture the measured distribution, confirming the need to include the treatment for fractal particles.

Figure 5. Time evolution of simulated (“PartMC”) and experimentally determined (“Barrel”) mean diameter, standard deviation of size distribution, and skewness of size distributions (top to bottom) for Experiment 1.

Figures S-5 and S-6 in the SI show the results for all three experiments. Except for one occasion (Experiment 3, after 7 min) all model results are within the range of the uncertainties. Overall, the good agreement between PartMC simulations and chamber measurement indicates that the model is able to capture the evolution of particles in a chamber environment undergoing Brownian coagulation and wall losses.

We further quantified the relative importance of particle loss due to coagulation and wall loss with two additional sensitivity runs for which coagulation and wall loss were disabled, respectively (Figure S-7). For Experiment 1, after around 5 h, wall loss and coagulation accounted for an additional 5% and 20% of particle loss, respectively, hence both processes are important in shaping the aerosol size distribution, but coagulation dominates.

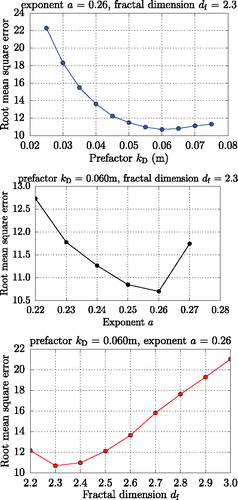
A potential concern with an optimization procedure as used in this work is that different combinations of free parameters may result in errors of similar magnitude. To investigate this, we show in Figure 6 the dependence of ε on each of the three parameters individually, while keeping the other two constant and equal to their optimal values. These curves should exhibit a clear minimum within the range of parameters used, which then indicates the optimal parameter combination. From this figure we also learn that the fractal dimension d_f is always the dominant factor determining ε, compared to k_D and a. This is in agreement with our finding that coagulation is relatively more important than wall loss (Figure S-7) and in line with the results by Naumann (2003).

Figure 6. Sensitivity of free parameters k_D, a, and d_f on model-measurement comparison results described by the value of root mean square error ε for the combined optimization procedure. When a parameter was varied, the other two parameters were fixed at their optimal value.

Lastly, we checked to what extent the parameters k_D, a, and d_f and the error ε change when the optimization procedure is performed on each experiment individually. As expected, the error decreases when the optimization is performed individually, namely, by 15%, 24%, and 4.5% for Experiments 1, 2, and 3, respectively. While the optimal parameter values are not identical for the three experiments, they remain in a relatively small range, with k_D between 0.040 m and 0.070 m, a between 0.22 and 0.26, and d_f between 2.2 and 2.4 (Table 2). This finding is consistent with our initial approach of performing the optimization procedure on the data from all experiments combined.

Table 2. Comparison of the optimal parameters obtained by optimizing over all three experiments combined and optimizing over each experiment individually.

Optimization	kD (m)	a	df
Combined	0.060	0.26	2.3
Indiv. Exp. 1	0.060	0.26	2.2
Indiv. Exp. 2	0.070	0.22	2.3
Indiv. Exp. 3	0.040	0.25	2.4

5. Conclusions

We conducted verification and validation of the stochastic particle-resolved aerosol model PartMC. Verification was performed against self-preserving analytical solutions, while for validation we performed three experiments with coagulating ammonium sulfate particles in a cylindrical stainless steel chamber under a range of input conditions and measured the evolving aerosol size distributions.

To compare with the chamber measurements, we extended PartMC to include the representation of fractal particle structure and wall loss. Including wall loss and fractal dynamics in the governing equation introduced five unknown parameters. We constrained two of them (radius of the primary particles R₀ and volume filling factor f) using SEM images and determined the remaining three parameters (wall loss parameters k_D and a, and fractal dimension d_f) by a global optimization procedure to fit the experimental data.

We showed that excellent agreement between modeled and measured size distributions can be achieved using the same set of parameters for all three experimental conditions, and we checked that estimating the parameters for each experiment individually did not substantially improve the fit. This creates the foundation for a model framework that can be applied to more complex experiments, for example, to investigate the evolution of aerosol mixing state when secondary aerosol material is coating the particles.

While the aim of this study was to verify and validate PartMC, we reach the following broader conclusions. The fact that our fitted value of a = 0.26 is close to the theoretically derived value of 0.25 is an excellent indication that our approach is valid. It would be interesting to determine the value of k_D for other chambers of similar design (i.e., stainless steel chambers) or of different type (e.g., teflon chambers). Further, it is likely that for aerosols generated as it was done in this study, a fractal dimension smaller than 3 is appropriate. These hypotheses should be tested on additional chamber datasets.

Currently, the model uses a constant value of fractal dimension throughout the simulation period. From the comparison of the model results to the experimental data, we conclude that using a constant d_f value is a good approximation for simulating coagulating particle populations in these experiments. At the same time, the strong sensitivity of the results to the fractal dimension value may justify the implementation of a more sophisticated model treatment, which, for example, would allow the simulation of particle restructuring during more complex mixing and coating processes. This could be easily achieved by adding fractal dimension as an additional per-particle entry in the particle-resolved representation using the PartMC model. At the same time, this would necessitate more detailed particle size measurements to constrain the rate of change of d_f during the evolution of particles in the chamber.

Acknowledgments

The authors thank Cate Wallace, Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, for performing the SEM imaging. The authors thank the editor, Dr. Yannis Drossinos, for insightful comments that greatly improved the manuscript.

Funding

J. T., B. T. B., T. C. B, M. J. R., and N. R. acknowledge DOE-ASR funding from grant DE-SC0006689. N. R. and M. W. acknowledge support from DOE-ASR DE-SC0011771, and M. W. acknowledges support from NSF CMMI 11-50490.